Downloaded 113 times
Uploaded byUnsa Shakir
decoder and encoder
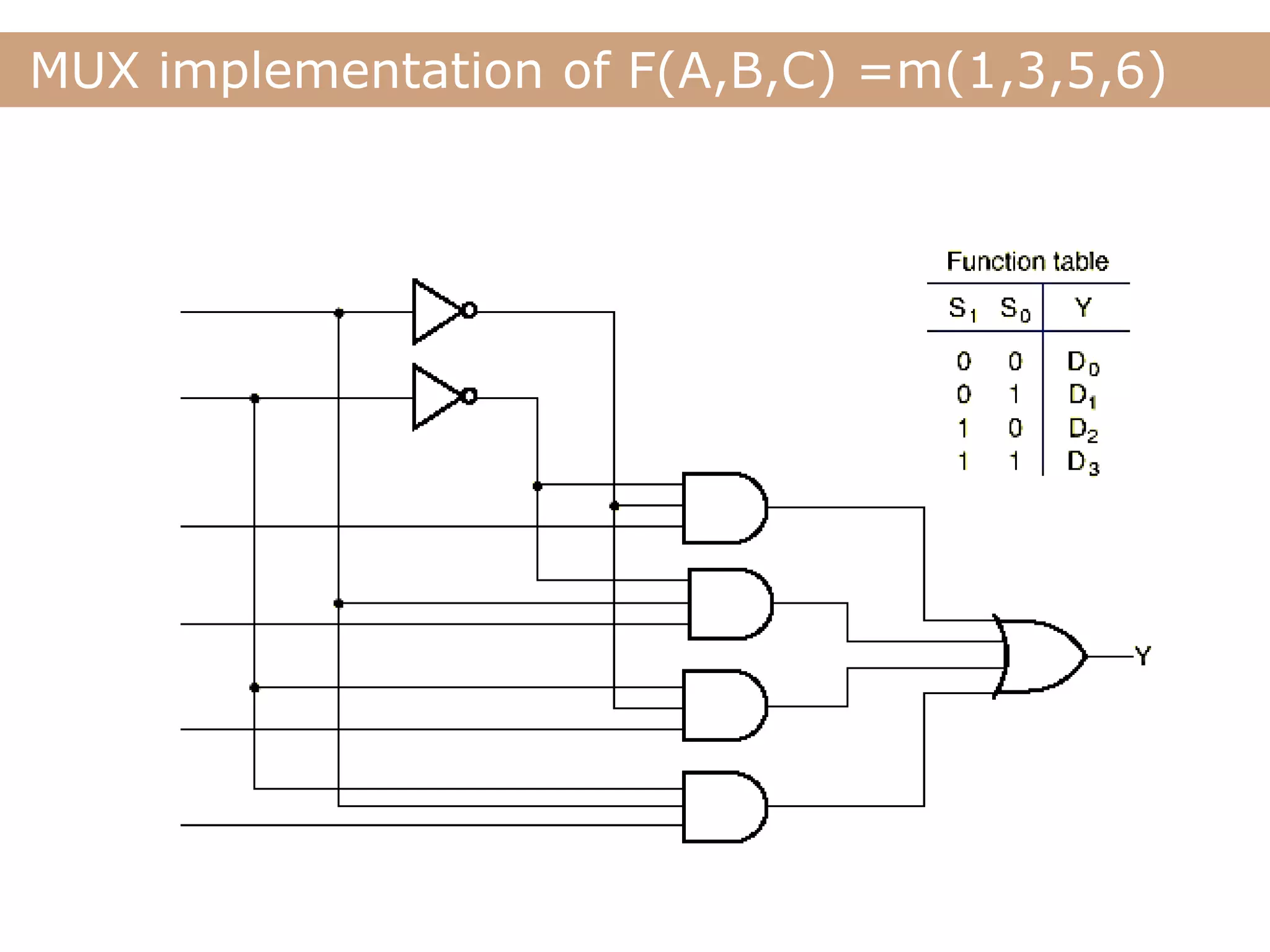
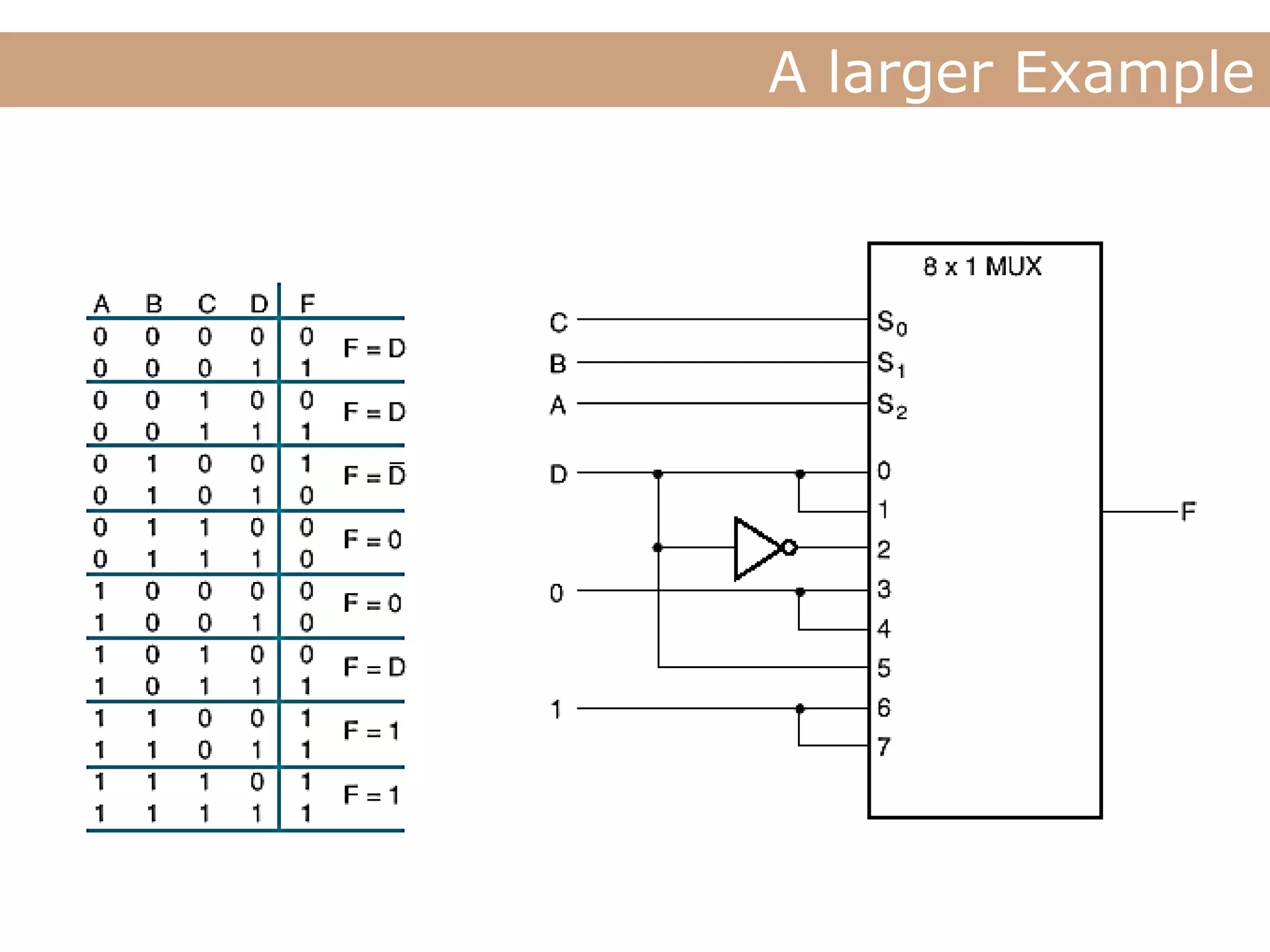
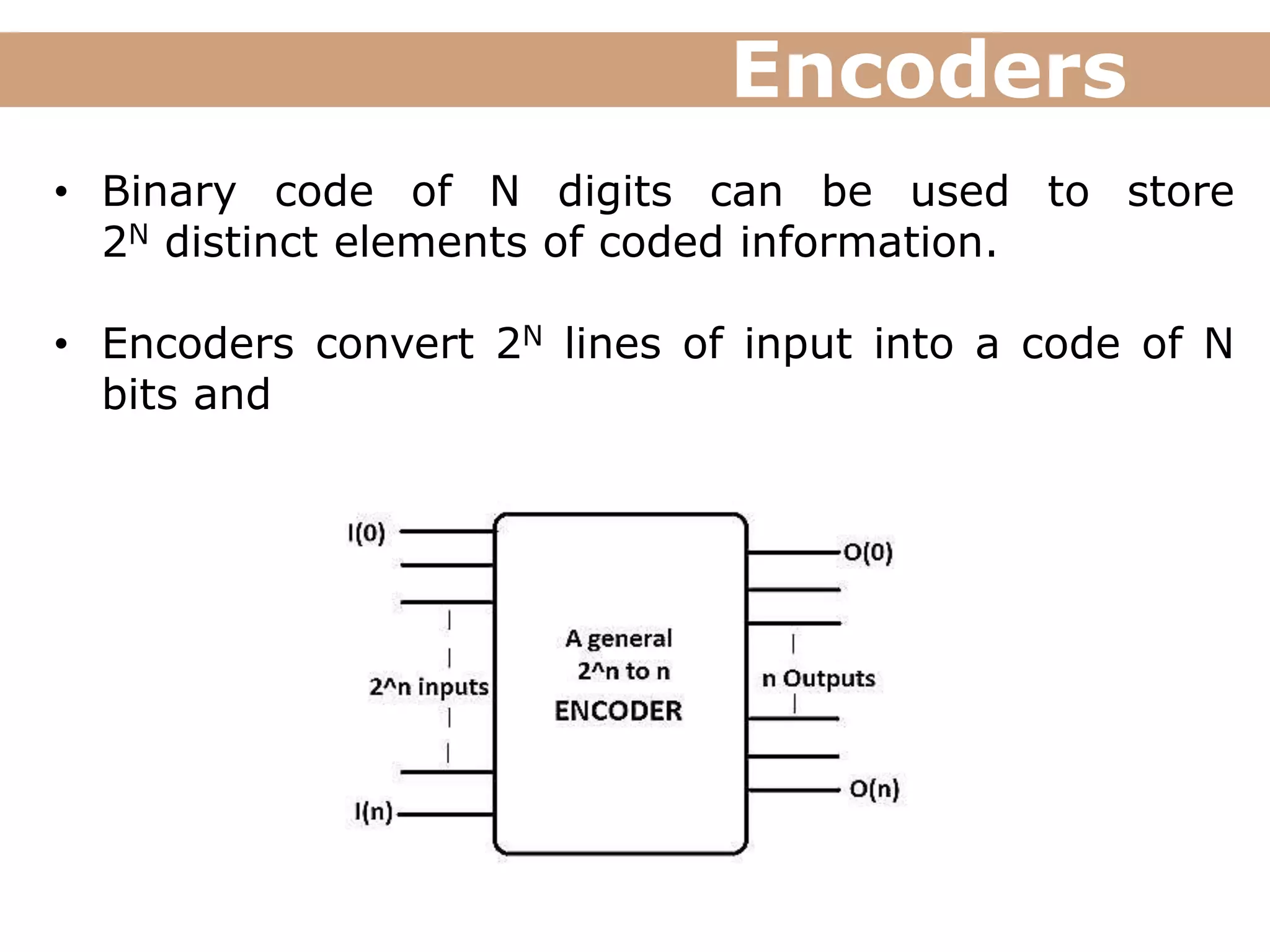
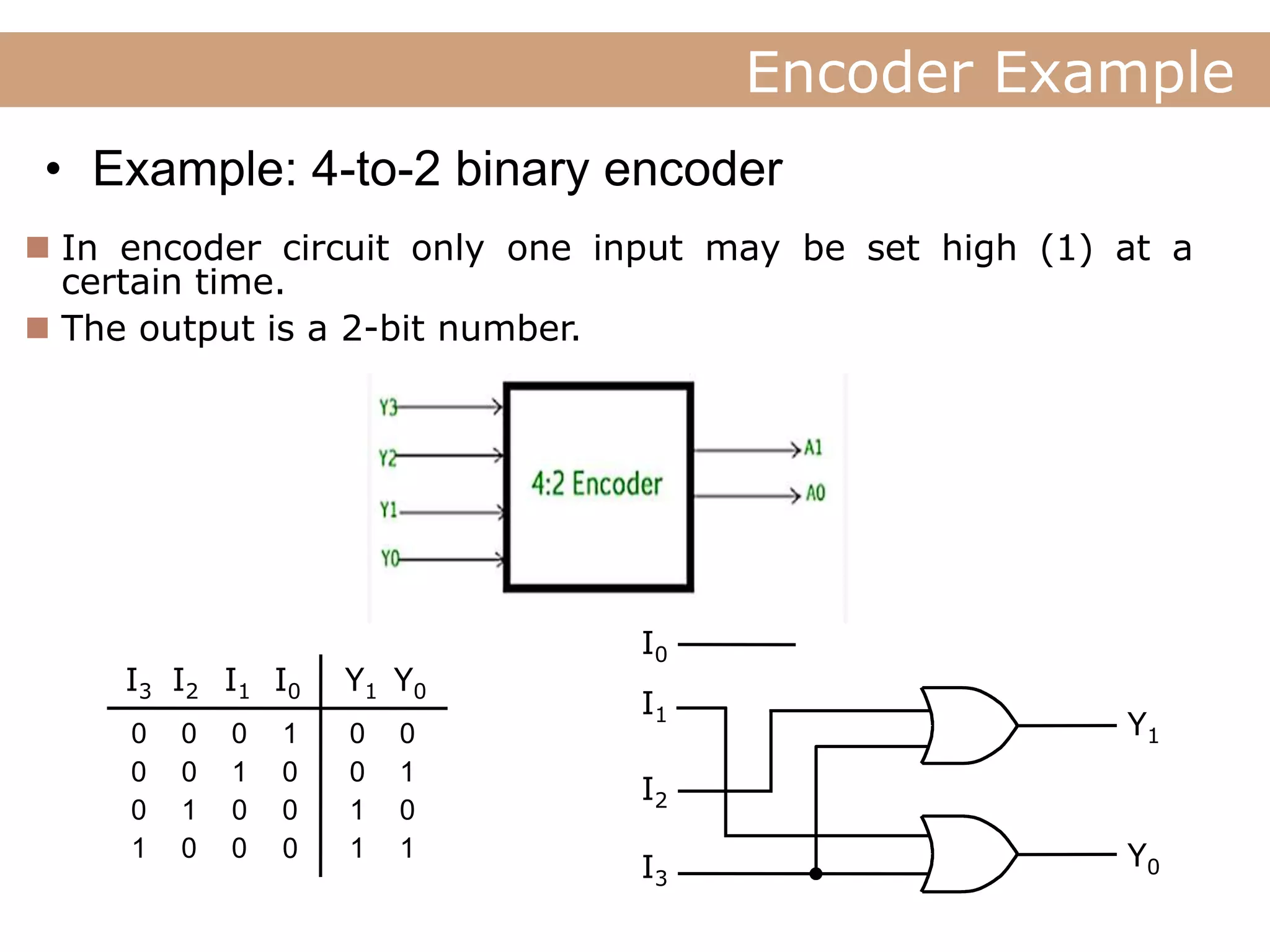
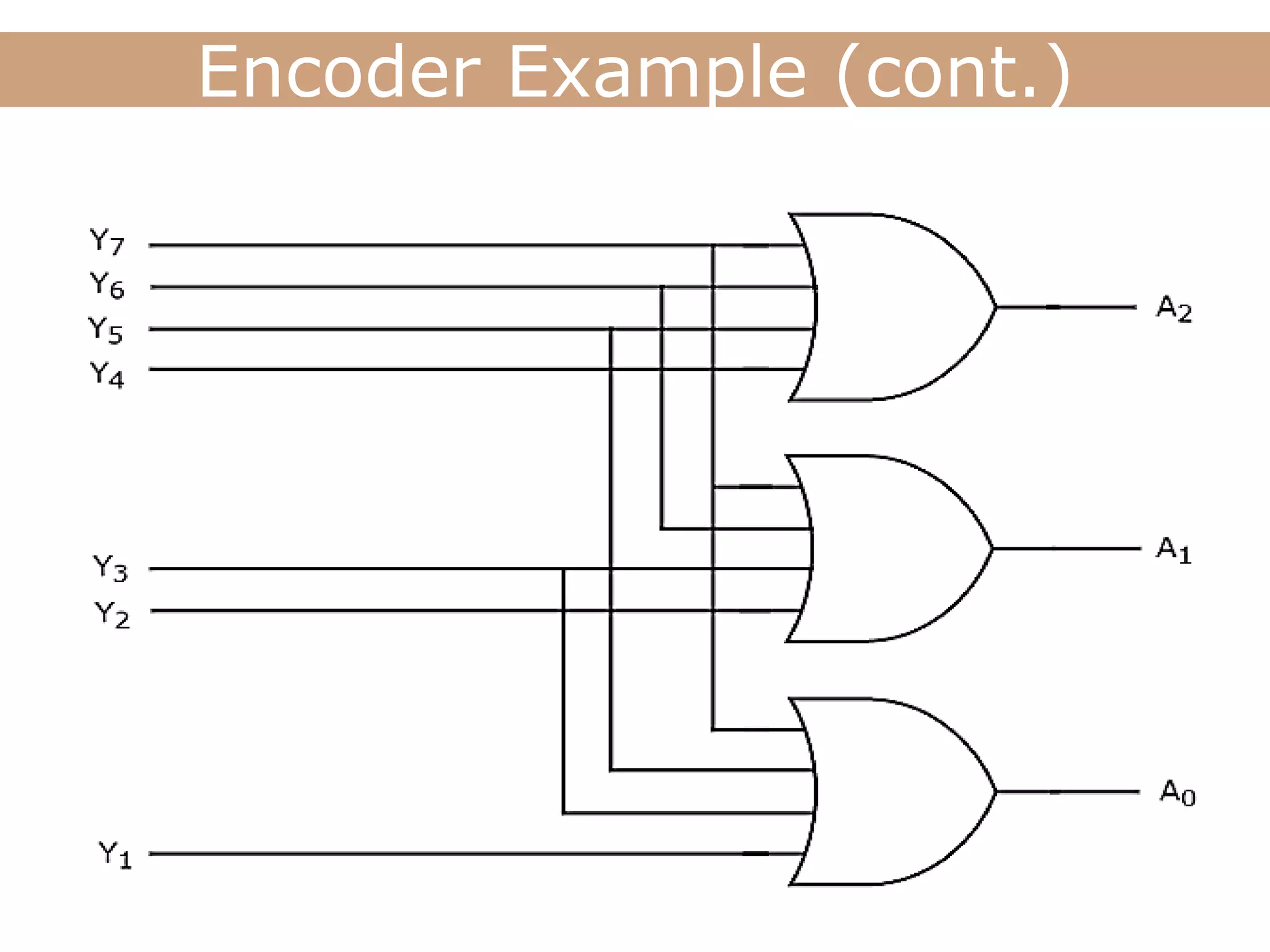
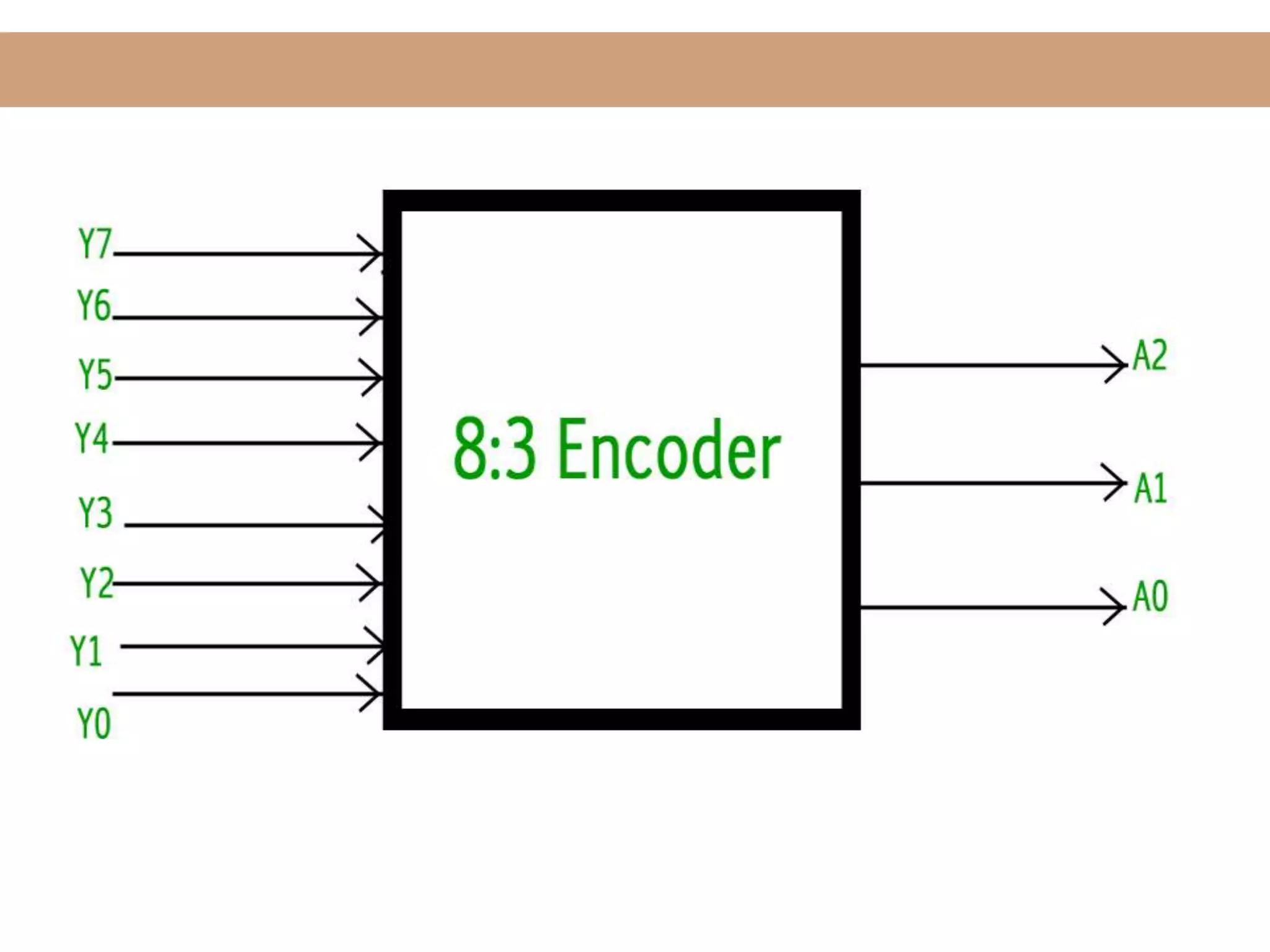
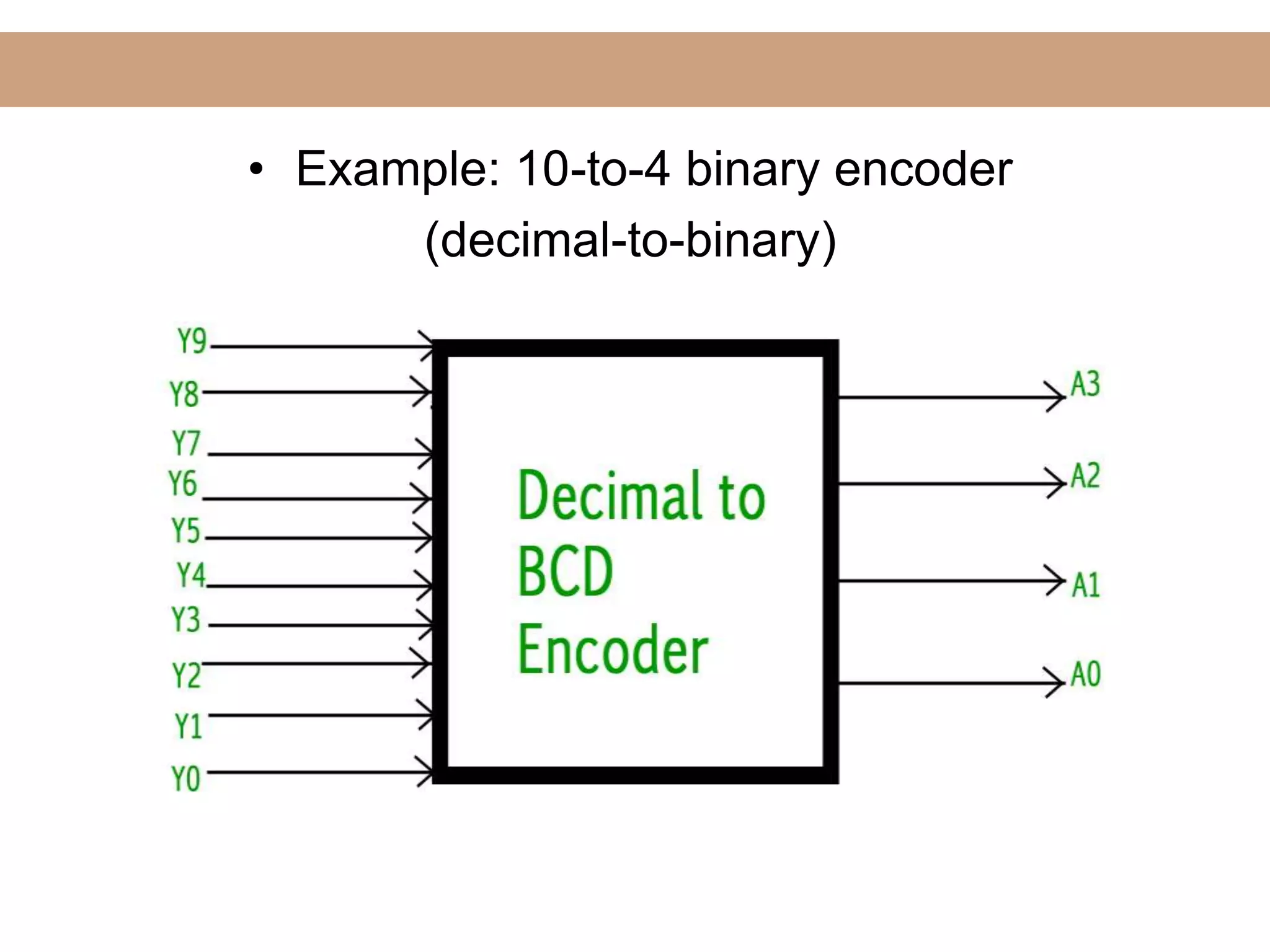
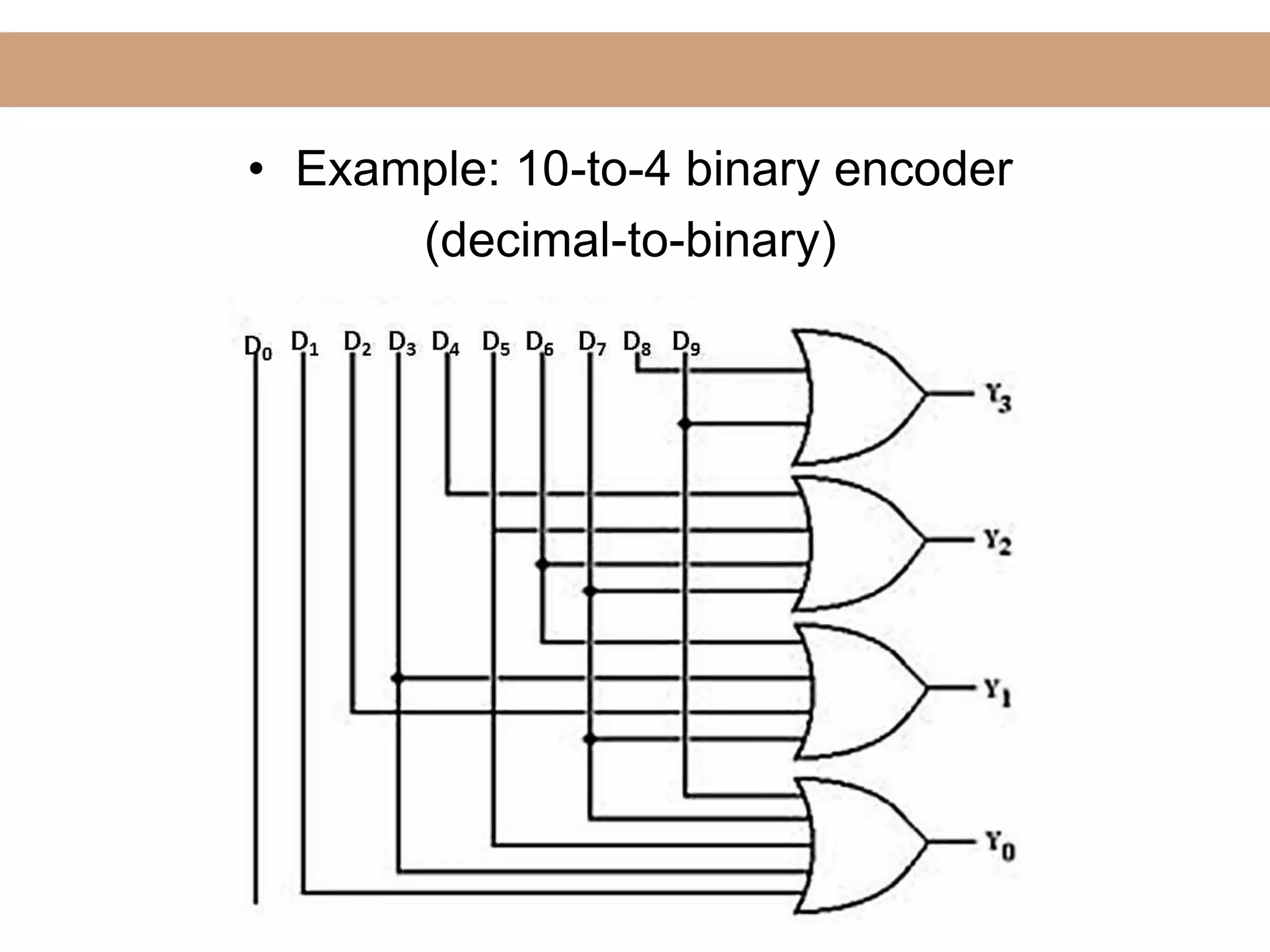
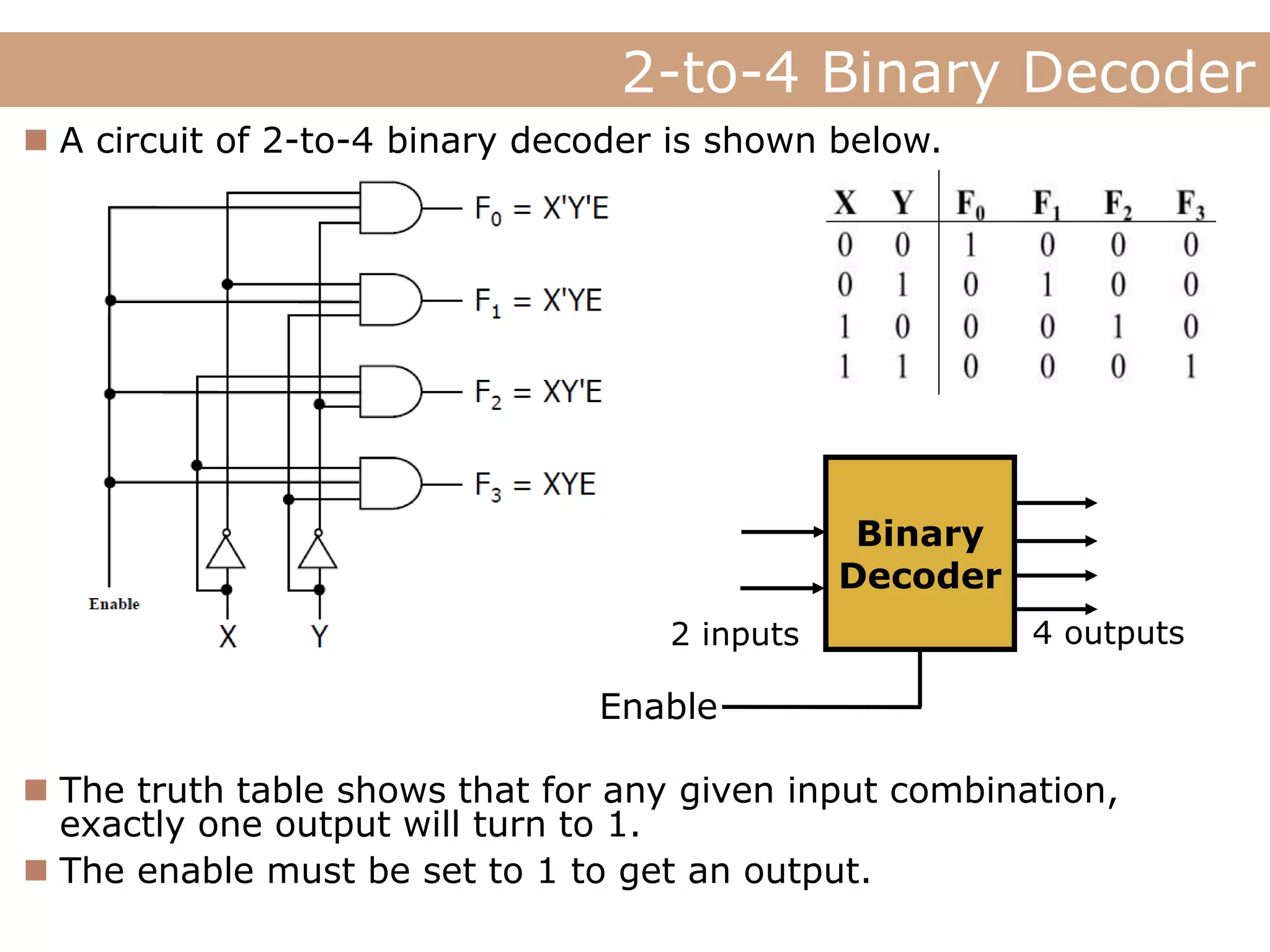
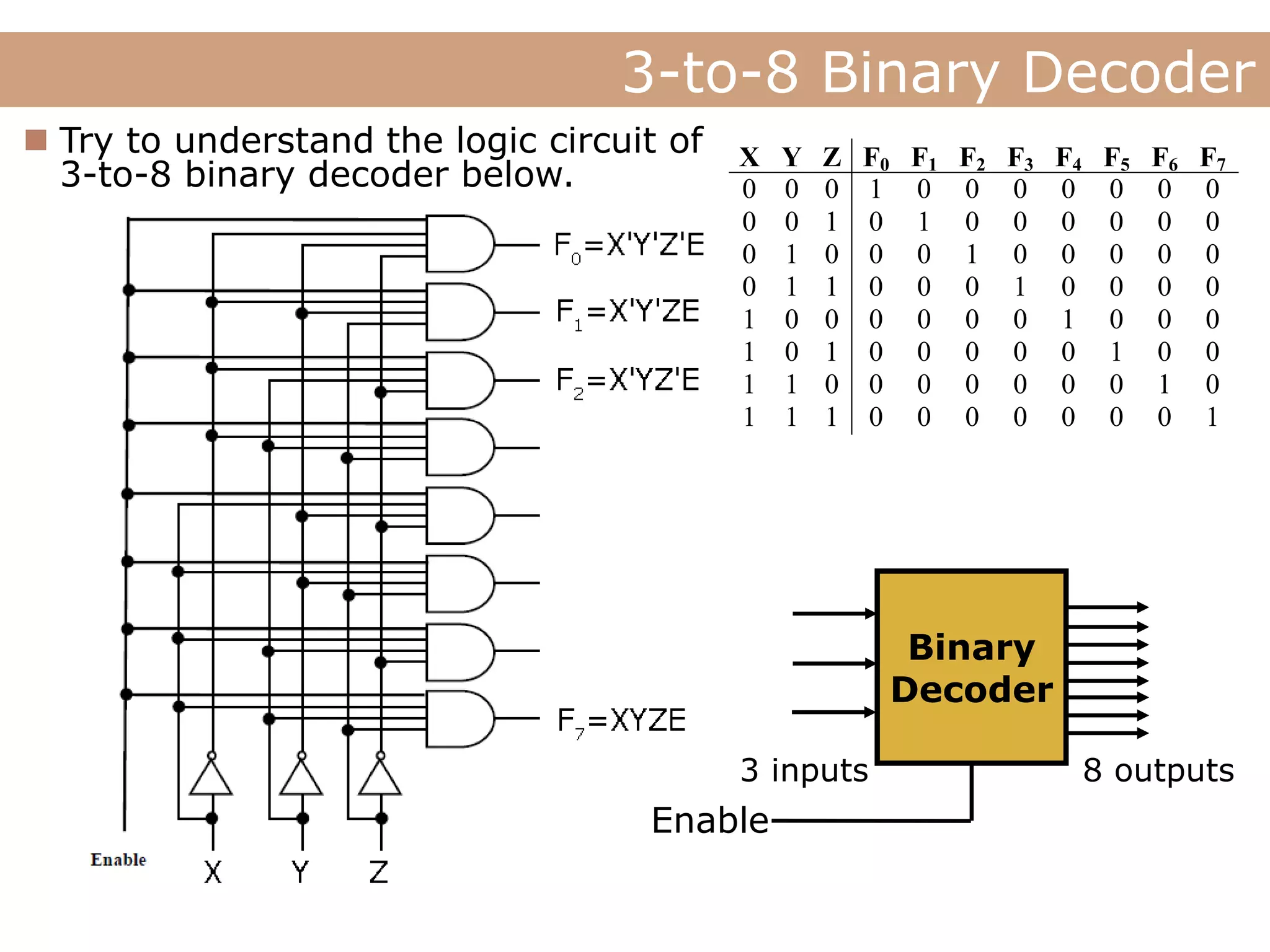
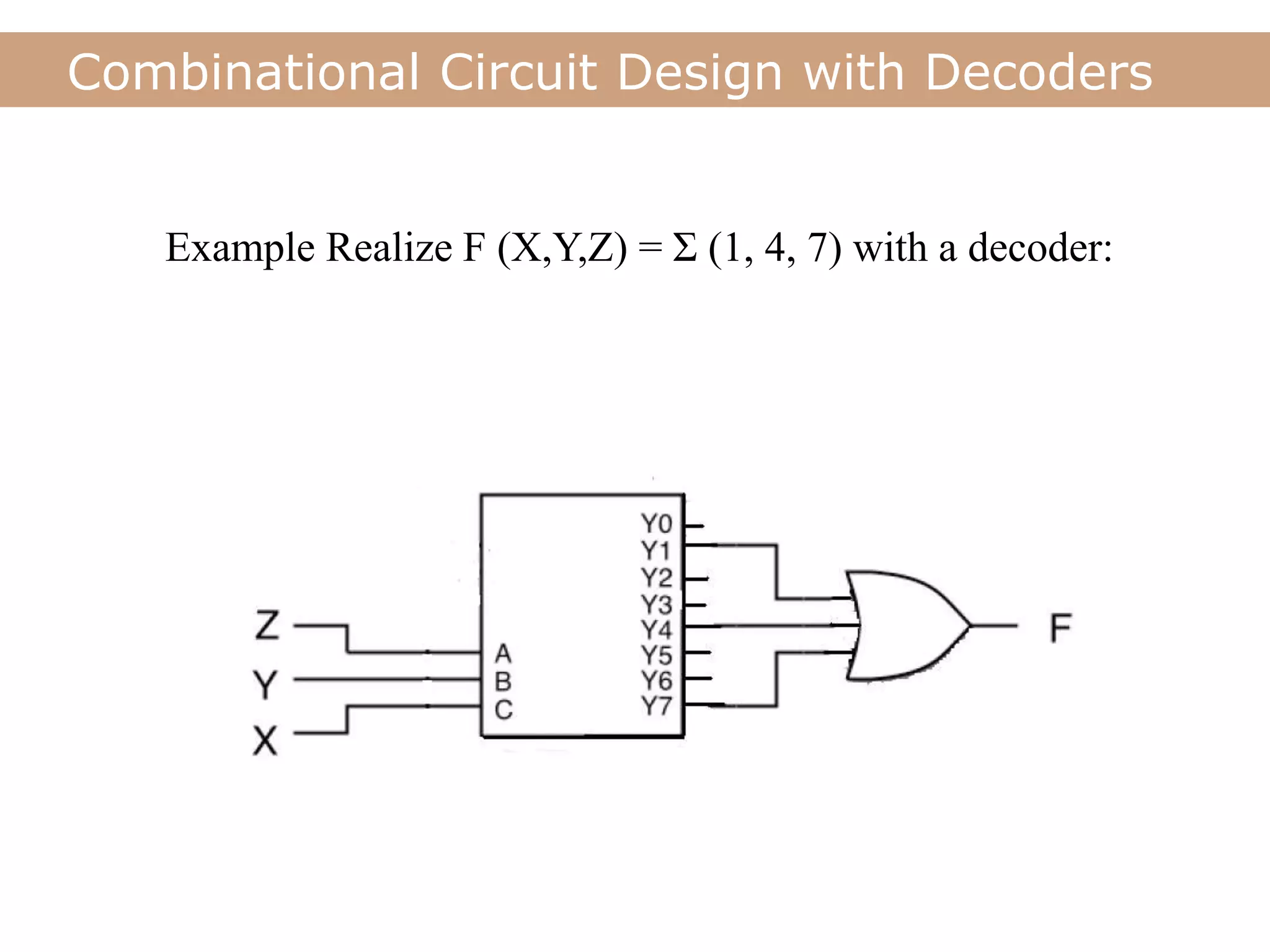
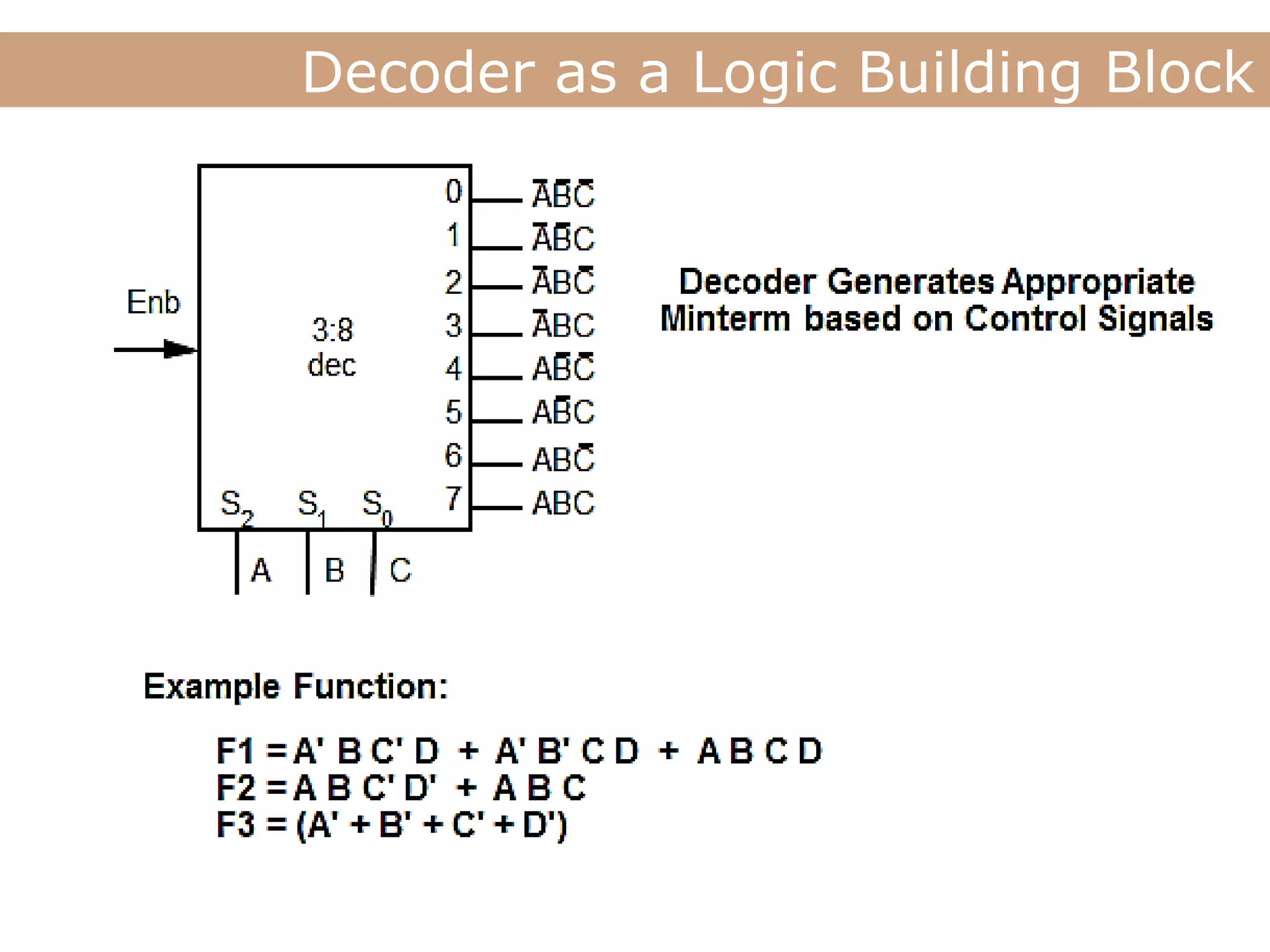
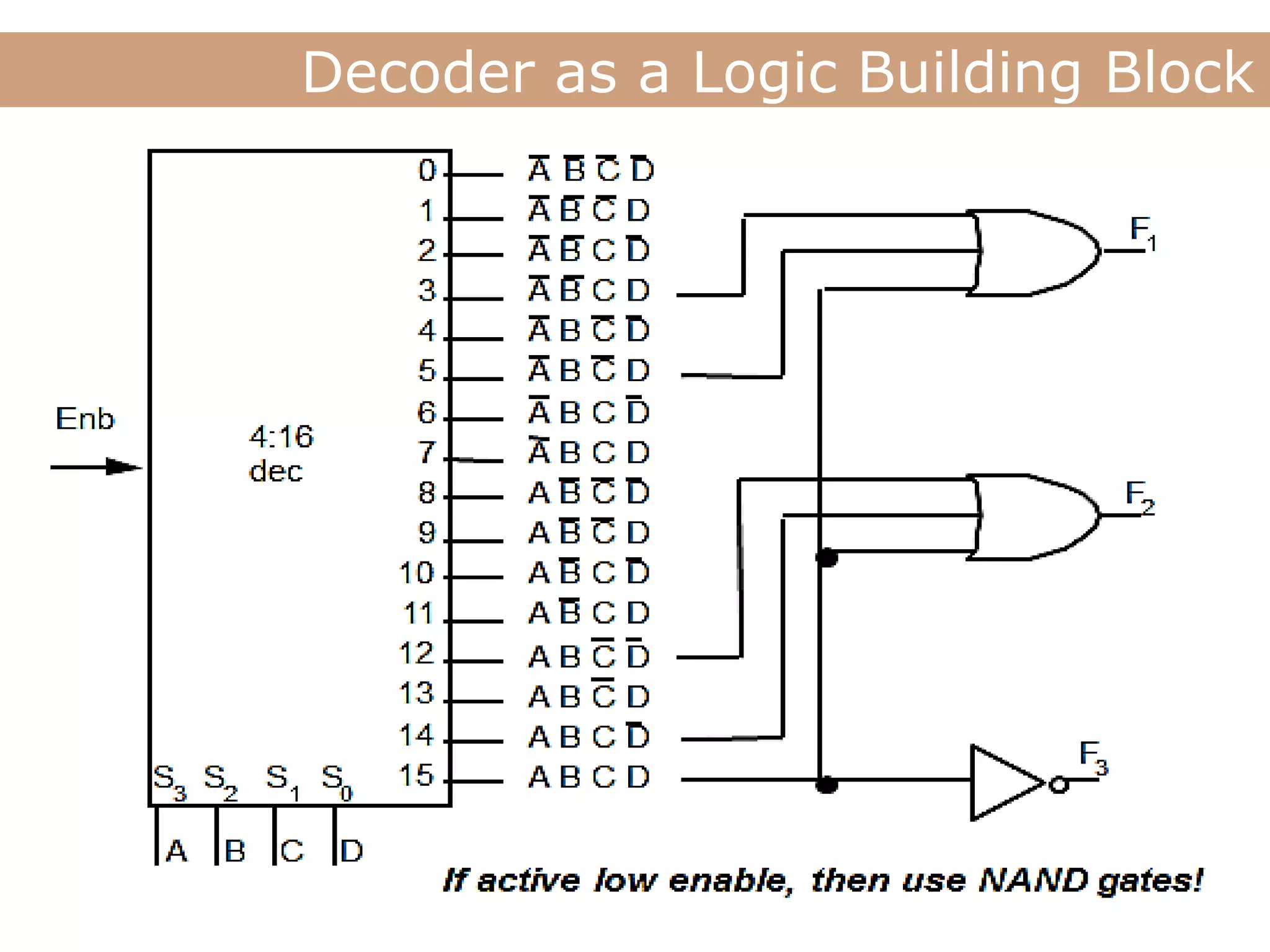
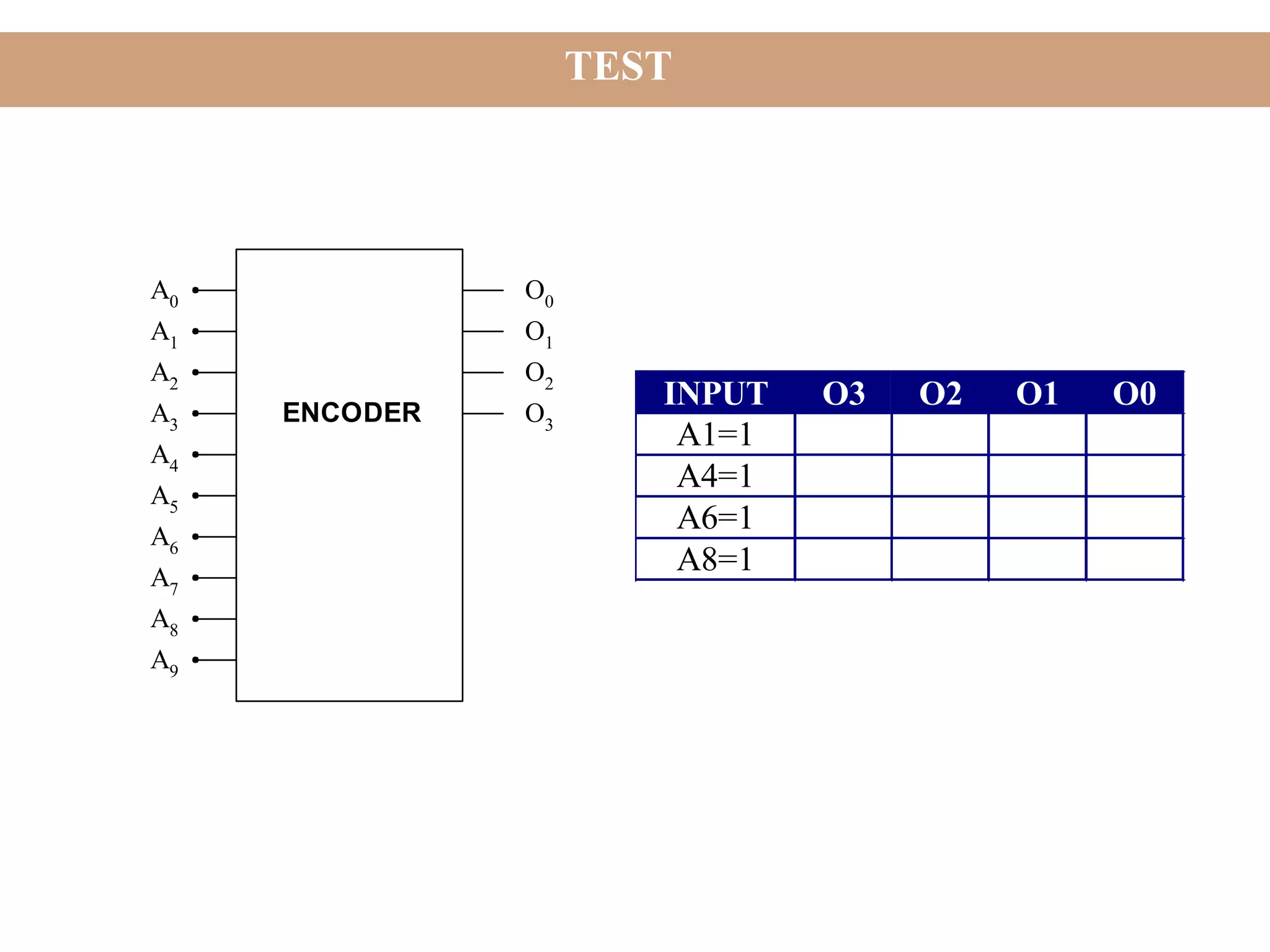
The document discusses encoders, decoders, multiplexers (MUX), and how they can be used to implement digital logic functions. It provides examples of using 4-to-1, 8-to-1 and 10-to-1 MUX to implement functions. It also gives examples of 4-to-2, 8-to-3 and 10-to-4 encoders. Decoder examples include a 2-to-4 and 3-to-8 binary decoder. The document explains how decoders can be used as logic building blocks to realize Boolean functions. It poses questions to be answered using terms like MUX, DEMUX, encoder, decoder.
decoder and encoder
- 1. BY UNSA SHAKIR Decodersand Encoders Digital Systems
- 2. Lecture Example • Implement F= XYZ + YZ with • 8:1 MUX • 4:1 MUX • Establish function in a truth table and design circuit diagram.
- 3. Lecture Example • Consider F(A,B,C)= m(1,3,5,6). We can implement this function using a 4-to-1 MUX as follows. • Establish function in a truth table and design circuit diagram.
- 4. Lecture MUX Example (cont.) AB C F 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 0 When A=B=0, F=C When A=0, B=1, F=C When A=1, B=0, F=C When A=B=1, F=C’
- 5. Lecture MUX implementation ofF(A,B,C) =m(1,3,5,6)
- 6. Lecture Example • Consider F(A,B,C)= m(1,3,4,11,12,13,14,15). We can implement this function using a 8-to-1 MUX as follows. • Establish function in a truth table and design circuit diagram.
- 7.
- 8. Lecture Encoder/Decoder ENCODER- a digitalcircuit that produces a binary output code depending on which of its inputs are activated. DECODER- a digital circuit that converts an input binary code into a single numeric output. A0 A1 A2 A3 A4 A5 A6 A7 ENCODER O0 O1 O2 A0 A1 A2 O0 O1 O2 O3 O4 O5 O6 O7 DECODER
- 9. Lecture Encoders • Binary codeof N digits can be used to store 2N distinct elements of coded information. • Encoders convert 2N lines of input into a code of N bits and
- 10. Lecture Encoder Example Lecture DigitalSystems In encoder circuit only one input may be set high (1) at a certain time. The output is a 2-bit number. 0 0 1 1 1 0 1 0 0 0 1 0 0 1 0 0 1 0 0 0 0 0 0 1 I3 I2 I1 I0 Y1 Y0 I0 I1 I2 I3 Y1 Y0 • Example: 4-to-2 binary encoder
- 11. Lecture Encoder Example • Example:8-to-3 binary encoder (octal-to-binary) A0 = D1 + D3 + D5 + D7 A1 = D2 + D3 + D6 + D7 A2 = D4 + D5 + D6 + D7
- 12.
- 13.
- 14. Lecture Encoder Example • Example:10-to-4 binary encoder (decimal-to-binary)
- 15. Lecture • Y0 =D1 + D3 + D5 + D7 + D9 • Y1 = D2 + D3 + D6 + D7 • Y2 = D4 + D5 + D6 + D7 • Y3 = D8 + D9 • Example: 10-to-4 binary encoder (decimal-to-binary)
- 16. Lecture • Example: 10-to-4binary encoder (decimal-to-binary)
- 17. Lecture • Example: 10-to-4binary encoder (decimal-to-binary)
- 18.
- 19. Lecture Binary Decoders Lecture DigitalSystems Binary decoders convert an n-bit input to a single output. It uses its n-bit input to determine which of the 2n outputs will be uniquely activated. Binary decoders can be developed using AND or OR Gates. Later on, binary decoders can be implemented in logic circuits. The outputs of a decoder are minterms. That is why decoders are sometimes called as minterm generators. We can easily use a decoder to implement any sum of minterms expression. Note: A minterm is a Boolean expression resulting in 1 only for the output of a single row (in a truth table) or a single cell (in a Karnaugh map), and 0s for all other row or cells, respectively.
- 20. Lecture 2-to-4 Binary Decoder LectureDigital Systems A circuit of 2-to-4 binary decoder is shown below. Binary Decoder 2 inputs 4 outputs Enable The truth table shows that for any given input combination, exactly one output will turn to 1. The enable must be set to 1 to get an output.
- 21. Lecture 3-to-8 Binary Decoder LectureDigital Systems X Y Z F0 F1 F2 F3 F4 F5 F6 F7 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 1 0 1 1 1 0 0 0 0 0 0 0 1 Try to understand the logic circuit of 3-to-8 binary decoder below. Binary Decoder 3 inputs 8 outputs Enable
- 22. Lecture Combinational Circuit Designwith Decoders Example Realize F (X,Y,Z) = Σ (1, 4, 7) with a decoder:
- 23. Lecture Decoder as aLogic Building Block
- 24. Lecture Decoder as aLogic Building Block
- 25. Lecture TEST A0 A1 A2 A3 A4 A5 A6 A7 ENCODER O0 O1 O2 O3 A8 A9 INPUT O3 O2O1 O0 A1=1 A4=1 A6=1 A8=1
- 26. Lecture A0 A1 A2 O0 O1 O2 O3 O4 O5 O6 O7 DECODER O8 O9 A3 A3 A2 A1A0 OUTPUT 0 0 0 0 0 1 0 1 0 1 1 1 1 0 0 1 TEST
- 27. Lecture ANSWER THE FOLLOWINGQUESTIONS WITH ONE OR MORE OF THESE WORDS: MUX, DEMUX, ENCODER, DECODER. A. Has more inputs than outputs. ENCODER, MUX B. Uses select inputs. MUX, DEMUX C. Can be used in parallel-to-serial conversion. MUX D. Produces a binary code at its output. ENCODER E. Only one of its outputs is activated at one time. DEMUX, DECODER F. Used to route input signals to one of several outputs. MUX G. Used to generate arbitrary logic functions. MUX, DEMUX H. 3 line-to-8 line or binary to octal. DECODER I. Data Selectors are also MUX