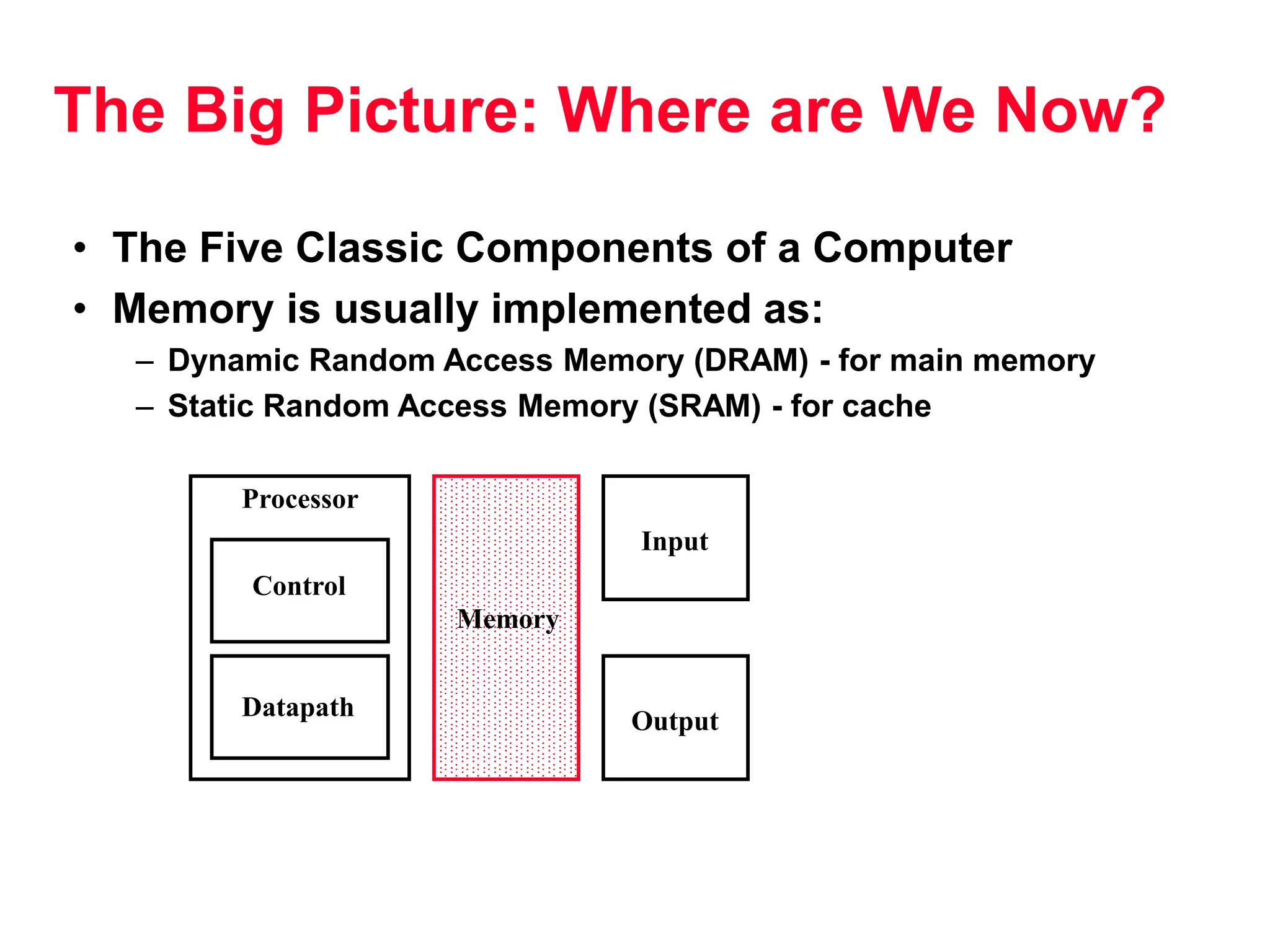
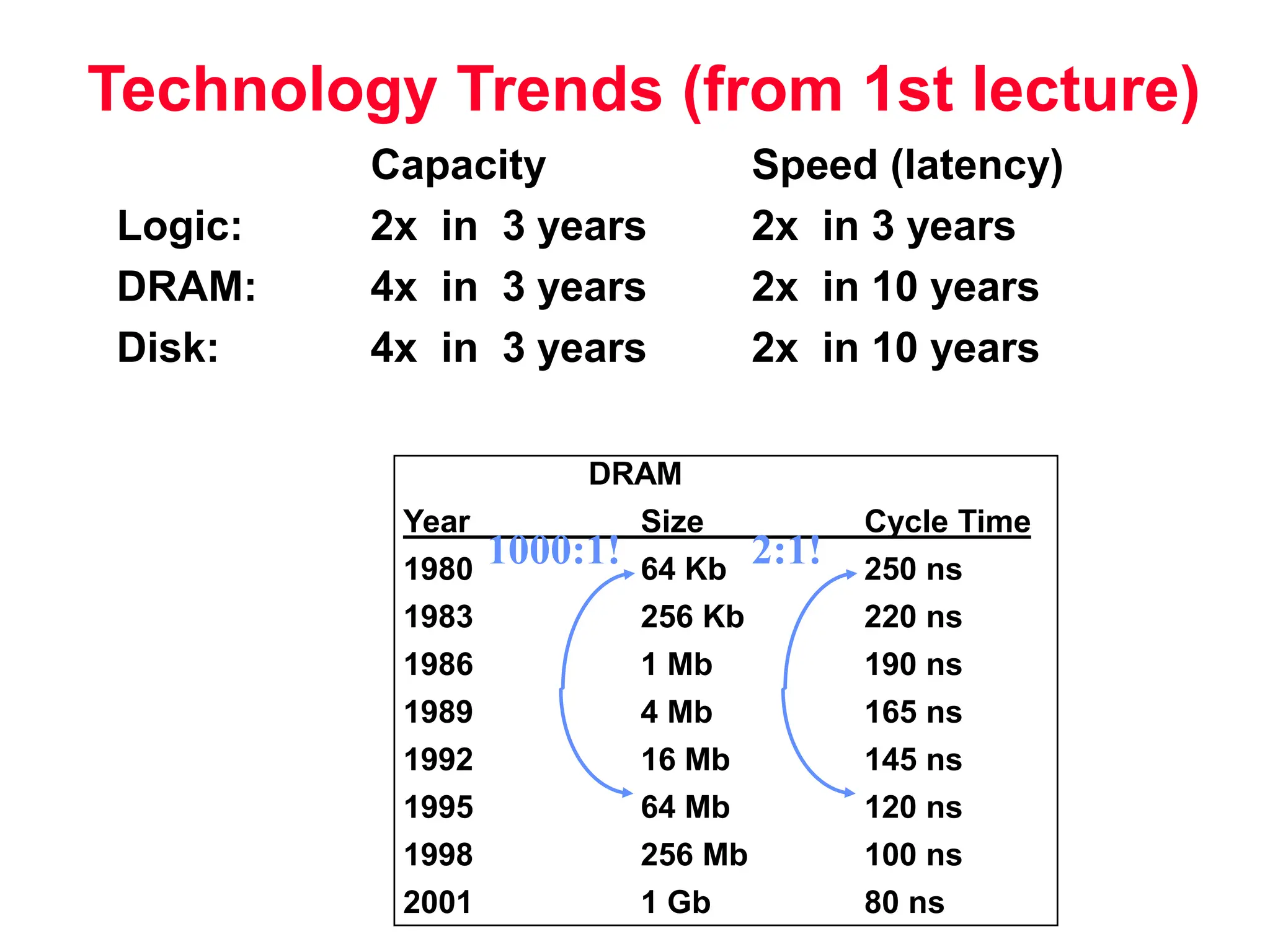
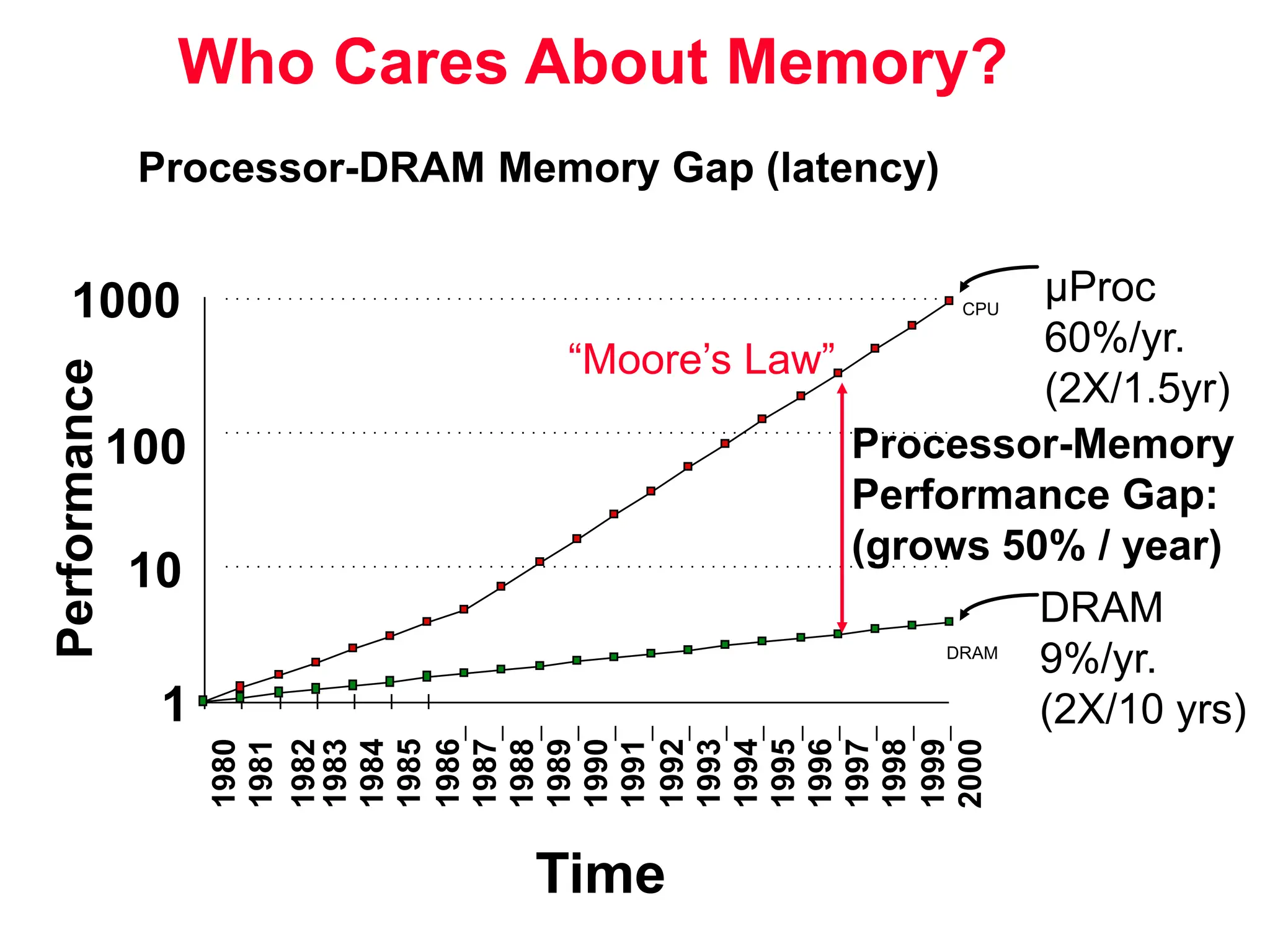
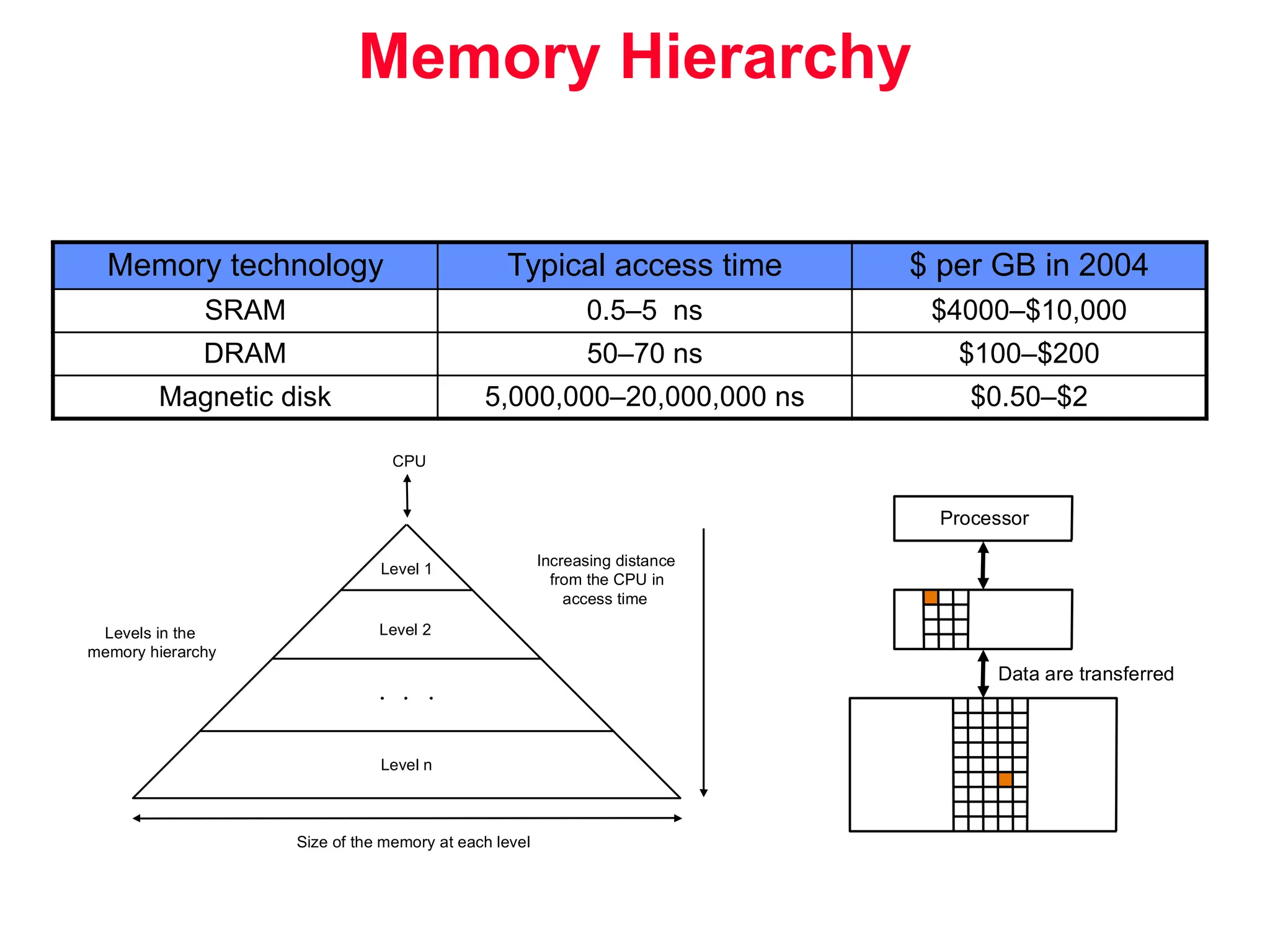
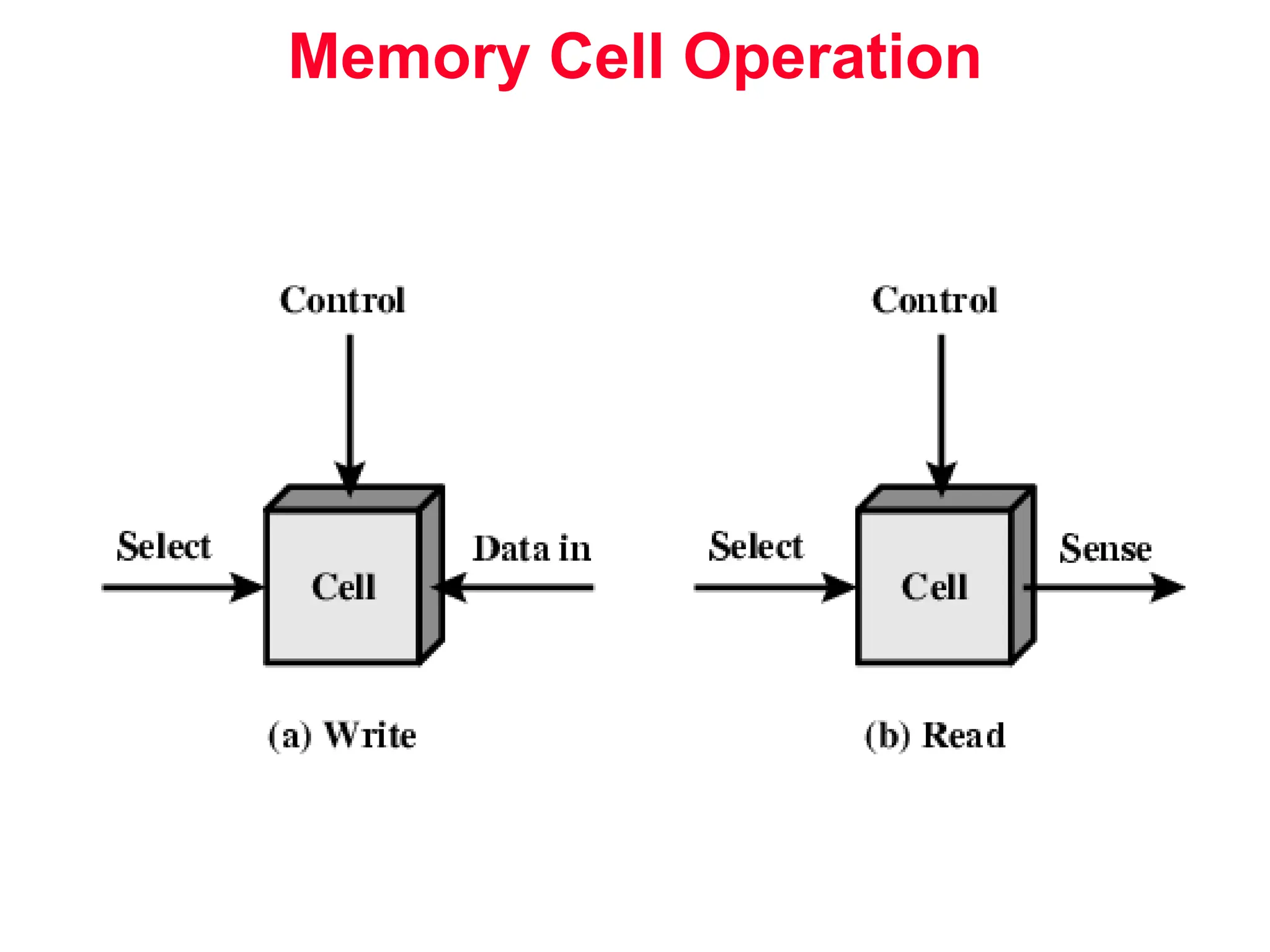
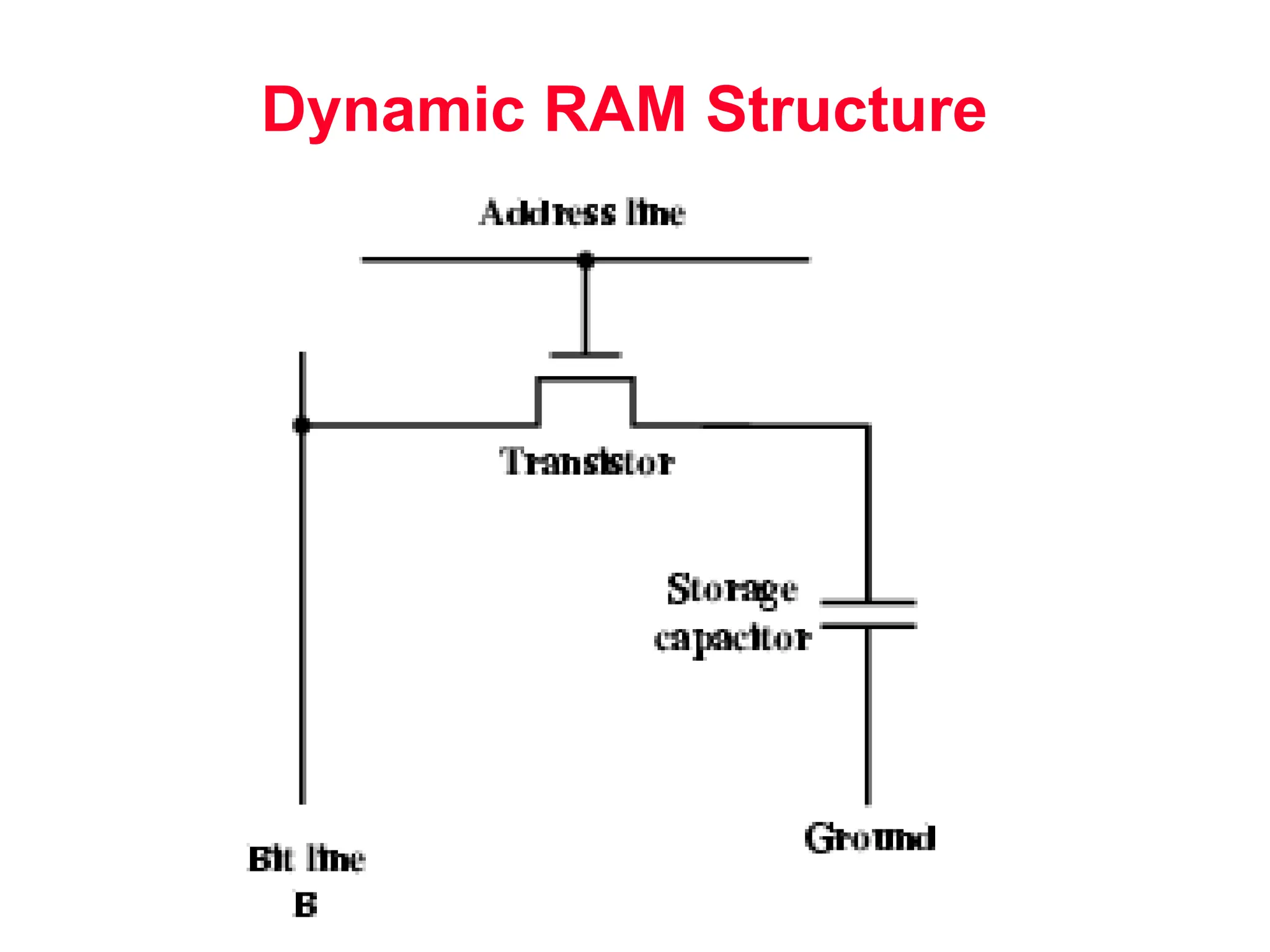
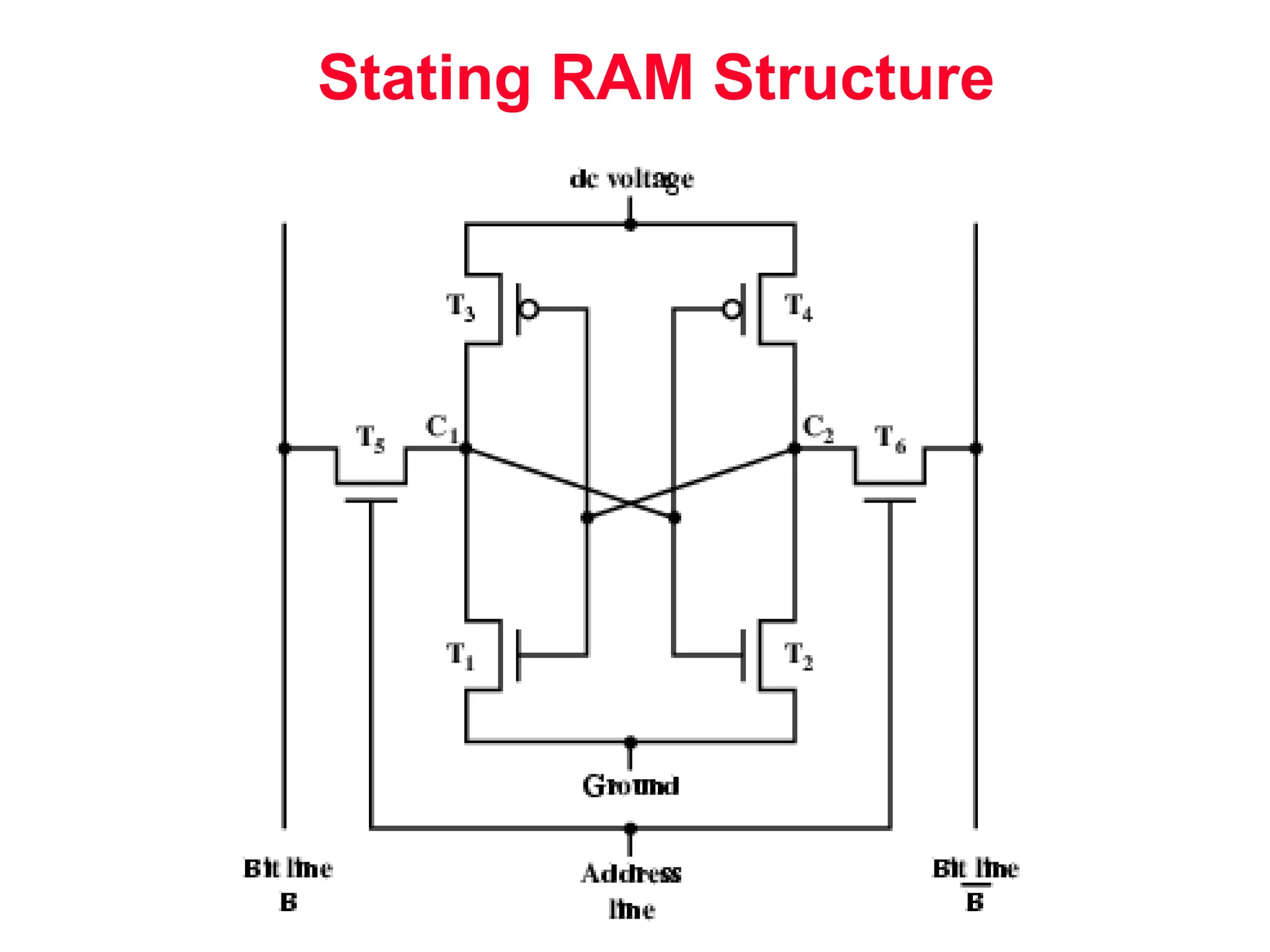
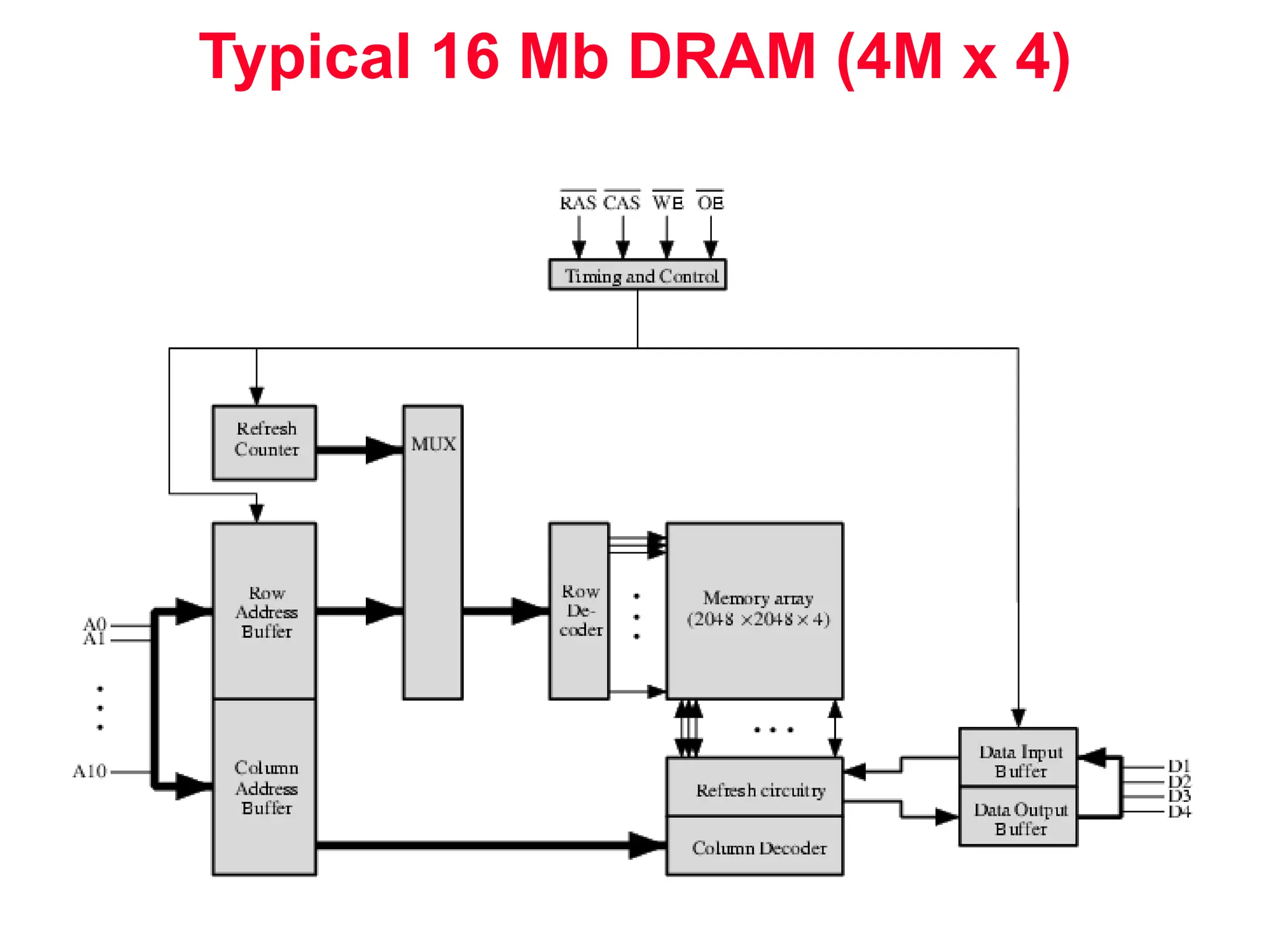
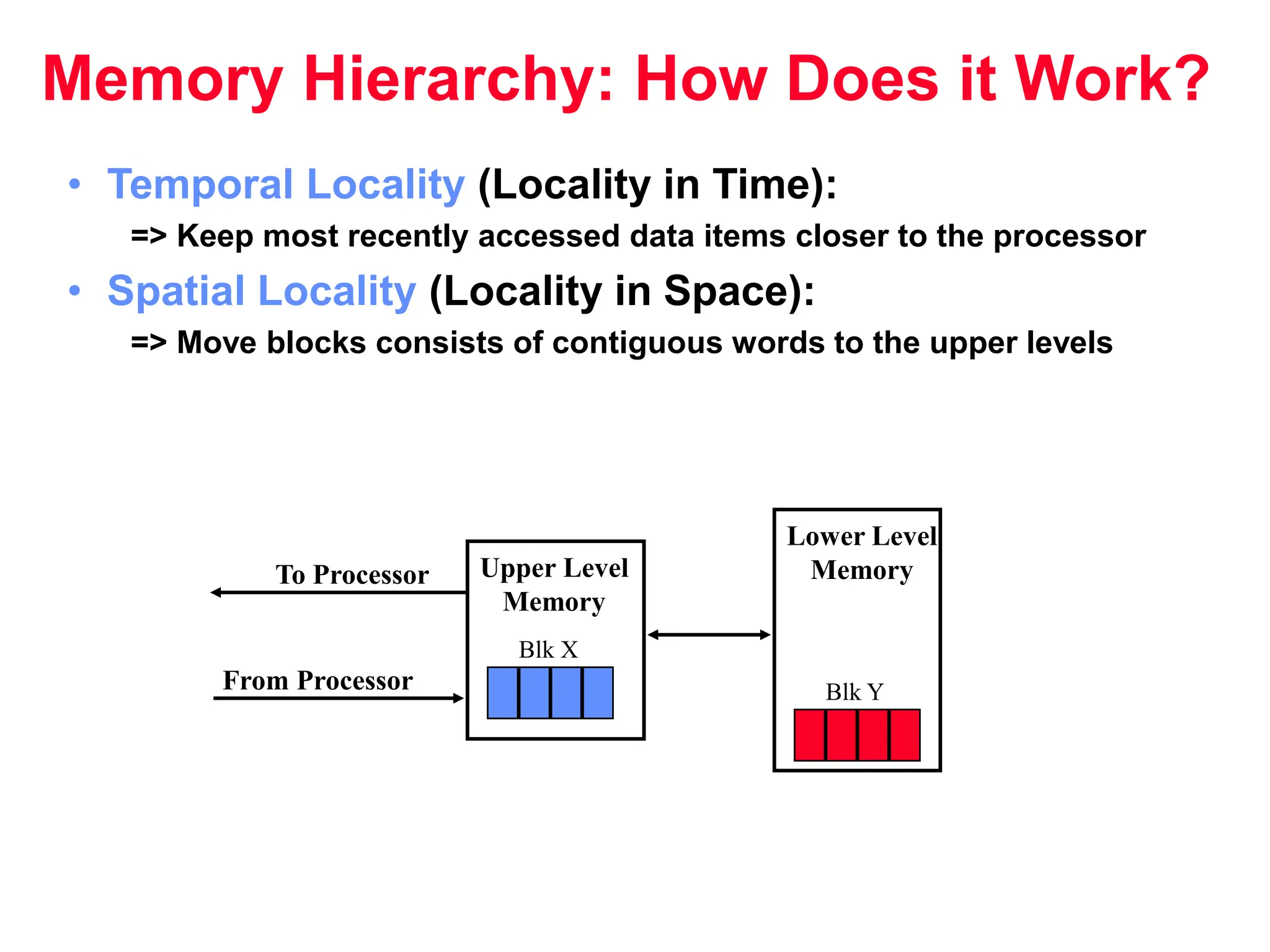
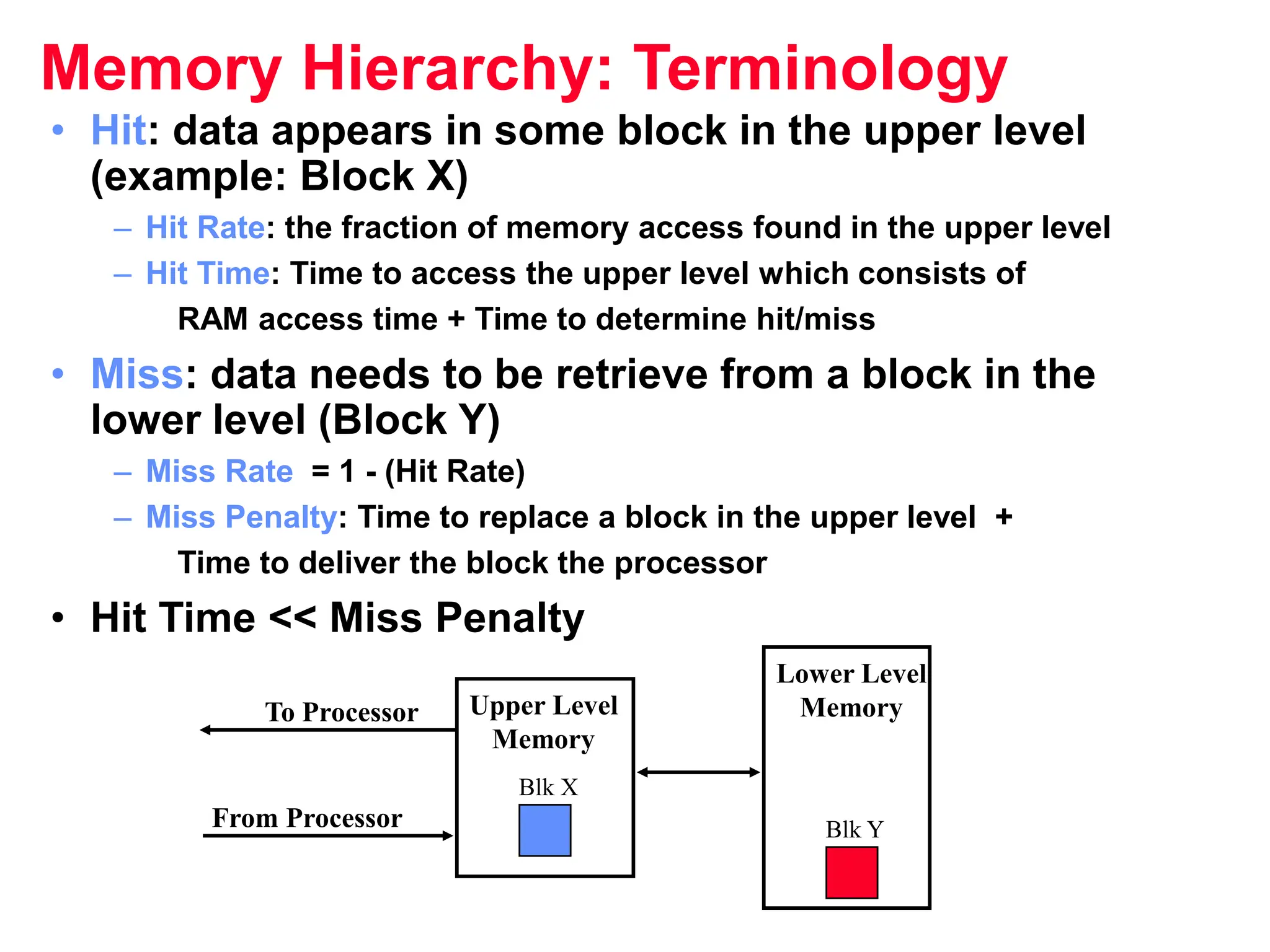
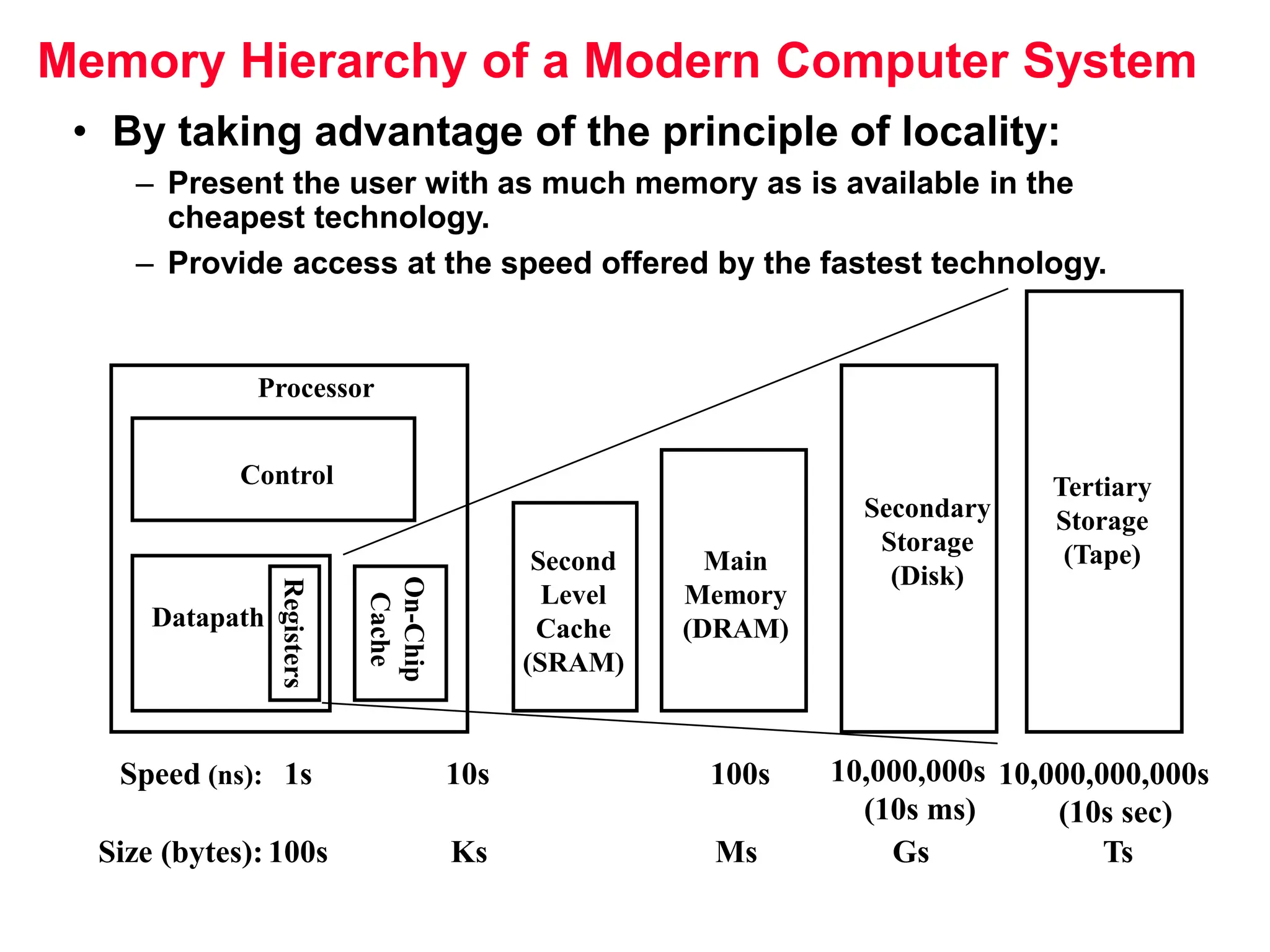
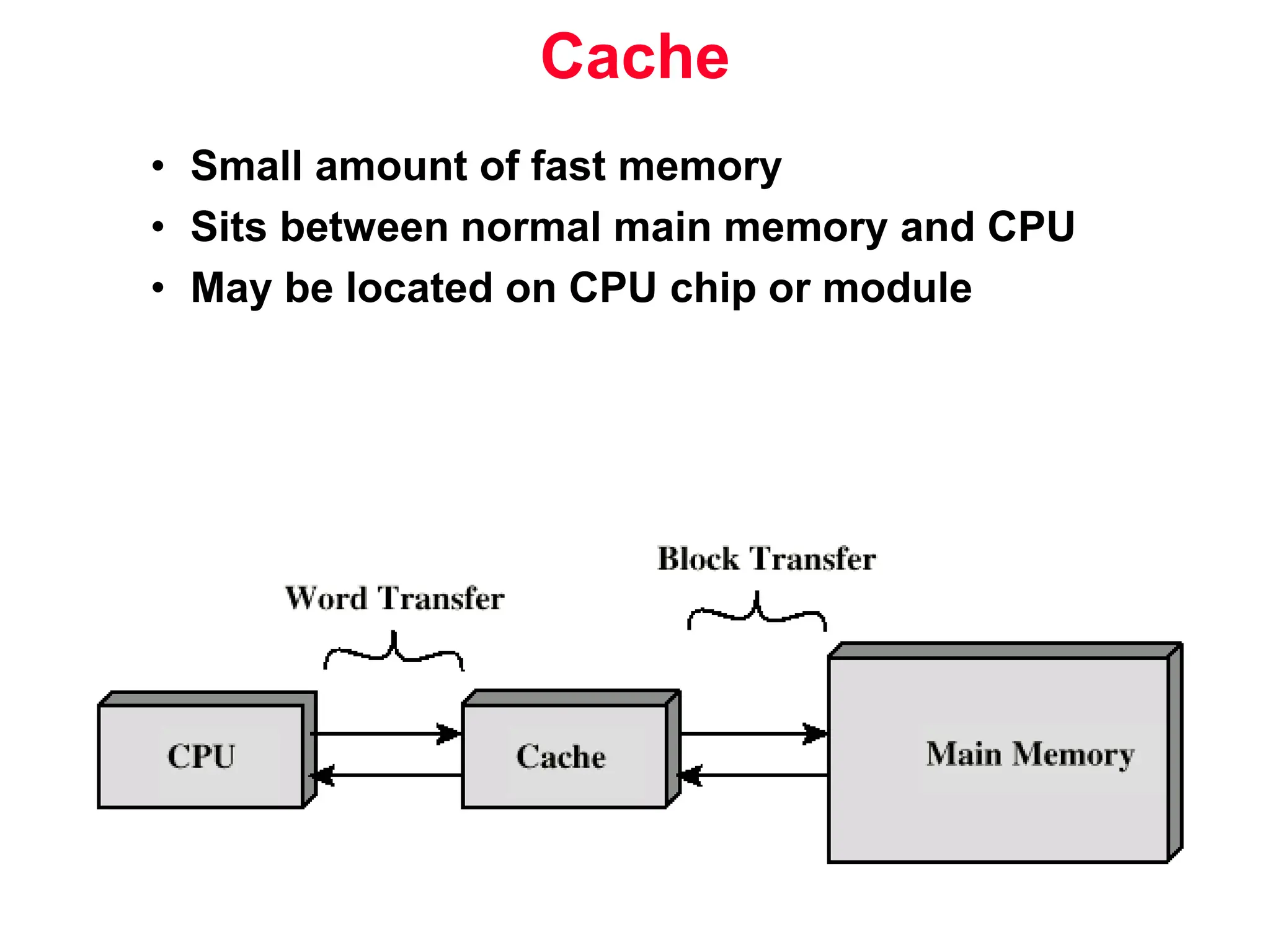
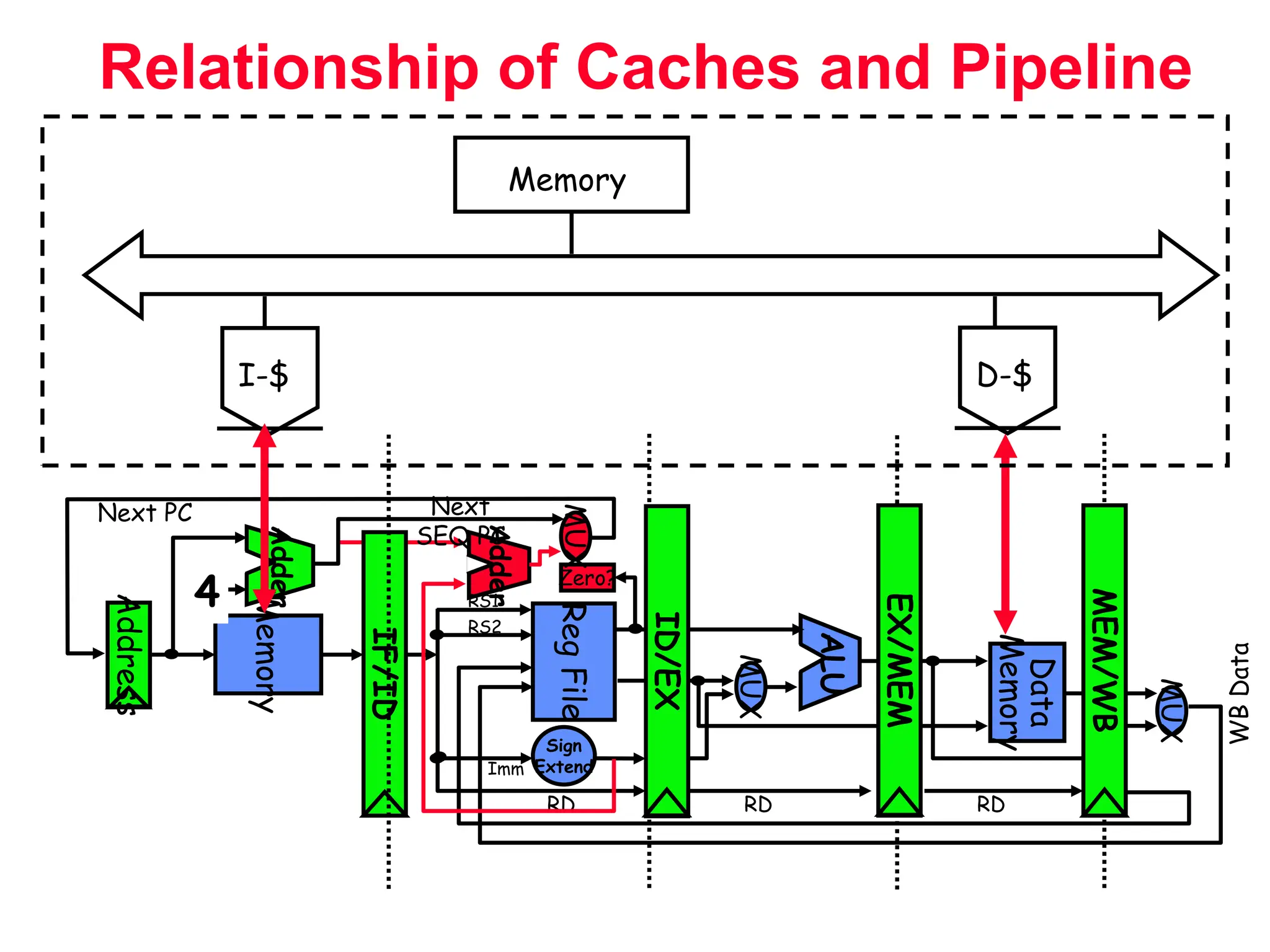
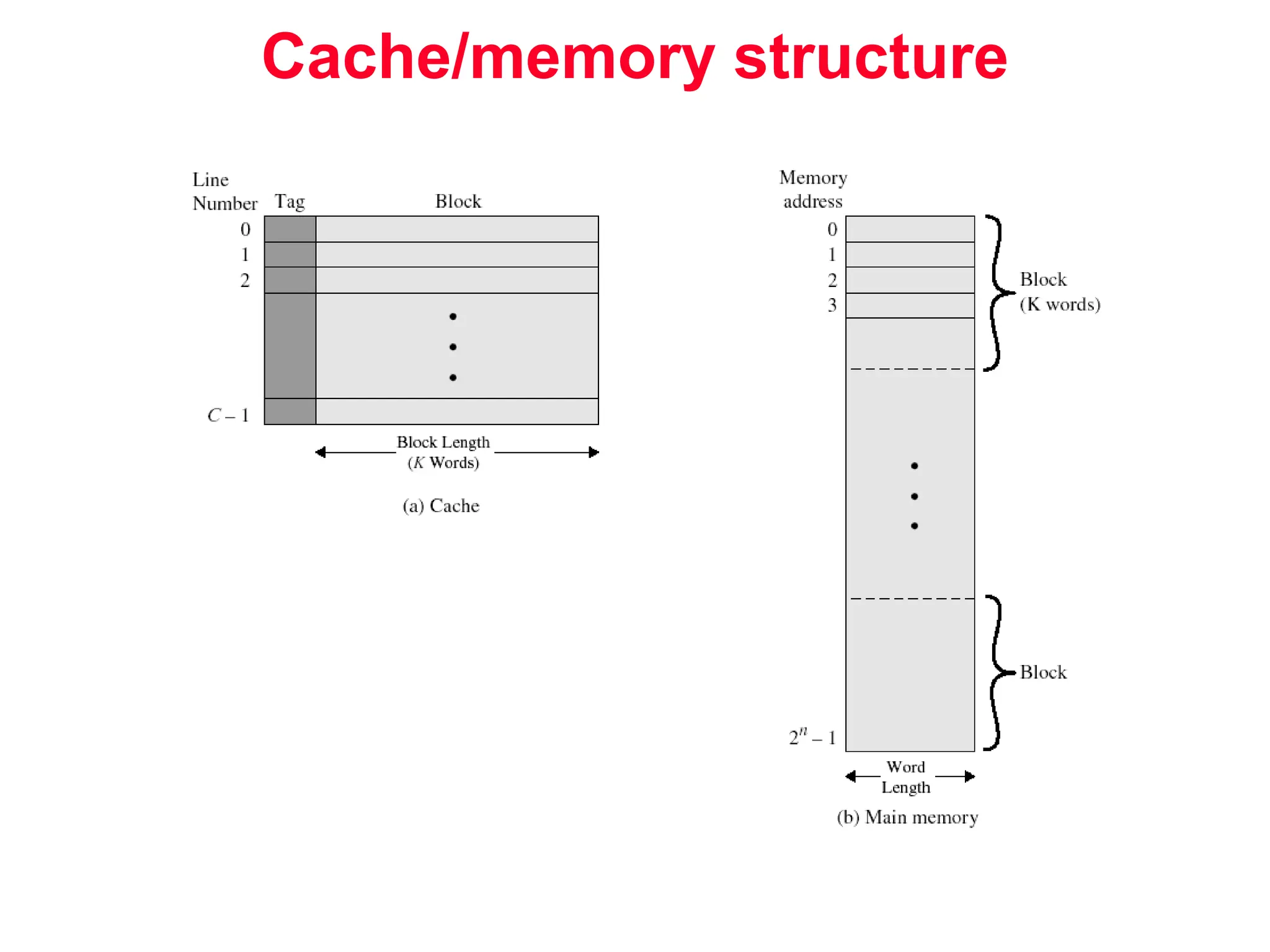
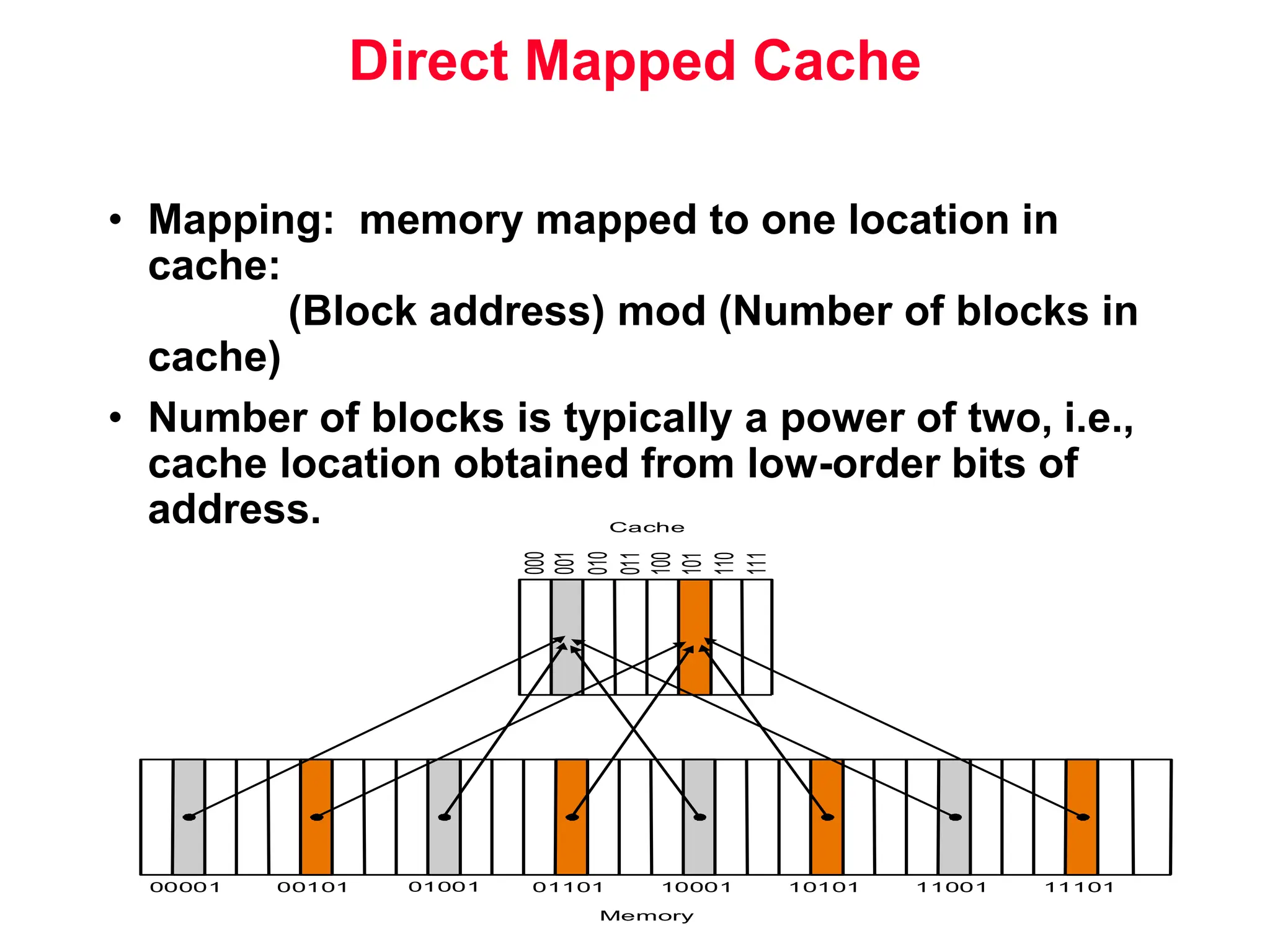
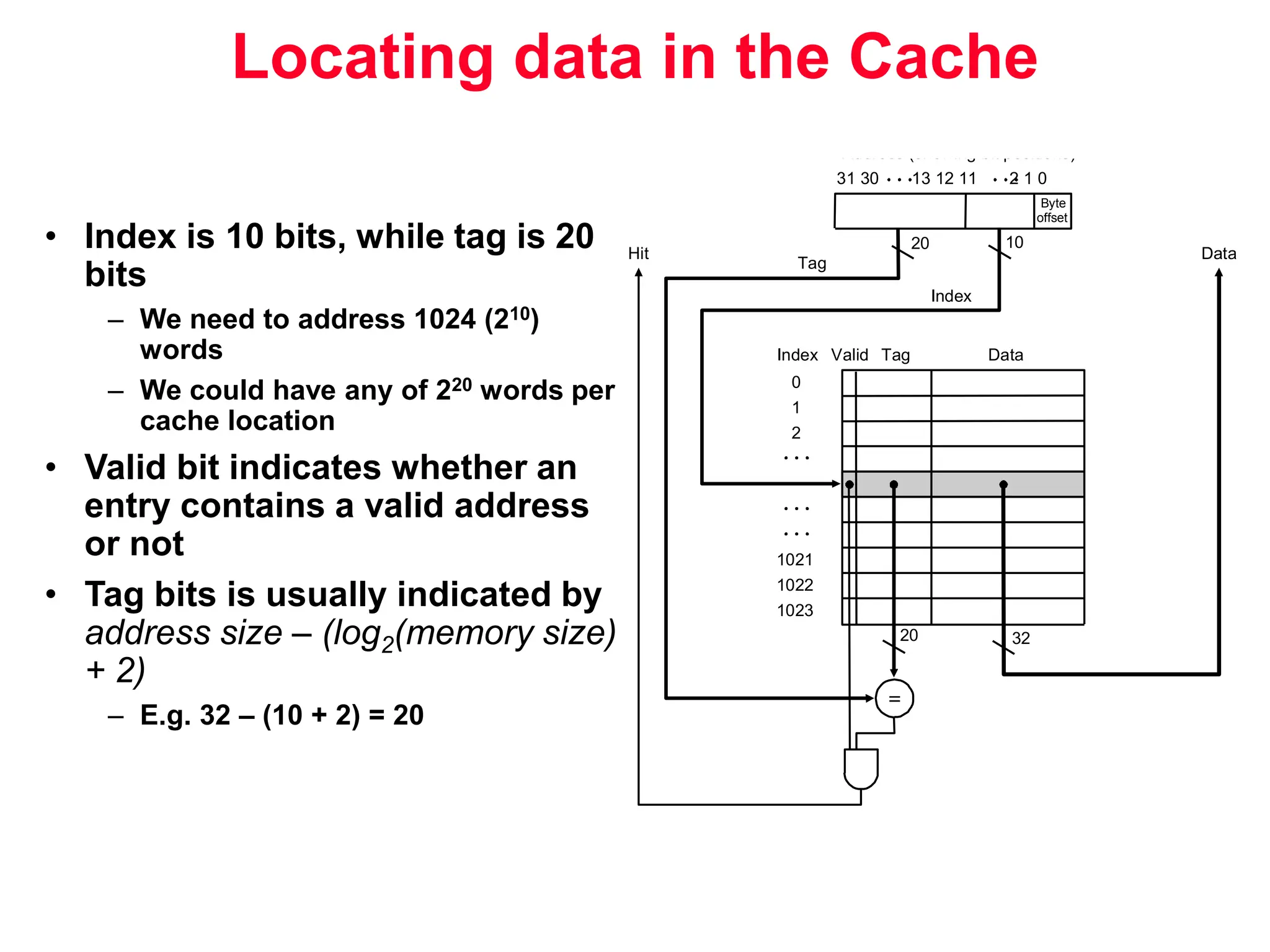
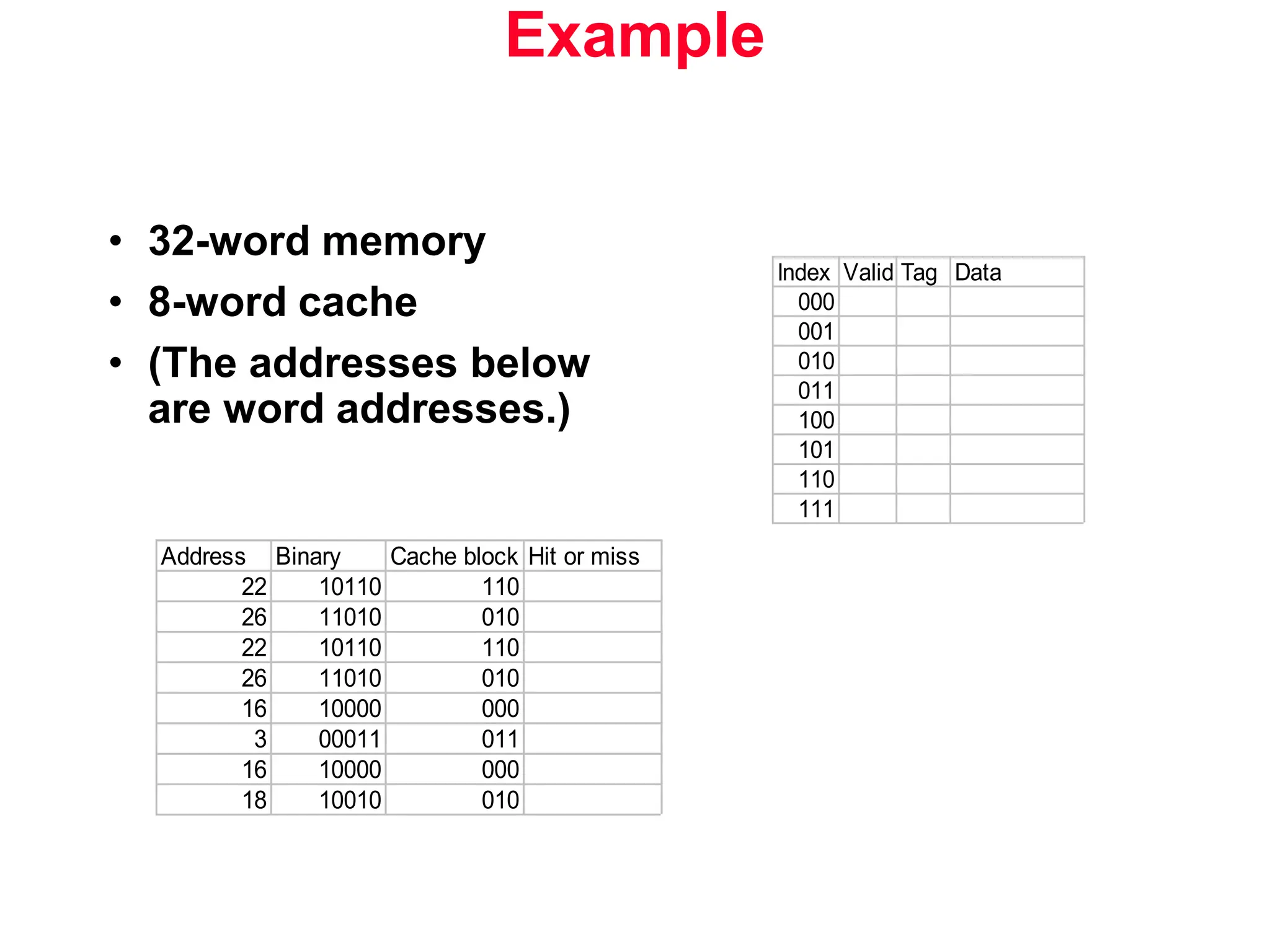
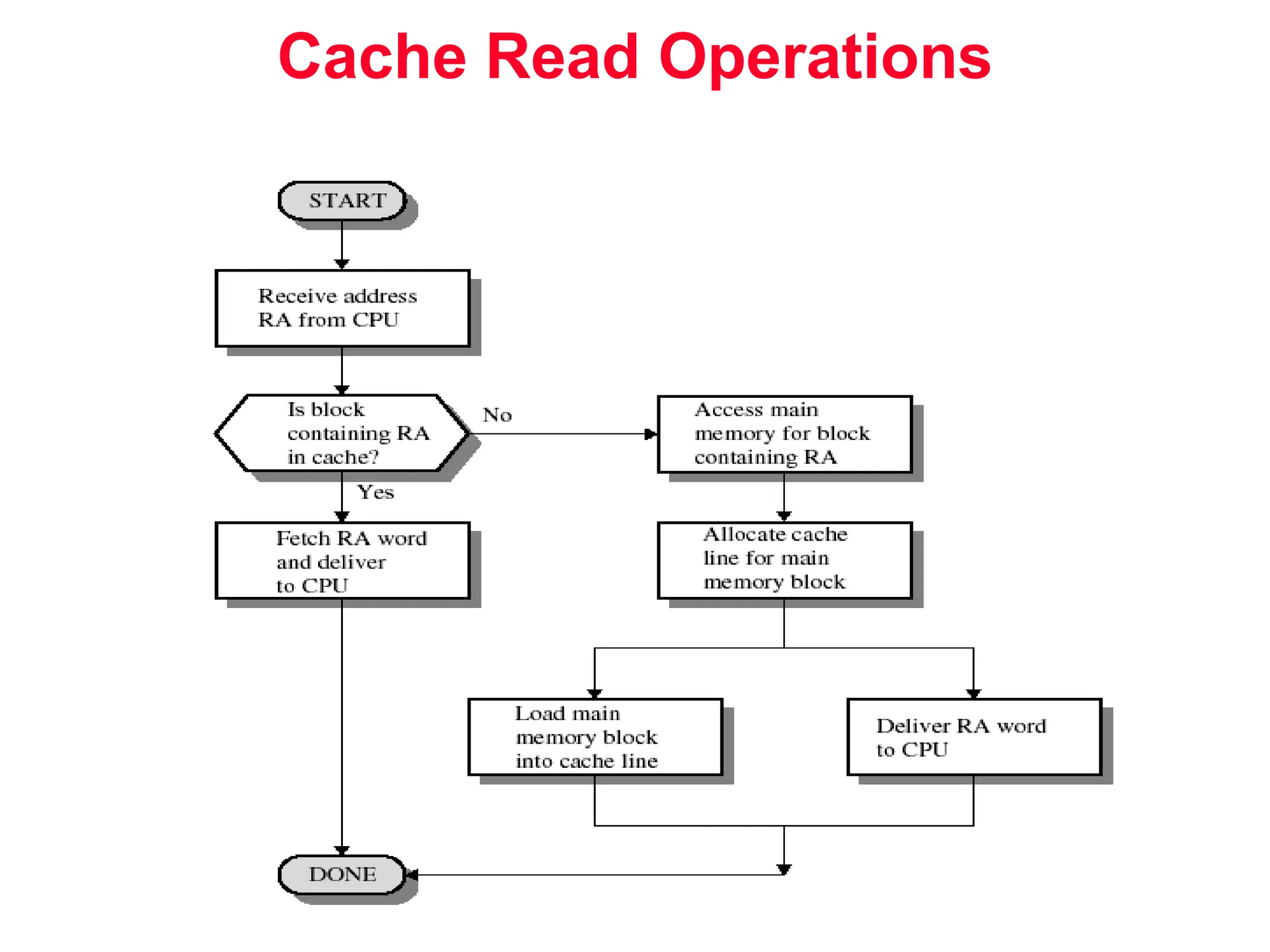
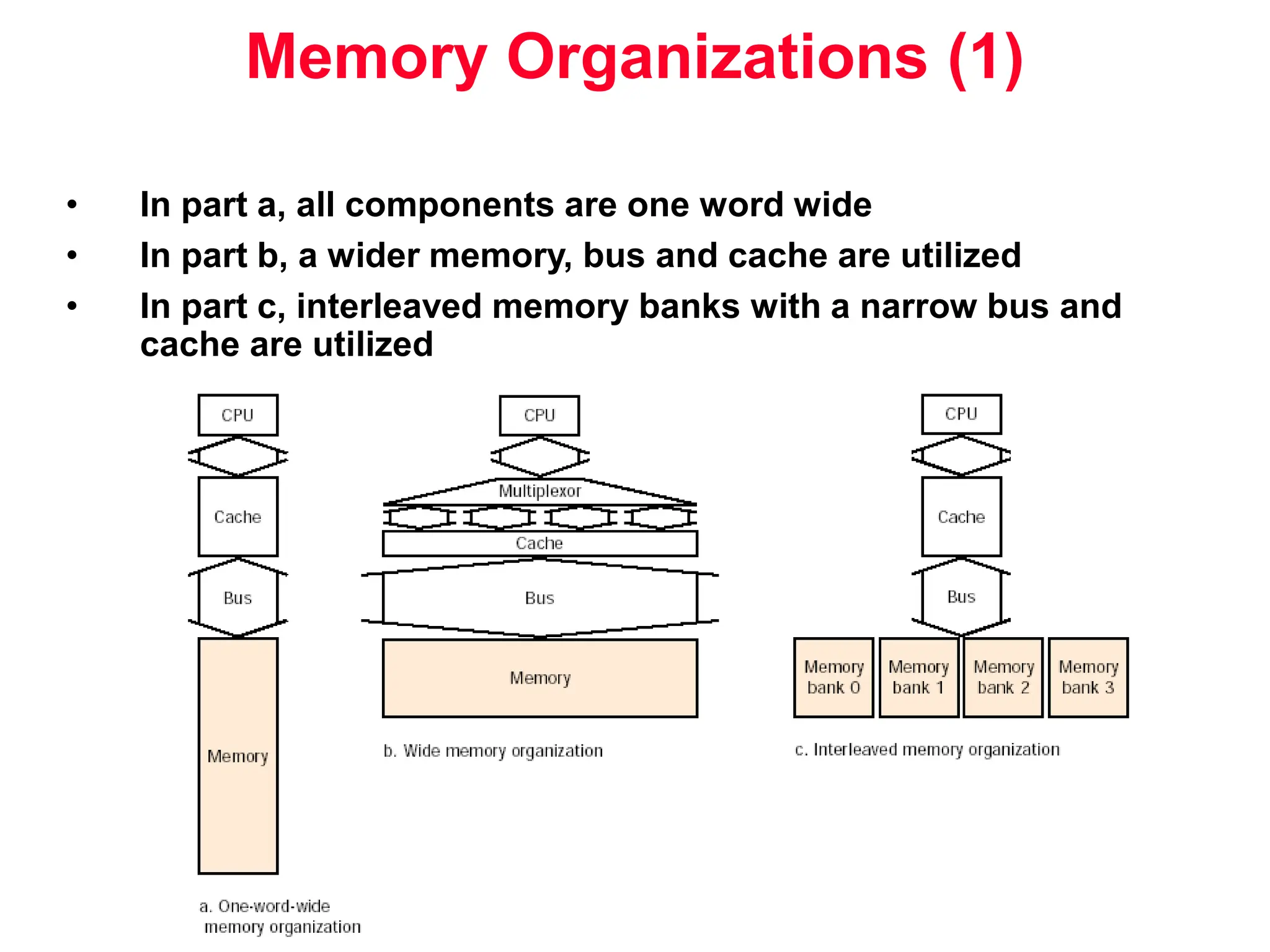
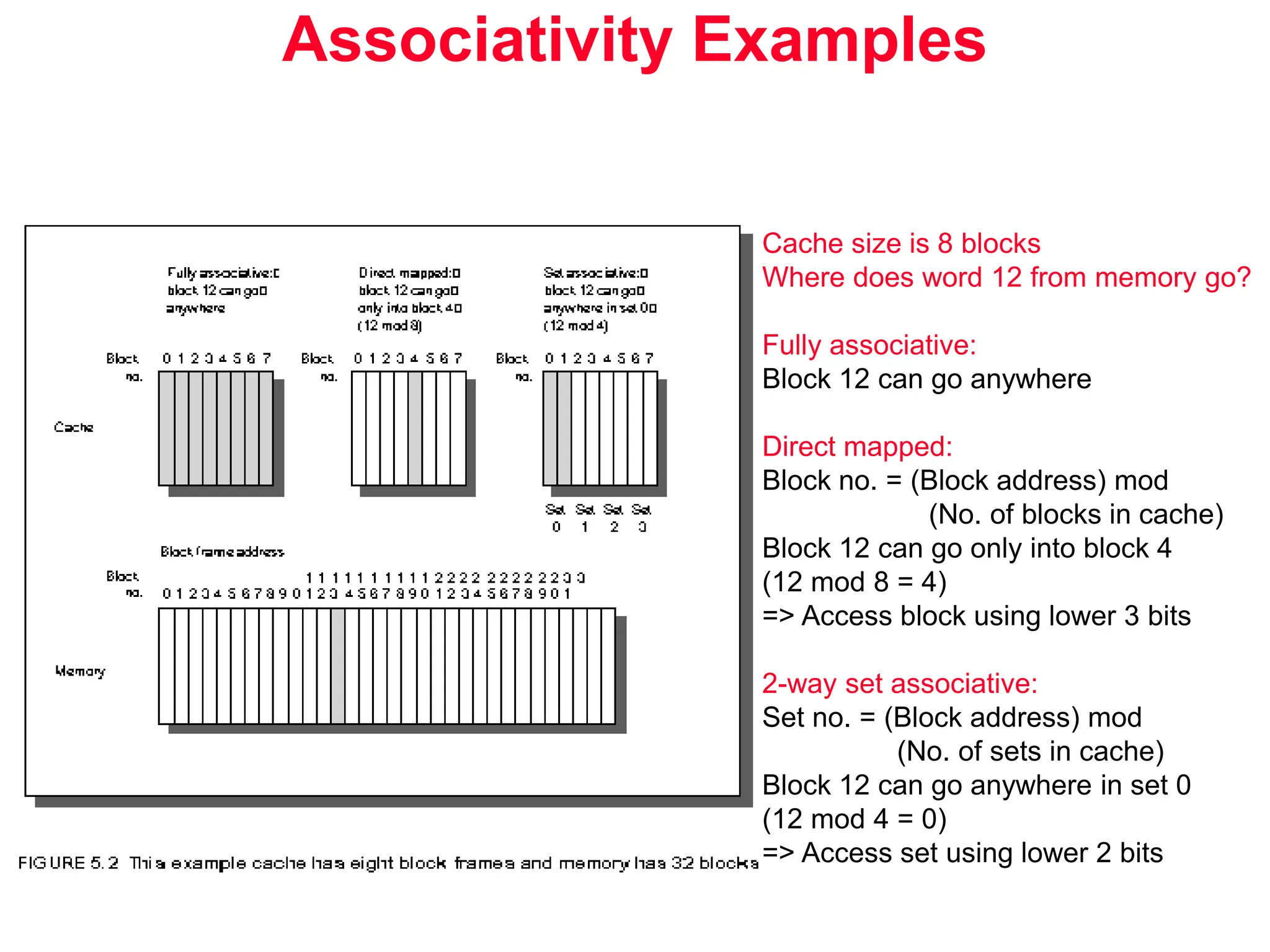
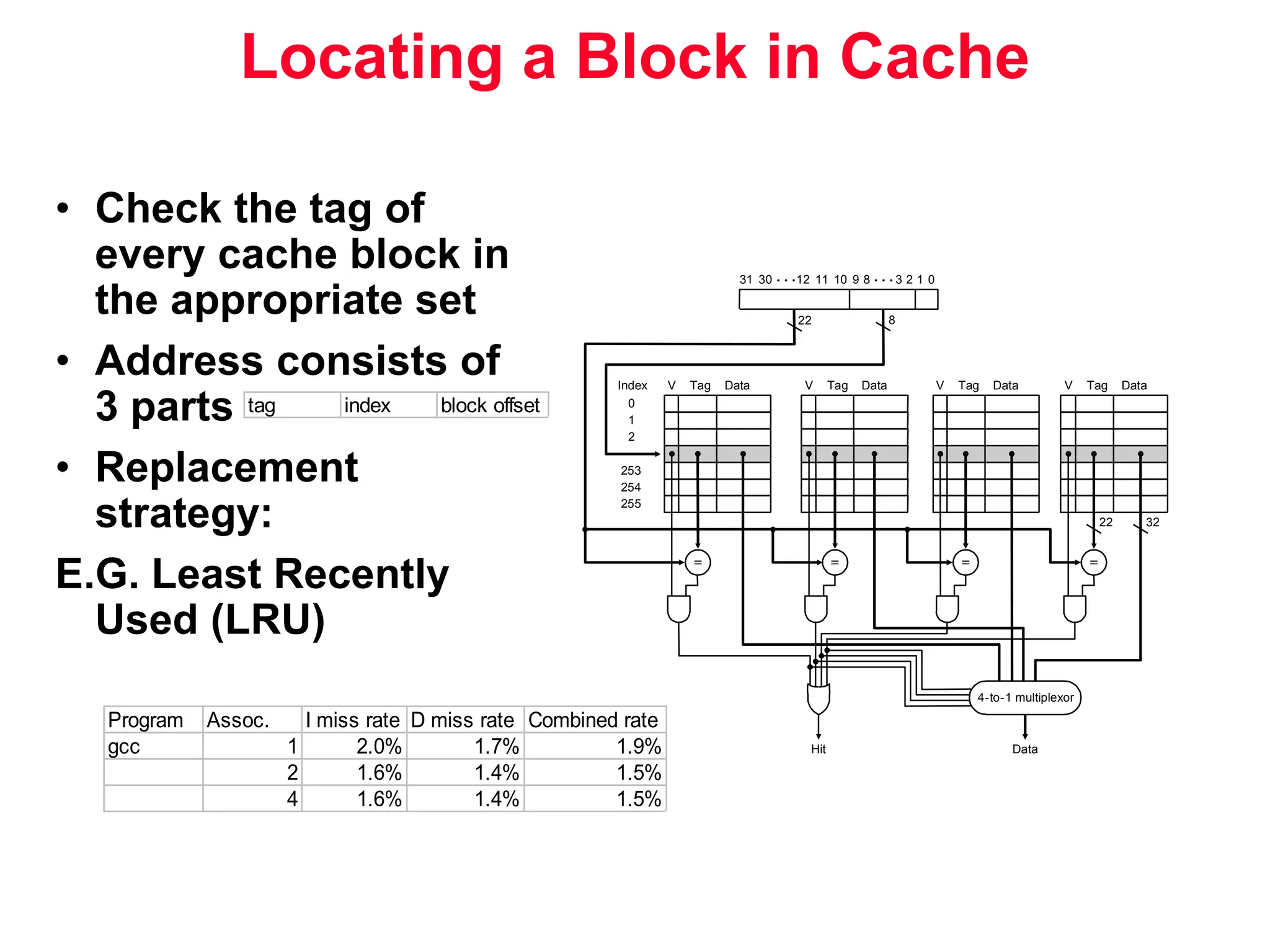
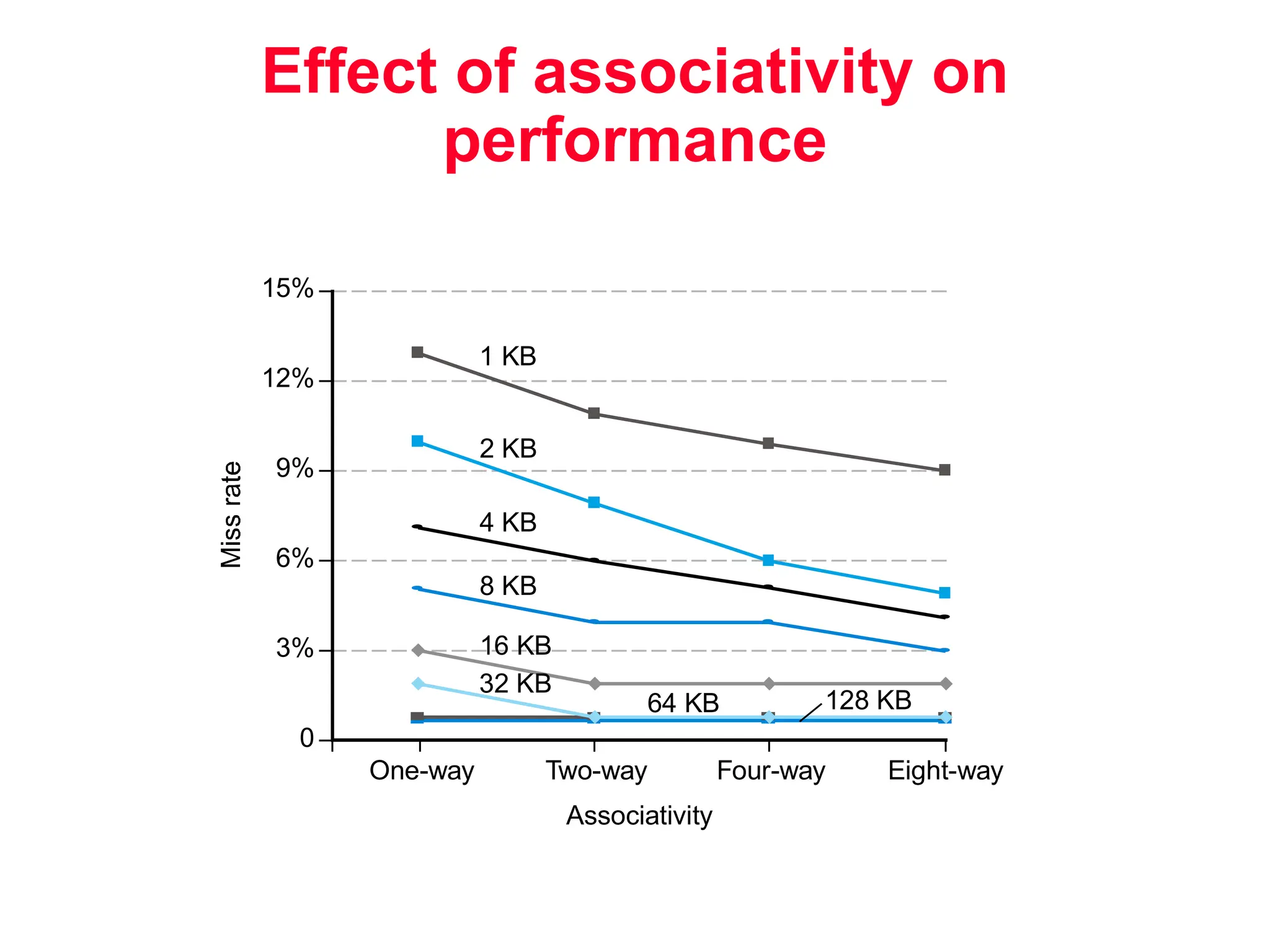
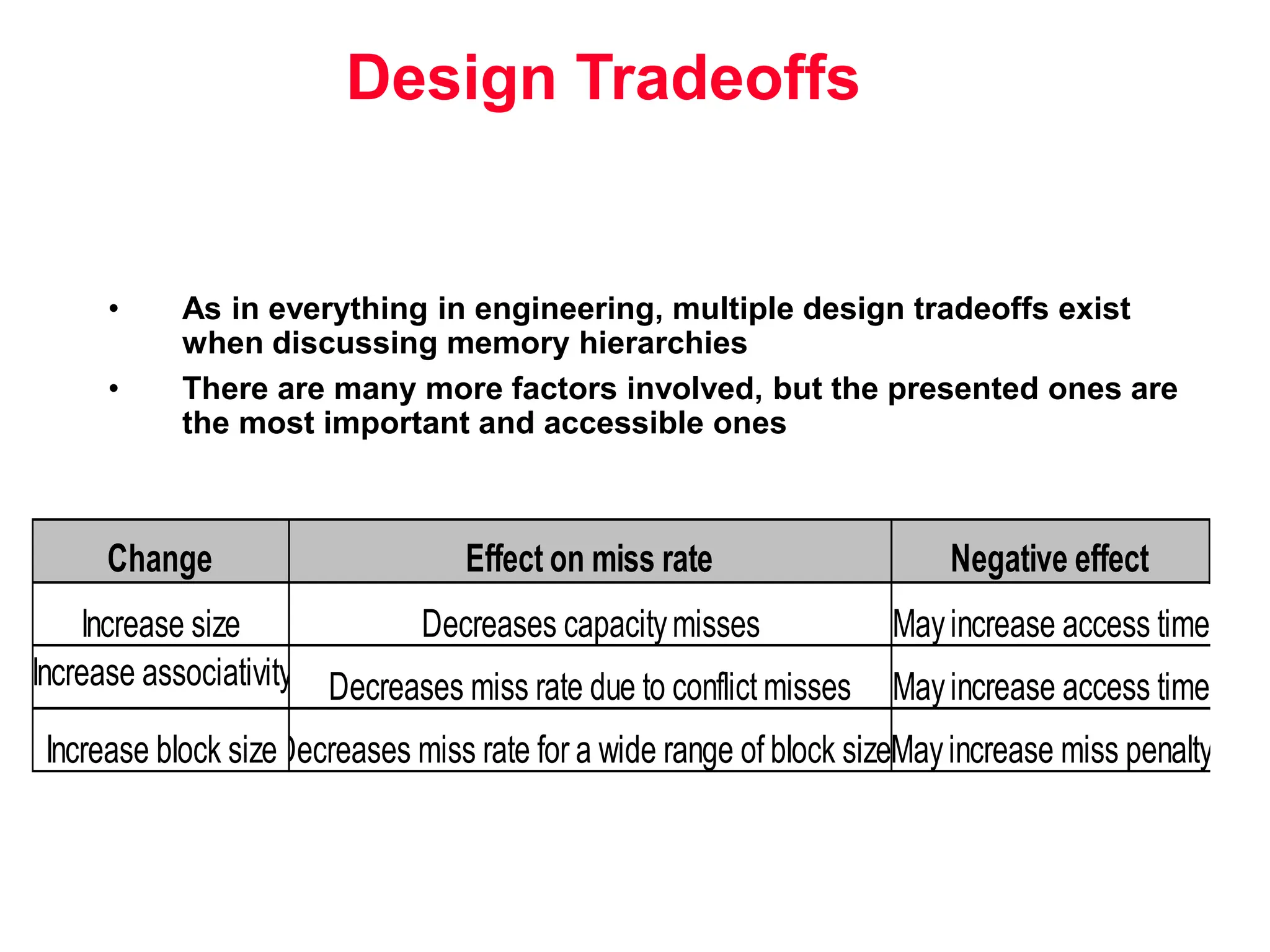
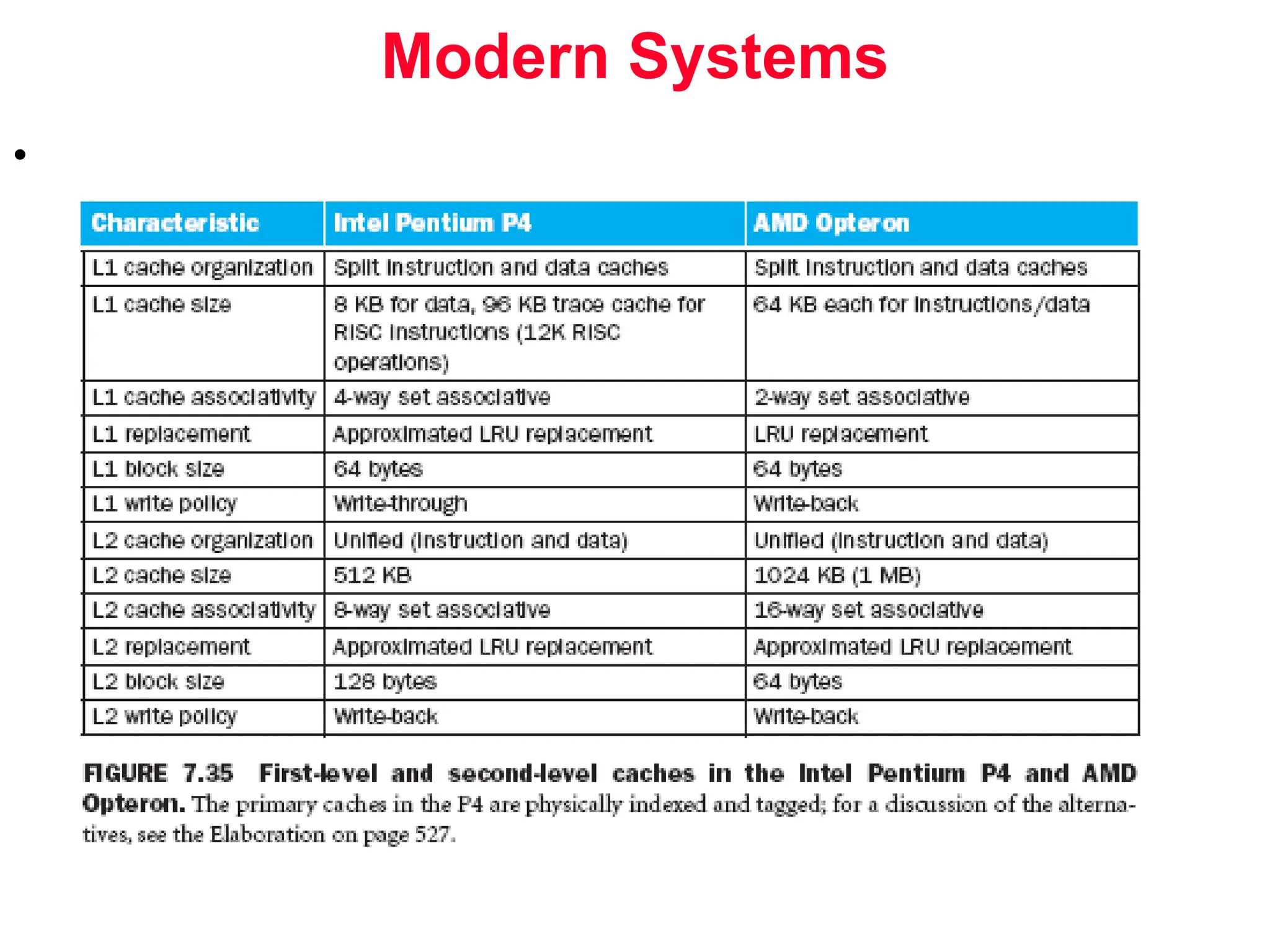
The document discusses memory hierarchy and cache design. It begins by listing sources used to create slides on this topic. It then provides definitions of key terms like cache hit, miss, hit time, and miss penalty. The document explains the principles of memory hierarchy, including exploiting locality of reference and implementing multiple memory levels with decreasing size but increasing speed. It discusses technologies like SRAM and DRAM that are commonly used for caches and main memory. The document also addresses four important questions in cache design: block placement, block identification, block replacement, and write strategy.