Matrix Factorizations at Scale: a Comparison of Scientific Data Analytics on Spark and MPI Using Three Case Studies with Michael Mahoney

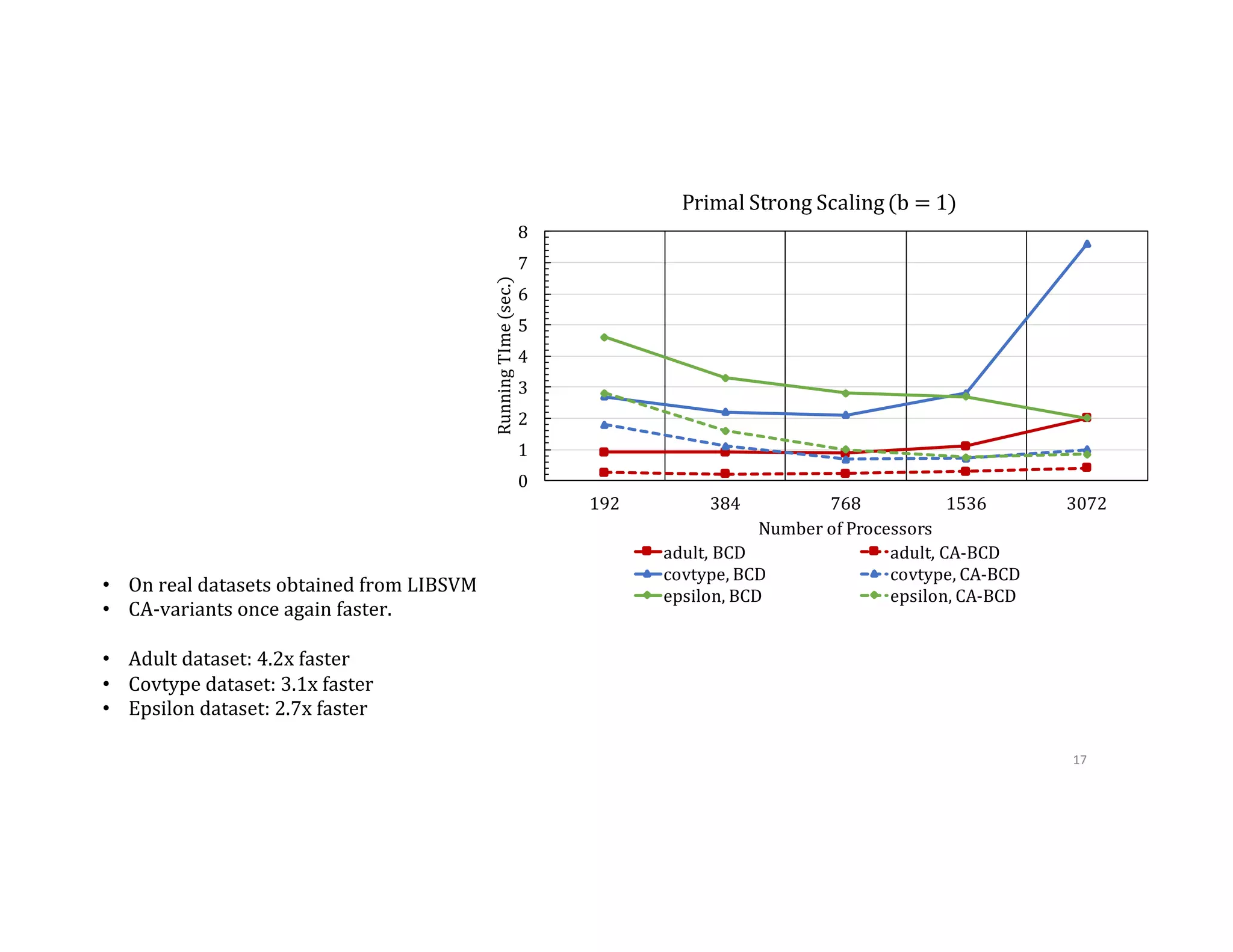
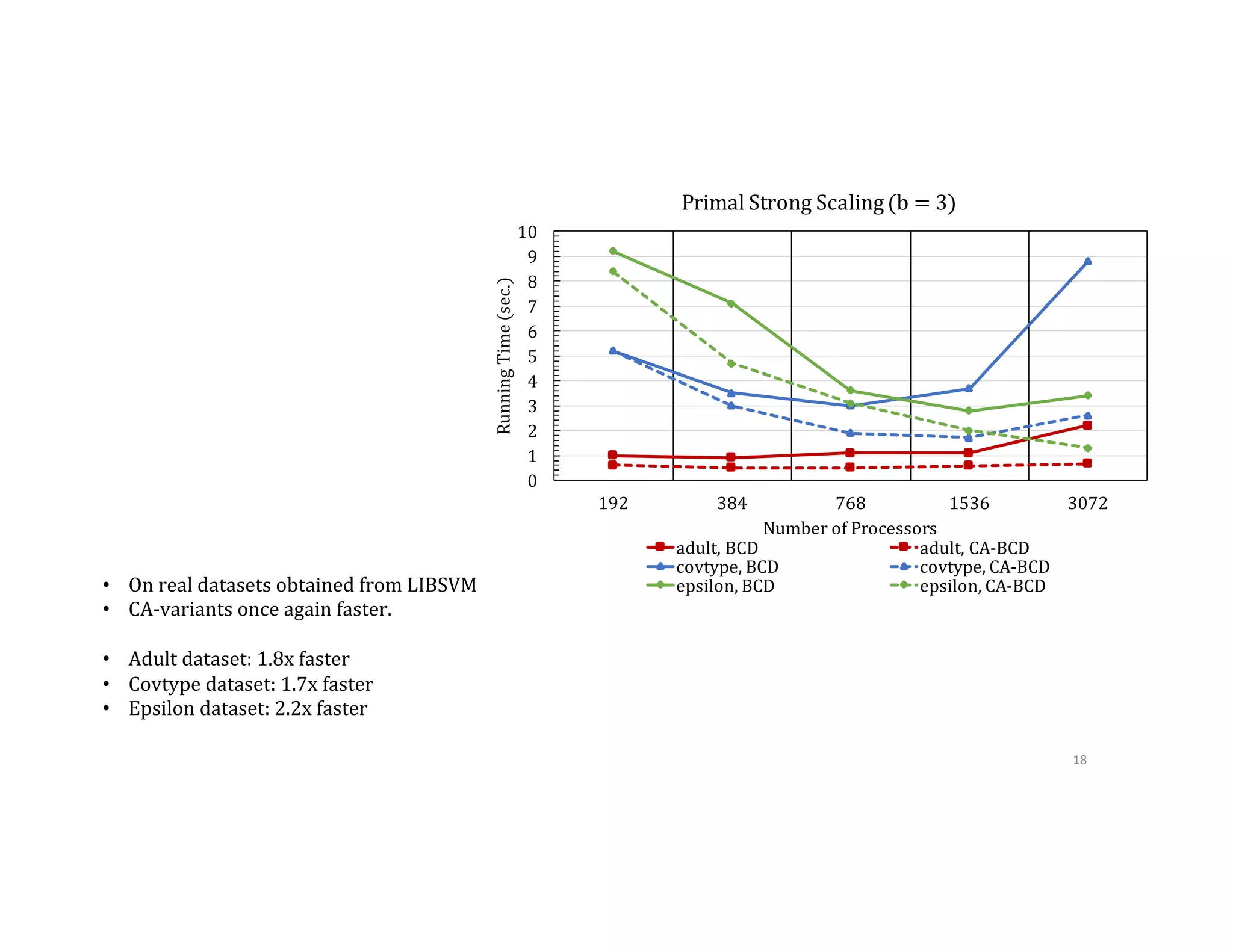
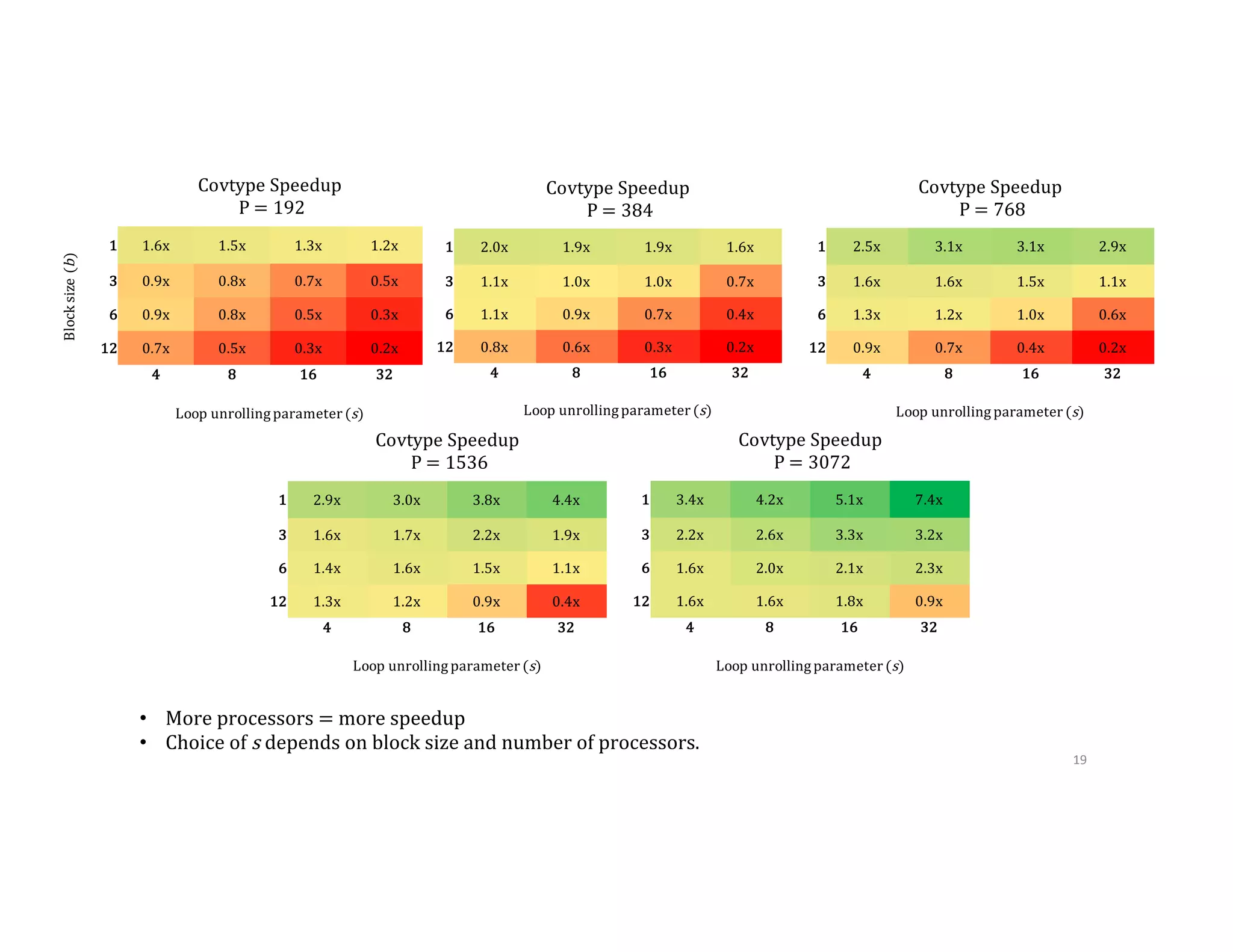
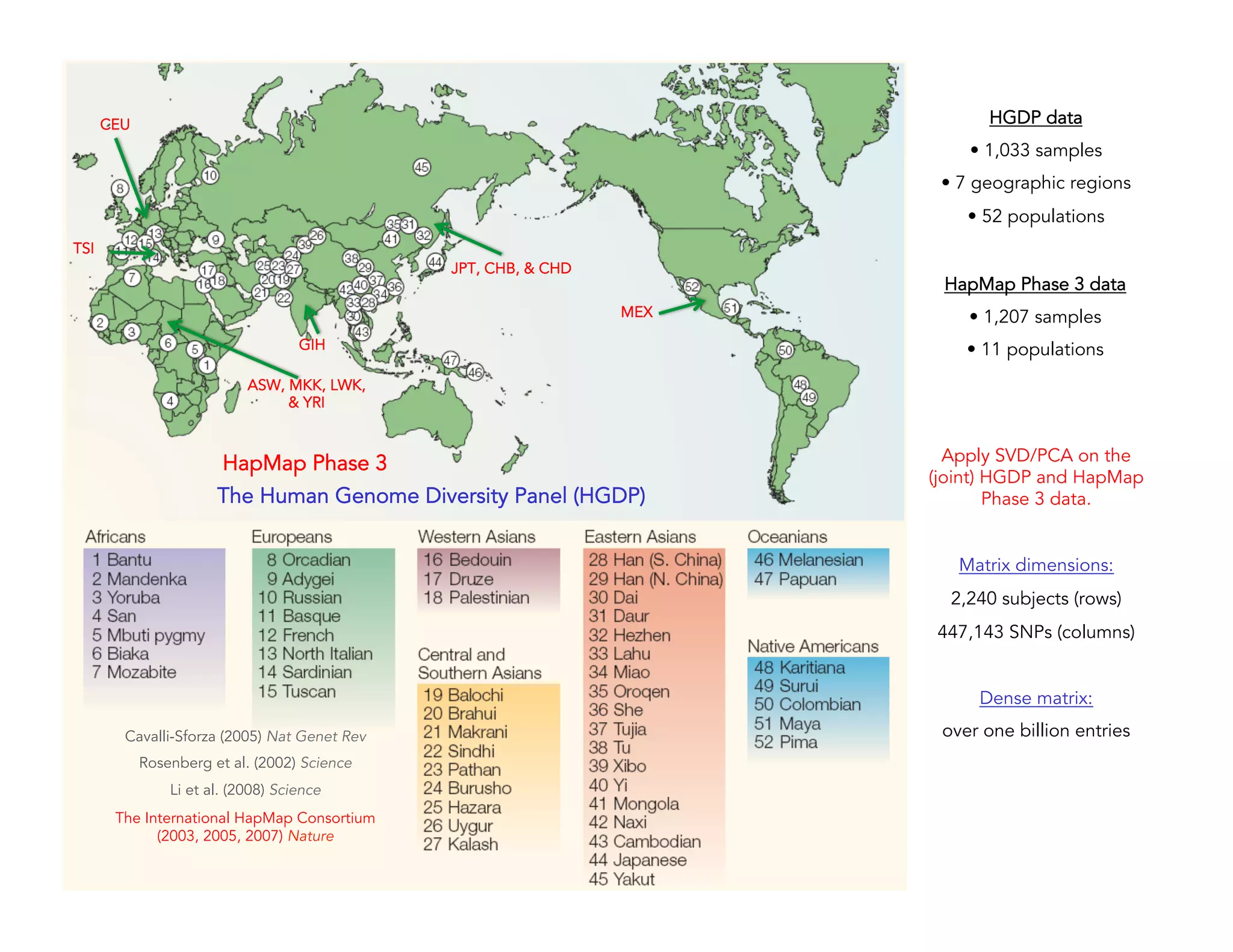
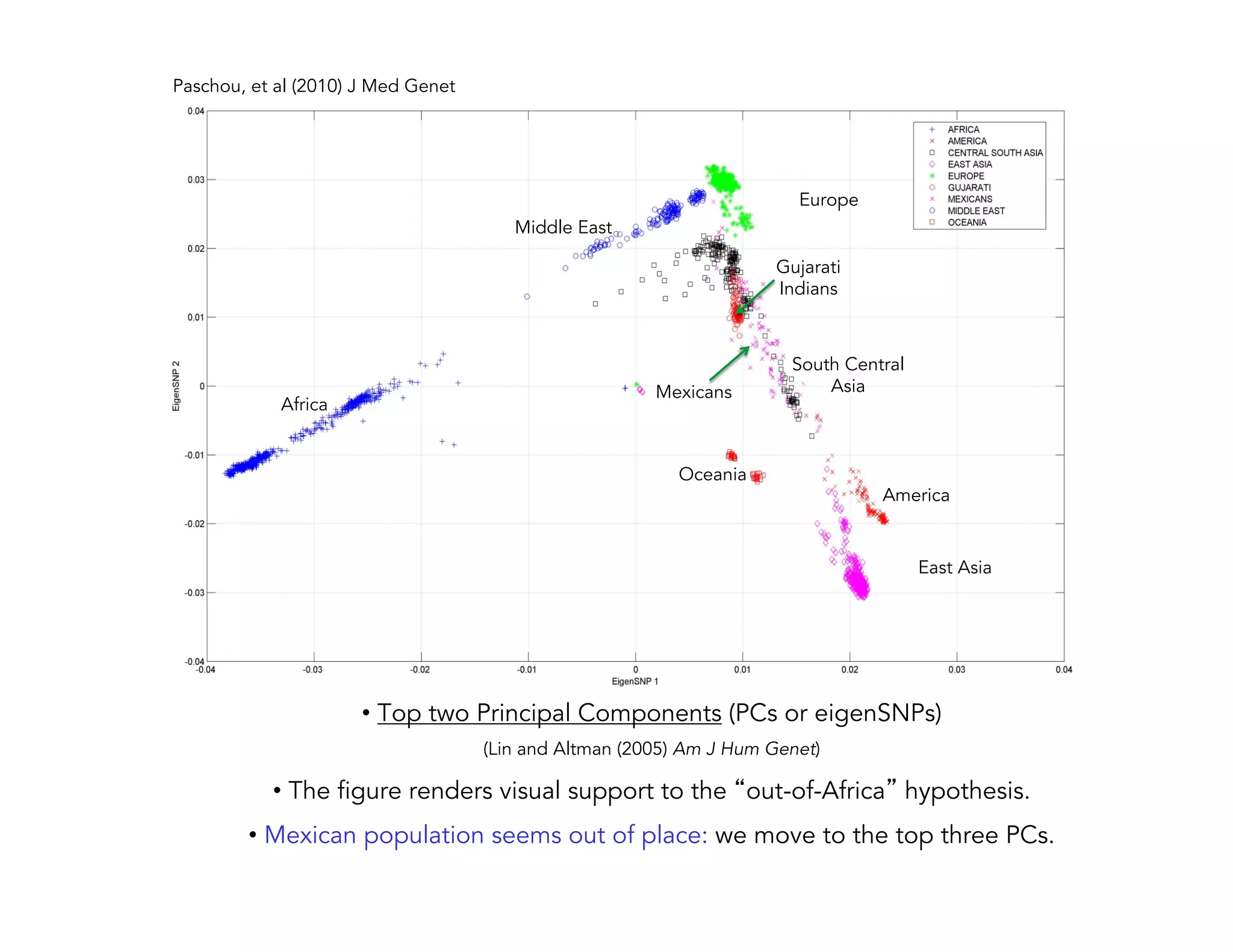
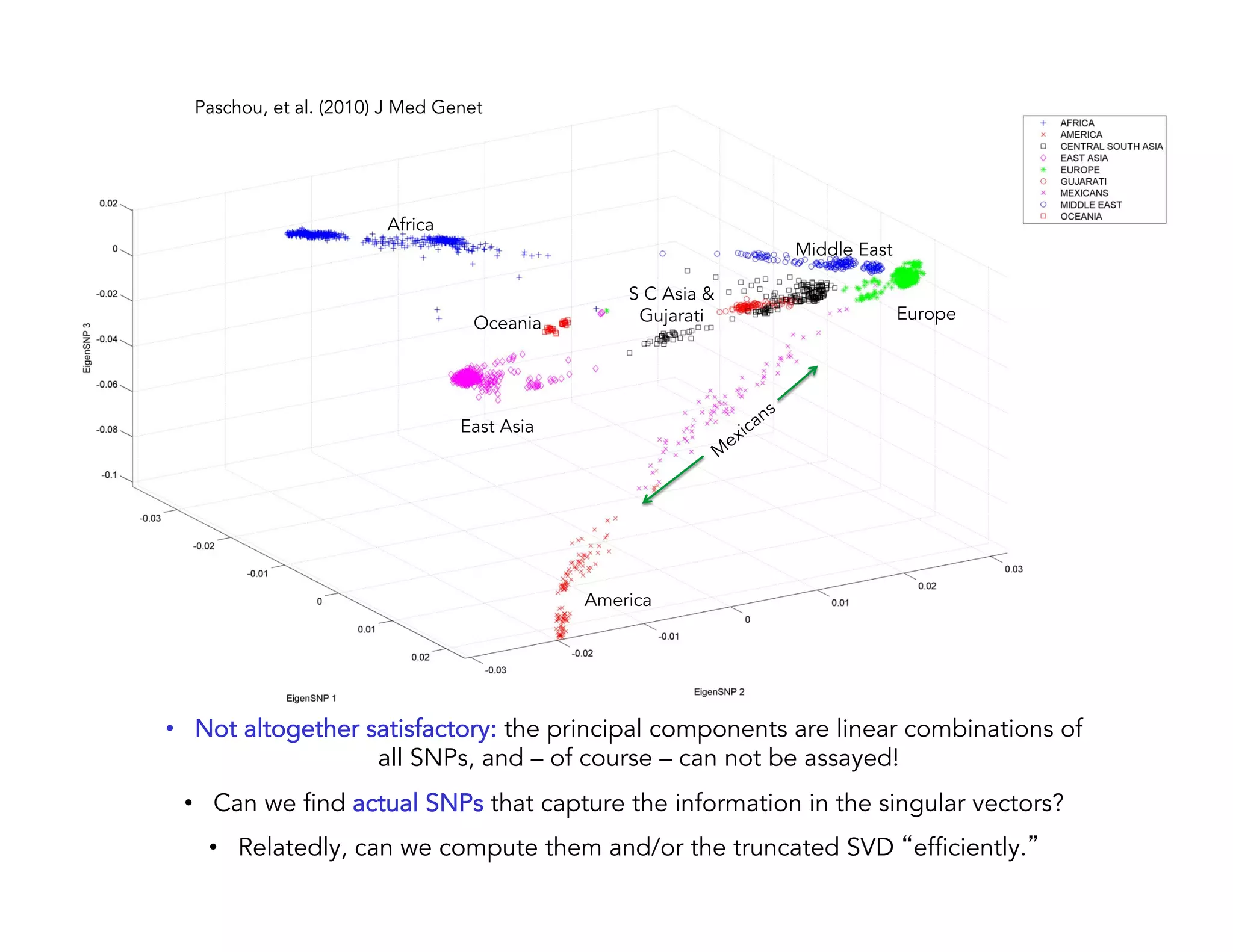
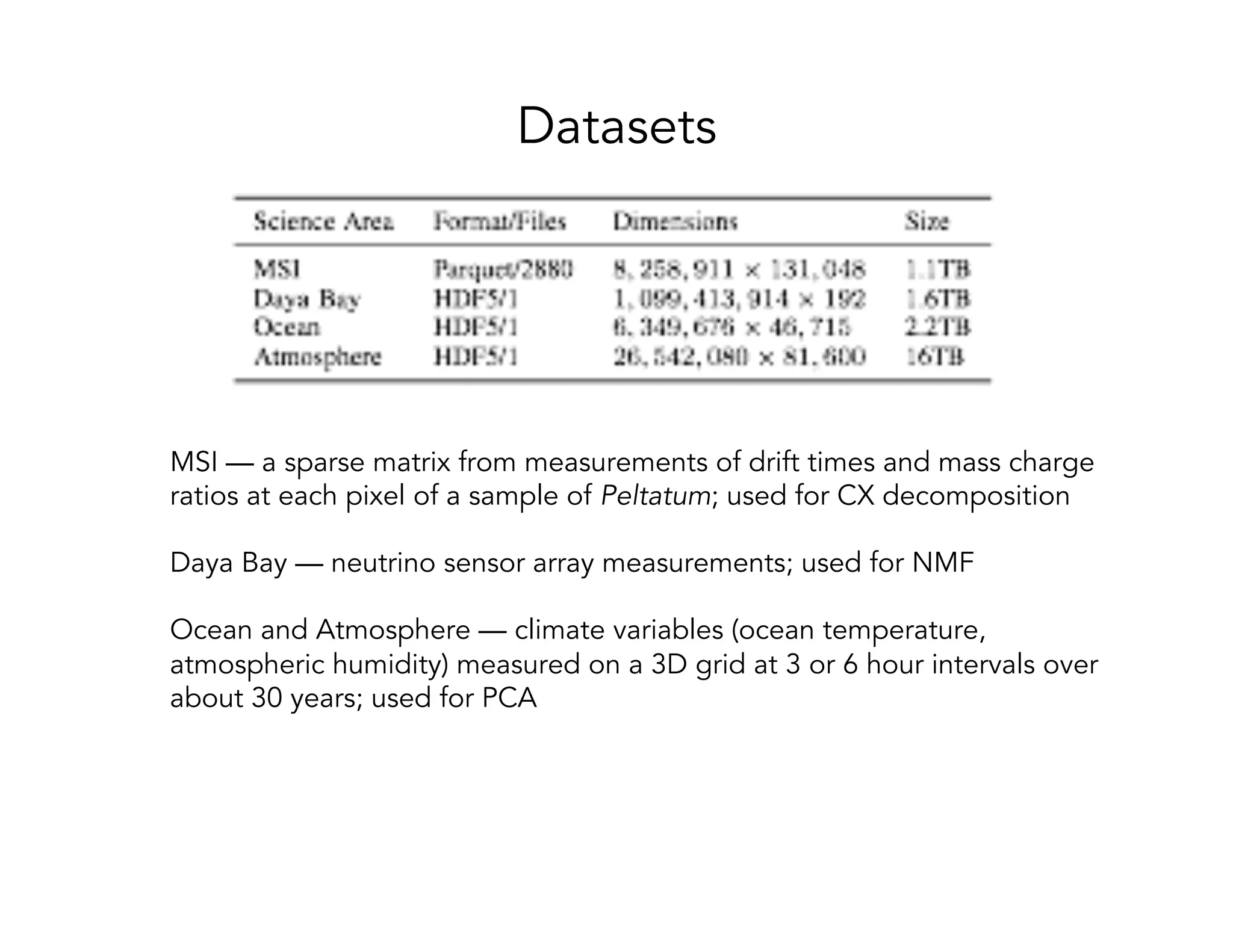
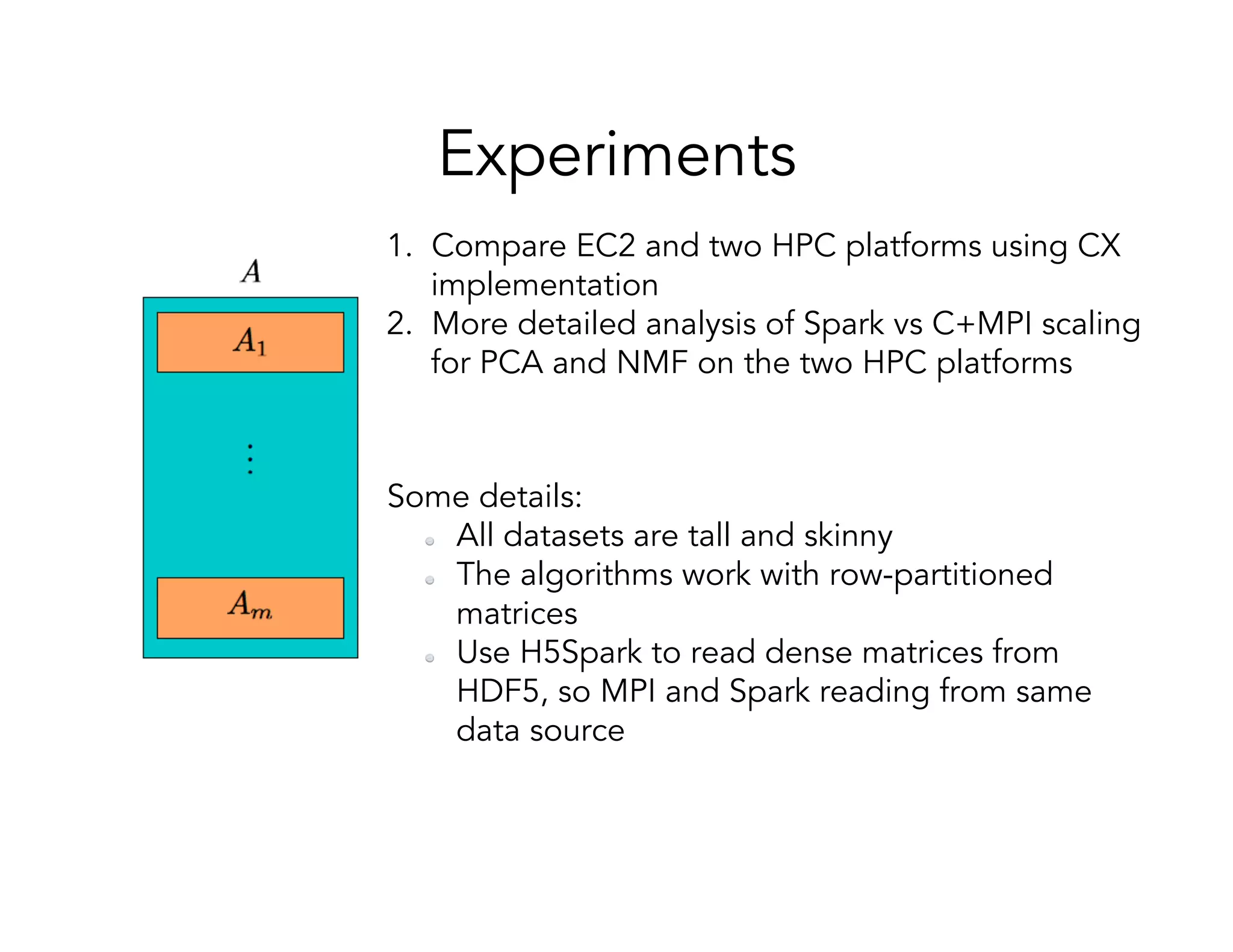
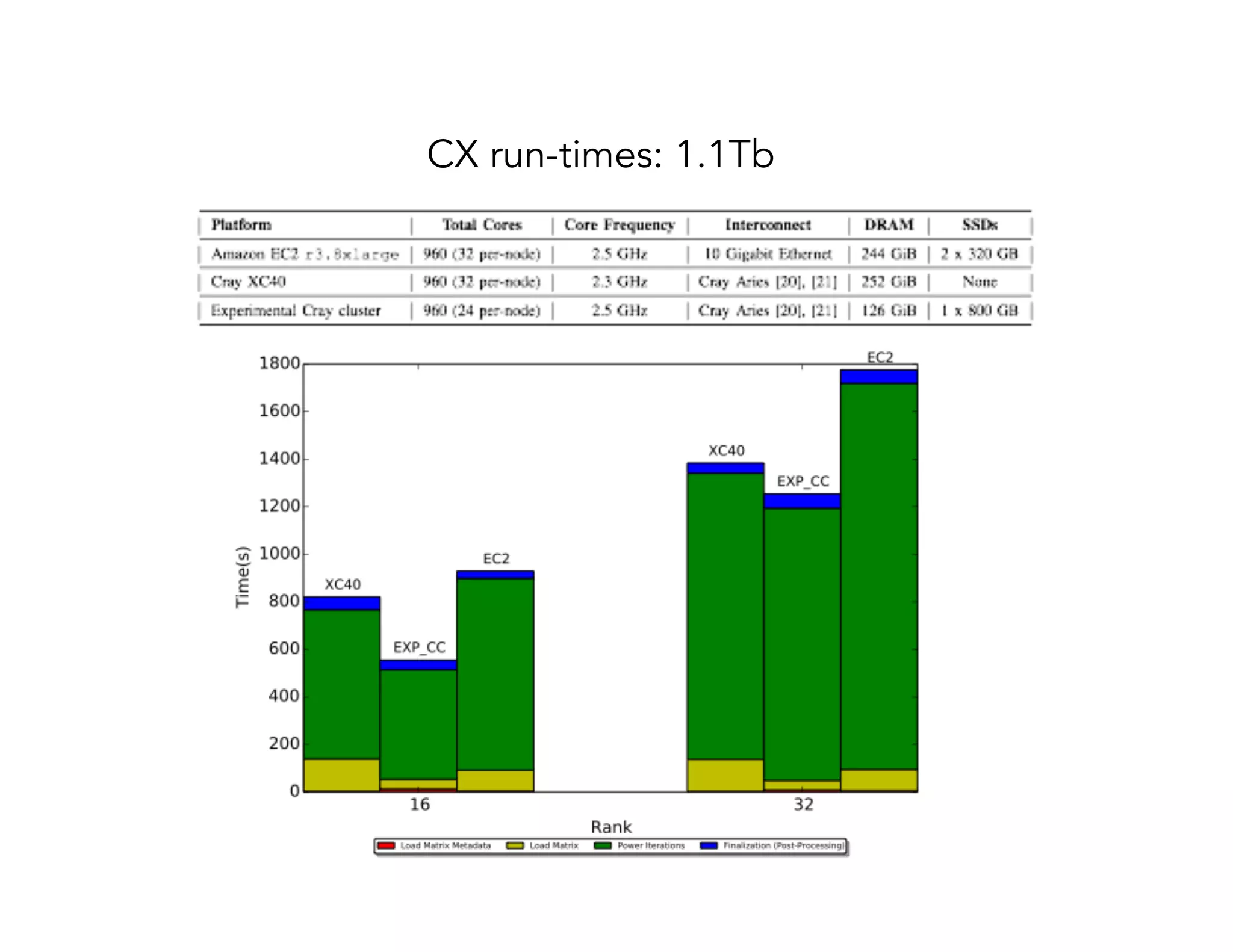
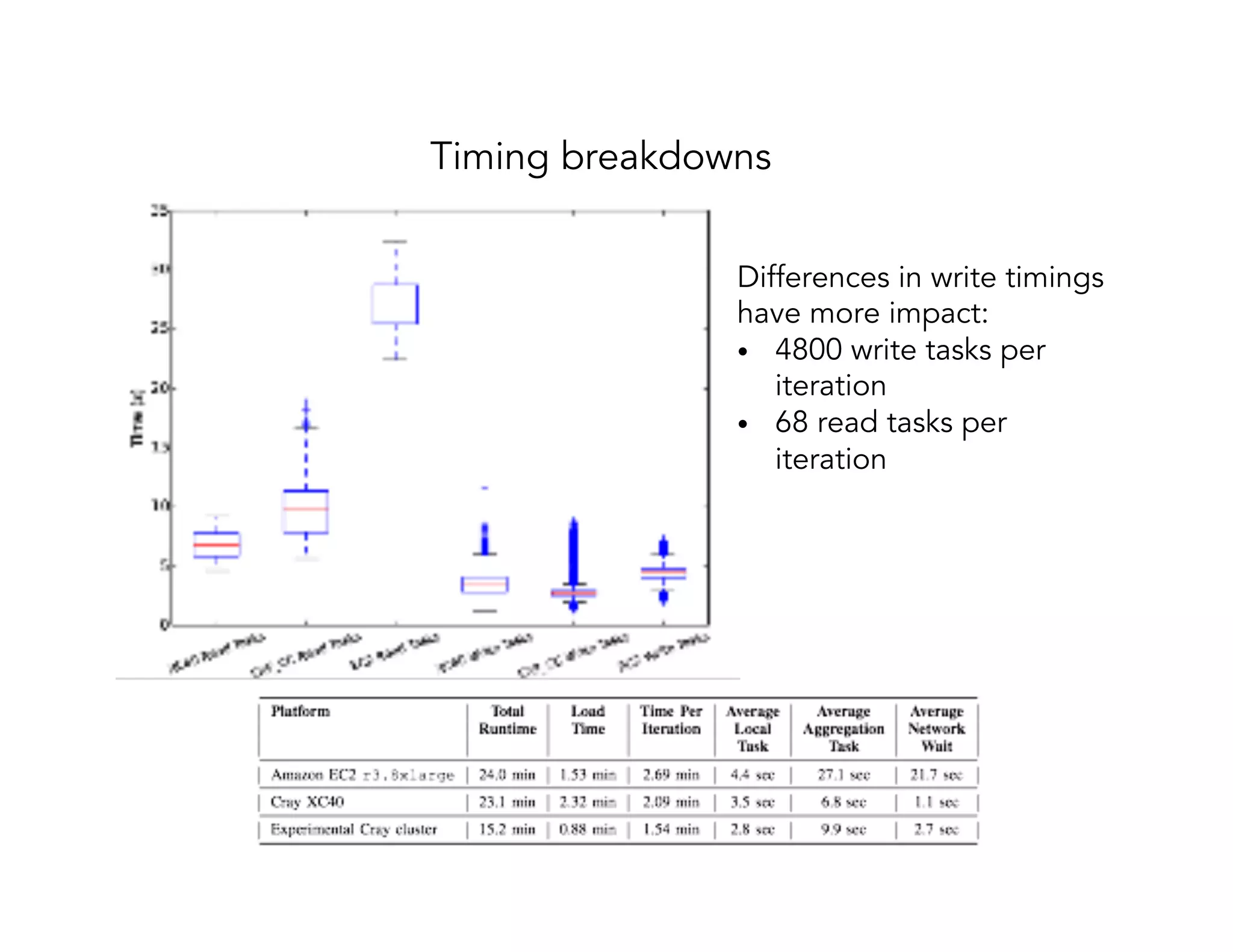
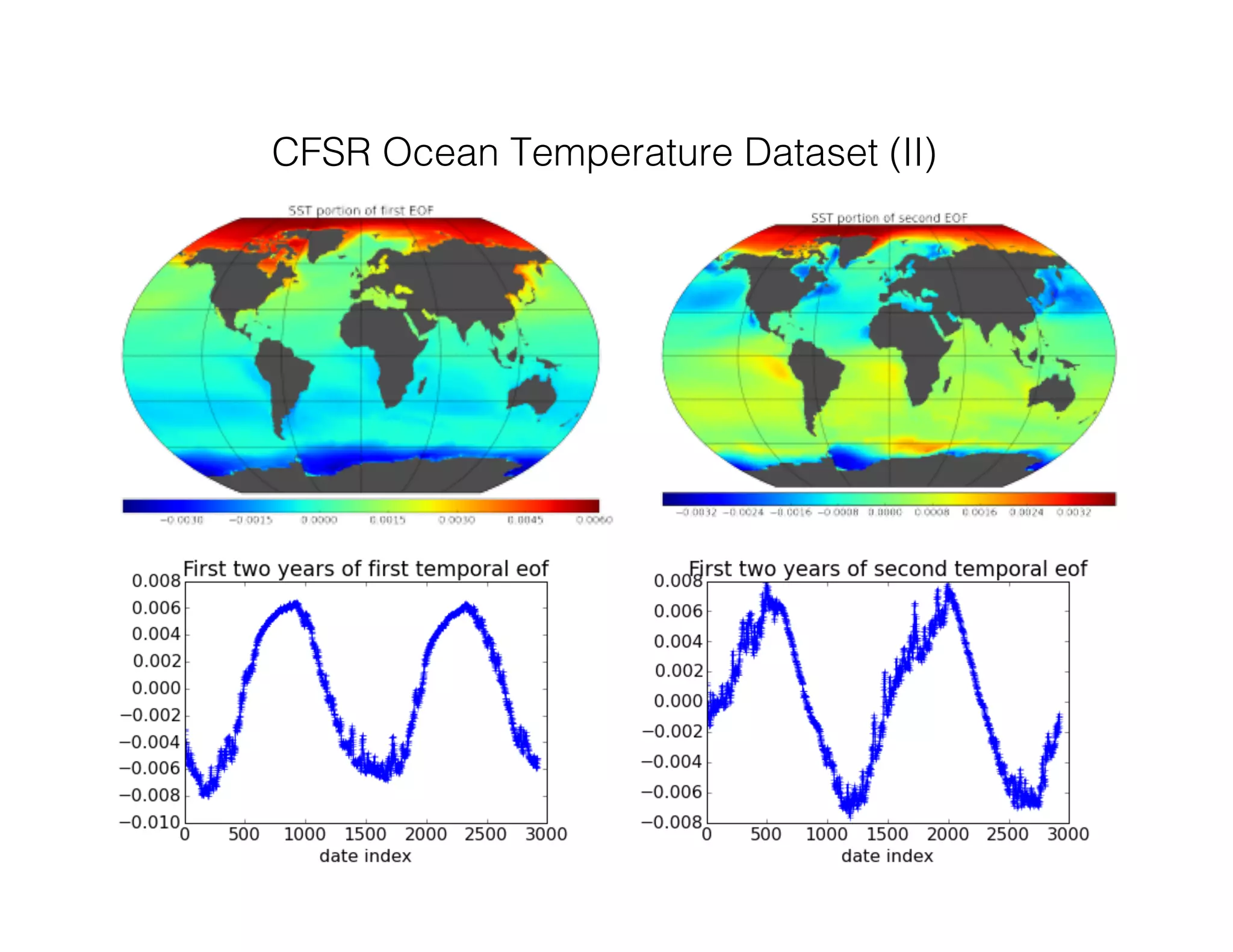
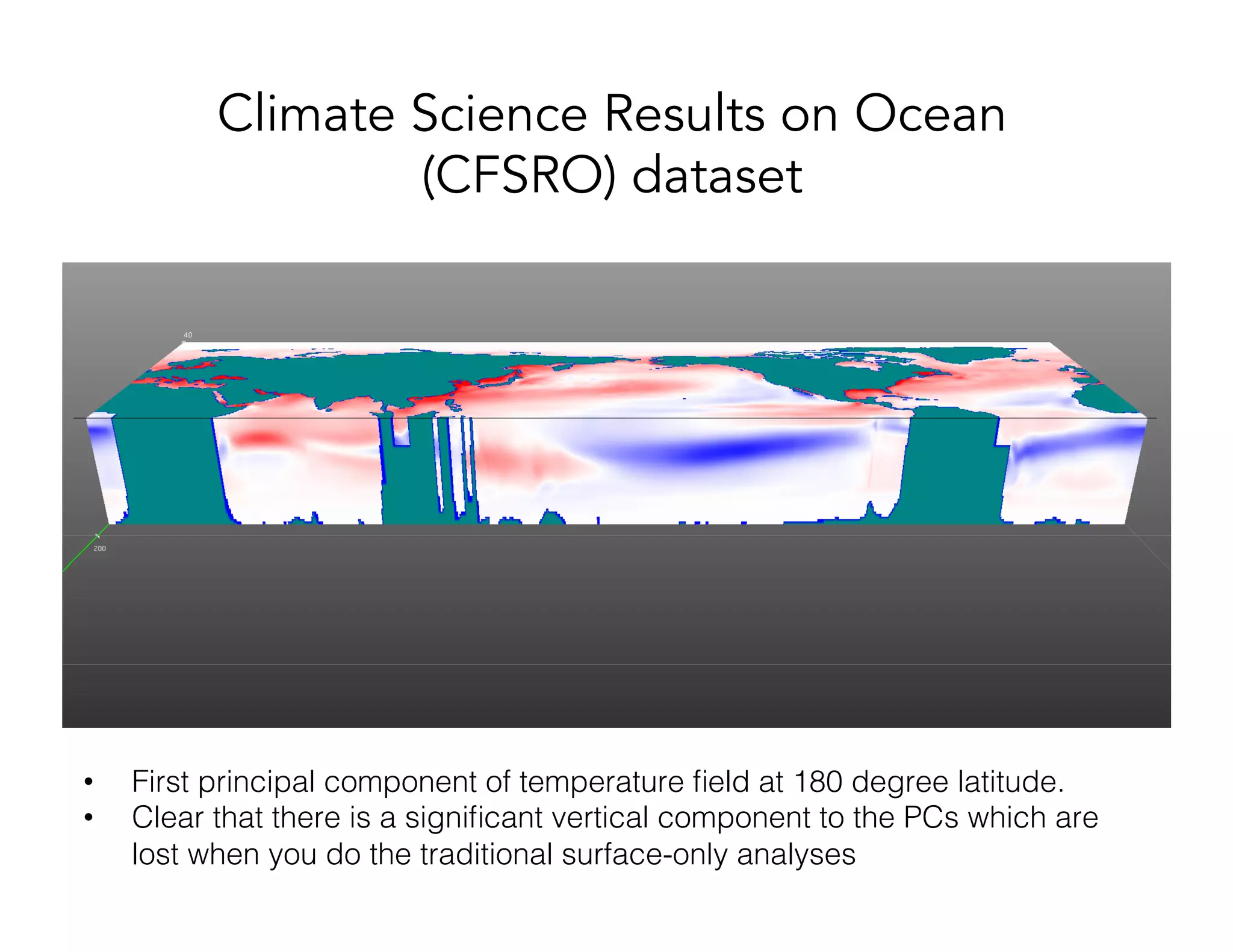
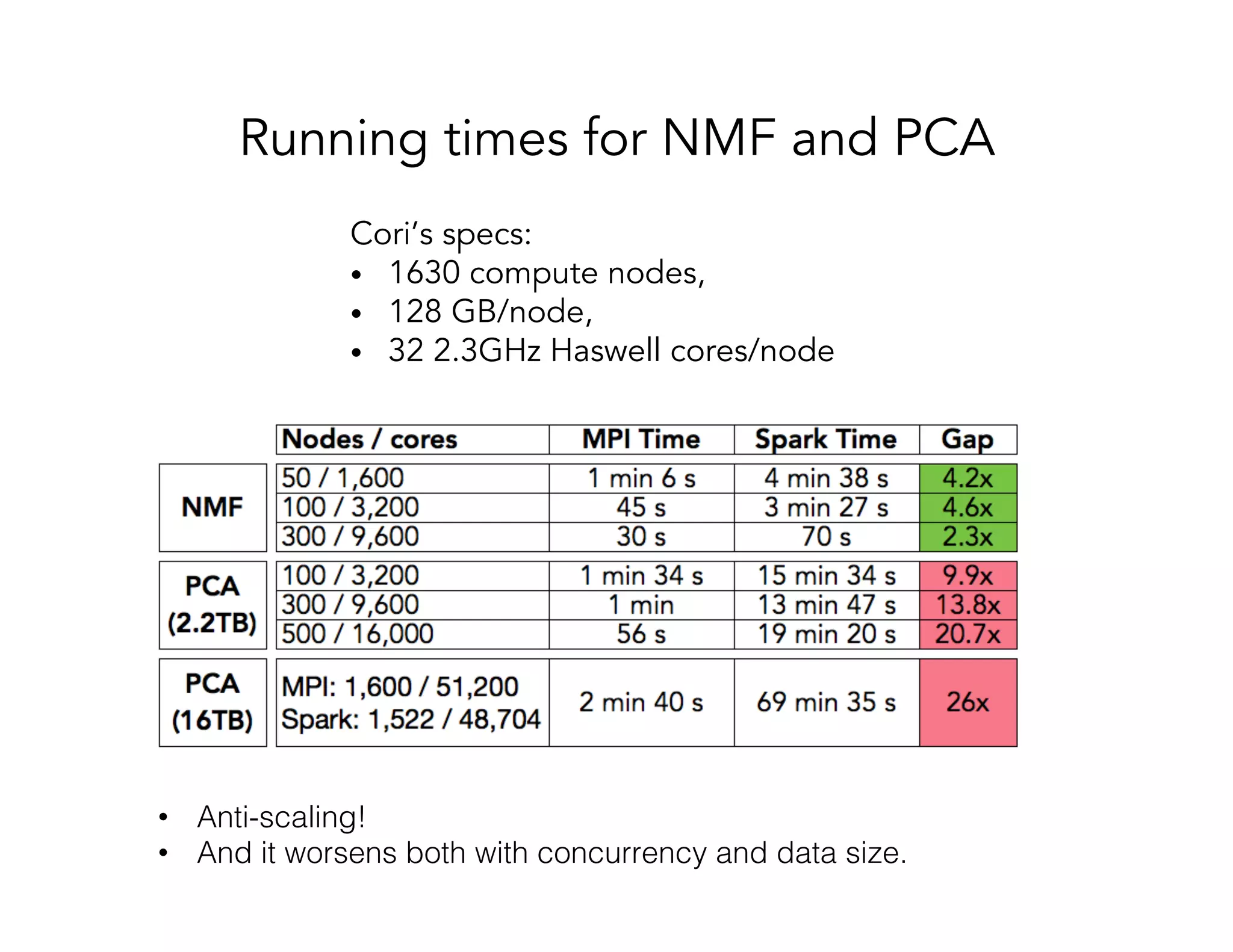
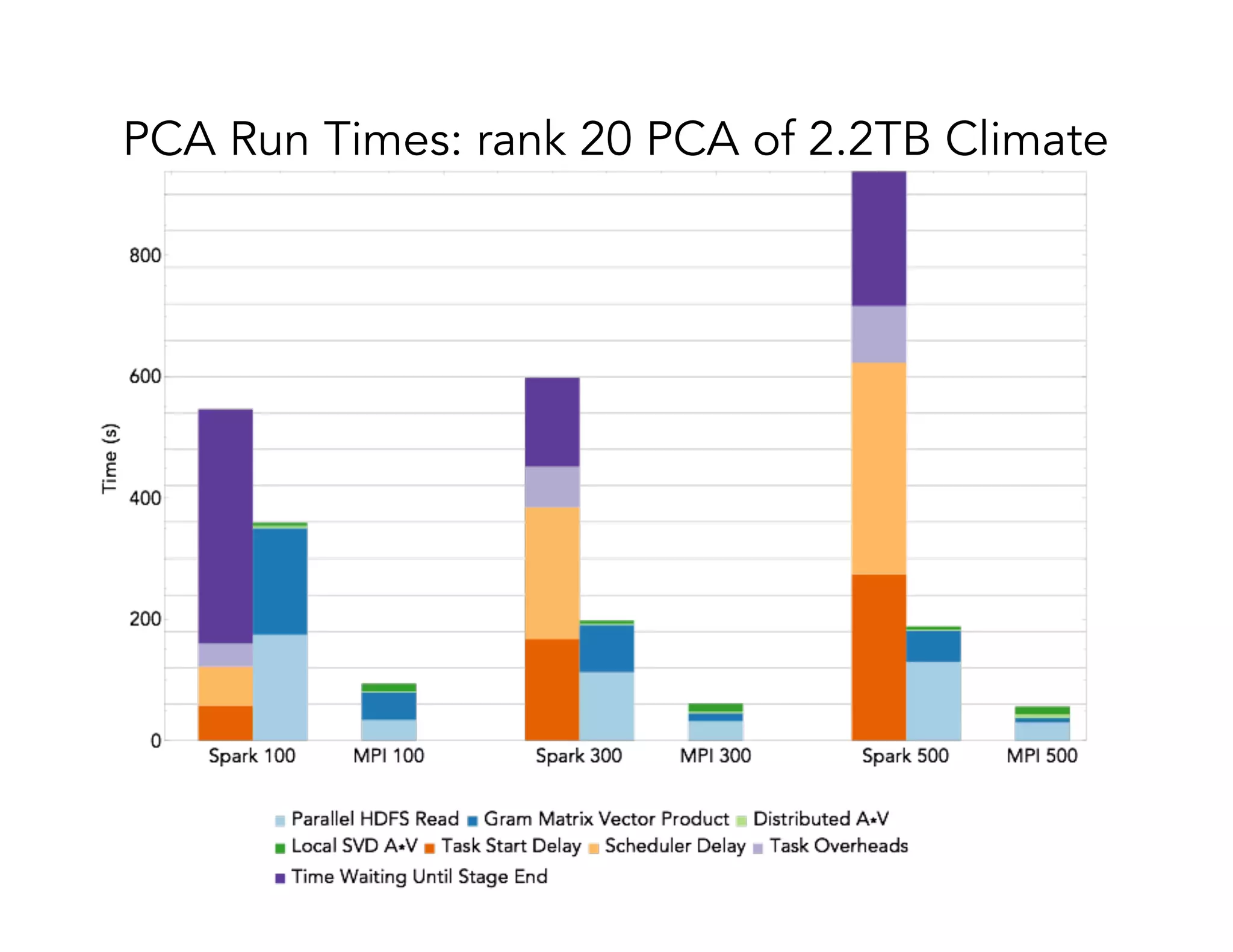
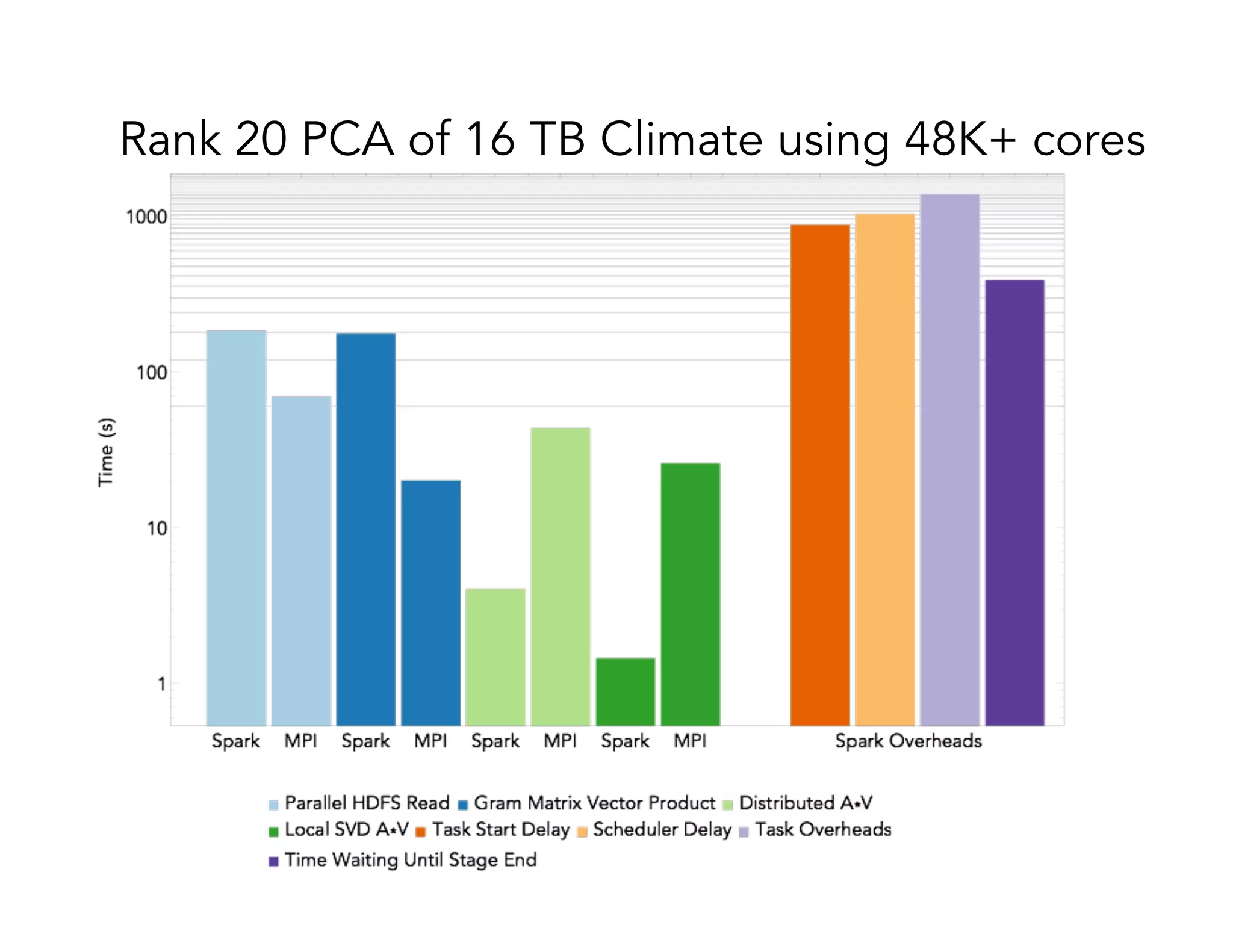
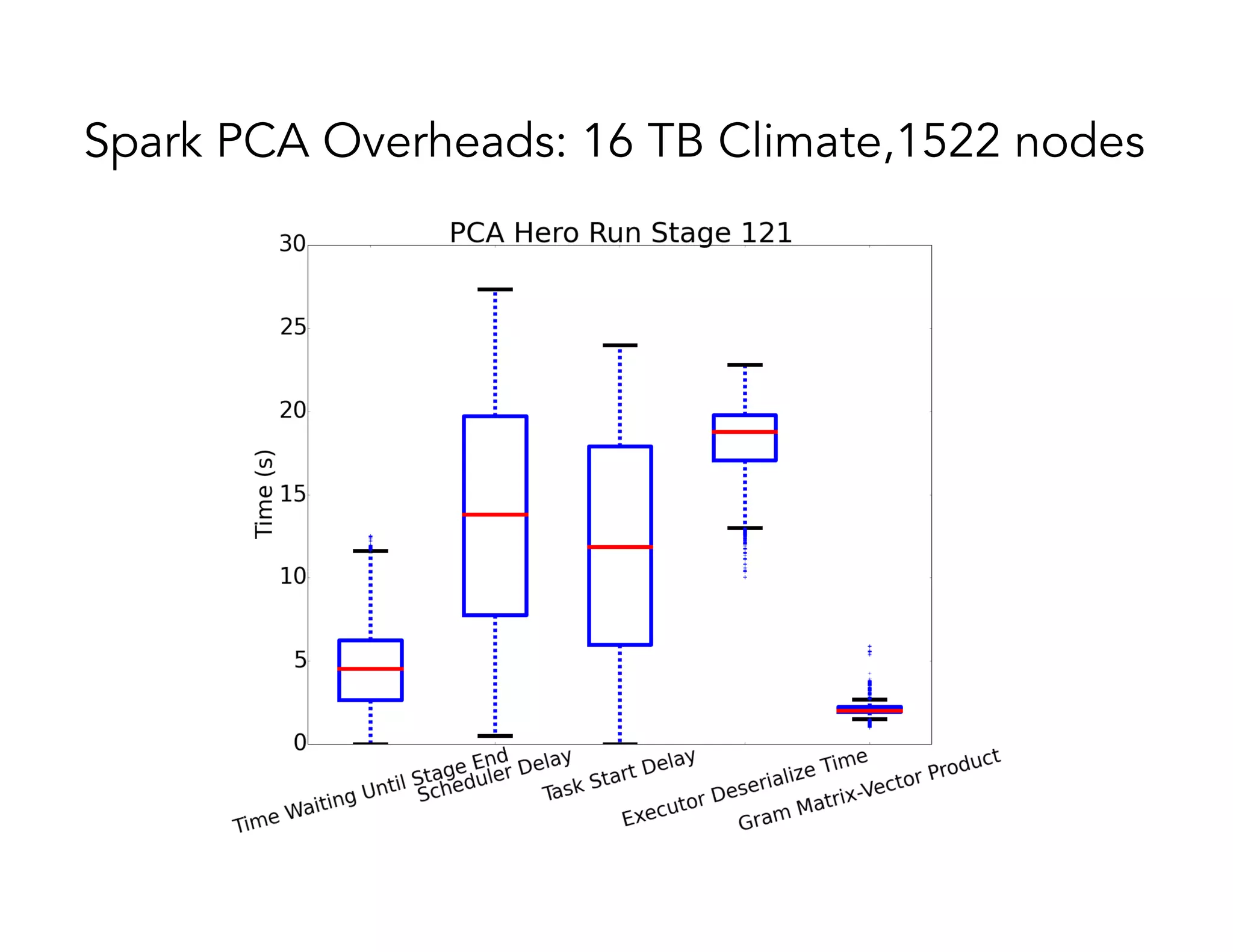
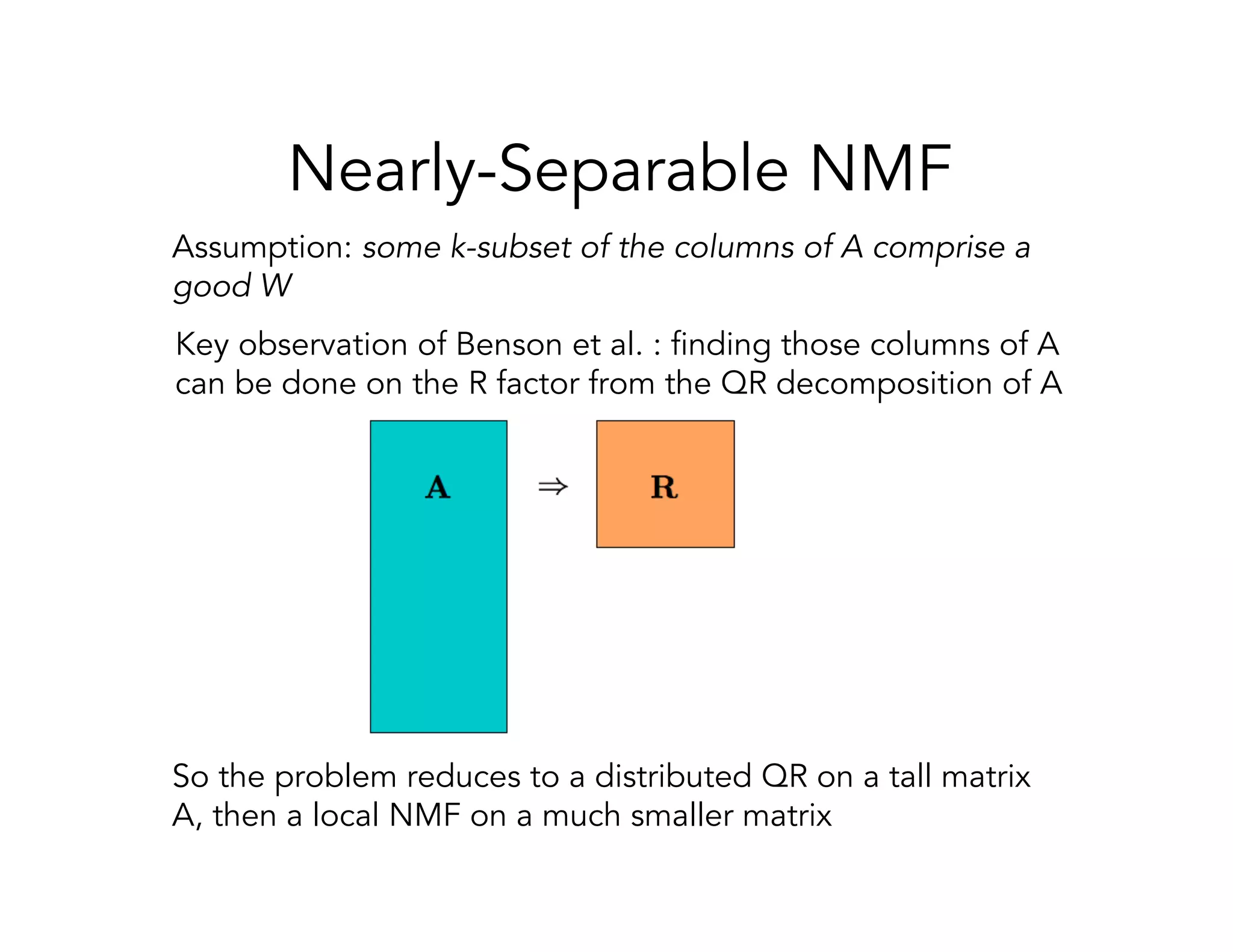
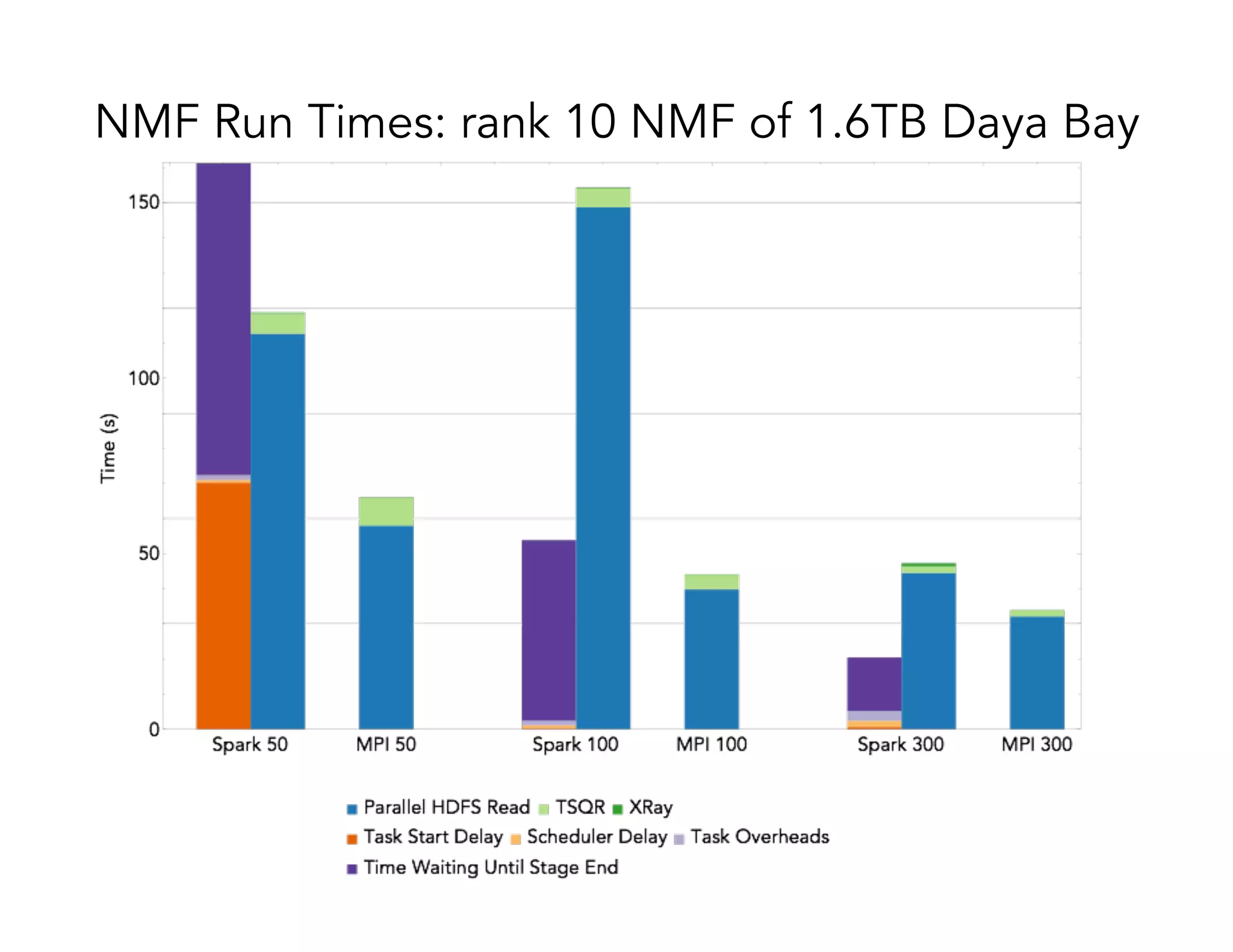
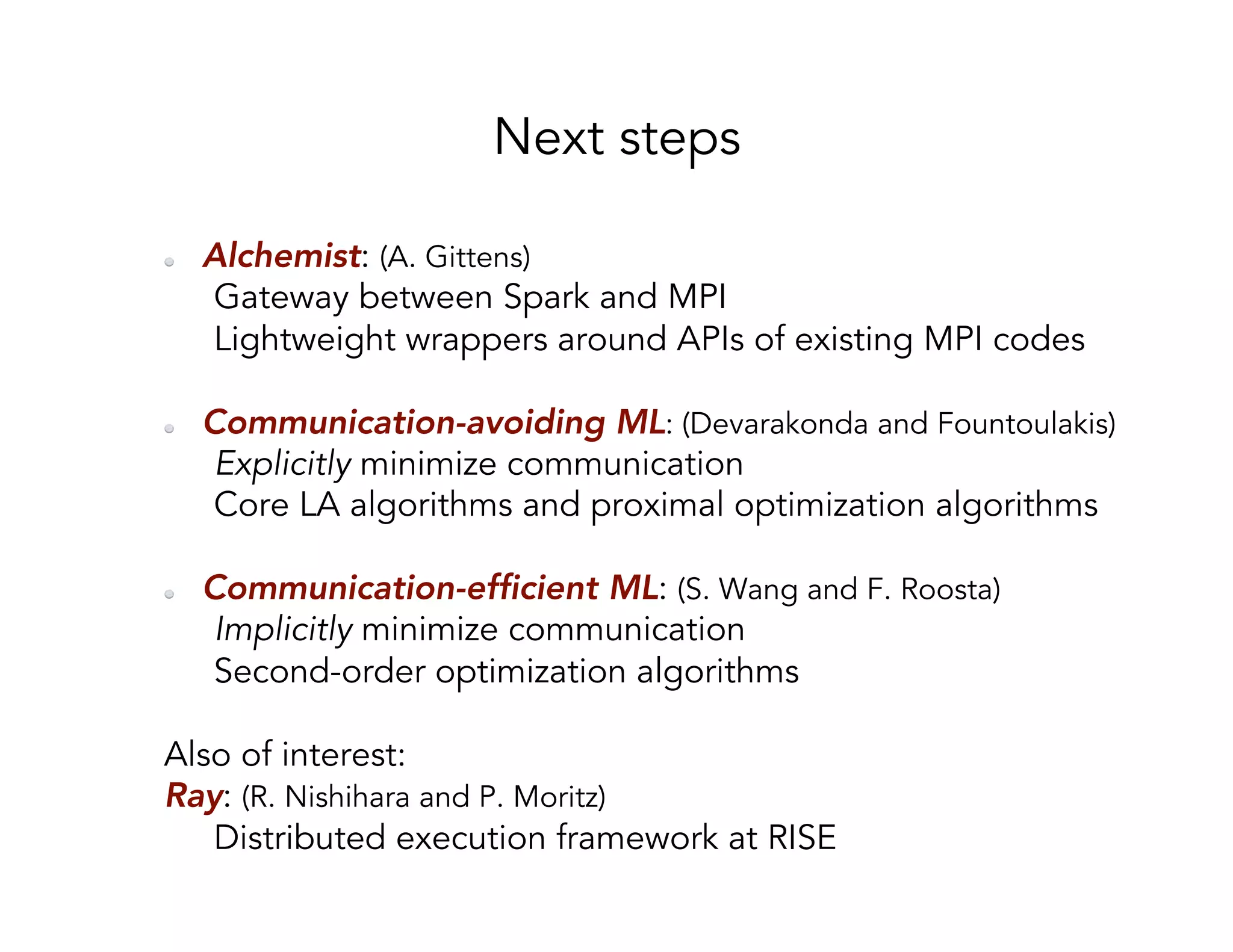
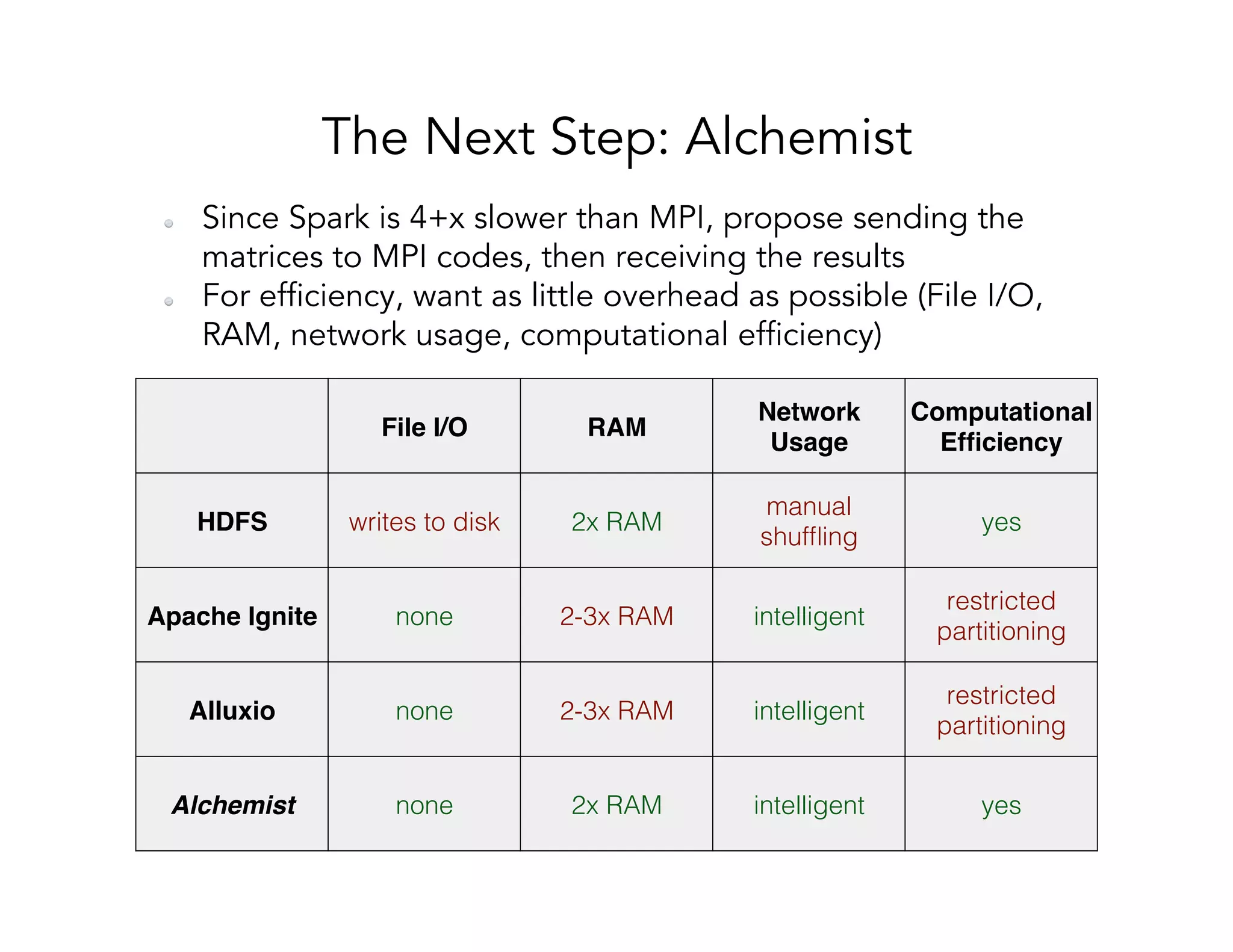
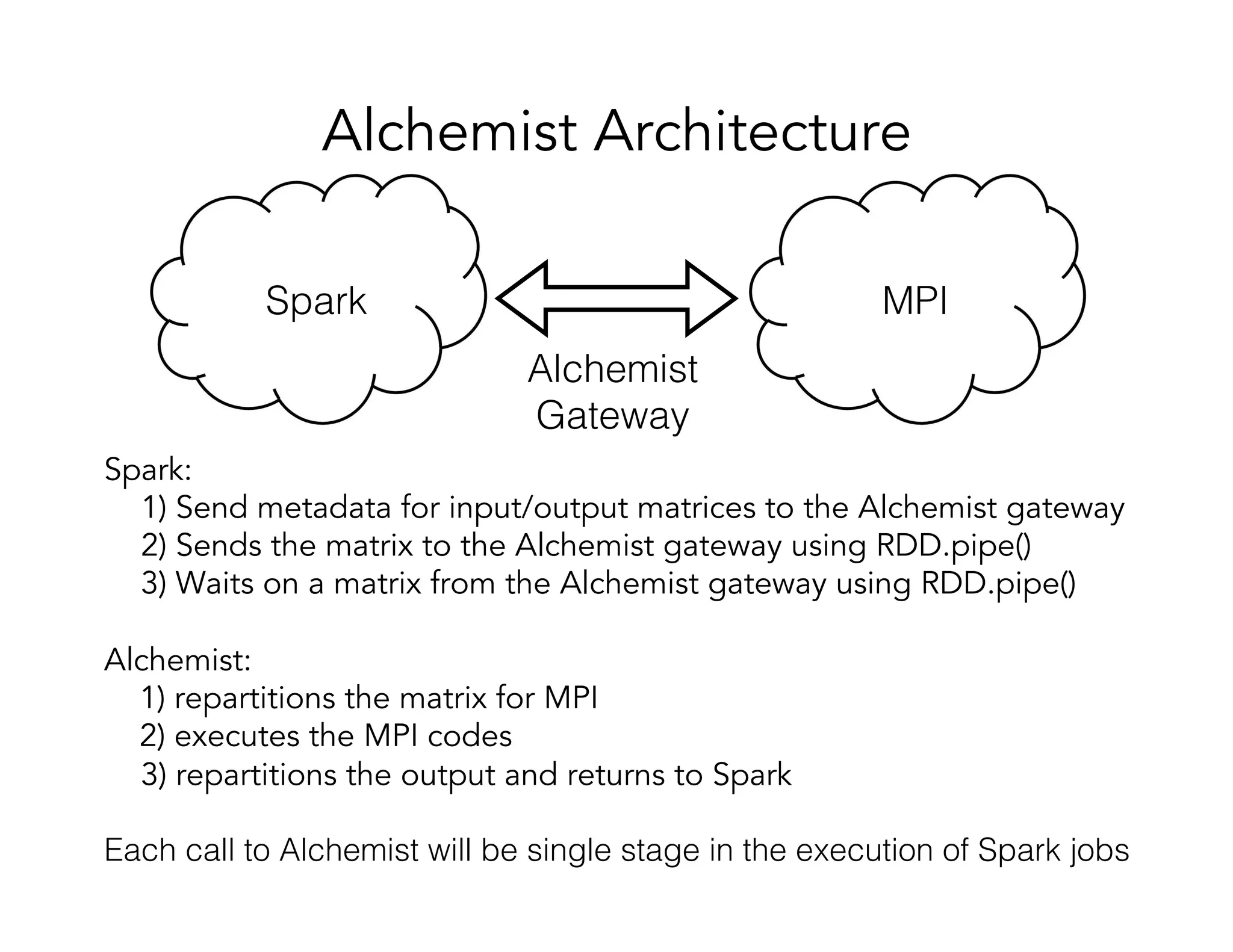
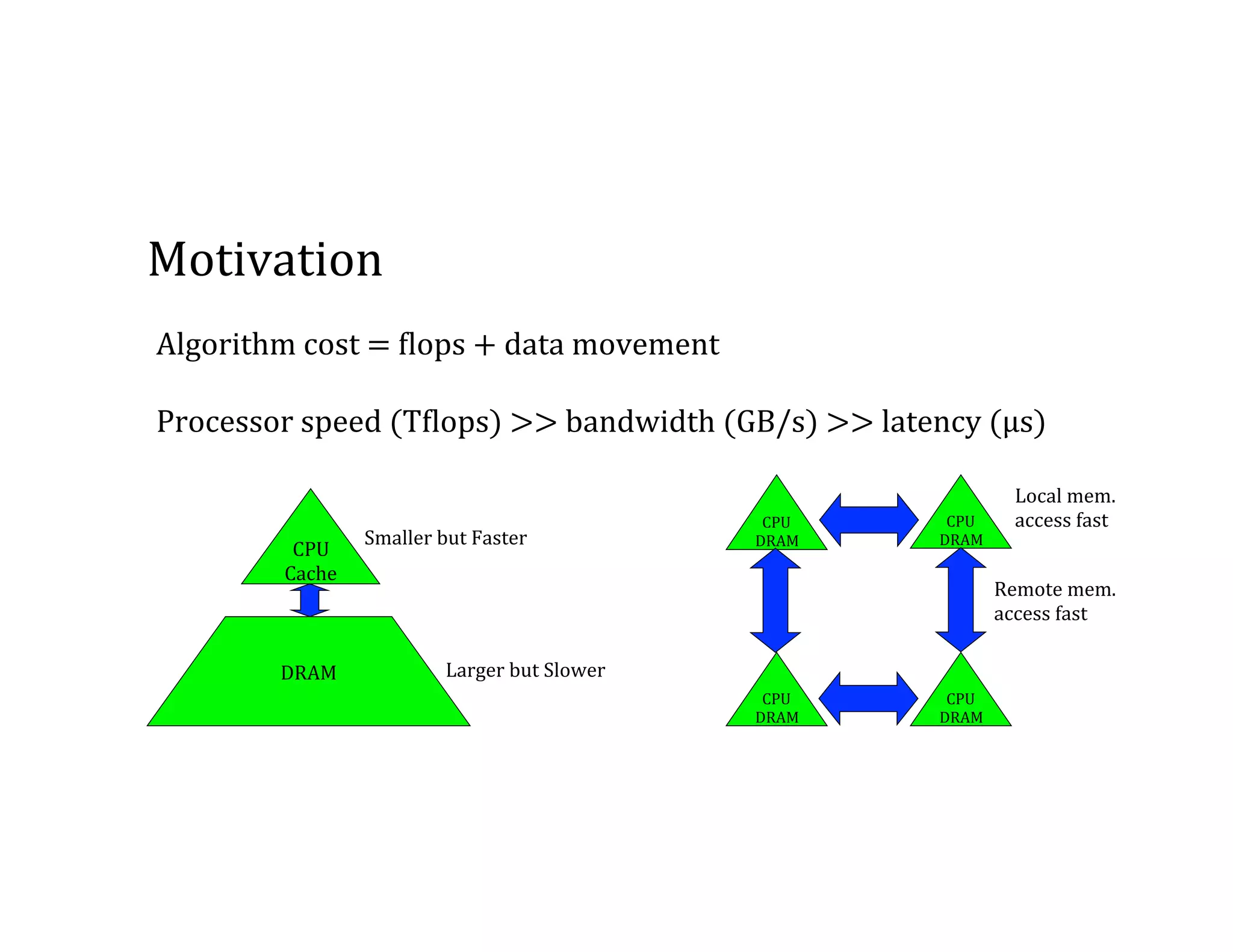
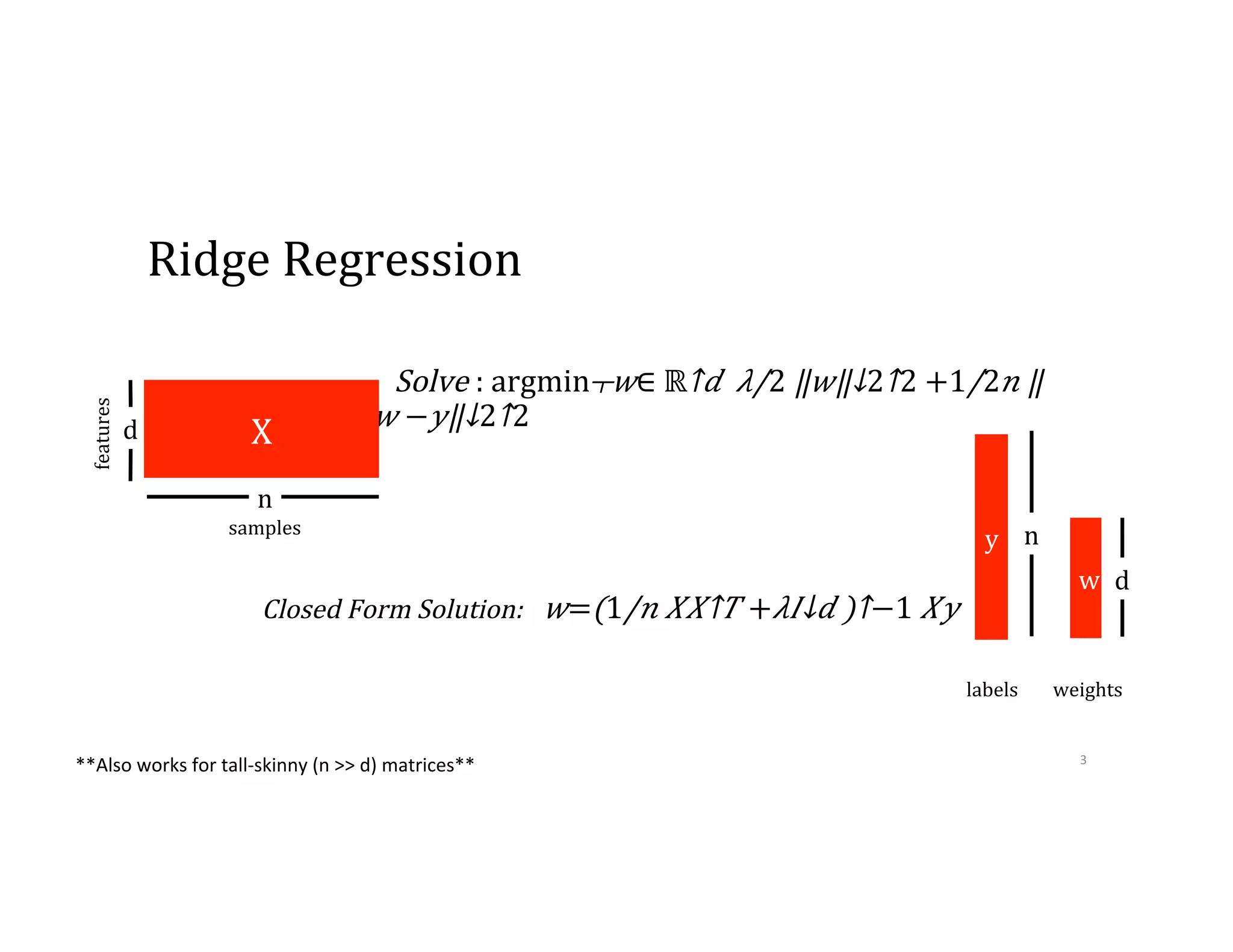
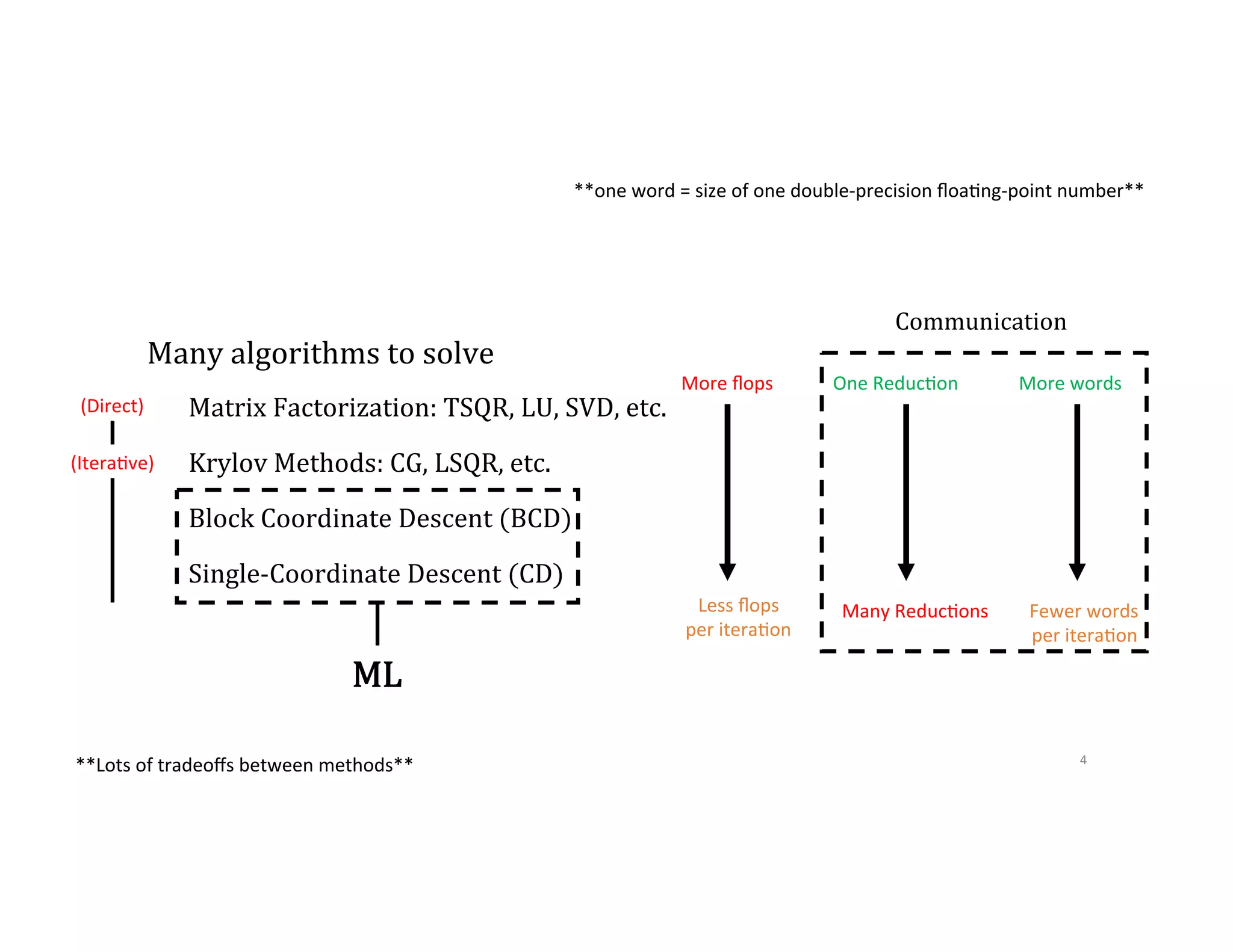
Computationally-intensive machine learning at the tera-scale Michael W. Mahoney (AMPLab, ICSI, and Department of Statistics, UC Berkeley) December 2016

Thoughts on data, large data, massive data, big data, etc. Linear Algebra in Spark for science problems •  CX and SVD/PCA implementations and performance •  Applications of the CX and PCA matrix decompositions •  To mass spec imaging, climate science, etc. •  The Next Step: Alchemist Communication-avoiding Linear Algebra for Machine Learning Overview

Algorithmic & Statistical Perspectives ... Computer Scientists • Data: are a record of everything that happened. • Goal: process the data to find interesting patterns and associations. • Methodology: Develop approximation algorithms under different models of data access since the goal is typically computationally hard. Statisticians (and Natural Scientists, etc) • Data: are a particular random instantiation of an underlying process describing unobserved patterns in the world. • Goal: is to extract information about the world from noisy data. • Methodology: Make inferences (perhaps about unseen events) by positing a model that describes the random variability of the data around the deterministic model. Lambert (2000), Mahoney (2010)

... are VERY different paradigms Statistics, natural sciences, scientific computing, etc: • Problems often involve computation, but the study of computation per se is secondary • Only makes sense to develop algorithms for well-posed* problems • First, write down a model, and think about computation later Computer science: • Easier to study computation per se in discrete settings, e.g., Turing machines, logic, complexity classes • Theory of algorithms divorces computation from data • First, run a fast algorithm, and ask what it means later *Solution exists, is unique, and varies continuously with input data

E.g., application in: Human Genetics Scientific data and choosing good columns as features Single Nucleotide Polymorphisms: the most common type of genetic variation in the genome across different individuals. They are known locations at the human genome where two alternate nucleotide bases (alleles) are observed (out of A, C, G, T). SNPs individuals … AG CT GT GG CT CC CC CC CC AG AG AG AG AG AA CT AA GG GG CC GG AG CG AC CC AA CC AA GG TT AG CT CG CG CG AT CT CT AG CT AG GG GT GA AG …! … GG TT TT GG TT CC CC CC CC GG AA AG AG AG AA CT AA GG GG CC GG AA GG AA CC AA CC AA GG TT AA TT GG GG GG TT TT CC GG TT GG GG TT GG AA …! … GG TT TT GG TT CC CC CC CC GG AA AG AG AA AG CT AA GG GG CC AG AG CG AC CC AA CC AA GG TT AG CT CG CG CG AT CT CT AG CT AG GG GT GA AG …! … GG TT TT GG TT CC CC CC CC GG AA AG AG AG AA CC GG AA CC CC AG GG CC AC CC AA CG AA GG TT AG CT CG CG CG AT CT CT AG CT AG GT GT GA AG …! … GG TT TT GG TT CC CC CC CC GG AA GG GG GG AA CT AA GG GG CT GG AA CC AC CG AA CC AA GG TT GG CC CG CG CG AT CT CT AG CT AG GG TT GG AA …! … GG TT TT GG TT CC CC CG CC AG AG AG AG AG AA CT AA GG GG CT GG AG CC CC CG AA CC AA GT TT AG CT CG CG CG AT CT CT AG CT AG GG TT GG AA …! … GG TT TT GG TT CC CC CC CC GG AA AG AG AG AA TT AA GG GG CC AG AG CG AA CC AA CG AA GG TT AA TT GG GG GG TT TT CC GG TT GG GT TT GG AA …! Matrices including thousands of individuals and hundreds of thousands (large for some people, small for other people) if SNPs are available.

HGDP data • 1,033 samples • 7 geographic regions • 52 populations Cavalli-Sforza (2005) Nat Genet Rev Rosenberg et al. (2002) Science Li et al. (2008) Science The International HapMap Consortium (2003, 2005, 2007) Nature Apply SVD/PCA on the (joint) HGDP and HapMap Phase 3 data. Matrix dimensions: 2,240 subjects (rows) 447,143 SNPs (columns) Dense matrix: over one billion entries The Human Genome Diversity Panel (HGDP) ASW, MKK, LWK, & YRI CEU TSI JPT, CHB, & CHD GIH MEX HapMap Phase 3 data • 1,207 samples • 11 populations HapMap Phase 3

Africa Middle East South Central Asia Europe Oceania East Asia America Gujarati Indians Mexicans • Top two Principal Components (PCs or eigenSNPs) (Lin and Altman (2005) Am J Hum Genet) • The figure renders visual support to the “out-of-Africa” hypothesis. • Mexican population seems out of place: we move to the top three PCs. Paschou, et al (2010) J Med Genet

Africa Middle East S C Asia & Gujarati Europe Oceania East Asia America •  Not altogether satisfactory: the principal components are linear combinations of all SNPs, and – of course – can not be assayed! •  Can we find actual SNPs that capture the information in the singular vectors? •  Relatedly, can we compute them and/or the truncated SVD “efficiently.” Paschou, et al. (2010) J Med Genet

Two related issues with eigen-analysis Computing large SVDs: computational time •  In commodity hardware (e.g., a 4GB RAM, dual-core laptop), using MatLab 7.0 (R14), the computation of the SVD of the dense 2,240-by-447,143 matrix A takes ca 20 minutes. •  Computing this SVD is not a one-liner, since we can not load the whole matrix in RAM (runs out-of-memory in MatLab). •  Instead, compute the SVD of AAT. •  In a similar experiment, compute 1,200 SVDs on matrices of dimensions (approx.) 1,200- by-450,000 (roughly, a full leave-one-out cross-validation experiment) (DLP2010) Selecting actual columns that “capture the structure” of the top PCs •  Combinatorial optimization problem; hard even for small matrices. •  Often called the Column Subset Selection Problem (CSSP). •  Not clear that such “good” columns even exist. •  Avoid “reification” problem of “interpreting” singular vectors! • (Solvable in “random projection time” with CX/CUR decompositions! (PNAS, MD09))

Where do you run your linear algebra? Single machine • Think about RAM, call LAPACK, etc. • Someone else thought about numerical issues, memory hierarchies, etc. • This is the 99% Supercomputer • High end, compute-intensive. • Big emphasis on HPC (High Performance Computing) • C+MPI, etc. Distributed data center • High end, data-intensive • BIG emphasis on HPC (High Productivity Computing) • Databases, MapReduce/Hadoop, Spark, etc.

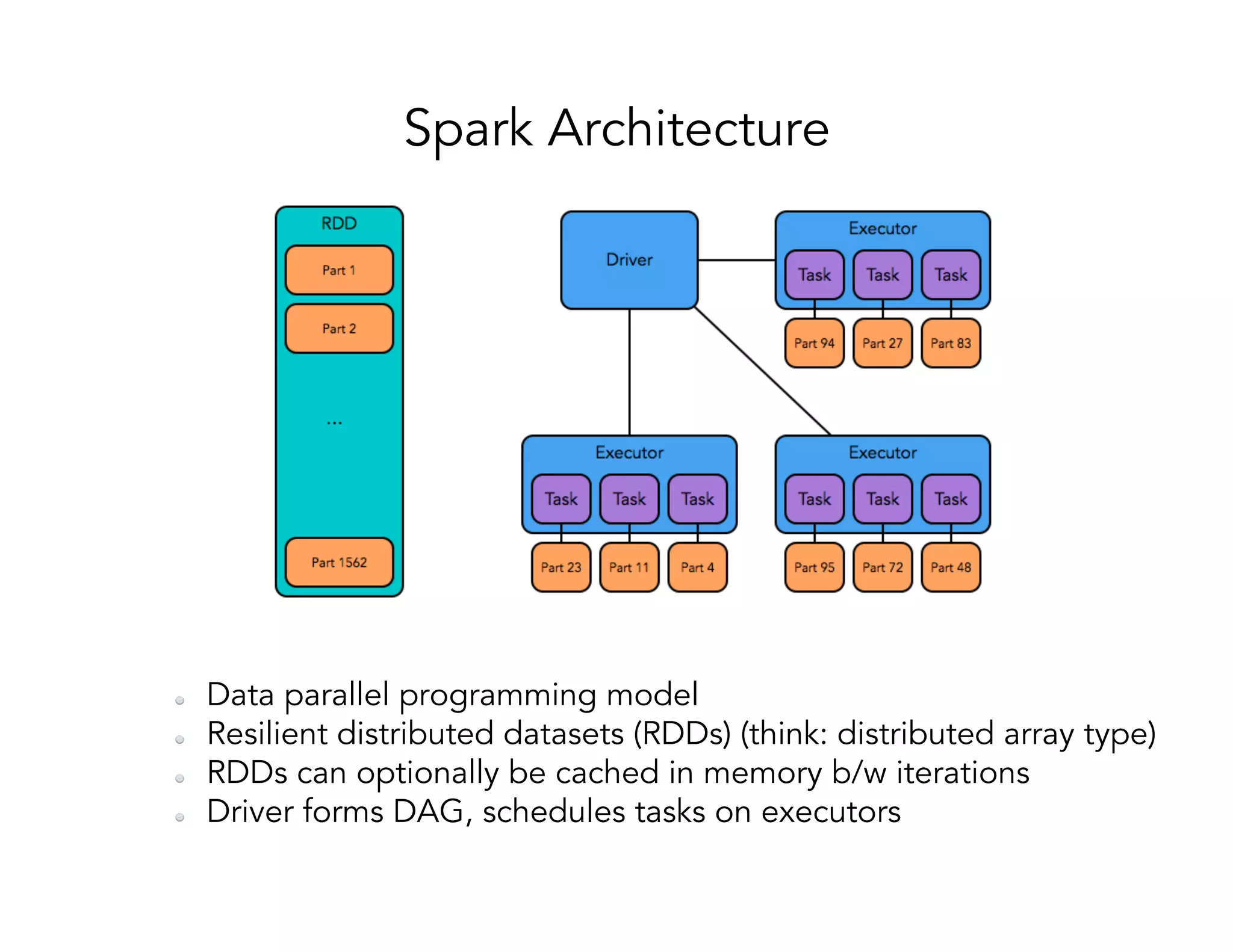
Spark Architecture   Data parallel programming model   Resilient distributed datasets (RDDs) (think: distributed array type)   RDDs can optionally be cached in memory b/w iterations   Driver forms DAG, schedules tasks on executors

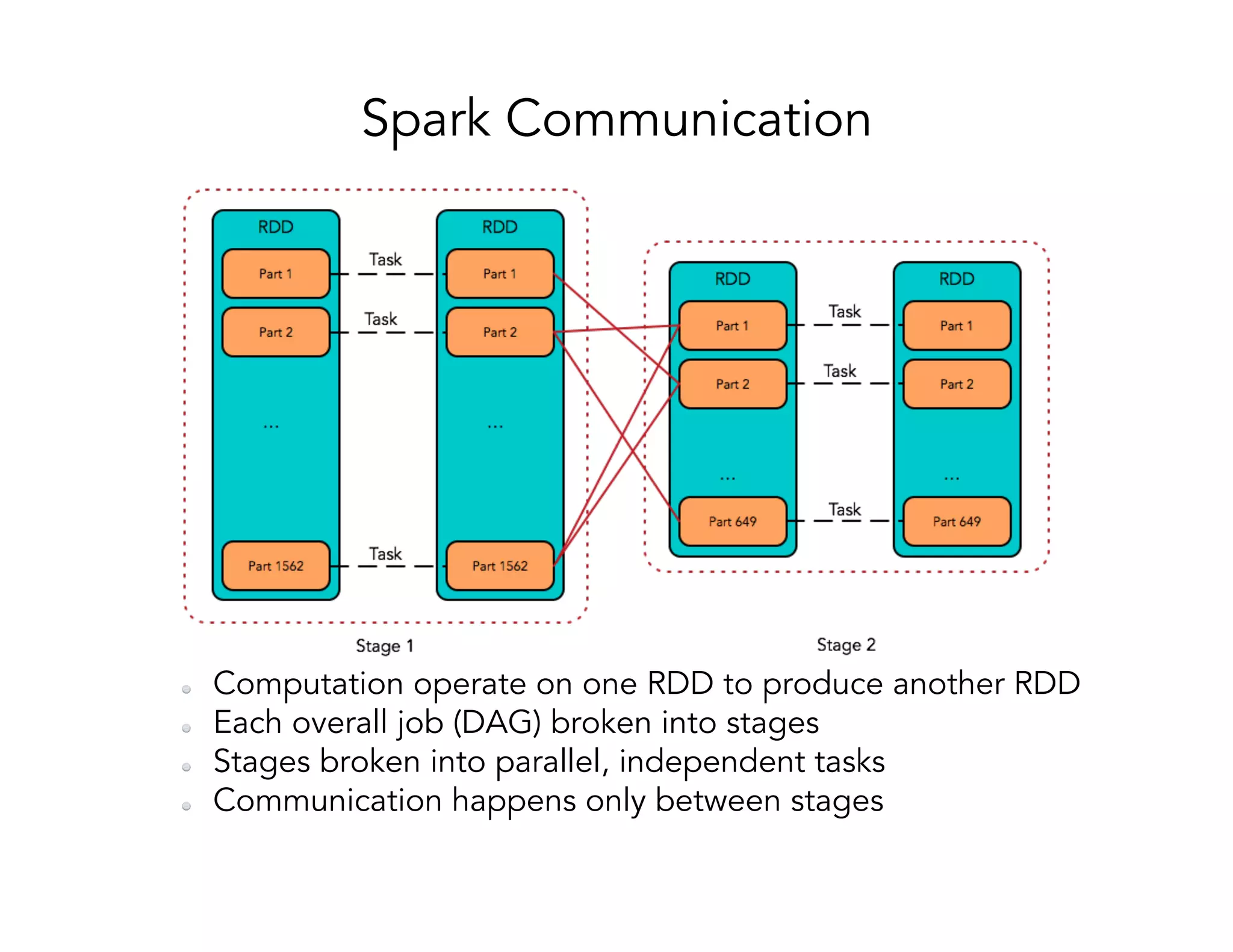
Spark Communication   Computation operate on one RDD to produce another RDD   Each overall job (DAG) broken into stages   Stages broken into parallel, independent tasks   Communication happens only between stages

Why do linear algebra in Spark?   Classical MPI-based linear algebra algorithms are faster and more efficient   No way, currently, to leverage legacy parallel linear algebra codes   JVM matrix size restrictions, and RDD rigidity Cons:   Widely used   Easier to use for non-experts   An entire ecosystem that can be used before and after the NLA computations   Spark can take advantage of available single-machine linear algebra codes (e.g. through netlib-java)   Automatic fault-tolerance   Transparent support for out of memory calculations Pros:

Our Goals   Provide implementations of low-rank factorizations (PCA, NMF, and randomized CX) in Spark   Apply low-rank matrix factorization methods to TB-scale scientiﬁc datasets in Spark   Understand Spark performance on commodity clusters vs HPC platforms   Quantify the scalability gaps between highly-tuned C/MPI and current Spark-based implementations   Provide a general-purpose interface for matrix-based algorithms between Spark and traditional MPI codes

Motivation   NERSC: Spark for data-centric workloads and scientific analytics   AMPLab: characterization of linear algebra in Spark (MLlib, MLMatrix)   Cray: customers demand for Spark; understand performance concerns

Three Science Drivers Climate Science: extract trends in variations of oceanic and atmospheric variables (PCA) Nuclear Physics: learn useful patterns for classification of subatomic particles (NMF) Mass Spectrometry: location of chemically important ions (CX)

Datasets MSI — a sparse matrix from measurements of drift times and mass charge ratios at each pixel of a sample of Peltatum; used for CX decomposition Daya Bay — neutrino sensor array measurements; used for NMF Ocean and Atmosphere — climate variables (ocean temperature, atmospheric humidity) measured on a 3D grid at 3 or 6 hour intervals over about 30 years; used for PCA

Experiments 1.  Compare EC2 and two HPC platforms using CX implementation 2.  More detailed analysis of Spark vs C+MPI scaling for PCA and NMF on the two HPC platforms Some details:   All datasets are tall and skinny   The algorithms work with row-partitioned matrices   Use H5Spark to read dense matrices from HDF5, so MPI and Spark reading from same data source

Platform comparisons Two Cray HPC machines and EC2, using CX

Randomized CX/CUR Decomposition   Dimensionality reduction is a ubiquitous tool in science (bio-imaging, neuro-imaging, genetics, chemistry, climatology, …), typical approaches include PCA and NMF which give approximations that rely on non- interpretable combinations of the data points in A   PCA, NMF lack reifiability. Instead, CX matrix decompositions identify exemplar data points (columns of A) that capture the same information as the top singular vectors, and give approximations of the form

The Randomized CX Decomposition   To get accuracy comparable to the truncated rank-k SVD, the randomized CX algorithm randomly samples O(k) columns with replacement from A according to the leverage scores where

The Randomized CX Decomposition   It is expensive to compute the right singular vectors   Since the algorithm is already randomized, we use a randomized algorithm to quickly approximate them

The Randomized SVD algorithm The matrix analog of the power method: requires only matrix-matrix multiplies against ATA assumes B ﬁts on one machine

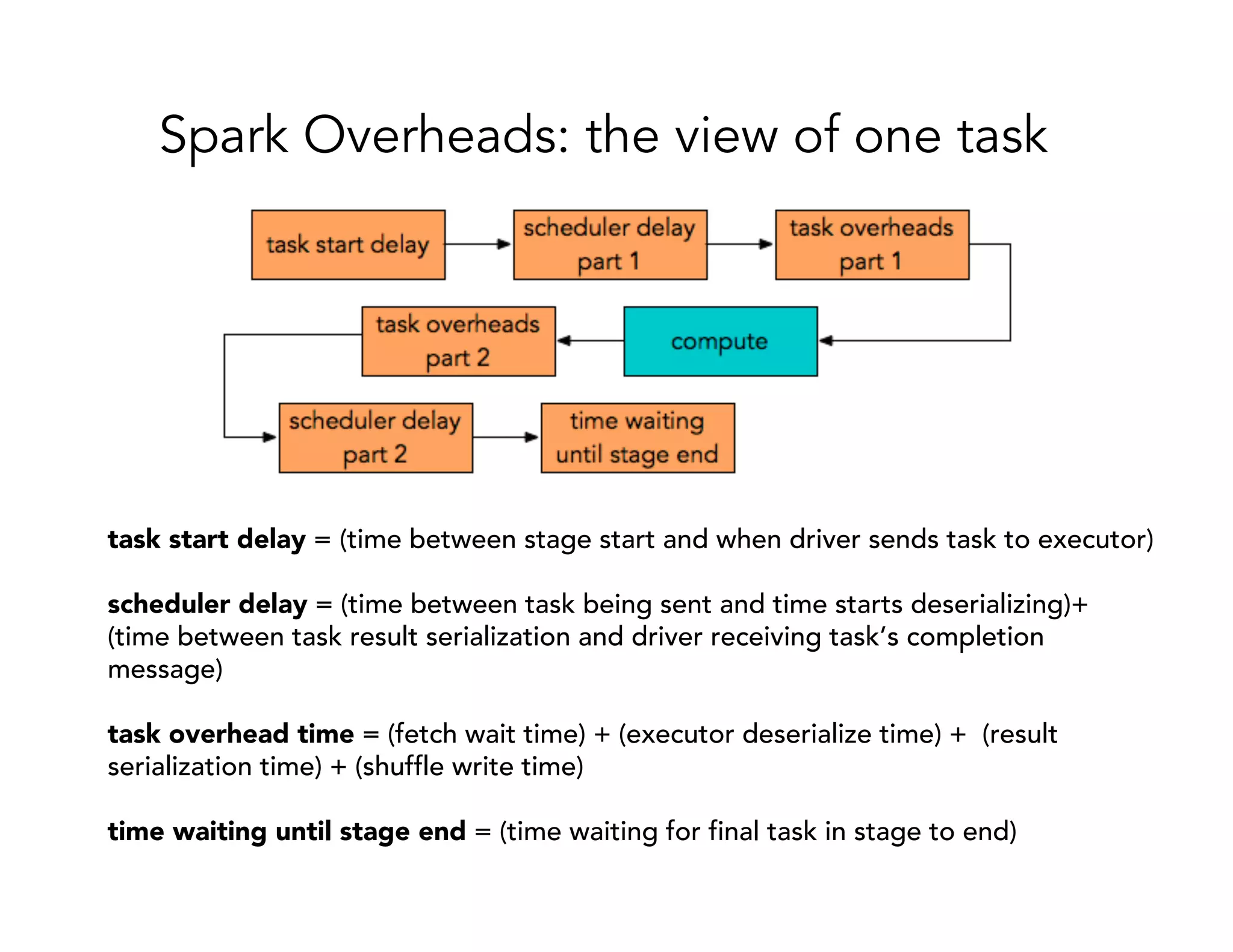
Computing the power iterations using Spark is computed using a treeAggregate operation over the RDD [src: https://databricks.com/blog/2014/09/22/spark-1-1-mllib-performance-improvements.html]!

Differences in write timings have more impact: •  4800 write tasks per iteration •  68 read tasks per iteration Timing breakdowns

Observations   EXP_CC outperforms EC2 and XC40 because of local storage and faster interconnect   On HPC platforms, can focus on modifying Spark to mitigate drawbacks of the global filesystem: 1.  clean scratch more often to help fit scratch entirely in RAM, no need to spill to Lustre 2.  allow user to specify order to ﬁll scratch directories (RAM disk, *then* Lustre) 3.  exploit fact that scratch on shared ﬁlesystem is global, to avoid wasted communication

Spark vs MPI PCA and NMF, on NERSC’s Cori supercomputer

CFSR Ocean Temperature Dataset (II)!

Climate Science Results on Ocean (CFSRO) dataset •  First principal component of temperature ﬁeld at 180 degree latitude.! •  Clear that there is a signiﬁcant vertical component to the PCs which are lost when you do the traditional surface-only analyses

Cori’s specs: •  1630 compute nodes, •  128 GB/node, •  32 2.3GHz Haswell cores/node Running times for NMF and PCA •  Anti-scaling! ! •  And it worsens both with concurrency and data size. !

Computing the truncated PCA The two steps in computing the truncated PCA of A are: 1.  Compute the truncated EVD of ATA to get Vk 2.  Compute the SVD of AVk to get Σk and Vk use Lanczos: requires only matrix vector multiplies assume this is small enough that the SVD can be computed locally Often (for dimensionality reduction, physical interpretation, etc.), the rank-k truncated PCA (SVD) is desired. It is defined as

Computing the Lanczos iterations using Spark If then the product can be computed as We call the spark.mllib.linalg.EigenvalueDecomposition interface to the ARPACK implementation of the Lanczos method This requires a function which computes a matrix-product against ATA

Spark Overheads: the view of one task task start delay = (time between stage start and when driver sends task to executor) scheduler delay = (time between task being sent and time starts deserializing)+ (time between task result serialization and driver receiving task’s completion message) task overhead time = (fetch wait time) + (executor deserialize time) + (result serialization time) + (shuffle write time) time waiting until stage end = (time waiting for final task in stage to end)

PCA Run Times: rank 20 PCA of 2.2TB Climate

Rank 20 PCA of 16 TB Climate using 48K+ cores

Spark PCA Overheads: 16 TB Climate,1522 nodes

Nonnegative Matrix Factorization Useful when the observations are positive, and assumed to be positive combinations of basis vectors (e.g., medical imaging modalities, hyperspectral imaging) In general, NMF factorizations are non-unique and NP- hard to compute for a fixed rank. We use the one-pass approach of Benson et al. 2014

Nearly-Separable NMF Assumption: some k-subset of the columns of A comprise a good W Key observation of Benson et al. : finding those columns of A can be done on the R factor from the QR decomposition of A So the problem reduces to a distributed QR on a tall matrix A, then a local NMF on a much smaller matrix

Tall-Skinny QR (TSQR) When A is tall and skinny, you can efficiently compute R:   uses a tree reduce   requires only one pass over A

NMF Run Times: rank 10 NMF of 1.6TB Daya Bay

MPI vs Spark: Lessons Learned   With favorable data (tall and skinny) and well-adapted algorithms, Spark LA is 4x-26x slower than MPI when IO is included   Spark overheads are orders of magnitude higher than the computations in PCA (time till stage end, scheduler delay, task start delay, executor deserialize time).   H5Spark performance is inconsistent this needs more work   The large gaps mean it is worthwhile to investigate efficiently interfacing MPI-based codes with Spark

Next steps   Alchemist: (A. Gittens) Gateway between Spark and MPI Lightweight wrappers around APIs of existing MPI codes   Communication-avoiding ML: (Devarakonda and Fountoulakis) Explicitly minimize communication Core LA algorithms and proximal optimization algorithms   Communication-efficient ML: (S. Wang and F. Roosta) Implicitly minimize communication Second-order optimization algorithms Also of interest: Ray: (R. Nishihara and P. Moritz) Distributed execution framework at RISE

The Next Step: Alchemist   Since Spark is 4+x slower than MPI, propose sending the matrices to MPI codes, then receiving the results   For efficiency, want as little overhead as possible (File I/O, RAM, network usage, computational efficiency) File I/O RAM Network Usage Computational Efﬁciency HDFS writes to disk! 2x RAM! manual shufﬂing! yes! Apache Ignite none! 2-3x RAM! intelligent! restricted partitioning! Alluxio none! 2-3x RAM! intelligent! restricted partitioning! Alchemist none! 2x RAM! intelligent! yes!

Alchemist Architecture Spark: 1) Send metadata for input/output matrices to the Alchemist gateway 2) Sends the matrix to the Alchemist gateway using RDD.pipe() 3) Waits on a matrix from the Alchemist gateway using RDD.pipe() Alchemist: 1) repartitions the matrix for MPI 2) executes the MPI codes 3) repartitions the output and returns to Spark Each call to Alchemist will be single stage in the execution of Spark jobs! Spark! MPI! Alchemist! Gateway!

What Alchemist Will Enable   Use MPI NLA/ML Codes from Spark: libSkylark, MaTeX, etc. … val xMat = alcMat(xRDD) val yMat = alcMat(yRDD) // Elemental NLA val (u,s,v) = alchemist.SVD(xMat,k).toIndexRowMatrices() // libSkylark ML val (rffweights,alpha) = alchemist.RFFRidgeRegression(xMat,yMat,lambda,D) // MaTeX ML val clusterIndicators = alchemist.kMeans(xMat,k) … It will be easy to write lightweight wrappers around APIs of existing MPI codes.!

Multi-platform evaluation of randomized CX/CUR (IPDPS 2016 Workshop) Poster presentations at climate science venues Technical Report on Spark performance for Terabyte-scale Matrix Decompositions (submitted): https://arxiv.org/abs/1607.01335 Attendant MPI and Spark codes: https://github.com/alexgittens/SparkAndMPIFactorizations End-to-end 3D Climate EOF codes: https://github.com/alexgittens/climate-EOF-suite CUG 2016 Paper on H5Spark: https://github.com/valiantljk/h5spark/files/261834/h5spark-cug16-final.pdf For more info, contact me or Alex Gittens: gittens@icsi.berkeley.edu

Sophisticated statistical data analysis involves strong control over linear algebra. Most workflows/applications currently do not demand much of the linear algebra. Low-rank matrix algorithms for interpretable scientific analytics on scores of terabytes of data! Complex data workflows invoke linear algebra as one step (of a multi-stage pipeline), and data/communication optimization might be needed across function calls. What is the “right” way to do linear algebra for large-scale data analysis? Conclusion 1

Motivation CPU Cache DRAM CPU DRAM CPU DRAM CPU DRAM CPU DRAM Algorithm cost = 9lops + data movement Processor speed (T9lops) >> bandwidth (GB/s) >> latency (µμs) Smaller but Faster Larger but Slower Local mem. access fast Remote mem. access fast

•  Recent developments: Communication-‐Avoiding Linear Algebra •  Direct and Iterative •  Our work: Extending to iterative ML •  Block Coordinate Descent (this presentation) 2

Closed Form Solution: 𝑤=(1/𝑛 𝑋 𝑋↑𝑇 + 𝜆 𝐼↓𝑑 )↑−1 𝑋𝑦 Ridge Regression Solve : argmin┬𝑤∈ ℝ↑𝑑  ⁠ 𝜆/2 ‖ 𝑤‖↓2↑2 +1/2 𝑛 ‖ 𝑋↑𝑇 𝑤 − 𝑦‖↓2↑2   X n d samples features w d y n labels weights **Also works for tall-‐skinny (n >> d) matrices** 3

Many algorithms to solve Matrix Factorization: TSQR, LU, SVD, etc. Krylov Methods: CG, LSQR, etc. Block Coordinate Descent (BCD) Single-‐Coordinate Descent (CD) **Lots of tradeoffs between methods** (Direct) (Itera@ve) More flops Less flops per itera@on One Reduc@on Many Reduc@ons More words Fewer words per itera@on **one word = size of one double-‐precision floa@ng-‐point number** Communication 4 ML

Block Coordinate Descent Original problem: argmin┬𝑤∈ ℝ↑𝑑  ⁠ 𝜆/2 ‖ 𝑤‖↓2↑2 +1/2 𝑛 ‖ 𝑋↑𝑇 𝑤 − 𝑦‖↓2↑2   Uniformly at random, select 𝑏 coordinates of 𝑤 to update. Update Rules looks like: 𝑤↓ℎ = 𝑤↓ℎ −1  + 𝕀↓ℎ Δ 𝑤 Δ 𝑤 is the solution to a 𝑏-‐dimensional subproblem. 𝕀↓ℎ  is a map from 𝑏-‐dimensions to 𝑑-‐dimensions.

Finding Δ 𝑤 𝑏-‐dimensional problem: argmin┬Δ 𝑤∈ ℝ↑𝑏  ⁠ 𝜆/2 ‖ 𝑤↓ℎ −1  + 𝕀↓ℎ Δ 𝑤 ‖↓2↑2 +1/2 𝑛 ‖ 𝑋↑𝑇 ( 𝑤↓ℎ −1   + 𝕀↓ℎ Δ 𝑤)− 𝑦‖↓2↑2   Just replace 𝑤 with update rule. Solve for Δ 𝑤=(1/𝑛  𝕀↓ℎ↑𝑇 𝑋 𝑋↑𝑇  𝕀↓ℎ + 𝜆𝐼)↑−1 (− 𝜆 𝕀↓ℎ↑𝑇  𝑤↓ℎ−1  −1/𝑛  𝕀↓ℎ↑𝑇 𝑋 𝑋↑𝑇  𝑤↓ℎ−1 +1/𝑛  𝕀↓ℎ↑𝑇 𝑋𝑦) Gram Matrix residual

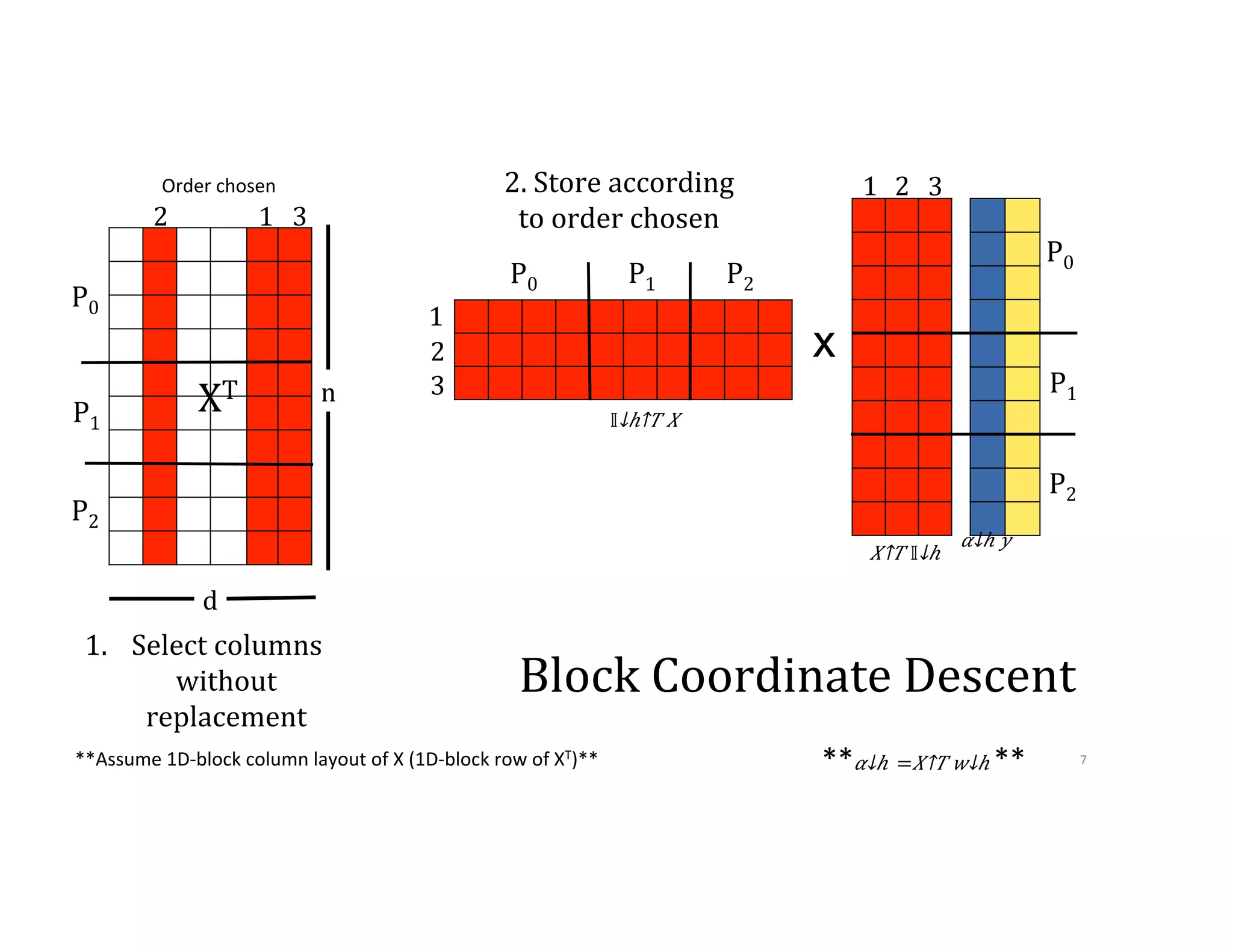
2 1 3 1 3 2 1.  Select columns without replacement 2. Store according to order chosen P0 P1 P2 P0 P1 P2 XT 1 3 2 n d P0 P1 P2 x 𝛼↓ℎ  𝑦 𝕀↓ℎ↑𝑇 𝑋 𝑋↑𝑇  𝕀↓ℎ  **Assume 1D-‐block column layout of X (1D-‐block row of XT)** 7 Block Coordinate Descent ** 𝛼↓ℎ  = 𝑋↑𝑇  𝑤↓ℎ ** Order chosen

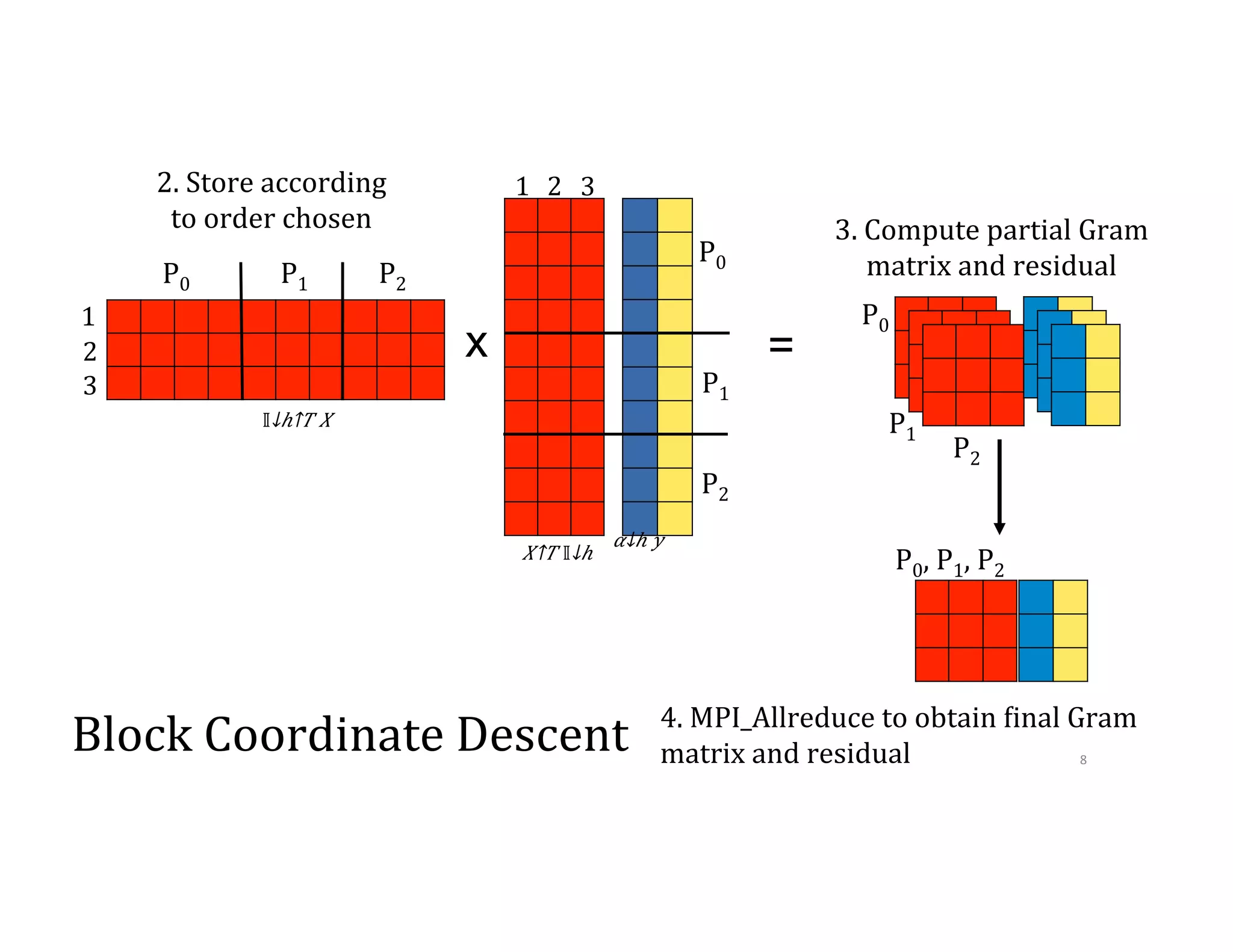
2 1 3 1 3 2 2. Store according to order chosen 3. Compute partial Gram matrix and residual 4. MPI_Allreduce to obtain 9inal Gram matrix and residual P0 P1 P2 P0 P1 P2 P0 P1 P2 P0, P1, P2 x 𝛼↓ℎ  𝑦 𝕀↓ℎ↑𝑇 𝑋 𝑋↑𝑇  𝕀↓ℎ  = 8 Block Coordinate Descent

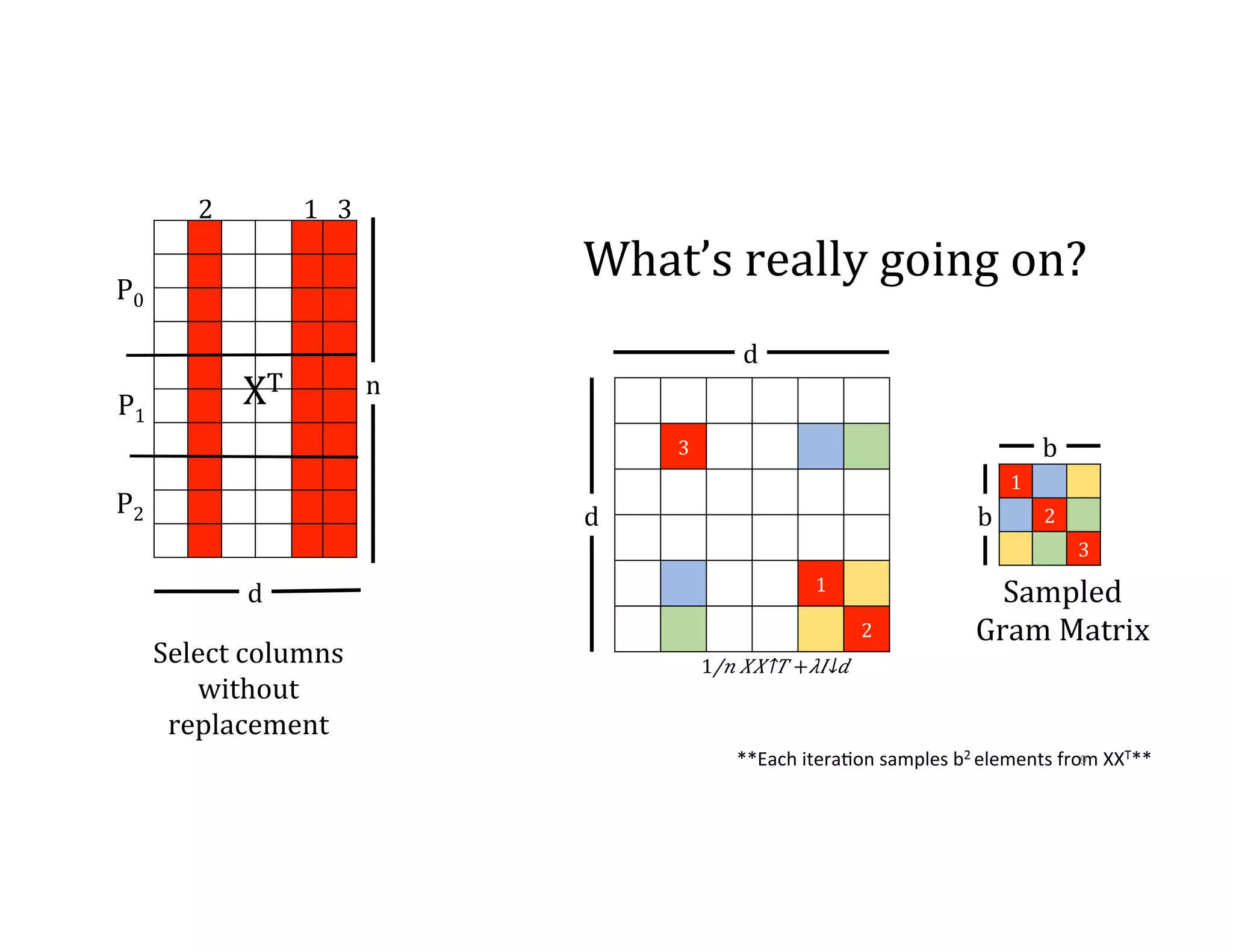
What’s really going on? 3 1 2 1 2 3 1/𝑛 𝑋 𝑋↑𝑇 + 𝜆 𝐼↓𝑑  Sampled Gram Matrix d d b b Select columns without replacement XT 1 3 2 n d P0 P1 P2 **Each itera@on samples b2 elements from XXT** 9

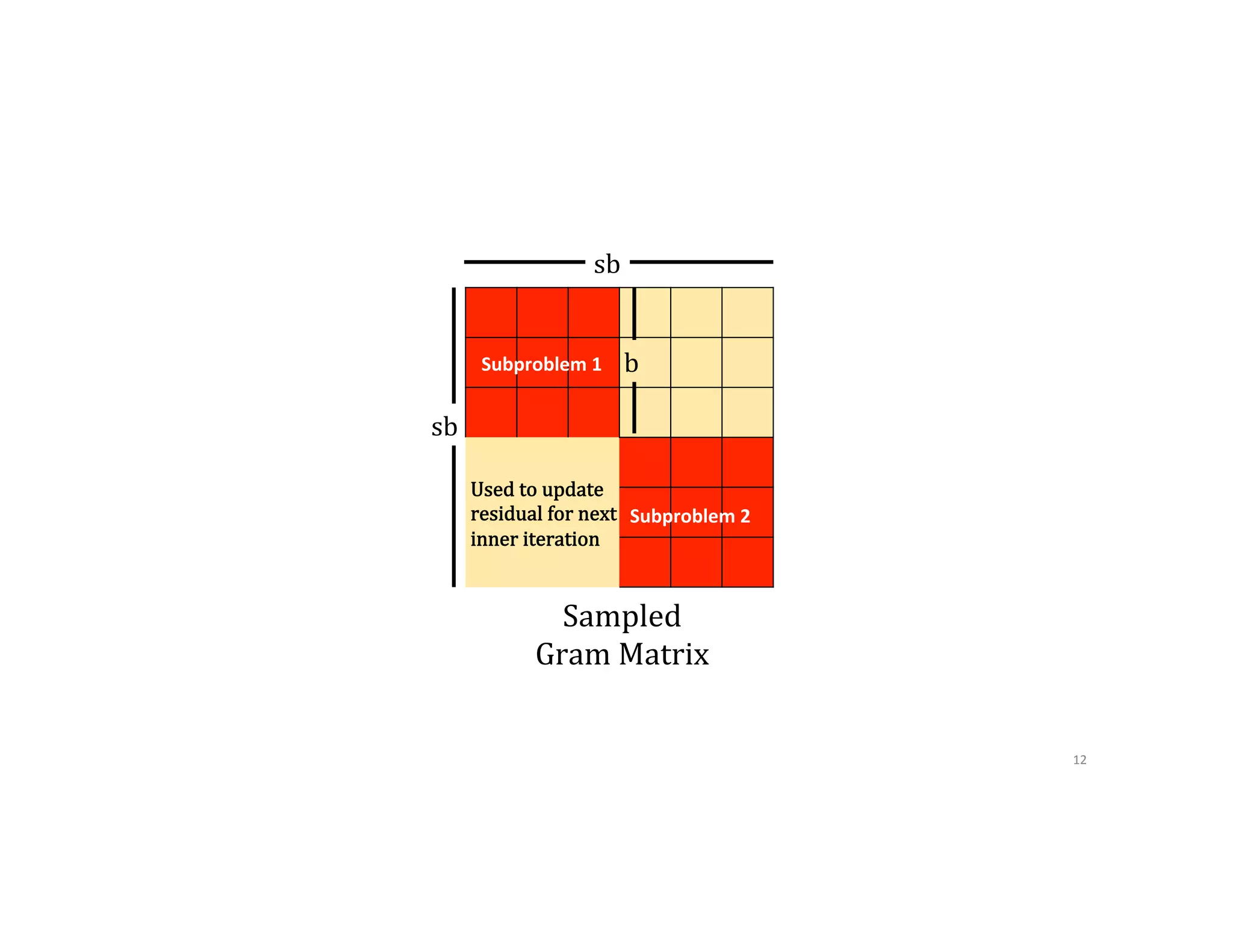
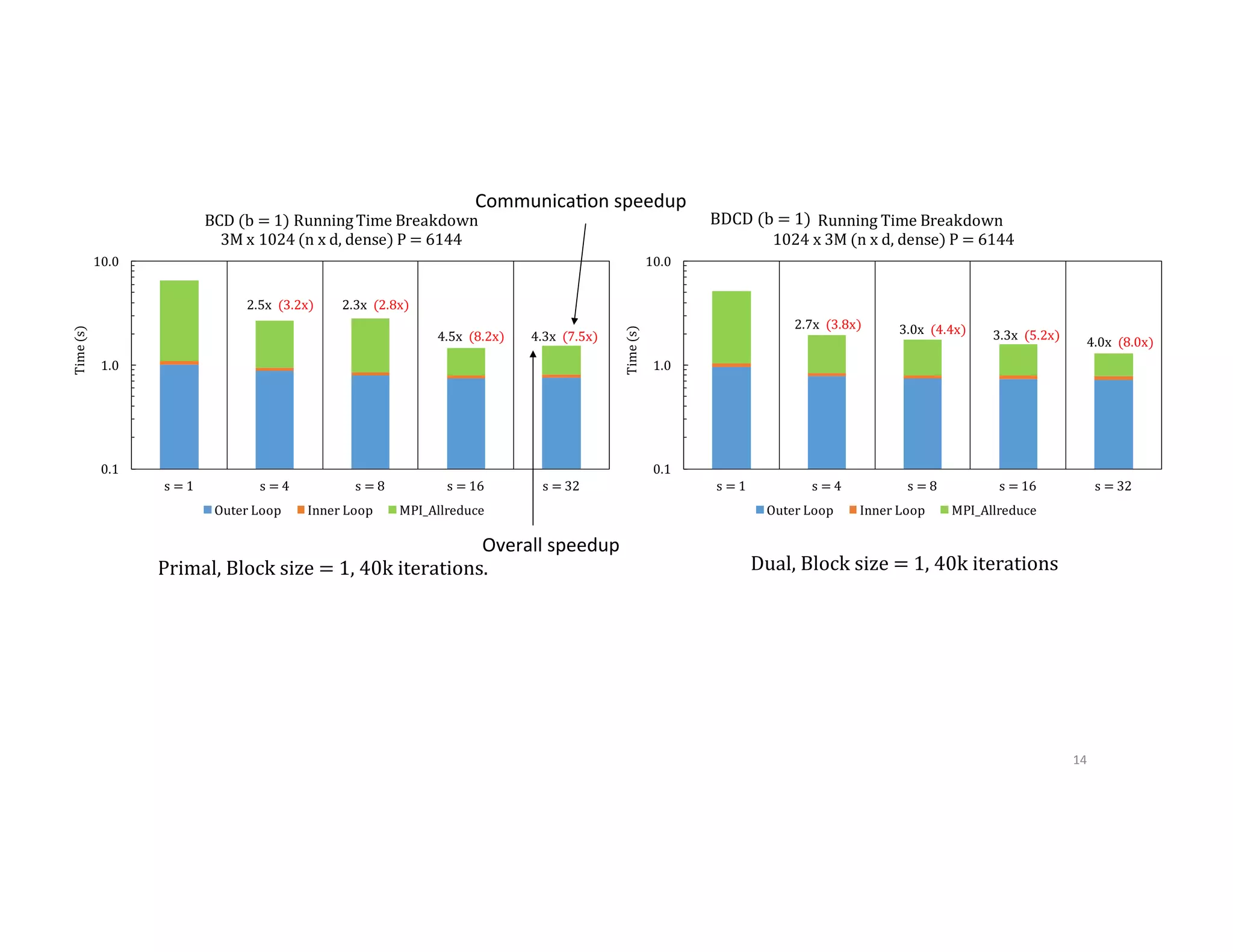
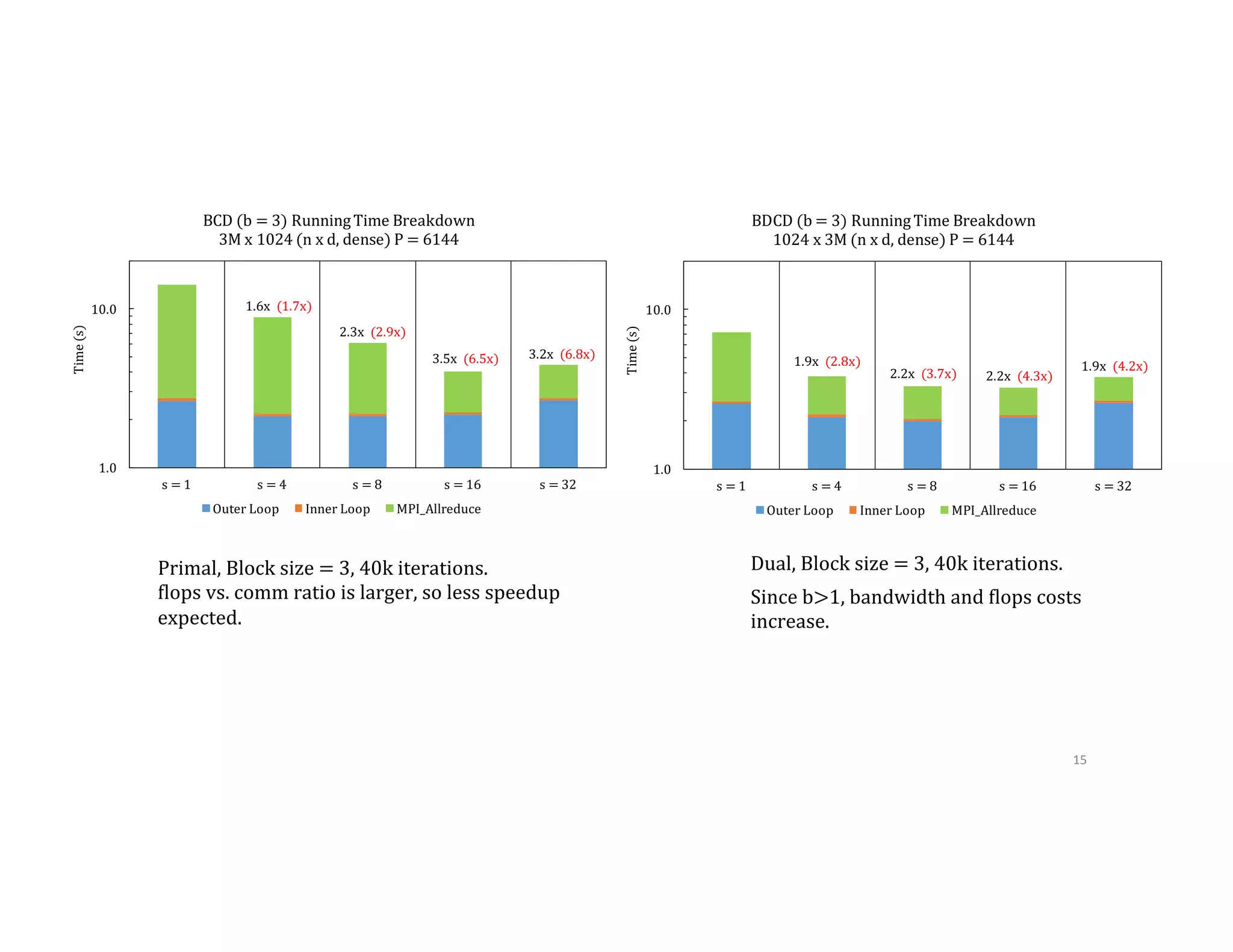
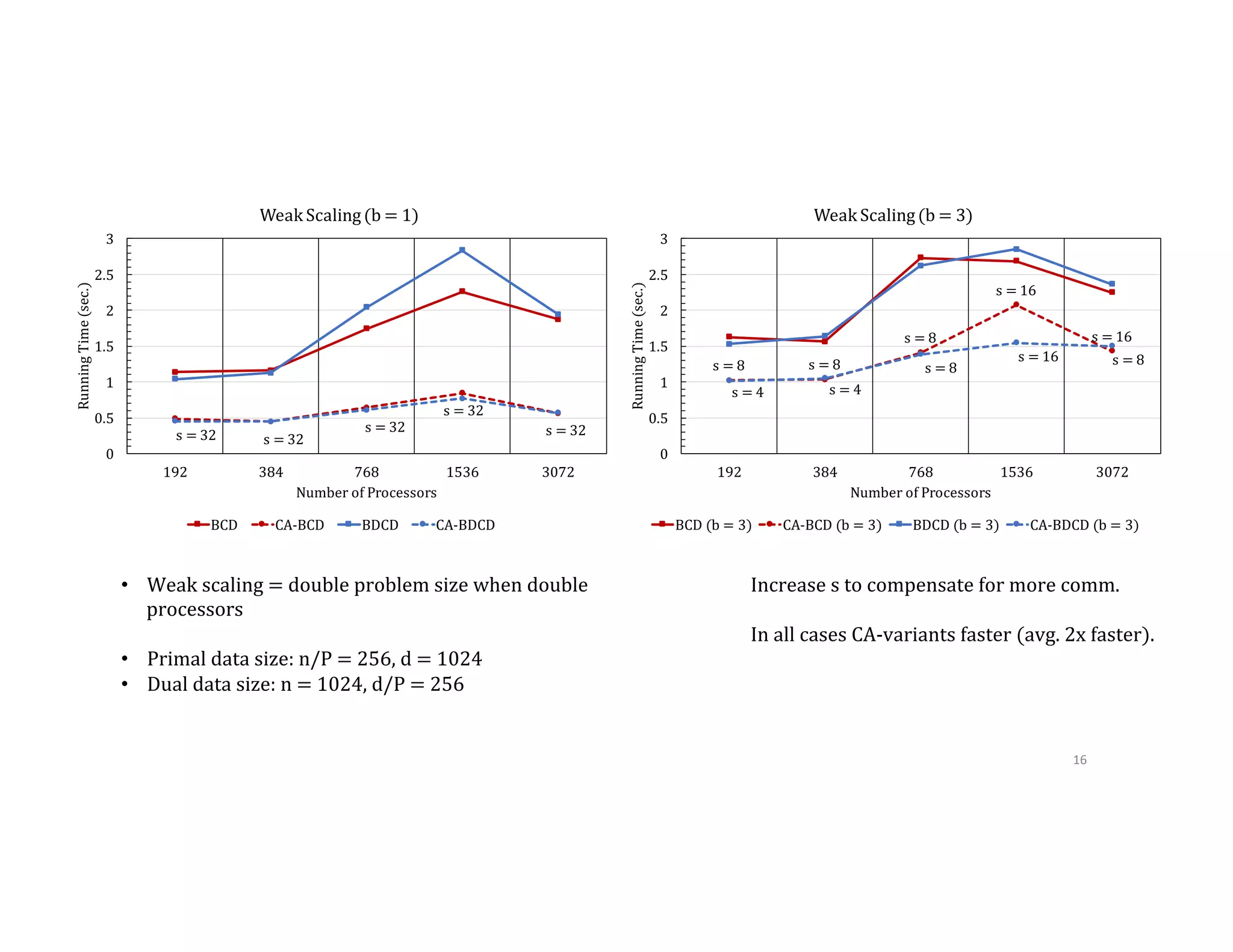
Communication Avoiding-‐BCD 2 1 3 1 3 2 1.  Select columns without replacement 2. Store according to order chosen P0 P1 P2 P0 P1 P2 XT 1,6 3 2,4 n d P0 P1 P2 x 𝛼↓ℎ  𝑦 𝑋↑𝑇 [𝕀↓𝑠𝑘+1  𝕀↓𝑠𝑘+2 ] [█■ 𝕀↓𝑠𝑘+1↑𝑇 ⁠ 𝕀↓𝑠𝑘 +2↑𝑇  ]𝑋 5 4 5 6 4 5 6 10

2 1 3 1 3 2 = 3. Store according to order chosen 4. Compute partial Gram matrix and residual 4. MPI_Allreduce to obtain 9inal Gram matrix and residual P0 P1 P2 P0 P1 P2 P0 P1 P2 P0, P1, P2 x 𝛼↓ℎ  𝑦 𝑋↑𝑇 [𝕀↓𝑠𝑘+1  𝕀↓𝑠𝑘+2 ] [█■ 𝕀↓𝑠𝑘+1↑𝑇 ⁠ 𝕀↓𝑠𝑘 +2↑𝑇  ]𝑋 4 5 6 4 5 6 11

Sampled Gram Matrix sb sb Used to update residual for next inner iteration Subproblem 1 Subproblem 2 b 12

Experimental Setup •  Using NERSC Edison •  Cray XC30 system with dragon9ly topology •  2.4 GHz Intel ”Ivy Bridge” •  24 cores per node •  Experiments performed on mix of real and synthetic problems •  Flat MPI with single-‐threaded MKL •  Storing in dense format 13 **sparse storage only reduces ﬂops, speedups should stay constant**

Primal, Block size = 1, 40k iterations. Dual, Block size = 1, 40k iterations 14 0.1 1.0 10.0 s = 1 s = 4 s = 8 s = 16 s = 32 Time (s) BCD (b = 1) Running Time Breakdown 3M x 1024 (n x d, dense) P = 6144 Outer Loop Inner Loop MPI_Allreduce 2.5x (3.2x) 2.3x (2.8x) 4.5x (8.2x) 4.3x (7.5x) Overall speedup 0.1 1.0 10.0 s = 1 s = 4 s = 8 s = 16 s = 32 Time (s) DCD Running Time Breakdown 1024 x 3M (n x d, dense) P = 6144 Outer Loop Inner Loop MPI_Allreduce 2.7x (3.8x) 3.0x (4.4x) 3.3x (5.2x) 4.0x (8.0x) BDCD (b = 1) Communica@on speedup

Primal, Block size = 3, 40k iterations. 9lops vs. comm ratio is larger, so less speedup expected. Dual, Block size = 3, 40k iterations. Since b>1, bandwidth and 9lops costs increase. 15 1.0 10.0 s = 1 s = 4 s = 8 s = 16 s = 32 Time (s) BDCD (b = 3) Running Time Breakdown 1024 x 3M (n x d, dense) P = 6144 Outer Loop Inner Loop MPI_Allreduce 1.9x (2.8x) 2.2x (3.7x) 2.2x (4.3x) 1.9x (4.2x) 1.0 10.0 s = 1 s = 4 s = 8 s = 16 s = 32 Time (s) BCD (b = 3) Running Time Breakdown 3M x 1024 (n x d, dense) P = 6144 Outer Loop Inner Loop MPI_Allreduce 1.6x (1.7x) 2.3x (2.9x) 3.5x (6.5x) 3.2x (6.8x)

•  Weak scaling = double problem size when double processors •  Primal data size: n/P = 256, d = 1024 •  Dual data size: n = 1024, d/P = 256 Increase s to compensate for more comm. In all cases CA-‐variants faster (avg. 2x faster). 16 s = 32 s = 32 s = 32 s = 32 s = 32 0 0.5 1 1.5 2 2.5 3 192 384 768 1536 3072 Running Time (sec.) Number of Processors Weak Scaling (b = 1) BCD CA-BCD BDCD CA-BDCD s = 8 s = 8 s = 8 s = 16 s = 16 s = 4 s = 4 s = 8 s = 16 s = 8 0 0.5 1 1.5 2 2.5 3 192 384 768 1536 3072 Running Time (sec.) Number of Processors Weak Scaling (b = 3) BCD (b = 3) CA-BCD (b = 3) BDCD (b = 3) CA-BDCD (b = 3)

•  On real datasets obtained from LIBSVM •  CA-‐variants once again faster. •  Adult dataset: 4.2x faster •  Covtype dataset: 3.1x faster •  Epsilon dataset: 2.7x faster 17 0 1 2 3 4 5 6 7 8 192 384 768 1536 3072Running TIme (sec.) Number of Processors Primal Strong Scaling (b = 1) adult, BCD adult, CA-BCD covtype, BCD covtype, CA-BCD epsilon, BCD epsilon, CA-BCD

•  On real datasets obtained from LIBSVM •  CA-‐variants once again faster. •  Adult dataset: 1.8x faster •  Covtype dataset: 1.7x faster •  Epsilon dataset: 2.2x faster 18 0 1 2 3 4 5 6 7 8 9 10 192 384 768 1536 3072Running Time (sec.) Number of Processors Primal Strong Scaling (b = 3) adult, BCD adult, CA-BCD covtype, BCD covtype, CA-BCD epsilon, BCD epsilon, CA-BCD

19 Covtype Speedup P = 1536 1 2.9x 3.0x 3.8x 4.4x 3 1.6x 1.7x 2.2x 1.9x 6 1.4x 1.6x 1.5x 1.1x 12 1.3x 1.2x 0.9x 0.4x 4 8 16 32 Loop unrolling parameter (s) Covtype Speedup P = 3072 1 3.4x 4.2x 5.1x 7.4x 3 2.2x 2.6x 3.3x 3.2x 6 1.6x 2.0x 2.1x 2.3x 12 1.6x 1.6x 1.8x 0.9x 4 8 16 32 Loop unrolling parameter (s) Covtype Speedup P = 192 Block size (b) 1 1.6x 1.5x 1.3x 1.2x 3 0.9x 0.8x 0.7x 0.5x 6 0.9x 0.8x 0.5x 0.3x 12 0.7x 0.5x 0.3x 0.2x 4 8 16 32 Loop unrolling parameter (s) Covtype Speedup P = 384 1 2.0x 1.9x 1.9x 1.6x 3 1.1x 1.0x 1.0x 0.7x 6 1.1x 0.9x 0.7x 0.4x 12 0.8x 0.6x 0.3x 0.2x 4 8 16 32 Loop unrolling parameter (s) Covtype Speedup P = 768 1 2.5x 3.1x 3.1x 2.9x 3 1.6x 1.6x 1.5x 1.1x 6 1.3x 1.2x 1.0x 0.6x 12 0.9x 0.7x 0.4x 0.2x 4 8 16 32 Loop unrolling parameter (s) •  More processors = more speedup •  Choice of s depends on block size and number of processors.

Conclusions 2 •  CA-‐variants faster in all experiments (validates theory) •  Speedups vary based on 9lops v. comm ratio. •  Highlights importance of avoiding communication •  Same convergence behavior and rates as original algorithms 20

Matrix Factorizations at Scale: a Comparison of Scientific Data Analytics on Spark and MPI Using Three Case Studies with Michael Mahoney

More Related Content

What's hot

Similar to Matrix Factorizations at Scale: a Comparison of Scientific Data Analytics on Spark and MPI Using Three Case Studies with Michael Mahoney

More from Databricks

Recently uploaded

Matrix Factorizations at Scale: a Comparison of Scientific Data Analytics on Spark and MPI Using Three Case Studies with Michael Mahoney