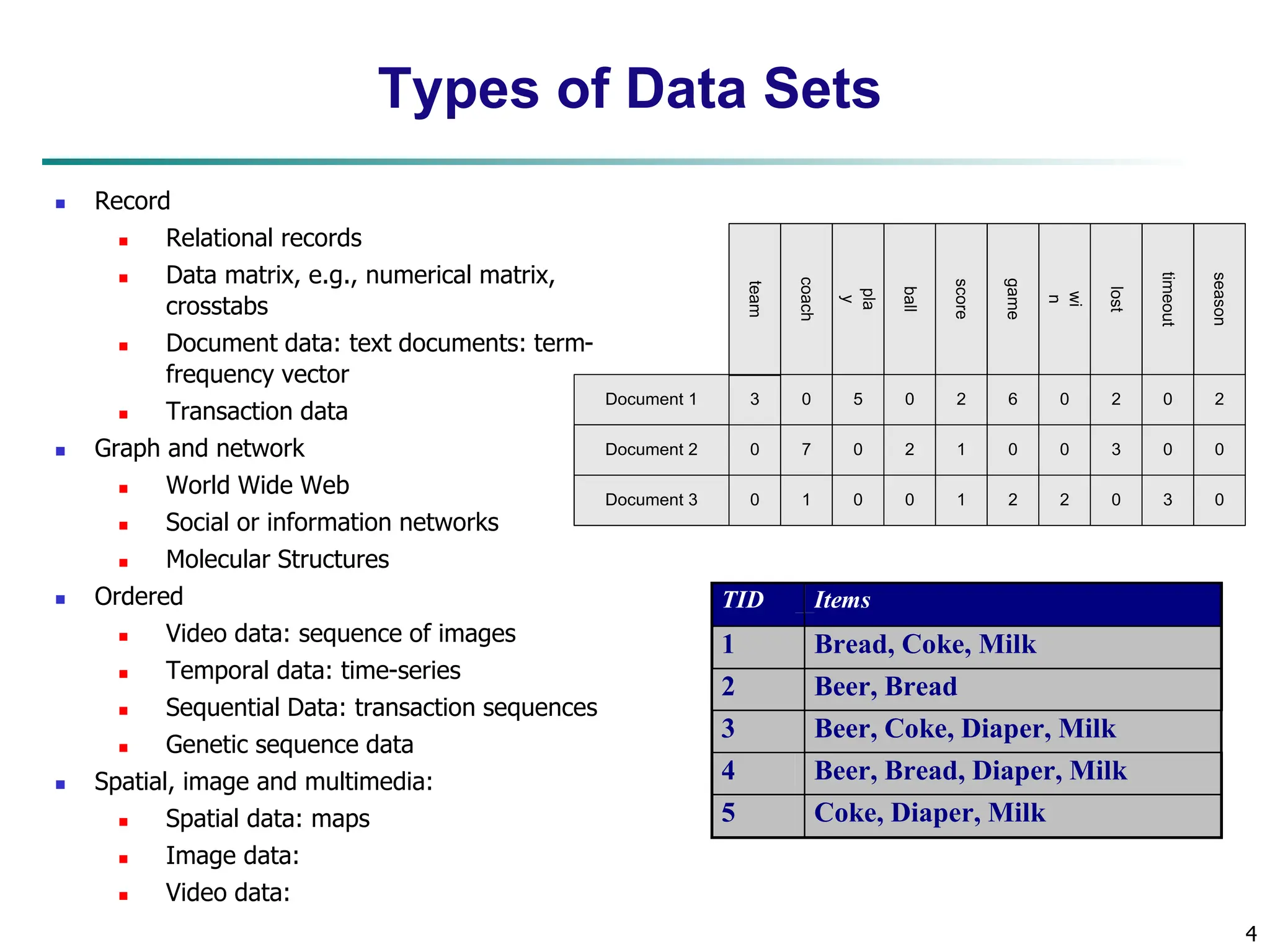
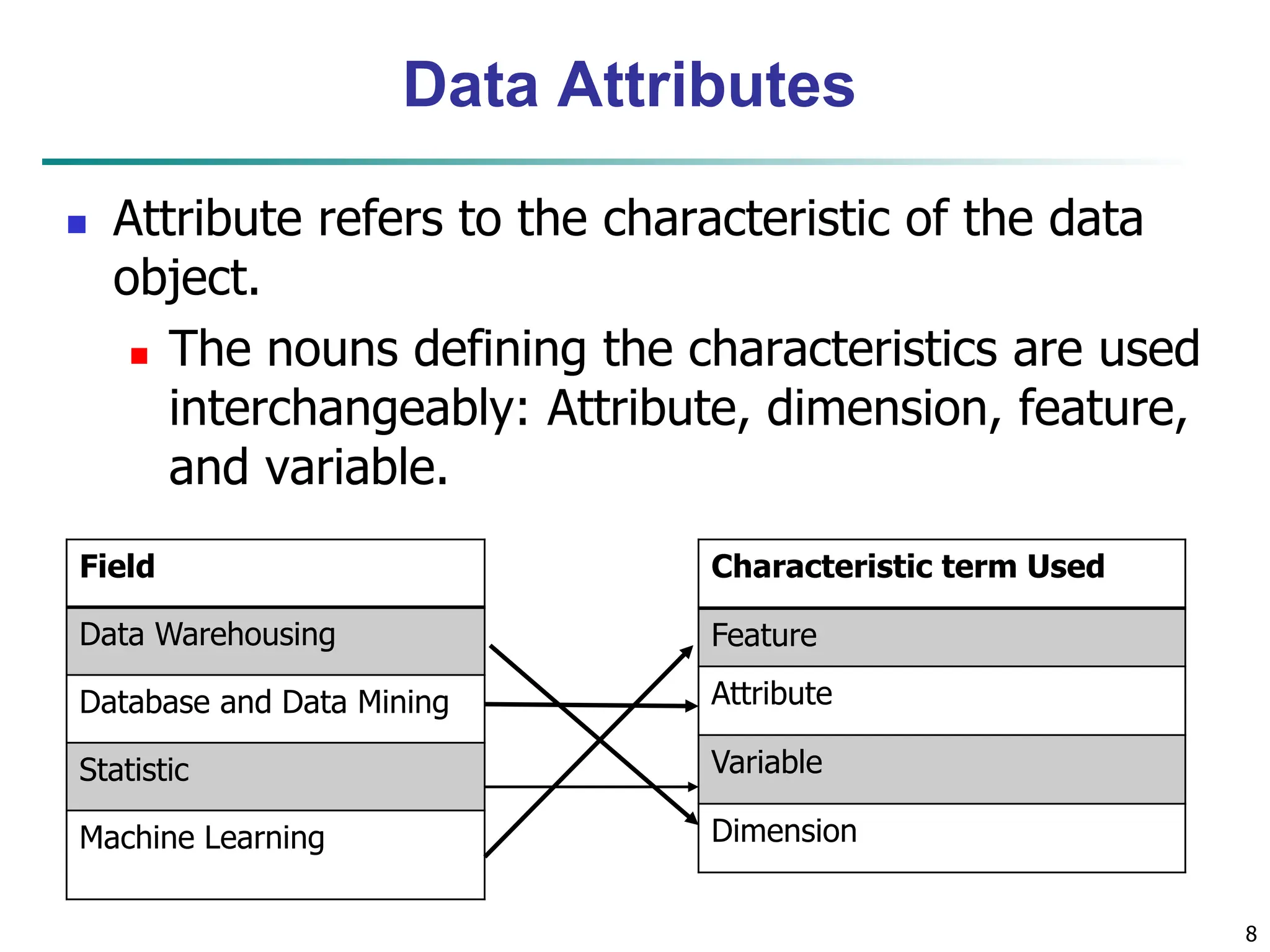
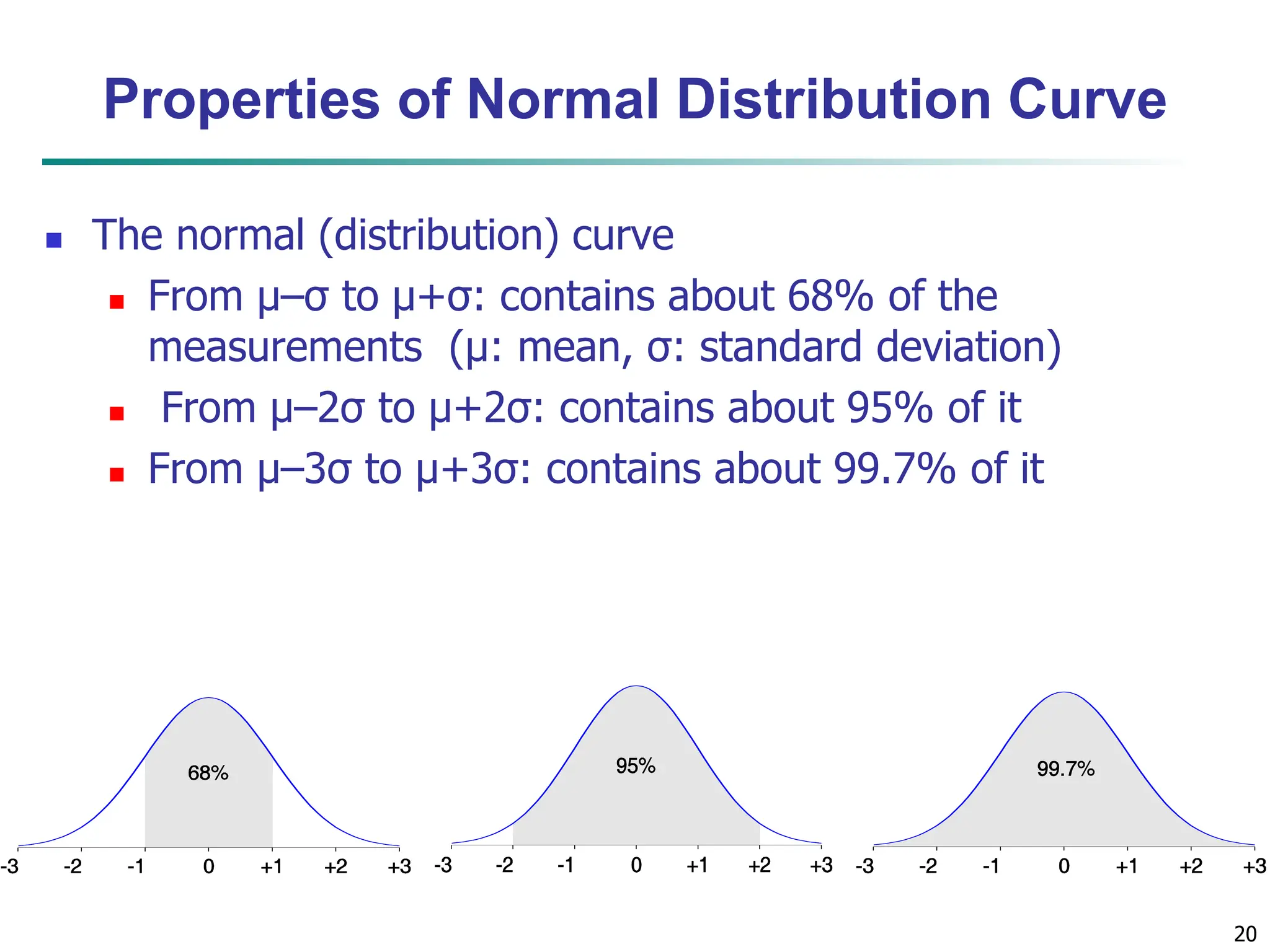
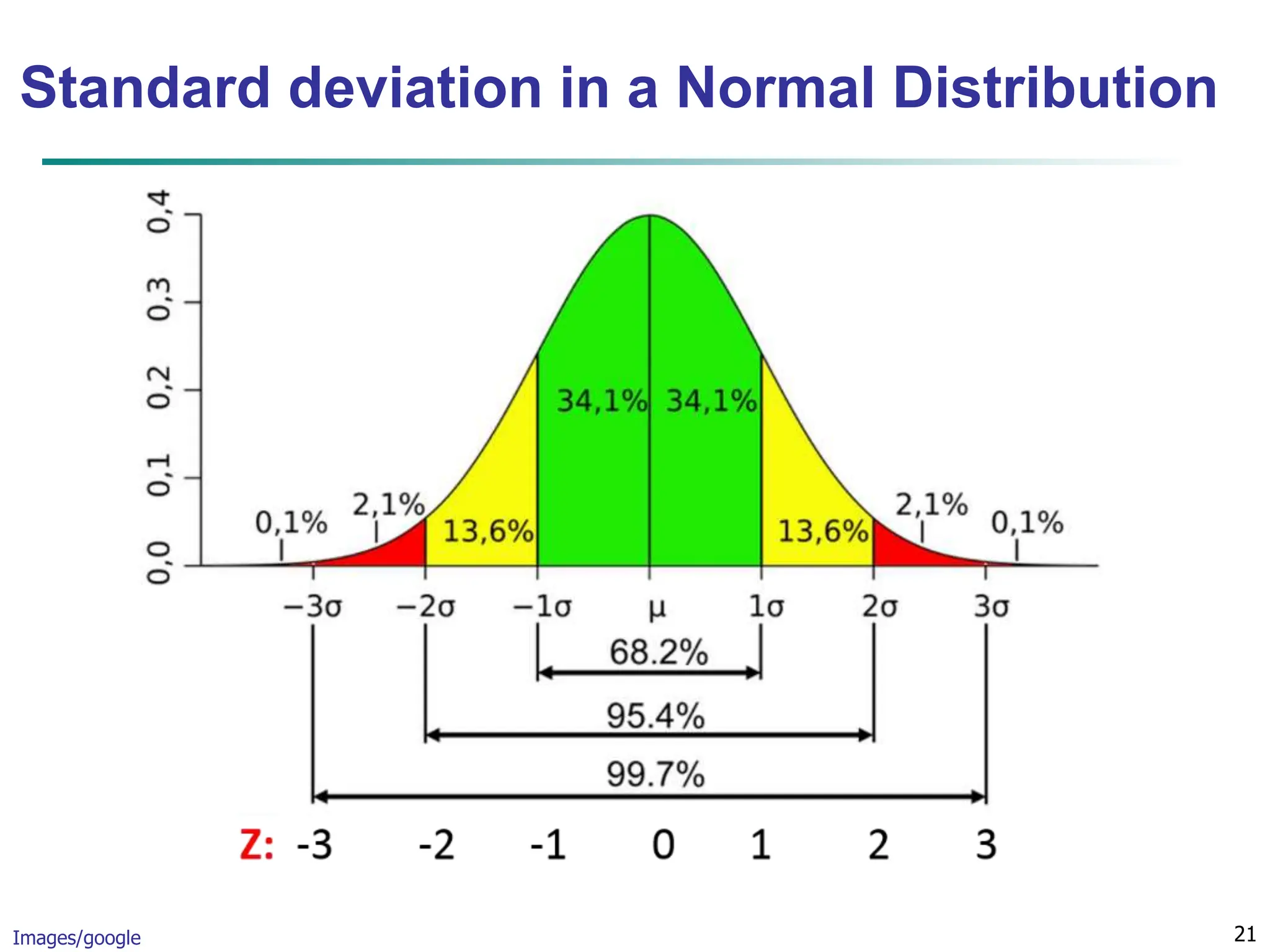
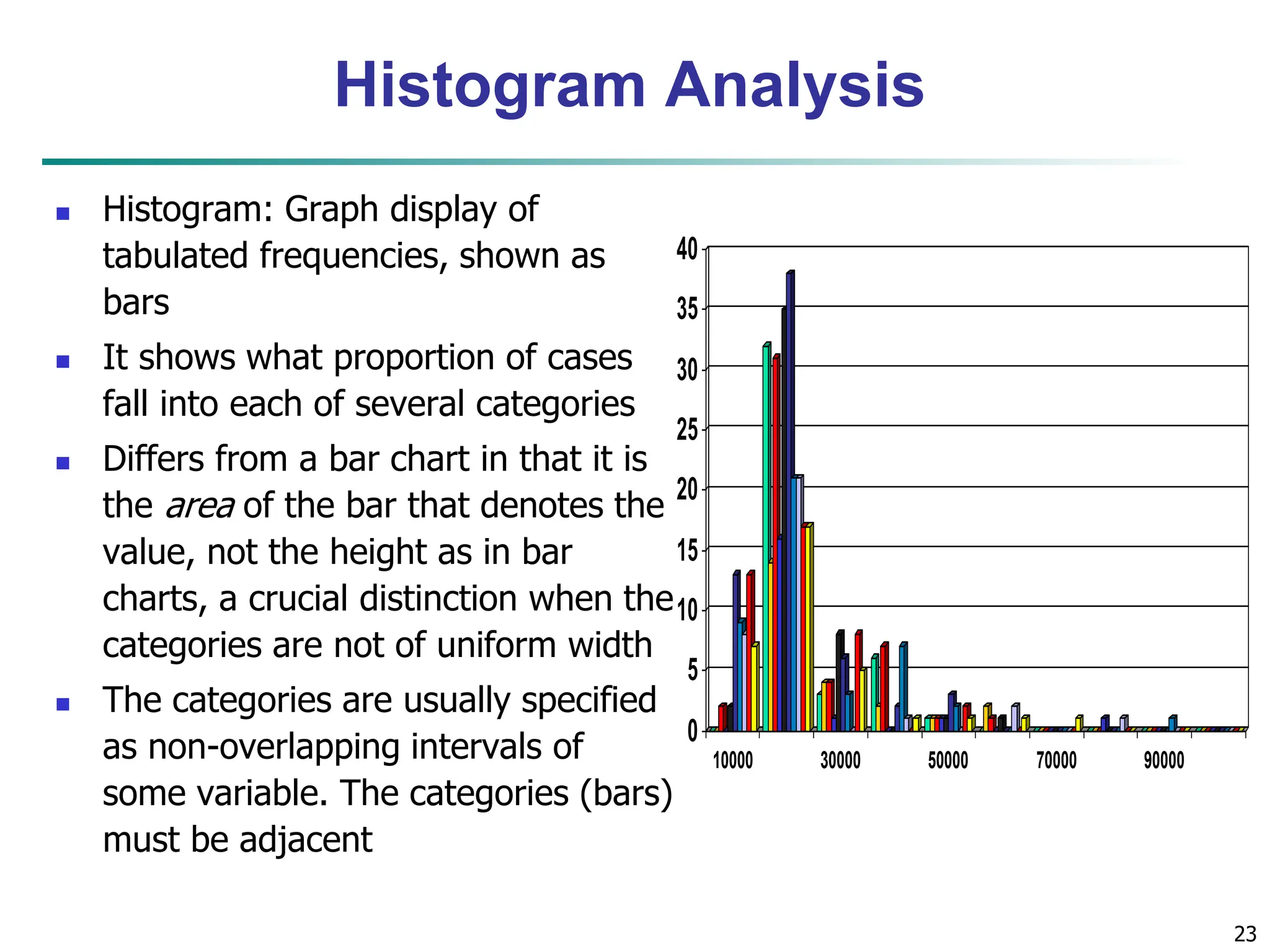
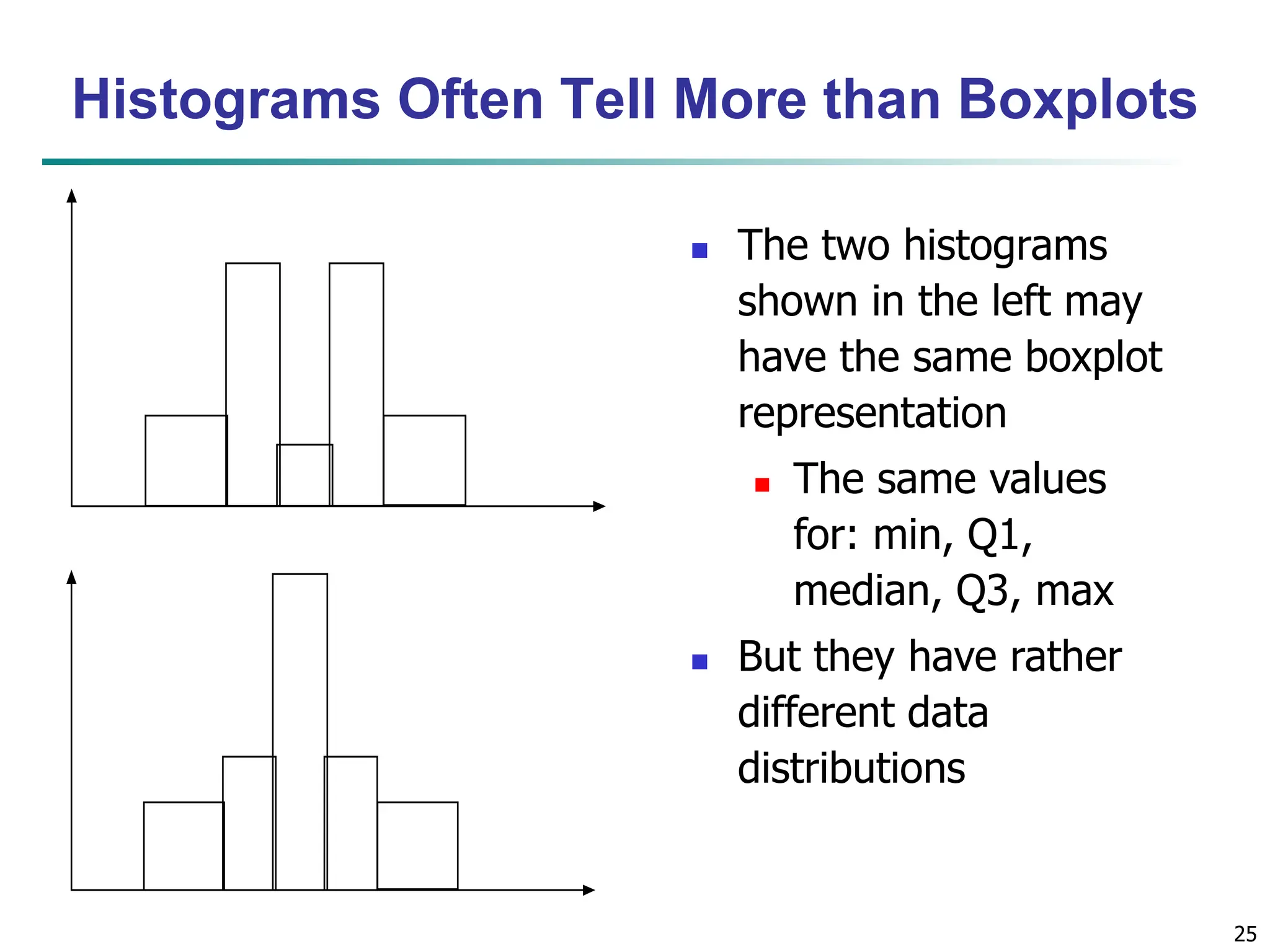
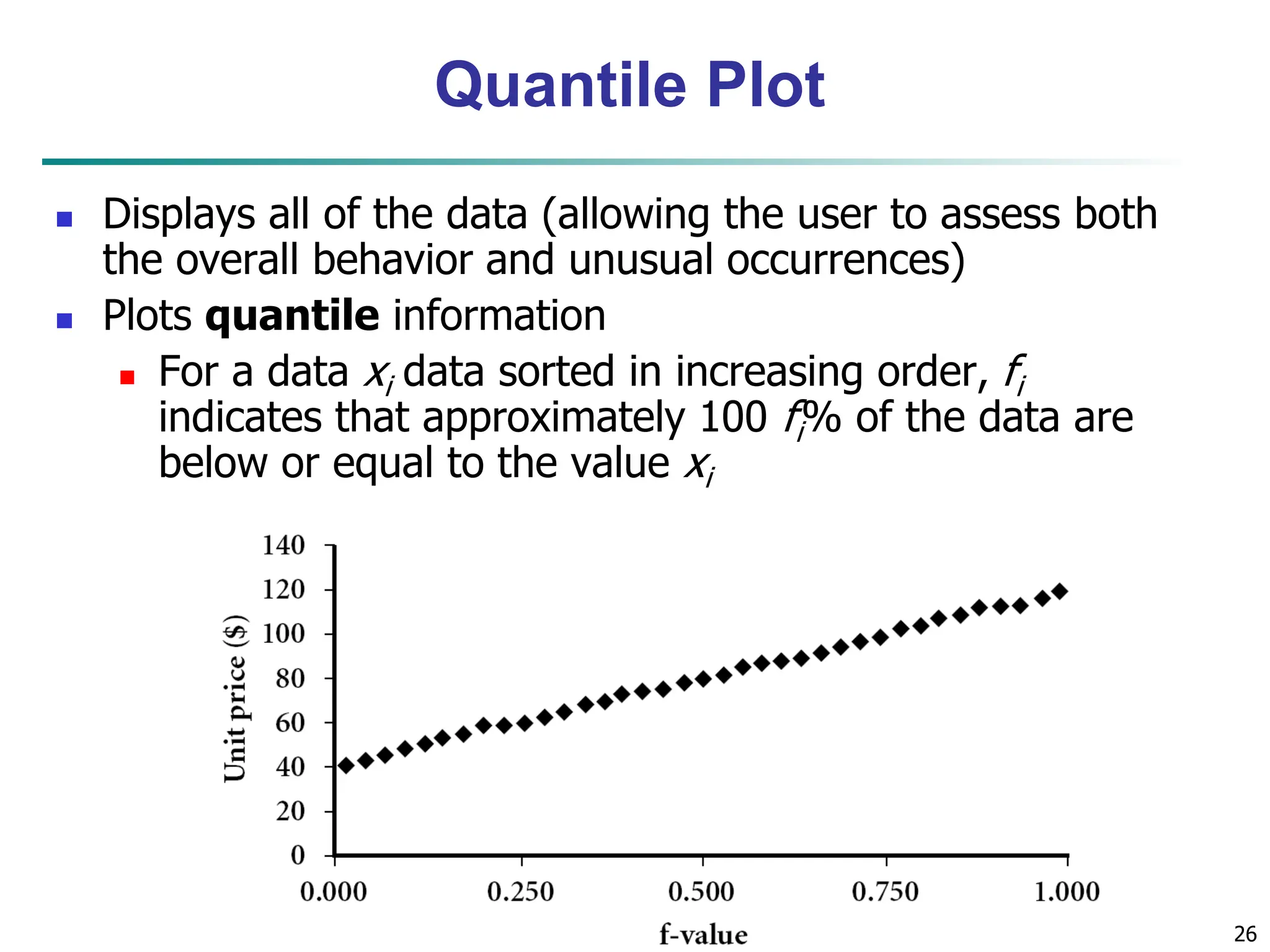
The document outlines concepts related to data mining, particularly focusing on understanding data objects, attribute types, and statistical descriptions. It discusses various types of data sets, how to visualize data, and the measures of similarity and dissimilarity between data objects. Key methodologies for statistical analysis and visualization techniques, such as box plots and histograms, are also highlighted.













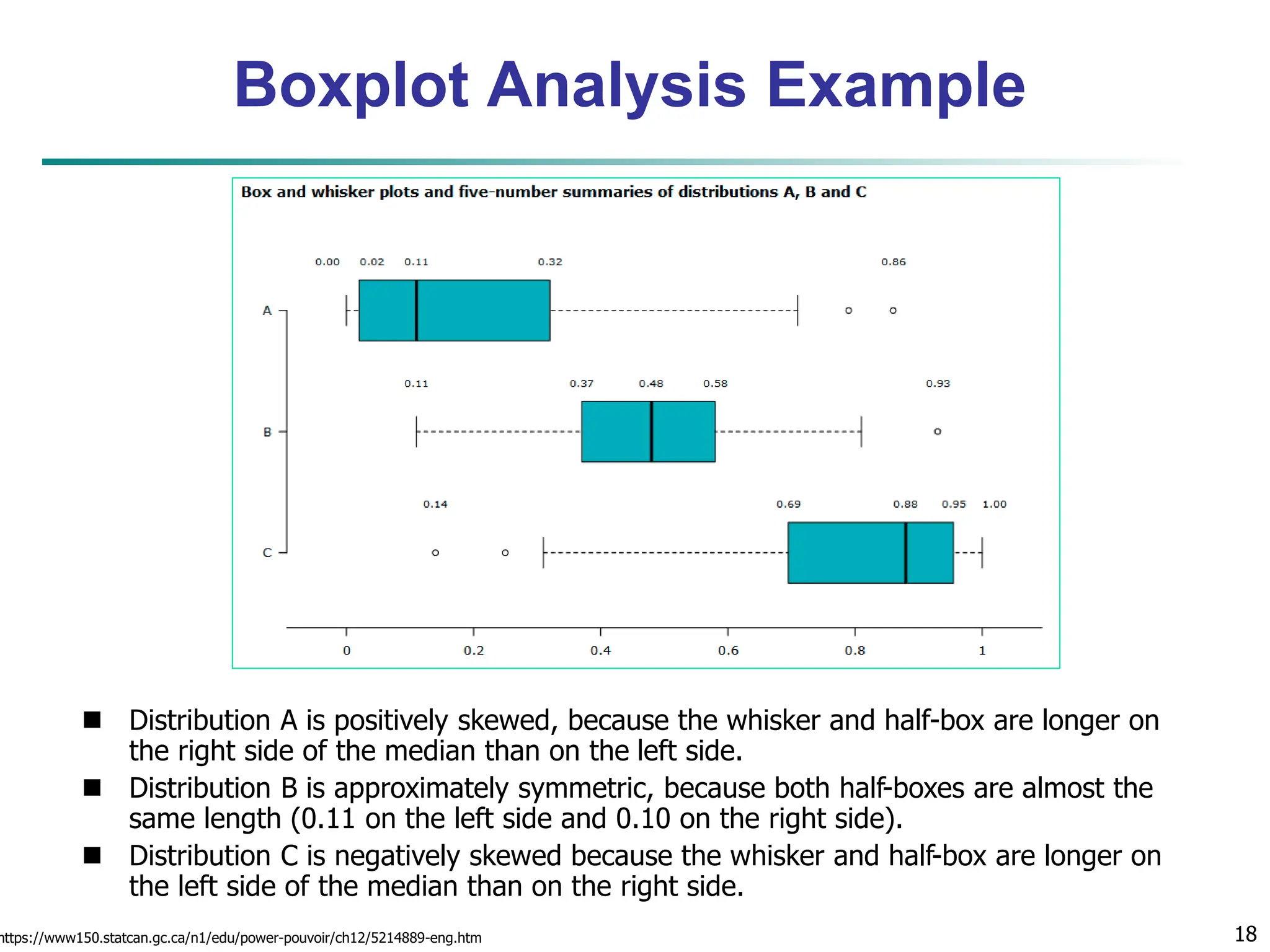
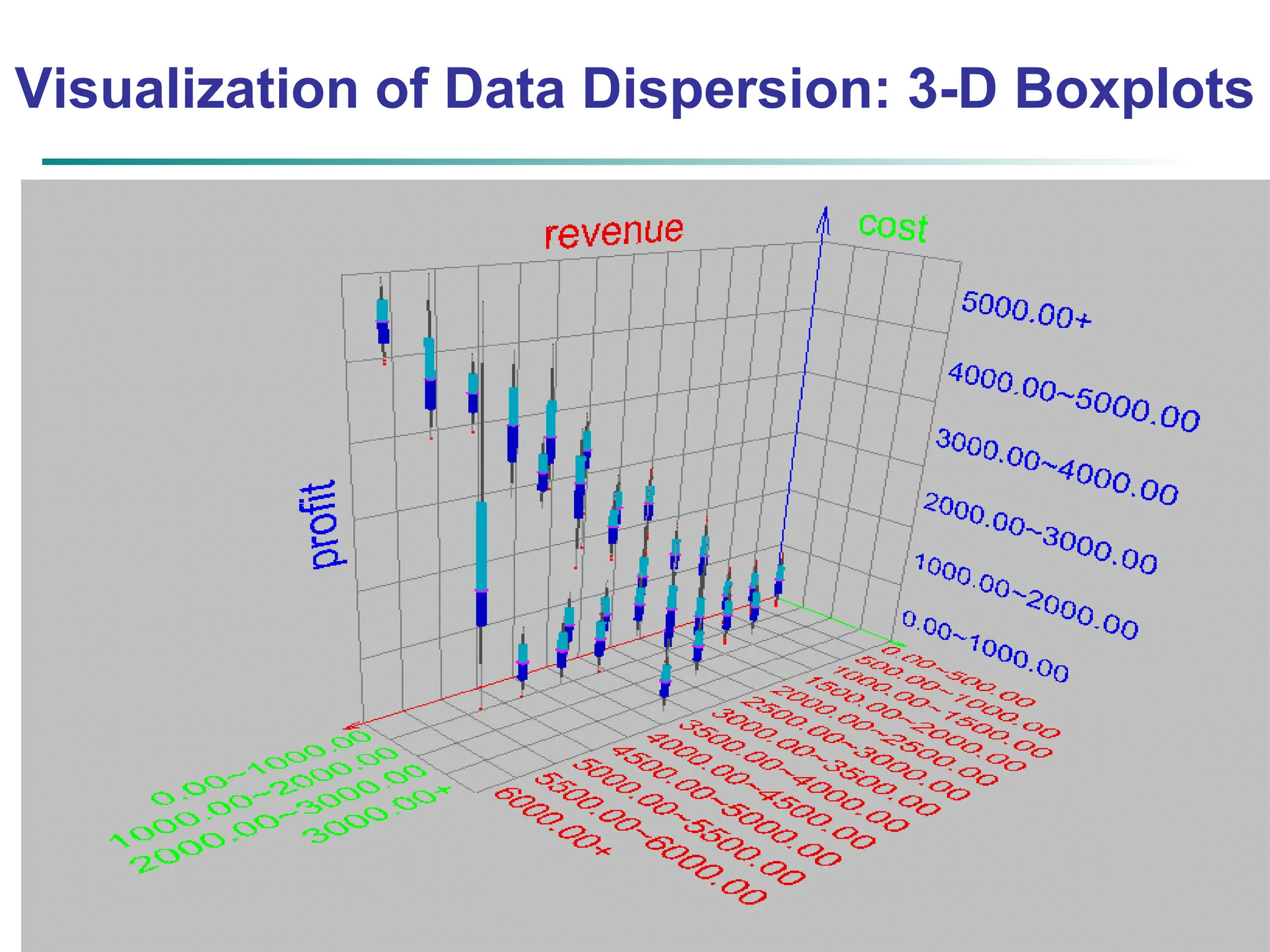
![16 Measuring the Dispersion of Data Quartiles, outliers and boxplots Quartiles: Q1 (25th percentile), Q3 (75th percentile) Inter-quartile range: IQR = Q3 – Q1 Five number summary: min, Q1, median, Q3, max Boxplot: ends of the box are the quartiles; median is marked; add whiskers, and plot outliers individually Outlier: usually, a value higher/lower than Q3 + 1.5 x IQR or Q1 – 1.5 x IQR Variance and standard deviation (sample: s, population: σ) Variance: (algebraic, scalable computation) Standard deviation s (or σ) is the square root of variance s2 (or σ2) n i n i i i n i i x n x n x x n s 1 1 2 2 1 2 2 ] ) ( 1 [ 1 1 ) ( 1 1 n i i n i i x N x N 1 2 2 1 2 2 1 ) ( 1 ](https://image.slidesharecdn.com/02knowyourdata-lecture2-3-240508102118-9b4520bb/75/Know-Your-Data-in-data-mining-applications-16-2048.jpg)



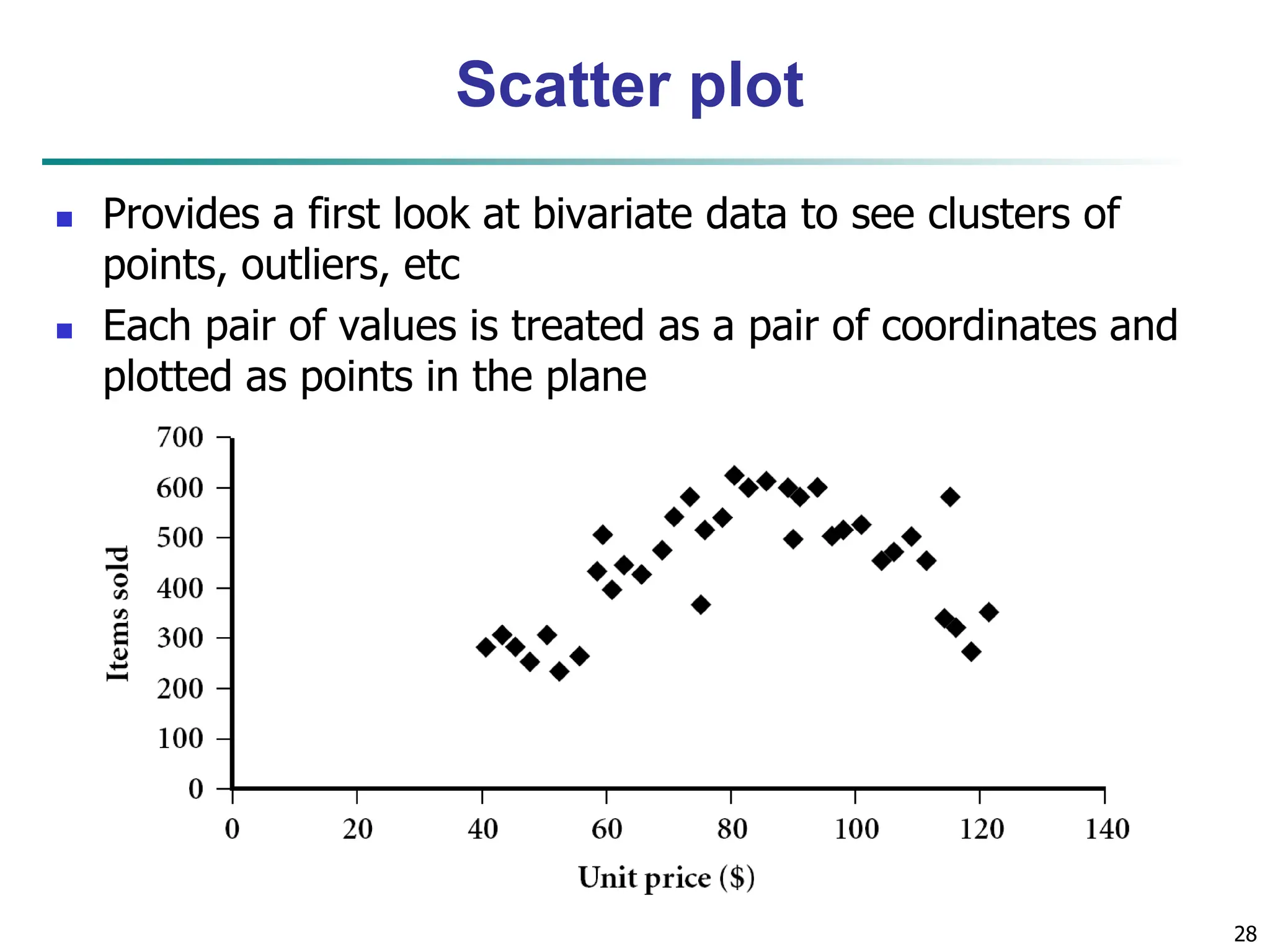
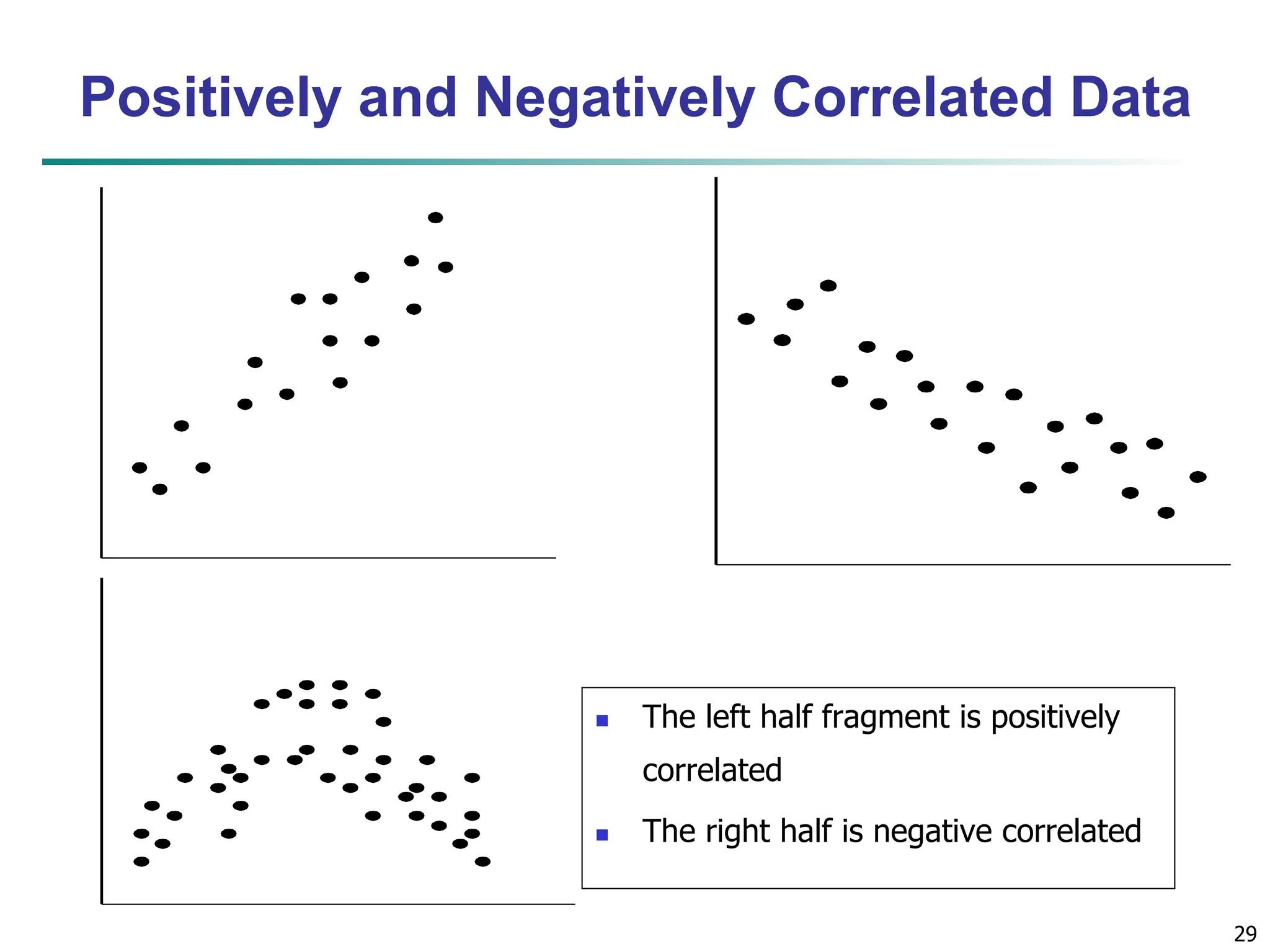


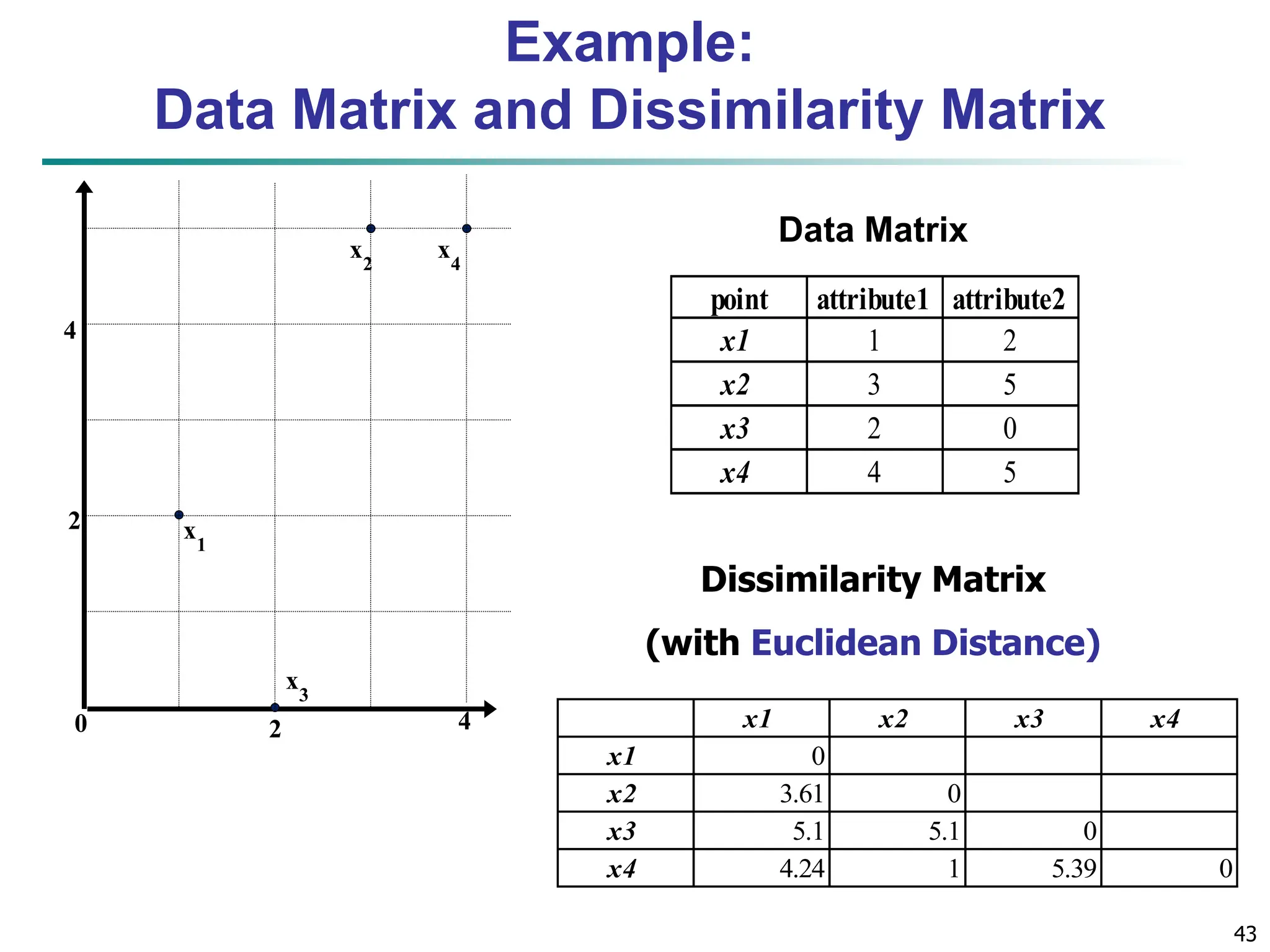
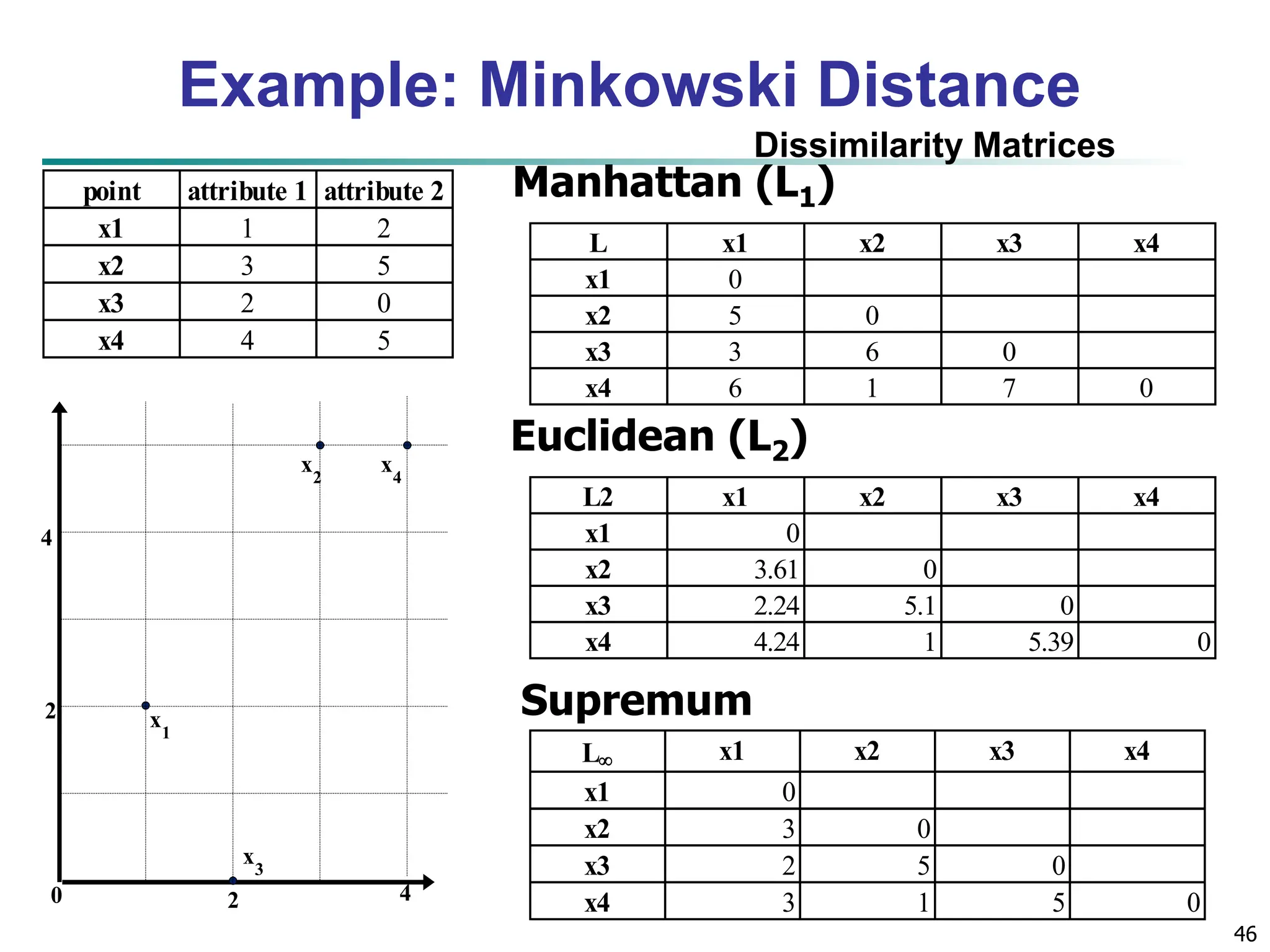
![32 Similarity and Dissimilarity Similarity Numerical measure of how alike two data objects are Value is higher when objects are more alike Often falls in the range [0,1] Dissimilarity (e.g., distance) Numerical measure of how different two data objects are Lower when objects are more alike Minimum dissimilarity is often 0 Upper limit varies Proximity refers to a similarity or dissimilarity](https://image.slidesharecdn.com/02knowyourdata-lecture2-3-240508102118-9b4520bb/75/Know-Your-Data-in-data-mining-applications-32-2048.jpg)












![47 Ordinal Variables An ordinal variable can be discrete or continuous Order is important, e.g., rank Can be treated like interval-scaled replace xif by their rank map the range of each variable onto [0, 1] by replacing i-th object in the f-th variable by compute the dissimilarity using methods for interval- scaled variables 1 1 f if if M r z } ,..., 1 { f if M r ](https://image.slidesharecdn.com/02knowyourdata-lecture2-3-240508102118-9b4520bb/75/Know-Your-Data-in-data-mining-applications-47-2048.jpg)





