Ang Chen, profile picture
Uploaded byAng Chen
647 views

Java Code Generation from Formal Models: The CO-OPN Framework

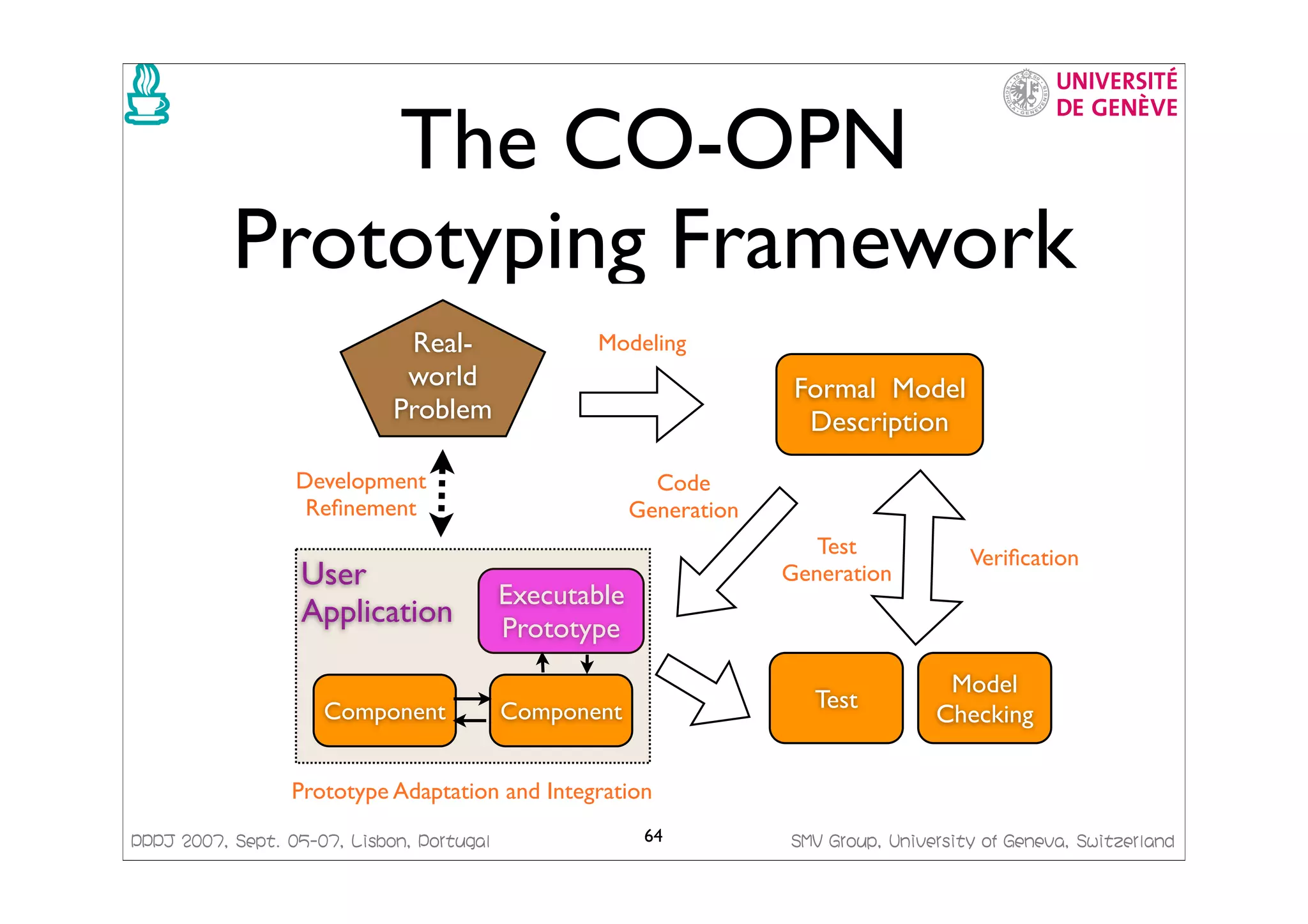
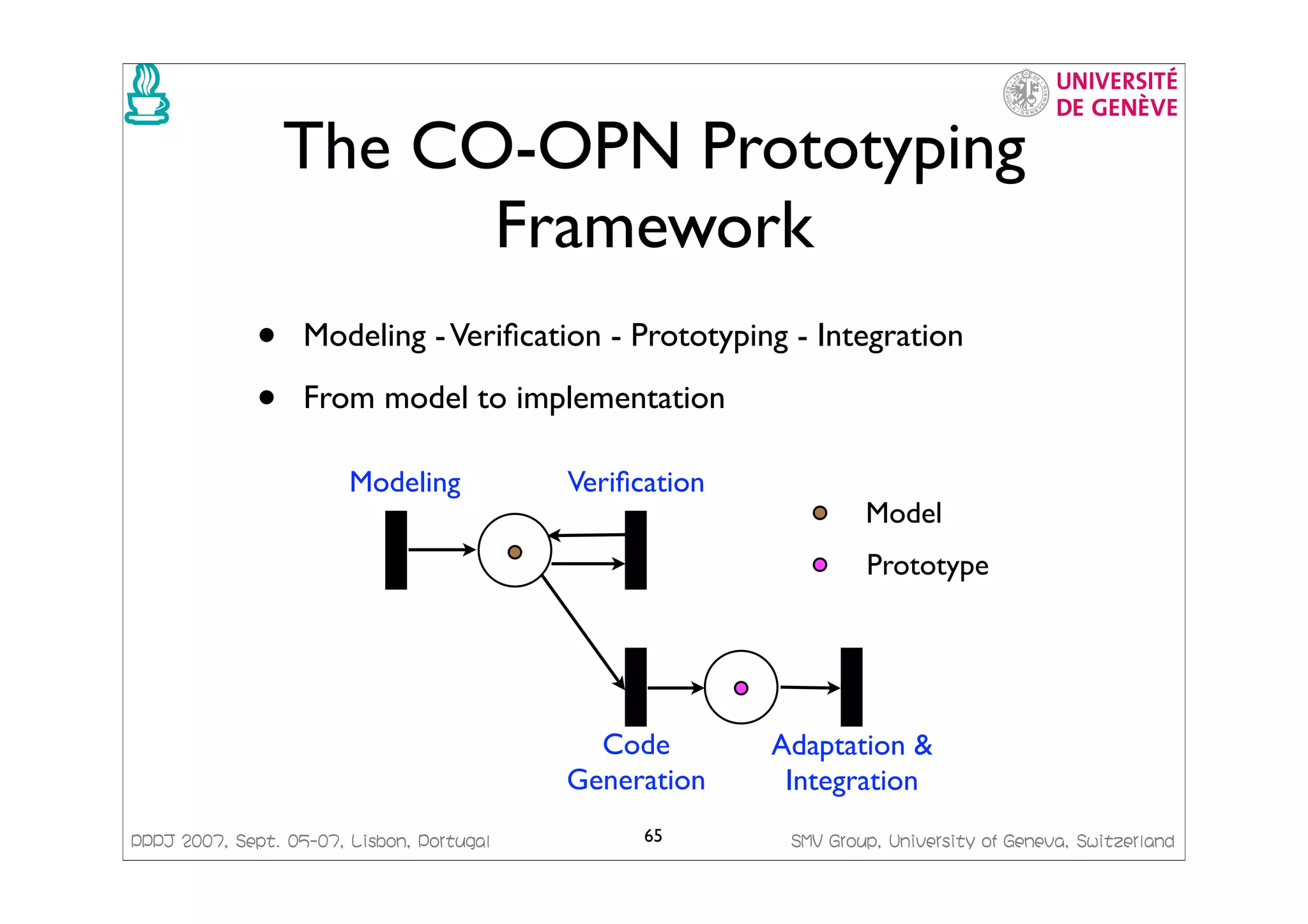
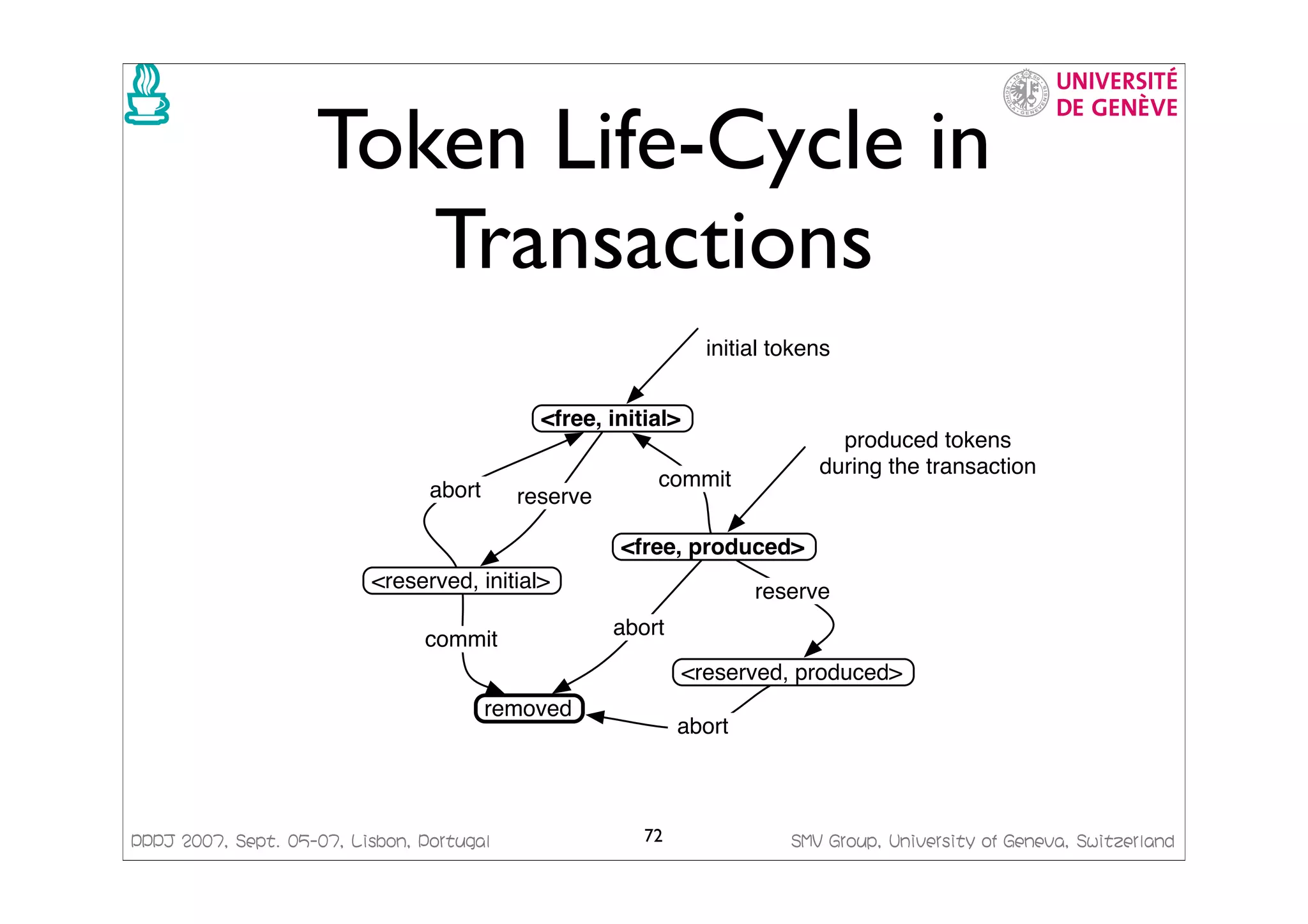
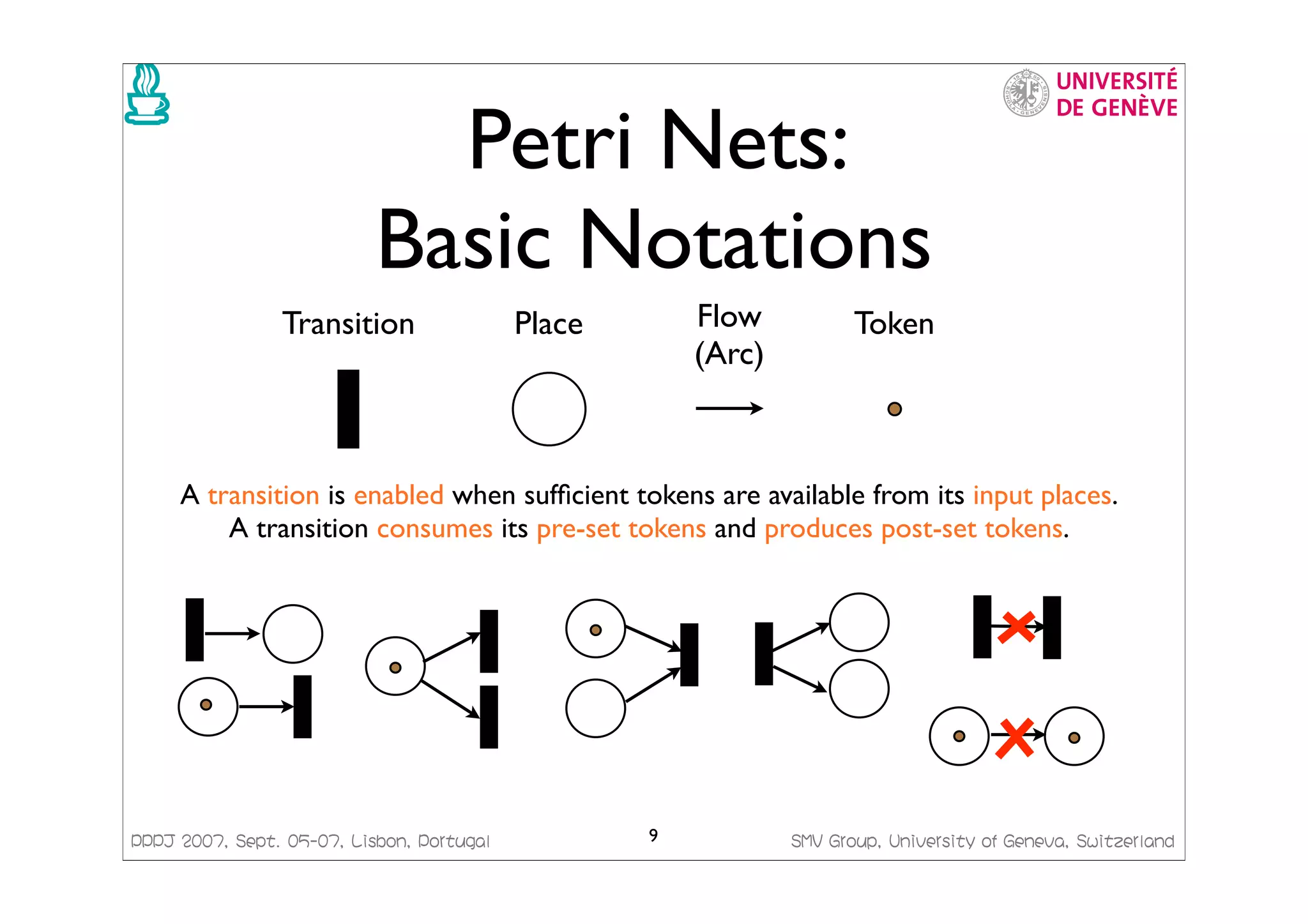
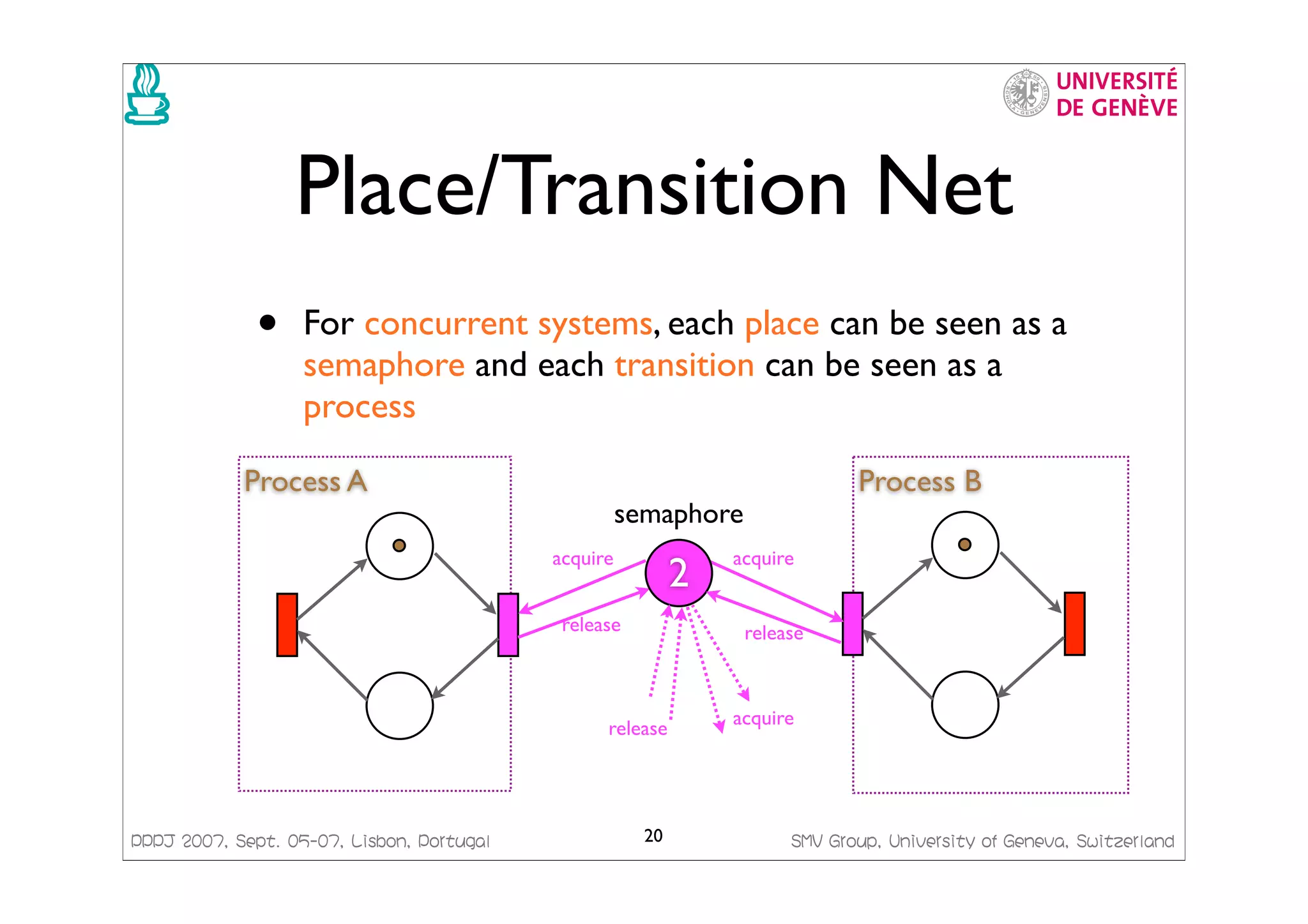
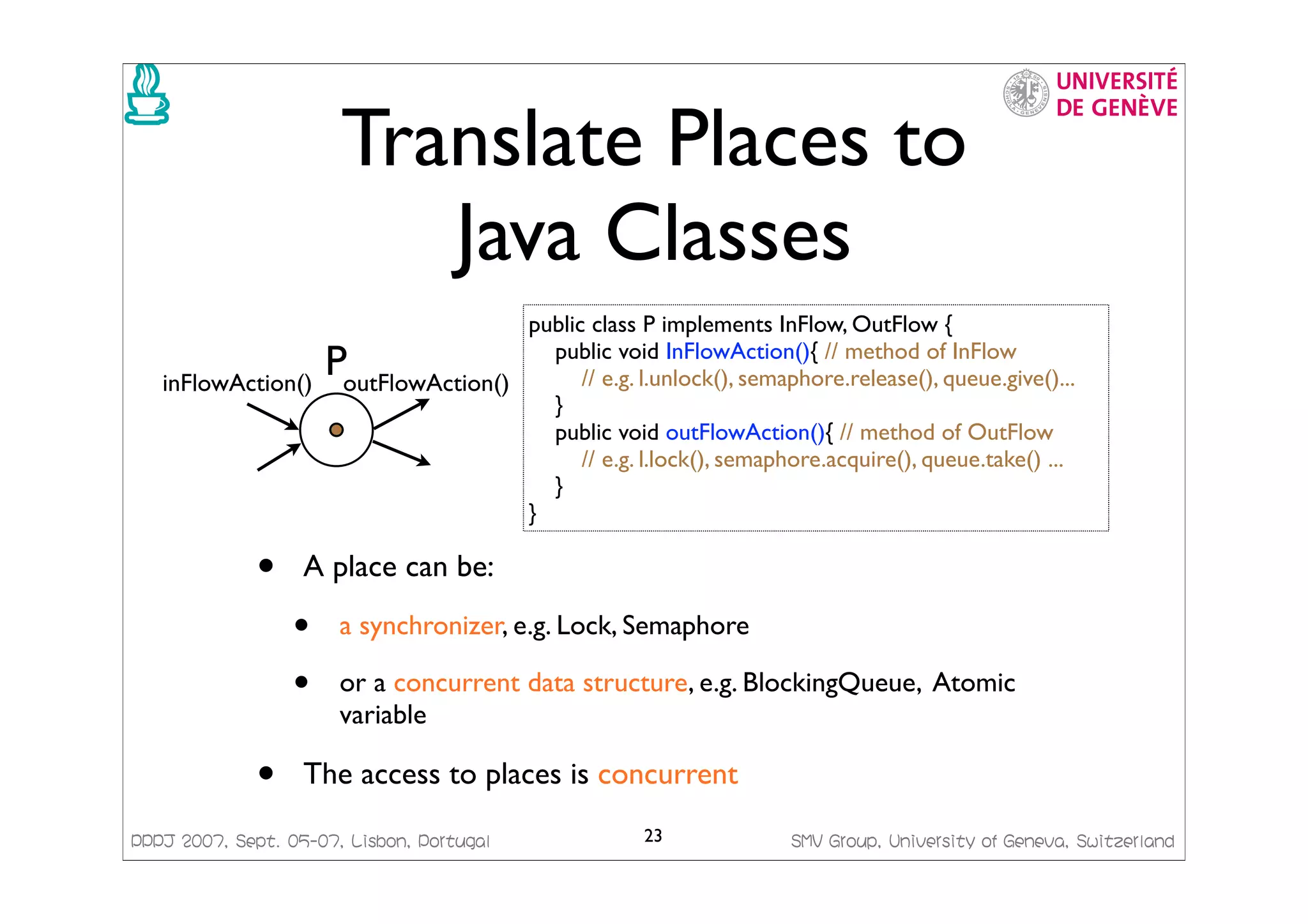
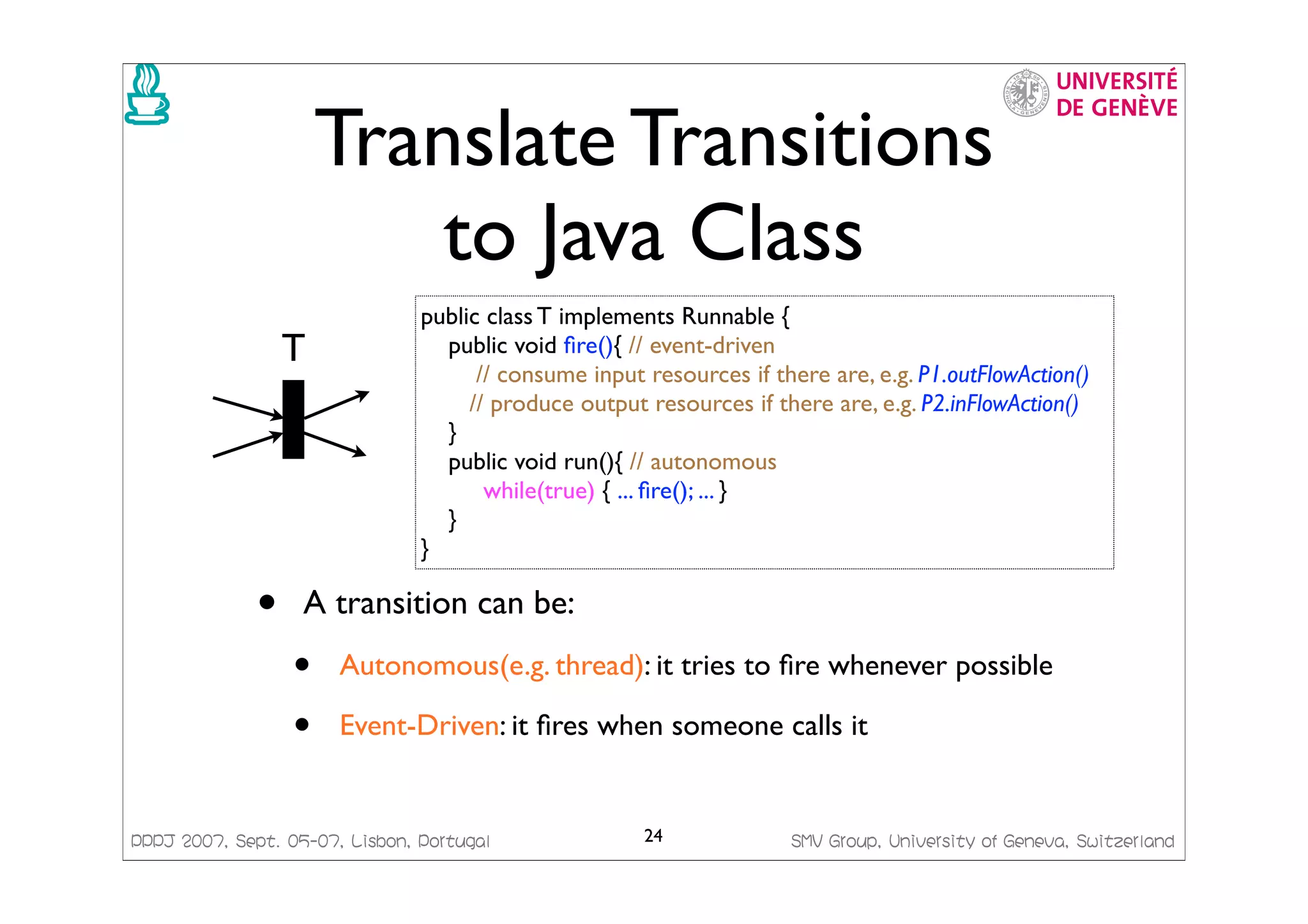
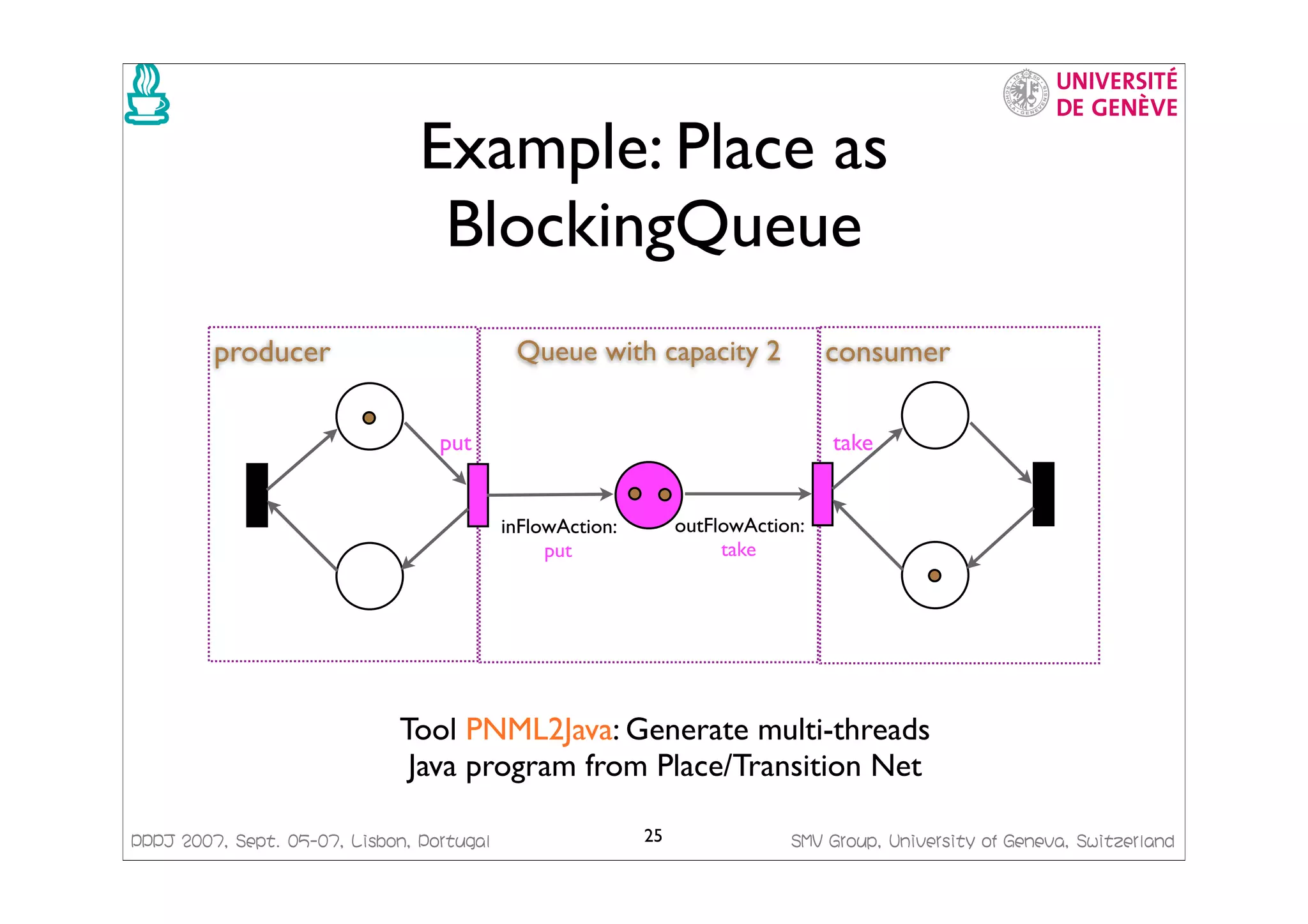
This document presents a framework for generating Java code from formal models. It discusses managing concurrency with Petri nets, modeling transactional systems with Concurrent Object-Oriented Petri Nets (CO-OPN), and the CO-OPN code generation framework. The tutorial aims to demonstrate the advantages of model-based development using formal models like Petri nets, including precise semantics, platform independence, and automatic model checking, testing and code generation.

Downloaded 25 times
Java Code Generation from Formal Models The CO-OPN Framework Ang Chen, Matteo Risoldi, Didier Buchs System Modeling and Verification Group University of Geneva, Switzerland {ang.chen, matteo.risoldi, didier.buchs}@cui.unige.ch Principles
and
Practices
of
Programming
in
Java
 Sept.
05-07,2007
Lisbon,
Portugal
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Objective of this tutorial • Present a framework to develop concurrent, transactional systems and applications from high-level concurrent models to executable Java code • Show the advantages of model-based development with formal models such as Petri nets: • Precise semantics, non-ambiguity • Platform independent • Automatic model checking, test, and code generation (model transformation) 2
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Outline • Part I: Manage Concurrency with Petri Nets • Petri nets for concurrent modeling • From PN models to concurrent Java programs • Part II: Concurrent Object-Oriented Petri Nets • Modeling transactional systems with CO-OPN • CO-OPN code generation framework • Conclusion 3
Part I: Manage Concurrency with Petri Nets 4
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Concurrent System • The world is concurrent • Autonomous: the system runs independently from others • Reactive (or interactive): it reacts to external events and actions • Parallel: things (events, actions) happen in parallel • Example: distributed computers, control system (e.g. aircraft), workflow • In computer science, concurrency means resources sharing which may cause race conditions 5
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Java Concurrency Utilities (JSR 166) • Tasks scheduling, e.g. Executor • Concurrent collections • Atomic variables • Semaphores, barriers, latches, exchangers • Locks Threads Data Structures Synchronizers 6
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Why Formal Models? • Concurrent and distributed systems are complex, difficult to develop and manage • To ensure the safety of critical systems, e.g. prove that the system can operate without failures before implementation • Widely used formal methods: relational algebra in DB, boolean algebra in circuit design, Finite State Machines in many systems ... 7
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Petri Net: Definition • A Petri net is a directed bipartite graph (P, T, F, M): • P is a finite set of places • T is a finite set of transitions • P and T are disjoint, (P∩T =Φ) • F (P×T)∪(T×P) is the flow relation • Marking M is the distribution of tokens in the PN • Token is defined according to the type of PN 8
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Petri Nets: Basic Notations Transition Place Flow (Arc) Token A transition is enabled when sufficient tokens are available from its input places. A transition consumes its pre-set tokens and produces post-set tokens. 9
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland PN: Concurrency T1P1 P3 T2P2 P4 T1 andT2 are concurrent and independent Simultaneously enabled and firable transitions are called concurrent 10
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland PN: Concurrency T1 T2 P1 T1 andT2 are simultaneously enabled, but they have a conflict on P1 Interleaving 11
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland PN: Concurrency T1 T2 P1 T1 andT2 are simultaneously enabled, but they have a conflict on P1 The can be fired concurrently only when sufficient resources are available in P1 (e.g. >=2 tokens) 12
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland PN: Join • When a transition has multiple incoming flow T3 is not enabled until bothT1 andT2 have terminated. Also called barrier, join point, rendez-vous T1 P1 P3 P2T2 T3 13
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland PN: Split • When a transition has multiple outgoing flow T1 P2 P3 P1 Also called fork or parallel split e.g. creating new threads, parallel tasks 14
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland PN: Non-determinism • When a place has multiple outgoing flow Consumer 1 resource container Producer Consumer 2 Consumer 3 ? 15
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Petri Nets: Modeling • Different PN formalisms propose different constraints for place, token, and firing rules. • Petri net models and their properties are independent of the application domain • For a concrete application domain, an operational semantics or interpretation is needed for the PN formalism This is a deadlock-free PN What is the meaning of each place, transition, token, and flow? 16
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Petri Net: Modeling • For example, in workflow and manufacturing systems, we use: • Transitions to represent tasks; places to represent steps • Tokens to represent documents and physical objects receive order schedule shipping schedule production schedule collect payment order payment invoice send invoice create invoice An E-CommerceWorkflow 17
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Petri Nets:Applications Railway Network Telephony System Communication Protocol Petri Nets Theory Control System Distributed System Workflow We will apply the Place/Transition Nets for the problem of concurrent programming Concurrent Programming 18
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Place/Transition Net • Tokens are indistinguishable • The marking of a place is represented by an integer n≥0, the number of tokens in the place • The incoming arcs increase the value of n • The outgoing arcs of a place decrease the value of n 01210 19
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Place/Transition Net • For concurrent systems, each place can be seen as a semaphore and each transition can be seen as a process Process A Process B semaphore 2 acquire release acquire release release acquire 20
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland PN in Concurrent Programming: Rules • Rule 1: Each transition is a schedulable task which tries to consume resources from its input flow • Rule 2: Simultaneously enabled transitions are concurrent or in conflict • Rule 3: The task is hanged if the necessary resources are not available • Rule 4: The task is eligible to run if it is enabled (acquired all necessary resources) TP1 P2 while(true) { if (all pre-tokens are ready) { P1.take() ... P2.put() ... } else suspend(); } 21
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland PN in Concurrent Programming: Rules • Rule 5:The acquisition of resources is sequential and transactional, i.e. the taken resources are released in case of failure • Rule 6:The output flow of a transition will produce or release resources to the corresponding places, it is also sequential and transactional Conflicts on multiple resources may imply deadlocks during sequential execution: T3 is holding P1 and waiting on P2 T4 is holding P2 and waiting on P1 Thus, a transition should release its taken resources in case of failure. T3 T4 P1 P2 P3 P4 22
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Translate Places to Java Classes • A place can be: • a synchronizer, e.g. Lock, Semaphore • or a concurrent data structure, e.g. BlockingQueue, Atomic variable • The access to places is concurrent public class P implements InFlow, OutFlow { public void InFlowAction(){ // method of InFlow // e.g. l.unlock(), semaphore.release(), queue.give()... } public void outFlowAction(){ // method of OutFlow // e.g. l.lock(), semaphore.acquire(), queue.take() ... } } inFlowAction() outFlowAction() P 23
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Translate Transitions to Java Class • A transition can be: • Autonomous(e.g. thread): it tries to fire whenever possible • Event-Driven: it fires when someone calls it public class T implements Runnable { public void fire(){ // event-driven // consume input resources if there are, e.g. P1.outFlowAction() // produce output resources if there are, e.g. P2.inFlowAction() } public void run(){ // autonomous while(true) { ... fire(); ... } } } T 24
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Queue with capacity 2 Example: Place as BlockingQueue producer consumer put take outFlowAction: take inFlowAction: put Tool PNML2Java: Generate multi-threads Java program from Place/Transition Net 25
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Translation of PN to Java Concurrent Program Petri Nets Java Autonomous transition Runnable Class Event-Driven transition Class Method Place Lock, Semaphore, BlockingQueue, Synchronized Channel ... Token Thread-safe data and resources Deadlock-free PN Deadlock-free program 26
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Dining Philosophers • 5 philosophers sitting around the table with 5 forks • each philosopher passes time for thinking and eating • in order to eat, he or she should have the left-side fork and the right-side fork in hands • after eating, the two forks are released •Deadlocked when each philosopher is holding one fork and waiting for the other one and nobody releases a fork 27
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Statement I “If all the philosophers are leftie* or all of them are rightie, the system has deadlock” Is it true? How to prove it? Manually or automatically? 28 *A leftie takes the left fork first, then the right fork; the contrary for a rightie.
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland A Philosopher (Leftie) Thinking Eating GoThinking Left Fork Right Fork Take Left Take Right While(true) { TakeLeft(); TakeRight(); eating ... GoThinking(); } 29
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Thinking Eating GoThinking Take Left Take Right Thinking Eating GoThinking Take Left TakeRight Thinking Eating GoThinking TakeLeft Take Right Thinking Eating GoThinking TakeLeft Take Right Thinking Eating GoThinking TakeLeft TakeRightFork 0 Fork 1 Fork 2 Fork 3 Fork 4 Philosopher 0 Philosopher 1 Philosopher 2 Philosopher 3 Philosopher 4 PN: 5 leftie at the table Deadlock found with PN model-checking. The shortest path to deadlock is given. Tool used: Platform Independent Petri net Editor http://pipe2.sourceforge.net/ 30
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Statement II “It will be deadlock-free if there are at least one leftie and at least one rightie at the table” Is it true? How to prove it? 31
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland PN: 1 rightie + 4 leftie at the table Philosopher 0 is a rightie Deadlock-free proved by PN model-checking Thinking Eating GoThinking Take Left Take Right Thinking Eating GoThinking Take Left TakeRight Thinking Eating GoThinking TakeLeft Take Right Thinking Eating GoThinking TakeLeft Take Right Thinking Eating GoThinking TakeRight TakeLeft Fork 0 Fork 1 Fork 2 Fork 3 Fork 4 Philosopher 0 Philosopher 1 Philosopher 2 Philosopher 3 Philosopher 4 32
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Statement II “If only 4 philosophers are allowed at the table at a time, deadlock is impossible” Is it true? How to prove it? 33
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland More Statements “If a philosopher takes the two forks at the same time, deadlock is impossible” Are these statements true? Build the PN models and verify them! “If the philosophers can communicate with each other and ...” 34
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Part I: Summary • PN for concurrent programming: 1. Use Petri net to design concurrent programs: threads, semaphores, locks, channels. Do model checking for liveness, deadlock-freedom, fairness etc. 2. Generate project skeleton from the correct PN model 3. Implement the functionalities of threads without thinking about concurrency • This principle only works with Place/Transition Nets • What is still missing: encapsulation, transactional behavior, system coordination 35
Part II: Concurrent Object- Oriented Petri Net 36
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland CO-OPN Concurrent Object-Oriented Petri Nets • OO modeling language based on Petri Nets • Algebraic Abstract data types • Concurrency, transactionality • Can generate Java code 37
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
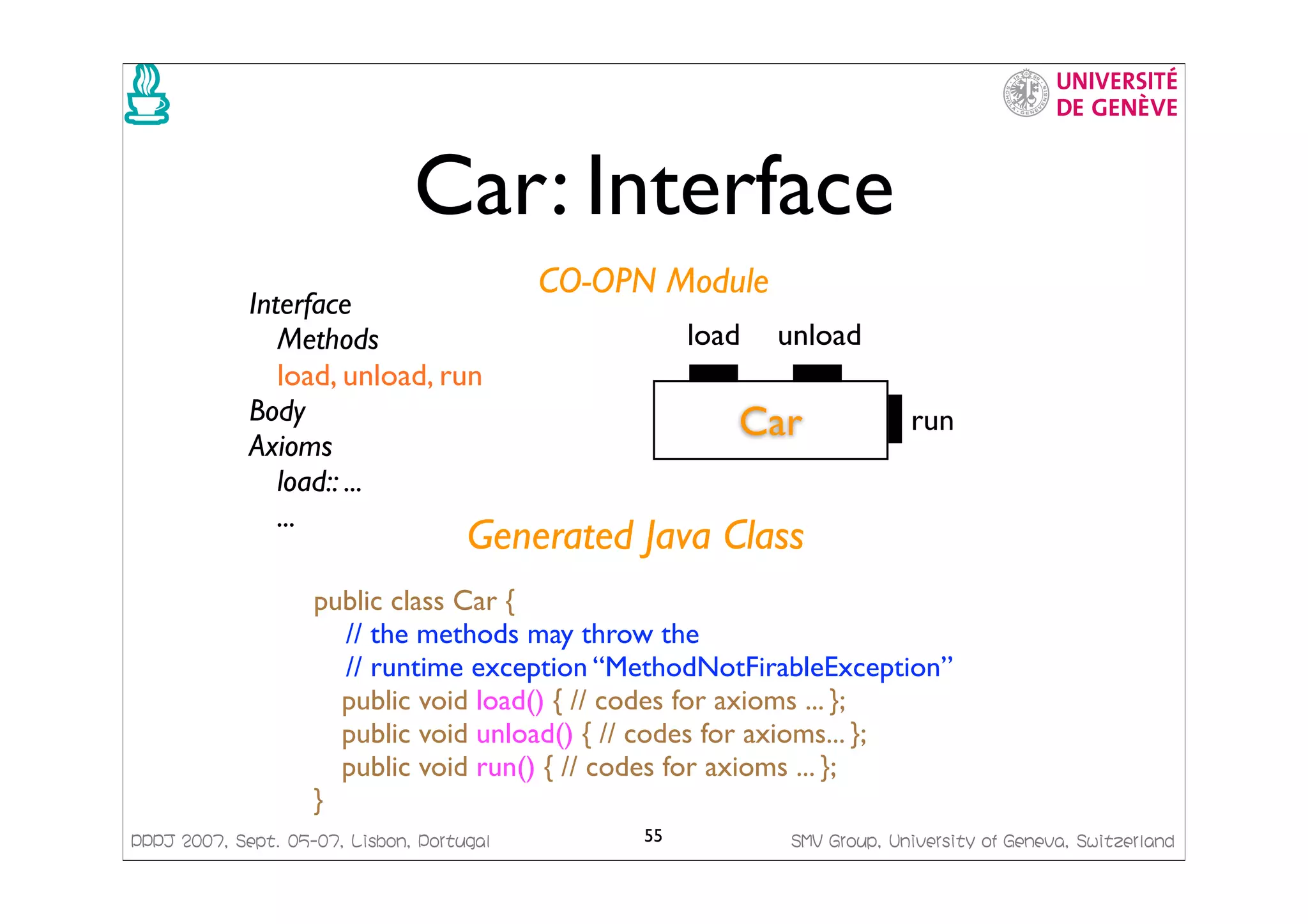
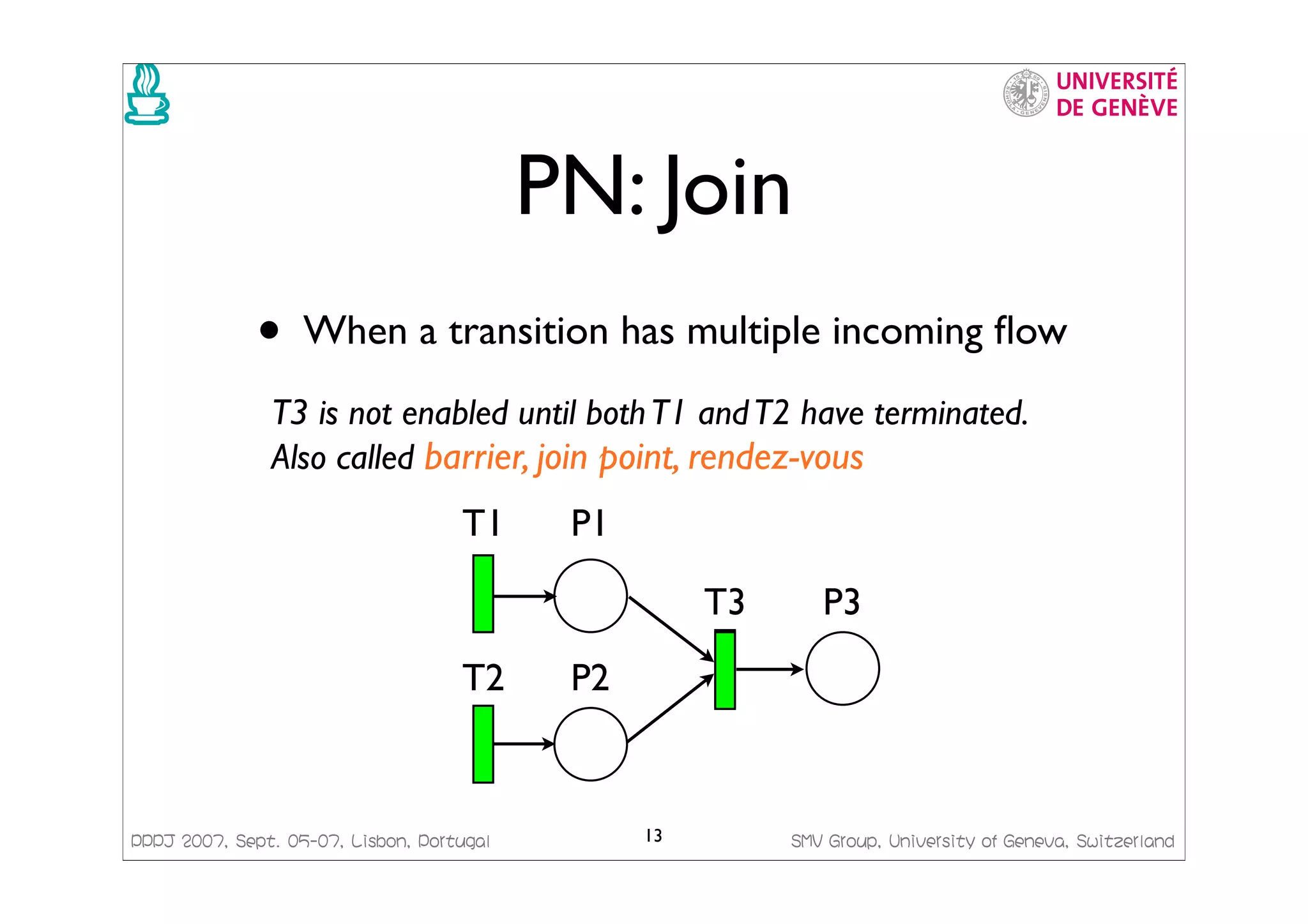
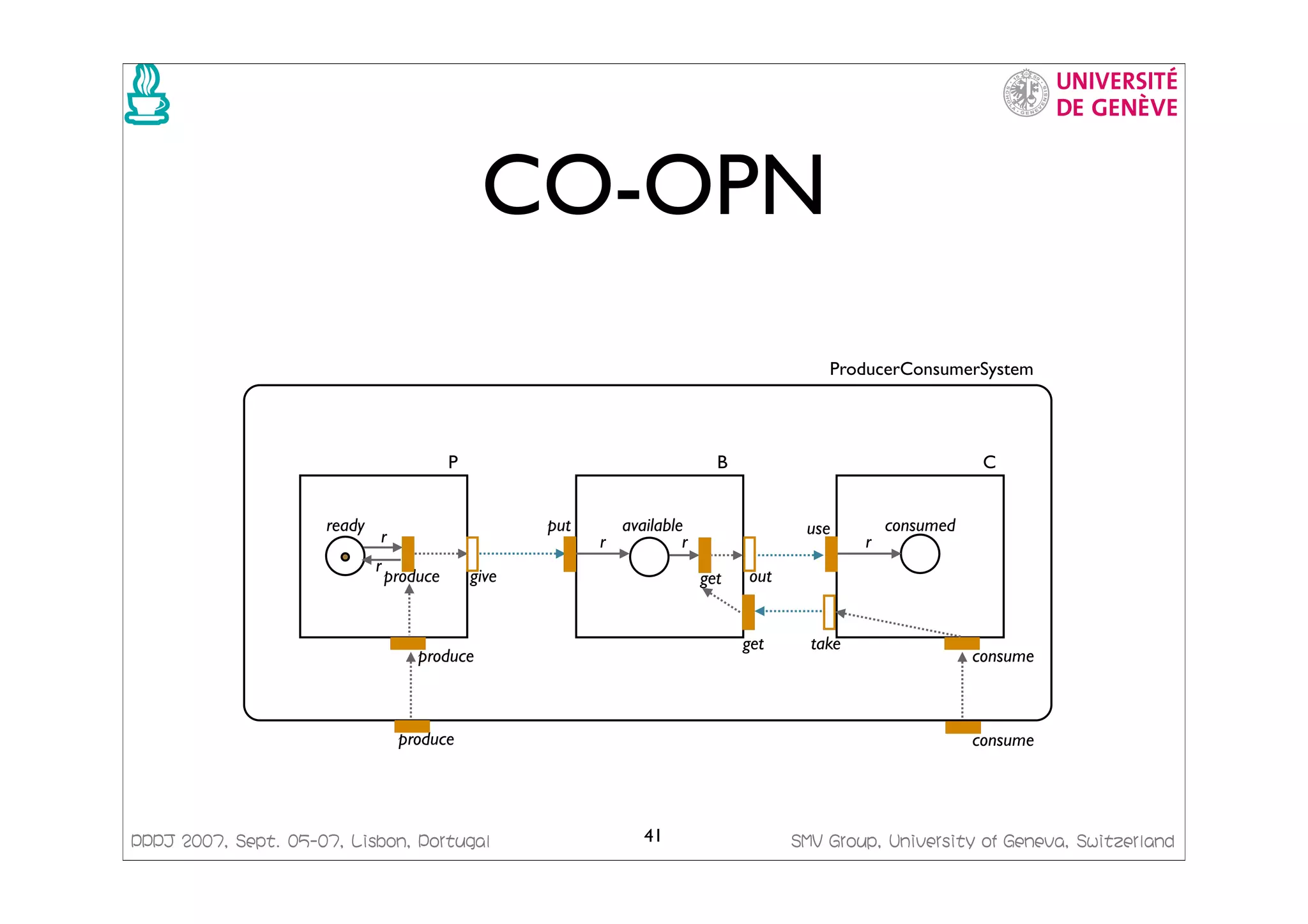
Switzerland CO-OPN Modules • Classes - encapsulate a Petri Net - have methods and gates (events) Producer produce produce ready give r r Class Producer; Interface Methods produce; Gates give; Body Places ready [...] End Producer; 38
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland CO-OPN Modules • Contexts - instantiate and coordinate objects P produce produce ready give r r C use consumed r ProducerConsumerSystem produce Context ProducerConsumerSystem; Interface Methods produce; [...] Body Objects P: Producer; C: Consumer; Axioms produce with P.produce; P.give with C.use; [...] End ProducerConsumerSystem; 39
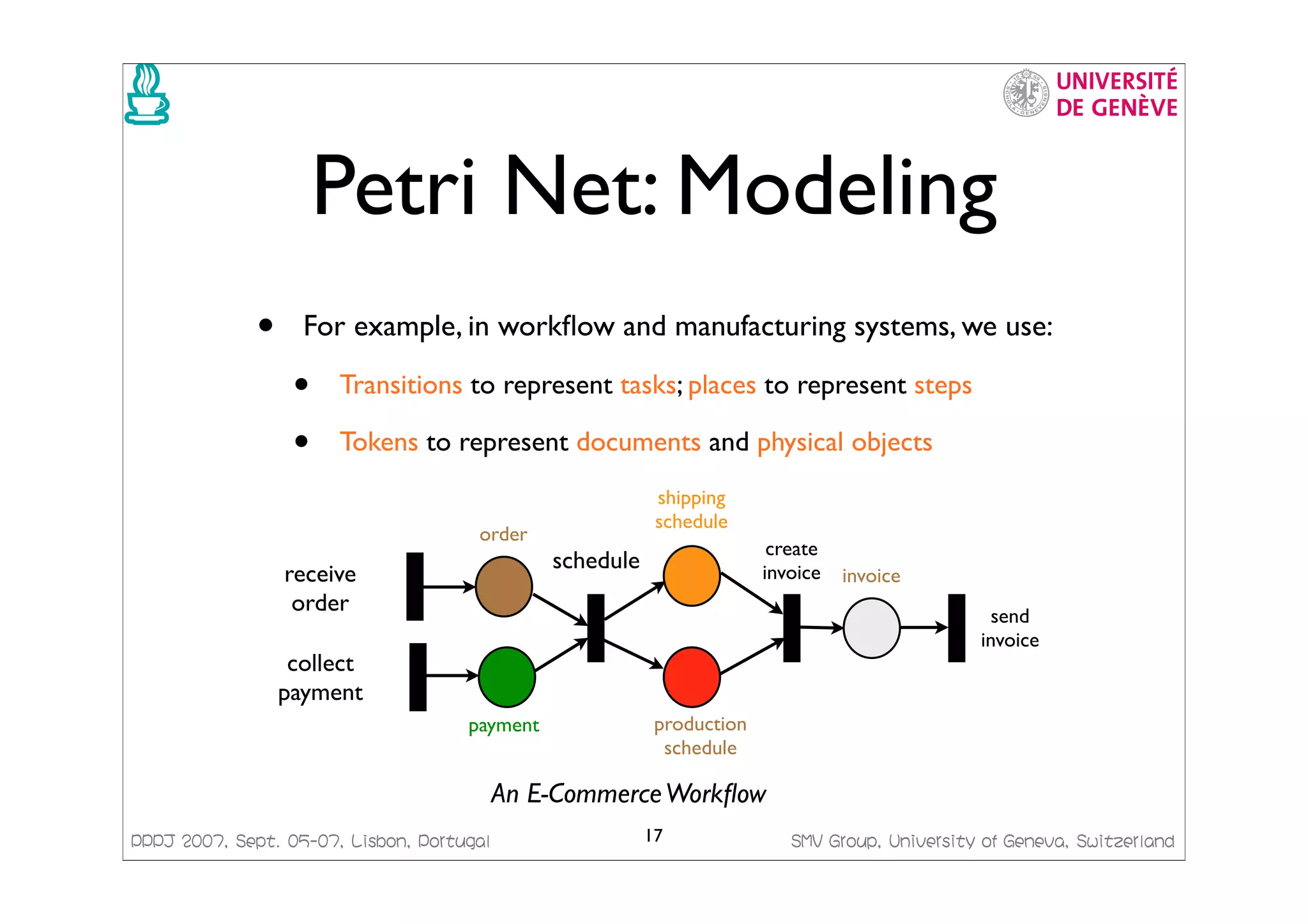
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland CO-OPN Modules • ADT (Abstract algebraic Data Types) - define data types (primitive + structured) • Generators • Operations • Theorems • Algebraic definition of data ADT Booleans; Interface Generators true:->boolean; false:->boolean; Operations _ and _: boolean, boolean -> boolean; [...] Axioms true and b = b; false and b = false; [...] End Booleans; 40
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland produce CO-OPN P B C produce produce take get put use consume ProducerConsumerSystem consume ready available consumed give out r r r r r get 41
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland CO-OPN Axiom syntax in brief Condition => transition with event :: pre -> post ; Condition Any boolean expression evaluated on tokens, parameters, values... Transition A method call or an event Event One or more method calls or events Pre Precondition of the transition, evaluated on tokens in the places Post Postcondition of the transition, evaluated on tokens in the places Ex. => produce with give :: ready t -> ready t ; Producer produce produce ready givet t 42
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland CO-OPN Transactions Operators Parallel // : m1//m2, m1 and m2 occur simultaneously, i.e. concurrent access of resources Sequence .. : m1..m2, m2 occurs after the success of m1 Alternative + : m1 + m2, m1 or m2 can have success (nondeterministic) Ex: => m with m1//m2:: ->; • ACID* Properties respected *Atomicity, Consistency, Isolation, Durability 43
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland CO-OPN Transactions transition with event1 .. (event2 // event3) What happens to transition, event1 and event2 if something in event3 fails? 44
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland CO-OPN Transactions • Transactional semantics: firing a transaction results in either: • success: at least one solution found • failure: no solution found • A solution is a resource allocation plan for the transaction • Try to achieve "success" plan, until no more plans are possible 45
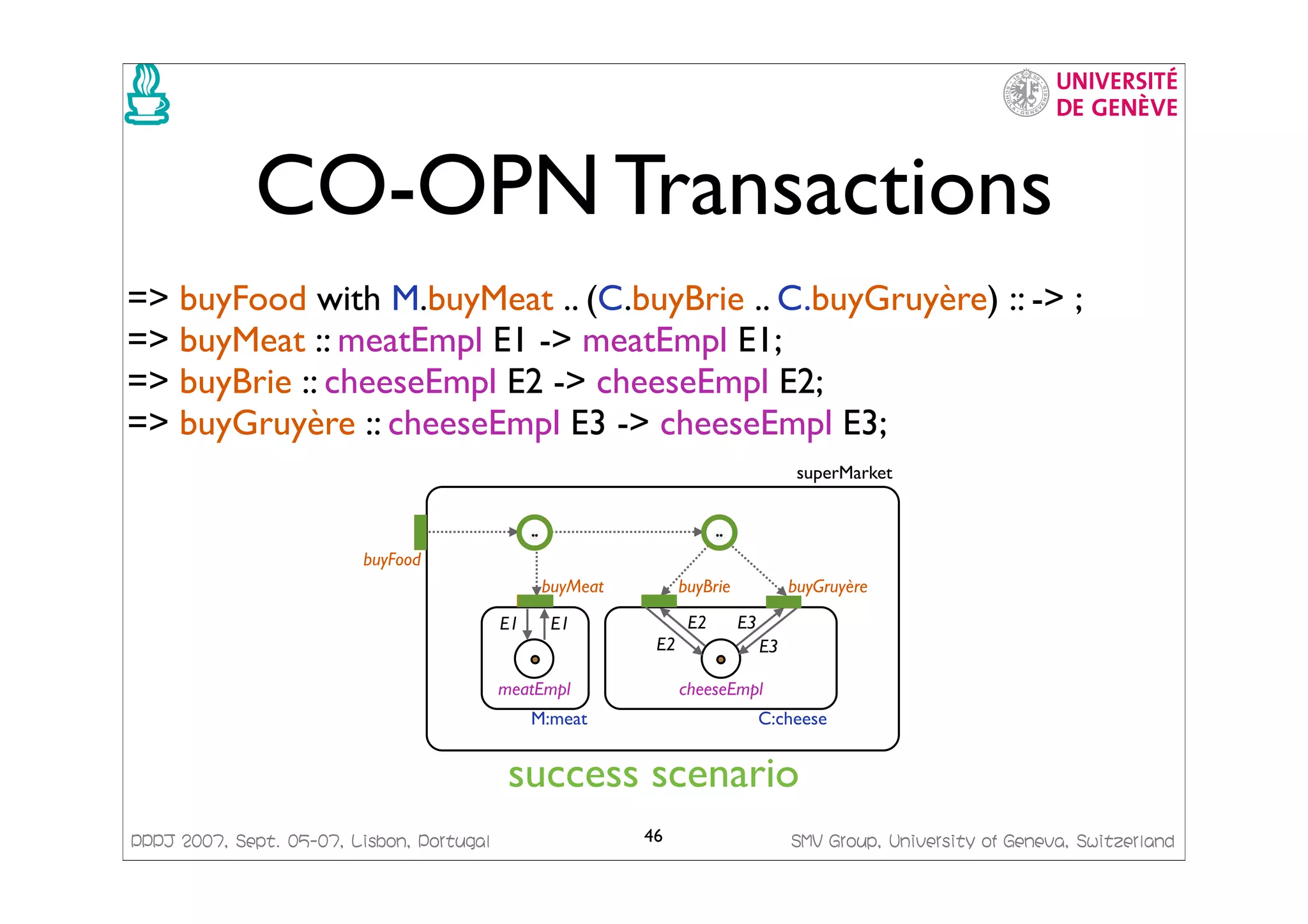
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland CO-OPN Transactions superMarket buyFood meatEmpl cheeseEmpl .. .. buyMeat buyBrie buyGruyère success scenario M:meat C:cheese E1 E2 E3 => buyFood with M.buyMeat .. (C.buyBrie .. C.buyGruyère) :: -> ; => buyMeat :: meatEmpl E1 -> meatEmpl E1; => buyBrie :: cheeseEmpl E2 -> cheeseEmpl E2; => buyGruyère :: cheeseEmpl E3 -> cheeseEmpl E3; E1 E2 E3 46
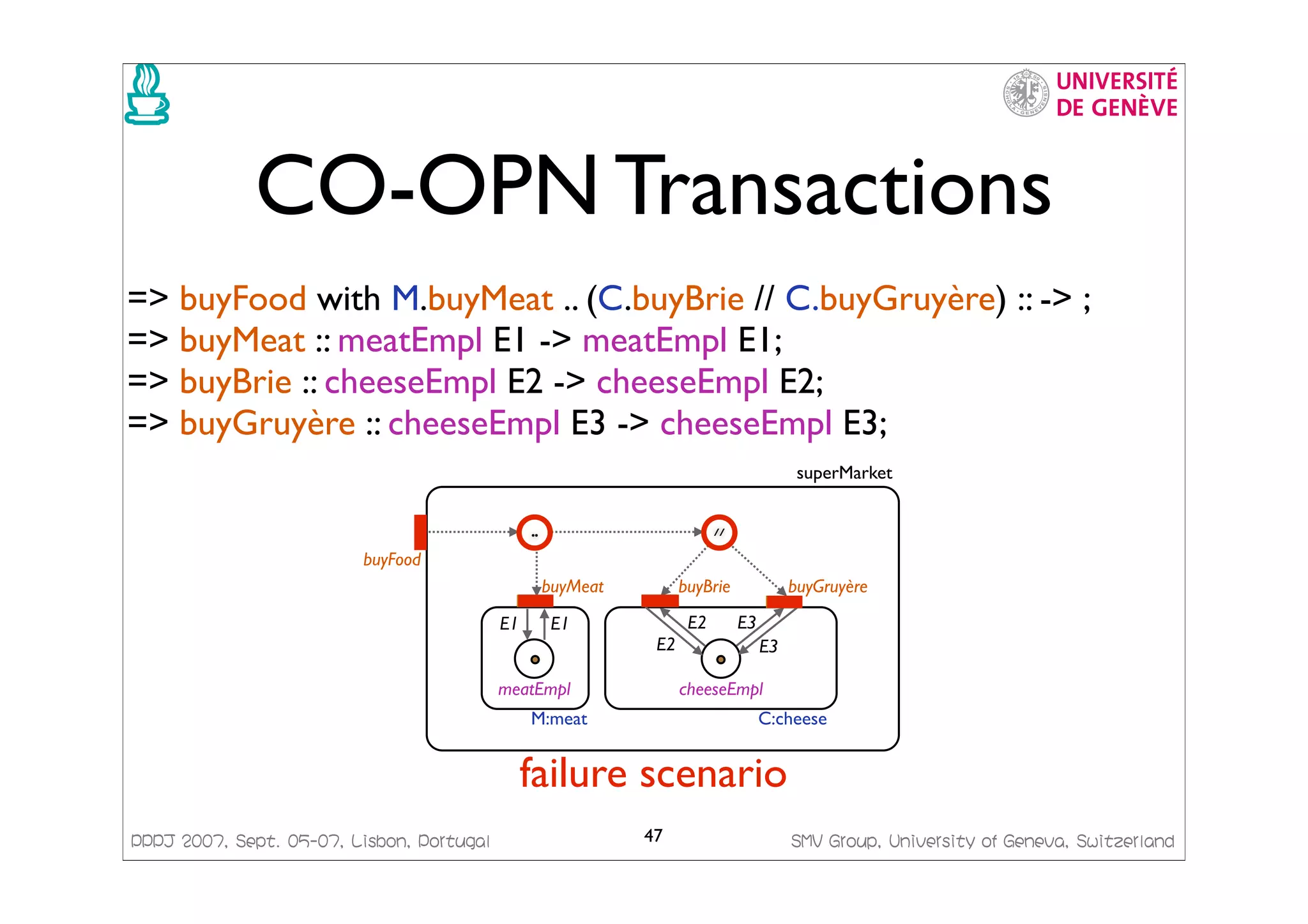
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland CO-OPN Transactions superMarket buyFood meatEmpl cheeseEmpl .. // buyMeat buyBrie buyGruyère failure scenario M:meat C:cheese E1 E2 E3 => buyFood with M.buyMeat .. (C.buyBrie // C.buyGruyère) :: -> ; => buyMeat :: meatEmpl E1 -> meatEmpl E1; => buyBrie :: cheeseEmpl E2 -> cheeseEmpl E2; => buyGruyère :: cheeseEmpl E3 -> cheeseEmpl E3; E1 E2 E3 47
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland CO-OPN example The roller coaster problem 48
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland The roller coaster (single car) • 5 passengers,1 car • The passengers repeatedly wait to take rides in the car, which can hold 4 passengers • The car can go around the tracks only when it is full. 49
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland The roller coaster (single car) •Passengers cannot board until the car has invoked load() •The car cannot depart until 4 passengers are onboard •Passengers cannot unboard until the car has invoked unload() board() unboard() passenger load() unload() run() passengers: int car enters 50
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland The roller coaster (single car) Object diagram Passenger state machine Car state machine passengers=0 c: car p1: passenger p2: passenger p3: passenger p4: passenger p5: passenger boardedoffboard board unboard loadingunloading running load [passengers=0] run [passengers=5] unload 51
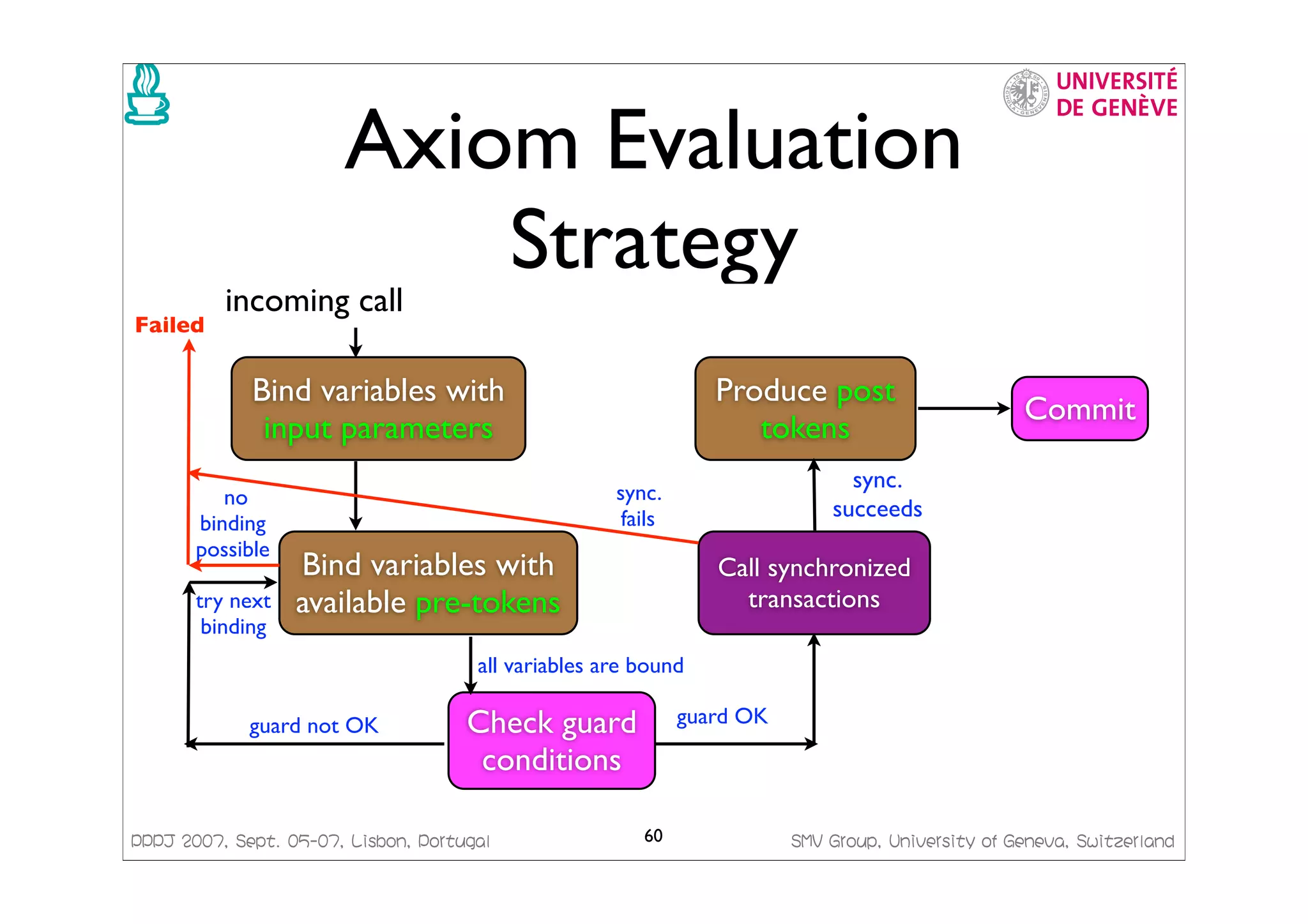
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland The roller coaster (in CO-OPN) C rollercoaster p1:passenger wantToExit board offboard board boarded unboard wantToEnter unboard p2:passenger wantToExit board offboard board boarded unboard wantToEnter unboard p5:passenger wantToExit board offboard board boarded unboard wantToEnter unboard [...] unload c:car run 0 runningunloading passengers exit enter load run [n=4] load [n=0] unload n n n n exit [n>0] enter [n<4] n n-1 n+1 n loading runload unload unboard _ board _ 52
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Demo 53
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland CO-OPN Interface Methods Gates ✦ The visible part of a module, as Java interface ✦ Provided Services (incoming signals): Methods ✦ Requested Services (outgoing signals): Gate ✦ Services can have parameters, specified by its signature 54
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Car: Interface Generated Java Class public class Car { // the methods may throw the // runtime exception “MethodNotFirableException” public void load() { // codes for axioms ... }; public void unload() { // codes for axioms... }; public void run() { // codes for axioms ... }; } Car load unload run CO-OPN Module Interface Methods load, unload, run Body Axioms load:: ... ... 55
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Integration of Prototype Car car=new Car(...); try { CoopnTransaction T=new CoopnTransaction(); car.load(T); T.commit(); } catch (CoopnMethodNotFirableException e) { System.out.println(“Car loading fails”); } Create a Car object and try to call its load() method 56
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland CO-OPN to Java Translation • Names preserved if possible • Modular structure preserved • CO-OPN Module Java classes • Component architecture preserved • CO-OPN Methods Java methods • CO-OPN Gates Java Events • Weird aspects hidden as possible • non-determinism, atomicity, backtracking ... 57
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Example of backtracking and non-determinism 0,1,2 1,2,3 out_ _: natural, natural m_: natural x y x+y=z? P1 P2 Initial marking: P1{0,1,2}, P2{1,2,3} (x+y)=z :: m z with this.out x y :: P1 x, P2 y -> The token selection is nondeterministic Method m z will trigger the gate out x y and output the tokens which satisfy the condition: x +y=z Possible solutions: m 3 with out (0,3) or (1,2) or (2,1) m 2 with out (0,2) or (1,1) 58
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Axiom Translation Condition :: method with sync. :: pre -> post (x+y)=z :: m z with this.out x y :: P1 x, P2 y ->Example: 0,1,2 1,2,3 out_ _: natural, natural m_: natural x y x+y=z? P1 P2 z = 3; for (x: tokens in P1){ for (y: tokens in P2){ if (x+y==z) { // check guard condition SaveStackState(); this.out(x,y); return; } } } throws new NotFirableException(); Variable binding when calling “m 3”: 59
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Axiom Evaluation Strategy Bind variables with input parameters Bind variables with available pre-tokens incoming call Check guard conditions all variables are bound try next binding guard not OK Call synchronized transactions guard OK Commit Produce post tokens sync. succeedsno binding possible Failed sync. fails 60
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Transaction Tree An example of COOPN transaction tree Places P_: natural, P1_: natural , P2_: natural Initial P 0, P1 0, P2 0; Methods m, m1, m2, m3, m4, m5, m6 Gates g1_: natural, g2_: natural m with m1 // m2 :: P x -> P x m1 with m3 .. m4 :: P1 x, P1 x+1 m2 with m5 + m6 :: P1 x, P1 x+2 m3 :: P1 x -> P1 x+3 m4 :: P1 x -> P1 x+4 m5 with g1 x :: P2 x -> P2 x+5 m6 with g2 x :: P2 x -> P2 x+6 m with // m1 m2 m3 m4 m5 m6 with .. with + with with g1_ g2_ allocation order 61
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Eligibility of Tokens during Transactions • During the exploration of the transaction tree, the rules to determinate the eligibility of token are: • All reserved tokens are not eligible • Tokens produced by the simultaneous transactions are not eligible, e.g.With and // • Free tokens produced by precedent sequential transactions are eligible • E.g. in seq1..(sim1//sim2), tokens produced by seq1 are eligible for transaction sim1 and sim2. However, sim1 and sim2 may have concurrent access of the tokens. 62
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland CO-OPN Runtime Architecture User Application Java Platform and APIs Other Components The generated code can be annotated by CO-OPN specifications Concurrency and Transactionality are managed here! CO-OPN Runtime Classes Generated Code with Annotations 63
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland The CO-OPN Prototyping Framework Real- world Problem Formal Model Description Modeling Prototype Adaptation and Integration Code Generation Executable Prototype User Application Component Component Development Refinement Model Checking Verification Test Test Generation 64
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland The CO-OPN Prototyping Framework • Modeling -Verification - Prototyping - Integration • From model to implementation Modeling Verification Code Generation Adaptation & Integration Prototype Model 65
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Conclusion • Formal models with rich expressive power provide facilities for model-driven development for: • test generation and model checking • automatic code generation • rapid system prototyping • incremental, iterative development • Cost effective for safety-critical systems 66
Thank you. Question time. 67
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Backup slides 68
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Life-Cycle of Tokens ReservedFree produce consume reserve rollback Operationally, PN transitions uses the 2 phases commit protocol to avoid deadlocks T3 T4 P1 P2 P3 P4 69
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland CO-OPN to Java Translation • Declarative Language Imperative Language • Operational aspects • Logical term evaluation (e.g. conditions) and backtracking • Implementation of atomicity and nested transactions • Event-driven execution & simulation • Architectural aspects • Service-oriented architecture: interface, methods, gates • Reusable & substitutable components 70
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Tokens Stamping • There are 4 kinds of tokens in the system • Free initial tokens • Reserved initial tokens • Free intermediate tokens • Reserved intermediate tokens 71
PPPJ
2007,
Sept.
05-07,
Lisbon,
Portugal SMV
Group,
University
of
Geneva,
Switzerland Token Life-Cycle in Transactions <free, initial> <free, produced> <reserved, initial> <reserved, produced> removed abort reserve abort commit abort reserve commit initial tokens produced tokens during the transaction 72

More Related Content

PDF
Generating sentences from a continuous space
byShuhei Iitsuka
 
PDF
ETAPS03 SC.ppt
byPtidej Team
 
PDF
A benchmark evaluation for incremental pattern matching in graph transformation
byIstvan Rath
 
ODP
Syntax-based Simultaneous Translation through Prediction of Unseen Syntactic ...
byYusuke Oda
 
PDF
SP Study1018 Paper Reading
byMori Takuma
 
PDF
High-Level Synthesis with GAUT
byAdaCore
 
PDF
Learning to Generate Pseudo-code from Source Code using Statistical Machine T...
byYusuke Oda
 
PDF
Data assimilation with OpenDA
bynilsvanvelzen
 
Generating sentences from a continuous space
byShuhei Iitsuka
 
ETAPS03 SC.ppt
byPtidej Team
 
A benchmark evaluation for incremental pattern matching in graph transformation
byIstvan Rath
 
Syntax-based Simultaneous Translation through Prediction of Unseen Syntactic ...
byYusuke Oda
 
SP Study1018 Paper Reading
byMori Takuma
 
High-Level Synthesis with GAUT
byAdaCore
 
Learning to Generate Pseudo-code from Source Code using Statistical Machine T...
byYusuke Oda
 
Data assimilation with OpenDA
bynilsvanvelzen
 

What's hot

PDF
Preliminary study on using vector quantization latent spaces for TTS/VC syste...
byYamagishi Laboratory, National Institute of Informatics, Japan
 
PDF
エンドツーエンド音声合成に向けたNIIにおけるソフトウェア群 ～ TacotronとWaveNetのチュートリアル (Part 2)～
byYamagishi Laboratory, National Institute of Informatics, Japan
 
PPT
2009 CSBB LAB 新生訓練
byAbner Huang
 
PDF
Post-graduate course: Object technology: Implementation of object-oriented pr...
byBaltasar García Perez-Schofield
 
PPTX
Transformer Zoo
byGrigory Sapunov
 
PPTX
Transformer Mods for Document Length Inputs
bySujit Pal
 
PPTX
Transformer Zoo (a deeper dive)
byGrigory Sapunov
 
PDF
简历
by? ?
 
Preliminary study on using vector quantization latent spaces for TTS/VC syste...
byYamagishi Laboratory, National Institute of Informatics, Japan
 
エンドツーエンド音声合成に向けたNIIにおけるソフトウェア群 ～ TacotronとWaveNetのチュートリアル (Part 2)～
byYamagishi Laboratory, National Institute of Informatics, Japan
 
2009 CSBB LAB 新生訓練
byAbner Huang
 
Post-graduate course: Object technology: Implementation of object-oriented pr...
byBaltasar García Perez-Schofield
 
Transformer Zoo
byGrigory Sapunov
 
Transformer Mods for Document Length Inputs
bySujit Pal
 
Transformer Zoo (a deeper dive)
byGrigory Sapunov
 
简历
by? ?
 

Similar to Java Code Generation from Formal Models: The CO-OPN Framework

PDF
Concurrency in Java
byLakshmi Narasimhan
 
PDF
Concurrent Programming in Java
byLakshmi Narasimhan
 
PDF
Gpars workshop
byVaclav Pech
 
PPT
Petri Nets financial problems solution with
byAssadLeo1
 
PPTX
Concurrency Programming in Java - 07 - High-level Concurrency objects, Lock O...
bySachintha Gunasena
 
PDF
Groovy concurrency
byAlex Miller
 
ODP
Concurrency on the JVM
byVaclav Pech
 
KEY
Modern Java Concurrency (OSCON 2012)
byMartijn Verburg
 
PPTX
G pars
byNexThoughts Technologies
 
ODP
Java Concurrency, Memory Model, and Trends
byCarol McDonald
 
PPTX
all about petri netis model and simulation
byAssadLeo1
 
PPTX
Concurrency in Java
byAllan Huang
 
PPT
petri-nets: definition and its application
bynicholas507559
 
PDF
Java Tutorials - Concurrency
byChristian Rubiales
 
PPTX
GPARS: Lessons from the parallel universe - Itamar Tayer, CoolaData
byCodemotion Tel Aviv
 
PDF
Loom Virtual Threads in the JDK 19
byJosé Paumard
 
PPT
Java Core | Modern Java Concurrency | Martijn Verburg & Ben Evans
byJAX London
 
PPTX
Concurrent talk
byrahulrevo
 
PDF
Java Concurrency and Performance | Multi Threading | Concurrency | Java Conc...
byAnand Narayanan
 
PPTX
Evolution of JDK Tools for Multithreaded Programming
byGlobalLogic Ukraine
 
Concurrency in Java
byLakshmi Narasimhan
 
Concurrent Programming in Java
byLakshmi Narasimhan
 
Gpars workshop
byVaclav Pech
 
Petri Nets financial problems solution with
byAssadLeo1
 
Concurrency Programming in Java - 07 - High-level Concurrency objects, Lock O...
bySachintha Gunasena
 
Groovy concurrency
byAlex Miller
 
Concurrency on the JVM
byVaclav Pech
 
Modern Java Concurrency (OSCON 2012)
byMartijn Verburg
 
G pars
byNexThoughts Technologies
 
Java Concurrency, Memory Model, and Trends
byCarol McDonald
 
all about petri netis model and simulation
byAssadLeo1
 
Concurrency in Java
byAllan Huang
 
petri-nets: definition and its application
bynicholas507559
 
Java Tutorials - Concurrency
byChristian Rubiales
 
GPARS: Lessons from the parallel universe - Itamar Tayer, CoolaData
byCodemotion Tel Aviv
 
Loom Virtual Threads in the JDK 19
byJosé Paumard
 
Java Core | Modern Java Concurrency | Martijn Verburg & Ben Evans
byJAX London
 
Concurrent talk
byrahulrevo
 
Java Concurrency and Performance | Multi Threading | Concurrency | Java Conc...
byAnand Narayanan
 
Evolution of JDK Tools for Multithreaded Programming
byGlobalLogic Ukraine
 

More from Ang Chen

KEY
Defence: A multi-dimensional compositional approach for business process (sem...
byAng Chen
 
PDF
A Multi-Dimensional Compositional Approach for Business Process Engineering
byAng Chen
 
KEY
A Proposition for Business Process Modeling
byAng Chen
 
PDF
Synchronized Composition Of Labeled Transition SystemTS
byAng Chen
 
PDF
Jsp & Ajax
byAng Chen
 
PDF
Semantics (requirements) of Business Process
byAng Chen
 
PDF
Business Process Modeling
byAng Chen
 
PDF
Composing Business Process with ID-Net
byAng Chen
 
PDF
Prototyping Business Processes
byAng Chen
 
PPT
Towards Service-based Business Process Modeling, Prototyping and Integration
byAng Chen
 
Defence: A multi-dimensional compositional approach for business process (sem...
byAng Chen
 
A Multi-Dimensional Compositional Approach for Business Process Engineering
byAng Chen
 
A Proposition for Business Process Modeling
byAng Chen
 
Synchronized Composition Of Labeled Transition SystemTS
byAng Chen
 
Jsp & Ajax
byAng Chen
 
Semantics (requirements) of Business Process
byAng Chen
 
Business Process Modeling
byAng Chen
 
Composing Business Process with ID-Net
byAng Chen
 
Prototyping Business Processes
byAng Chen
 
Towards Service-based Business Process Modeling, Prototyping and Integration
byAng Chen
 

Recently uploaded

PPTX
Green-Digital-Hub-for-Startups-and-Social-Enterprises_FOCUS_GROUP (1) (1).pptx
byChristinaFortunova
 
PDF
Function of Words in Context_V-N-ADJ-ADV.pdf
byNetziValdelomar1
 
PPTX
Schacher Record Store Report Full Sail University
byChrisSchacher
 
PDF
Friday Night Blockbuster 2025 - Intra UEM Online MELA Quiz of Jigisha 4.0
byPragya - UEM Kolkata Quiz Club
 
PDF
'25 BC An Hour with Bonner Alumni–Meet, Mingle, Move.pdf
byBonner Foundation
 
PDF
Slit lamp parts 1/ppt/pdf/notes/save.pdf
byanmols3059
 
PDF
2025 Bonner Congress Strategy Session– Student Leadership Bonner and Beyond.pdf
byBonner Foundation
 
PPTX
unit-2 PATIENT CARE UNIT. pptx
byAneetaSharma15
 
PDF
Master Plan Produktivitas Nasional 2025–2029
byDadang Solihin
 
PPTX
COMMON ETHICAL PROBLEMS SHILPA HOTAKAR PROFESSIONALISM .pptx
bySHILPA HOTAKAR
 
PPTX
Ancient Educational Institutions: Taxsila, Nalanda, Vikramshila, Kashi
byBanaras Hindu University
 
PPTX
SCOPE OF NURSING. pptx
byAneetaSharma15
 
PDF
2025 Bonner Congress Opening Engage Now.pdf
byBonner Foundation
 
PPTX
ETHICAL DILEMMAS SHILPA H .pptx PROFESSIONALISM BSC NURSING STUDENTS
bySHILPA HOTAKAR
 
PPTX
Hudson Vitale "AI Essentials: From Tools to Strategies: A 2025 NISO Training ...
byNational Information Standards Organization (NISO)
 
PPTX
Staircase: Types, Design & Indian Standards
byMrunali Vasava
 
PPTX
Chemical Properties of Construction Materials
byMrunali Vasava
 
PDF
The Ghana Chamber of Construction Industry (GhCCI) has appealed to the govern...
bynservice241
 
PPTX
How to Manage Vehicle Model in Odoo 18 Fleet
byCeline George
 
PDF
LDMMIA Reiki Yoga 20th Workshop Study Lounge
byLDMMia YogaOm Reiki
 
Green-Digital-Hub-for-Startups-and-Social-Enterprises_FOCUS_GROUP (1) (1).pptx
byChristinaFortunova
 
Function of Words in Context_V-N-ADJ-ADV.pdf
byNetziValdelomar1
 
Schacher Record Store Report Full Sail University
byChrisSchacher
 
Friday Night Blockbuster 2025 - Intra UEM Online MELA Quiz of Jigisha 4.0
byPragya - UEM Kolkata Quiz Club
 
'25 BC An Hour with Bonner Alumni–Meet, Mingle, Move.pdf
byBonner Foundation
 
Slit lamp parts 1/ppt/pdf/notes/save.pdf
byanmols3059
 
2025 Bonner Congress Strategy Session– Student Leadership Bonner and Beyond.pdf
byBonner Foundation
 
unit-2 PATIENT CARE UNIT. pptx
byAneetaSharma15
 
Master Plan Produktivitas Nasional 2025–2029
byDadang Solihin
 
COMMON ETHICAL PROBLEMS SHILPA HOTAKAR PROFESSIONALISM .pptx
bySHILPA HOTAKAR
 
Ancient Educational Institutions: Taxsila, Nalanda, Vikramshila, Kashi
byBanaras Hindu University
 
SCOPE OF NURSING. pptx
byAneetaSharma15
 
2025 Bonner Congress Opening Engage Now.pdf
byBonner Foundation
 
ETHICAL DILEMMAS SHILPA H .pptx PROFESSIONALISM BSC NURSING STUDENTS
bySHILPA HOTAKAR
 
Hudson Vitale "AI Essentials: From Tools to Strategies: A 2025 NISO Training ...
byNational Information Standards Organization (NISO)
 
Staircase: Types, Design & Indian Standards
byMrunali Vasava
 
Chemical Properties of Construction Materials
byMrunali Vasava
 
The Ghana Chamber of Construction Industry (GhCCI) has appealed to the govern...
bynservice241
 
How to Manage Vehicle Model in Odoo 18 Fleet
byCeline George
 
LDMMIA Reiki Yoga 20th Workshop Study Lounge
byLDMMia YogaOm Reiki
 

Java Code Generation from Formal Models: The CO-OPN Framework