Downloaded 305 times
![خان سنور Algorithm Analysis Algorithm Greedy-fractional-knapsack (w, v, W) FOR i =1 to do x[i] =0 weight = 0 while weight < W do i = best remaining item IF weight + w[i] ≤ W then x[i] = 1 weight = weight + w[i] else x[i] = (w - weight) / w[i] weight = W return x](https://image.slidesharecdn.com/greedyalgorithm-190528012359/75/Greedy-algorithm-35-2048.jpg)
Uploaded byInternational Islamic University
Greedy algorithm
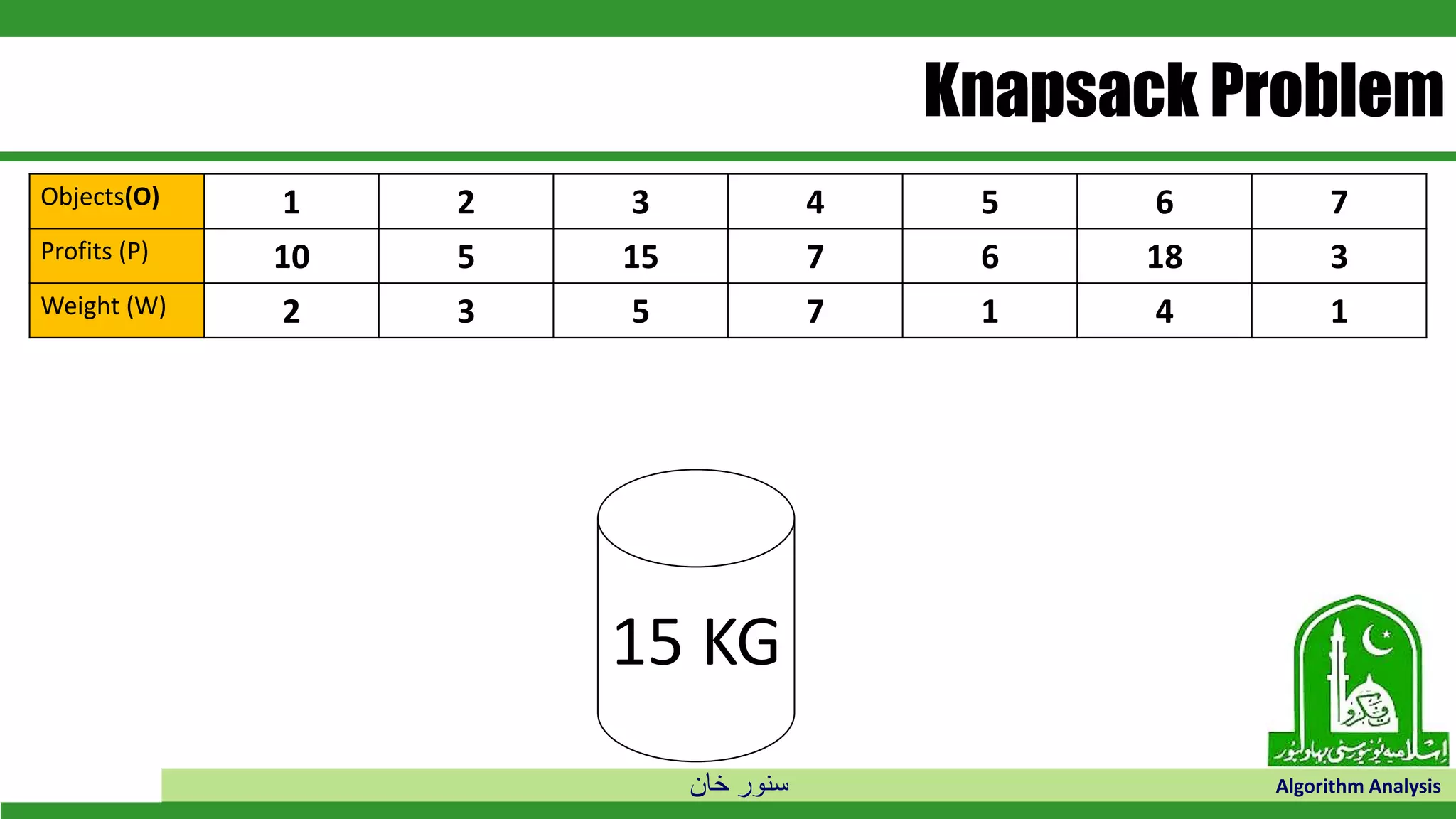
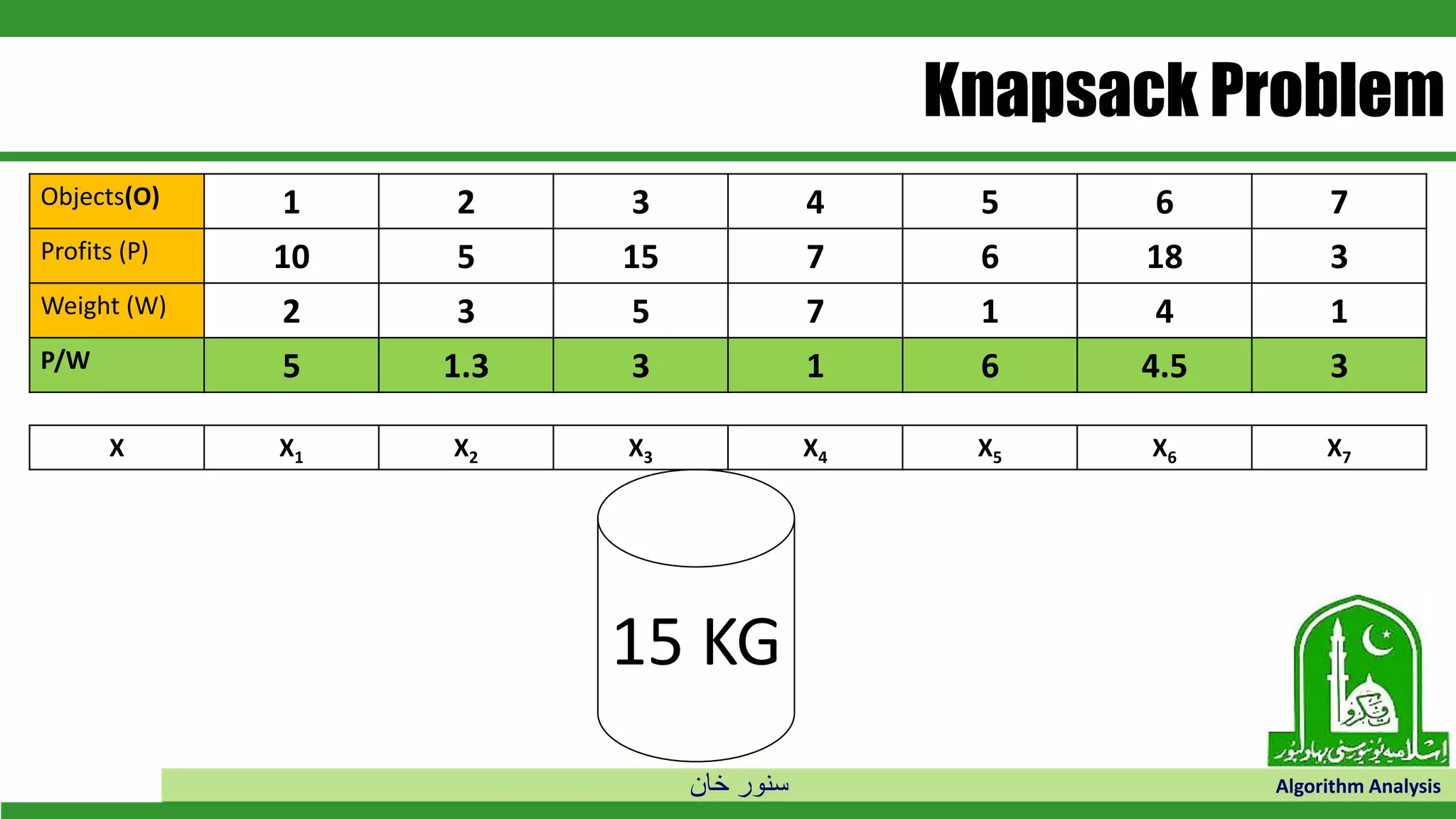
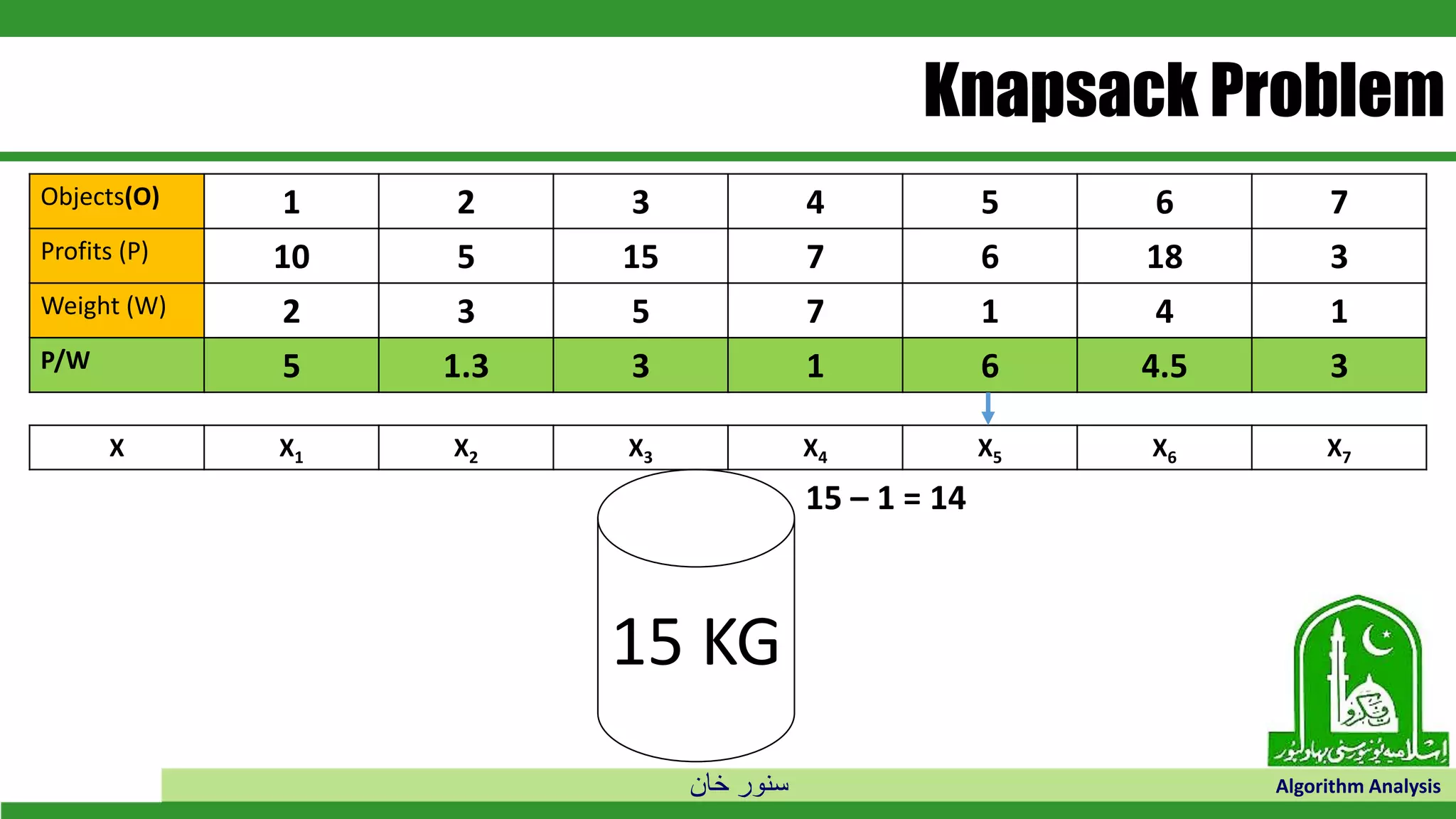
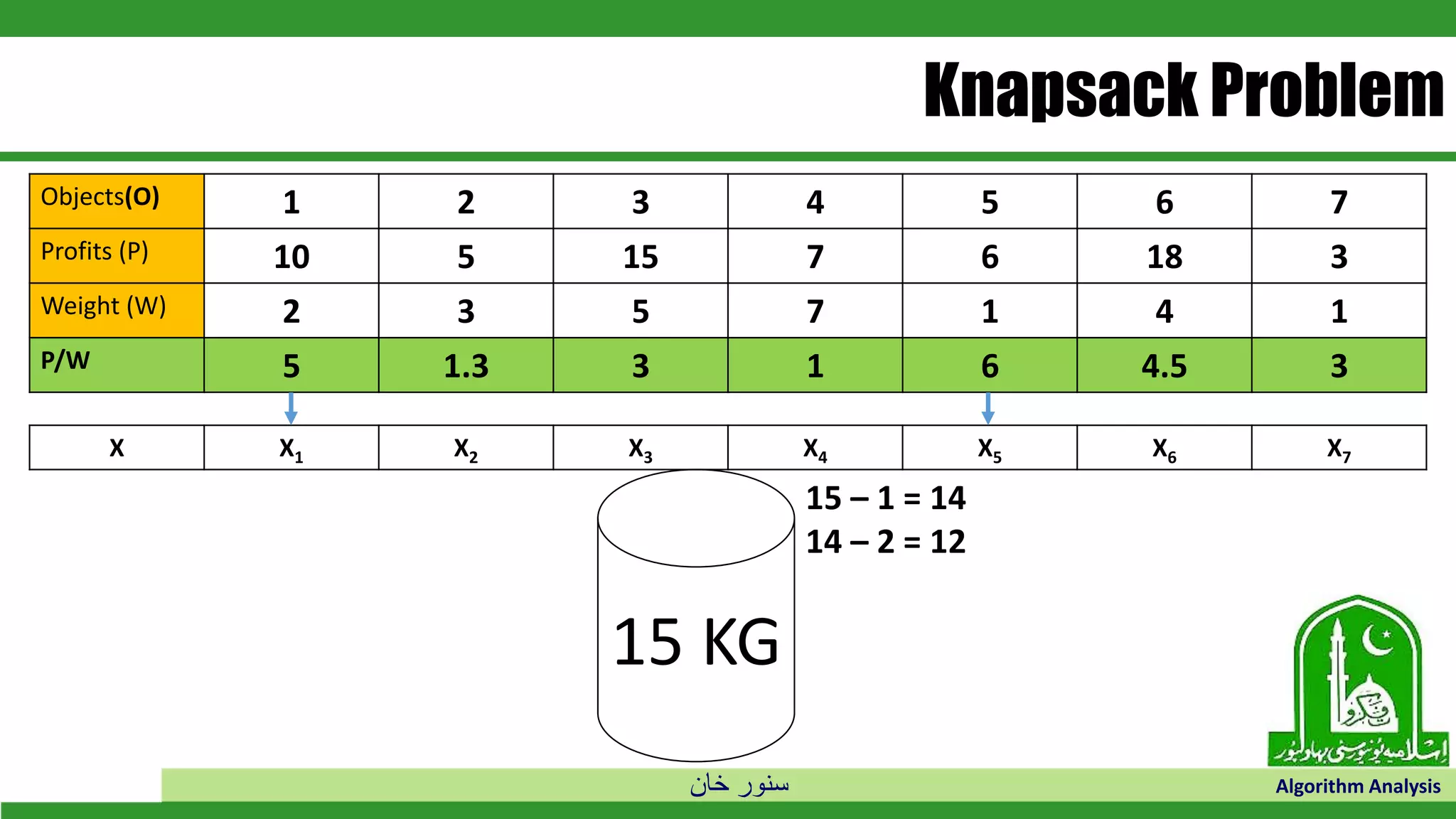
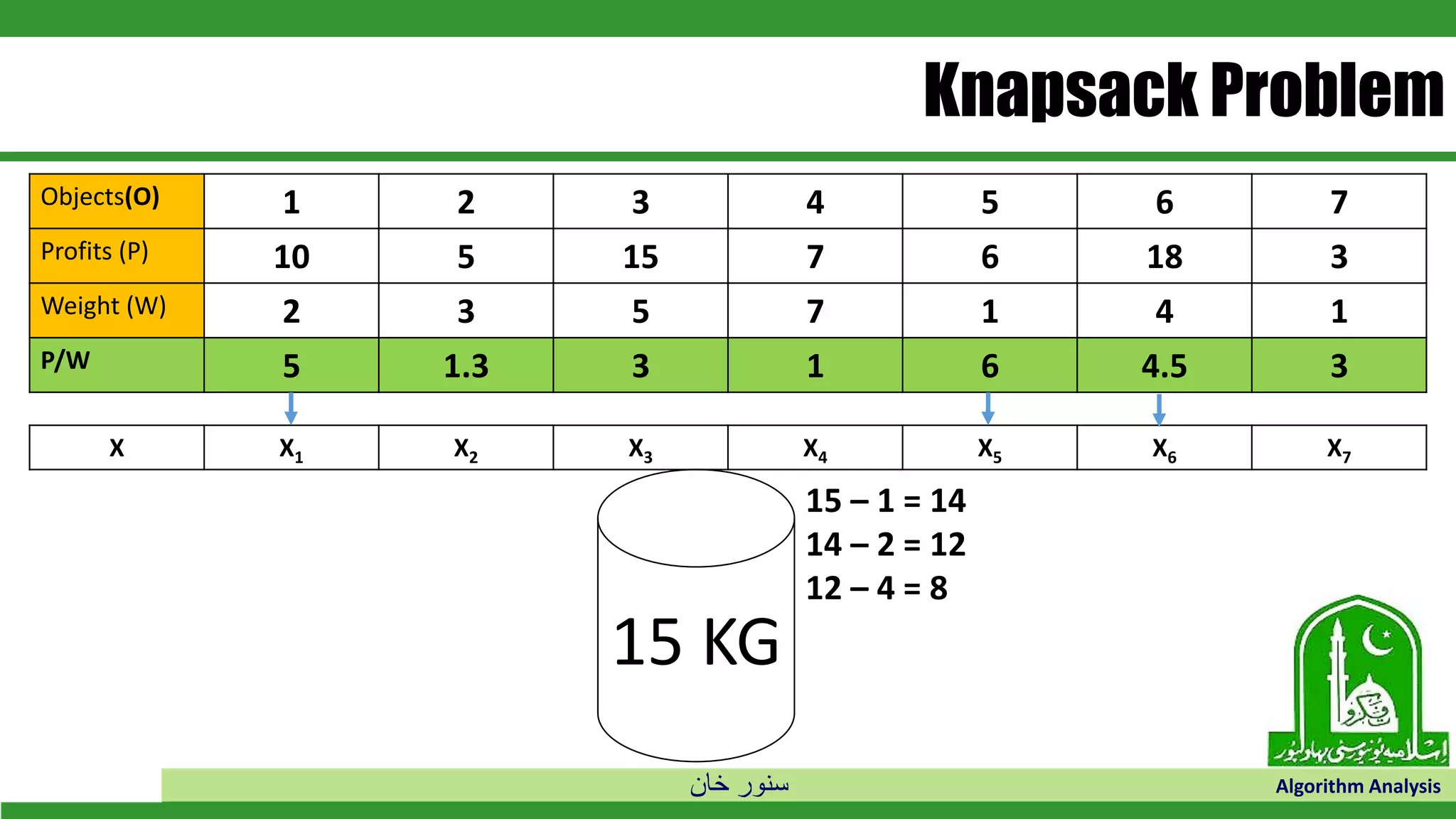
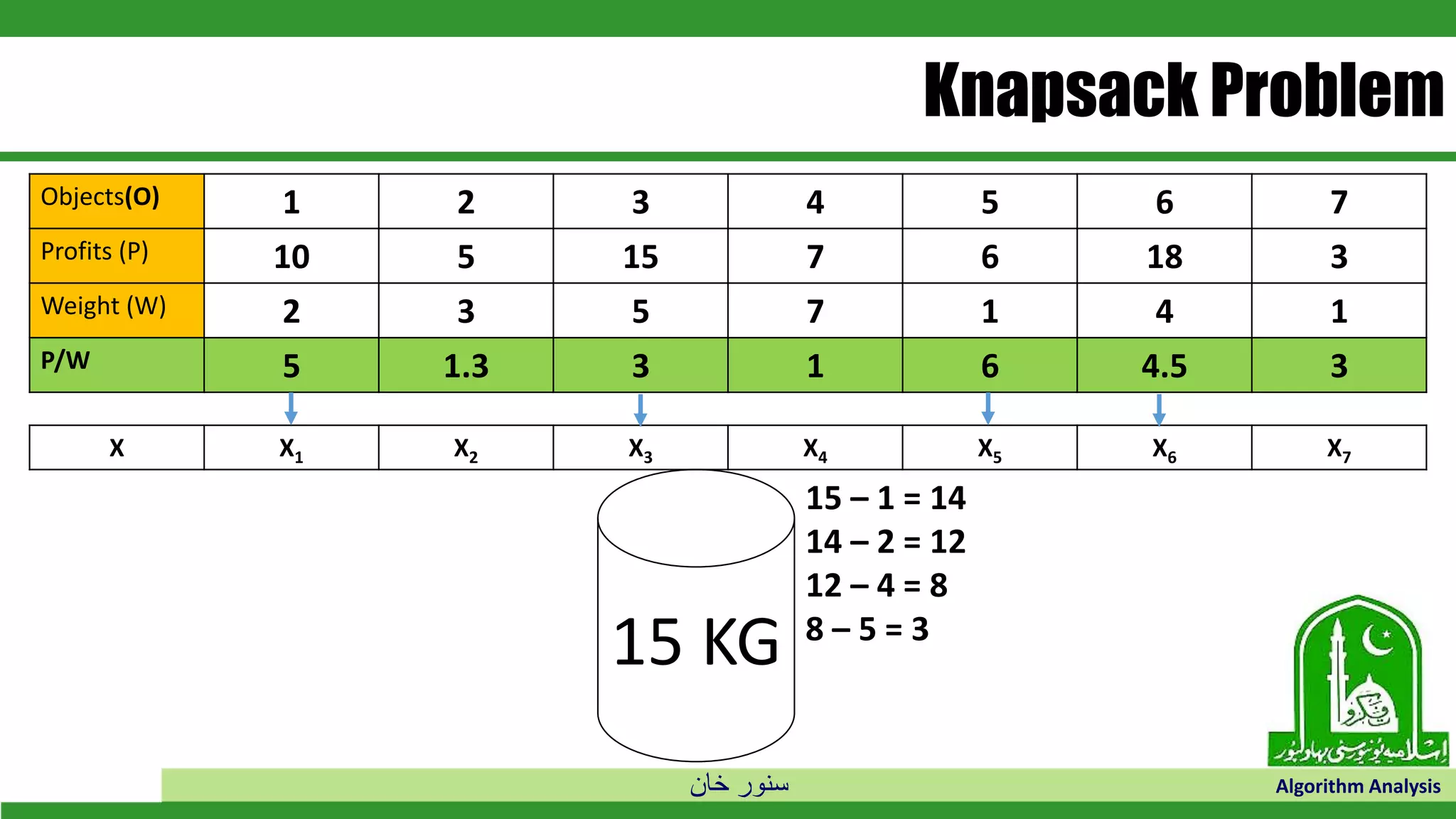
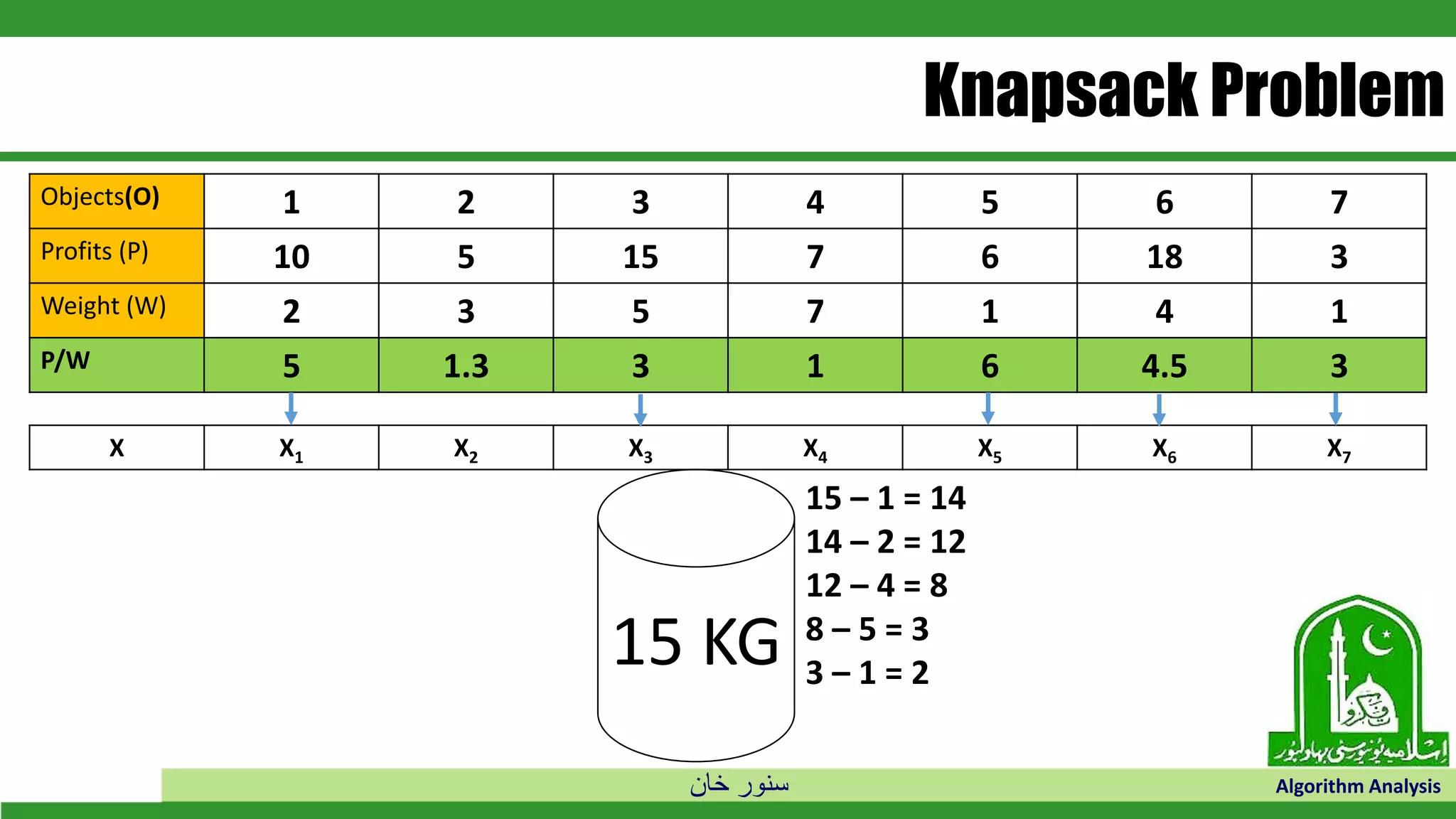
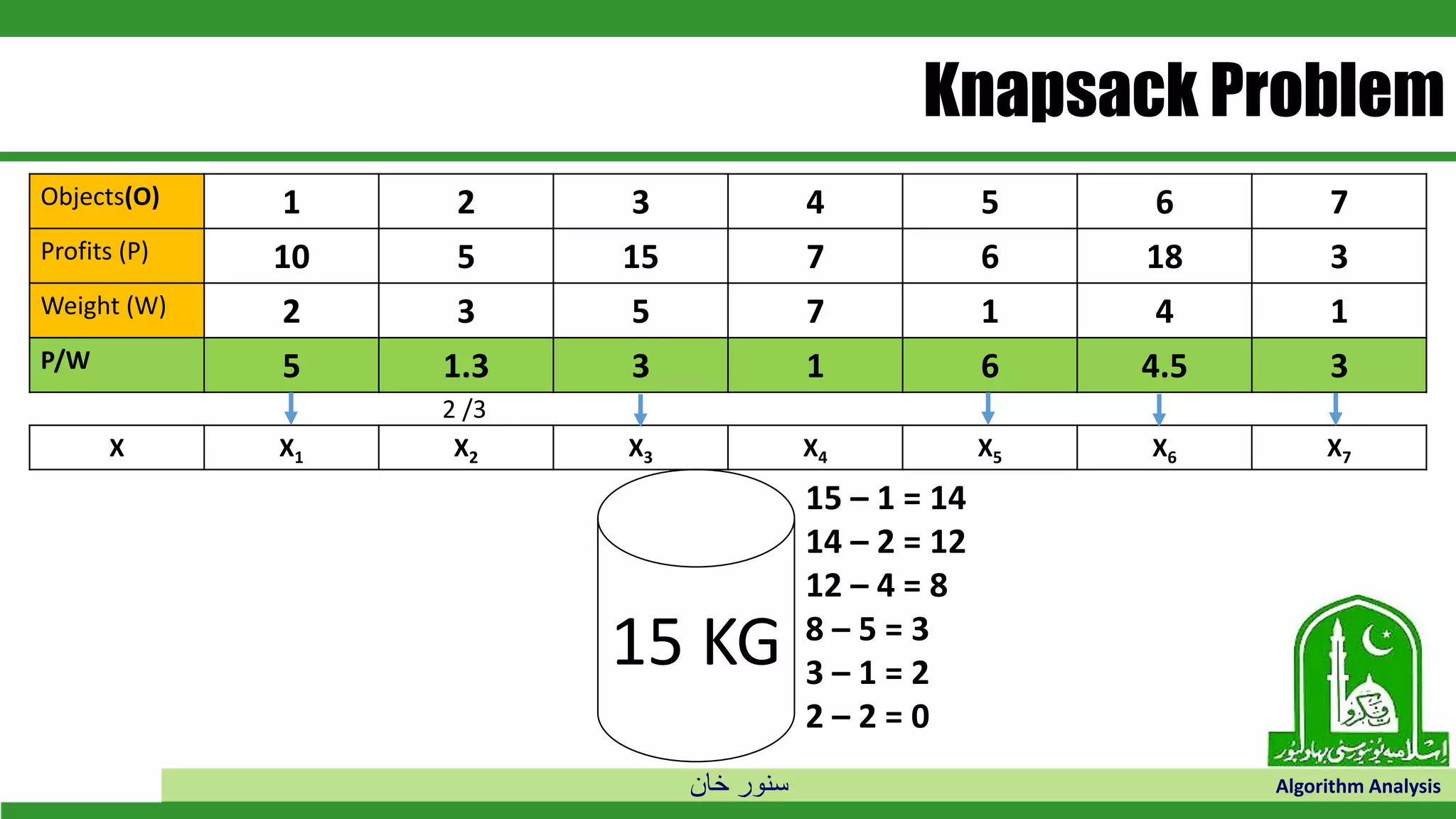
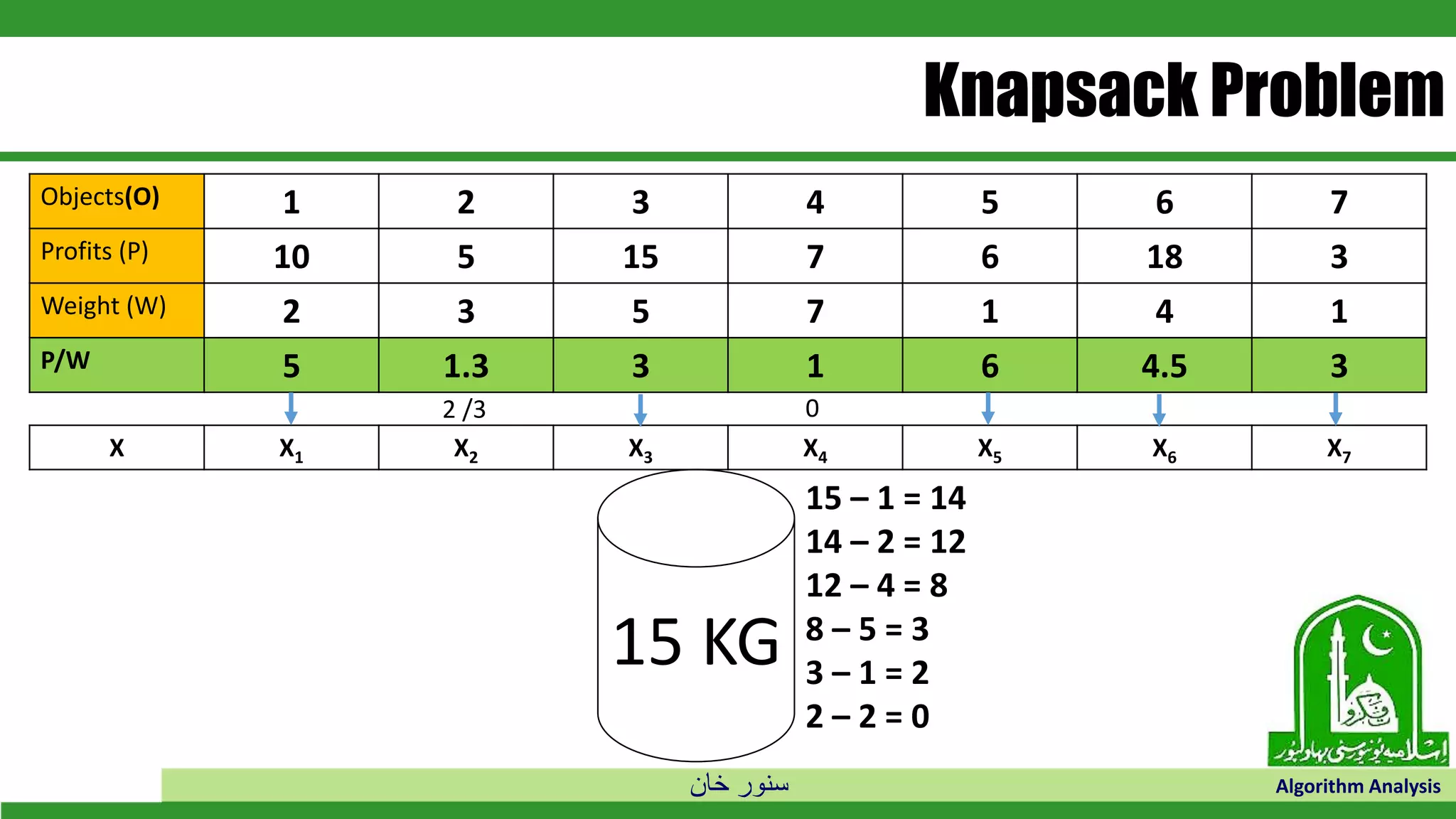
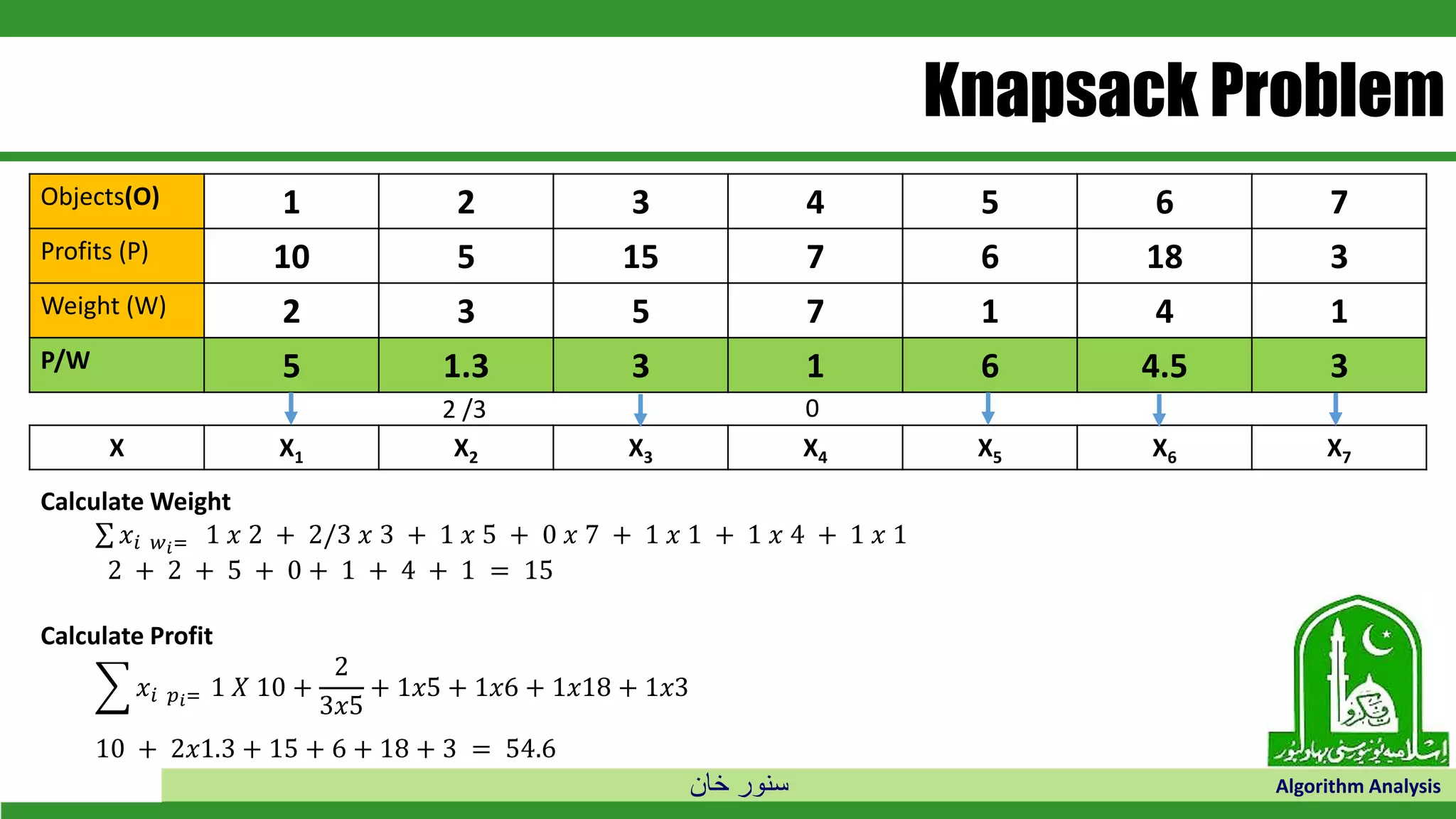
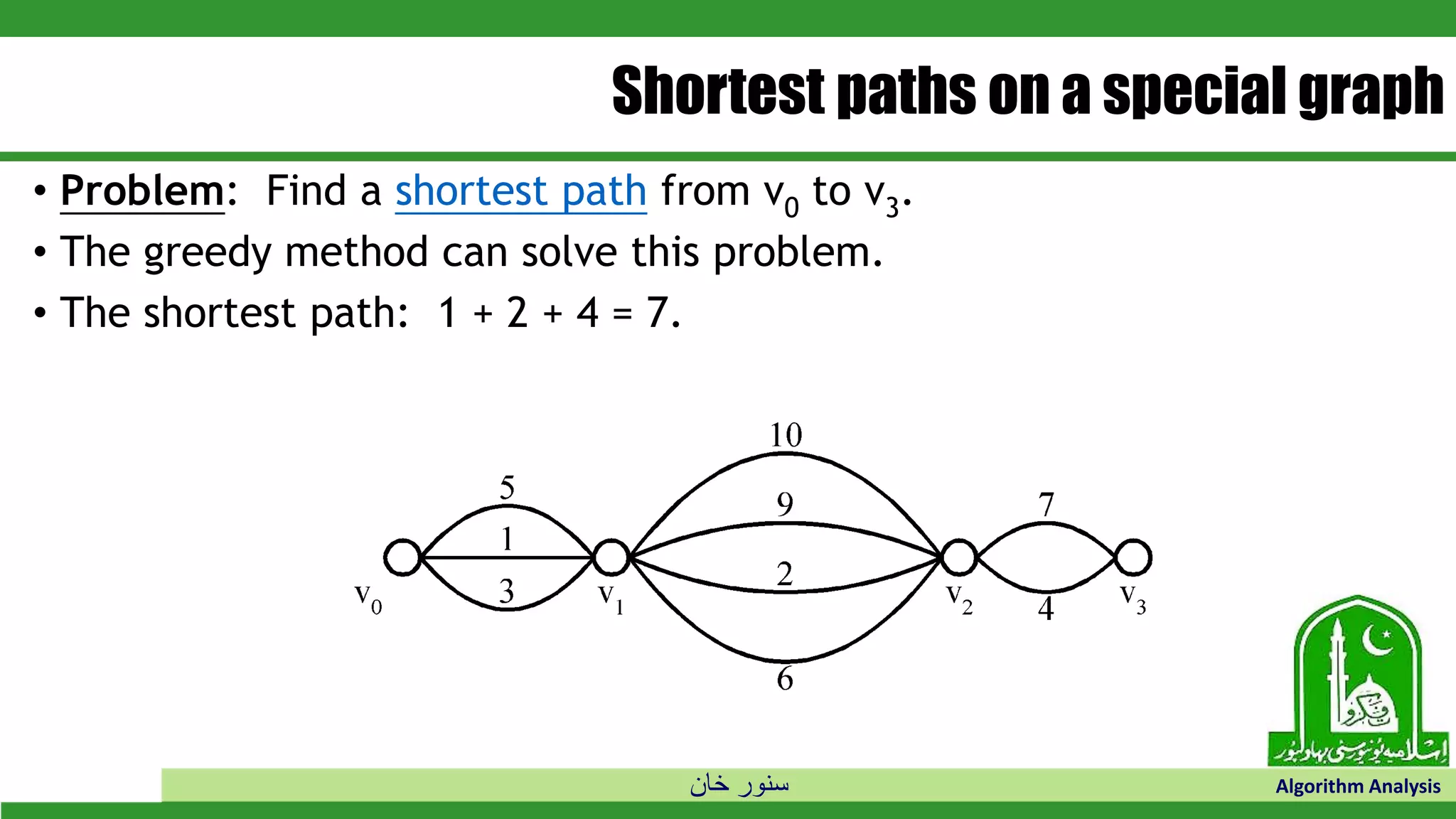
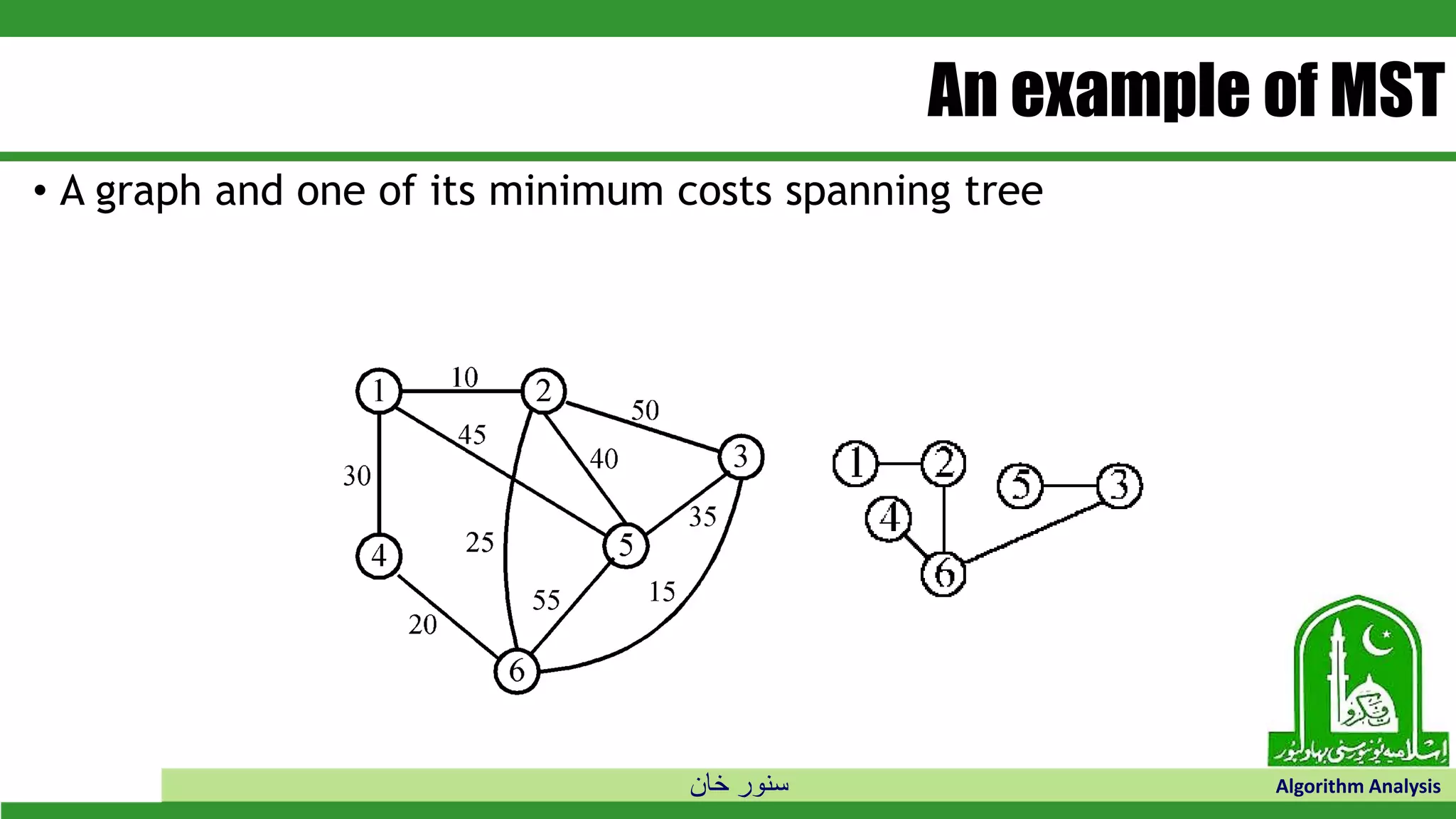
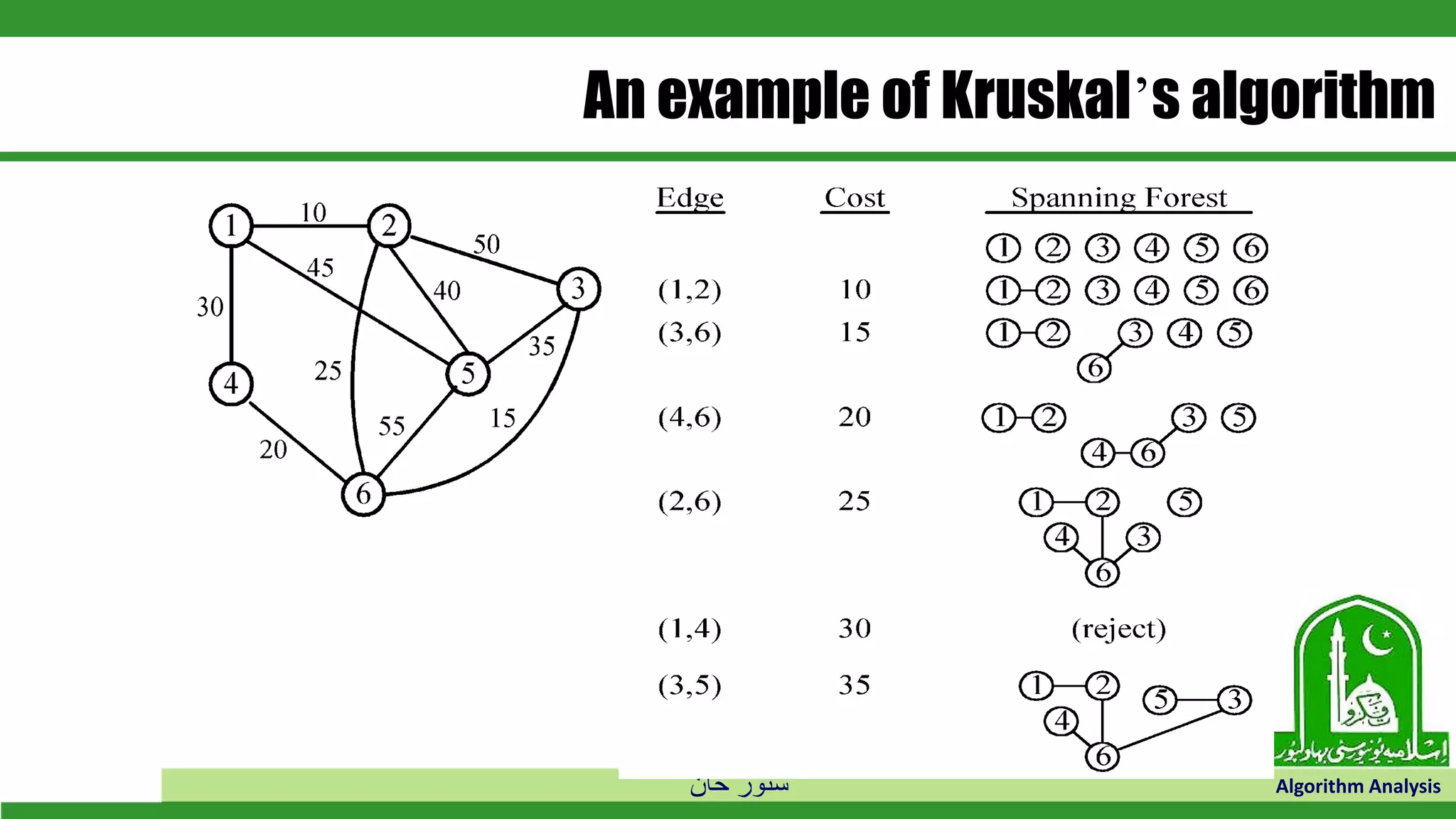
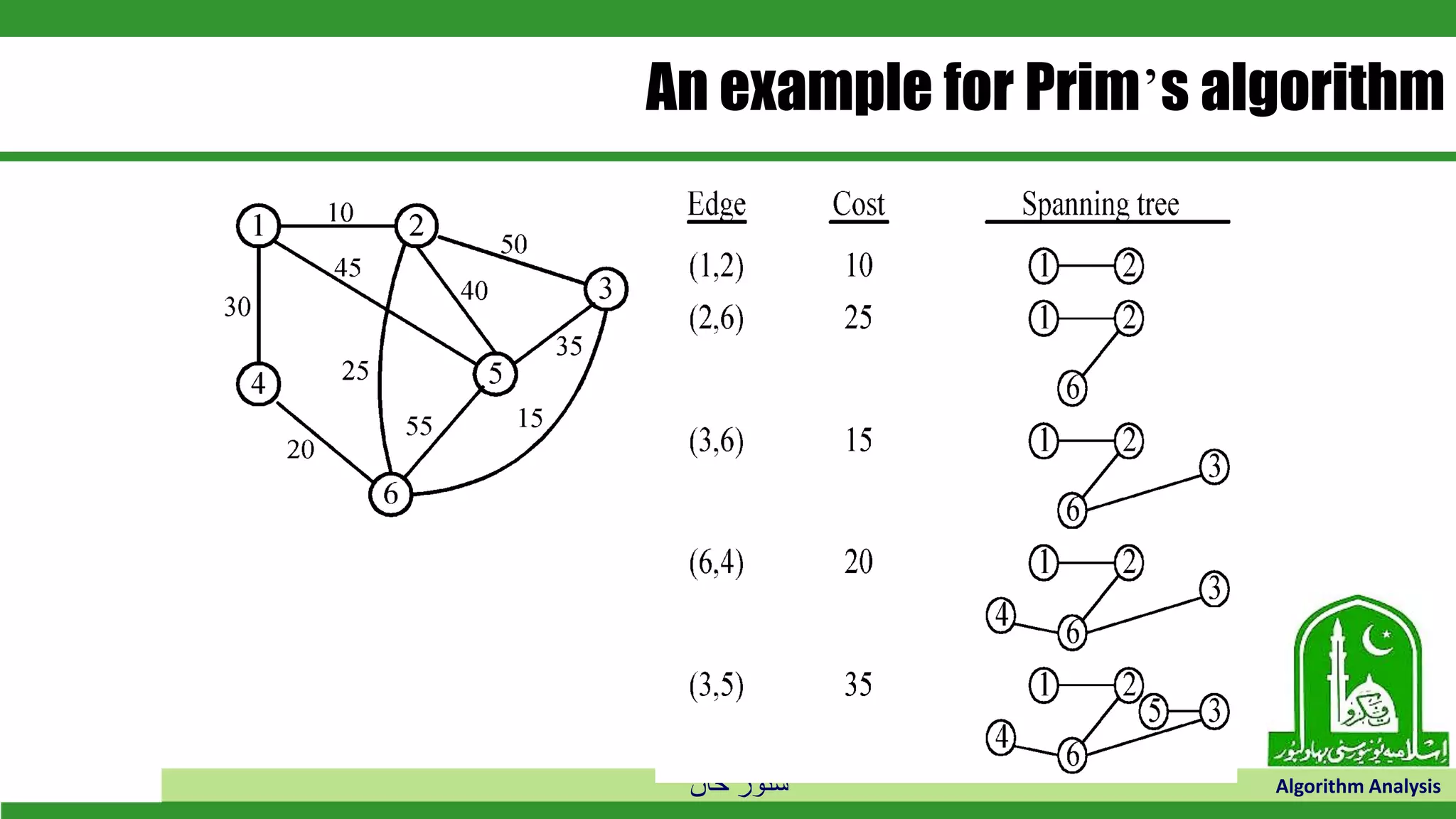
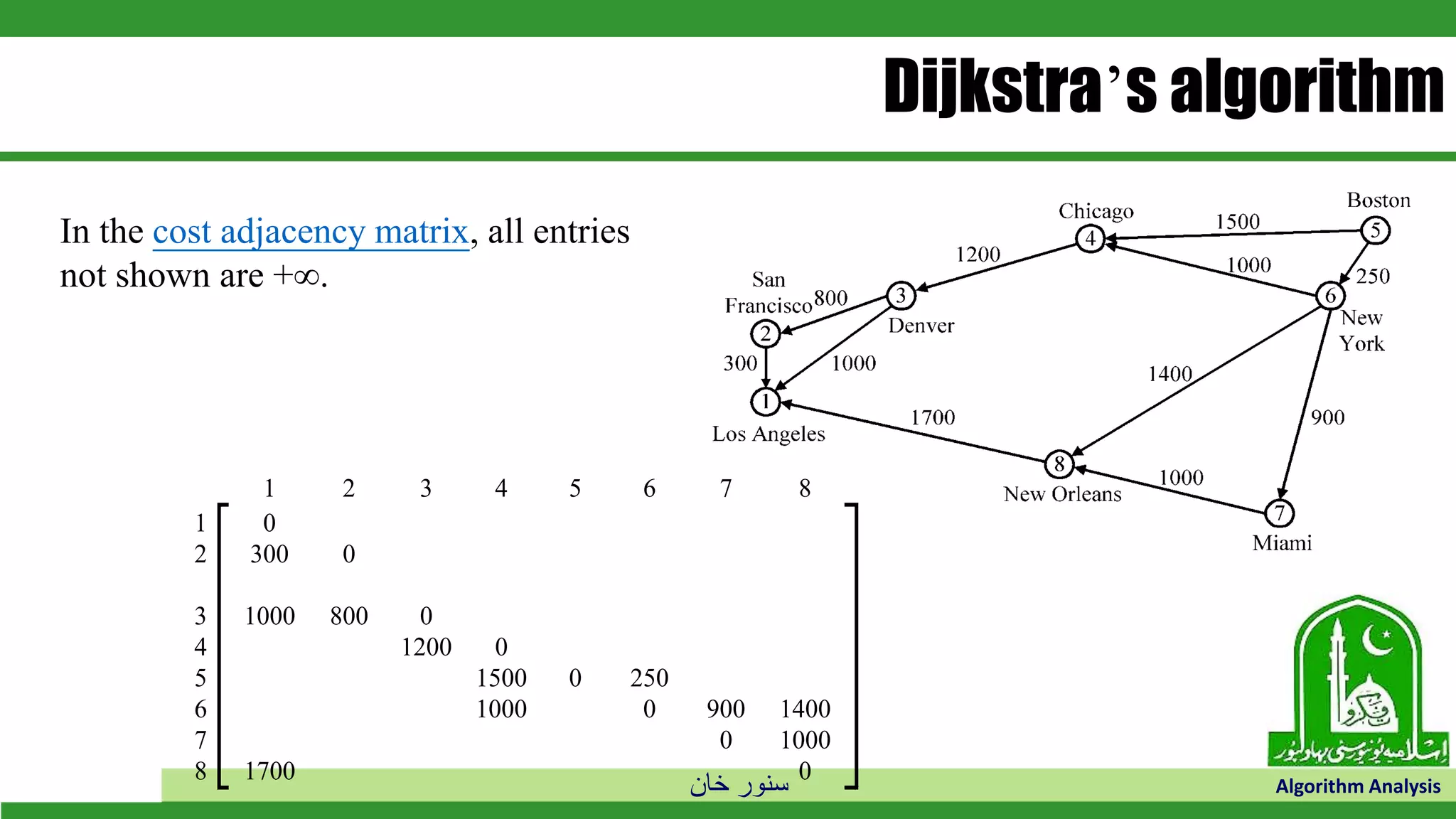
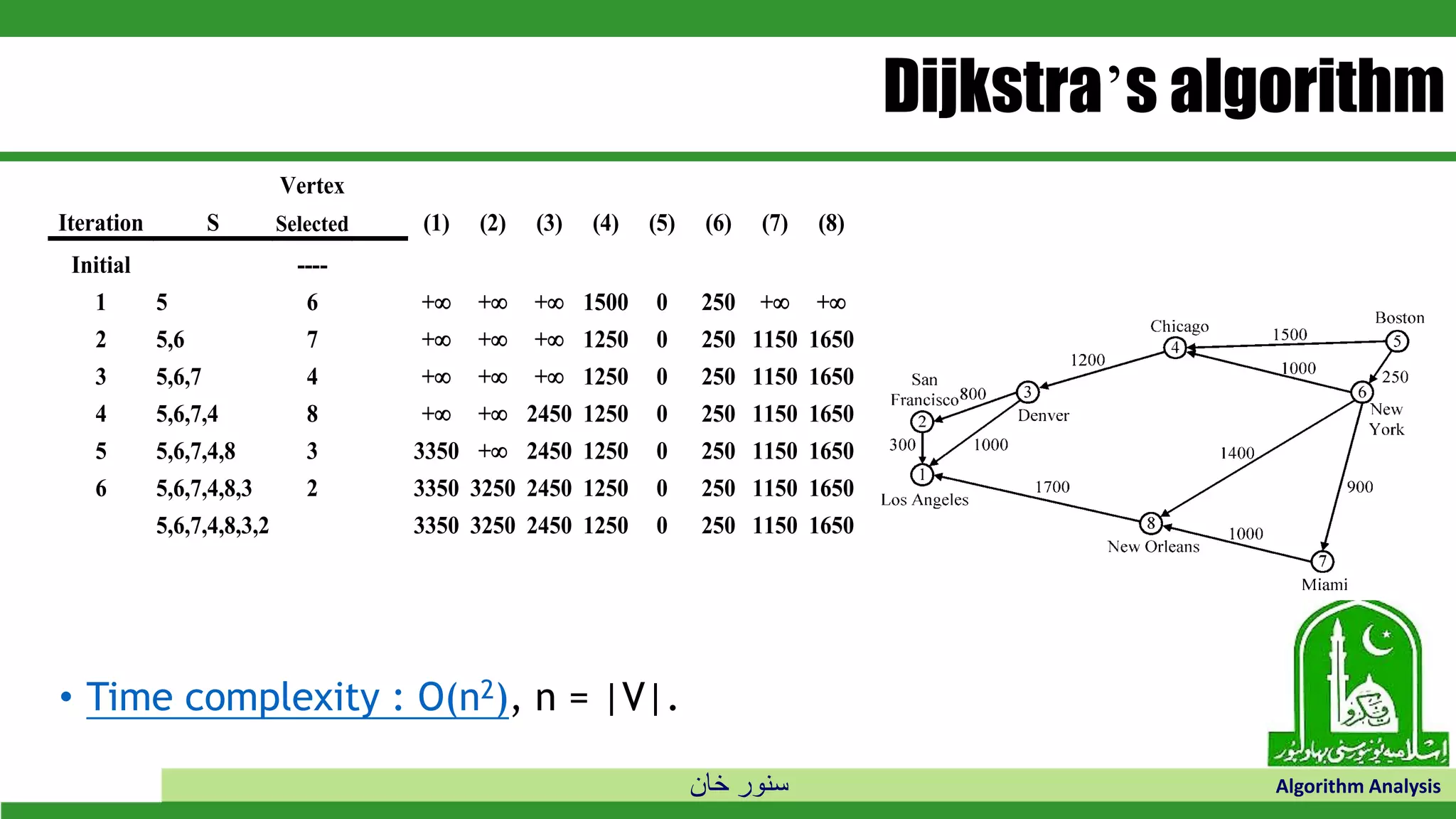
The document discusses greedy algorithms and their application to optimization problems. It provides examples of problems that can be solved using greedy approaches, such as fractional knapsack and making change. However, it notes that some problems like 0-1 knapsack and shortest paths on multi-stage graphs cannot be solved optimally with greedy algorithms. The document also describes various greedy algorithms for minimum spanning trees, single-source shortest paths, and fractional knapsack problems.
Greedy algorithm
- 1. Sunawar Khan Islamia Universityof Bahawalpur Bahawalnagar Campus Analysis o f Algorithm
- 2. خان سنور AlgorithmAnalysis Areas of Greedy Introduction to Greedy Algorithm Contents Components of Greedy Technique 0-1 Knapsack Problem
- 3. خان سنور AlgorithmAnalysis Optimization Problems • A problem that may have many feasible solutions. • Each solution has a value • In maximization problem, we wish to find a solution to maximize the value • In the minimization problem, we wish to find a solution to minimize the value
- 4. خان سنور AlgorithmAnalysis Technique to Solve a Problem • Greedy Method • Dynamic Programming • Branch and Bound
- 5. خان سنور AlgorithmAnalysis Greedy Algorithms • Many optimization problems can be solved using a greedy approach • The basic principle is that local optimal decisions may be used to build an optimal solution • But the greedy approach may not always lead to an optimal solution overall for all problems • The key is knowing which problems will work with this approach and which will not • We will study • The Knapsack Problem
- 6. خان سنور AlgorithmAnalysis Greedy algorithms • A greedy algorithm always makes the choice that looks best at the moment • My everyday examples: • Driving in Los Angeles, NY, or Boston for that matter • Playing cards • Invest on stocks • Choose a university • The hope: a locally optimal choice will lead to a globally optimal solution • For some problems, it works • Greedy algorithms tend to be easier to code
- 7. خان سنور AlgorithmAnalysis Greedy Technique • Greedy algorithms are simple and straightforward. • They are shortsighted in their approach in the sense that they take decisions on the basis of information at hand without worrying about the effect these decisions may have in the future. • They are easy to invent, easy to implement and most of the time quite efficient. • Many problems cannot be solved correctly by greedy approach. Greedy algorithms are used to solve optimization problems
- 8. خان سنور AlgorithmAnalysis Greedy Approach • Greedy Algorithm works by making the decision that seems most promising at any moment; it never reconsiders this decision, whatever situation may arise later.
- 9. خان سنور AlgorithmAnalysis Algorithm Algorithm Greedy(a, n){ for i=1 to n do X = Select(a); If feasible(x) then Solution = Solution + x; }
- 10. خان سنور AlgorithmAnalysis A simple example • Problem: Pick k numbers out of n numbers such that the sum of these k numbers is the largest. • Algorithm: FOR i = 1 to k pick out the largest number and delete this number from the input. ENDFOR
- 11. خان سنور AlgorithmAnalysis The greedy method • Suppose that a problem can be solved by a sequence of decisions. The greedy method has that each decision is locally optimal. These locally optimal solutions will finally add up to a globally optimal solution. • Only a few optimization problems can be solved by the greedy method.
- 12. خان سنور AlgorithmAnalysis Another Example • As an example consider the problem of "Making Change". • Coins available are: • dollars (100 cents) • quarters (25 cents) • dimes (10 cents) • nickels (5 cents) • pennies (1 cent)
- 13. خان سنور AlgorithmAnalysis Making Change Problem • Problem Make a change of a given amount using the smallest possible number of coins. • Informal Algorithm • Start with nothing. • at every stage without passing the given amount. • add the largest to the coins already chosen.
- 14. خان سنور AlgorithmAnalysis Formal Algorithm • Make change for n units using the least possible number of coins. • MAKE-CHANGE (n) C ← {100, 25, 10, 5, 1}// constant. Sol ← {}; // set that will hold the solution set. Sum ← 0 sum of item in solution set WHILE sum not = n x = largest item in set C such that sum + x ≤ n IF no such item THEN RETURN "No Solution" S ← S {value of x} sum ← sum + x RETURN S
- 15. خان سنور AlgorithmAnalysis Features of Problems solved by Greedy Algorithms • To construct the solution in an optimal way. Algorithm maintains two sets. One contains chosen items and the other contains rejected items. • The greedy algorithm consists of four (4) function. • A Candidate Set:- Solution is created from this set. • A Selection Set:- A Function used to chose the best candidate to be added to the solution. • A Feasibility Set:- A function that checks the feasibility of a set. • A Objective Function:- A Function which is used to assign value to a solution or partial solution. • A Solution Function:- A Function which is used to indicate whether a complete solution has been reached
- 16. خان سنور AlgorithmAnalysis Structure of Greedy Algorithm • Initially the set of chosen items is empty i.e., solution set. • At each step • item will be added in a solution set by using selection function. • IF the set would no longer be feasible • reject items under consideration (and is never consider again). • ELSE IF set is still feasible THEN • add the current item.
- 17. خان سنور AlgorithmAnalysis Definition of Feasibility • A feasible set (of candidates) is promising if it can be extended to produce not merely a solution, but an optimal solution to the problem. In particular, the empty set is always promising why? (because an optimal solution always exists) • Unlike Dynamic Programming, which solves the subproblems bottom-up, a greedy strategy usually progresses in a top-down fashion, making one greedy choice after another, reducing each problem to a smaller one. • Greedy-Choice Property • The "greedy-choice property" and "optimal substructure" are two ingredients in the problem that lend to a greedy strategy. • Greedy-Choice Property • It says that a globally optimal solution can be arrived at by making a locally optimal choice.
- 18. خان سنور AlgorithmAnalysis Shortest paths on a special graph • Problem: Find a shortest path from v0 to v3. • The greedy method can solve this problem. • The shortest path: 1 + 2 + 4 = 7.
- 19. خان سنور AlgorithmAnalysis Shortest paths on a multi-stage graph • Problem: Find a shortest path from v0 to v3 in the multi-stage graph. • Greedy method: v0v1,2v2,1v3 = 23 • Optimal: v0v1,1v2,2v3 = 7 • The greedy method does not work.
- 20. خان سنور AlgorithmAnalysis Minimum spanning trees (MST) • It may be defined on Euclidean space points or on a graph. • G = (V, E): weighted connected undirected graph • Spanning tree : S = (V, T), T E, undirected tree • Minimum spanning tree(MST) : a spanning tree with the smallest total weight.
- 21. خان سنور AlgorithmAnalysis An example of MST • A graph and one of its minimum costs spanning tree
- 22. خان سنور AlgorithmAnalysis Kruskal’s algorithm for finding MST Step 1: Sort all edges into nondecreasing order. Step 2: Add the next smallest weight edge to the forest if it will not cause a cycle. Step 3: Stop if n-1 edges. Otherwise, go to Step2.
- 23. خان سنور AlgorithmAnalysis An example of Kruskal’s algorithm
- 24. خان سنور AlgorithmAnalysis Prim’s algorithm for finding MST Step 1: x V, Let A = {x}, B = V - {x}. Step 2: Select (u, v) E, u A, v B such that (u, v) has the smallest weight between A and B. Step 3: Put (u, v) in the tree. A = A {v}, B = B - {v} Step 4: If B = , stop; otherwise, go to Step 2. • Time complexity : O(n2), n = |V|. (see the example on the next page)
- 25. خان سنور AlgorithmAnalysis An example for Prim’s algorithm
- 26. خان سنور AlgorithmAnalysis The single-source shortest path problem • shortest paths from v0 to all destinations
- 27. خان سنور AlgorithmAnalysis Dijkstra’s algorithm 1 2 3 4 5 6 7 8 1 0 2 300 0 3 1000 800 0 4 1200 0 5 1500 0 250 6 1000 0 900 1400 7 0 1000 8 1700 0 In the cost adjacency matrix, all entries not shown are +.
- 28. خان سنور AlgorithmAnalysis • Time complexity : O(n2), n = |V|. Vertex Iteration S Selected (1) (2) (3) (4) (5) (6) (7) (8) Initial ---- 1 5 6 + + + 1500 0 250 + + 2 5,6 7 + + + 1250 0 250 1150 1650 3 5,6,7 4 + + + 1250 0 250 1150 1650 4 5,6,7,4 8 + + 2450 1250 0 250 1150 1650 5 5,6,7,4,8 3 3350 + 2450 1250 0 250 1150 1650 6 5,6,7,4,8,3 2 3350 3250 2450 1250 0 250 1150 1650 5,6,7,4,8,3,2 3350 3250 2450 1250 0 250 1150 1650 Dijkstra’s algorithm
- 29. خان سنور AlgorithmAnalysis Knapsack Problem • Statement A thief robbing a store and can carry a maximal weight of w into their knapsack. There are n items and ith item weigh wi and is worth vi dollars. What items should thief take? • There are two versions of problem
- 30. خان سنور AlgorithmAnalysis Fractional knapsack problem • The setup is same, but the thief can take fractions of items, meaning that the items can be broken into smaller pieces so that thief may decide to carry only a fraction of xi of item i, where 0 ≤ xi ≤ 1.Exhibit greedy choice property. • Greedy algorithm exists. • Exhibit optimal substructure property. • ?????
- 31. خان سنور AlgorithmAnalysis 0-1 knapsack problem • The setup is the same, but the items may not be broken into smaller pieces, so thief may decide either to take an item or to leave it (binary choice), but may not take a fraction of an item.Exhibit No greedy choice property. • No greedy algorithm exists. • Exhibit optimal substructure property. • Only dynamic programming algorithm exists.
- 32. خان سنور AlgorithmAnalysis Greedy Solution - Fractional Knapsack Problem • There are n items in a store. For i =1,2, . . . , n, item i has weight wi > 0 and worth vi> 0. Thief can carry a maximum weight of W pounds in a knapsack. • In this version of a problem the items can be broken into smaller piece, so the thief may decide to carry only a fraction xi of object i, where 0 ≤ xi ≤ 1. Item i contributes xiwi to the total weight in the knapsack, and xivi to the value of the load. • In Symbol, the fraction knapsack problem can be stated as follows. maximize nSi=1 xivi subject to constraint nSi=1 xiwi ≤ W • It is clear that an optimal solution must fill the knapsack exactly, for otherwise we could add a fraction of one of the remaining objects and increase the value of the load. Thus in an optimal solution nSi=1 xiwi = W.
- 33. خان سنور AlgorithmAnalysis The knapsack problem • n objects, each with a weight wi > 0 a profit pi > 0 capacity of knapsack: M Maximize Subject to 0 xi 1, 1 i n p xi i i n1 w x Mi i i n1
- 34. خان سنور AlgorithmAnalysis The knapsack Pseudo Code • The greedy algorithm: Step 1: Sort pi/wi into nonincreasing order. Step 2: Put the objects into the knapsack according to the sorted sequence as possible as we can.
- 35. خان سنور AlgorithmAnalysis Algorithm Greedy-fractional-knapsack (w, v, W) FOR i =1 to do x[i] =0 weight = 0 while weight < W do i = best remaining item IF weight + w[i] ≤ W then x[i] = 1 weight = weight + w[i] else x[i] = (w - weight) / w[i] weight = W return x
- 36. خان سنور AlgorithmAnalysis Knapsack Problem Objects(O) 1 2 3 4 5 6 7 Profits (P) 10 5 15 7 6 18 3 Weight (W) 2 3 5 7 1 4 1 15 KG
- 37. خان سنور AlgorithmAnalysis Knapsack Problem Objects(O) 1 2 3 4 5 6 7 Profits (P) 10 5 15 7 6 18 3 Weight (W) 2 3 5 7 1 4 1 15 KG X X1 X2 X3 X4 X5 X6 X7
- 38. خان سنور AlgorithmAnalysis Knapsack Problem Objects(O) 1 2 3 4 5 6 7 Profits (P) 10 5 15 7 6 18 3 Weight (W) 2 3 5 7 1 4 1 P/W 5 1.3 3 1 6 4.5 3 15 KG X X1 X2 X3 X4 X5 X6 X7
- 39. خان سنور AlgorithmAnalysis Knapsack Problem Objects(O) 1 2 3 4 5 6 7 Profits (P) 10 5 15 7 6 18 3 Weight (W) 2 3 5 7 1 4 1 P/W 5 1.3 3 1 6 4.5 3 15 KG X X1 X2 X3 X4 X5 X6 X7 15 – 1 = 14
- 40. خان سنور AlgorithmAnalysis Knapsack Problem Objects(O) 1 2 3 4 5 6 7 Profits (P) 10 5 15 7 6 18 3 Weight (W) 2 3 5 7 1 4 1 P/W 5 1.3 3 1 6 4.5 3 15 KG X X1 X2 X3 X4 X5 X6 X7 15 – 1 = 14 14 – 2 = 12
- 41. خان سنور AlgorithmAnalysis Knapsack Problem Objects(O) 1 2 3 4 5 6 7 Profits (P) 10 5 15 7 6 18 3 Weight (W) 2 3 5 7 1 4 1 P/W 5 1.3 3 1 6 4.5 3 15 KG X X1 X2 X3 X4 X5 X6 X7 15 – 1 = 14 14 – 2 = 12 12 – 4 = 8
- 42. خان سنور AlgorithmAnalysis Knapsack Problem Objects(O) 1 2 3 4 5 6 7 Profits (P) 10 5 15 7 6 18 3 Weight (W) 2 3 5 7 1 4 1 P/W 5 1.3 3 1 6 4.5 3 15 KG X X1 X2 X3 X4 X5 X6 X7 15 – 1 = 14 14 – 2 = 12 12 – 4 = 8 8 – 5 = 3
- 43. خان سنور AlgorithmAnalysis Knapsack Problem Objects(O) 1 2 3 4 5 6 7 Profits (P) 10 5 15 7 6 18 3 Weight (W) 2 3 5 7 1 4 1 P/W 5 1.3 3 1 6 4.5 3 15 KG X X1 X2 X3 X4 X5 X6 X7 15 – 1 = 14 14 – 2 = 12 12 – 4 = 8 8 – 5 = 3 3 – 1 = 2
- 44. خان سنور AlgorithmAnalysis Knapsack Problem Objects(O) 1 2 3 4 5 6 7 Profits (P) 10 5 15 7 6 18 3 Weight (W) 2 3 5 7 1 4 1 P/W 5 1.3 3 1 6 4.5 3 15 KG X X1 X2 X3 X4 X5 X6 X7 15 – 1 = 14 14 – 2 = 12 12 – 4 = 8 8 – 5 = 3 3 – 1 = 2 2 – 2 = 0 2 /3
- 45. خان سنور AlgorithmAnalysis Knapsack Problem Objects(O) 1 2 3 4 5 6 7 Profits (P) 10 5 15 7 6 18 3 Weight (W) 2 3 5 7 1 4 1 P/W 5 1.3 3 1 6 4.5 3 15 KG X X1 X2 X3 X4 X5 X6 X7 15 – 1 = 14 14 – 2 = 12 12 – 4 = 8 8 – 5 = 3 3 – 1 = 2 2 – 2 = 0 2 /3 0
- 46. خان سنور AlgorithmAnalysis Knapsack Problem Objects(O) 1 2 3 4 5 6 7 Profits (P) 10 5 15 7 6 18 3 Weight (W) 2 3 5 7 1 4 1 P/W 5 1.3 3 1 6 4.5 3 X X1 X2 X3 X4 X5 X6 X7 2 /3 0 Calculate Weight σ 𝑥𝑖 𝑤 𝑖= 1 𝑥 2 + 2/3 𝑥 3 + 1 𝑥 5 + 0 𝑥 7 + 1 𝑥 1 + 1 𝑥 4 + 1 𝑥 1 2 + 2 + 5 + 0 + 1 + 4 + 1 = 15 Calculate Profit 𝑥𝑖 𝑝 𝑖= 1 𝑋 10 + 2 3𝑥5 + 1𝑥5 + 1𝑥6 + 1𝑥18 + 1𝑥3 10 + 2𝑥1.3 + 15 + 6 + 18 + 3 = 54.6
- 47. خان سنور AlgorithmAnalysis Conclusion •Constraints σ 𝑥𝑖 𝑤𝑖 ≤ m where m = 15 •Objective 𝑀𝐴𝑋 𝑥𝑖 𝑝 𝑖=
- 48. خان سنور AlgorithmAnalysis Analysis • If the items are already sorted into decreasing order of vi / wi, then the while-loop takes a time in O(n); Therefore, the total time including the sort is in O(n log n). • If we keep the items in heap with largest vi/wi at the root. Then • creating the heap takes O(n) time • while-loop now takes O(log n) time (since heap property must be restored after the removal of root) • Although this data structure does not alter the worst-case, it may be faster if only a small number of items are need to fill the knapsack.