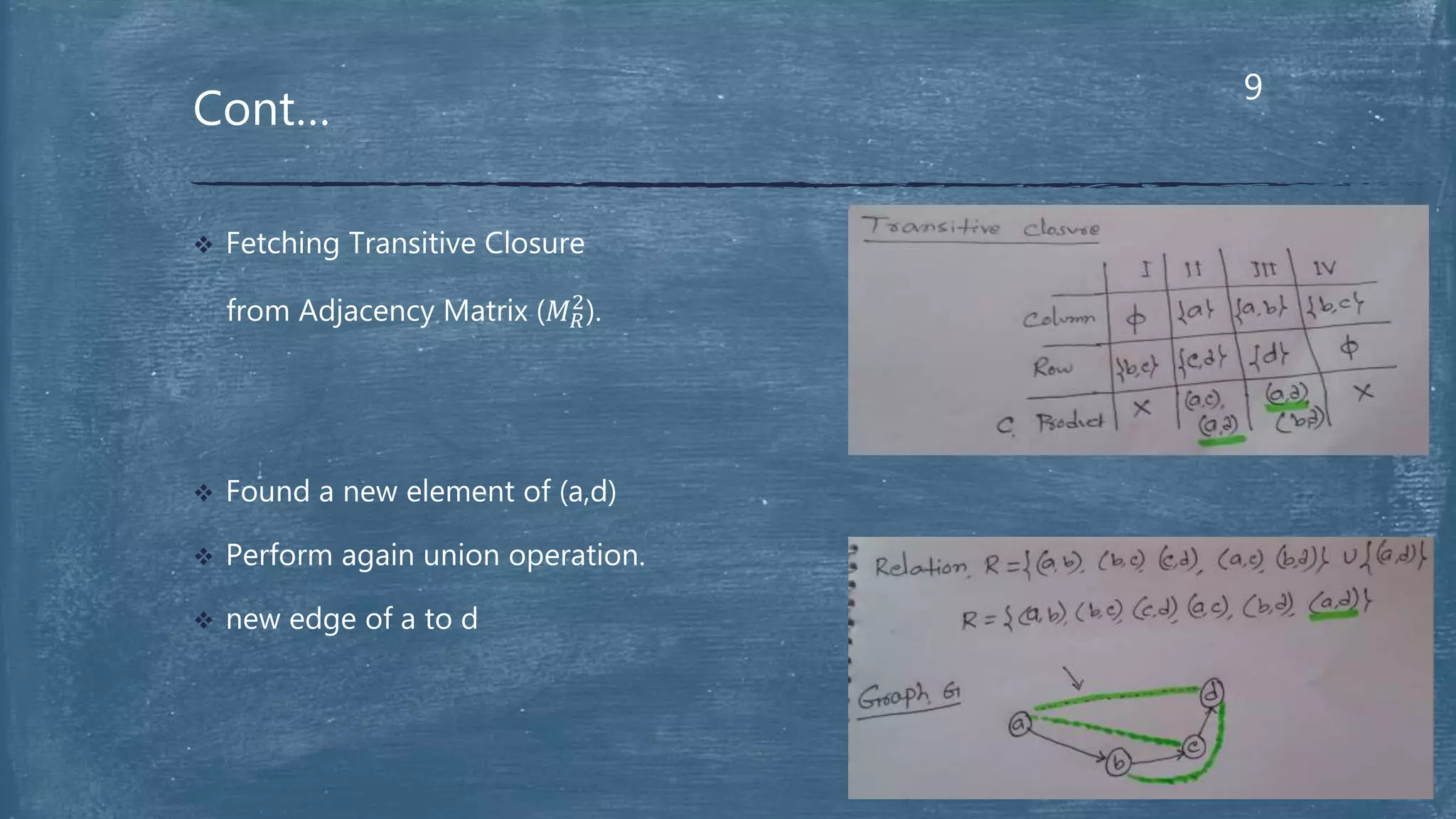
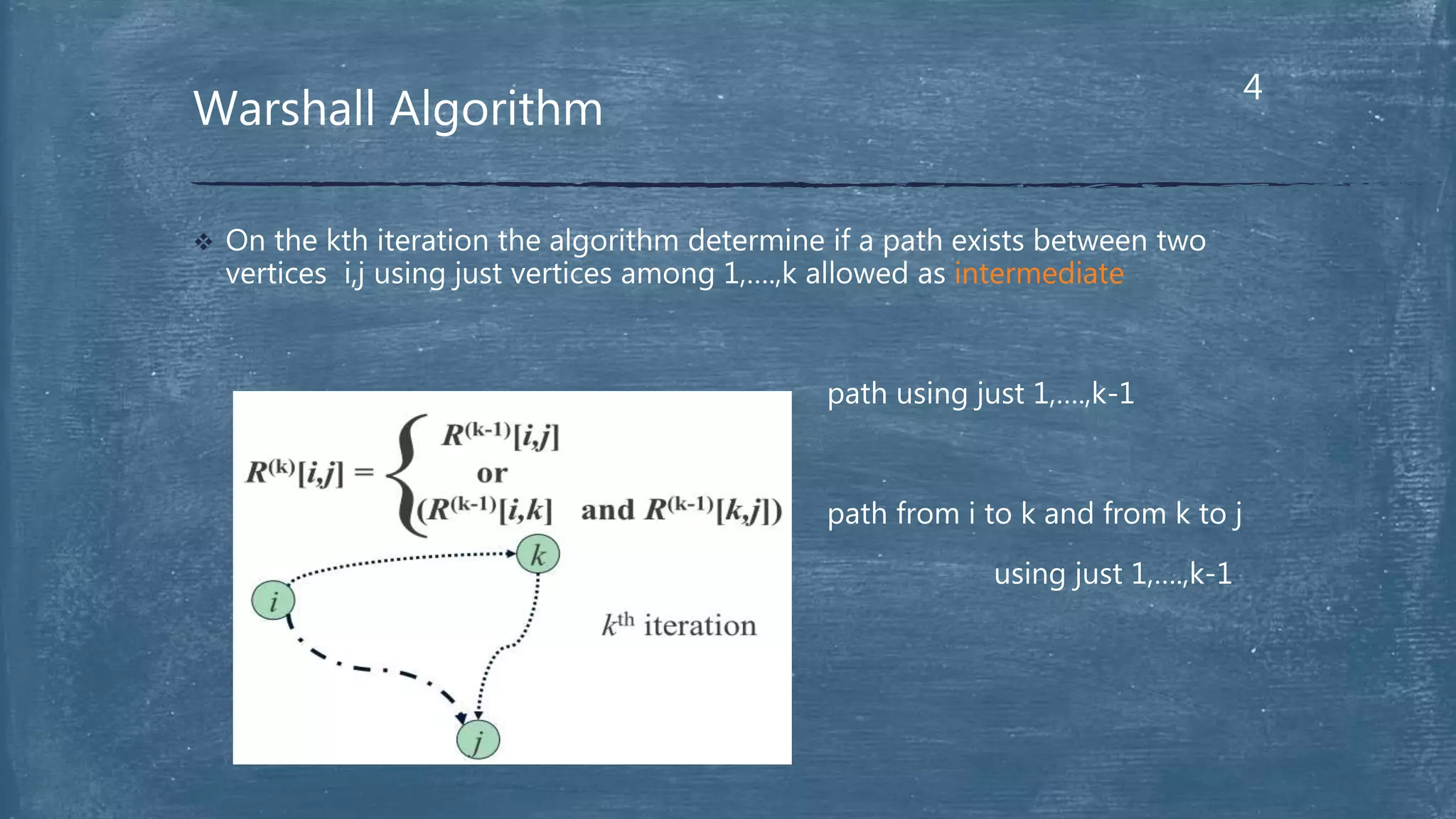
The document presents the Floyd-Warshall algorithm for finding the transitive closure of a graph. It defines transitive closure as determining if there is a path between any two vertices in the graph. The algorithm works by iterating through the vertices and using union operations to update the adjacency matrix at each step, adding new paths found by going through intermediate vertices. It runs in O(n3) time and requires additional space to store the updated matrices at each step. In the end, the final adjacency matrix represents the transitive closure of the original graph.



![ Algorithm to find Transitive Closure Input: The given graph. Output: Transitive Closure matrix. TransitiveClosure { R(0) A //copy adjacency matrix into another matrix for k = 1 to n do for i = 1 to n do for j = 1 to n do R(k) [i,j] := R(k-1) [i,j] OR ( R(k-1)[i,k] AND R(k-1) [k,j]); } Warshall Algorithm : Transitive Closure 5](https://image.slidesharecdn.com/findtransitiveclosureusingfloyd-warshallalgorithm-191125183439/75/Find-Transitive-Closure-Using-Floyd-Warshall-Algorithm-5-2048.jpg)