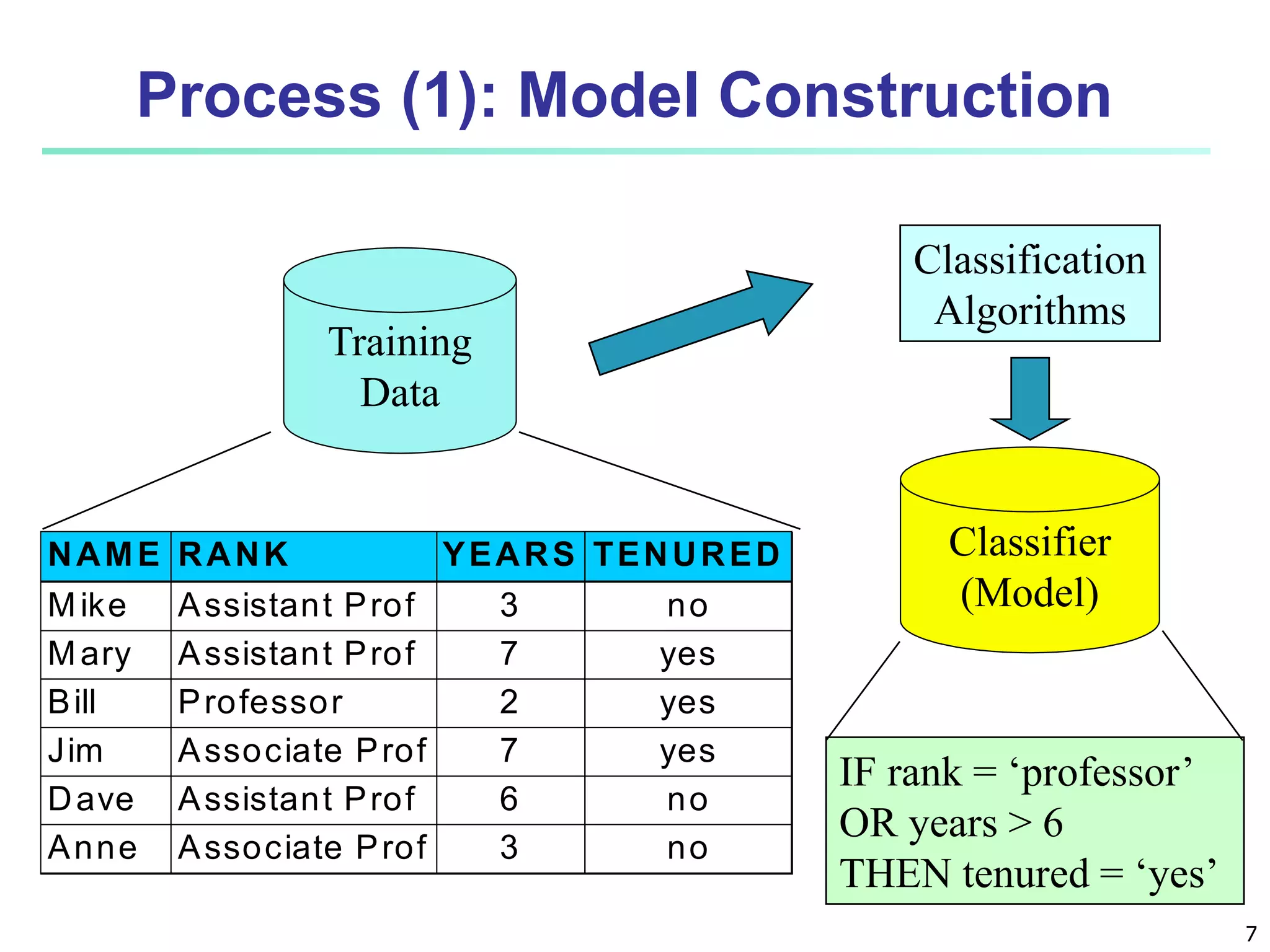
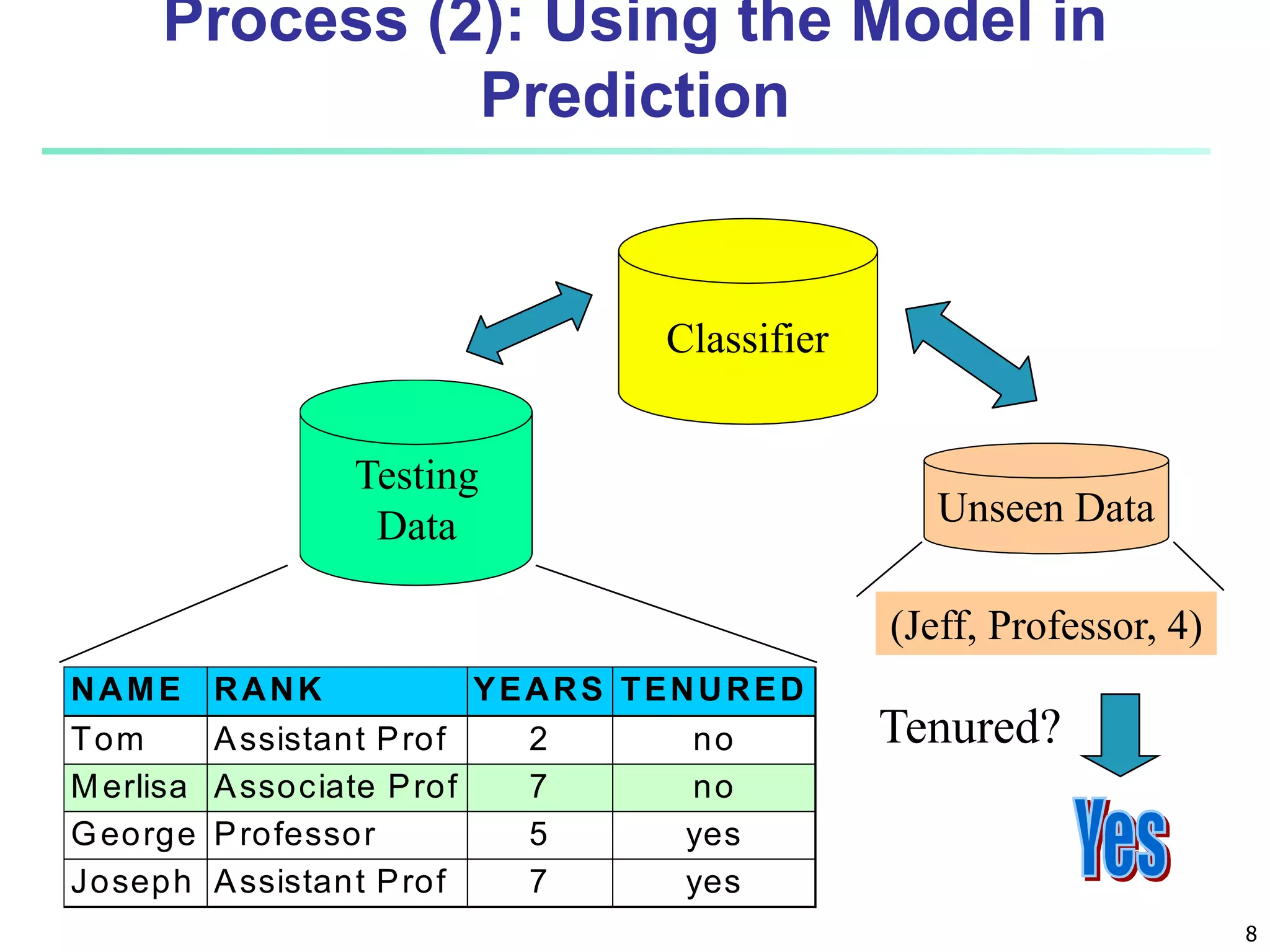
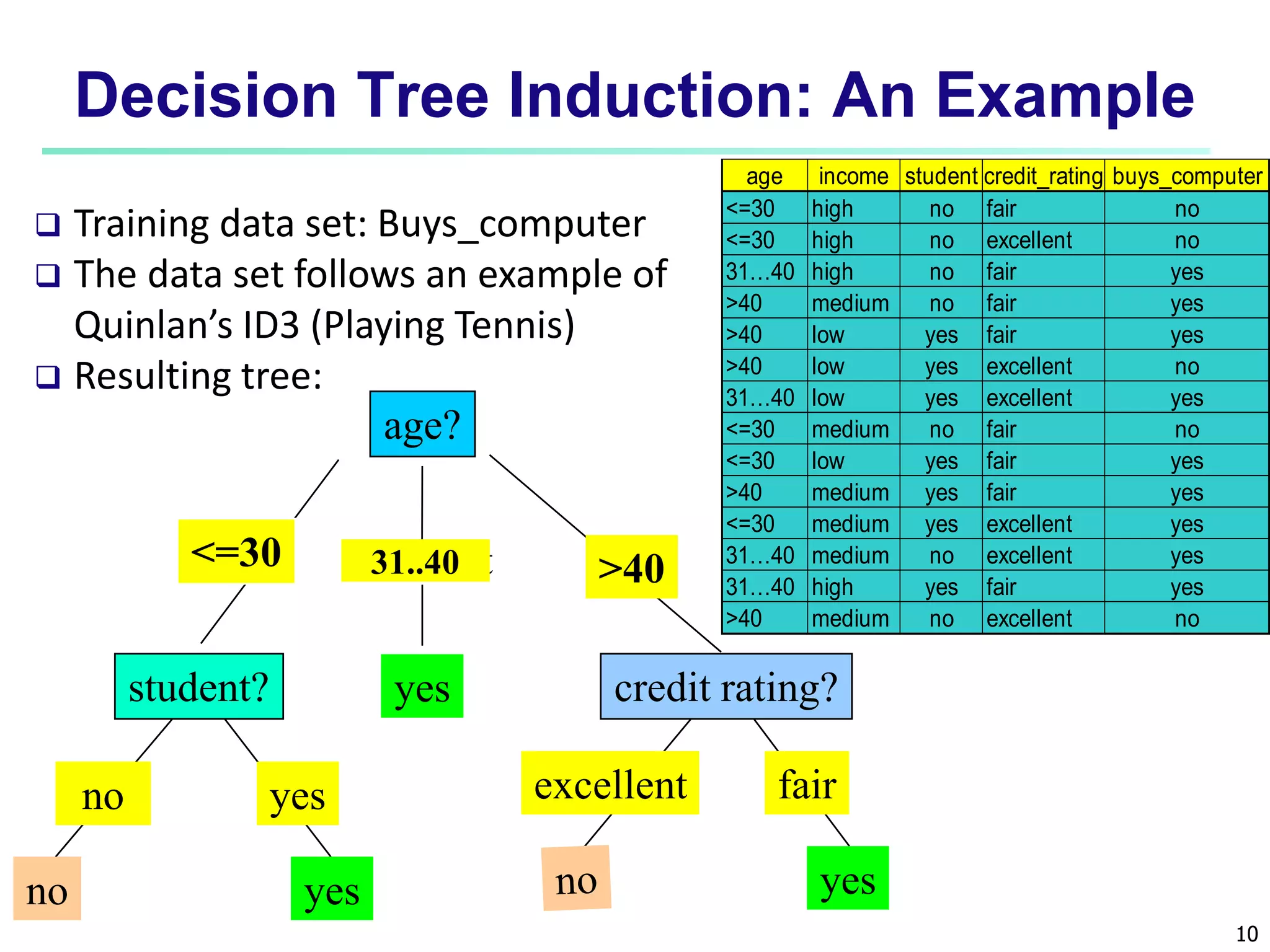
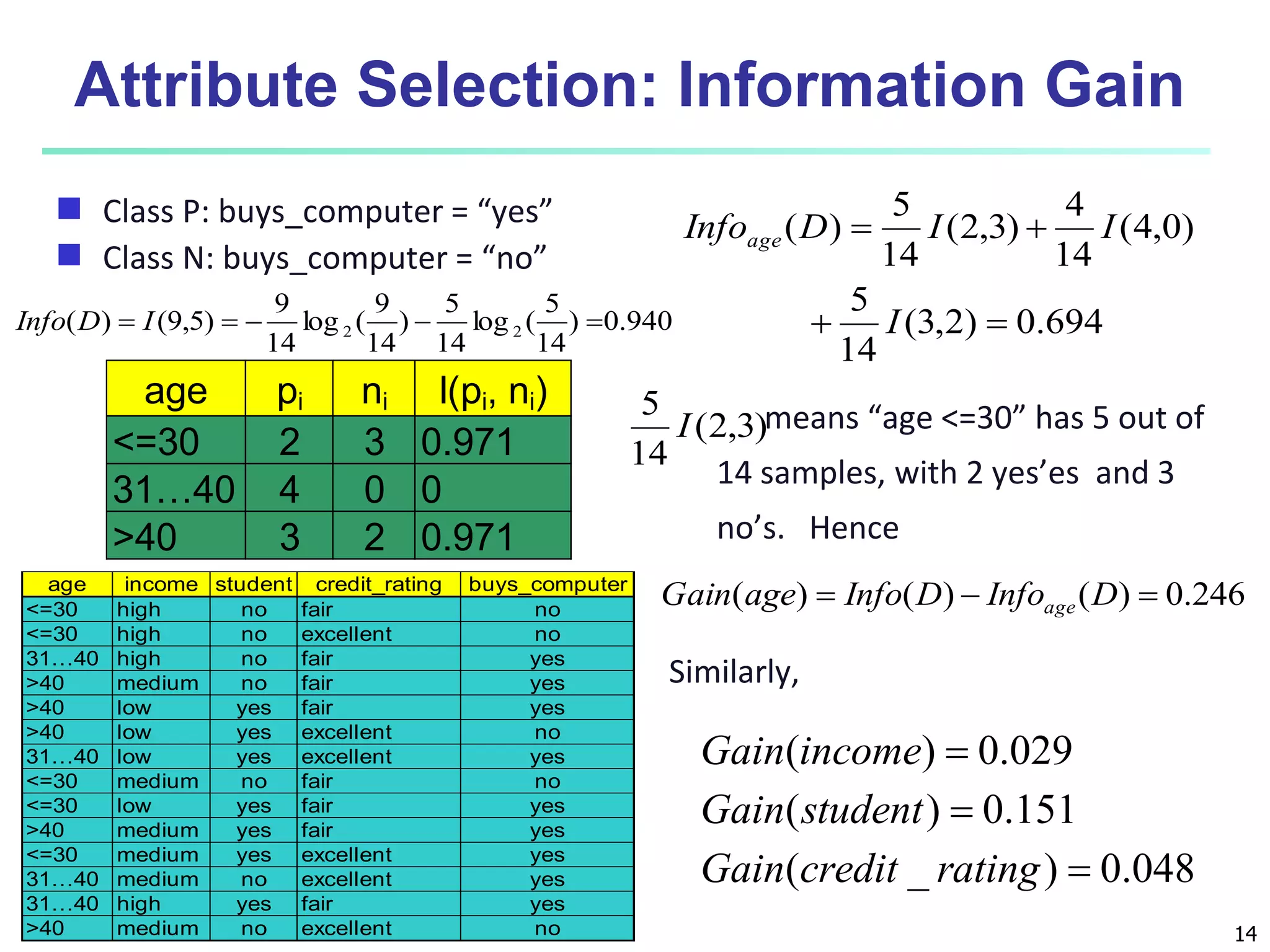
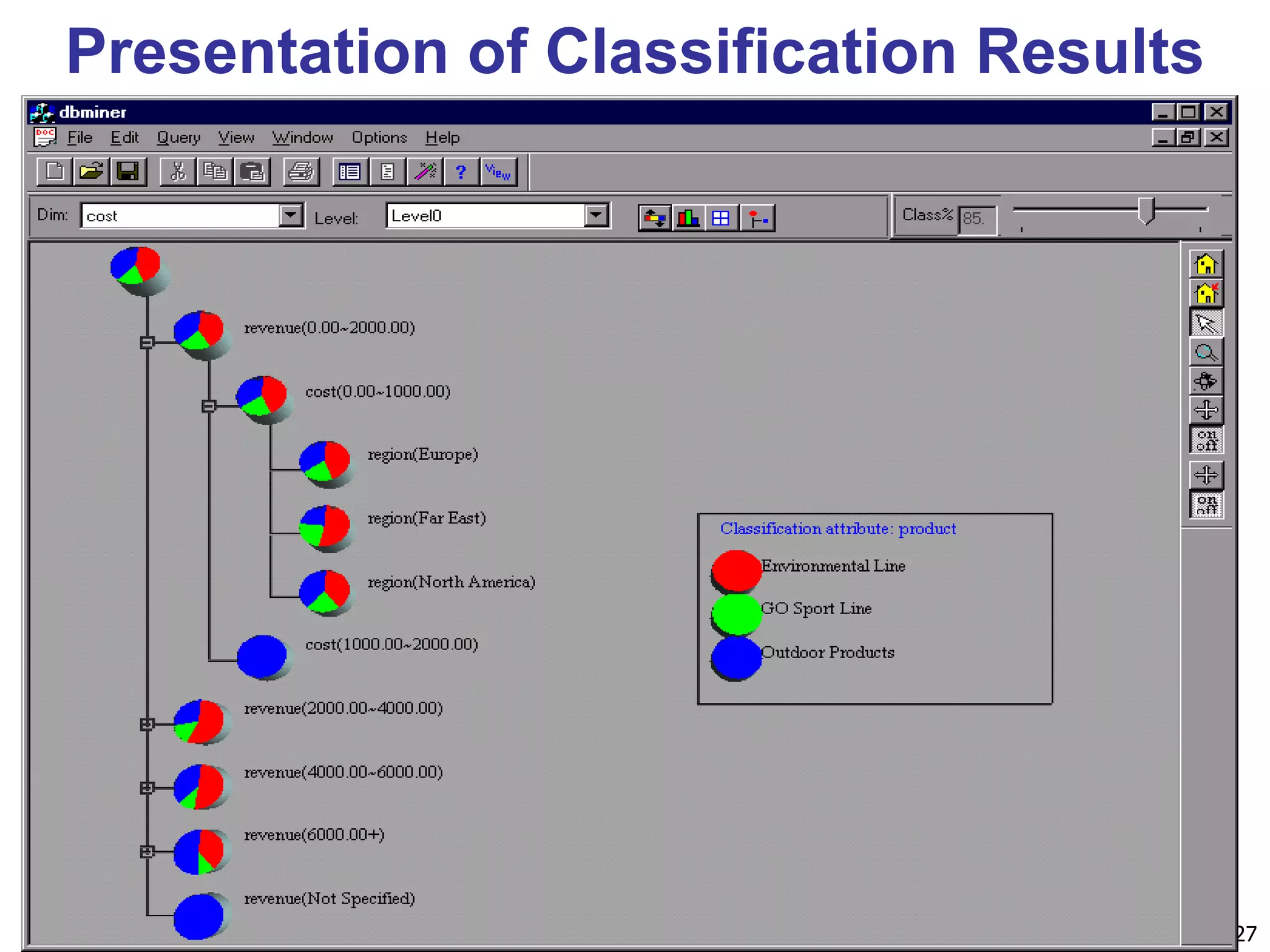
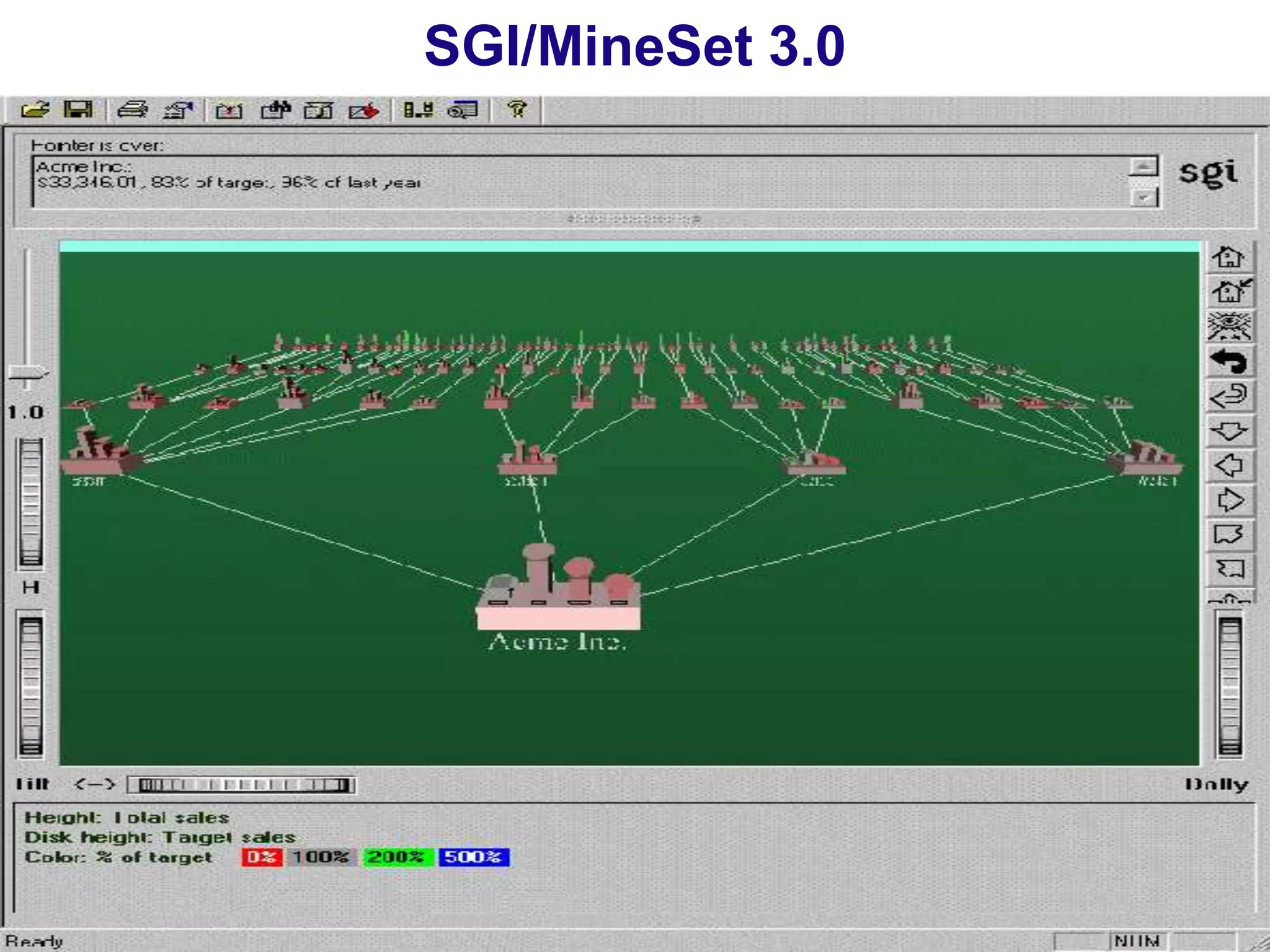
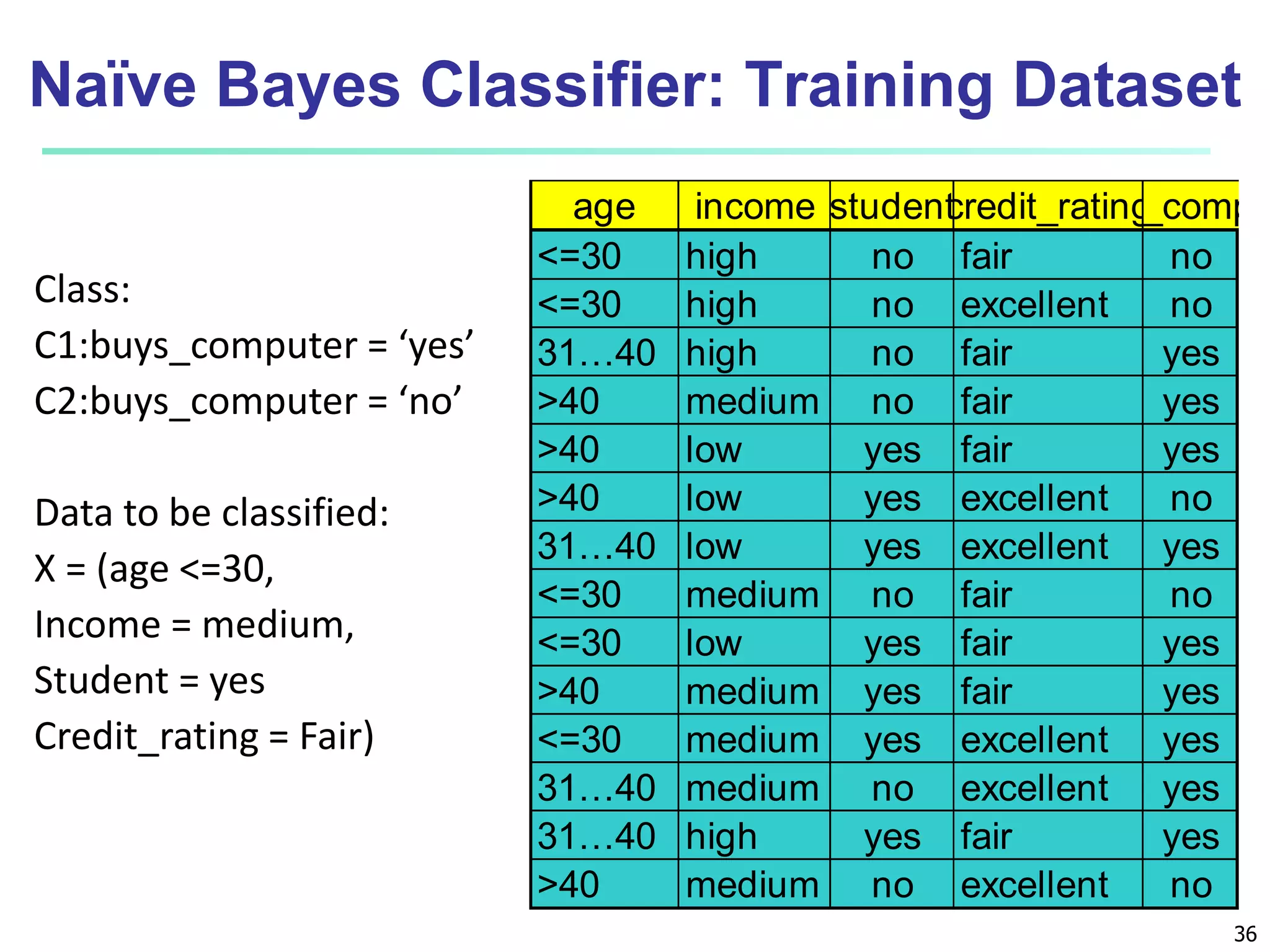
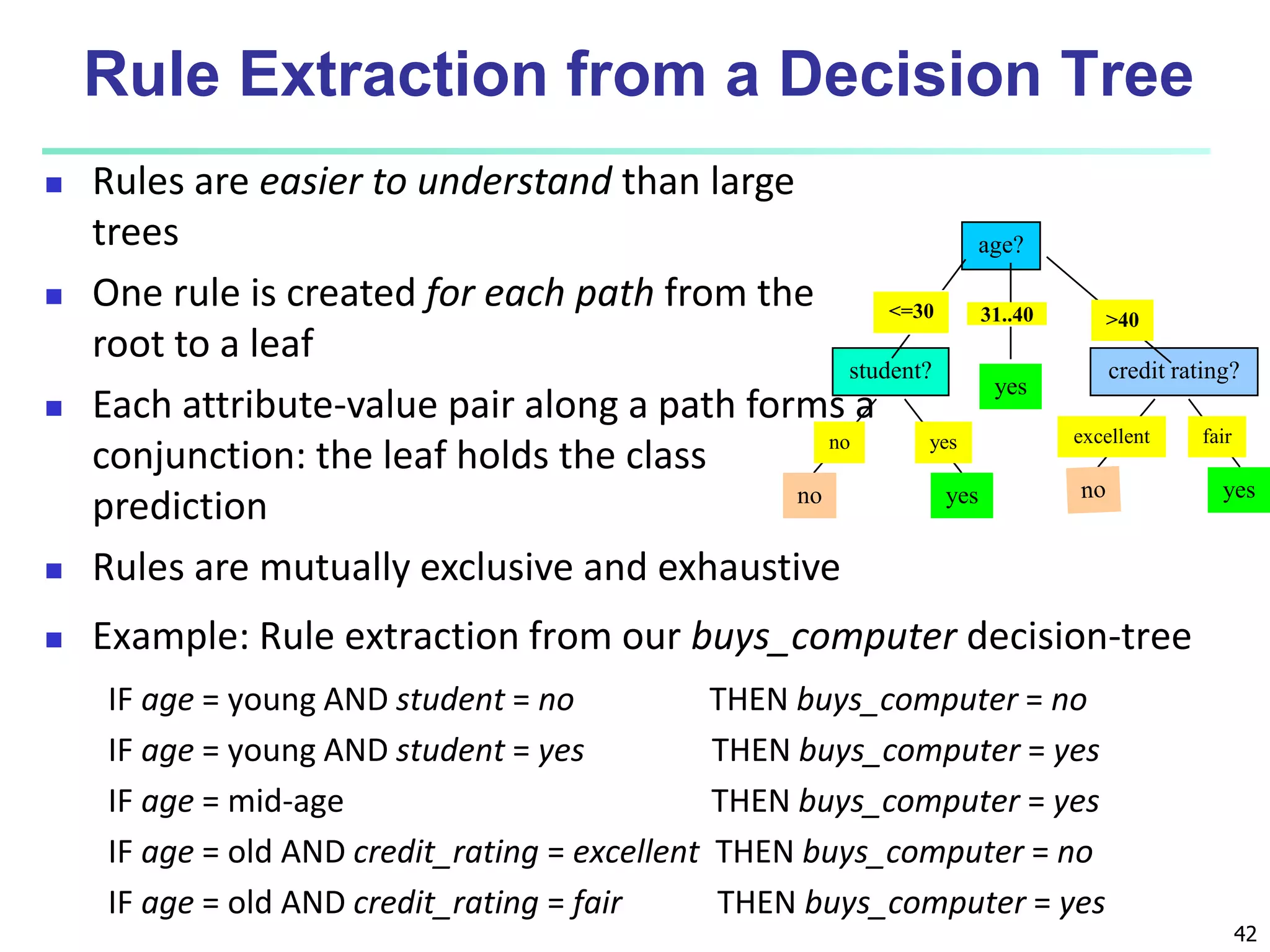
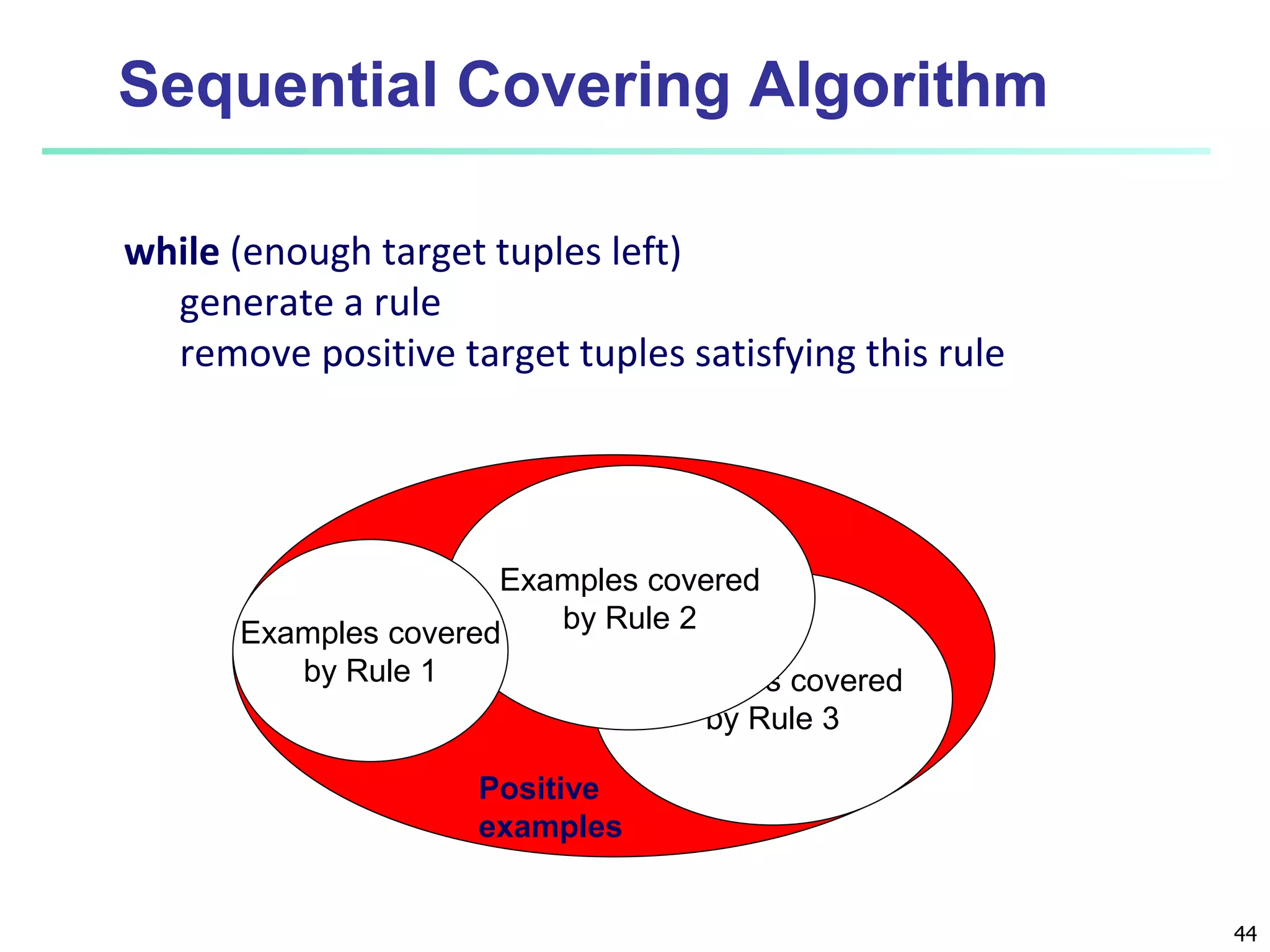
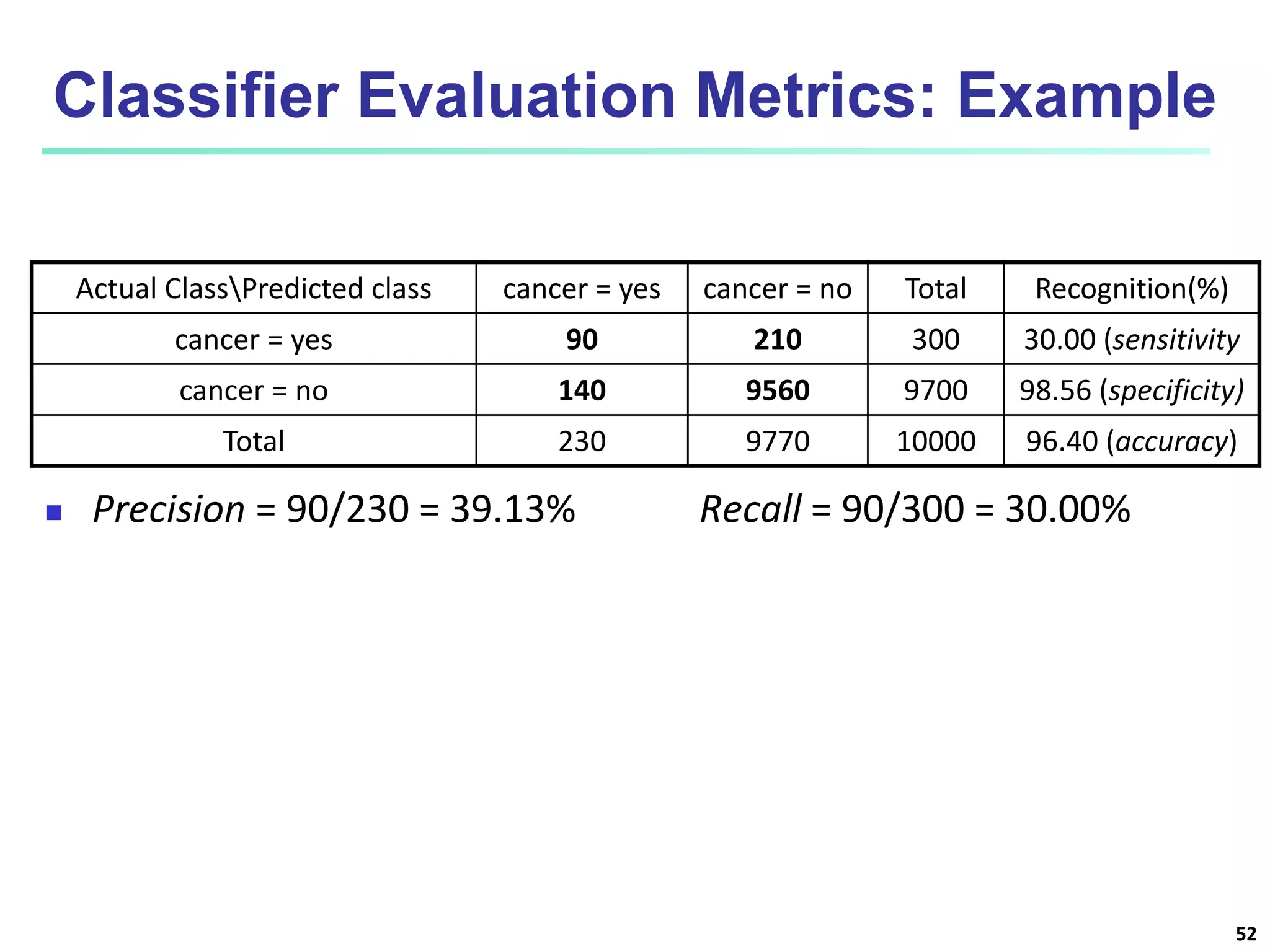
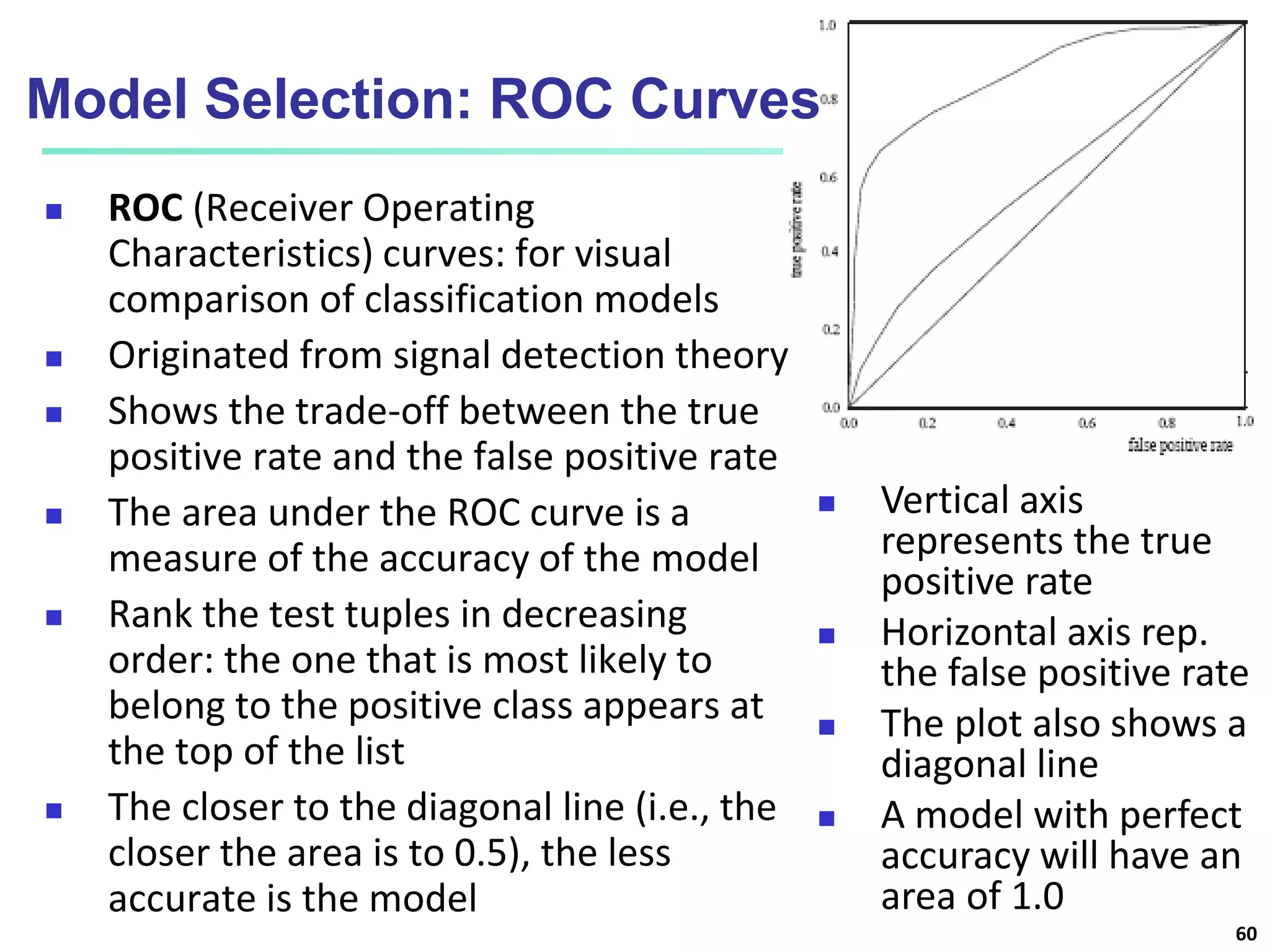
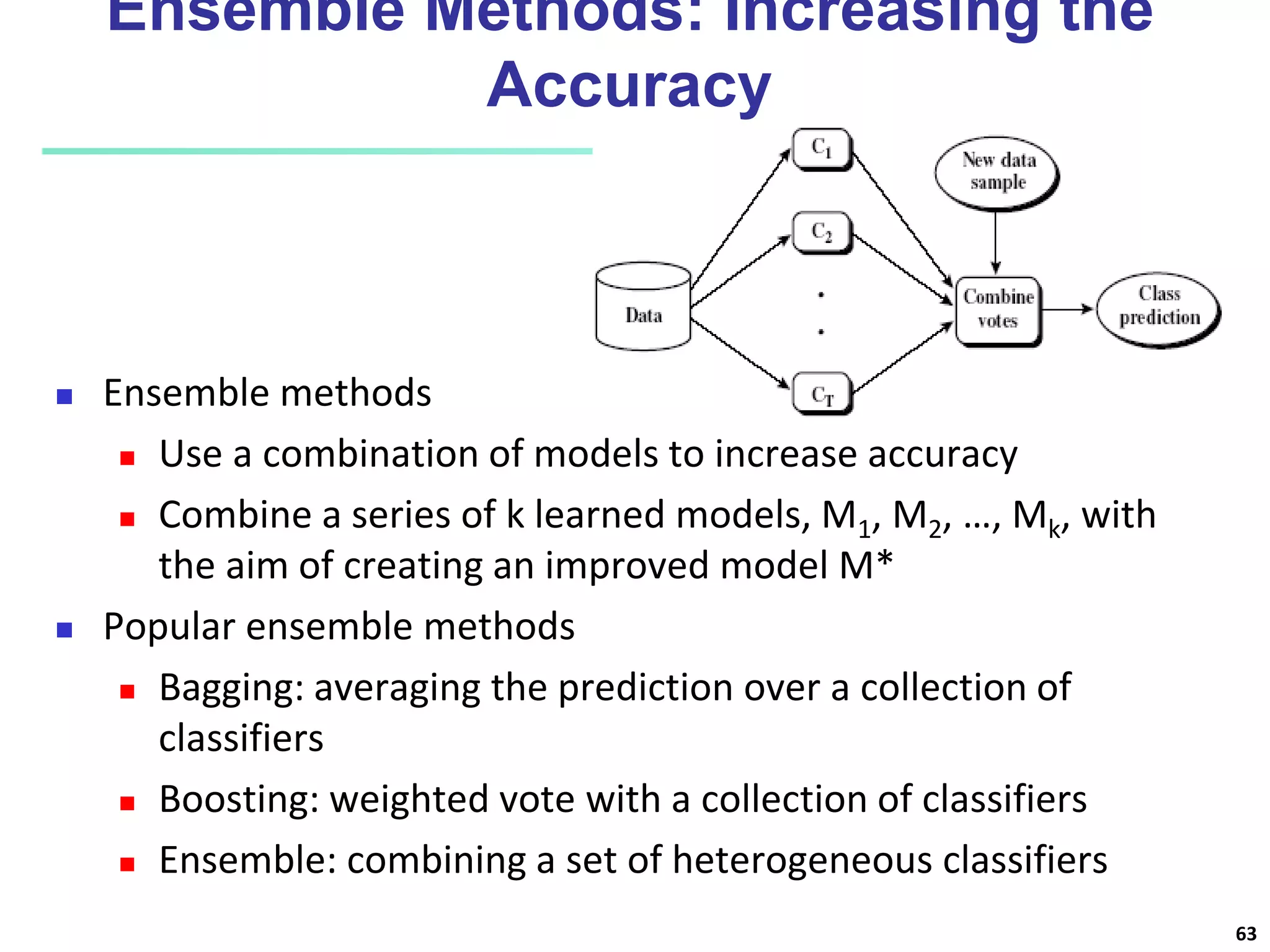
Chapter 8 of 'Data Mining: Concepts and Techniques' covers classification basics, including supervised and unsupervised learning, decision tree induction, Bayesian classification, and evaluation techniques. It discusses how to construct models using training data, apply these models to classify new data, and improve accuracy through ensemble methods. The chapter emphasizes key concepts like overfitting, model evaluation, and important classification algorithms such as decision trees and Bayesian classifiers.