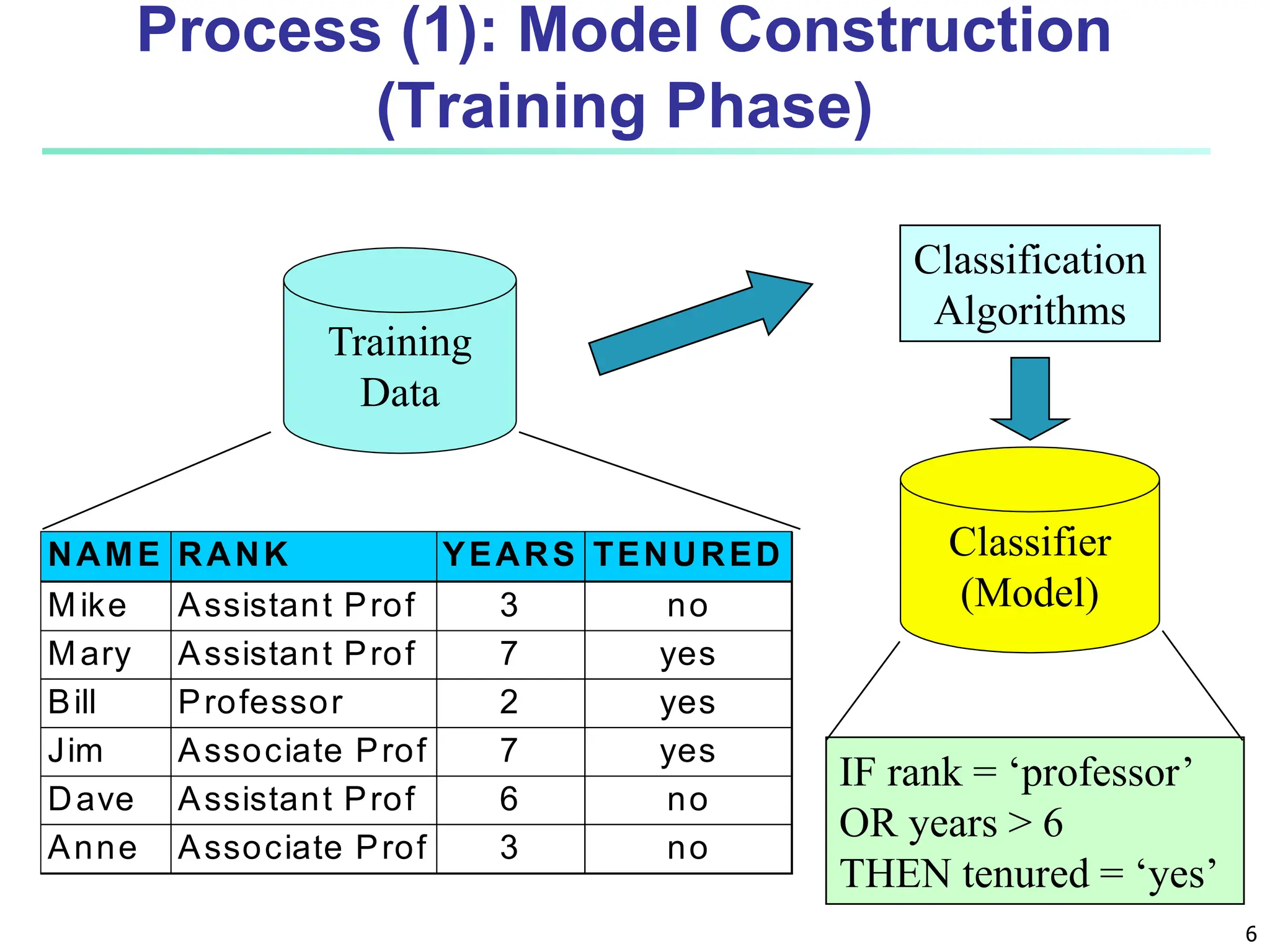
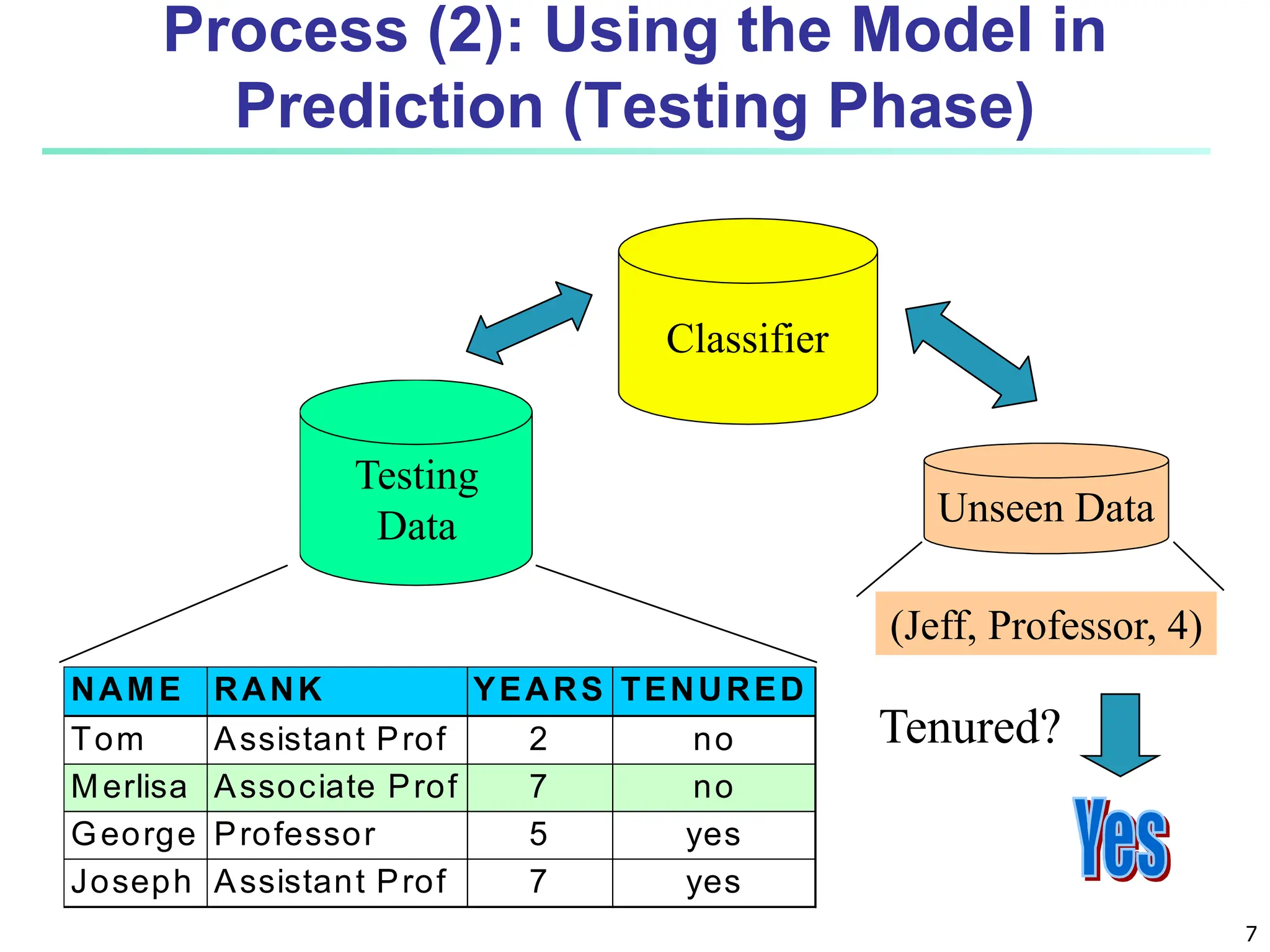
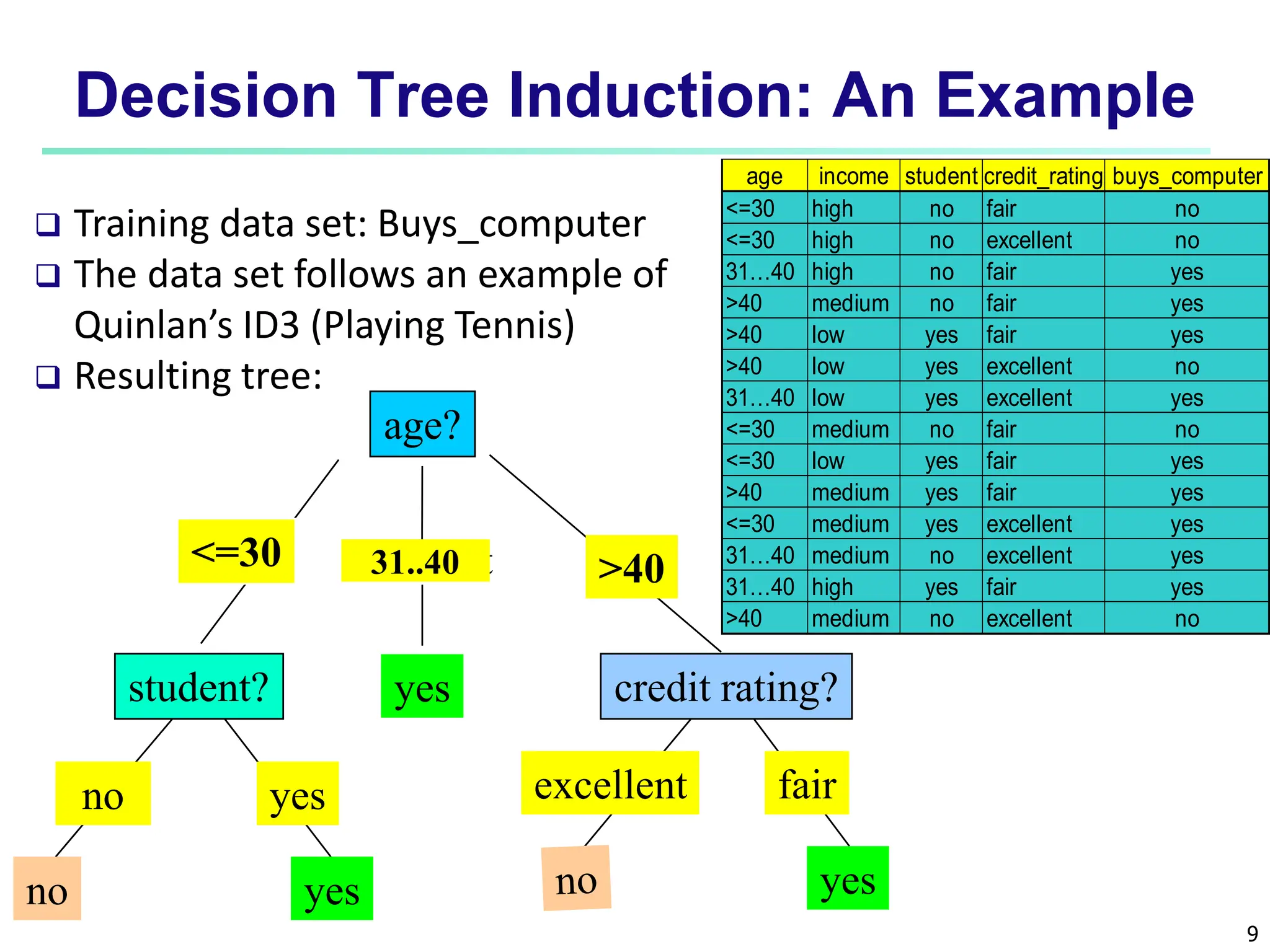
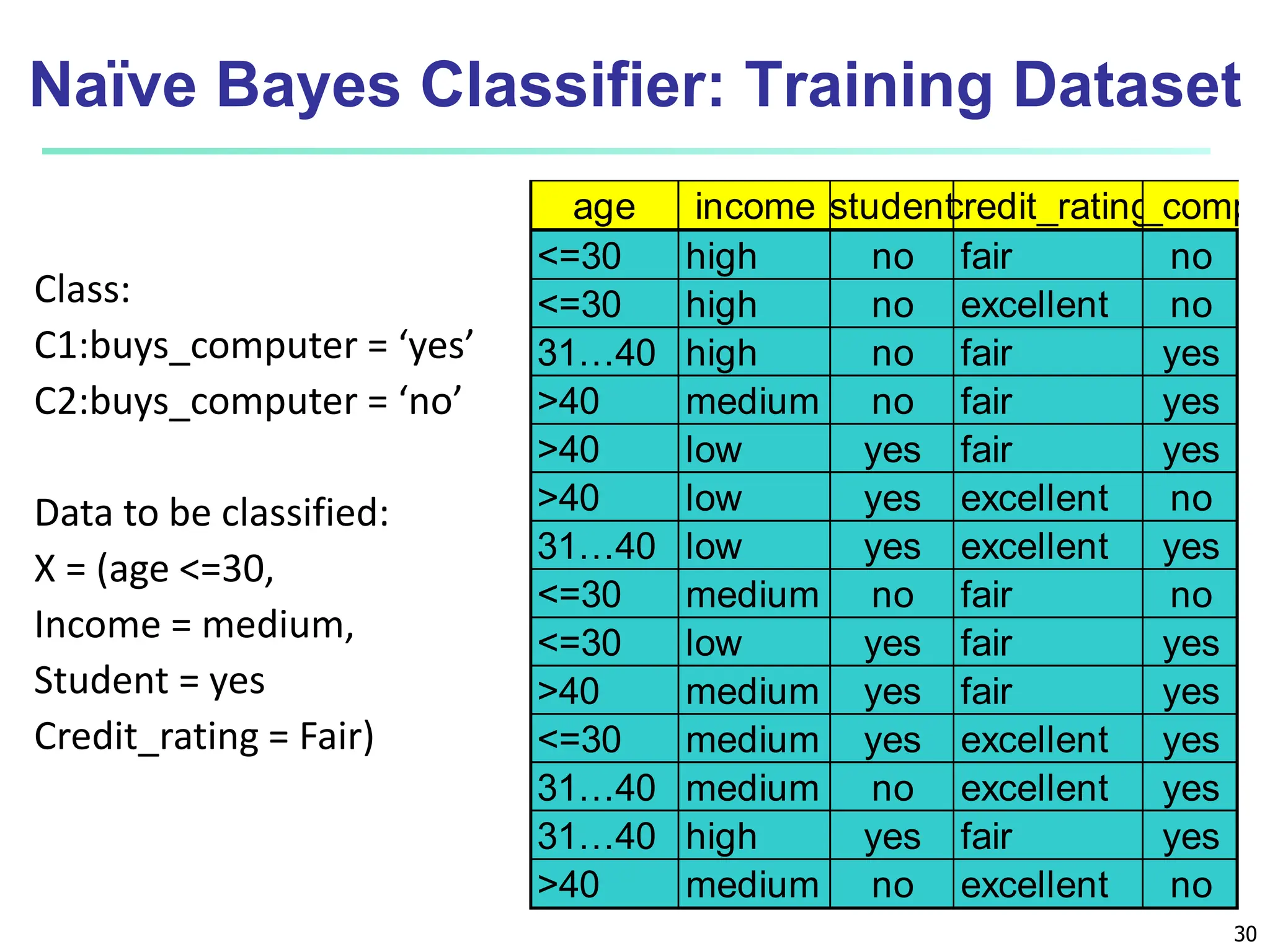
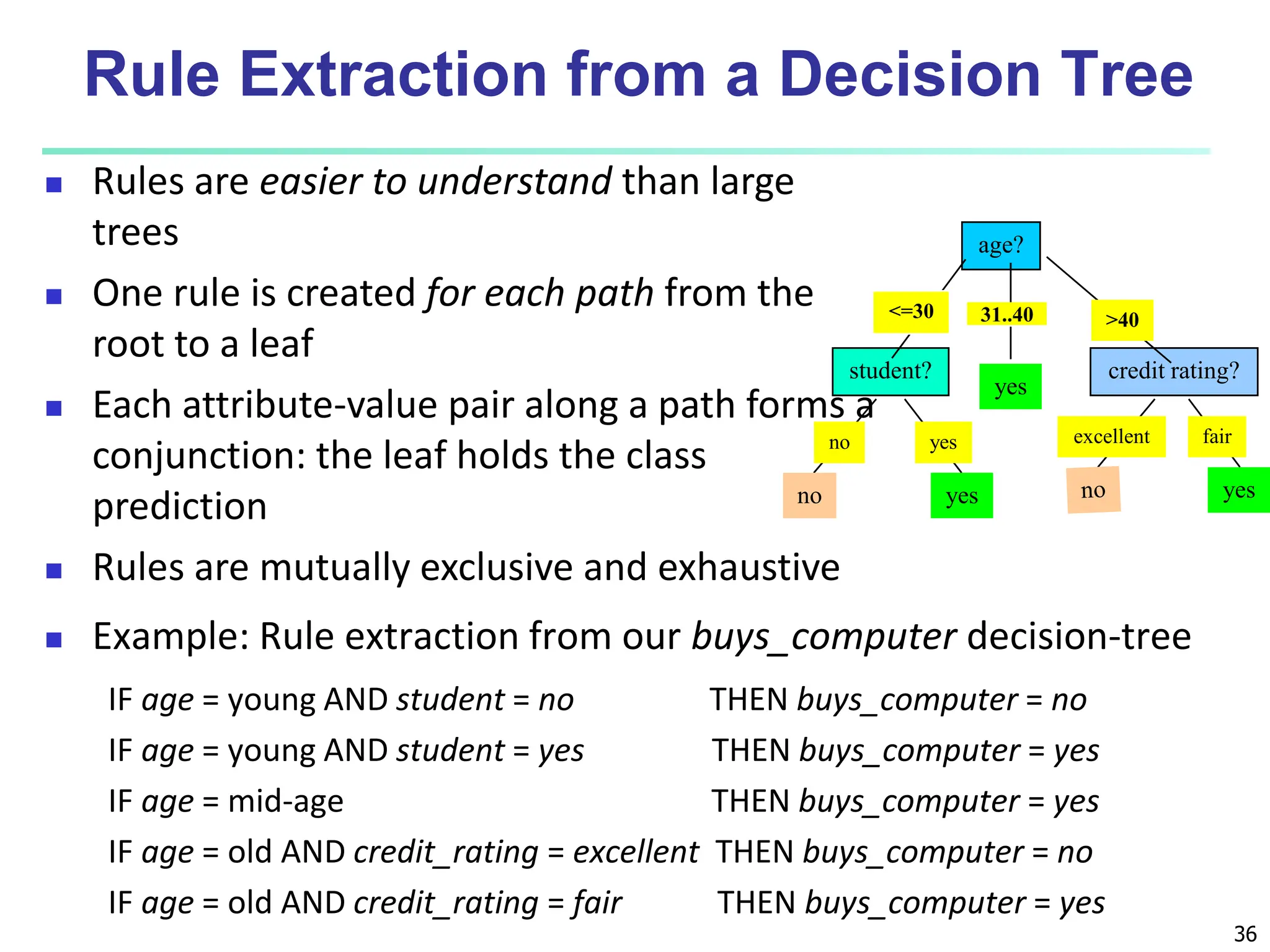
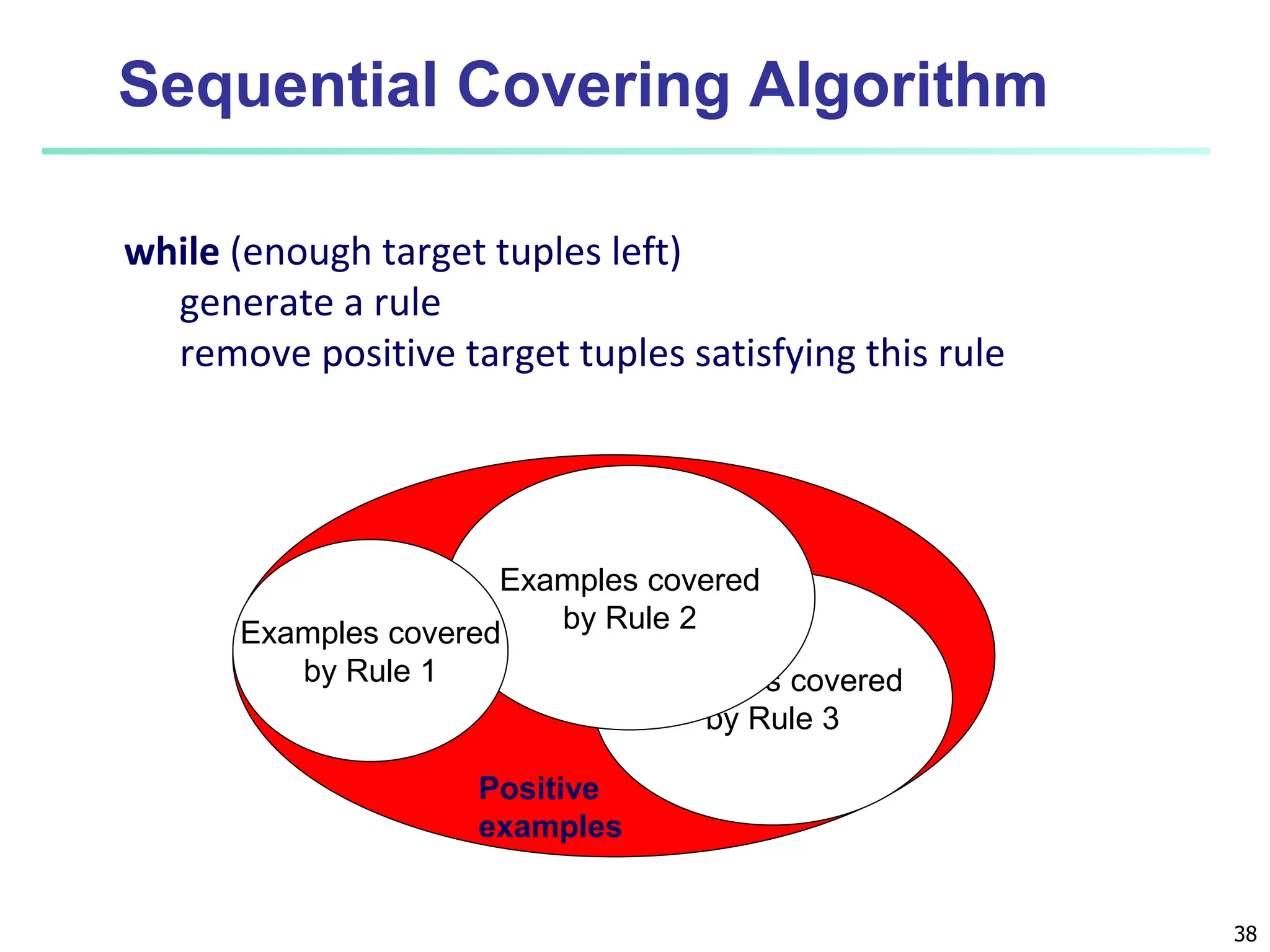
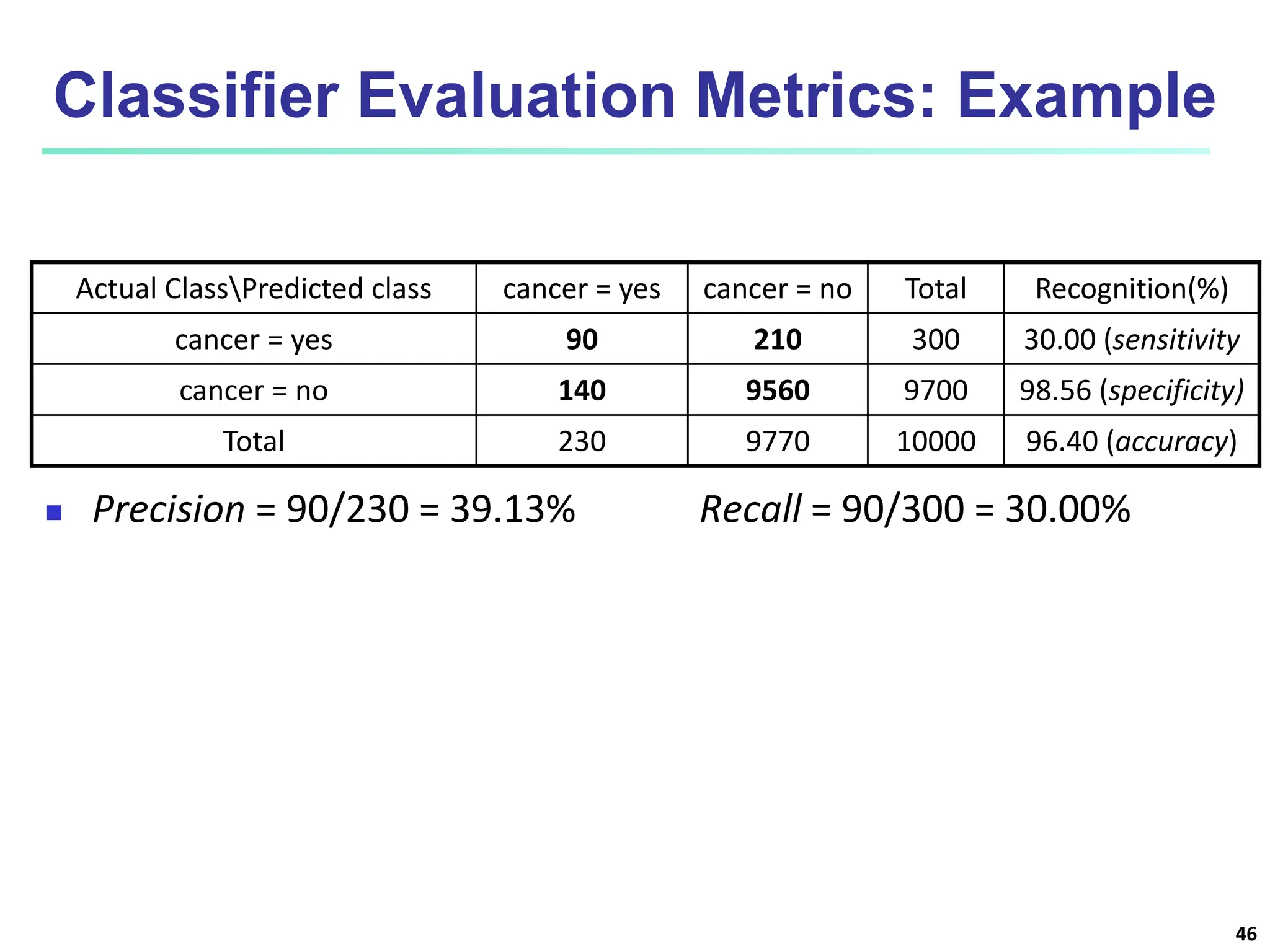
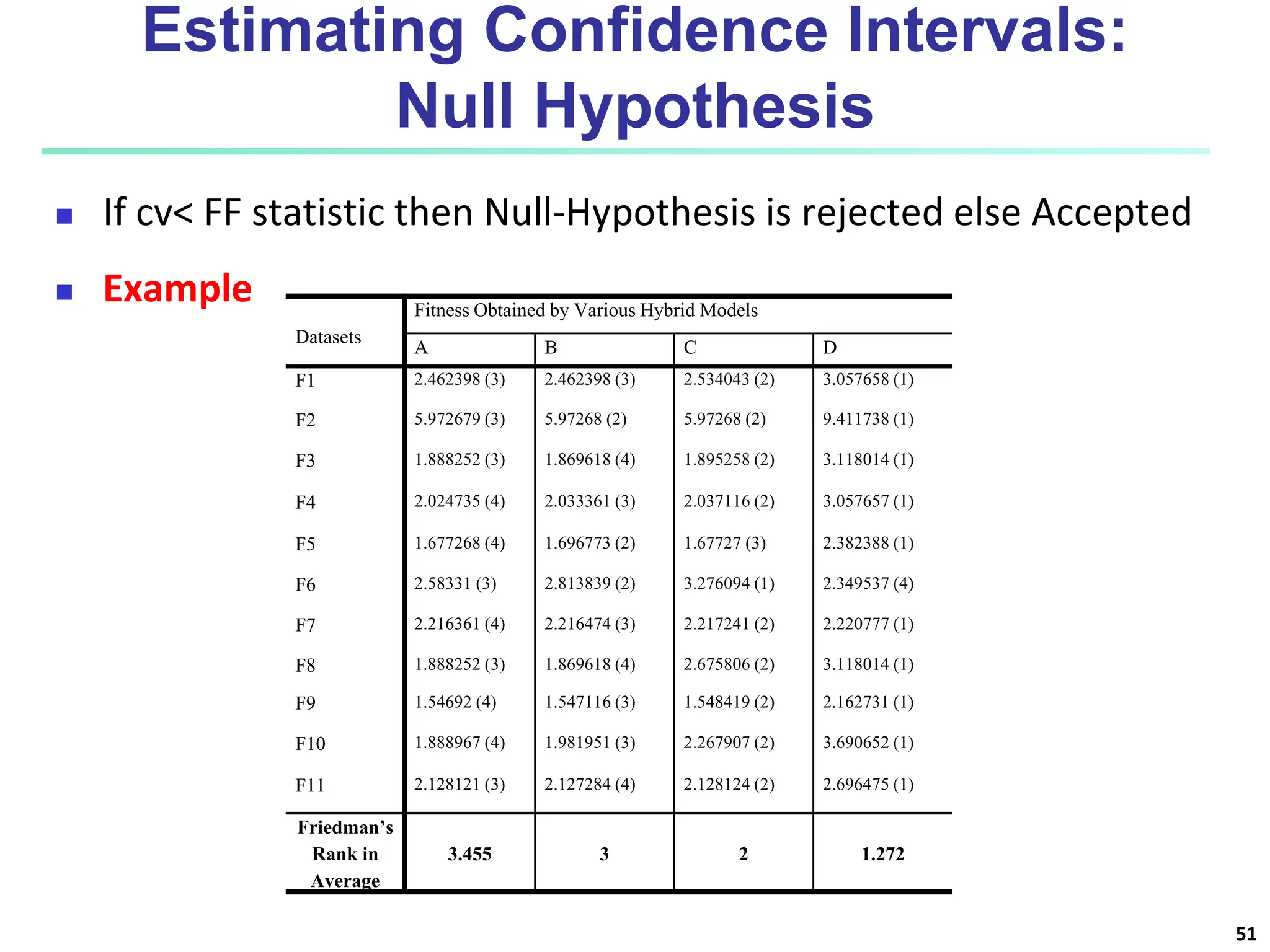
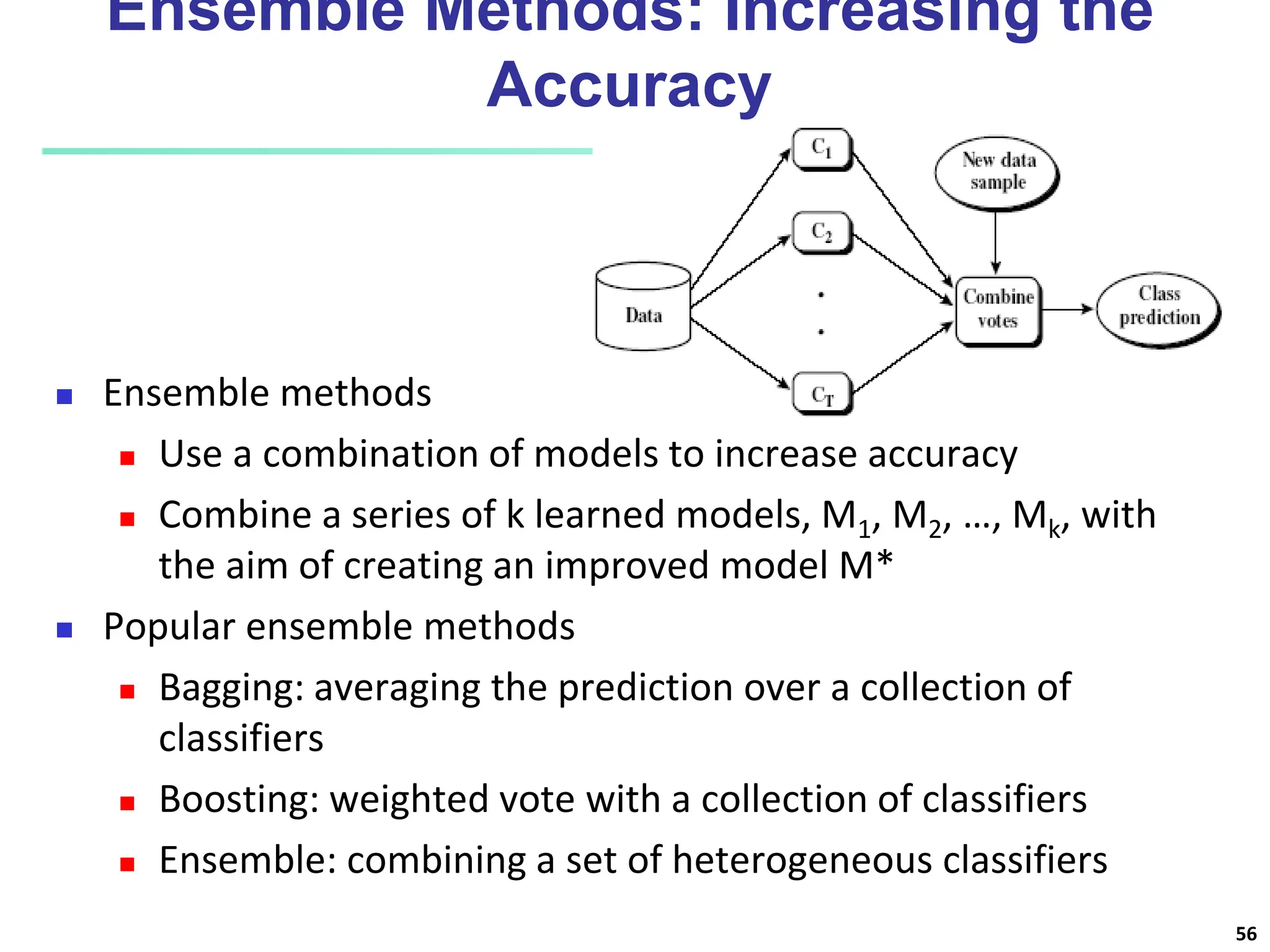
The document covers basic concepts of machine learning classification, focusing on supervised and unsupervised learning, predictive models, and decision tree induction. It details the processes involved in model construction and usage, classification accuracy evaluation, and various classification algorithms including Bayesian methods and decision trees. Additionally, it discusses enhancements to decision trees to avoid overfitting, along with the importance of scalability in large databases.