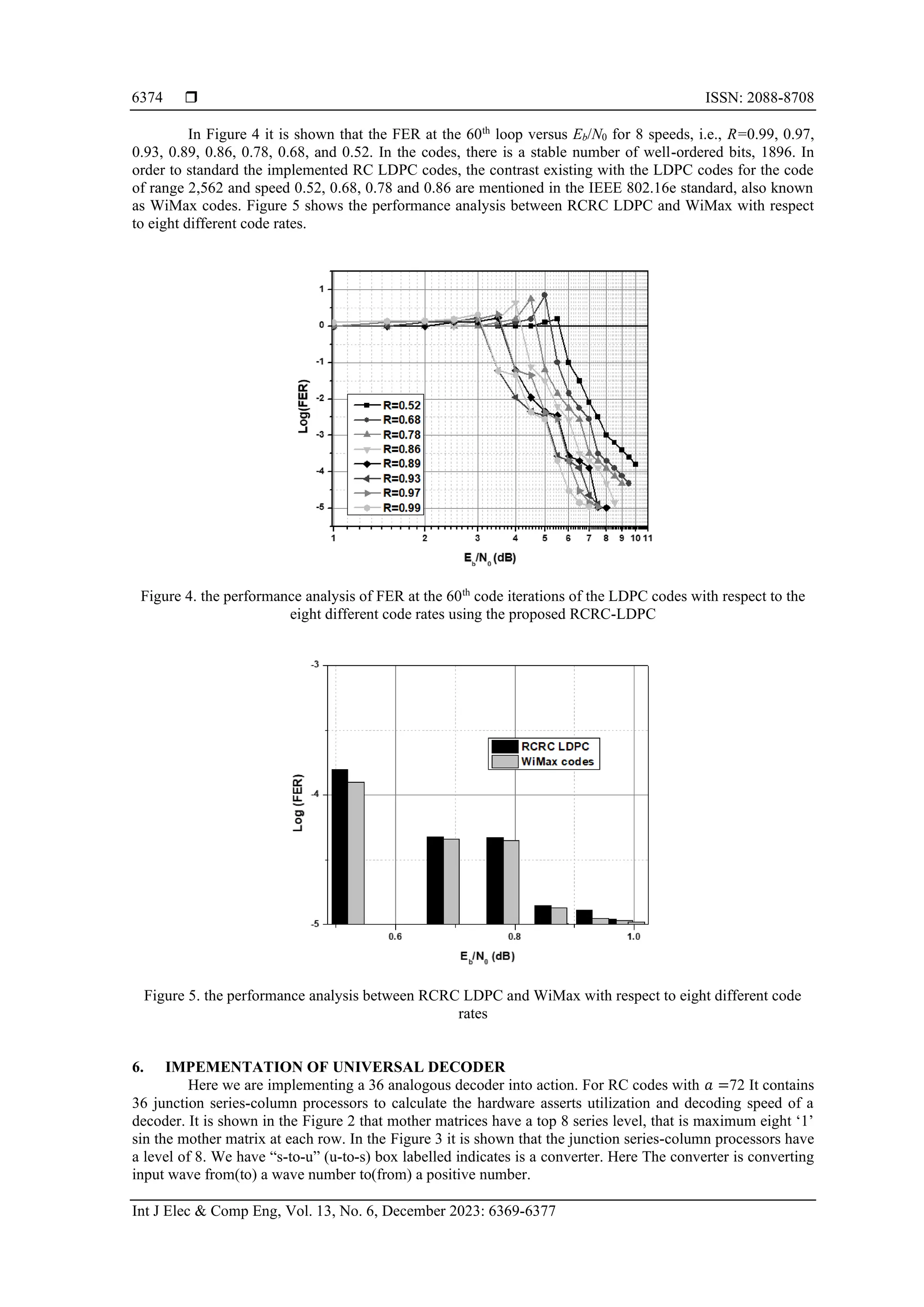
The article proposes a reconfigurable code rate cooperative (RCRC) and low-density parity check (LDPC) method to optimize digital communication processes, achieving a maximum code rate of 0.98. Implemented via MATLAB on FPGA, it demonstrates a throughput efficiency exceeding 8.2 Gbps with a clock frequency of 160 MHz. The comparison shows that the RCRC-LDPC outperforms existing methods in terms of efficiency and code rate adaptability.
![International Journal of Electrical and Computer Engineering (IJECE) Vol. 13, No. 6, December 2023, pp. 6369~6377 ISSN: 2088-8708, DOI: 10.11591/ijece.v13i6.pp6369-6377 6369 Journal homepage: http://ijece.iaescore.com An efficient reconfigurable code rate cooperative low-density parity check codes for gigabits wide code encoder/decoder operations Divyashree Yamadur Venkatesh1 , Komala Mallikarjunaiah1 , Mallikarjunaswamy Srikantaswamy2 1 Department of Electronics and Communication Engineering, SJB Institute of Technology, Bengaluru, India 2 Department of Electronics and Communication Engineering, JSS Academy of Technical Education, Bengaluru, India Article Info ABSTRACT Article history: Received Apr 3, 2023 Revised Jul 11, 2023 Accepted Jul 17, 2023 In recent days, extensive digital communication process has been performed. Due to this phenomenon, a proper maintenance of authentication, communication without any overhead such as signal attenuation code rate fluctuations during digital communication process can be minimized and optimized by adopting parallel encoder and decoder operations. To overcome the above-mentioned drawbacks by using proposed reconfigurable code rate cooperative (RCRC) and low-density parity check (LDPC) method. The proposed RCRC-LDPC is capable to operate over gigabits/sec data and it effectively performs linear encoding, dual diagonal form, widens the range of code rate and optimal degree distribution of LDPC mother code. The proposed method optimize the transmission rate and it is capable to operate on 0.98 code rate. It is the highest upper bounded code rate as compared to the existing methods. The proposed method optimizes the transmission rate and is capable to operate on a 0.98 code rate. It is the highest upper bounded code rate as compared to the existing methods. the proposed method's implementation has been carried out using MATLAB and as per the simulation result, the proposed method is capable of reaching a throughput efficiency greater than 8.2 (1.9) gigabits per second with a clock frequency of 160 MHz. Keywords: Bit error rate Field programming gate array Frame error rate Low-density-parity-check Signal to noise ratio This is an open access article under the CC BY-SA license. Corresponding Author: Mallikarjunaswamy Srikantaswamy Department of Electronics and Communication Engineering, JSS Academy of Technical Education Bengaluru, India Email: mallikarjunaswamys@jssateb.ac.in 1. INTRODUCTION A challenge of designing rate-compatible low-density parity check (RC LDPC) codes, which need to improve size of rate of code, because to widen the overall channel size and to give a good and proper service depending on channel conditions. Among many paths, puncturing method gives an advantageous approach to gain a list of RC codes, where maximum daughter codes rate can be obtained from mother codes, following a method of puncturing, i.e., puncturing some parity bits [1]–[5]. code designs major challenge with specified way to maintain the performance of both codes are nearer to potential. Piercing leads to modification of degree distribution, is a main element for finding the decoding act, it is complex to get the best daughter codes at highest code levels. A group of RC LDPC codes is recommended by document with different code levels. By asserting a perfect transmission pattern with a zero-filling encryption algorithm, the method to get RC codes does not change daughter codes degree of distribution. Thus, the method forces rates to a 0.98.](https://image.slidesharecdn.com/3832484emf-240104041950-339a3968/75/An-efficient-reconfigurable-code-rate-cooperative-low-density-parity-check-codes-for-gigabits-wide-code-encoder-decoder-operations-1-2048.jpg)
![ ISSN: 2088-8708 Int J Elec & Comp Eng, Vol. 13, No. 6, December 2023: 6369-6377 6370 Designed from shifted identity matrices, the codes match the implementation of high-speed parallel encoders and decoders. The deployment results to a design of field programmable gate array (FPGA) devices, which show that a 32-parallel encoder for the said LDPC codes having rates from 0.5 to 0.98 is having a capacity to reach an outturn of 8.2 (1.9) gigabits per second (Gbps) with the help of a clock frequency of 180 MHz and absorbing only 0.3% (12%) of Xilinx Virtex-5’s overall resources. Rate- compatible LDPC codes system is as shown in Figure 1. The information 'm' bits are applied to the RC-LDPC and the output of RC-LDPC generates a codeword 'C', which is then applied to modulation process. the modulated output is applied to the channel. Figure 1. The fundamental block diagram of RC-LDPC codes 2. METHOD 2.1. Build rate compatible LDPC codes RC LDPC codes have been considered using a subsequent parent matrix, which is having a set of i X (I+J) sub-matrices as shown in (1). 𝑀 = [ 𝑚1,1 . . 𝑚1,𝑗 𝐾 . . 𝑚1,1 . . 𝑚2,𝑗 𝐾 𝐾 . . . 𝑚𝑖−1,1 𝑚𝑖 . . . . . . . 𝑚𝑖−1,𝑗 𝑚𝑖,𝑗 . . . 𝐾 𝐾 𝐾 . 𝐾 𝐾 ] (1) where ‘K’ is represented the it is an 𝑎 𝑋 𝑎 identity matrix and the null matrices are indicated by unmarked spaces. For 1 ≤ 𝑖 ≤ 𝐼 and 1 ≤ 𝑗 ≤ 𝐽 the submatrix 𝑚𝑖,𝑗 within ‘M’ at position (𝑖, 𝑗) is either a shifted identity matrix [6], [7]. The shifted identity matrix is gained by performing a circularly shifting the rows of ‘K’ to the right by 𝑆𝑖,𝑗 positions i.e., 𝑚𝑖,𝑗 = 𝐾(𝑆𝑖,𝑗). 𝑆𝑖,𝑗 shows shifting coefficient, and has been selected from the restricted set-in range 0 and ‘a’. The main purpose is to prevent short and medium length cycles depending on the methods in [6], [7]. The submatrix size is represented by ‘a’. To differentiate among conventional rows and columns, we access column of submatrices, which is present like a block column inside M. It has I block-rows and (𝐽 + 𝐼) block columns inside the matrix (1) [8], [9]. 2.2. Transmission and encoding algorithm Assume splitting of a codeword ‘X’ into (J+K) parts, as shown in (2). 𝑋 = [𝑝1, 𝑝2, 𝑝3, … … … 𝑝𝑗, 𝑞1, 𝑞2, 𝑞3, … … 𝑞𝑖 ] (2) where 𝑝𝑗 is presented partitioning codewords with 1 ≤ 𝑗 ≤ 𝐽 shows systematic bits of ‘a’ vector and ‘q’ with 1 ≤ 𝑖 ≤ 𝐽 , that is a vector of q parity bits. With coding basics, 𝑀𝑋𝑇 =0𝑇 , results to a parity bit as (3) and (4): 𝑄1 𝑇 = ∑ 𝑚1,𝑘𝑃𝑘 𝑇 𝐽 𝑗=1 (3) 𝑄𝑖 𝑇 = ∑ 𝑚𝑖,𝑗𝑃𝑘 𝑇 𝐾 𝑘=1 + 𝑄𝑖−1 𝑇 (4)](https://image.slidesharecdn.com/3832484emf-240104041950-339a3968/75/An-efficient-reconfigurable-code-rate-cooperative-low-density-parity-check-codes-for-gigabits-wide-code-encoder-decoder-operations-2-2048.jpg)
![Int J Elec & Comp Eng ISSN: 2088-8708 An efficient reconfigurable code rate cooperative low-density parity … (Divyashree Yamadur Venkatesh) 6371 with 2 ≤ 𝑖 ≤ 𝐼,. it is agreed that the introduction of LDPC codes is linear time encoded. The code presented in (1) possess leas rate 𝑅𝐿 is given in (5). 𝑅𝐿 = 𝐽/(𝐽 + 𝐼) (5) The daughter code having highest rate, 𝑅𝐻 as shown in (6) is resulted by passing only one parity bit vector 𝑞𝐼. 𝑅𝐻 = 𝐽/(𝐽 + 1) (6) For ARQ which is called as automatic repeat request transmission, step-by-step transmission of systematic and parity bits are as follows: - transmit parity bit vector 𝑞𝑖 and systematic bit vector 𝑝. - transfer parity bit vectors [𝑞1, 𝑞2, … … … . 𝑞𝑖−1] according to the following order, if asked. 𝑞𝑗 2 ; 𝑞𝑗/4 , 𝑞3𝑗/4; 𝑞2, 𝑞4, 𝑞6 … … … … . . (𝑡ℎ𝑒 𝑟𝑒𝑠𝑡 𝑒𝑣𝑒𝑛 𝑛𝑢𝑚𝑏𝑒𝑟𝑠) 𝑞1, 𝑞3, 𝑞5 … … … … . . (𝑡ℎ𝑒 𝑟𝑒𝑠𝑡 𝑂𝐷𝐷 𝑛𝑢𝑚𝑏𝑒𝑟𝑠) 2.3. Case study For instance, assume a 32×48 array of sub-matrices, which is considered as a mother matrix, across the entire text [10], [11]. It is simple to extend the suggested approach to LDPC codes having any numbers of block-rows and block-columns. Solid bars in a Figure 2 shows an offset ID matrix with unmarked spaces shows null matrices. A least code rate of 𝑅𝐿 = 0.5 is associated with mother code. Figure 2. 32×48 sub matrix array constitutes a LDPC mother matrix. Shifted identity matrix forms solid bars and null matrices found unmarked spaces We assume splitting a codeword x to smaller parts, say 64, is given in (7) 𝑋 = [𝑝1, 𝑝2, 𝑝3, … … … 𝑝32, 𝑞1, 𝑞2, 𝑞3, … … 𝑞32 ] (7) where, 𝑝𝑗 with 1 ≤ 𝑗 ≤ 32 indicates a vector of ‘a’ systematic bits and 𝑞𝑖 with 1 ≤ 𝑖 ≤ 32 is a vector of ‘a’ parity bits. A systematic bit vector ‘p’ is initially transmitted by the transmitter along with the parity bit vector 𝑞32. It is discovered that; daughter code has the maximum rate 𝑅𝑀 = 0.98 . Send the other parity bit vectors in the following order if requested: 𝑞12, 𝑞6, 𝑞18, 𝑞2, 𝑞4, 𝑞8, 𝑞10, 𝑞14, 𝑞16, 𝑞20, 𝑞22, 𝑞1, 𝑞3, 𝑞5, 𝑞7, 𝑞9, 𝑞11, 𝑞13, 𝑞15, 𝑞17, 𝑞19, 𝑞21, 𝑞23. We shall discuss the benefits of transmitting the parity bit vectors 𝑝32 first, in section 4.](https://image.slidesharecdn.com/3832484emf-240104041950-339a3968/75/An-efficient-reconfigurable-code-rate-cooperative-low-density-parity-check-codes-for-gigabits-wide-code-encoder-decoder-operations-3-2048.jpg)
![ ISSN: 2088-8708 Int J Elec & Comp Eng, Vol. 13, No. 6, December 2023: 6369-6377 6372 2.4. Comparative analysis of rate-compatible code and rate-adaptive code Rate-adaptive LDPC codes are created in [12]–[14] which are indicated with the help of mother matrix, and it also includes an array of circularly shifted identity sub-matrices. By deleting the highest rows from the mother matrix, the parity-check matrices of daughter codes with higher levels are obtained i.e., by row-deleting approach, the rates are adapted. By piercing few of the parity bits of the mother code, the daughter codes of rate-compatible LDPC codes are obtained. By deleting few columns from the parity portion of the mother matrix, the greater rates of parity-check matrices of daughter codes are generated. Table 1 show the performance analysis between reconfigurable code rate cooperative (RCRC) and rate- adaptive LDPC codes. Table 1. Performance analysis between RCRC and rate-adaptive LDPC codes Particulars Rate adaptive LDPC code RCRC System parity check bits matrix for code length applications This method is constant in various row removal adaptive modulation and coding algorithm This method is constant in various column removal adaptive modulation and coding algorithm 3. IMPLEMENTATION PROCESS OF UNIVERSAL ENCODER: The fact is that usage of single encoder/decoder pair, decoding and encoding of RC LDPC codes can be done and is one of its key benefits [15]. In this section, we walk through how the universal encoder is implemented in practice. Think about the following code having ‘I’ as 24 and ‘j’ as 24 in II.B). Due to the fact that 𝑚𝑖,𝑗 is either a null matrix or a shifted identity matrix, the matrix vector multiplications in (3) and (4) is computed as (8): 𝑋𝑖,𝑗 𝑇 = 𝑚𝑖,𝑗𝑝𝑗 𝑇 (8) where 𝑋𝑖,𝑗 𝑇 with 1 ≤ 𝑖 ≤ 32 and 1 ≤ 𝑗 ≤ 32 indicates a vector of ‘a’ bits. 𝑚𝑖,𝑗 indicates shifted identity matrix i.e., 𝑚𝑖,𝑗 = 𝑘 (𝑆𝑖,𝑗). By shifting 𝑝𝑗 to the left side by 𝑆𝑖,𝑗 places, 𝑋𝑖,𝑗 is obtained. 𝑚𝑖,𝑗 is a null matrix and 𝑋𝑖,𝑗 is a zero vector. Using a simple XOR processor, the computation in (3) and (4) can be implemented [16], [17]. 𝑞𝑖(𝑘) = ∑ 𝑥𝑖,𝑗(𝑘) 24 𝑗=1 + 𝑠𝑖−1(𝑘) (9) where 𝑞0(𝑘) = 0, 1 ≤ 𝑖 ≤ 24 and 1 ≤ 𝑗 ≤ 𝑎. The 𝑘 − 𝑏𝑖𝑡𝑠 in the bit vector 𝑥𝑖,𝑗 is represented by every signal to the input 𝑥𝑖,𝑗(𝑘). To shorten the time, it takes for signals to propagate from input to output, a tree design is used. A made up of 32 XOR processors are used to design a 32-parallel encoder and integrated into MATLAB and FPGA devices. The target XC5VFX200T device's created implementation was placed and routed using the Xilinx development system tool suite (ISE 10.1) with the speed option set to -2. Estimation of highest clock frequency was carried out using Xilinx static time analysis. The results give the following observation: 80 LUTs, slices of 416 with 467 flip-flops were used by 32 parallel encoders. Thus, the total resources consumed by encoder were only 3/10 percentage in an XC5VFX200T device [18], [19]. Static timing analysis is a critical process in digital design, particularly in the context of field-programmable gate arrays (FPGAs) like those manufactured by Xilinx. It involves analyzing the timing behavior of a digital circuit to ensure that it meets the required timing constraints, such as setup and hold times, and that it operates correctly within its intended clock frequency. Analysis of the Xilinx static timing shows that, in an XC5VFX200T device the highest encoding clock frequency of 32 parallel encoder attained is 460 MHz. An encoding speed of 7,200 Mbps was attained by the encoder with the use of 180 MHz frequency for the encoding clock. 4. DECODING ALGORITHM AND PERFORMANCE ANALYSIS Here we are using Sum product algorithm to decode the implemented RC LDPC codes effectively. Sum and product of external communication in every column and each row is performed by this algorithm [19], [20]. Rather than using different series column processing in classical sum product method here we are using junction sum product sort out method. This decoding algorithm includes the computation of external communication in column processing into series processing. That is, we are using a processor called junction series column processor to operate each series from bottom series to top series in every loop.](https://image.slidesharecdn.com/3832484emf-240104041950-339a3968/75/An-efficient-reconfigurable-code-rate-cooperative-low-density-parity-check-codes-for-gigabits-wide-code-encoder-decoder-operations-4-2048.jpg)
![Int J Elec & Comp Eng ISSN: 2088-8708 An efficient reconfigurable code rate cooperative low-density parity … (Divyashree Yamadur Venkatesh) 6373 4.1. Zero filling decoding algorithm Before introducing the null-filling method for decoding the implemented RC codes. We shall talk over about the mother code. Assume the mother matrix as ‘M’ consisting of 𝑖 𝑋 𝑎 series and (𝑗 + 𝑖) 𝑋 𝑎 columns, in which (𝑗 + 𝑖) and I are block columns and series. Hence this code is sort out with the junction processor from bottom series to top series inside the matrix 𝑀 in every loop [21], [22]. When sort out is processing the series column processor captures the pair extrinsic messages 𝑦𝑚𝑛 from matrix and log likelihood ratio (LLR) (𝑍𝑛) from matrix after then it calculates the new ratio 𝑍′𝑛 and extrinsic communication 𝑦′𝑚𝑛 with 1 ≤ 𝑚 ≤ 𝑖 𝑋 𝑎 and 1 ≤ 𝑛 ≤ (𝐽 + 𝑖)𝑋𝑎 . The extracted n-bits LLR at received signal is given by (10). 𝑍𝑛 = log(𝑠𝑛 0 /𝑠𝑛 1 ) (10) where 𝑠𝑛 0 and 𝑠𝑛 1 is described as nth bit probabilities of ‘0’ or ‘1’ respectively. The mother code with the least speed: systematic segment and parity segment are sent, where Log Likelihood ratio of all the segments can be captured out of the signal collected [23]–[25]. For daughter code: few parity segments are not sent, where Nth segment is large positive constant which is not sent and assigned to 𝑍𝑛 with value 0. 5. PERFORMANCE ANALYSIS Implemented RCRC-LDPC code has to evolved for its performance. Hence the simulations are performed along with the binary phase-shift keying modulation in additive white gaussian noise channel for representing RC codes by Mother code matrices which is as shown in Figure 2 where 𝑎 = 72. This method will finish if the correct code is originated else when it reaches 50 loops in the cycle. The proposed RCRC- LDPC has an advantage when it pushes upper rates (R) to 0.98 by transmitting a single parity bit vector (P24). The 𝑞32 code performs well so it is sent to loop. The frame error rate at 60th loop vs signal to noise ratio is given in Figure 2 which has 𝑙𝑒𝑛𝑔𝑡ℎ = 1900 and 𝑅𝑎𝑡𝑒 = 0.98. The query is that why we are sending the segment vector 𝑞32. The contrast occurred for frame error rate (FER) at 60th loop with the signal-to-noise ratio (SNR) per bit 𝐸𝑏 𝑁0 as shown in Figure 3 for those source code with the distance 1,900 and a speed of 0.98. This clearly says the source code with the segment vector 𝑞32 gives top and best result. We are rewriting the (3) and (4) by sending a vector 𝑆𝑖 to describe why transferral plan attains the good performance which is given (11). 𝑠𝑖 𝑇 = ∑ (∑ 𝑚𝑖,𝑗 𝐽 𝑗=1 𝑝𝑗 𝑇 ) 𝑖 𝑘=1 (11) with 1 ≤ 𝑖 ≤ 𝐽. It is shown in (11) here the vector 𝑠𝑖 is encoding with the matrix 𝑚𝑖, here 𝑚𝑖, indicates the top a block series in structured portion of M. Dispatching 𝑠𝑖 with 𝑖 < 𝐼, since the level sharing in M a is dissimilar from ideal sharing in M, degradation of decoding result takes place. If we send vector 𝑠𝑖, the ideal level sharing keeps no change and the best performance is attained by transmission scheme. Figure 3. 60th code iteration with a range of 1900 and 0.98 code rate with respect to the transmission parity bit vector](https://image.slidesharecdn.com/3832484emf-240104041950-339a3968/75/An-efficient-reconfigurable-code-rate-cooperative-low-density-parity-check-codes-for-gigabits-wide-code-encoder-decoder-operations-5-2048.jpg)
![Int J Elec & Comp Eng ISSN: 2088-8708 An efficient reconfigurable code rate cooperative low-density parity … (Divyashree Yamadur Venkatesh) 6375 The Figure 6 that there is a processor which consists of both inputs and outputs, eight in number. The processor is designed using fifteen XOR gates and its carryout sign functioning as given in (12) and (13). 𝑃 = ∏ 𝑠𝑖𝑔𝑛 (𝑥𝑗) 8 𝑖=1 (12) 𝑃𝑖 = 𝑃 𝑋 𝑠𝑖𝑔𝑛 (𝑥𝑗) (13) with 1 ≤ 𝑖 ≤ 8. The magnitude operation is performed by the processor known as magnitude processor which has 8 inputs and 8 outputs in Figure 6. 𝑦𝑗 = ∅[∑ |𝑥𝑖| 8 𝑖=1,𝑖≠𝑘 ] (14) where 𝑦𝑗 is represented the magnitude operation, ∅ is describe the 7-bit look-up-table (LUT) function using 4 bits for fractional part. The measurement for the considered case code’s submatrices is 72, the 36 analogous decoder is implemented with a MATLAB-XC5VFX200T FPGA tool with the rate of -2, it intakes below expedient: chop 8%, flipflop 12%, and look up table 12%. Timing analysis publishes above results, for 36 parallel decoder the maximum decoding clock frequency attained is 250 MHz with 180 MHz as decoding clock frequency and iteration number of 6 decoder is capable of attaining a decoding rate of 1.9 Gbps. Figure 6. RCRC LDPC row-column processor with respect to the eight degrees 7. CONCLUSION The proposed method RCRC LDPC code enhances the code rates and it is capable to optimize the transmission rate. The proposed method efficiently distributes the unchanged degree codes used for the more communication operation to increase the switching operation. Due to these activities, the mother code and all daughter codes very desired result. The proposed method optimizes the transmission rate and is capable to operate on a 0.98 code rate. It is the highest upper bounded code rate as compared to the existing methods. The proposed method enhances parallel operations of 32 encoders and 44 decoders with a throughput rate of 8.2 with 1.9 Gbps by using a clock frequency of 180 MHz and power consumption is reduced by 0.54% as compared to the existing methods and FER is reduced to 0.12% and signal to noise ratio increases to 1.2% as compared to the existing method (WiMAX). Due to this, the proposed method is capable to operate high bit rate data without any overheads, and millions of electric components are integrated efficiently with more accelerated performance. FUTURE SCOPE Nowadays, 5G LTE communication is an emerging field. Due to more devices being connected to the 5G LTE network, this research work will be enhanced to 128-bit operational and increases the switching speed.](https://image.slidesharecdn.com/3832484emf-240104041950-339a3968/75/An-efficient-reconfigurable-code-rate-cooperative-low-density-parity-check-codes-for-gigabits-wide-code-encoder-decoder-operations-7-2048.jpg)
![ ISSN: 2088-8708 Int J Elec & Comp Eng, Vol. 13, No. 6, December 2023: 6369-6377 6376 ACKNOWLEDGMENTS The authors would like to thank SJB Institute of Technology, JSS Academy of Technical Education, Bengaluru, Visvesvaraya Technological University (VTU), Belagavi and Vision Group on Science and Technology (VGST) Karnataka Fund for Infrastructure Strengthening in Science and Technology level–2 sponsored “Establishment of renewable smart grid laboratory” for all the support and encouragement provided by them to take up this research work and publish this paper REFERENCES [1] E. A. Papatheofanous, D. Reisis, and K. Nikitopoulos, “LDPC hardware acceleration in 5G open radio access network platforms,” IEEE Access, vol. 9, pp. 152960–152971, 2021, doi: 10.1109/ACCESS.2021.3127039. [2] B.-S. Su, C.-H. Lee, and T.-D. Chiueh, “A 58.6/91.3 pJ/b dual-mode belief-propagation decoder for LDPC and polar codes in the 5G communications standard,” IEEE Solid-State Circuits Letters, vol. 5, pp. 98–101, 2022, doi: 10.1109/LSSC.2022.3167423. [3] S. Belhadj and M. L. Abdelmounaim, “On error correction performance of LDPC and polar codes for the 5G machine type communications,” in 2021 IEEE International IOT, Electronics and Mechatronics Conference (IEMTRONICS), Apr. 2021, pp. 1–4, doi: 10.1109/IEMTRONICS52119.2021.9422665. [4] N.-I. Kim and J.-U. Kim, “Early termination scheme for 5G NR LDPC code,” in 2021 International Conference on Information and Communication Technology Convergence (ICTC), Oct. 2021, pp. 933–935, doi: 10.1109/ICTC52510.2021.9621117. [5] V. L. Petrovic and D. M. El Mezeni, “Reduced-complexity offset min-sum based layered decoding for 5G LDPC codes,” in 2020 28th Telecommunications Forum (TELFOR), Nov. 2020, pp. 1–4, doi: 10.1109/TELFOR51502.2020.9306590. [6] M. T. N., M. S., K. M., S. N., and M. K. S., “An efficient hybrid reconfigurable wind gas turbine power management system using MPPT algorithm,” International Journal of Power Electronics and Drive Systems (IJPEDS), vol. 12, no. 4, pp. 2501–2510, Dec. 2021, doi: 10.11591/ijpeds.v12.i4.pp2501-2510. [7] L. Li et al., “Performance analysis of finite length non-binary raptor codes under ordered statistics decoder,” in 2019 IEEE 90th Vehicular Technology Conference (VTC2019-Fall), Sep. 2019, pp. 1–5, doi: 10.1109/VTCFall.2019.8891217. [8] P. Dayananda, M. Srikantaswamy, S. Nagaraju, R. Velluri, and D. M. Kumar, “Efficient detection of faults and false data injection attacks in smart grid using a reconfigurable Kalman filter,” International Journal of Power Electronics and Drive Systems (IJPEDS), vol. 13, no. 4, pp. 2086–2097, Dec. 2022, doi: 10.11591/ijpeds.v13.i4.pp2086-2097. [9] S. Thazeen, M. S, M. N. Saqhib, and S. N, “DOA method with reduced bias and side lobe suppression,” in 2022 International Conference on Communication, Computing and Internet of Things (IC3IoT), Mar. 2022, pp. 1–6, doi: 10.1109/IC3IOT53935.2022.9767996. [10] H. N. Mahendra, S. Mallikarjunaswamy, and S. R. Subramoniam, “An assessment of vegetation cover of Mysuru City, Karnataka State, India, using deep convolutional neural networks,” Environmental Monitoring and Assessment, vol. 195, no. 4, Apr. 2023, doi: 10.1007/s10661-023-11140-w. [11] T. Lu, X. He, P. Kang, J. Xing, and X. Tang, “Parity-check matrix partitioning for efficient layered decoding of QC-LDPC codes,” IEEE Transactions on Communications, vol. 71, no. 6, pp. 3207–3220, Jun. 2023, doi: 10.1109/TCOMM.2023.3261380. [12] J.-C. Liu, H.-C. Wang, C.-A. Shen, and J.-W. Lee, “Low-complexity LDPC decoder for 5G URLLC,” in 2018 IEEE Asia Pacific Conference on Postgraduate Research in Microelectronics and Electronics (PrimeAsia), Oct. 2018, pp. 43–46, doi: 10.1109/PRIMEASIA.2018.8597812. [13] C.-Y. Liang, M.-R. Li, H.-C. Lee, H.-Y. Lee, and Y.-L. Ueng, “Hardware-friendly LDPC Decoding Scheduling for 5G HARQ Applications,” in ICASSP 2019 - 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), May 2019, pp. 1418–1422, doi: 10.1109/ICASSP.2019.8682481. [14] A. Katyushnyj, A. Krylov, A. Rashich, C. Zhang, and K. Peng, “FPGA implementation of LDPC decoder for 5G NR with parallel layered architecture and adaptive normalization,” in 2020 IEEE International Conference on Electrical Engineering and Photonics (EExPolytech), Oct. 2020, pp. 34–37, doi: 10.1109/EExPolytech50912.2020.9243997. [15] C. Y. Lin, L. W. Liu, Y. C. Liao, and H. C. Chang, “A 33.2 Gbps/ITER. Reconfigurable LDPC decoder fully compliant with 5G NR applications,” in Proceedings - IEEE International Symposium on Circuits and Systems, May 2021, vol. 2021-May, doi: 10.1109/ISCAS51556.2021.9401329. [16] N. T. Nga, C. Huu Khanh, and N. Q. Tho, “An investigation of the 5G LDPC and polar decoding performance in spatial correlated MIMO-OFDMA system,” in 2022 16th International Conference on Ubiquitous Information Management and Communication (IMCOM), Jan. 2022, pp. 1–7, doi: 10.1109/IMCOM53663.2022.9721755. [17] A. L. Ortega-Ortega and J. F. Bravo-Torres, “Combining LDPC codes, M-QAM modulations, and IFDMA multiple-access to achieve 5G requirements,” in 2017 International Conference on Electronics, Communications and Computers (CONIELECOMP), 2017, pp. 1–5, doi: 10.1109/CONIELECOMP.2017.7891828. [18] E. A. Papatheofanous, D. Reisis, and K. Nikitopoulos, “The LDPC challenge in software-based 5G new radio physical layer processing,” in 2021 IEEE International Mediterranean Conference on Communications and Networking (MeditCom), Sep. 2021, pp. 312–317, doi: 10.1109/MeditCom49071.2021.9647697. [19] P. Vigneswari and S. Sivakumari, “Performance analysis of iterative minsum message passing decoding algorithm for 5G NR LDPC codes,” in 2021 Third International Conference on Intelligent Communication Technologies and Virtual Mobile Networks (ICICV), Feb. 2021, pp. 142–146, doi: 10.1109/ICICV50876.2021.9388463. [20] S. Mallikarjunaswamy, K. R. Nataraj, and K. R. Rekha, “Design of high-speed reconfigurable coprocessor for next-generation communication platform,” in Lecture Notes in Electrical Engineering, Springer India, 2014, pp. 57–67. [21] F. Li et al., “Review on 5G NR LDPC code: recommendations for DTTB system,” IEEE Access, vol. 9, pp. 155413–155424, 2021, doi: 10.1109/ACCESS.2021.3121587. [22] K. J. Sampath, N. K. Kumar, K. Yeswanth, K. Snehith, A. B, and B. T. S. B, “An efficient channel coding architecture for 5G wireless using high-level synthesis,” in 2021 5th International Conference on Trends in Electronics and Informatics (ICOEI), Jun. 2021, pp. 674–680, doi: 10.1109/ICOEI51242.2021.9453001. [23] J. Shrinidhi, P. S. Krishna, Y. B, and P. K., “Modified min sum decoding algorithm for low density parity check codes,” Procedia Computer Science, vol. 171, pp. 2128–2136, 2020, doi: 10.1016/j.procs.2020.04.230. [24] A. Muskan, T. Raj, T. Nisar, M. Abbas, S. Naz, and U. Tiwari, “Various channel coding schemes for 5G,” in 2023 IEEE International Students’ Conference on Electrical, Electronics and Computer Science (SCEECS), Feb. 2023, pp. 1–13, doi: 10.1109/SCEECS57921.2023.10062998.](https://image.slidesharecdn.com/3832484emf-240104041950-339a3968/75/An-efficient-reconfigurable-code-rate-cooperative-low-density-parity-check-codes-for-gigabits-wide-code-encoder-decoder-operations-8-2048.jpg)
![Int J Elec & Comp Eng ISSN: 2088-8708 An efficient reconfigurable code rate cooperative low-density parity … (Divyashree Yamadur Venkatesh) 6377 [25] A. Pramanik, S. P. Maity, and S. Sarkar, “Compressed sensing image reconstruction by low density parity check codes and soft decoding of space time block codes,” Computers and Electrical Engineering, vol. 72, pp. 553–565, Nov. 2018, doi: 10.1016/j.compeleceng.2018.01.014. BIOGRAPHIES OF AUTHORS Divyashree Yamadur Venkatesh is currently working as an Assistant Professor in Department of Electronics and Communication Engineering at SJB Institute of technology, Bangalore. She obtained her B. E degree in Electronics and Communication Engineering from Visvesvaraya Technological University Belgaum in 2008, M. Tech degree in VLSI Design and Embedded system design from Visvesvaraya Technological University Belgaum in 2011.She has 11 years of teaching experience. She has published 9 papers in various journals and conference. She can be contacted at email: divyapatel.gowda@gmail.com. Komala Mallikarjunaiah is working as Associate Professor who has around 22 years of teaching experience and has published 36 papers in international and national journals, author of two books and has applied for two patents. She is presently guiding 3 research scholars. She has also attended and conducted many workshops, FDP, and conferences. Her area of interest is communication and networking. She can be contacted at email: mkomala@sjbit.edu.in. Mallikarjunaswamy Srikantaswamy is currently working as an Associate Professor in Department of Electronics and Communication Engineering at JSS Academy of Technical Education, Bangalore. He obtained his B.E. degree in Telecommunication Engineering from Visvesvaraya Technological University Belgaum in 2008, M. Tech degree from Visvesvaraya Technological University Belgaum in 2010 and was awarded Ph. D from Jain University in 2015. He has 11+ years of teaching experience. His research work has been published in more than 65 International Journals and conference. He received funds from different funding agencies. Currently guiding five research scholars in Visvesvaraya Technological University Belgaum. He can be contacted at email: mallikarjunaswamys@jssateb.ac.in.](https://image.slidesharecdn.com/3832484emf-240104041950-339a3968/75/An-efficient-reconfigurable-code-rate-cooperative-low-density-parity-check-codes-for-gigabits-wide-code-encoder-decoder-operations-9-2048.jpg)