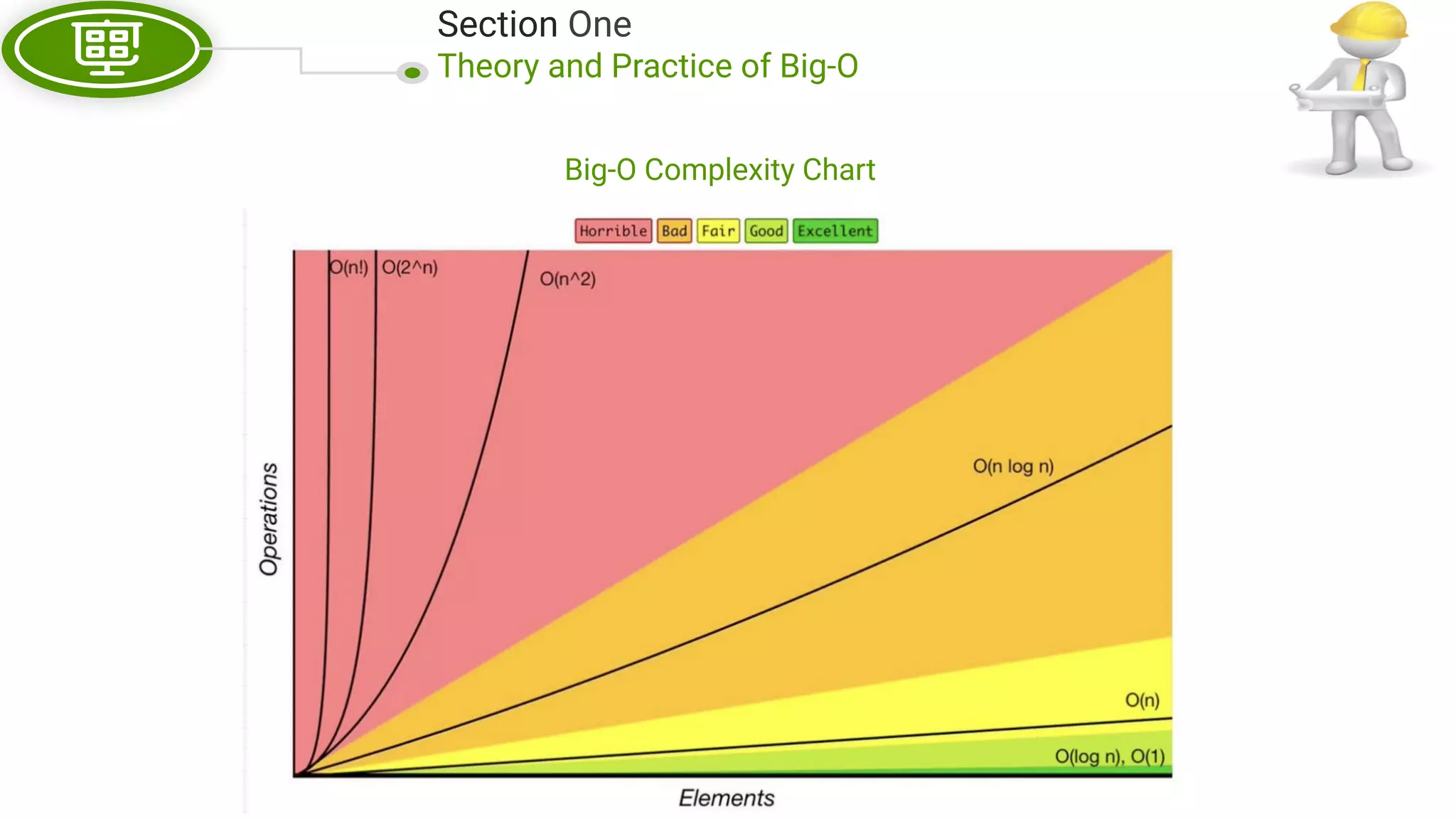
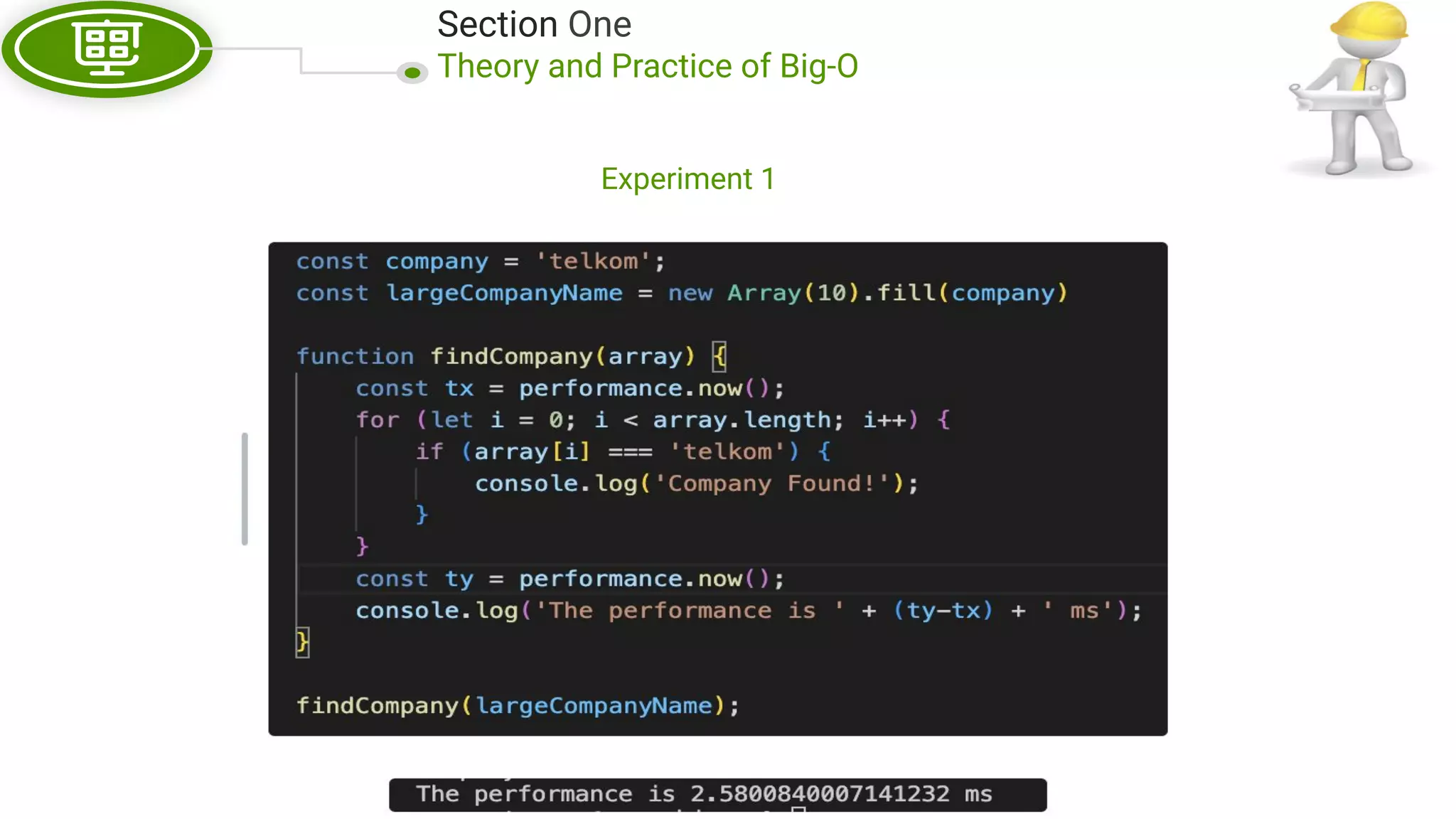
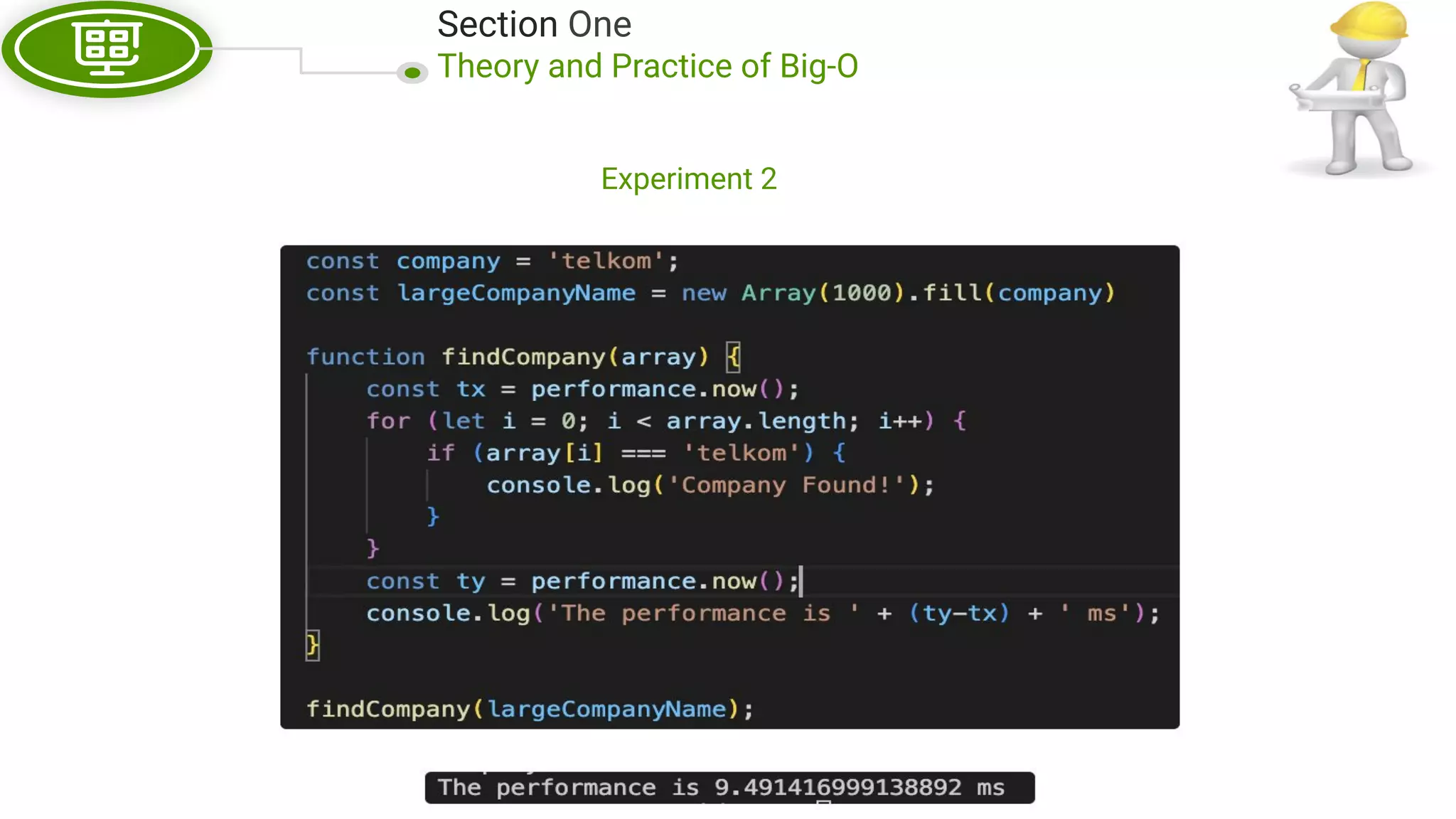
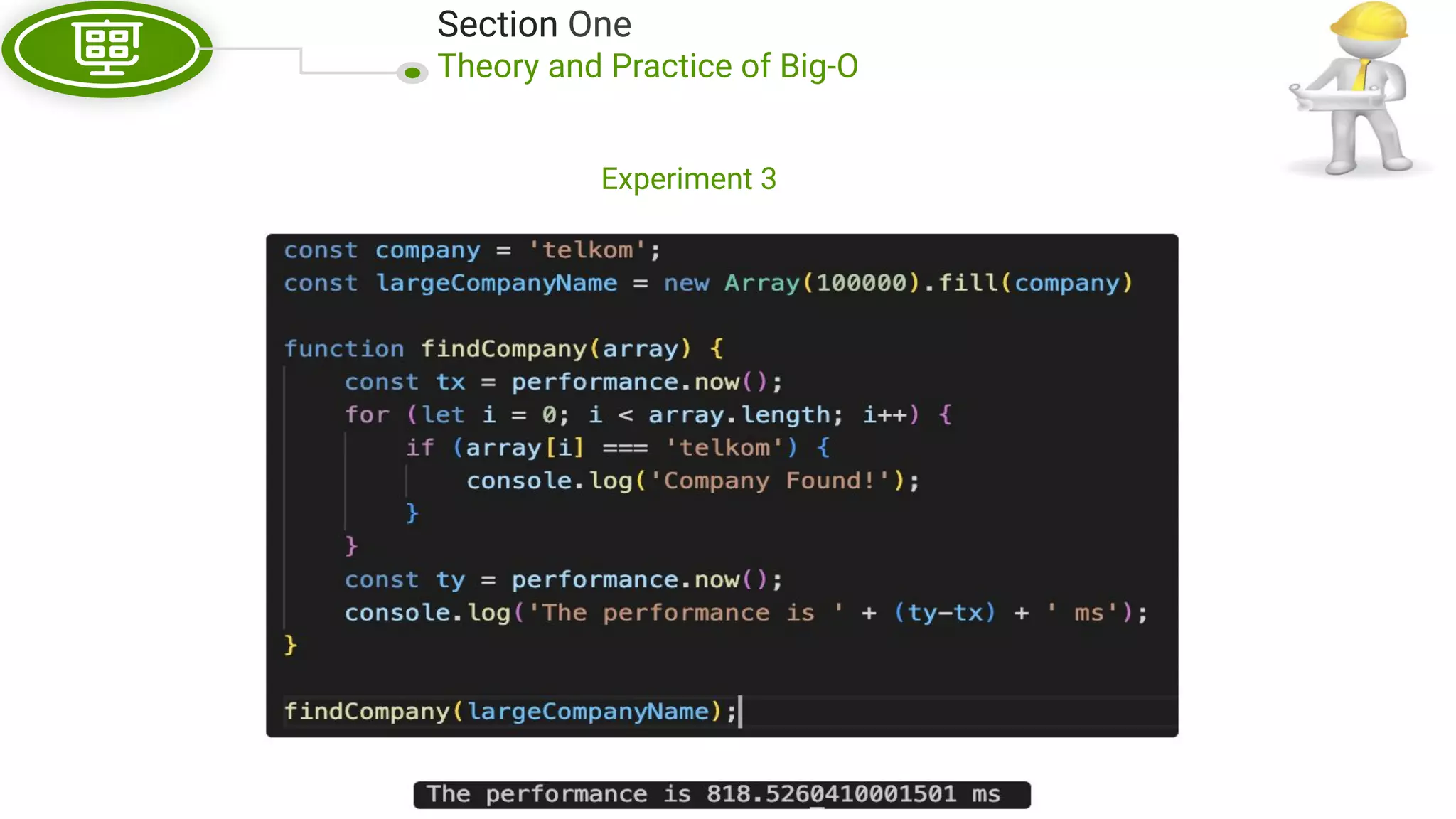
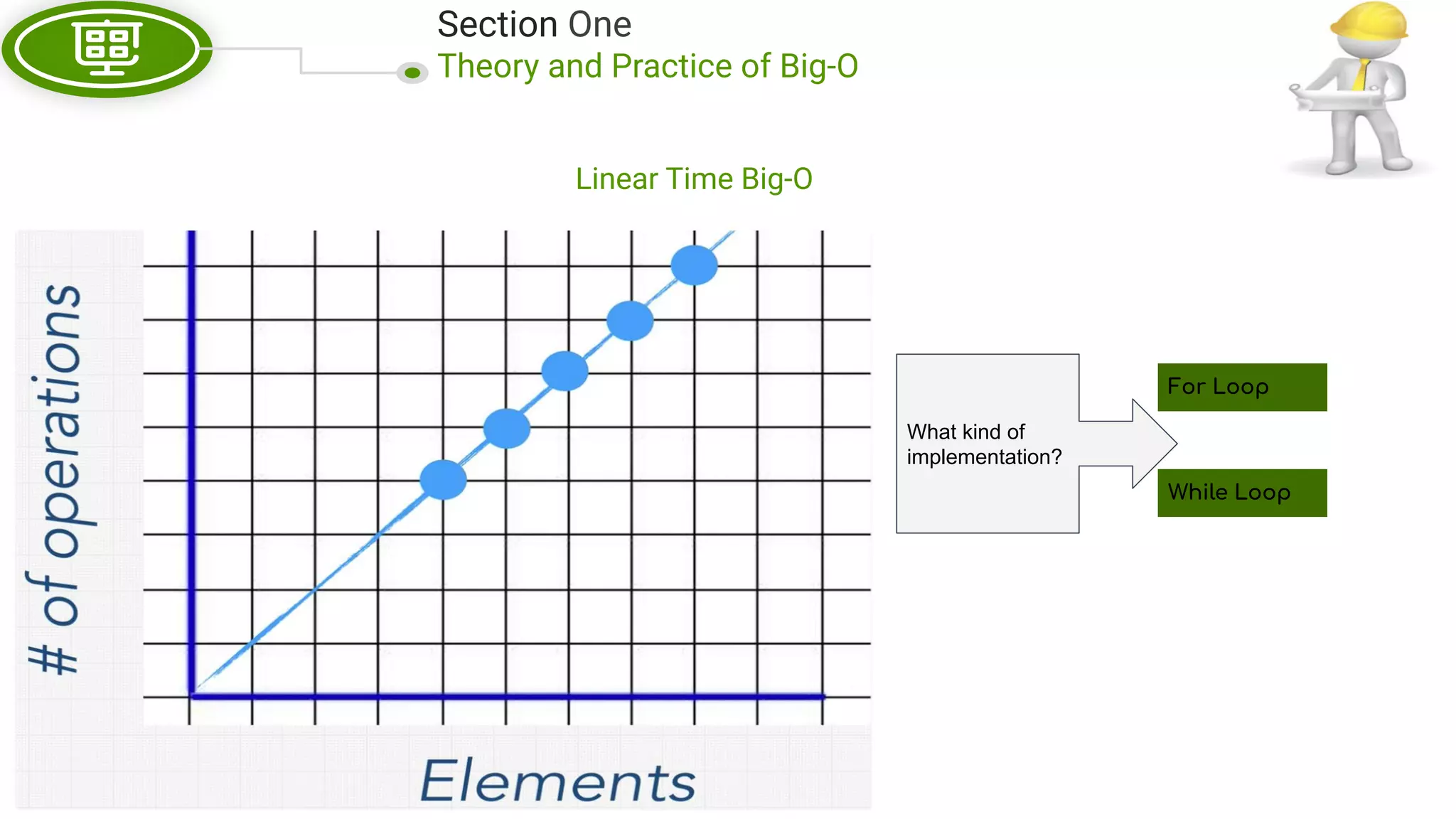
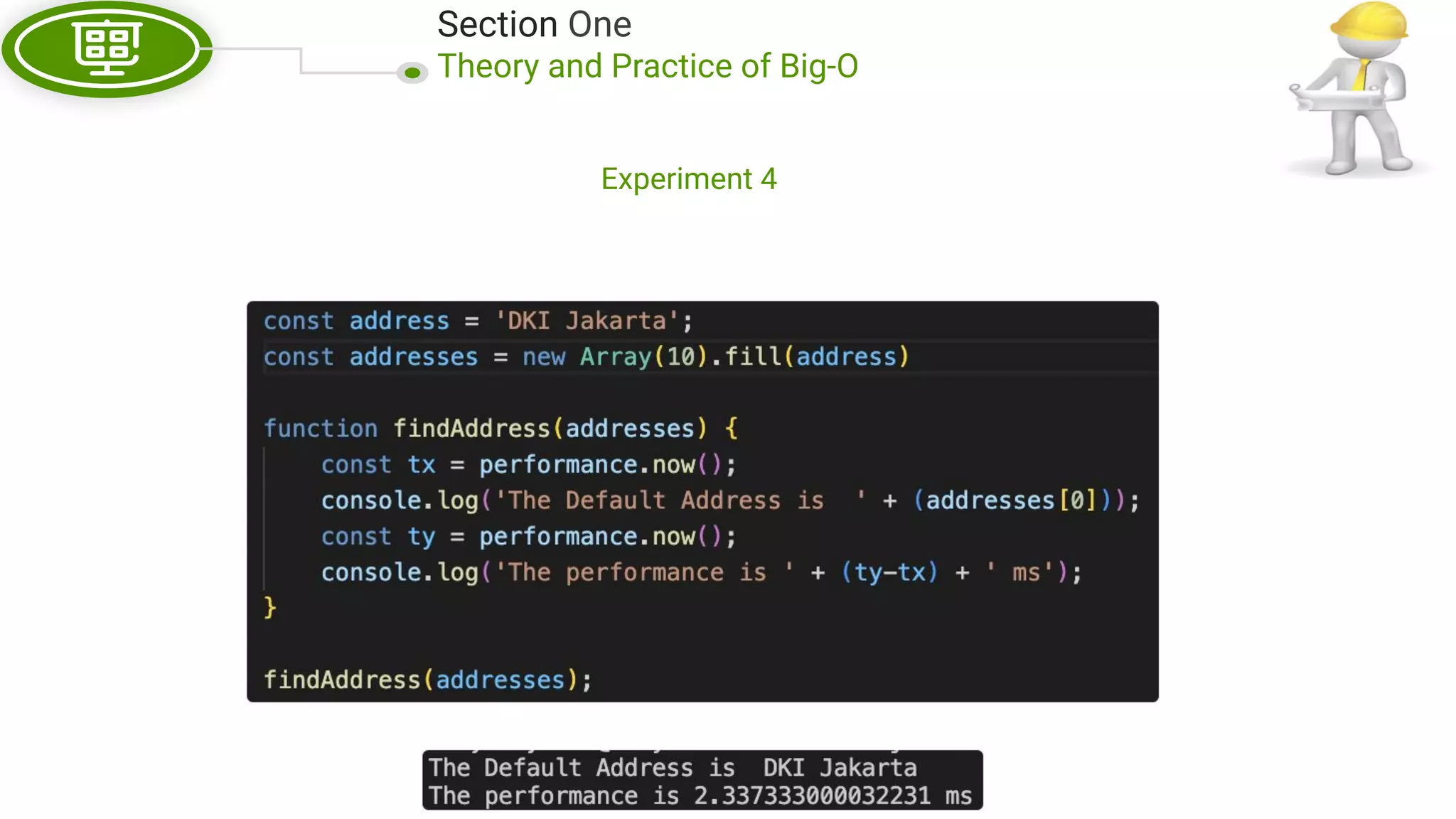
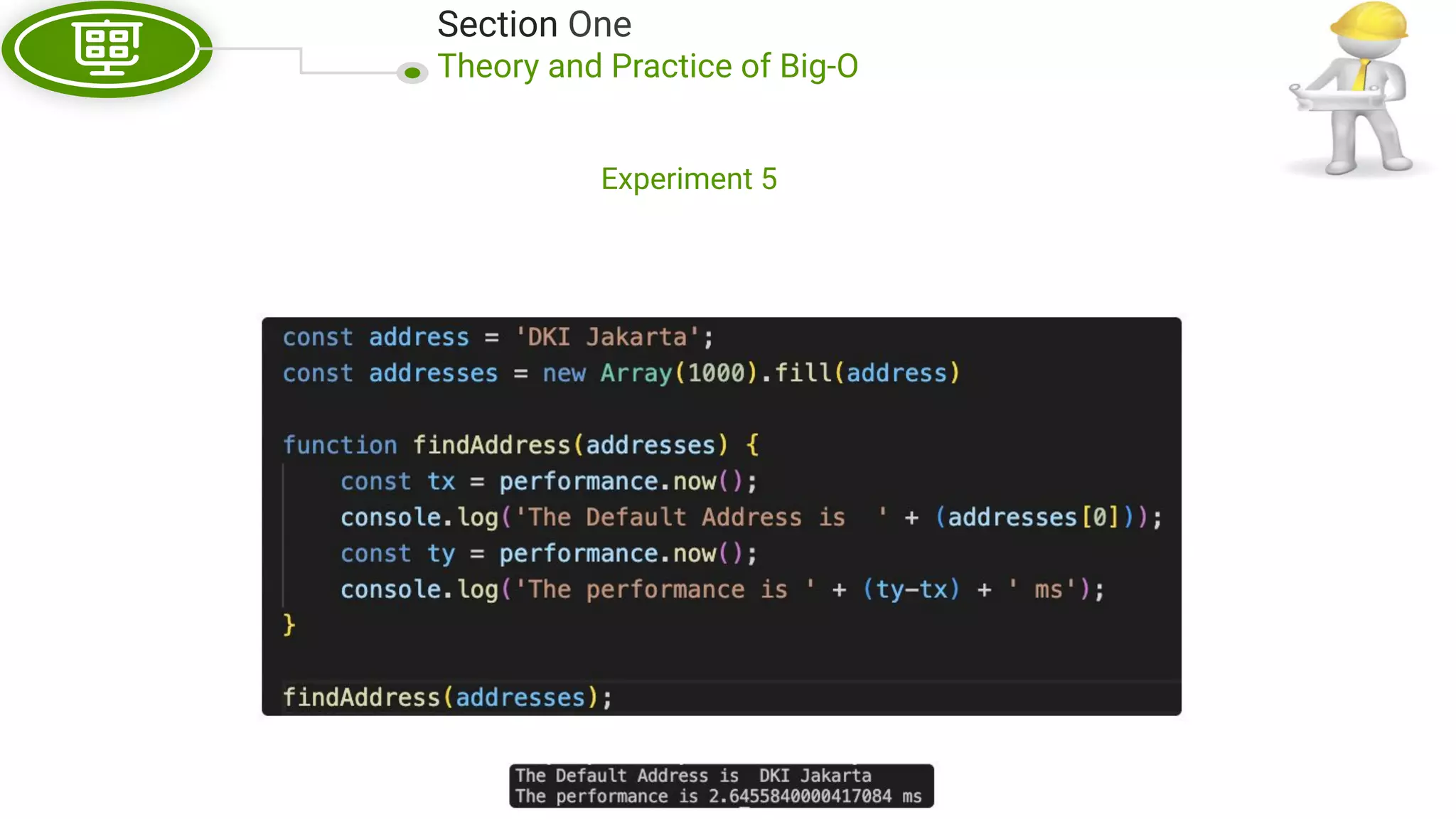
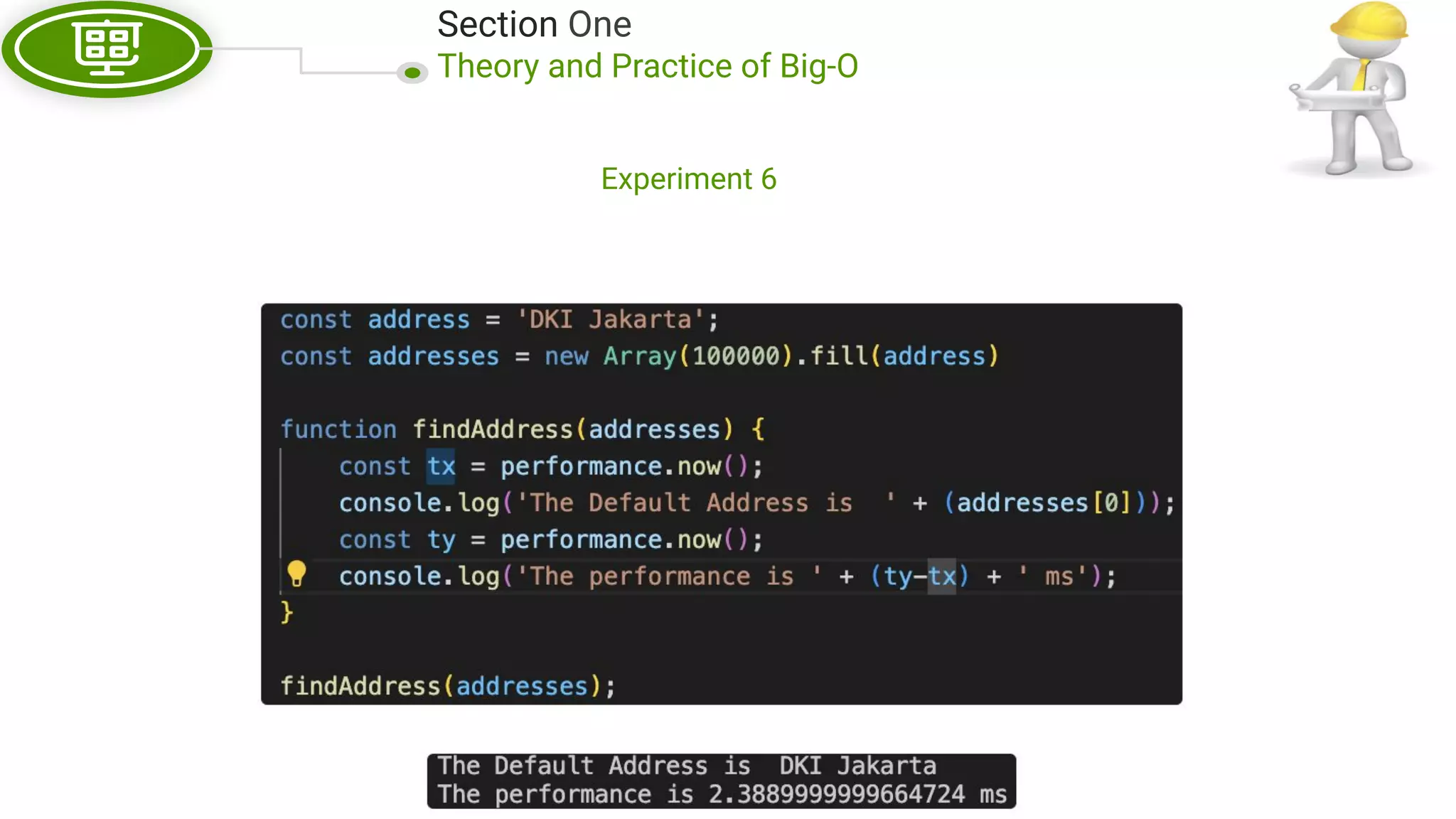
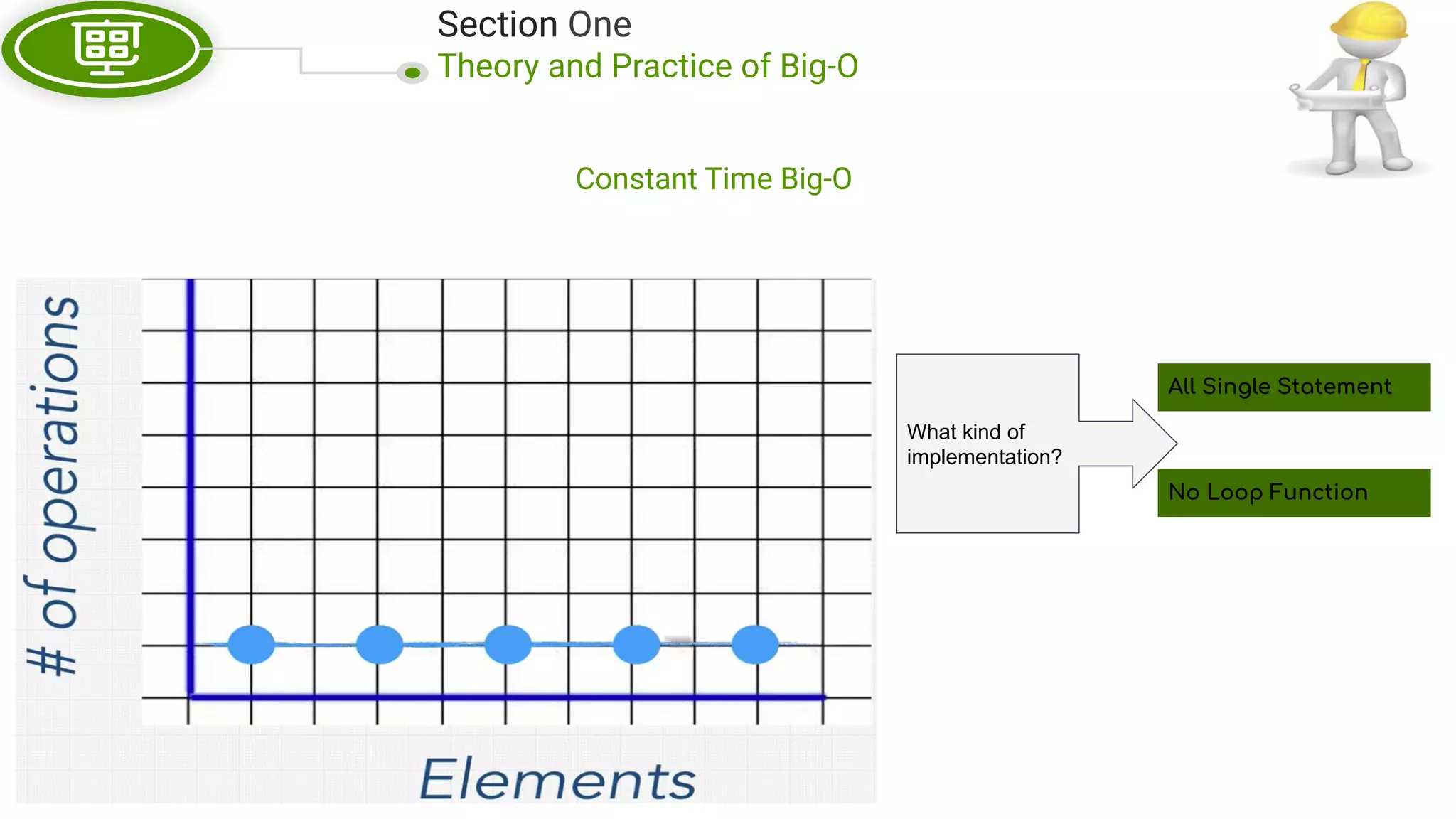
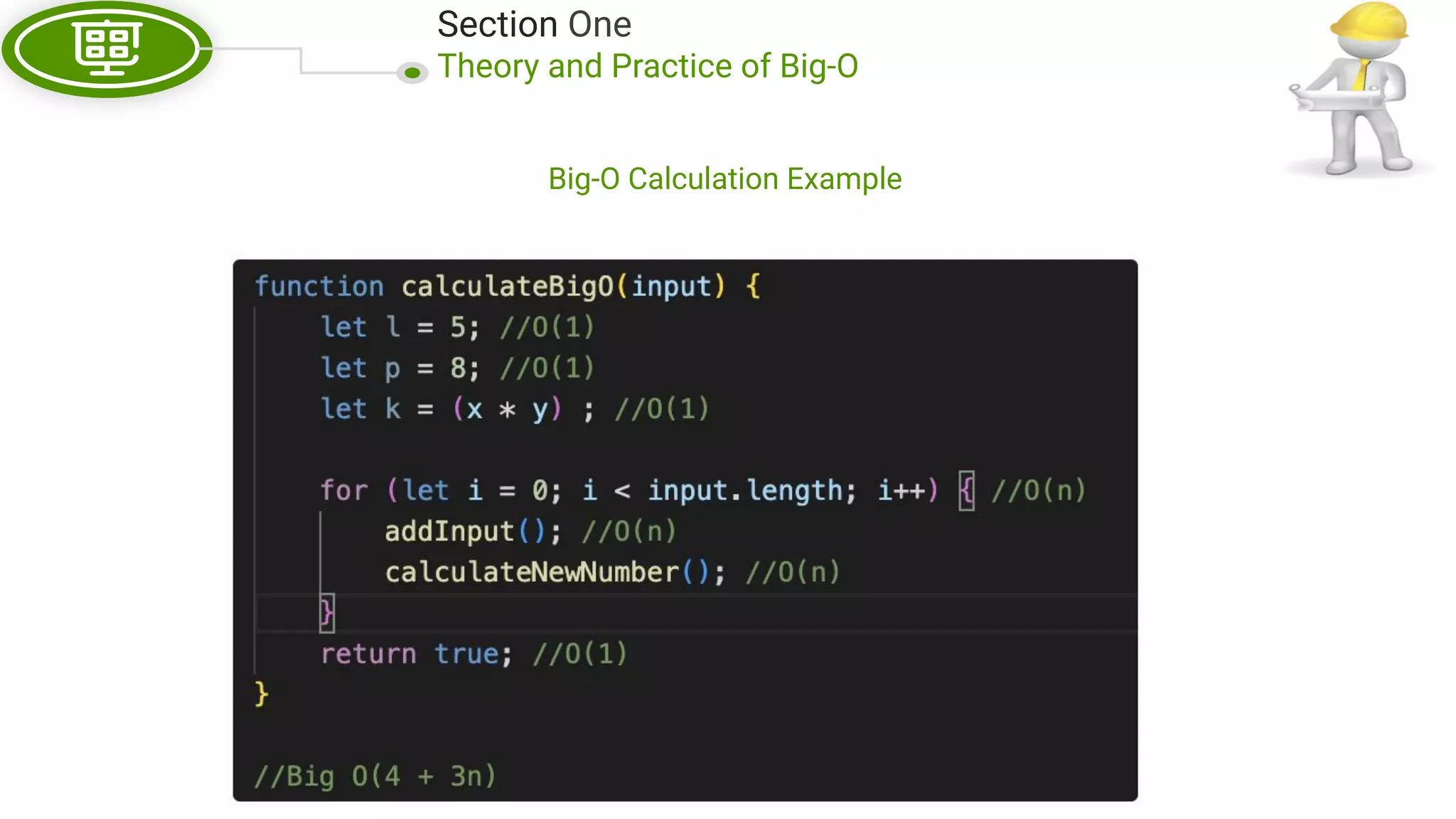
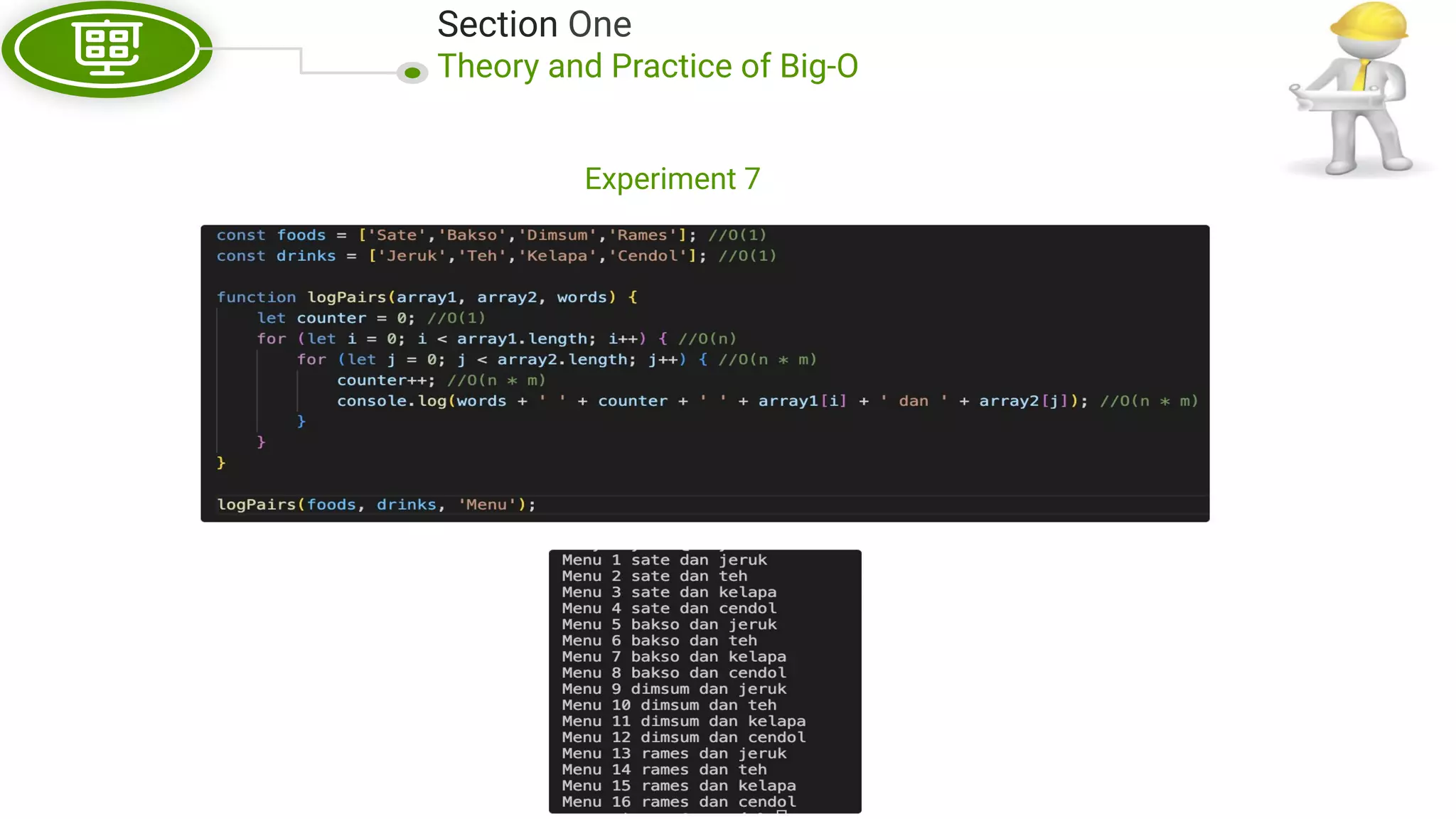
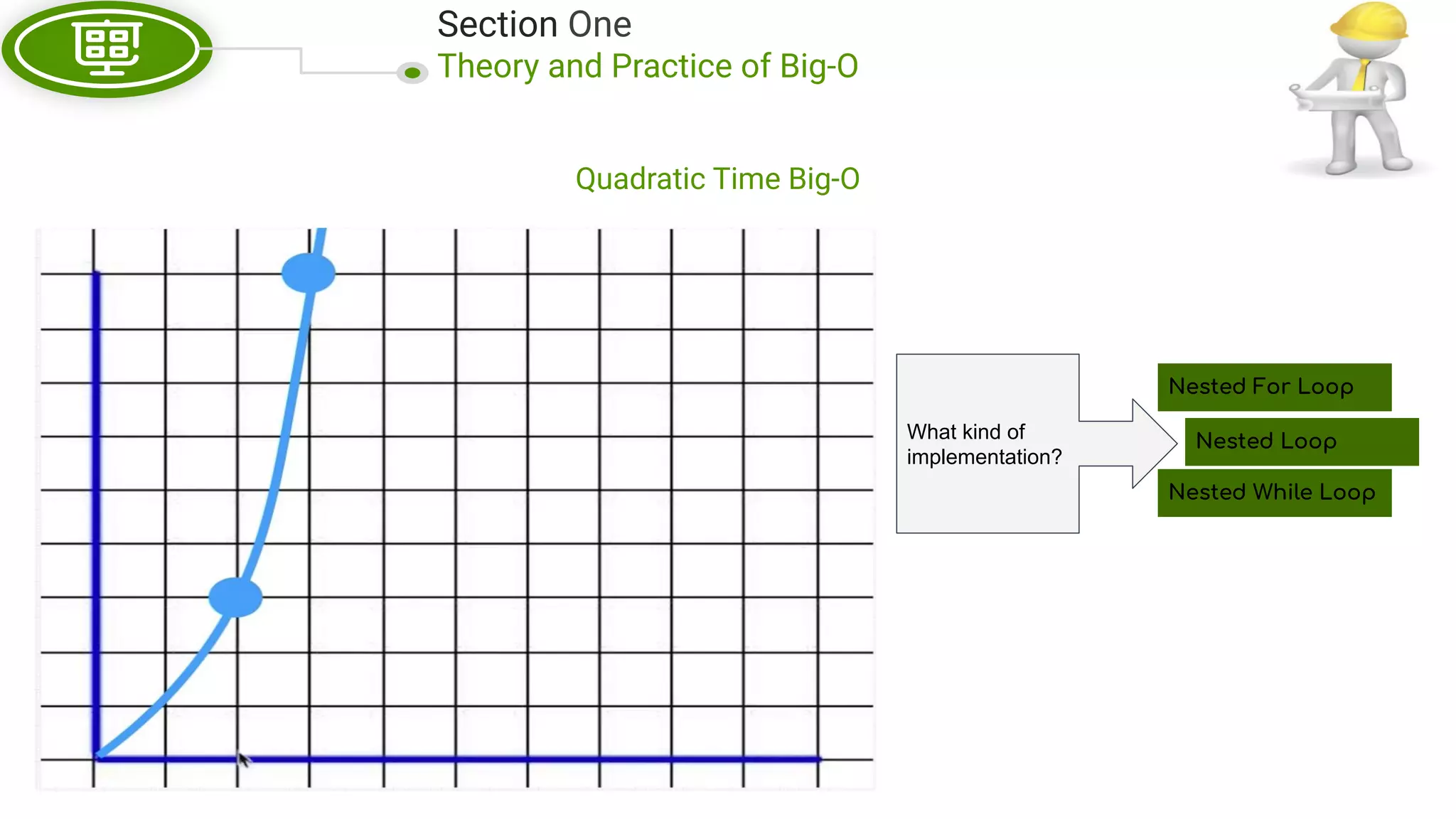
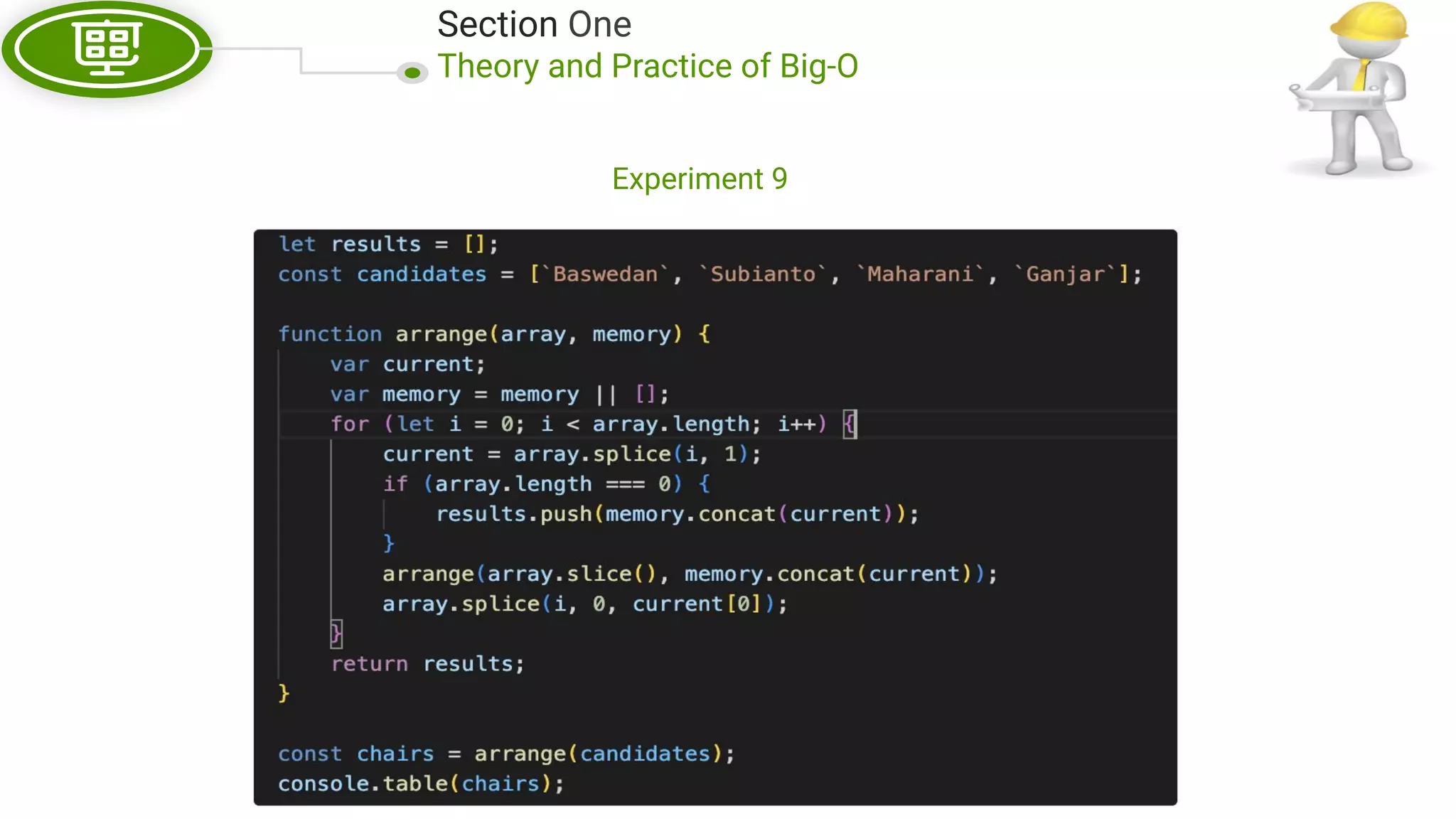
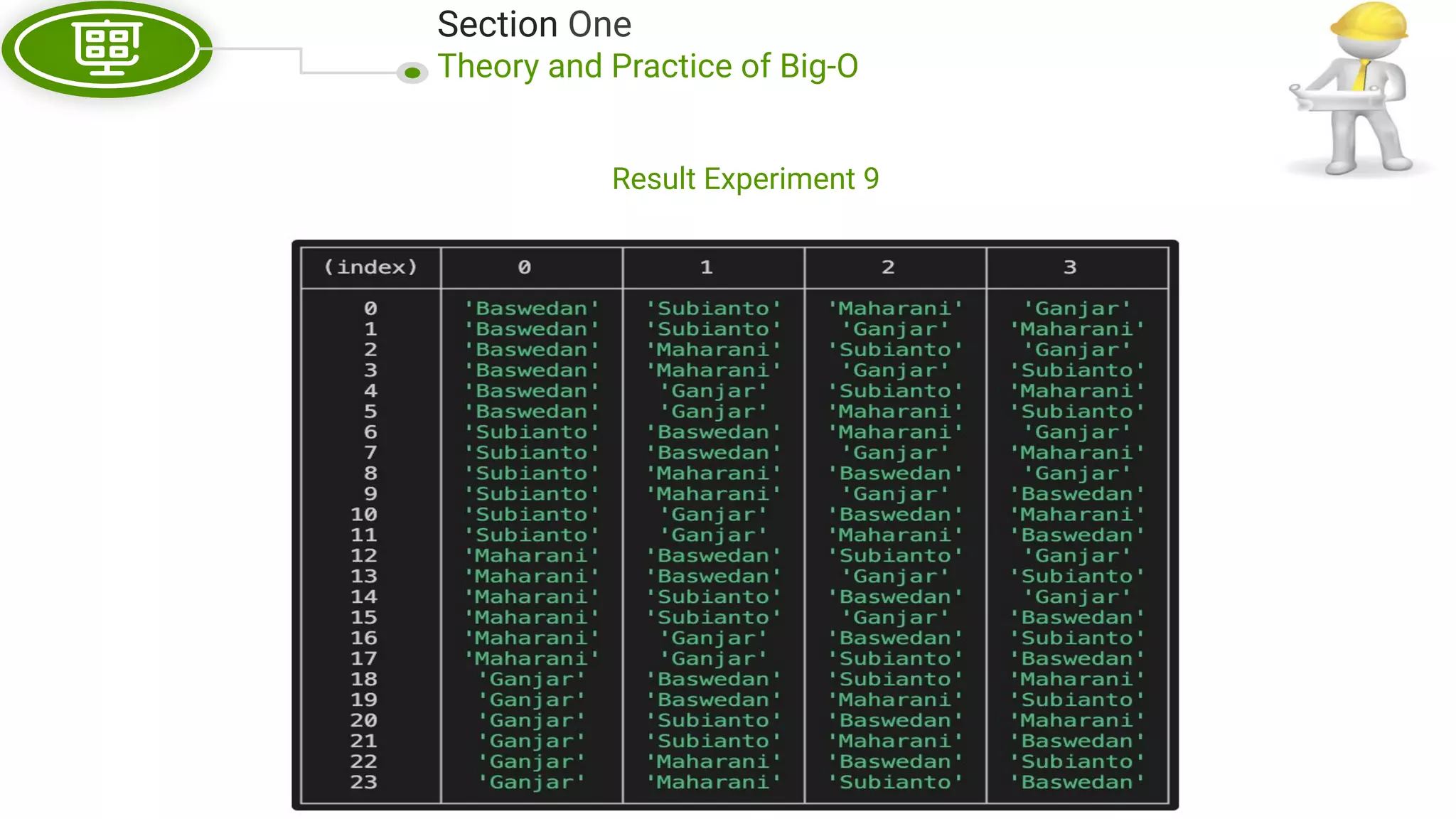
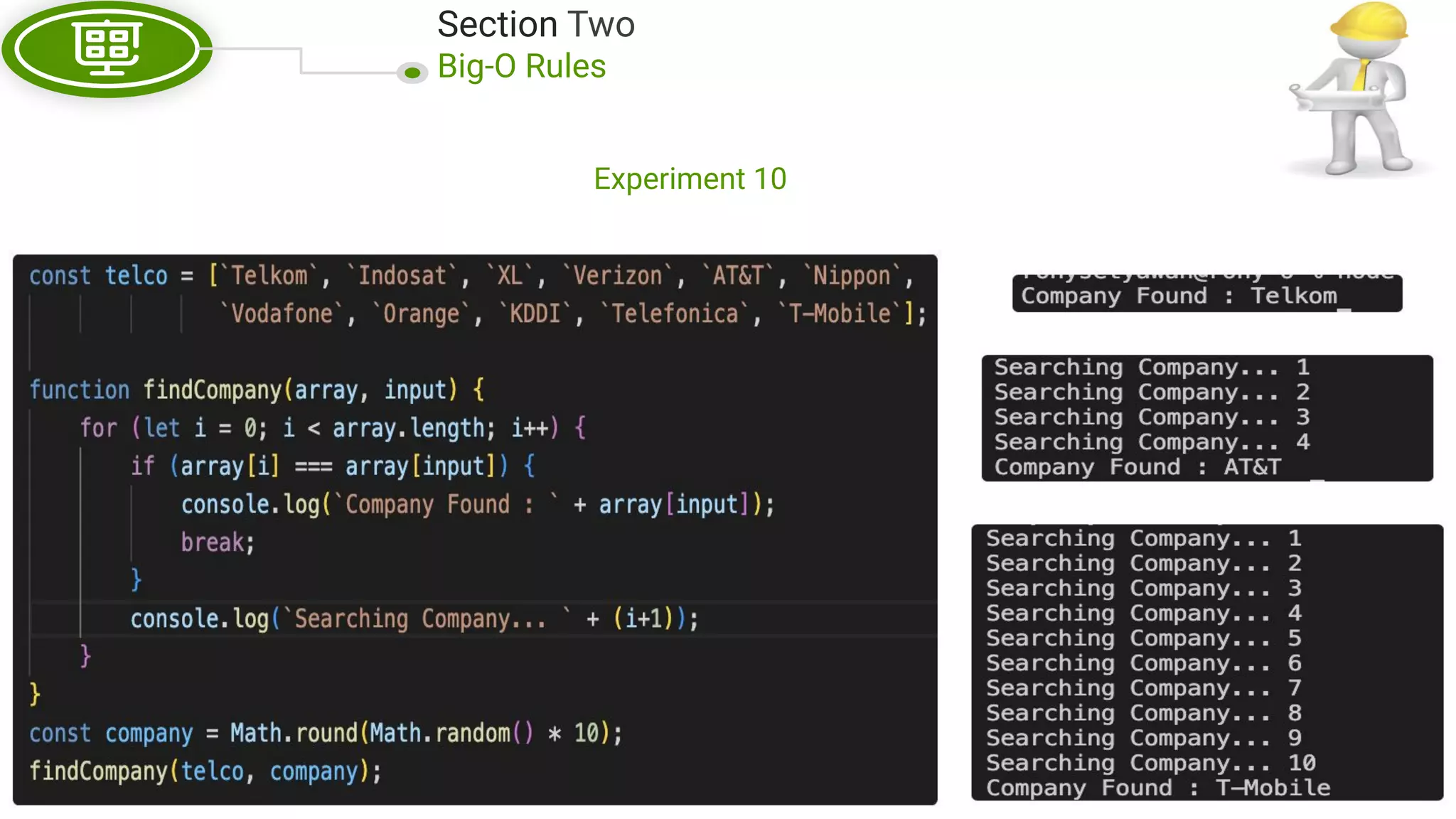
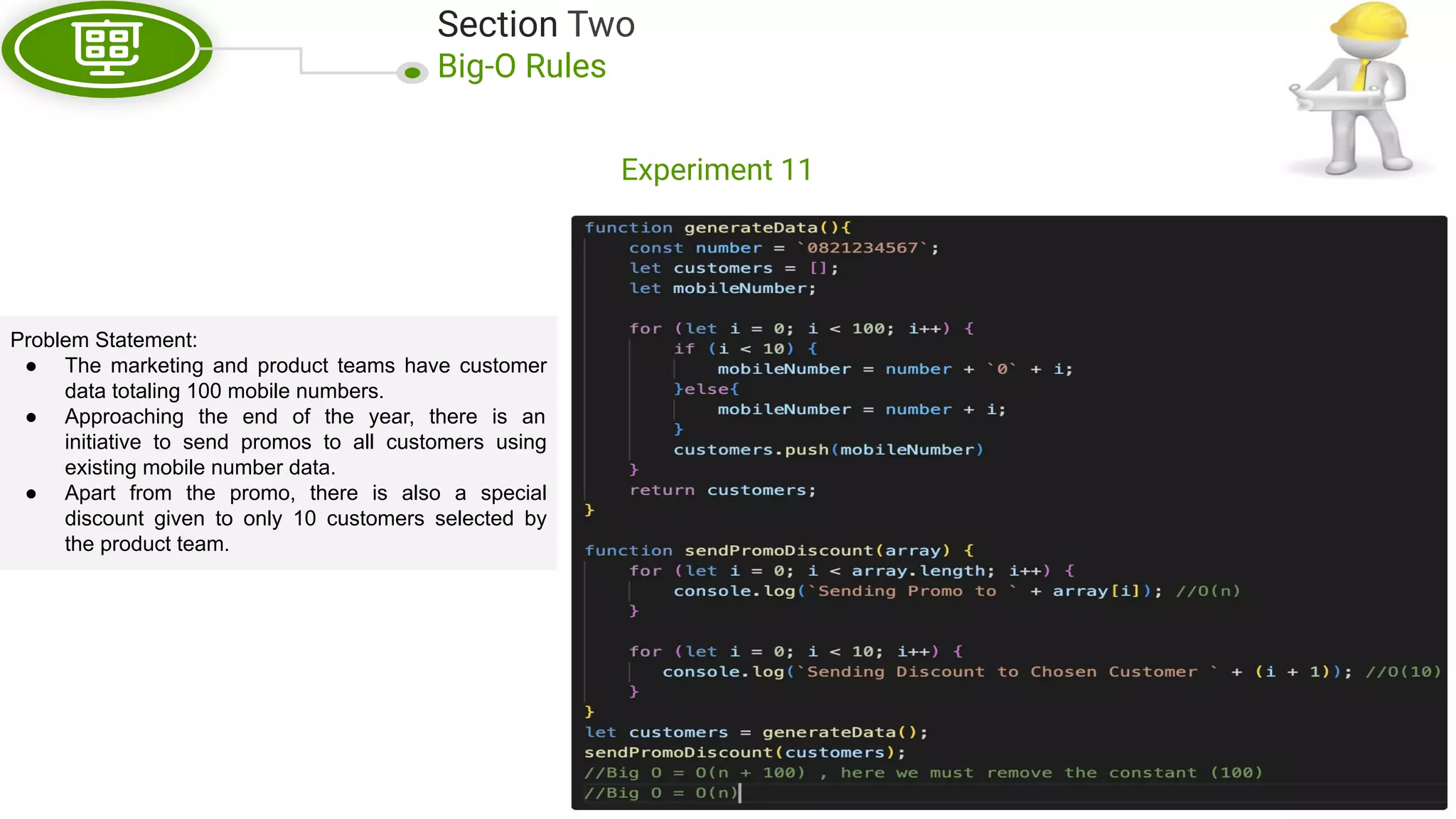
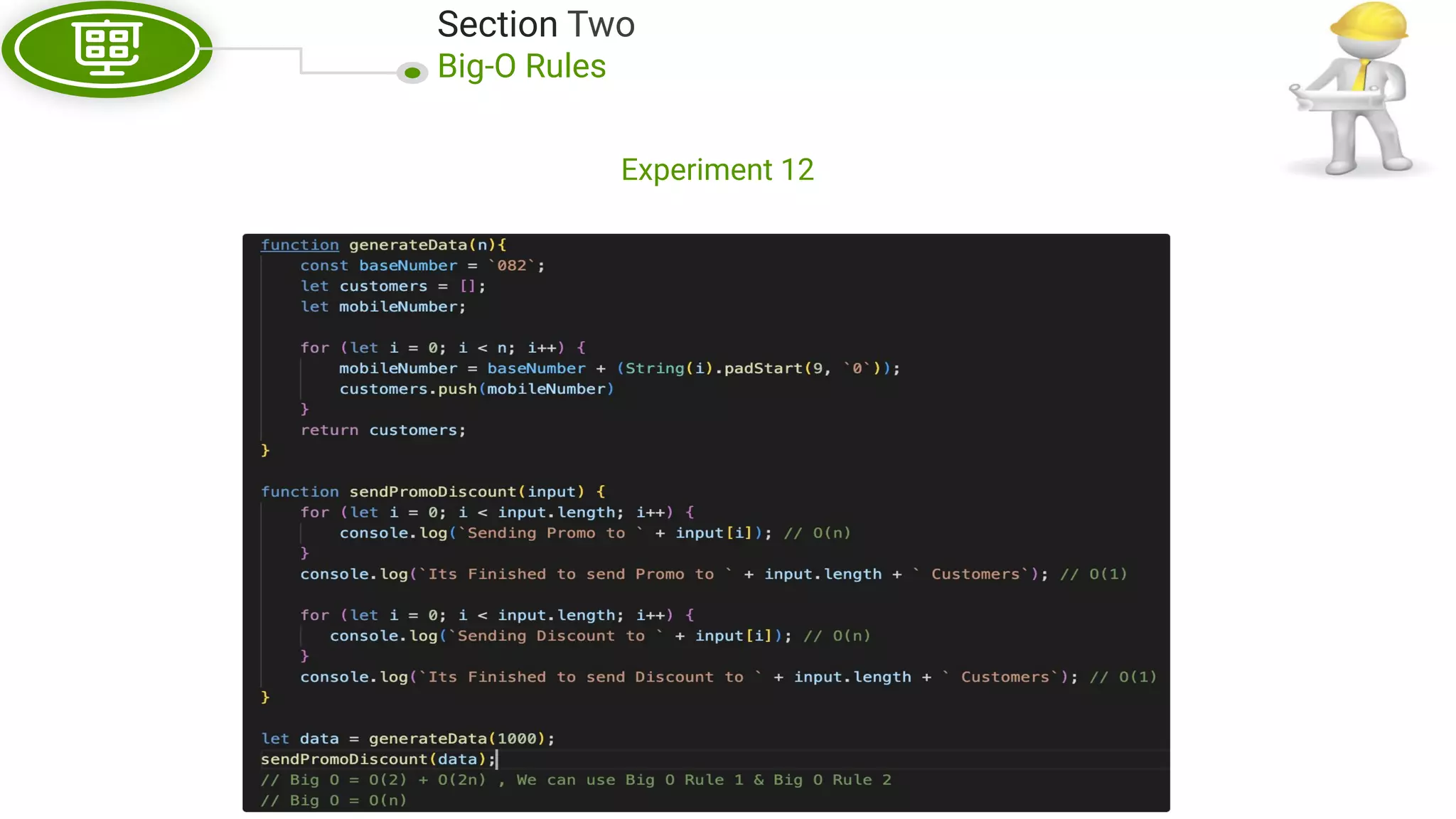
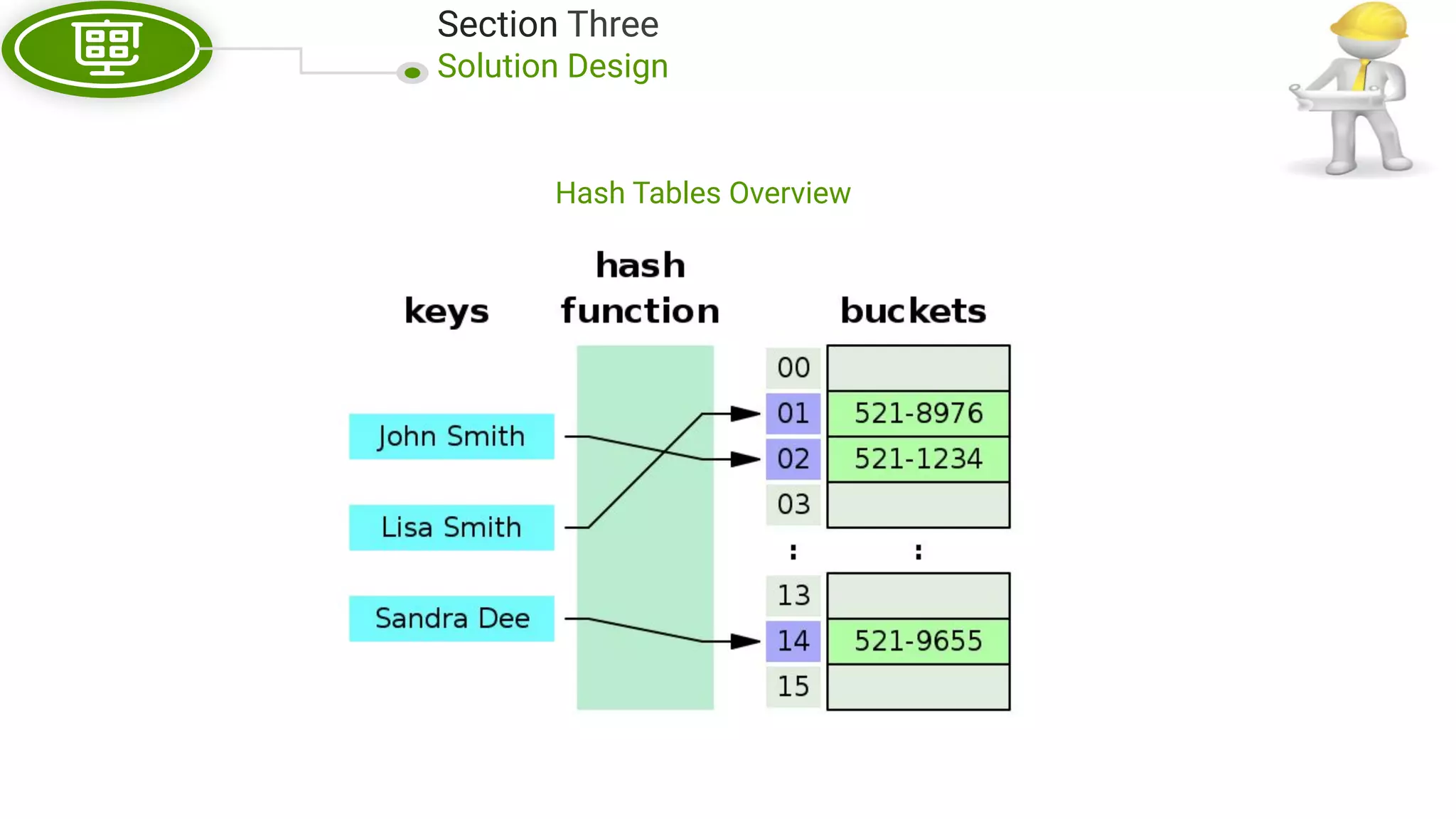
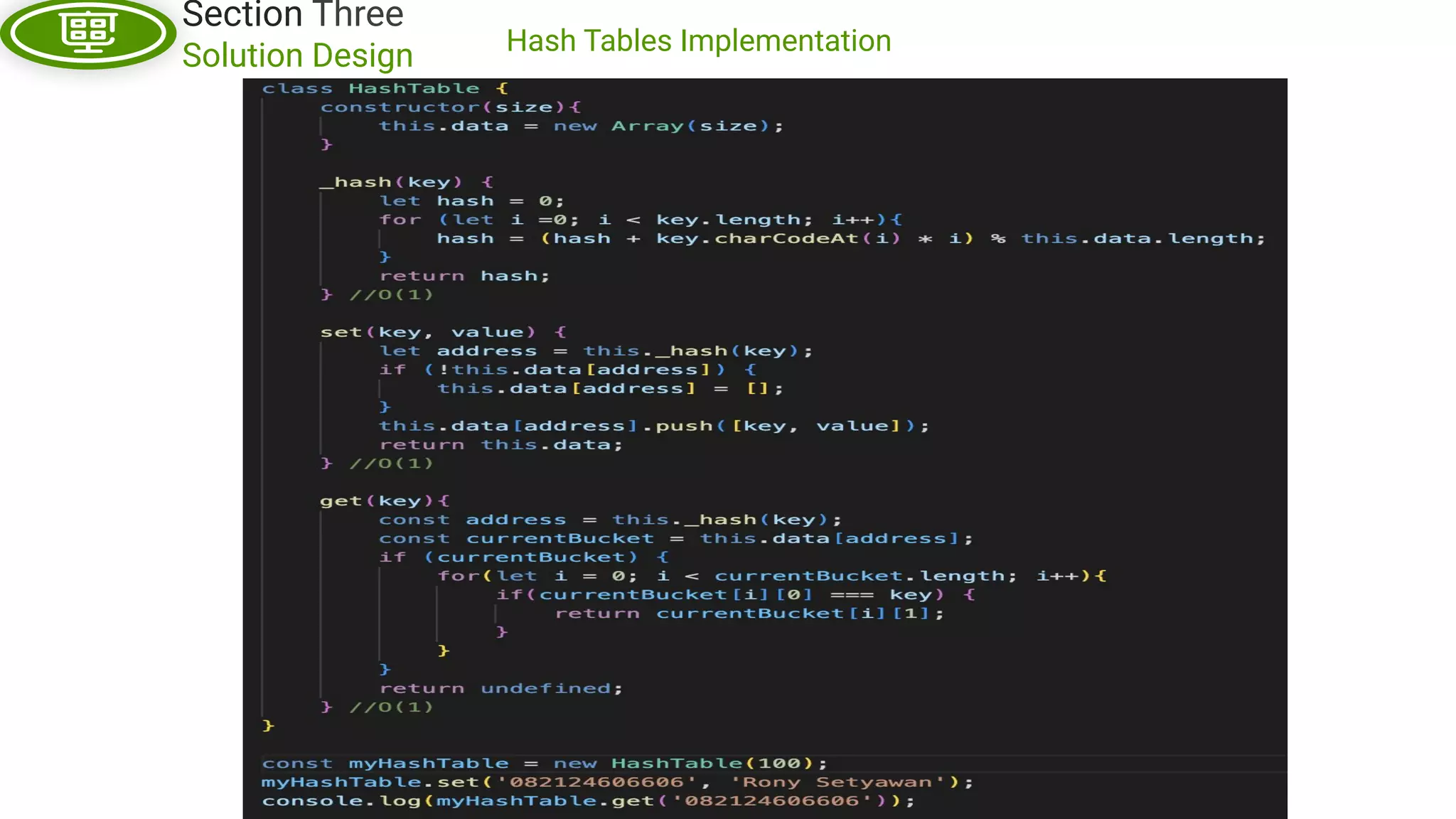
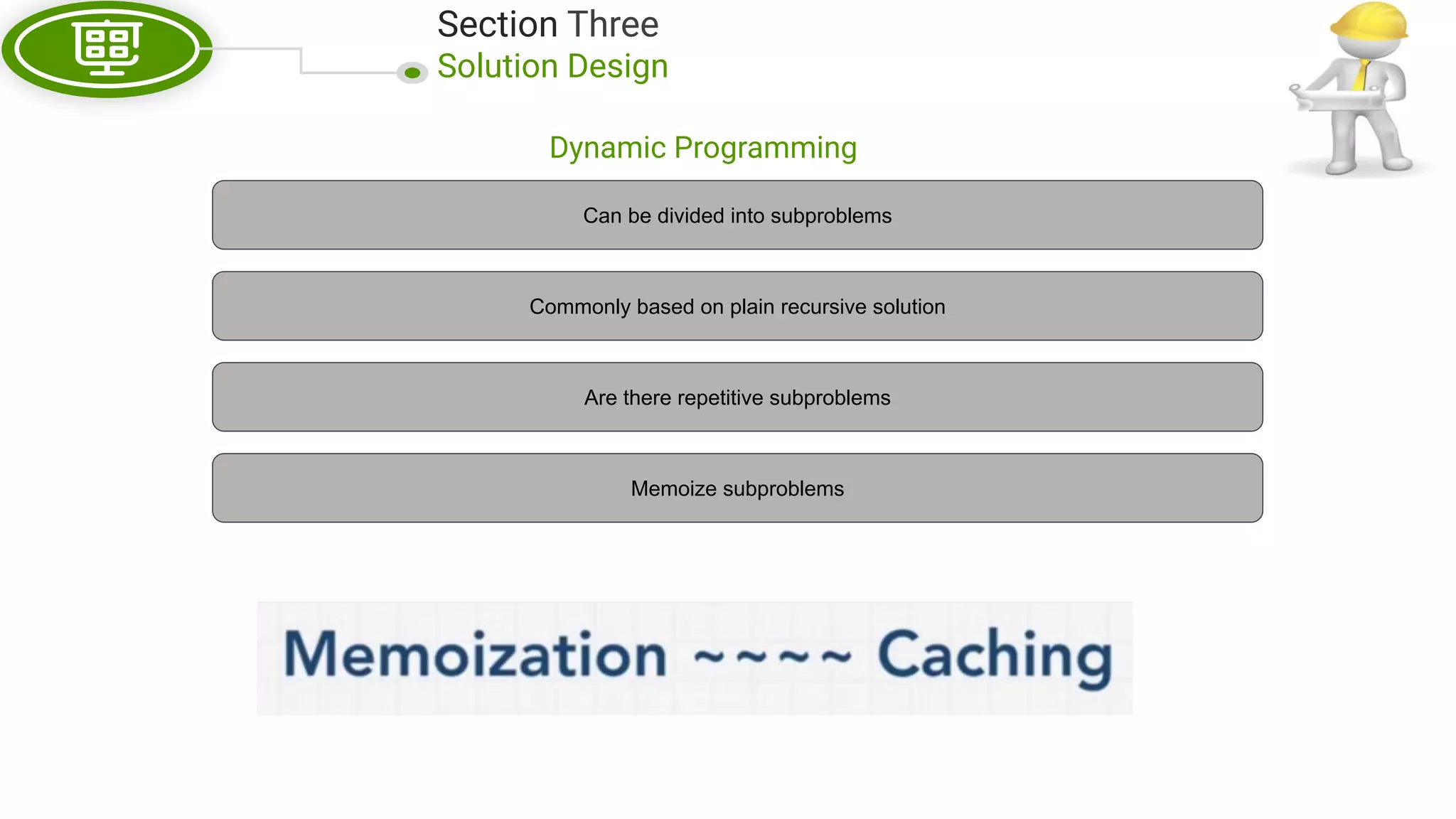
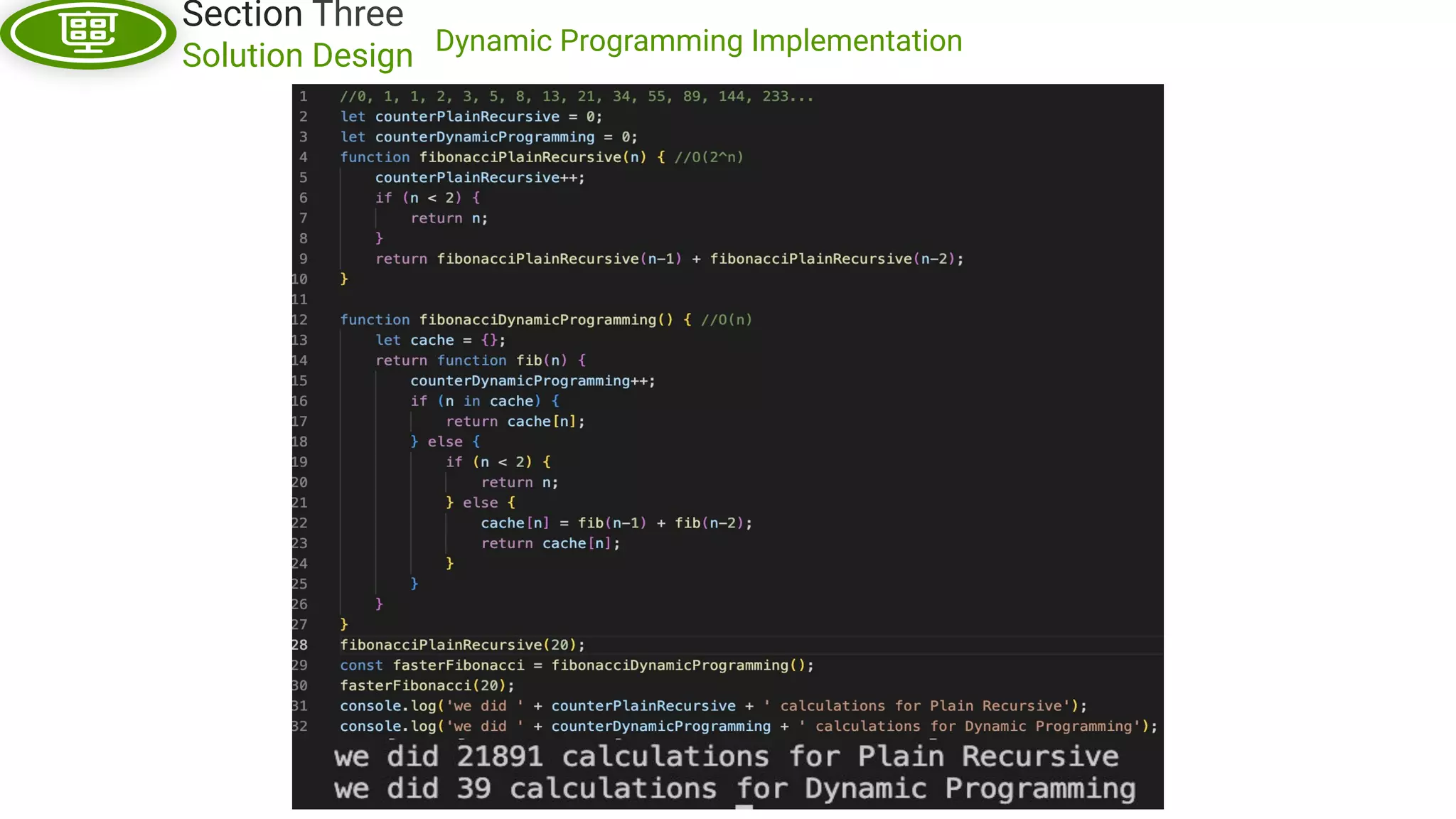
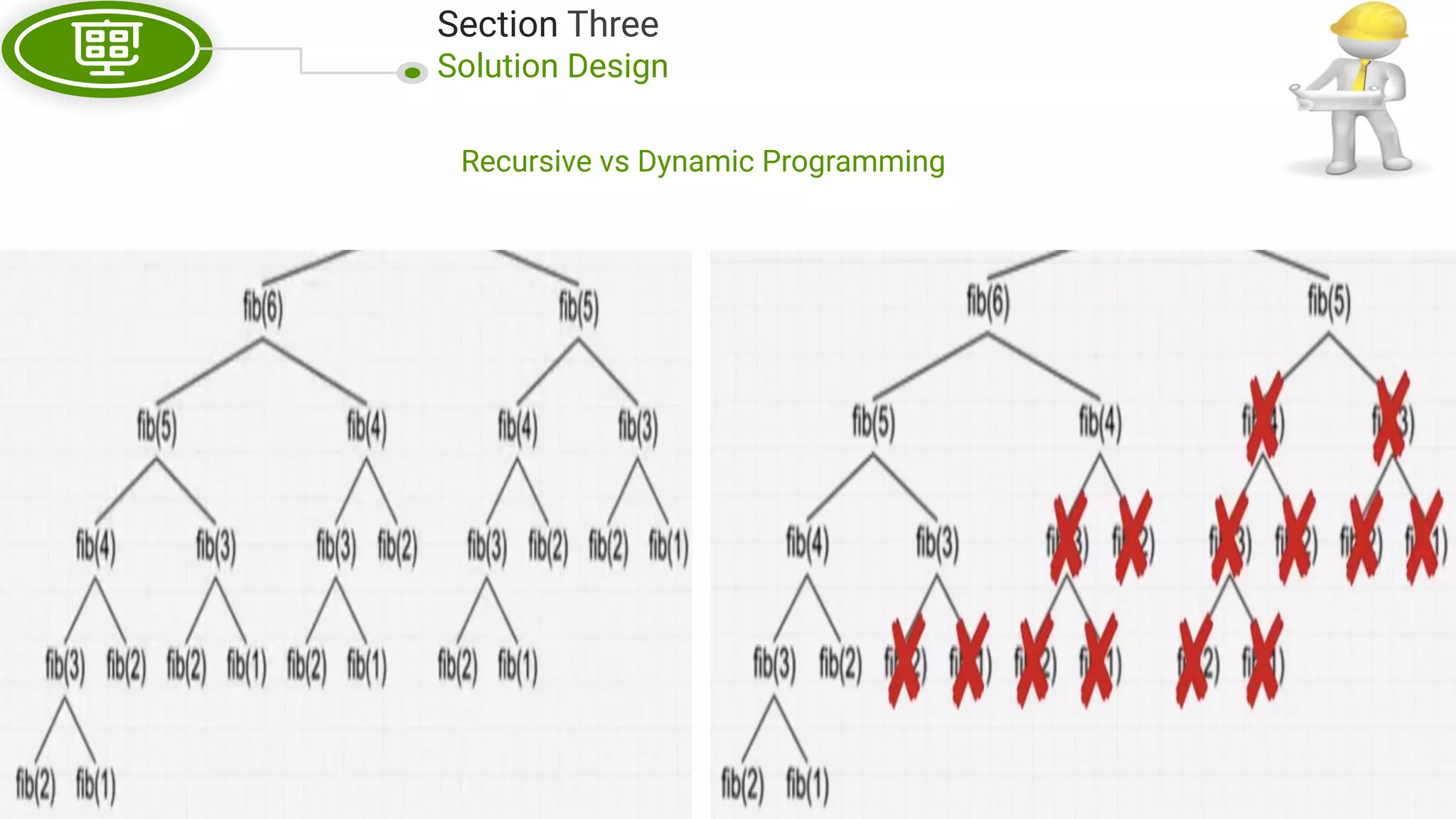
This document, written by Douglas Crockford and Rony Setyawan, explores algorithm analysis and design principles, particularly focusing on Big-O notation. It includes theoretical explanations, practical experiments, and rules for assessing algorithm efficiency, scalability, and complexity. Key concepts discussed include linear, constant, and factorial time complexities, as well as implementation techniques for hash tables and dynamic programming.