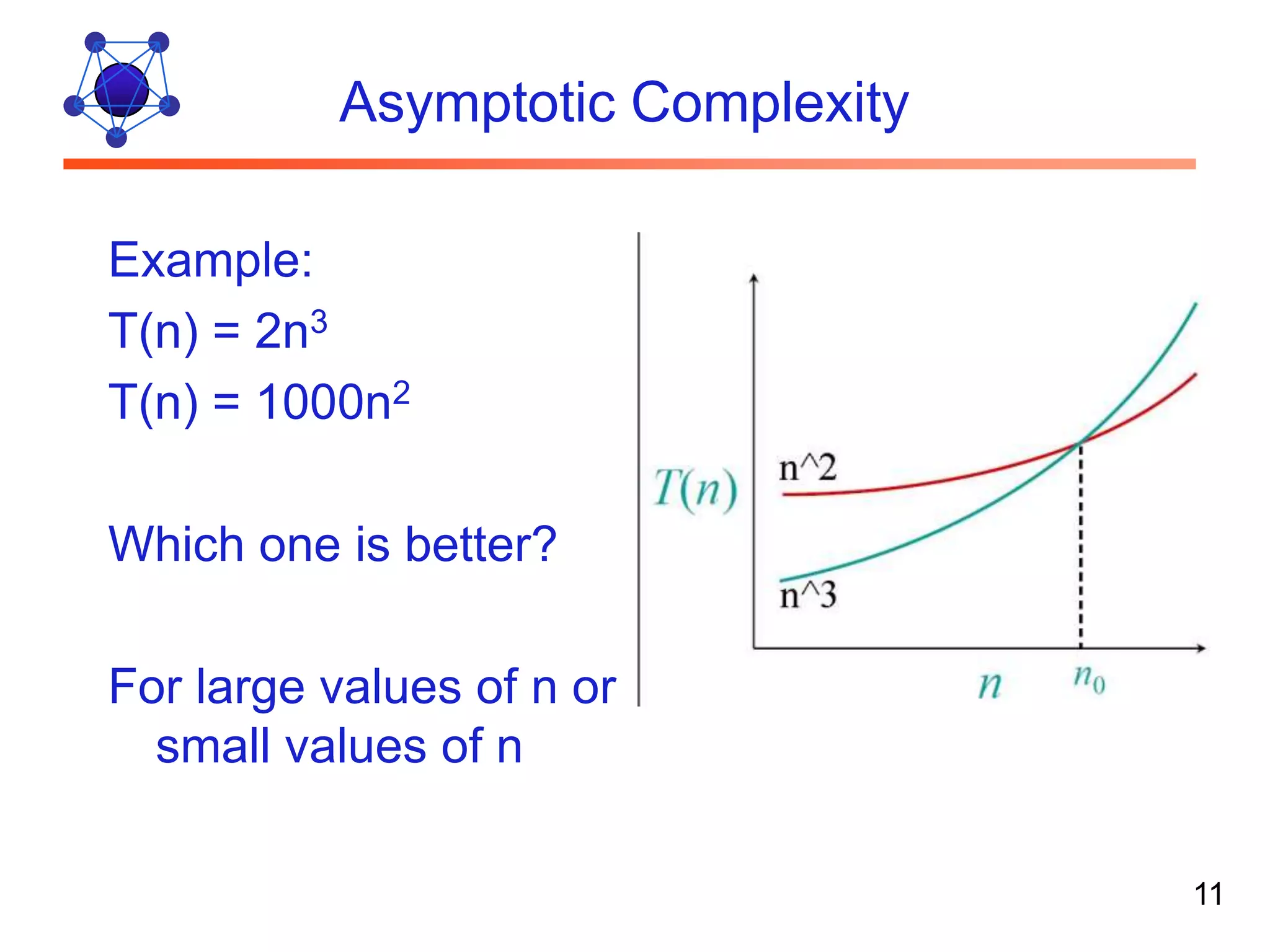
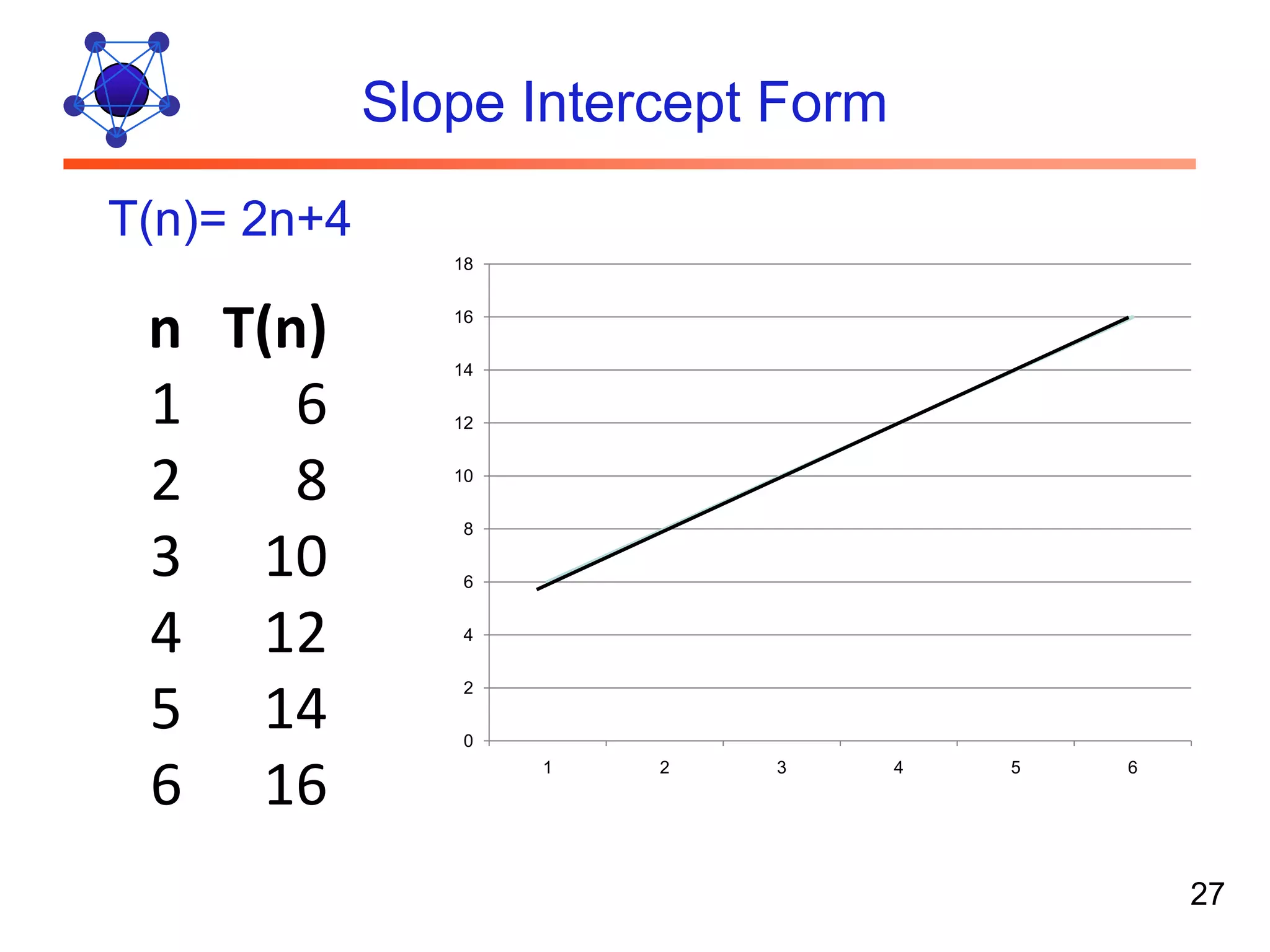
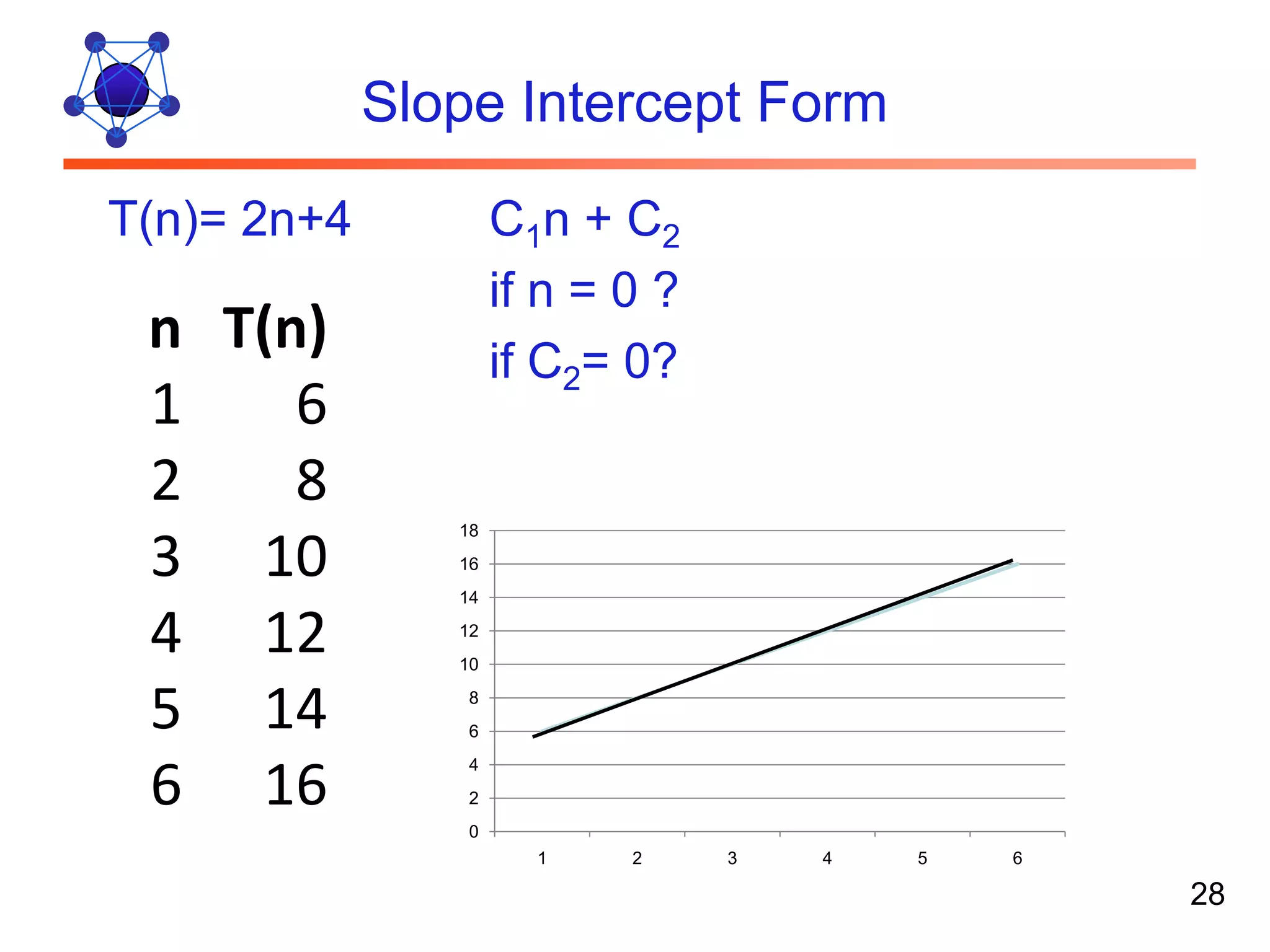
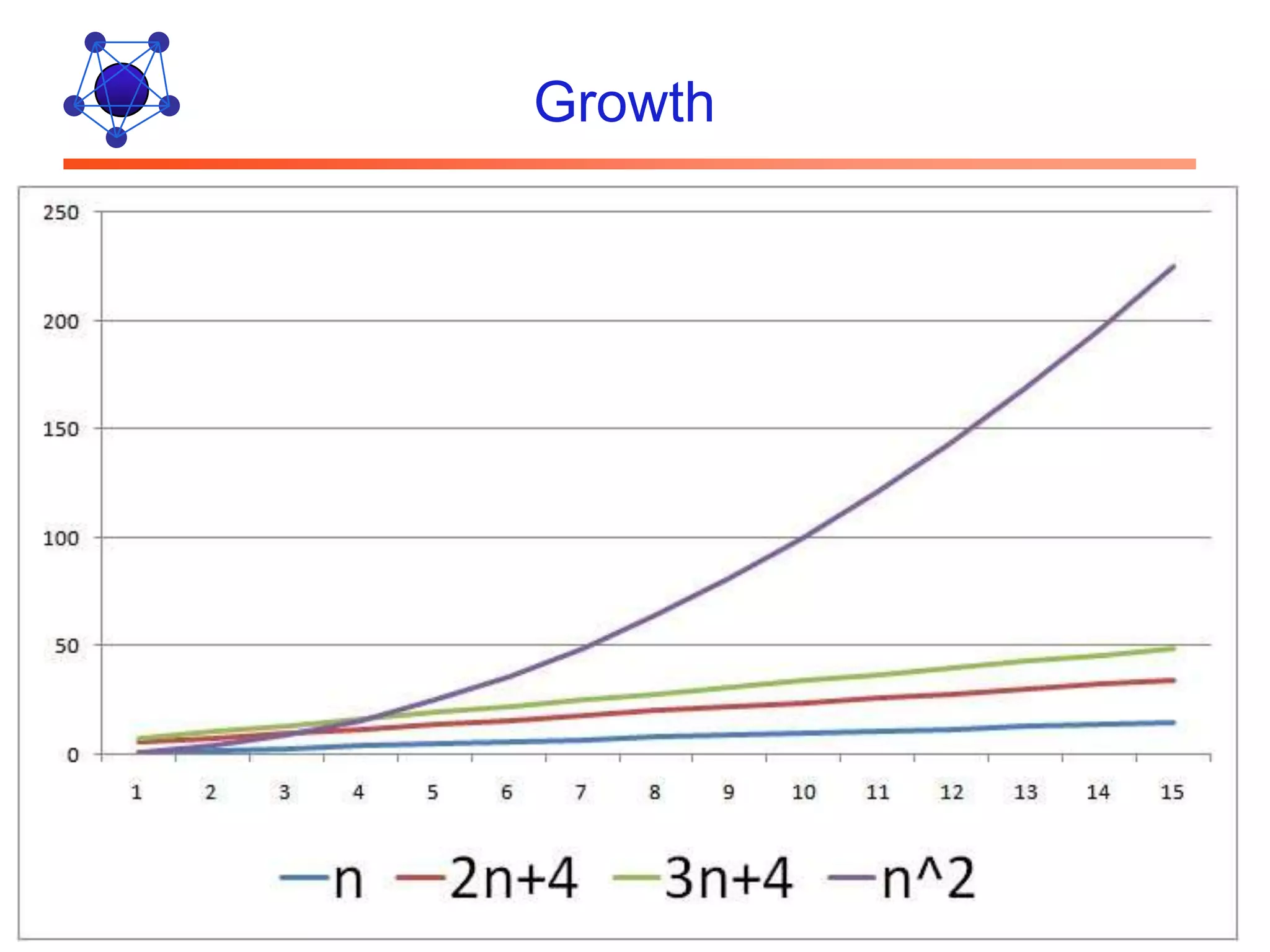
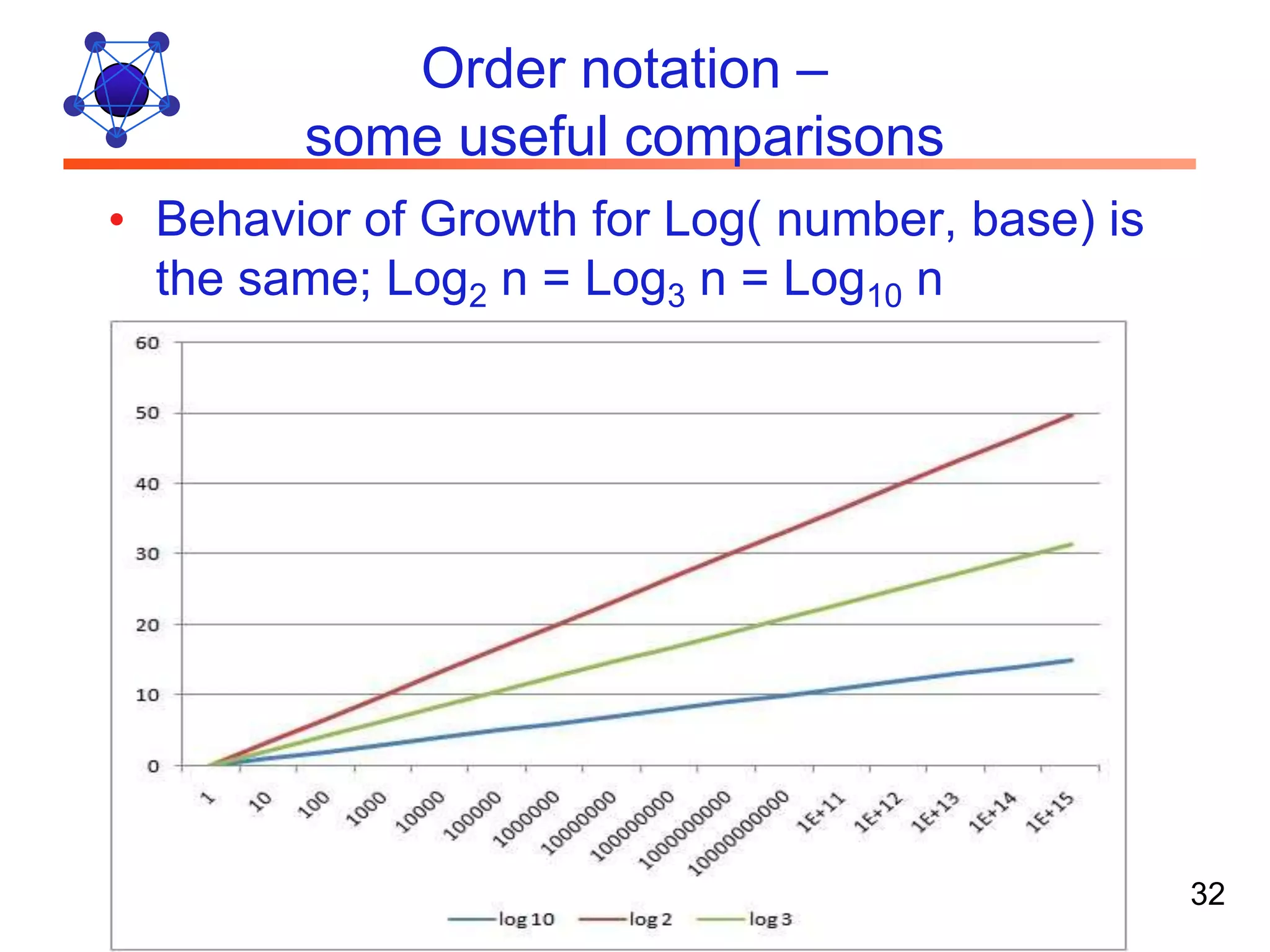
The document discusses algorithms and their analysis. It defines algorithms as well-defined problem solving steps and discusses analyzing their performance characteristics like time and space complexity. It explains the properties of algorithms like precision, determinism and finiteness. It also discusses different methods of analyzing algorithms like worst-case, average-case and best-case analysis and using asymptotic notations like Big-O to describe time complexity.