Download as PDF, PPTX
Uploaded byMarina Santini
Lecture 2: Computational Semantics
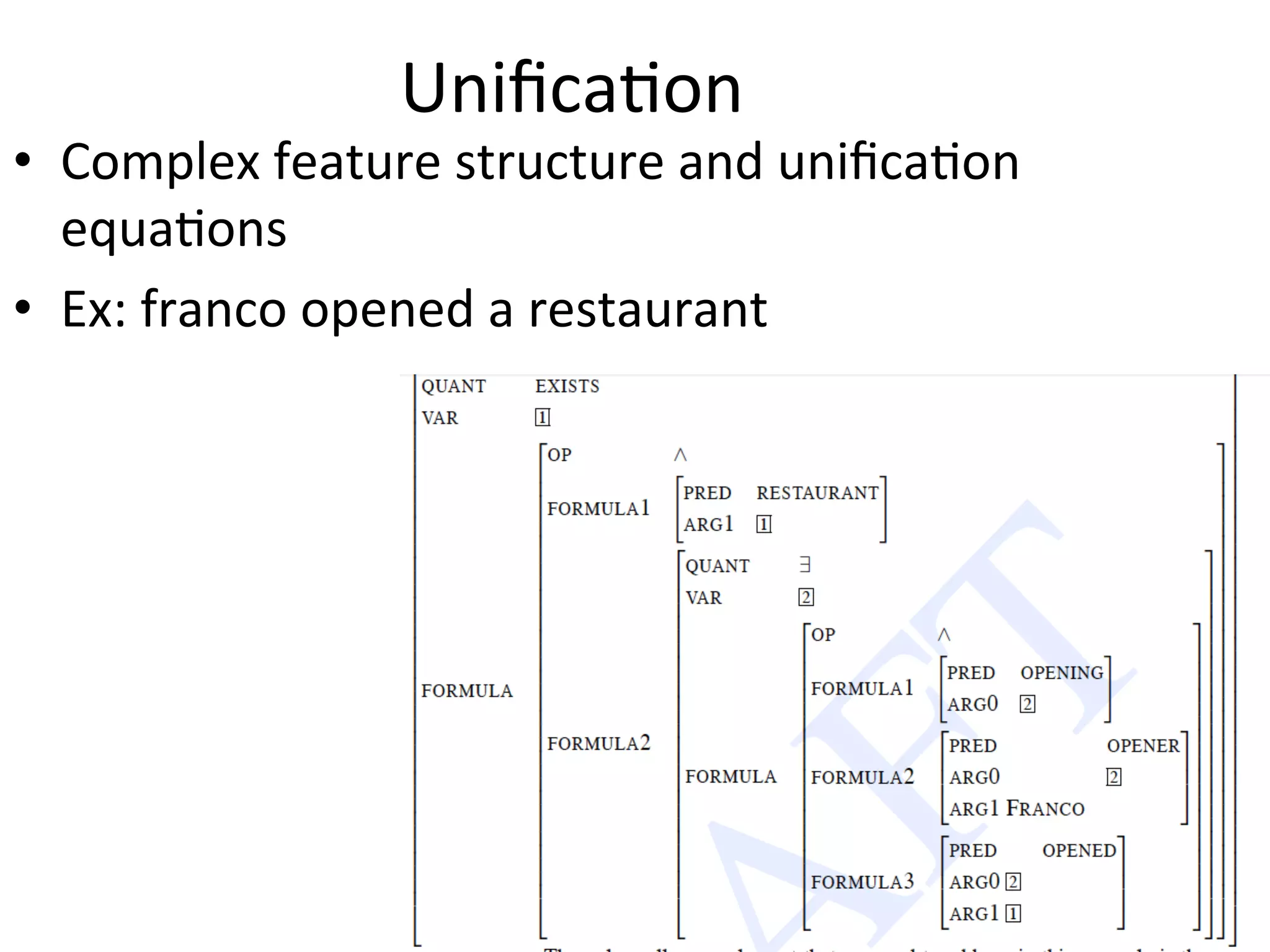
The document discusses computational semantics, focusing on the representation and analysis of meaning in linguistic expressions using formal structures such as first-order logic and event representations. It outlines the requirements of meaning representations, key concepts like predicates and quantifiers, and techniques for semantic analysis, including syntax-driven approaches and corpus-based methods. Additionally, it addresses challenges such as ambiguity and underspecification, while highlighting the importance of understanding the relationship between syntax and meaning.
Lecture 2: Computational Semantics
- 1. Seman&c Analysis in Language Technology http://stp.lingfil.uu.se/~santinim/sais/2014/sais_2014.htm Computa(onal Seman(cs Marina San(ni san$nim@stp.lingfil.uu.se Department of Linguis(cs and Philology Uppsala University, Uppsala, Sweden Autumn 2014 Lecture 2: Computational Semantics 1
- 2. Outline • Formal Representa(ons and Computa(onal approaches – The Seman(cs of First-‐Order Logic – Event Representa(ons – Descrip(on Logics & the Web Ontology Language – Syntax-‐Driven Seman(c Analysis: Composi(onality • Corpus-‐based approaches – Latent Seman&c Analysis – Topic models – Distribu&onal Seman&cs… Lecture 2: Computational Semantics 2
- 3. Generally speaking, seman(cs and meaning… In linguis(cs… • Seman&cs is the study of meaning • Meaning is the core of human communica(on. It is the msg that we want to convey (explicity or implicitly) • Meaning representa&ons are formal structures • Meaning representa&on languages are frameworks that speficy the syntax and seman(cs of these representa(ons Lecture 2: Computational Semantics 3
- 4. (Computa(onal) Seman(cs vs Pragma(cs • Roughly, seman(cs is the meaning that can be deduced directly from an expression, with no extra-‐linguis(c informa(on. – cf: ”the sun is rising” vs ”the bus” • Computa(onal Seman(cs focuses not only on the abstract accounts of meanings, but also in a concrete formaliza(ons that can support implementa&on Lecture 2: Computational Semantics 4
- 5. Seman(c Analysis… … is the process that we use to – create representa(ons of meaning – assign them to linguis(c inputs Lecture 2: Computational Semantics 5
- 6. WHAT IS NEEDED IN A MEANING REPRESENTATION? Ch 17 Lecture 2: Computational Semantics 6
- 7. The Representa(on of Meaning • Meaning of linguis(c expressions can be captured in formal structures that we call meaning representa&ons. • What we need are representa&on that bridge the gap from linguis&c inputs to the non linguis&c knowledge of the world • It requires access to the representa&ons that link the linguis&c elements involved in the task to the non-‐ linguisitc ’knowledge of the world’ needed to perform the task. Lecture 2: Computational Semantics 7
- 8. Seman(c processing… ”Learning to use a new piece of soWware by reading a manual” – knowledge about current computers – similar soWware applica(ons – knowledge about users in general Lecture 2: Computational Semantics 8
- 9. Requirements • The basic requirements that a meaning respresenta(on must fulfill: – Verifiability – Ambiguity – Inference – Expressiveness Lecture 2: Computational Semantics 9
- 10. First-‐Order Logic • FOL is a computa(onally tractable approach to the representa(on of knowledge that sa(sfies many of the previous requirements, namely: – Verifiability – Inference – Expressiveness Lecture 2: Computational Semantics 10
- 11. FOL (Wikipedia) http://en.wikipedia.org/wiki/First-order_logic • First-‐order logic is a formal system used in mathema(cs, philosophy, linguis(cs, and computer science. • It is also known as: – first-‐order predicate calculus – the lower predicate calculus – quan&fica&on theory – predicate logic – etc. Lecture 2: Computational Semantics 11
- 12. Why ”first-‐order”? Lecture 2: Computational Semantics 12 There are more powerful forms of logic, but first-‐‑ order logic is adequate for most everyday reasoning.
- 13. FOL • First-‐order logic is symbolized reasoning in which each sentence, or statement, is broken down into a subject and a predicate. • The predicate modifies or defines the proper(es of the subject. • In first-‐order logic, a predicate can only refer to a single subject. Lecture 2: Computational Semantics 13
- 14. But… undecidable (some(mes) • The Incompleteness Theorem , proven in 1930, demonstrates that first-‐order logic is in general undecidable. • That means there exist statements in this logic form that, under certain condi(ons, cannot be proven either true or false. • Ex: can’t solve the Hal(ng Problem Lecture 2: Computational Semantics 14
- 15. Hal(ng Problem • In 1936 Alan Turing proved that it's not possible to decide whether an arbitrary program will eventually halt, or run forever. • The official defini(on of the problem is to write a program (actually, a Turing Machine*) that accepts as parameters a program and its parameters. That program needs to decide, in finite (me, whether that program will ever halt running these parameters. • The hal(ng problem is a cornerstone problem in computer science. It is used mainly as a way to prove a given task is impossible, by showing that solving that task will allow one to solve the hal(ng problem. *A Turing machine is a hypothe(cal device that manipulates symbols according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, Lecture 2: Computational Semantics 15
- 16. Representa(on • A sentence in first-‐order logic is wrifen in the form Px or P(x), where P is the predicate and x is the subject, represented as a variable. • Complete sentences are logically combined and manipulated according to the same rules as those used in Boolean algebra. Lecture 2: Computational Semantics 16
- 17. FOL’s machinery • Terms: – Constants – Func(ons – Variables • Logical connec(ves • Quan(fiers • Lambda nota(on Lecture 2: Computational Semantics 17
- 18. The Seman(cs of FOL • Truth table • Inference Lecture 2: Computational Semantics 18
- 19. Predicates and terms • John is a sailor sailor(j) • In FOL we can represent the informa(on conveyed by NL entences sta(ng that an object is a member of a certain set by means of a predicate such as ”sailor” (deno(ng a set of object), and a term such as J, deno(ng John. • The atomic formula sailor(j) expresses the statement. Lecture 2: Computational Semantics 19
- 20. Arity • Using predicates of higher arity, we can also assign a seman(c interpreta(on to sentences sta(ng that certain objects stand in certain rela(on: • John likes Mary like(j,m) Lecture 2: Computational Semantics 20
- 21. Universal quan(fier: ∀ • The seman(c interpreta(on of sentences asser(ng that a set is included in another can be expressed by means of a universal quan(fier ∀ Dogs are mammals ∀xdogxàmammals(x)! Lecture 2: Computational Semantics 21
- 22. Existen(al quan(fier: Ǝ • The existen(al quan(fier Ǝ can be used to capture the informa(on that a certain set is not empty, as epressed by the sentence: I have a car Ǝxcar(x)∧own(spkr,x)! Lecture 2: Computational Semantics 22
- 23. 3 Connec(ves: ∧∨¬ John and Mary are happy happy(j) ∧ happy(m) John is not married ¬married(j) In certain applica(ons, represen(ng this info is all we need (eg. enquiry system for train transporta(on: a person travelling from sta(on a) to sta(on b) Lecture 2: Computational Semantics 23
- 24. λ nota(on & λ reduc(on • It is a way to ”abstract” from FOL formulae • λ followed by one or more variables, followed by a FOL formula that makes use of these variables. • Basically: manipula(on and aggrega(on of variables. Lecture 2: Computational Semantics 24
- 25. Example: lambda expressions • λx.λy.Near(x,y) = something near something else • λx.λy.Near(x,y)(uppsala) – Reduc(on: λy.Near(uppsala,y) • λy.Near(uppsala,y) (stockholm) – Reduc(on: Near(uppsala,stockholm) • More: Sec(ons 17.3.3 and 18.3; see also hfps://files.nyu.edu/cb125/public/Lambda/ Lecture 2: Computational Semantics 25
- 26. Proof Theory • What makes FOL a logic is that it also includes a specifica(on of the valid conclusions that can be derived from the info. a) All trains depar(ng from Stockholm and arriving at Gävle stop at Uppsala b) Train 531 departs from S and arrives at G. c) Train 531 stops at U Lecture 2: Computational Semantics 26
- 27. Inference rules 1. ∀x(train(x)∧depart(x,S)arrive(x, G) à stop(x, U)! 2. train(t531)∧depart(t531),S)∧arrive(t531,G)! 3. stop(t531,U)! • An inference rule consists of a set of statements called premises and a statement called conclusion. The inference rule is a claim that if all premises are true, then the conclusion is true. Lecture 2: Computational Semantics 27
- 28. Ex: Modus ponens = if-‐then reasoning • It is an example of a valid inference rule: – If P is the case, and P à Q is the case, than Q is the case. Lecture 2: Computational Semantics 28
- 29. Cf. Proposi(onal logic (wikipedia) http://en.wikipedia.org/wiki/Aristotelian_logic • Syllogism and inference: – Men are mortal = A – Socrates is a man = B – Socrates is mortal = C Proposi(onal logic (also called senten(al logic) is the logic the includes sentence lefers (A,B,C) and logical connec(ves, but not quan$fiers. The seman(cs of proposi(onal logic uses truth assignments to the lefers to determine whether a compound proposi(onal sentence is true. The syllogism is an inference in which one proposi(on (the "conclusion") follows of necessity from two others (the "premises"). A proposi(on may be universal or par(cular, and it may be affirma(ve or nega(ve. Syntac(cally, first-‐order logic has the same connec(ves as proposi(onal logic, but it also has variables for individual objects, quan(fiers, symbols for func(ons, and symbols for rela(ons. The seman(cs include a domain of discourse for the variables and quan(fiers to range over, along with interpreta(ons of the rela(on and func(on symbols. Lecture 2: Computational Semantics 29
- 30. Many Logic-‐s • logic of sentences (proposi(onal logic), • logic of objects (predicate logic), • logic involving uncertain(es, • logic dealing with fuzziness, • temporal logic etc. Lecture 2: Computational Semantics 30
- 31. Prac(cal use Of Modus Ponens • Forward chaining – Top-‐down: As soon as a new fact is added to the knowledge base, all applicable rules are found and applied, each esul(ng n the addi(on of new facts to then KB. Drawback: facts that will never be needed are deduced and stored • Backward chaining: – Bofom up: run in reverse to prove specific proposi(ons are true (à PROLOG). • Both incomplete: – Ie, there valid inferences that cannot be found by systems that use these methods alone. Lecture 2: Computational Semantics 31
- 32. State and Event Representa(ons • States and events – States are condi(ons, or proper(es, that remain unchanged over a period of (me – Events denote changes in some state of affairs Lecture 2: Computational Semantics 32
- 33. Predicates • Predicates in FOL have fixed arity: they take a fixed number of arguments – predicates have a fixed arity Lecture 2: Computational Semantics 33
- 34. Possible solu(on • event variables à (neo) Davidsonian event representa(on Ǝe eating(e) ∧ eater(e, speaker)∧ eaten(e,turkey sandwich) ∧ meal(e,lunch) ∧ location(e,desk)∧time(e,tuesday)# • No need to specify a fixed number of arguments • The event itself is a single argument. • Everything else is captured by addi(onal predica(on Lecture 2: Computational Semantics 34
- 35. Descrip(on Logics • DLs refer to a family of logical approaches that corrispond to different subsets of FOL. • We can use DLs to model an applica(on domain. The focus is then on: – Representa(on of knowledge about categories – The set of categories in an applica(on domain is called terminology – The terminology is arranged in a hierachical organiza(on called ontology, which capture superset & subset rela(ons among categoires/ concepts. – In order to specify a hierachical structure, we can use subsump$on rela(ons betw the appropriate concepts in a terminiology – Subsump$on is a form of inference. Determines whether a suprset/ subset rela(on (based on the fact asserted in a terminology) exists betw two concepts. Lecture 2: Computational Semantics 35
- 36. OWL and the Seman(c Web • A Descrip(on Logic roughly similar to the previous example is used in the Web Ontology Language (OWL). • OWL is a language used for the develoment of ontologies that should encapsulate the knowledge in the development of the Seman(c Web • The Seman(c Web is the effort to formally specify the seman(cs of the contents of the web . à lect 9 Lecture 2: Computational Semantics 36
- 37. Seman(c web (wikipedia) hfp://en.wikipedia.org/wiki/Seman(c_Web • The Seman(c Web is a collabora(ve movement led by interna(onal standards body the World Wide Web Consor(um (W3C). • By encouraging the inclusion of seman(c content in web pages, the Seman(c Web aims at conver(ng the current web, dominated by unstructured and semi-‐structured documents into a "web of data". • Web 3.0 – Tim Berners-‐Lee has described the seman(c web as a component of "Web 3.0". – "Seman(c Web" is some(mes used as a synonym for "Web 3.0", though each term's defini(on varies. Lecture 2: Computational Semantics 37
- 38. TECHNIQUES FOR ASSIGNING MEANINGS TO LINGUISTIC INPUT J&M -‐ Ch 18 see also Saeed, Ch 10: Formal se Lecture 2: Computational Semantics 38
- 39. Syntax-‐Driven Seman(c Analysis • : Meaning representa(ons are assigned to sentences on the basis of knowledge taken from the lexicon and grammar Lecture 2: Computational Semantics 39
- 40. Principle of Composi(onality • PoC: the meaning of a sentence can be constructed from the meaning of its parts. • Watch out! the meaning of a sentence is not based only on the words that make it up, but also on the ordering and grouping of words and on the rela(ons among the words in the sentence. • Basically, the meaning of a sentence is par(ally based on its syntac(c structure. Lecture 2: Computational Semantics 40
- 41. The rule-‐to-‐rule hypothesis • we do not define languages by enumera(ng the meanings that are permifed. • But we define a finite set of devices that generate the correct meaning for the context. • These devices are based on grammar rules and lexical entries. Lecture 2: Computational Semantics 41
- 42. Two constrained approaches 1. The first is based on FOL and lambda-‐ nota(on. 2. The second is based on feature-‐structure and unifica(on Lecture 2: Computational Semantics 42
- 43. 1: FOL • Every restaurant has a menu, 2 meanings: – All restaurants have a menu – There is a menu in the world and all the restarrants share it Lecture 2: Computational Semantics 43
- 44. 1. Quan(fier scope ambiguity • Expressions containing quan(fiers can create ambiguity even if there is no syntac(c, lexical or analphoric ambiguity. Lecture 2: Computational Semantics 44
- 45. Underspecifica(on and storage • The restaurant fills the haver role and the menu fills the had role. • it remain agnos(c about the placement of the quan(fies Lecture 2: Computational Semantics 45 We use λ-‐expressions and a store. The quan(fied expressions are in the form of λ-‐‑expressions thant can be combined with the core representaton in the right way. We have access to the quan(fier via the index. See Section 18.3
- 46. Drawback • fail to generated all the possible ambiguous representatons arising from the quan(fier scope ambigui(es. àunderspecifica(on = Including all possible readings without enumera(ng them (probabili(es?) Lecture 2: Computational Semantics 46
- 47. Idioms and Composi(onality (Sect 18.6) • What kind of meaning representa(on do we need for idioms? • The (p of the iceberg à flexible – iceberg’s (p – (p of an iceberg – (p of a rather large iceberg – (p of a larger iceberg • Kick the bucket à crystallized Lecture 2: Computational Semantics 47
- 48. CORPUS-‐BASED APPROACHES AND MACHINE LEARNING Lecture 2: Computational Semantics 48
- 49. Latent Seman(c Analysis (wikipedia) http://en.wikipedia.org/wiki/Latent_semantic_analysis • Latent seman(c analysis (LSA) is a technique of analyzing rela(onships between a set of documents and the terms they contain by producing a set of concepts related to the documents and terms. • LSA assumes that words that are close in meaning will occur in similar pieces of text. • A matrix containing word counts per paragraph is constructed from a large piece of text and a mathema(cal technique called singular value decomposi(on (SVD) is used to reduce the number of rows while preserving the similarity structure among columns. • Words are then compared . Values close to 1 represent very similar words while values close to 0 represent very dissimilar words.” Applica$ons and Limita$ons… Lecture 2: Computational Semantics 49
- 50. Topic Models (wikipedia) http://en.wikipedia.org/wiki/Topic_model ” a topic model is a type of sta(s(cal model for discovering the abstract "topics" that occur in a collec(on of documents. Intui(vely, given that a document is about a par(cular topic, one would expect par(cular words to appear in the document more or less frequently: "dog" and "bone" will appear more oWen in documents about dogs, "cat" and "meow" will appear in documents about cats, and "the" and "is" will appear equally in both. A document typically concerns mul(ple topics in different propor(ons; thus, in a document that is 10% about cats and 90% about dogs, there would probably be about 9 (mes more dog words than cat words. A topic model captures this intui(on in a mathema(cal framework, which allows examining a set of documents and discovering, based on the sta(s(cs of the words in each, what the topics might be and what each document's balance of topics is.” Latent Dirilecht Alloca$on (LDA) Lecture 2: Computational Semantics 50
- 51. Distribu(onal Seman(cs (wikipedia) http://en.wikipedia.org/wiki/Distributional_semantics ”Distribu$onal seman$cs is a research area that develops and studies theories and methods for quan(fying and categorizing seman(c similari(es between linguis(c items based on their distribu(onal proper(es in large samples of language data. The basic idea of distribu(onal seman(cs can be summed up in the so-‐called Distribu(onal hypothesis: linguis&c items with similar distribu&ons have similar meanings” Applica$ons and Limita$ons… Lecture 2: Computational Semantics 51
- 52. SemEval (wikipedia) http://en.wikipedia.org/wiki/SemEval • SemEval (Seman(c Evalua(on) is an ongoing series of evalua(ons of computa(onal seman(c analysis systems; it evolved from the Senseval word sense evalua(on series. The evalua(ons are intended to explore the nature of meaning in language. While meaning is intui(ve to humans, transferring those intui(ons to computa(onal analysis has proved elusive.This series of evalua(ons is providing a mechanism to characterize in more precise terms exactly what is necessary to compute in meaning. As such, the evalua(ons provide an emergent mechanism to iden(fy the problems and solu(ons for computa(ons with meaning. These exercises have evolved to ar(culate more of the dimensions that are involved in our use of language. They began with apparently simple afempts to iden(fy word senses computa(onally. They have evolved to inves(gate the interrela(onships among the elements in a sentence (e.g., seman(c role labeling), rela(ons between sentences (e.g., coreference), and the nature of what we are saying (seman(c rela(ons and sen(ment analysis). Lecture 2: Computational Semantics 52
- 53. In this course… • We are not going to focus on formalisms or on corpus-‐based approaches to seman(cs. We will focus some specific aspects of meaning that are useful for NLP and IR applica(ons, namely… Lecture 2: Computational Semantics 53
- 54. The End Lecture 2: Computational Semantics 54