Fractal Adaptive Moving Average (FrAMA) - MetaTrader 5のためのインディケータ

Fractal Adaptive Moving Average (FRAMA) は John Ehlers氏によって開発されました。

指数移動平均が現在のフラクタル次元に基づいて計算され、このインジケーターでは、その指数移動平均のアルゴリズムに基づいて構築されています。FRAMAには、強いトレンドの動きに従い、価格の動きが緩やかになるときに十分に速度を落とす優位性があります。

移動平均に使われるすべての分析方法は、このインジケーターにも適応可能です。

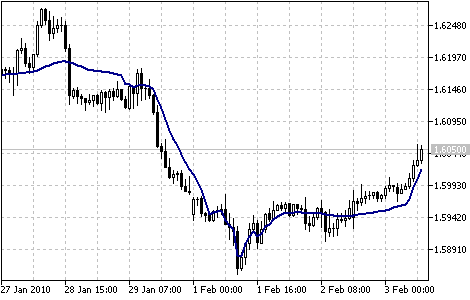
Fractal Adaptive Moving Average Indicator

計算:

ただし:

• FRAMA(i) - FRAMAの現在値;
• Price(i) - 現在の価格;
• FRAMA(i-1) - ひとつ前のFRAMAの値;
• A(i) - 指数平滑の現在要素

指数平滑要素は下記の公式から計算されます。:

ただし:

• D(i) - 現在のフラクタル次元;
• EXP() - 指数関数

直線のフラクタル次元は1D = 1の場合、 A = EXP(-4.6 *(1-1)) = EXP(0) = 1よりよって、価格変化が直線の場合、下記の式により、指数平滑は適応されない。:

つまり、このインジケーターは厳密に価格にしたがう。

平面のフラクタル次元は2D = 2の場合、スムージング要素は A = EXP(-4.6*(2-1)) = EXP(-4.6) = 0.01よりこのような小さな指数平滑要素は、価格が強いノコギリ状の動きをしたとき、瞬間的に得られる。強い減速は、200単純移動平均線に近似される。

フラクタル次元の公式:

これは次の追加公式によって計算される:

ただし:

• HighestPrice(i) - 長期期間の最高値;
• LowestPrice(i) - 長期間の最安値;

N1、N2、 N3 は、それぞれ下記の通り: