MetaTrader 5
Experts
Indicateurs
Scripts
Bibliothèque
StockageMoyenne Mobile Fractale Adaptative - Fractal Adaptive Moving Average (FrAMA) - indicateur pour MetaTrader 5
L'indicateur technique Fractal Adaptive Moving Average (FRAMA) a été développé par John Ehlers.
Cet indicateur est construit sur la base de l'algorithme de la Moyenne mobile exponentielle, dans laquelle le facteur de lissage est calculé en fonction de la dimension fractale actuelle de la série de prix. L'avantage de la FRAMA est la possibilité de suivre de forts mouvements de tendance et de ralentir suffisamment aux moments de consolidation des prix.
Tous les types d'analyse utilisés pour les moyennes mobiles peuvent être appliqués à cet indicateur.
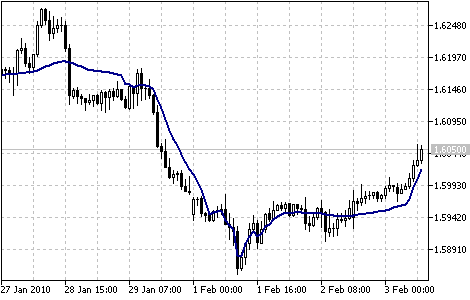
Indicateur de moyenne mobile adaptative fractale
Calcul :
FRAMA(i) = A(i) * Price(i) + (1 - A(i)) * FRAMA(i-1)
avec :
- FRAMA(i) - valeur actuelle de FRAMA ;
- Price(i) - prix actuel ;
- FRAMA(i-1) - valeur précédente de FRAMA ;
- A(i) - facteur actuel de lissage exponentiel.
Le facteur de lissage exponentiel est calculé selon la formule ci-dessous :
A(i) = EXP(-4.6 * (D(i) - 1))
avec :
- D(i) - dimension fractale actuelle ;
- EXP() - fonction mathématique de l'exposant.
La dimension fractale d'une ligne droite est égale à un. Il ressort de la formule que si D = 1, alors A = EXP(-4,6 *(1-1)) = EXP(0) = 1. Ainsi, si le prix change en lignes droites, le lissage exponentiel n'est pas utilisé, car dans un tel cas la formule ressemble à ceci :
FRAMA(i) = 1 * Price(i) + (1 - i) * FRAMA(i-1) = Price(i)
C'est à dire. l'indicateur suit exactement le prix.
La dimension fractale d'un plan est égale à deux. De la formule, nous obtenons que si D = 2, alors le facteur de lissage A = EXP(-4,6*(2-1)) = EXP(-4,6) = 0,01. Une si petite valeur du facteur de lissage exponentiel est obtenue aux moments où le prix effectue un fort mouvement en dents de scie. Un tel ralentissement correspond à une moyenne mobile simple d'environ 200 périodes.
Formule de dimension fractale :
D = (LOG(N1 + N2) - LOG(N3))/LOG(2)
Il est calculé sur la base de la formule supplémentaire :
N(Length,i) = (HighestPrice(i) - LowestPrice(i))/Length
avec :
- HighestPrice(i) - valeur maximale actuelle pour les périodes de longueur ;
- LowestPrice(i) - valeur minimale actuelle pour les périodes de longueur ;
Les valeurs N1, N2 et N3 sont respectivement égales à :
N1(i) = N(Length,i)
N2(i) = N(Length,i + Length)
N3(i) = N(2 * Length,i)
Traduit de l’anglais par MetaQuotes Ltd.
Code original : https://www.mql5.com/en/code/72