A Practical Walkthrough of Min-Max Scaling

Author(s): Amna Sabahat

Originally published on Towards AI.

In our previous discussion, we established why normalization is crucial for achieving success in machine learning. We saw how unscaled data can severely impact both distance-based and gradient-based algorithms.

Now, let’s get practical: How do we actually implement normalization, and which technique should you choose?

This article provides a comprehensive, hands-on guide to Min-Max Scaling one of the most fundamental normalization techniques. We’ll cover:

• The mathematical foundation of Min-Max Scaling
• When to use it (and when to avoid it)
• Step-by-step implementation with scikit-learn
• Proper handling of training and test data
• Visual demonstrations of the transformation

By the end, you’ll have a practical understanding of how to implement Min-Max Scaling in your own projects.

Understanding Min-Max Scaling:

Min-Max Scaling (often called Normalization) transforms features by rescaling their range to a predefined scale, typically between 0 and 1.

The core idea is simple: make the minimum value 0, the maximum value 1, and distribute all other values proportionally between them.

Mathematically

The transformation formula is:
x_norm = (x - x_min) / (x_max - x_min)

Where x = original value in the feature, x_min = minimum value in the feature,x_max = maximum value x_norm = normalized value between 0 and 1

What it does:

• Shifts the data so the minimum value becomes 0.
• Scales the data so the maximum value becomes 1.
• All other values are distributed between 0 and 1.

For Custom Range [a, b]

You can also scale the data to any arbitrary range [a, b] using this generalized formula:

where a,b are the min-max values.

For example, scaling to the range [-1, 1] is a common alternative.

When to Use Min-Max Scaling?

1. Puts Features on a Common Scale: This is the primary reason. Algorithms that rely on distance calculations between data points are particularly sensitive to feature scales. Examples include:

• K-Nearest Neighbors (KNN): Uses Euclidean distance. A feature with a larger scale would dominate the distance calculation.
• K-Means Clustering: Relies on the distance to centroids.
• Support Vector Machines (SVMs): Uses distance to define the margin.
• Principal Component Analysis (PCA): Aims to find directions of maximum variance, which are biased towards high-variance (often high-scale) features.

2. Improves Algorithm Convergence Speed: For algorithms that use gradient descent for optimization (like Linear Regression, Logistic Regression, and Neural Networks), scaled features help the model converge to the minimum loss much faster.

Imagine gradient descent trying to navigate a ravine; unscaled features create a long, narrow valley, while scaled features create a more spherical contour, allowing for a more direct path to the solution.

3. Intuitive Interpretation: After Min-Max Scaling, the value of a feature can be interpreted as its relative position within the original range. A value of 0.8 is very close to the maximum observed value.

When Should You Avoid Min-Max Scaling?

No technique is a silver bullet, and Min-Max Scaling is no exception. It’s crucial to understand its weaknesses.

1. Sensitive to Outliers: This is its biggest drawback. The formula depends entirely on Xmin​ and Xmax​. If your dataset has a single extreme outlier (e.g., a height of 250 cm in our previous example), the range will be stretched from 40 to 100. This will compress all the other “normal” data points into a very narrow range (e.g., 150 would be 0, 190 would become 190−150 / 100= 40 / 100 ​=0.4), losing a lot of the variance in the original data.
2. Produces a Fixed Range (0 to 1): The resulting data distribution is bounded. This can be a problem for algorithms that assume a Gaussian (normal) distribution of data, as Min-Max Scaling does not change the shape of the distribution.
3. Not Robust: Unlike other scalers like StandardScaler (which uses mean and standard deviation), Min-Max Scaling does not handle outliers robustly. A single outlier can distort the entire transformation.

Use Min-Max Scaling when you know your data doesn’t follow a Gaussian distribution or when you need a bounded range.

Min-Max Scaling vs. StandardScaler: A Quick Comparison

(While StandardScaler deserves its own deep dive, here’s a quick comparison)

We’ll explore StandardScaler in detail in our next article!

Practical Implementation: Min-Max Scaling in Action

Let’s implement Min-Max Scaling with a realistic multi-feature dataset using scikit-learn.

Sample Dataset with 3 Features

Consider a dataset of individuals with the following features:

• Age: Ranges from 25 to 75 years
• Salary: Ranges from 40,000 to 230,000 dollars
• Experience: Ranges from 1 to 23 years

Using scikit-learn’s MinMaxScaler (Recommended for Real Projects)

import numpy as np
from sklearn.preprocessing import MinMaxScaler

# Create sample data with 3 features: Age, Salary, Experience
data = np.array([
 [25, 40000, 1], 
 [35, 60000, 5], 
 [45, 80000, 10], 
 [55, 100000, 15], 
 [65, 120000, 20],
 [75, 230000, 23]
])

print("Original Data:")
print("Age Salary Experience")
print("-" * 25)
for row in data:
 print(f"{row[0]:<6} {row[1]:<7} {row[2]:<10}")
 
print(f"\nFeature ranges:")
print(f"Age: {data[:, 0].min()} - {data[:, 0].max()}")
print(f"Salary: {data[:, 1].min()} - {data[:, 1].max()}")
print(f"Experience: {data[:, 2].min()} - {data[:, 2].max()}")

Notice the dramatic scale differences! Salary ranges in hundreds of thousands while Experience is in single digits. This would cripple distance-based algorithms.

Applying Min-Max Scaling

# Create and fit the scaler on our training data
scaler = MinMaxScaler()
scaled_data = scaler.fit_transform(data)

print("\nScaled Data (0 to 1 range):")
print("Age Salary Experience")
print("-" * 35)
for row in scaled_data:
 print(f"{row[0]:<8.3f} {row[1]:<9.3f} {row[2]:<10.3f}")

print(f"\nScaler learned parameters:")
print(f"Data min: {scaler.data_min_}")
print(f"Data max: {scaler.data_max_}")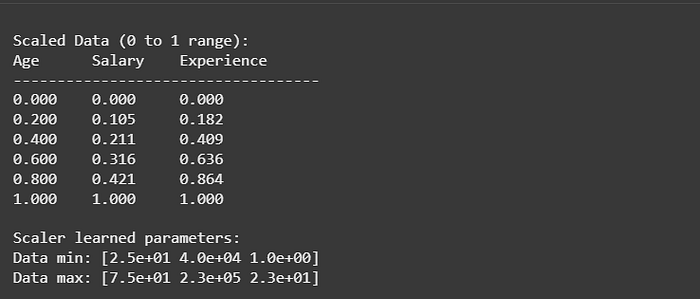

Critical: Proper Data Splitting Strategy

⚠️ Important Note: Always fit your scaler only on training data and use the same scaler to transform validation/test data

# Correct approach for new data
new_people = np.array([
 [30, 50000, 3], 
 [50, 90000, 12],
 [60, 100000, 13],
 [70, 110000, 14],
 [80, 130000, 15],
 [90, 150000, 19]
])

# Use the SAME scaler fitted on original training data
new_scaled = scaler.transform(new_people) # NOT fit_transform!

print("New unscaled data:")
print(new_people)
print("\nNew data scaled using ORIGINAL parameters:")
print(new_scaled)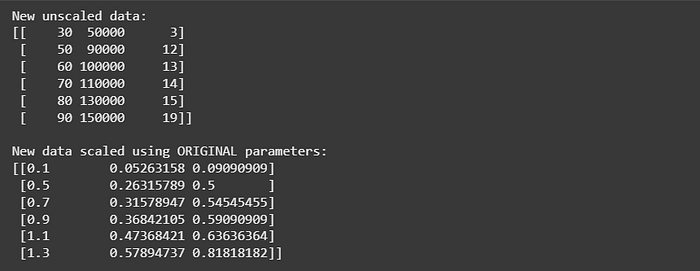

Notice some values exceed 1.0! This is expected and correct new data can fall outside the original training range.

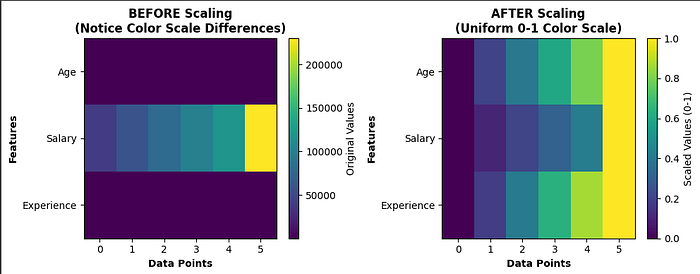
How Min-Max Scaling Transforms Your Data

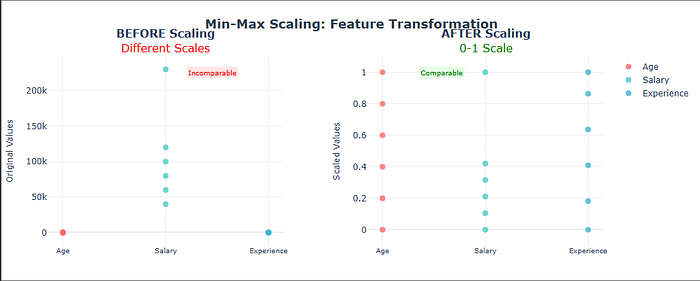
Notice how the color scales differ dramatically in the original data (left), making features incomparable.

After scaling (right), all features share the same 0–1 color scale, creating a level playing field for machine learning algorithms.

Conclusion

Throughout this practical walkthrough, we’ve seen how Min-Max Scaling solves a fundamental data preprocessing challenge: transforming features with incompatible units into a unified 0–1 scale that machine learning algorithms can properly interpret.

When to Reach for Min-Max Scaling:

• Your data has minimal outliers
• You need bounded output ranges
• Working with distance-based algorithms
• Dealing with non-Gaussian distributed data

While not a universal solution, Min-Max Scaling demonstrates how sometimes the simplest preprocessing steps, getting all your features to speak the same numerical language, deliver the most significant improvements in model performance.

In our next article, we’ll explore StandardScaler and when it might be a better choice for your specific dataset. Happy scaling!

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI