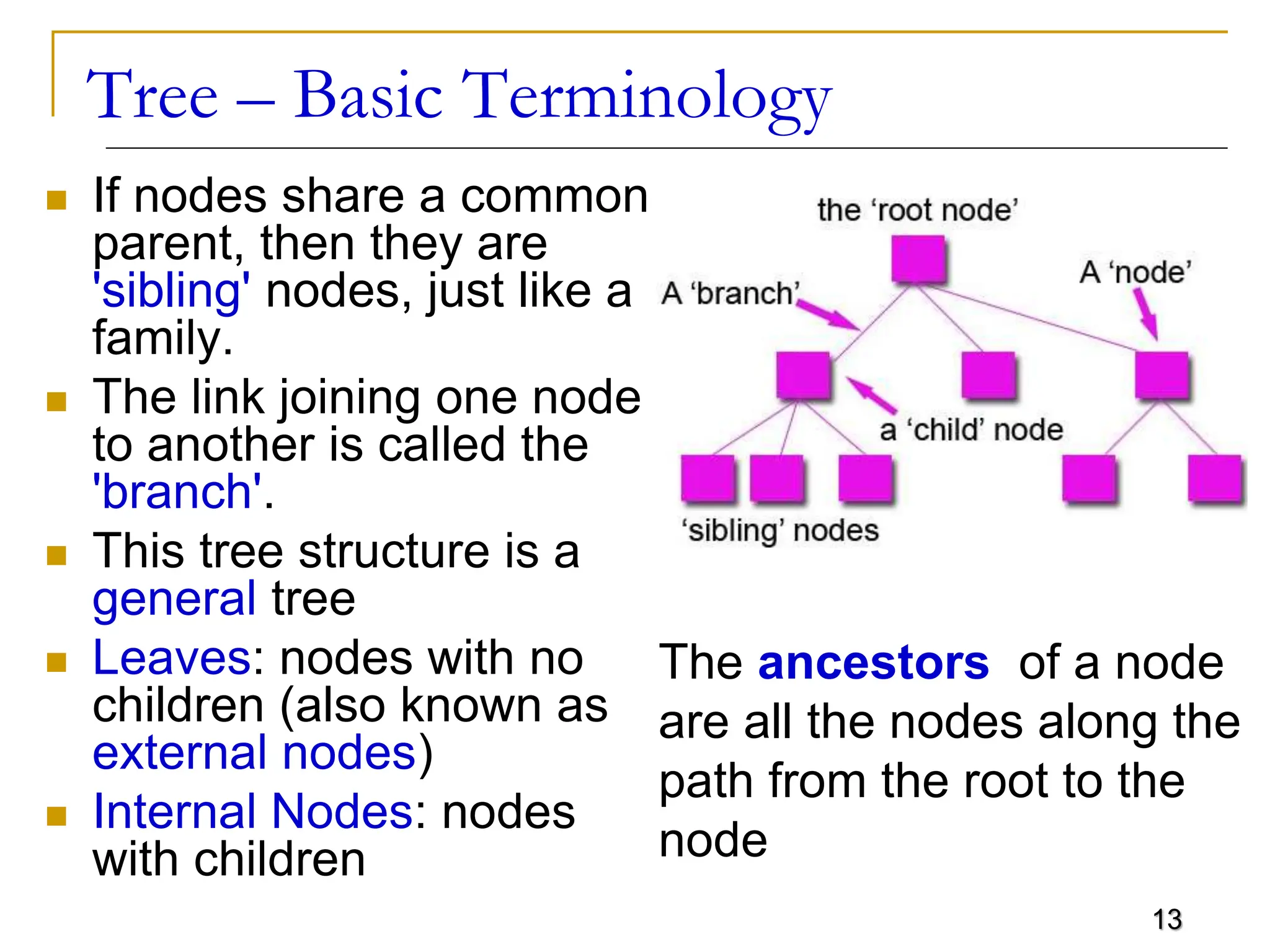
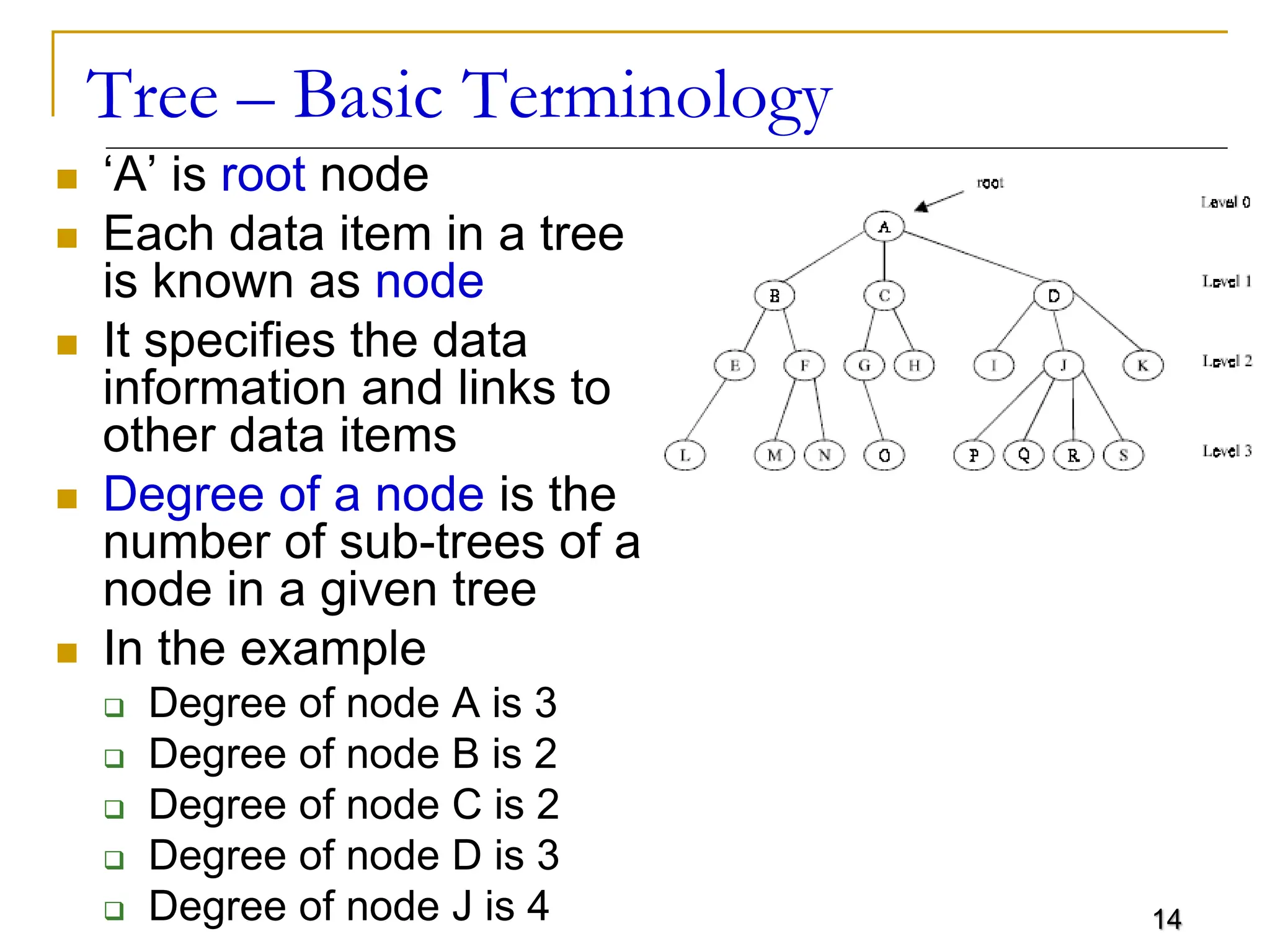
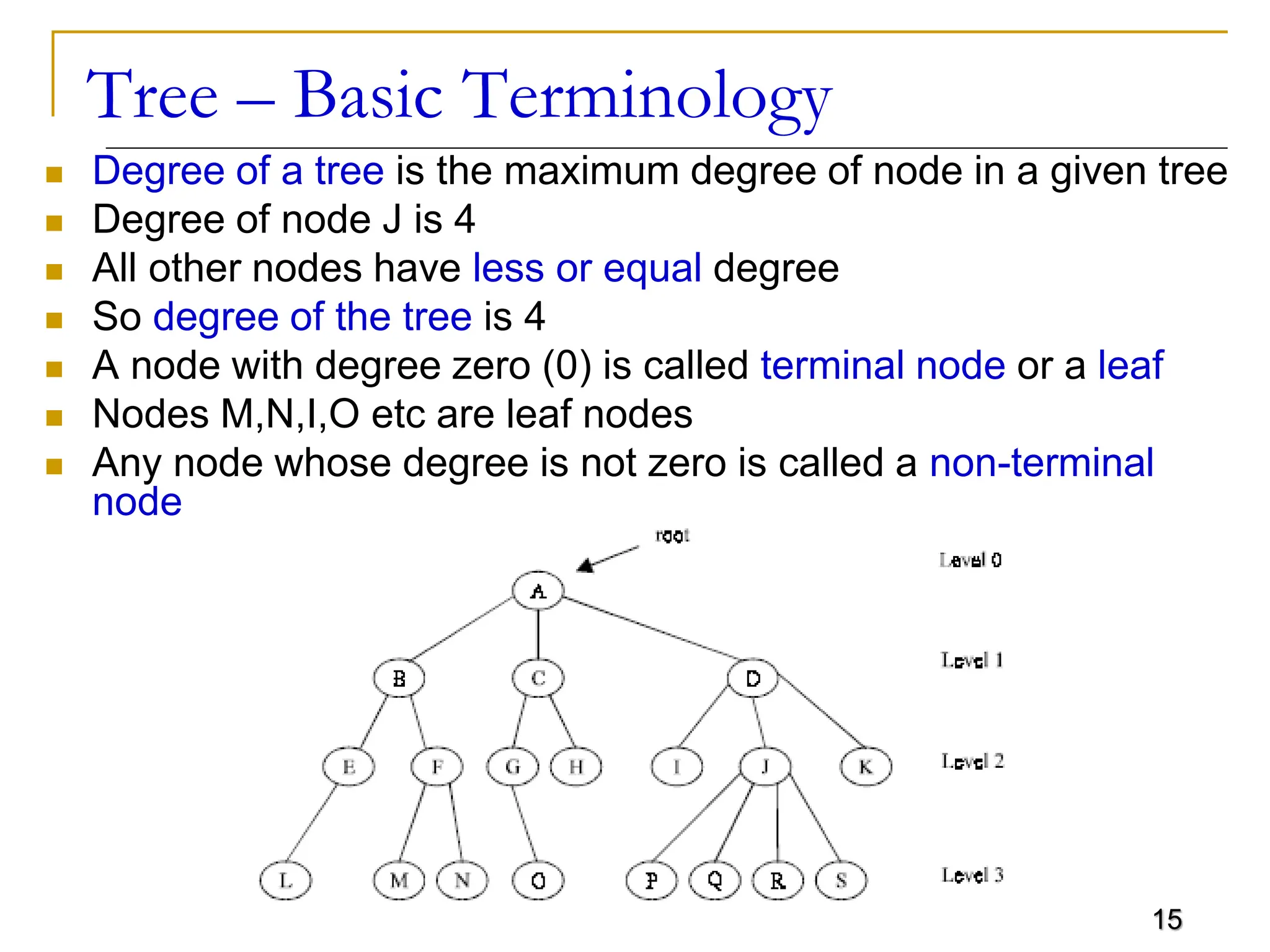
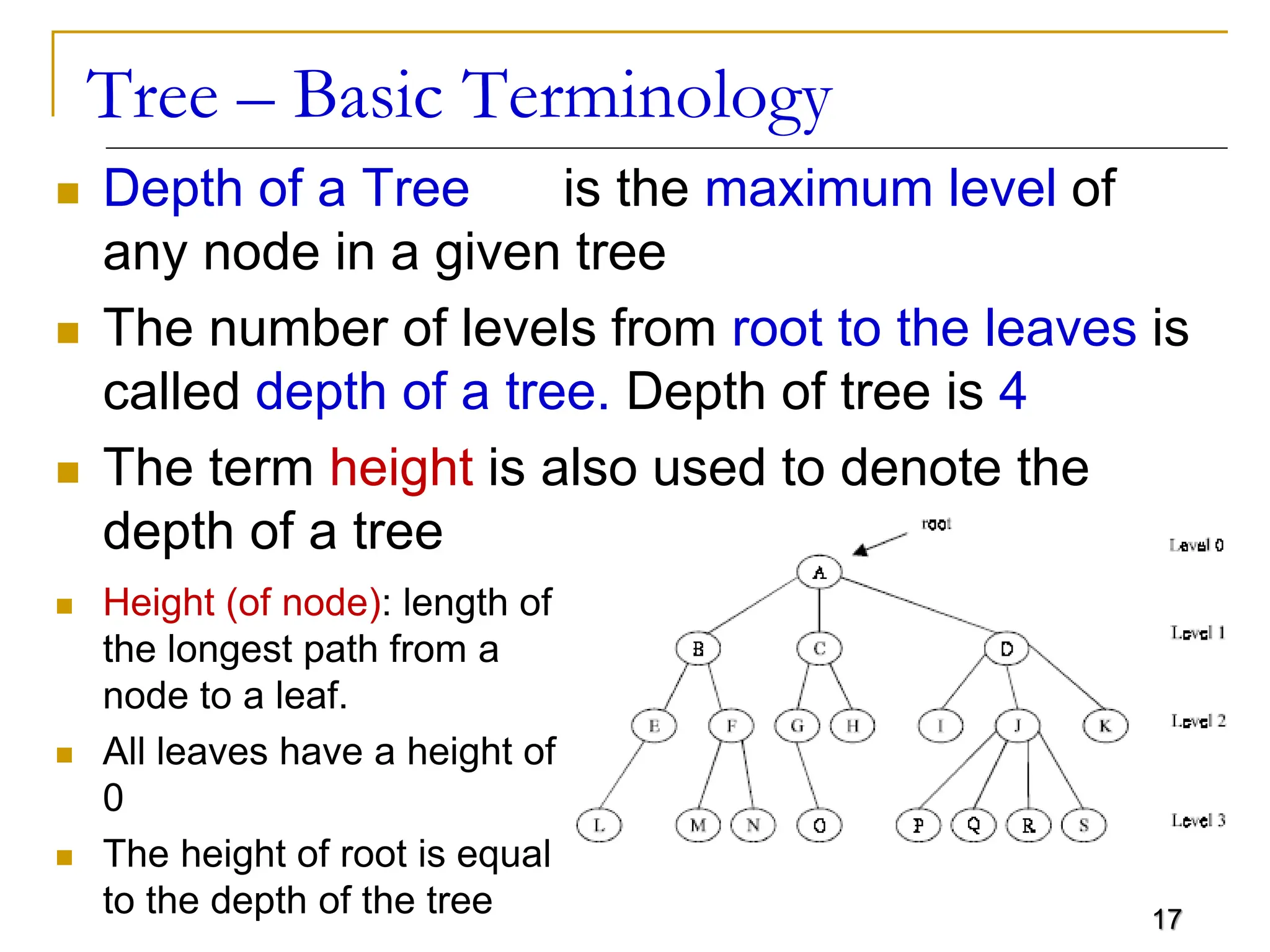
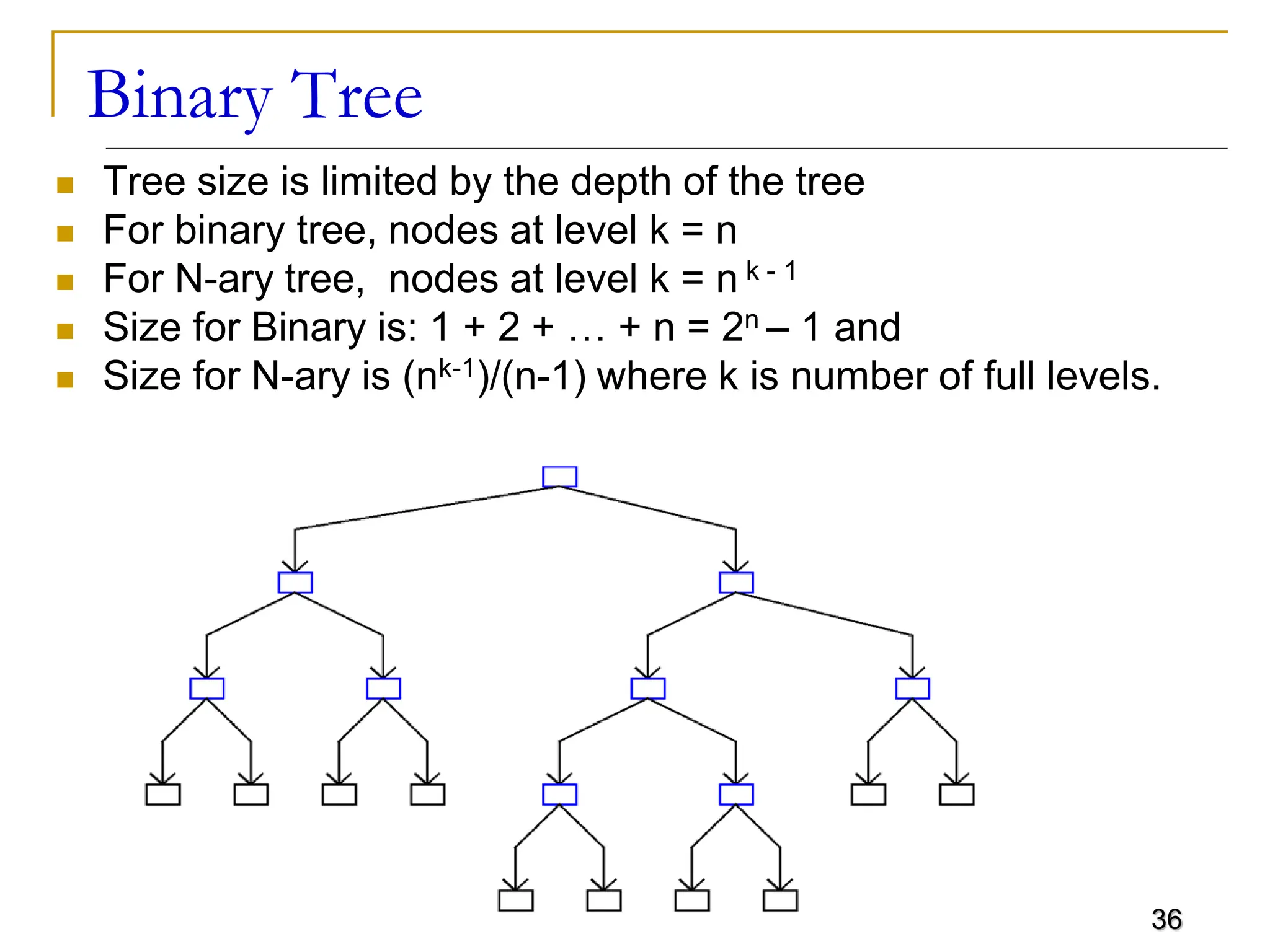
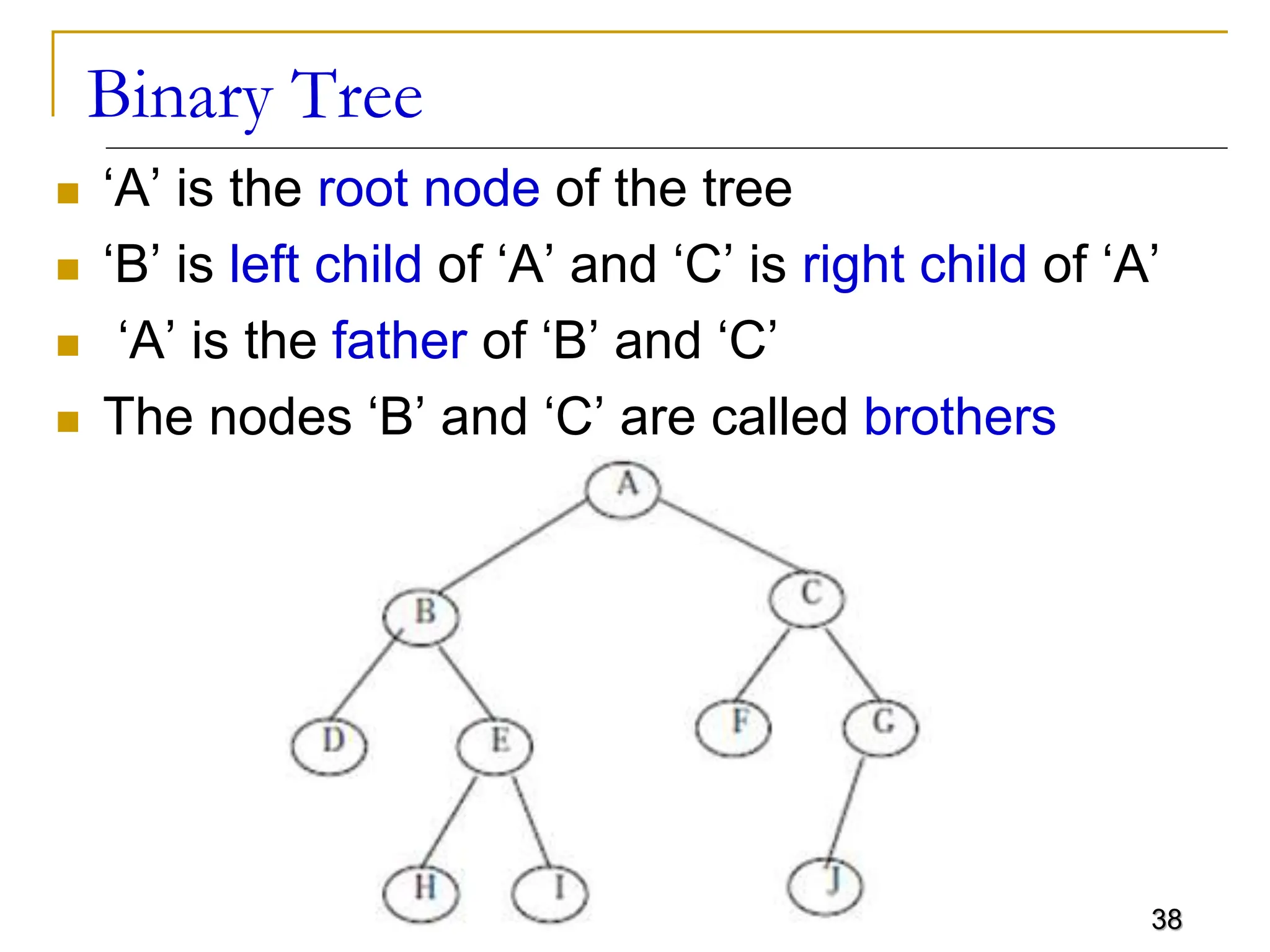
The document discusses trees as a flexible, non-linear data structure used for representing hierarchical relationships. It covers definitions, terminology, types of trees, and their applications in various fields including artificial intelligence and file organization. Additionally, it describes tree traversal methods and implementations, particularly focusing on binary trees.

























![44 Sequential Representation A B -- C -- -- -- D -- . E [1] [2] [3] [4] [5] [6] [7] [8] [9] . [16] A B E C D [1] [2] [3] [4] [5] [6] [7] [8] [9] A B C D E F G H I A B C G E I D H F (1) waste space (2) insertion/deletion problem](https://image.slidesharecdn.com/tree-240605075717-c47a9359/75/Tree-Data-Structure-Tree-Data-Structure-Details-44-2048.jpg)

