Binary Heap Tree, Data Structure

Binary Heap Tree, Data Structure

• 1.
  HEAP Anand Ingle Data Structure
• 2.
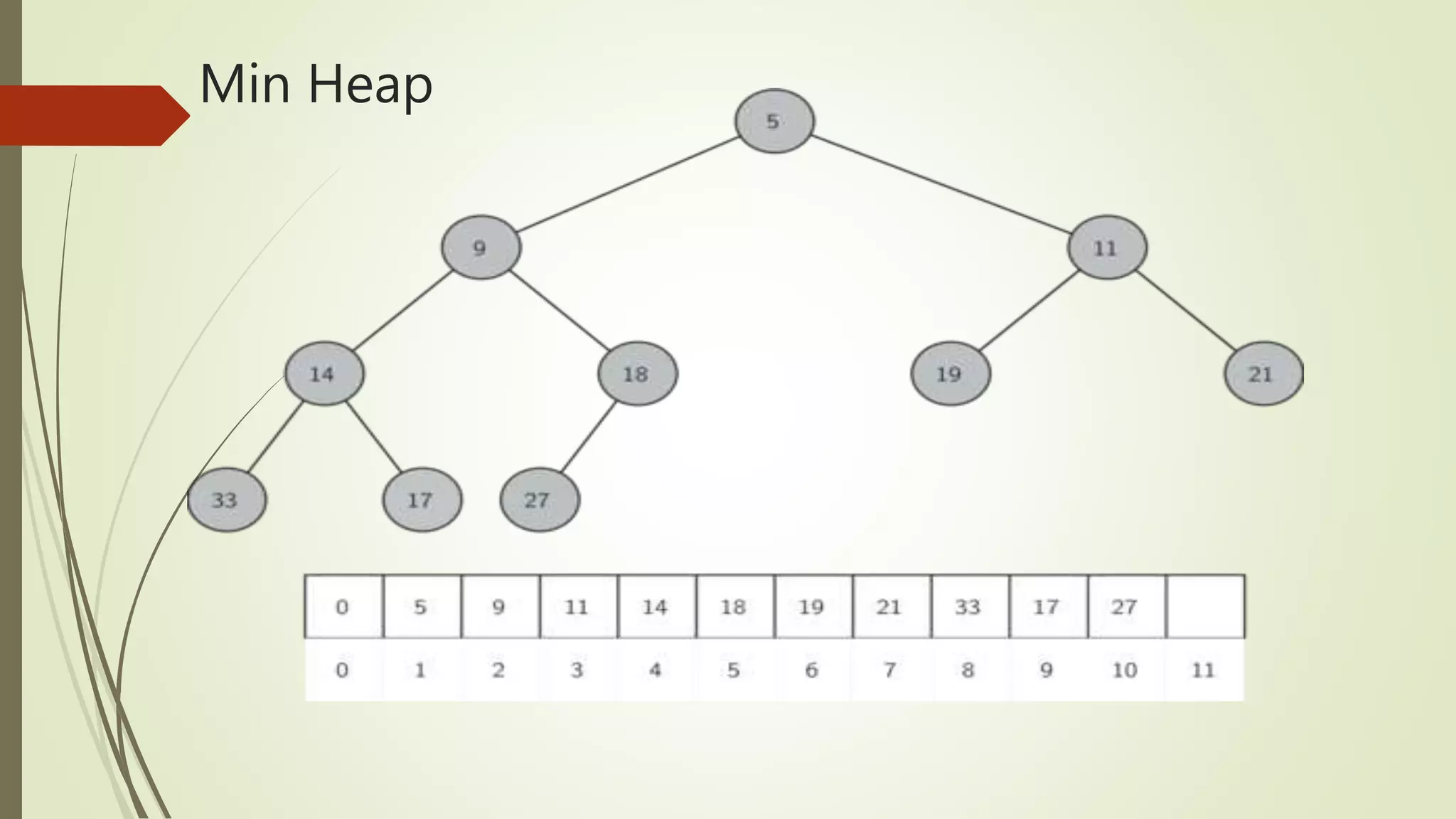
   Definition inData structure :  Heap: A special form of complete binary tree that key value of each node is no smaller or larger than the key value of its children (if any).  Types of Heap:-  Max-Heap: root node has the largest value.  Min-Heap : root node has the smallest value  What is complete Binary Tree:  A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
• 3.
  Max Heap
• 4.
  Min Heap
• 5.
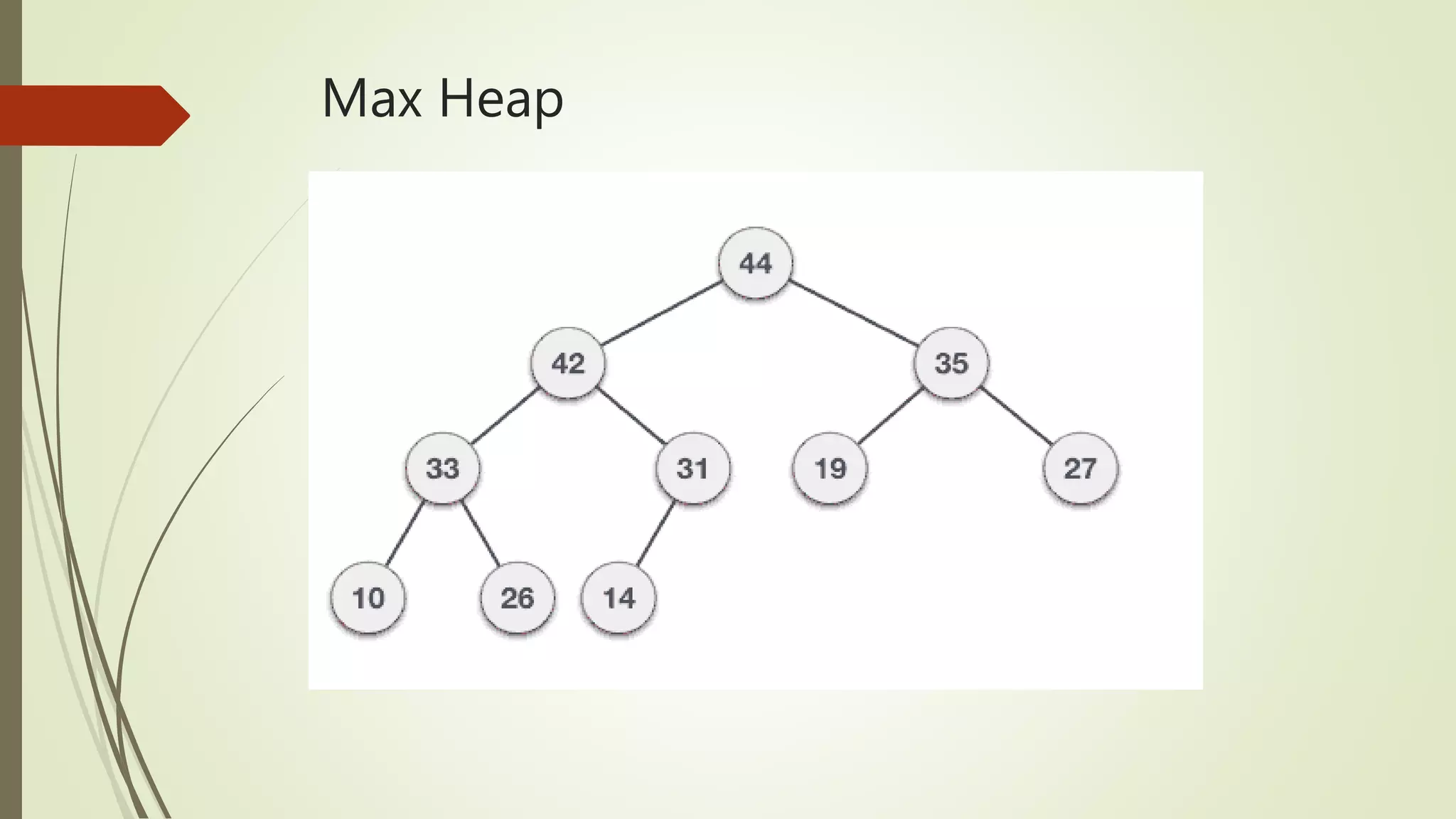
   How isHeap represented?  A Heap is a Complete Binary Tree.  A heap is typically represented as array.  Representation of Heap: The root element will be at Arr[0]. Below table shows indexes of other nodes for the ith node, i.e., Arr[i]: Arr[i/2] Returns the parent node Arr[(2*i)+1] Returns the left child node Arr[(2*i)+2] Returns the right child node
• 6.
  9 6 34 5 -1 -3 1 0 -7 0 1 2 3 4 5 6 7 8 9
• 7.
  Min Heap
• 8.
   Operations onHeap:  create-heap: create an empty heap  heapify: create a heap out of given array of elements  find-max or find-min: find a maximum item of a max-heap, or a minimum item of a min-heap  insert: adding a new key to the heap  delete-max or delete-min: removing the root node of a max- or min-heap, respectively  size: return the number of items in the heap.  merge (union): joining two heaps to form a valid new heap containing all the elements of both, preserving the original heaps
• 9.
  Application of Heap Heapsort: One of the best sorting methods being in-place and with no quadratic worst-case scenarios.  Finding the min, max, both the min and max, median, or even the k-th largest element can be done in linear time using heaps.  Priority Queue:: Priority queues can be efficiently implemented using Binary Heap because it supports insert(), delete() and extractmax(), decreaseKey() operations in O(logn) time.  Graph algorithms like Prim’s Algorithm and Dijkstra’s algorithm.
• 10.
  Thank you.......