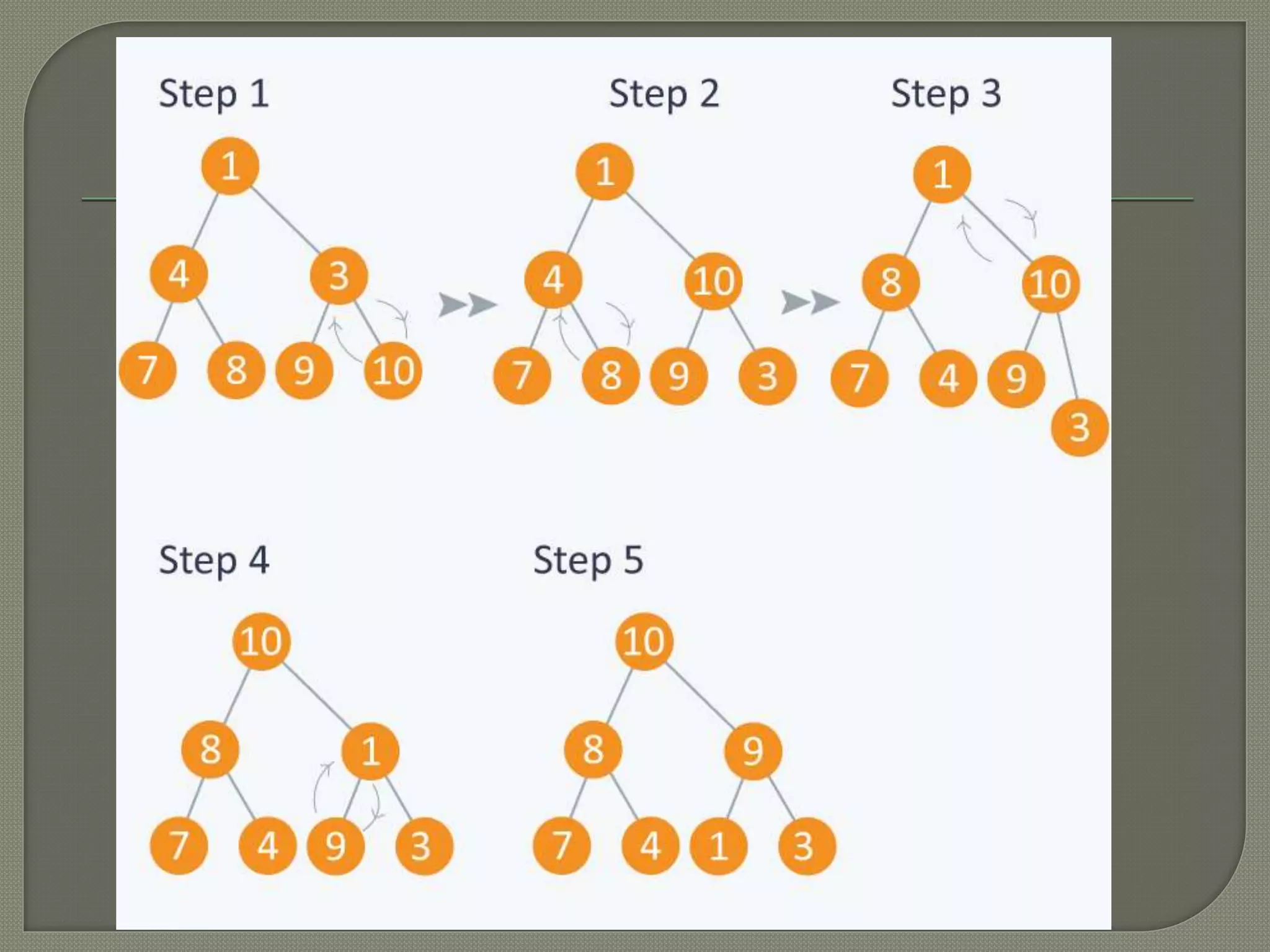
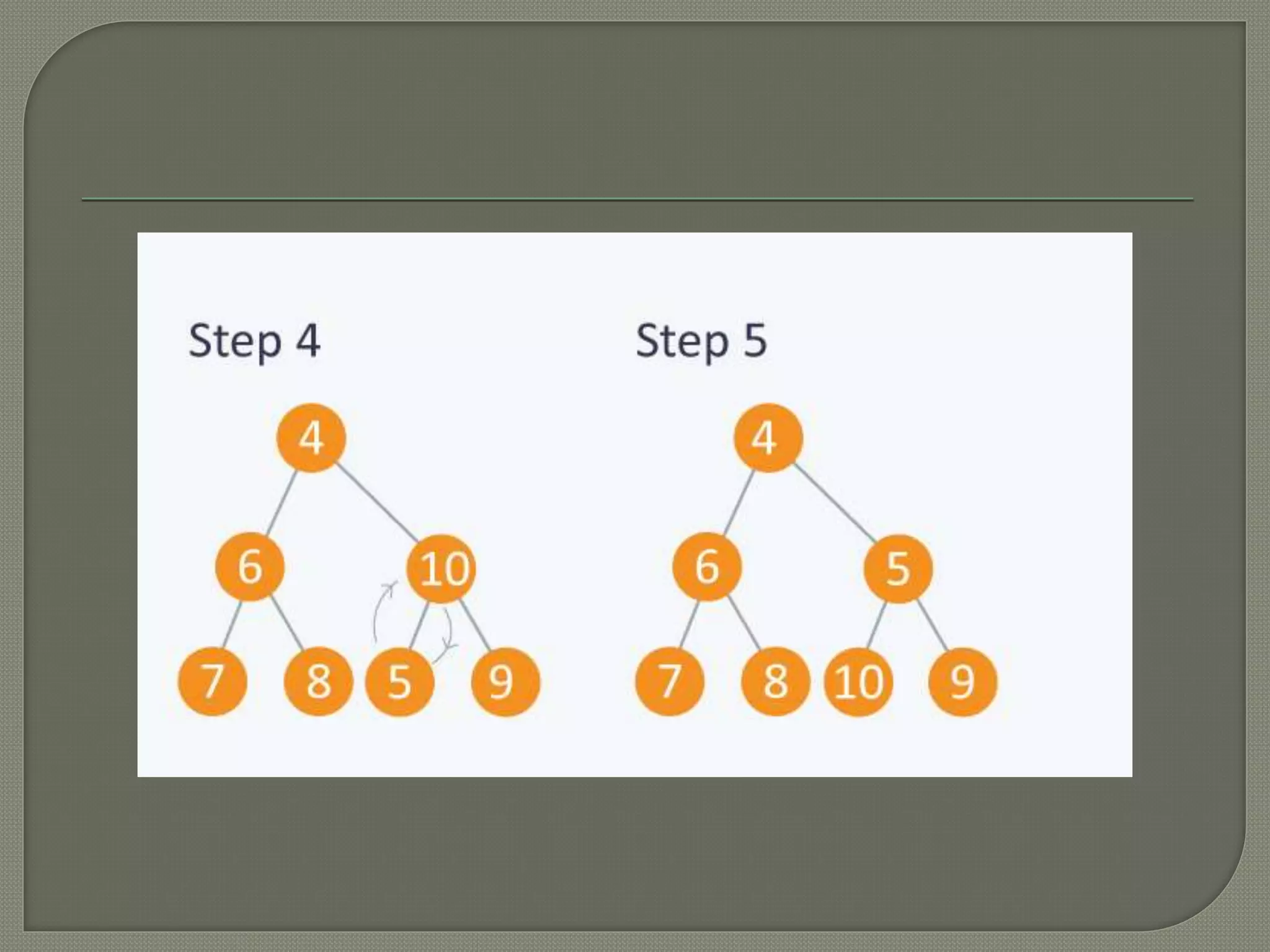
The document discusses heap data structures, which are complete binary trees that can be classified into max-heaps and min-heaps based on their node value properties. It describes the array representation of heaps, including the construction process and insertion algorithms for nodes. Heaps are also highlighted for their applications in sorting and implementing priority queues.



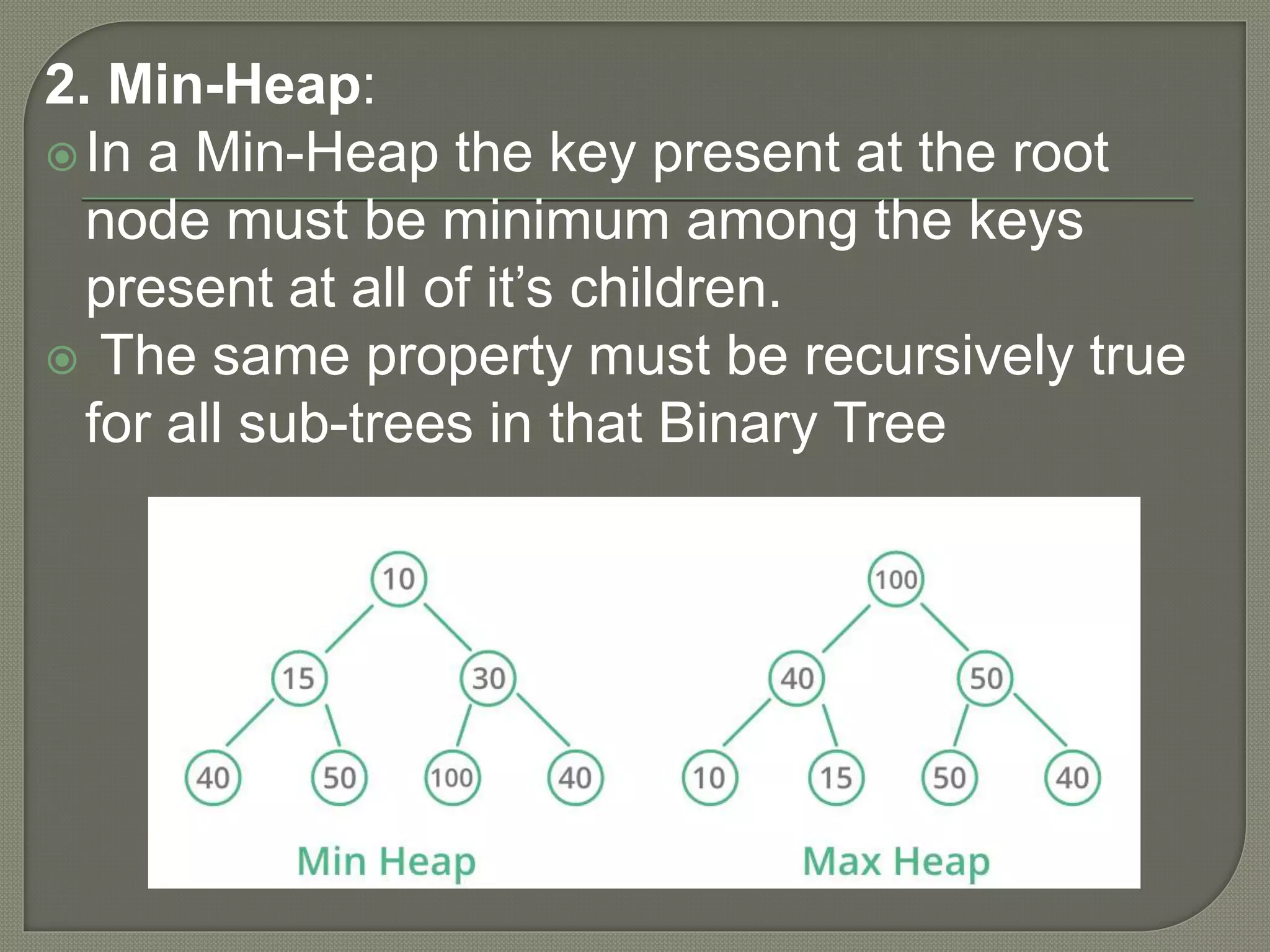
![A Binary Heap is a Complete Binary Tree. A binary heap is typically represented as array. The representation is done as: • The root element will be at Arr[0]. • Indexes of other nodes : Arr[(i-1)/2] Returns the parent node Arr[(2*i)+1] Returns the left child node Arr[(2*i)+2] Returns the right child node](https://image.slidesharecdn.com/21arunbrijwasi-200413102924/75/Array-implementation-Construction-of-Heap-5-2048.jpg)