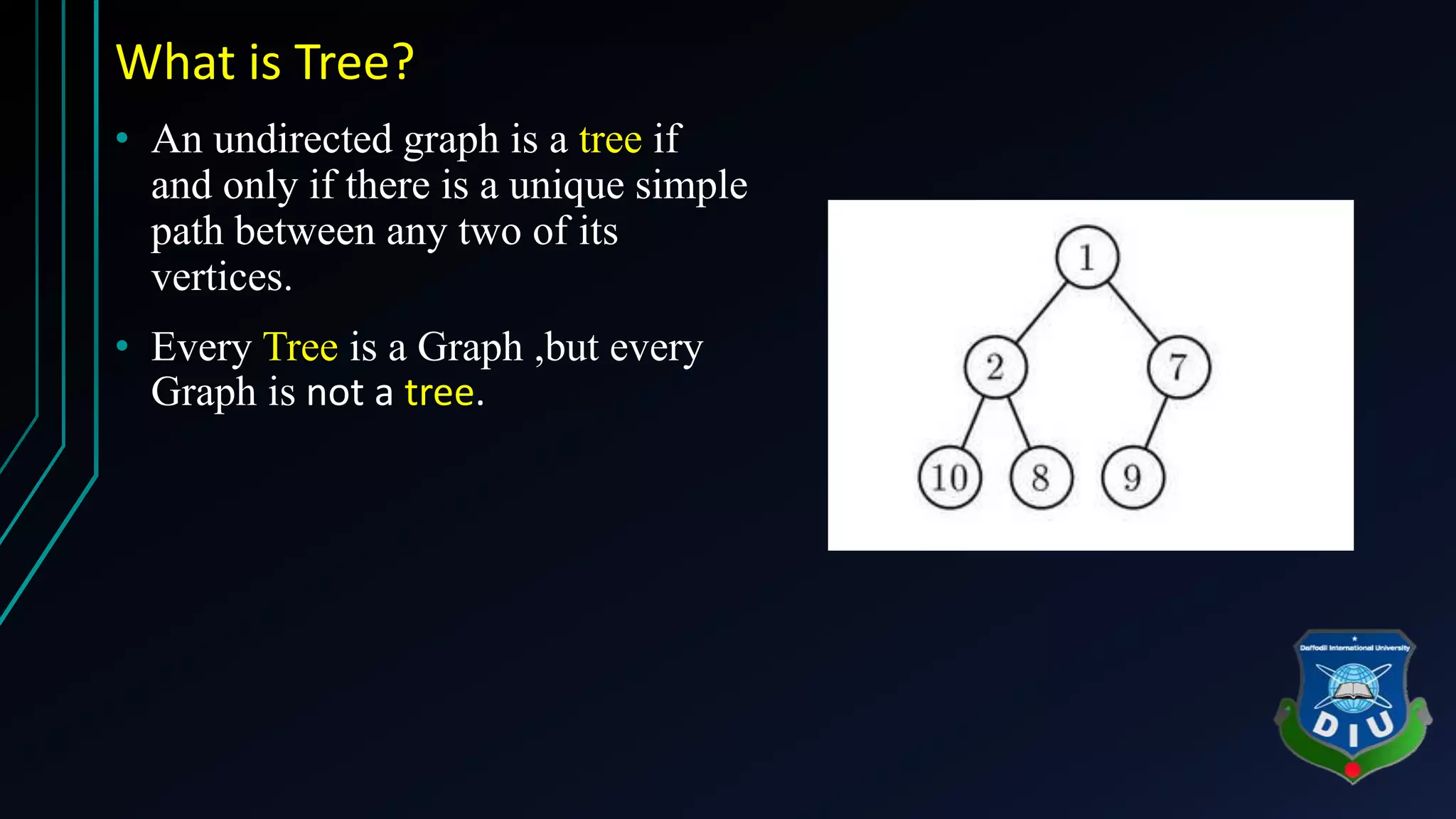
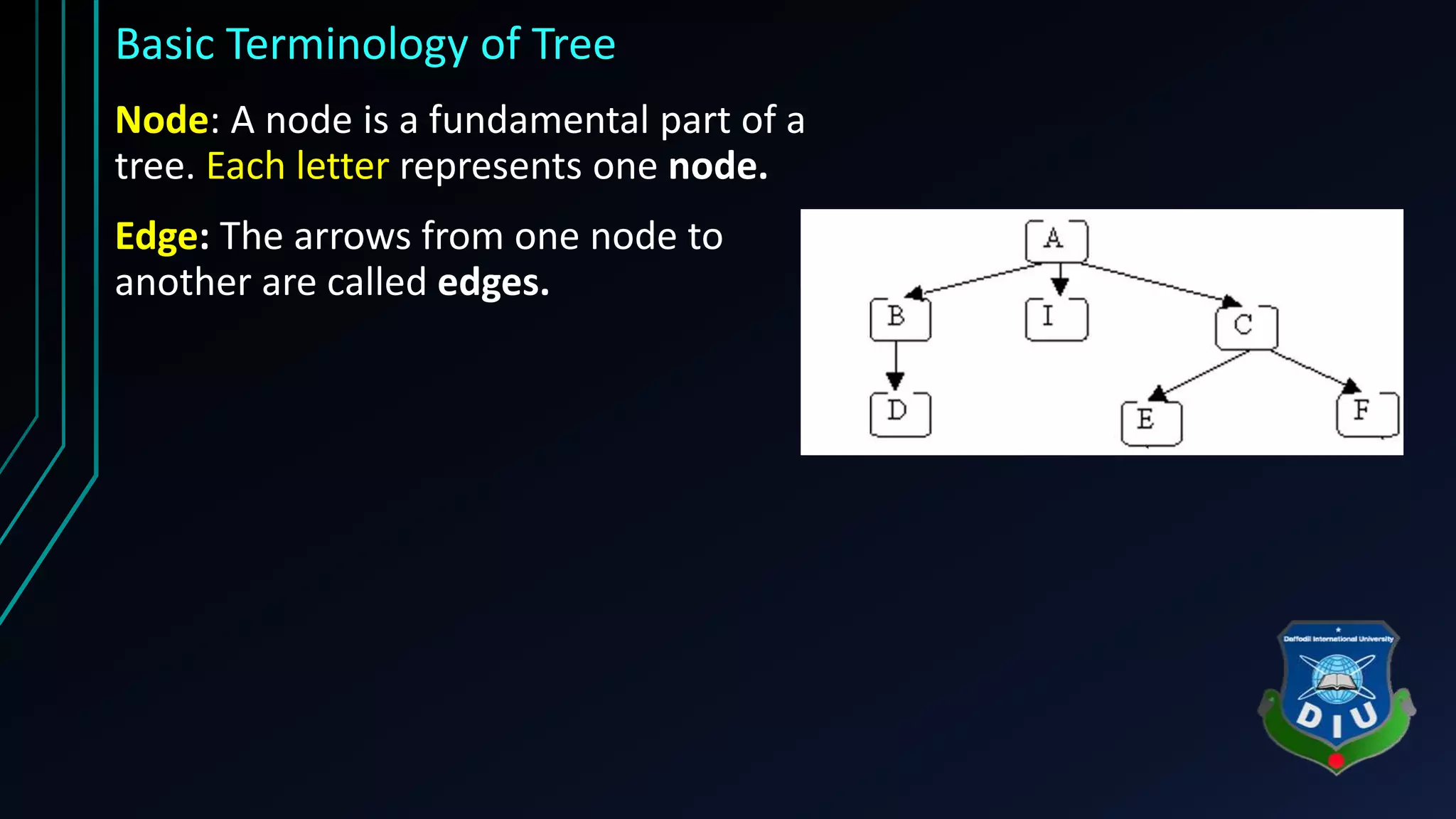
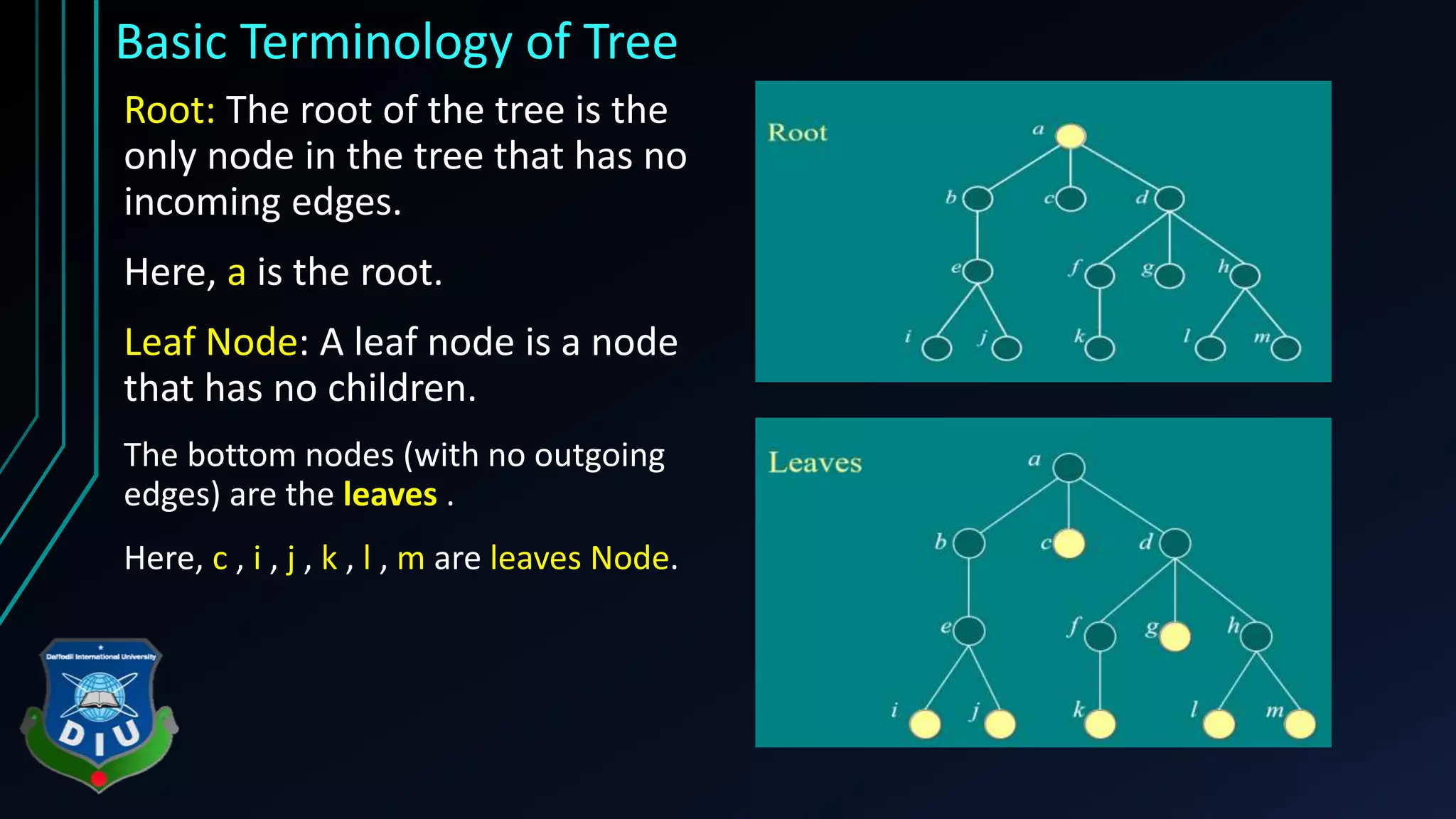
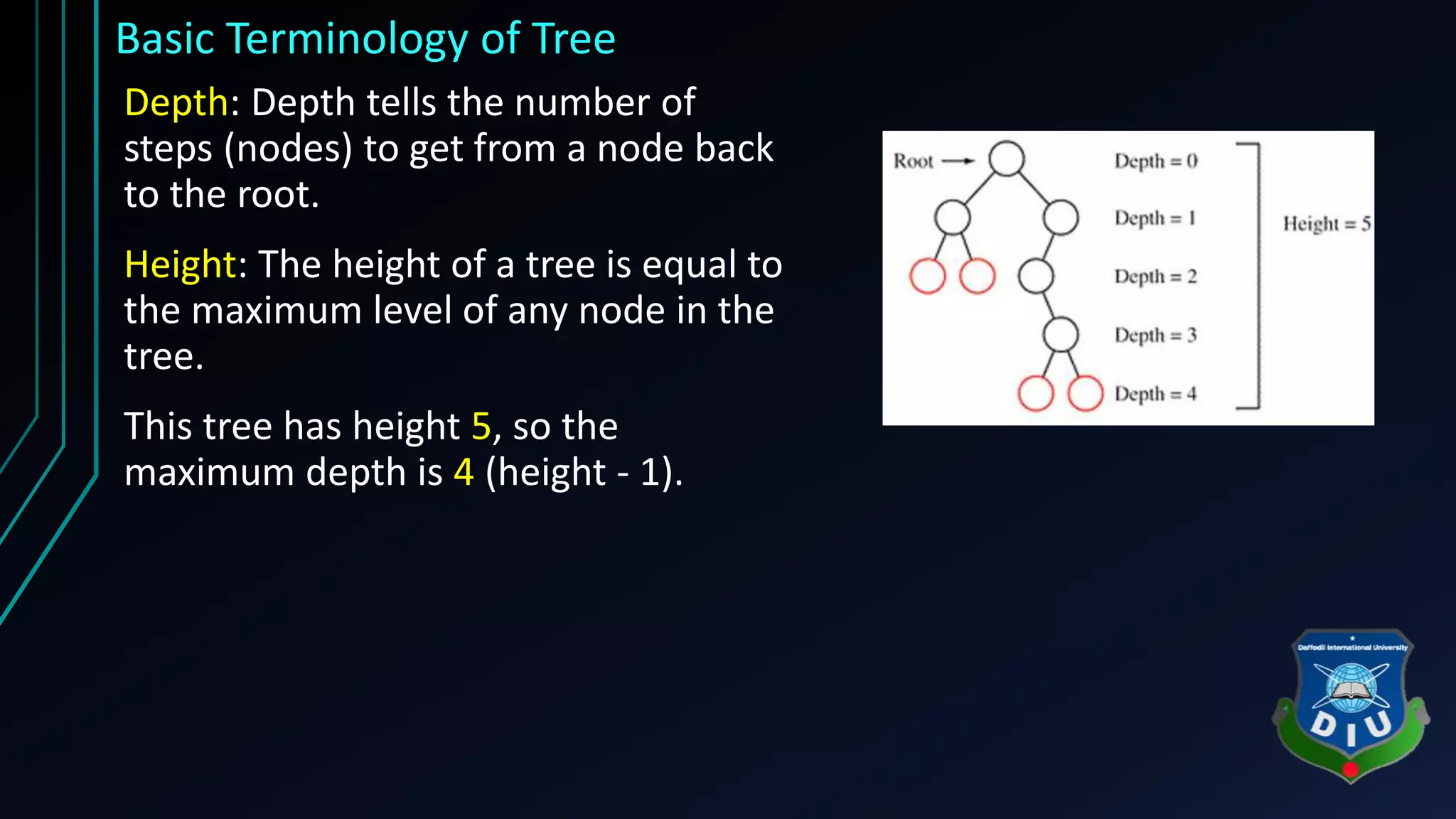
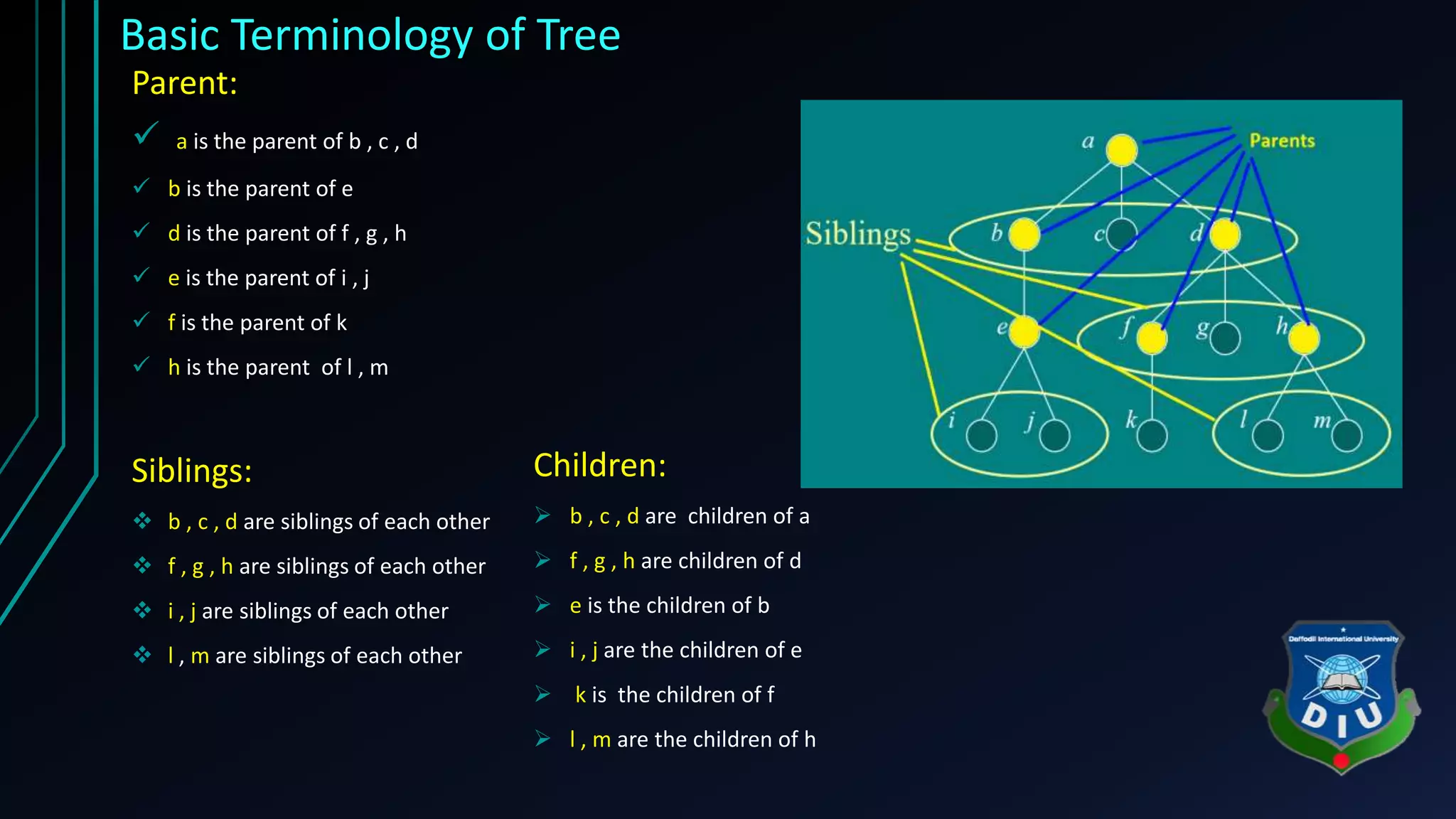
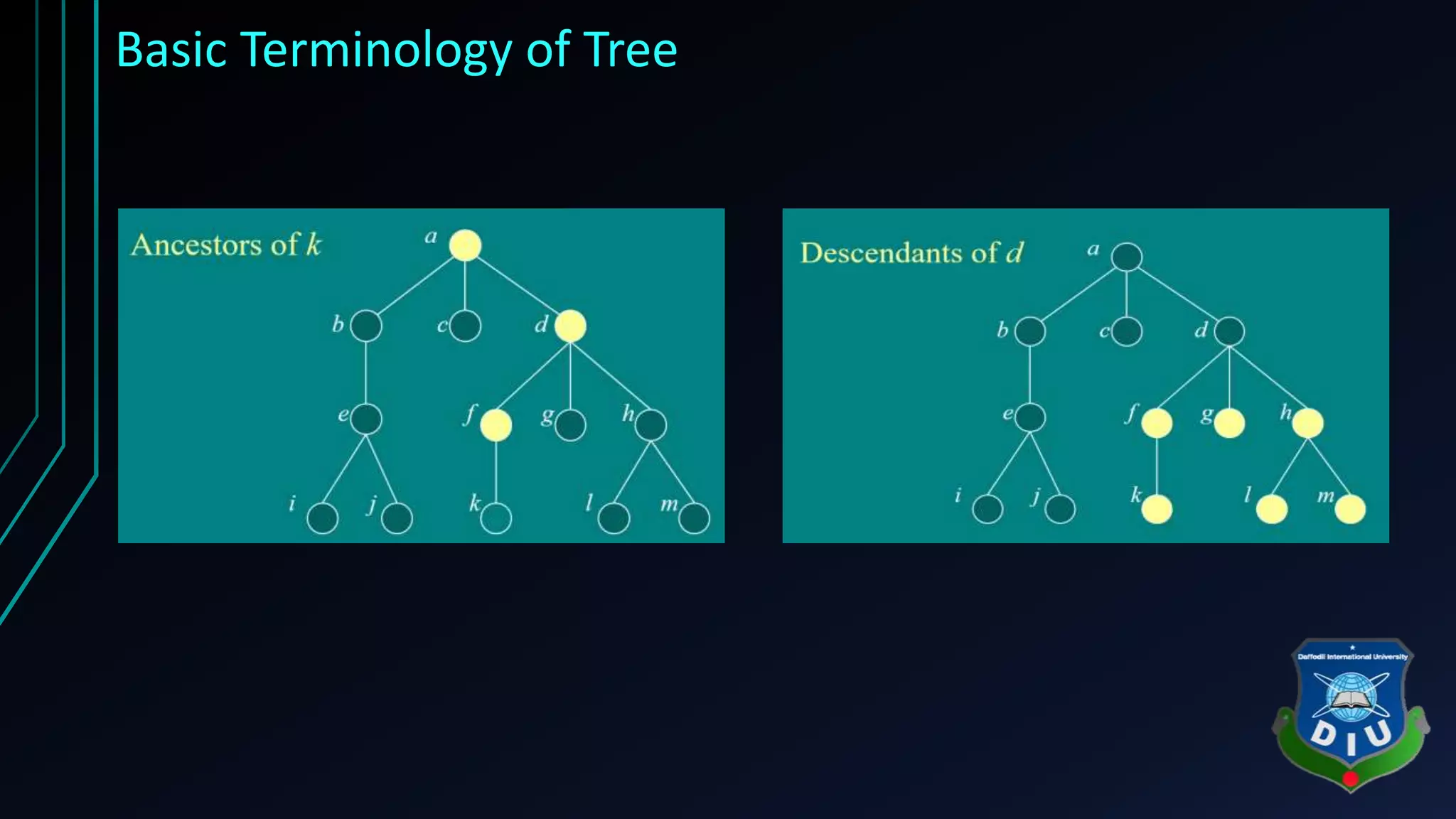
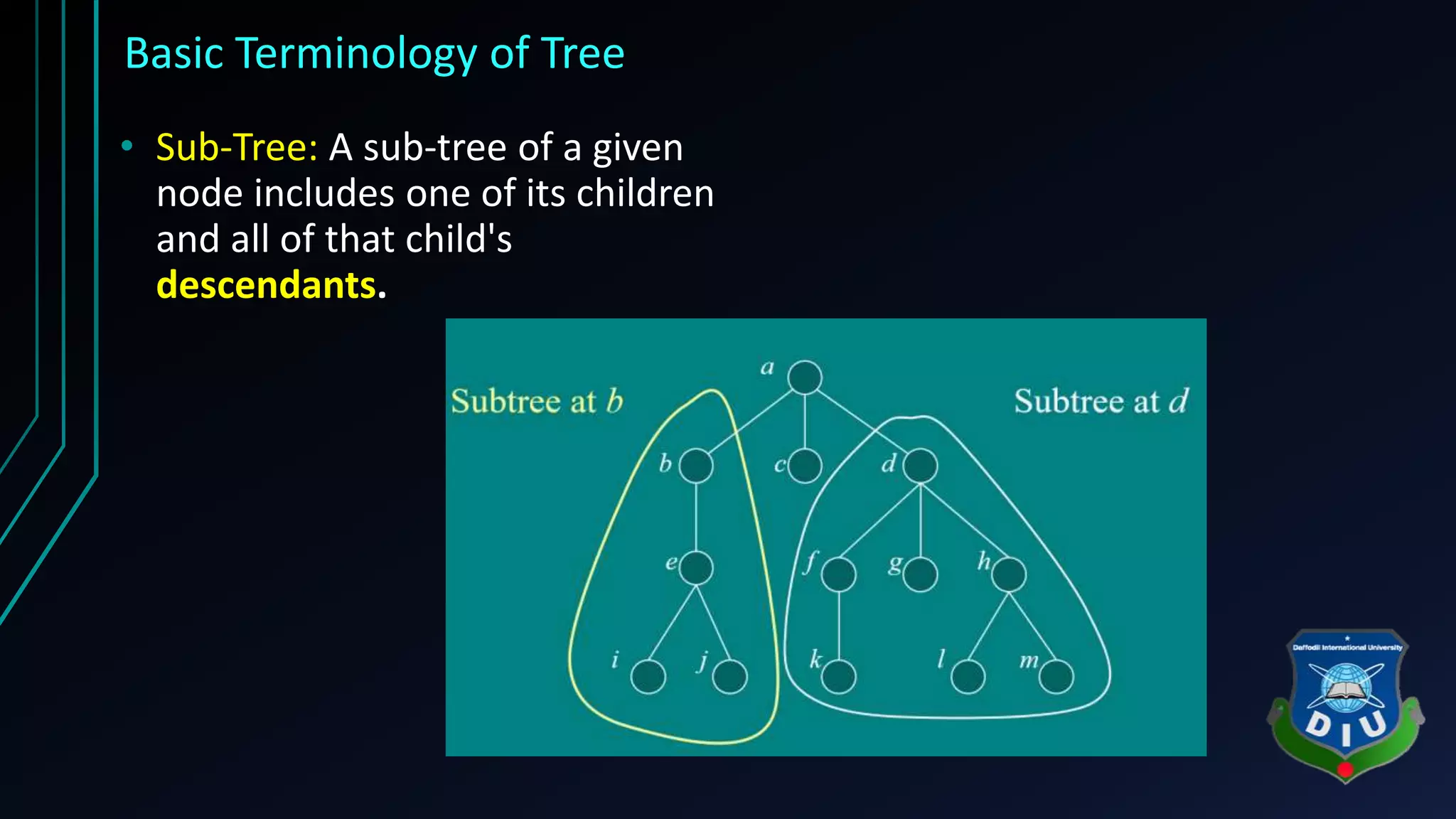
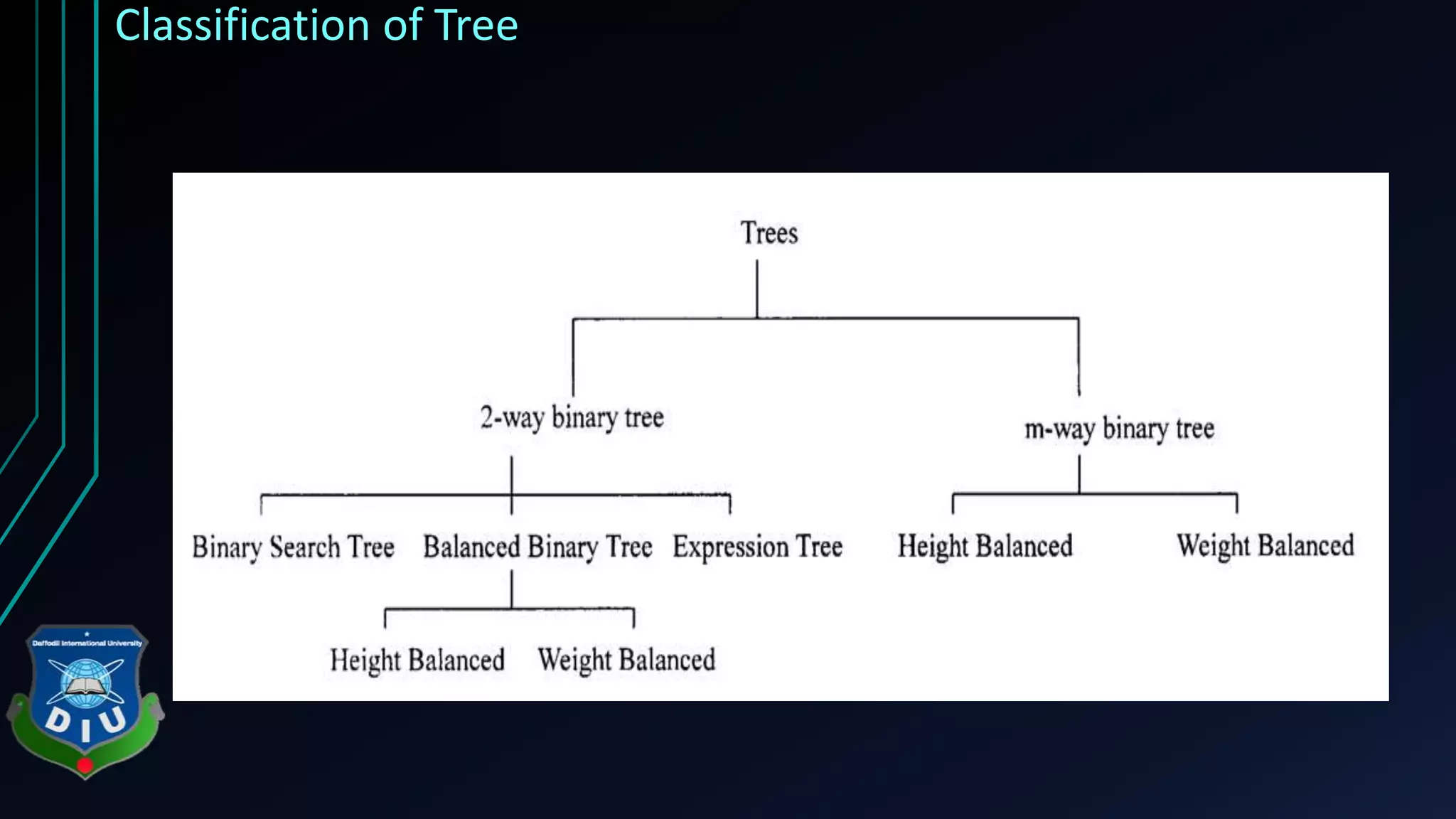
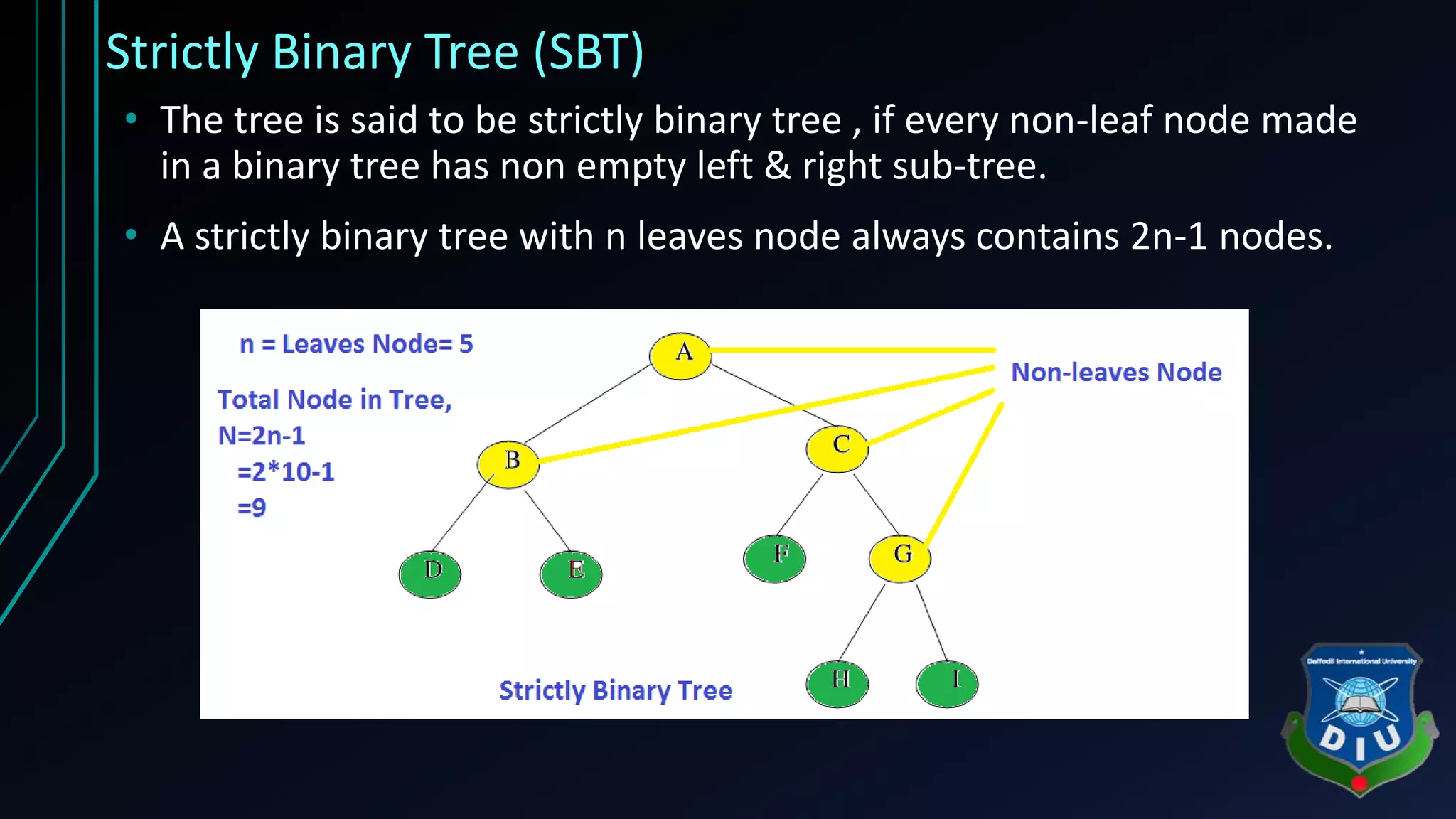
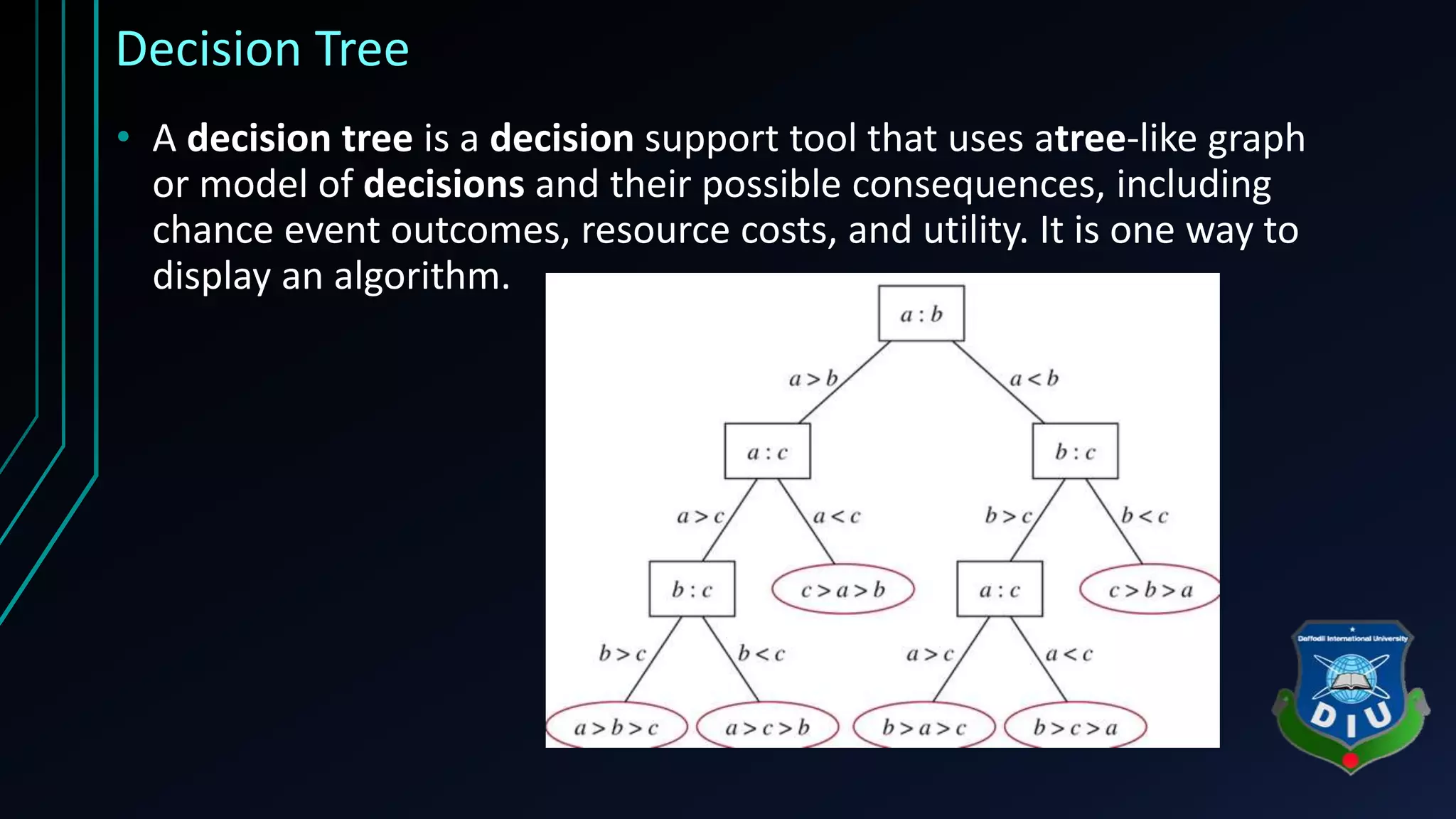
The document provides an overview of tree structures in discrete mathematics, including their definitions, terminology, and classifications such as m-ary trees, binary trees, and decision trees. Key concepts include nodes, edges, leaves, and various types of binary trees like complete and strictly binary trees. It also discusses the process of traversing binary trees through pre-order, in-order, and post-order methods.