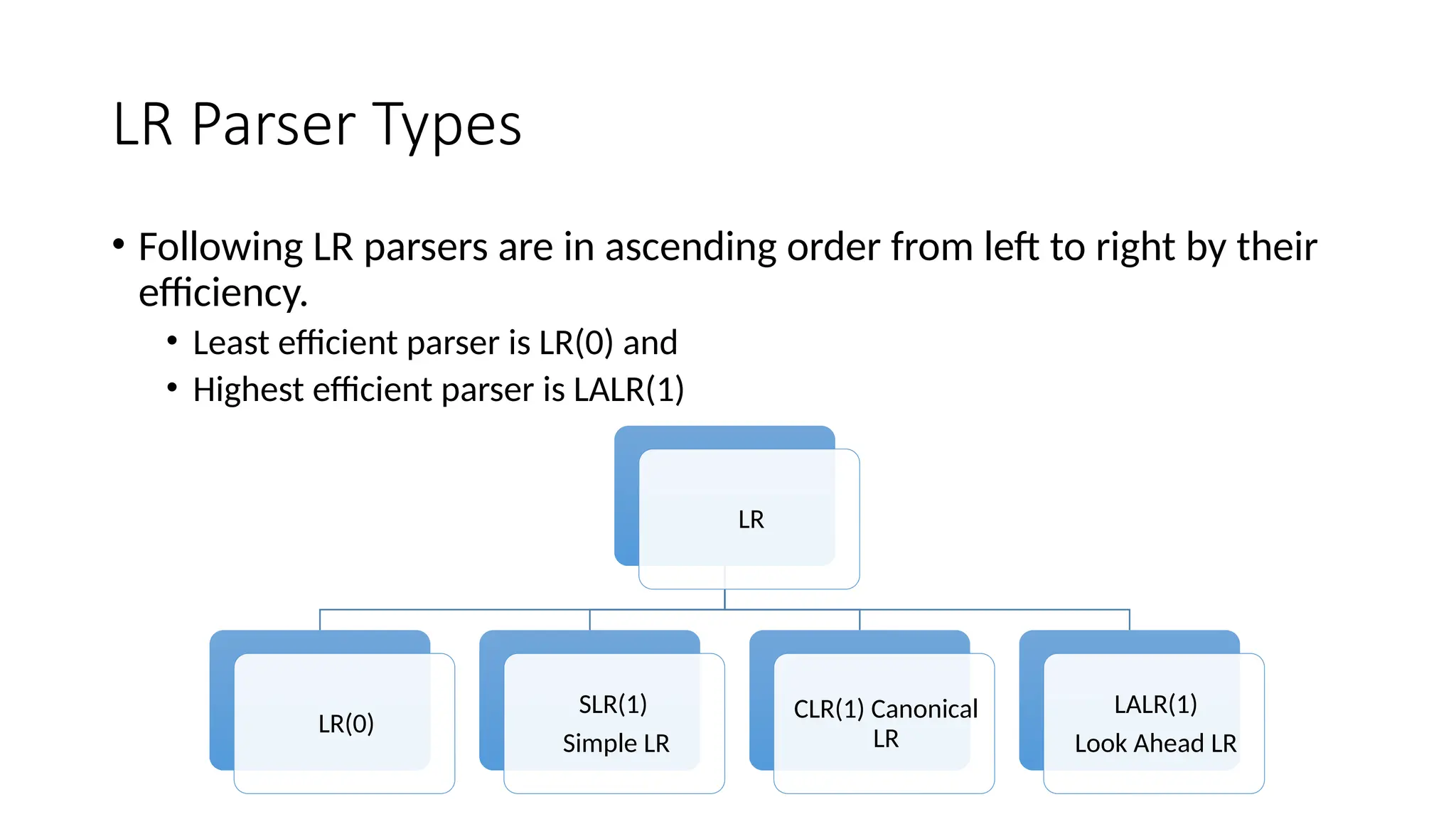
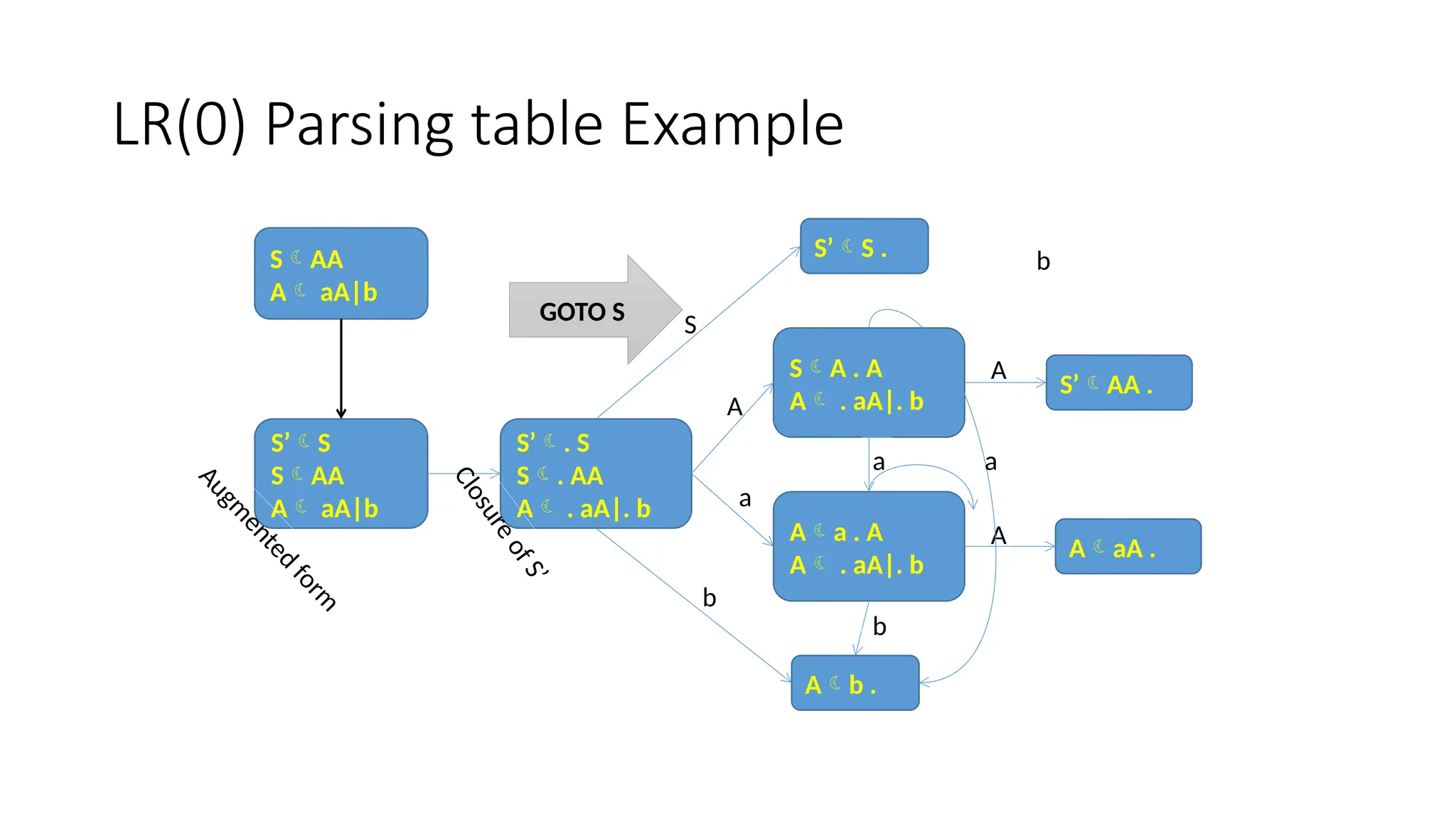
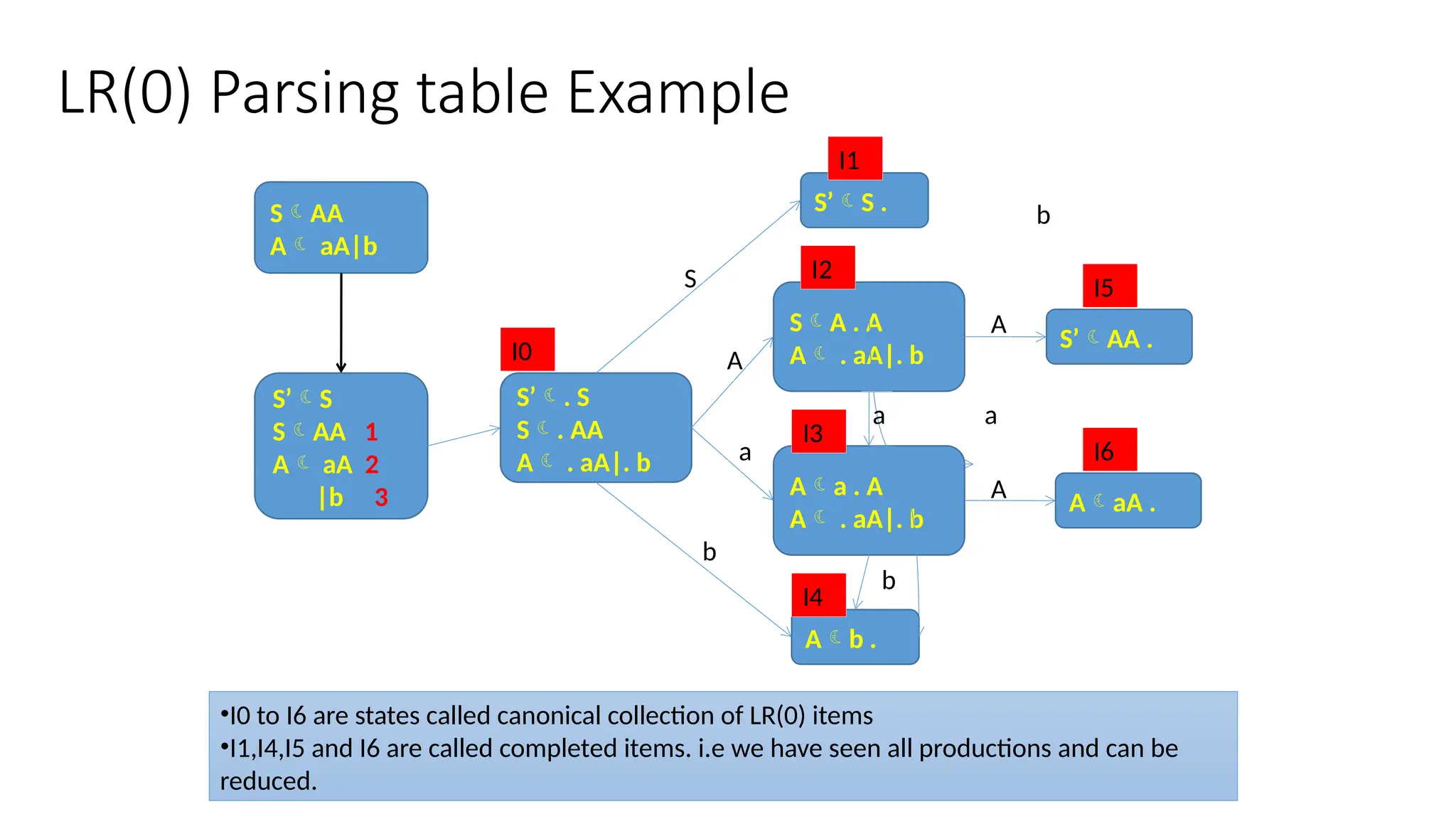
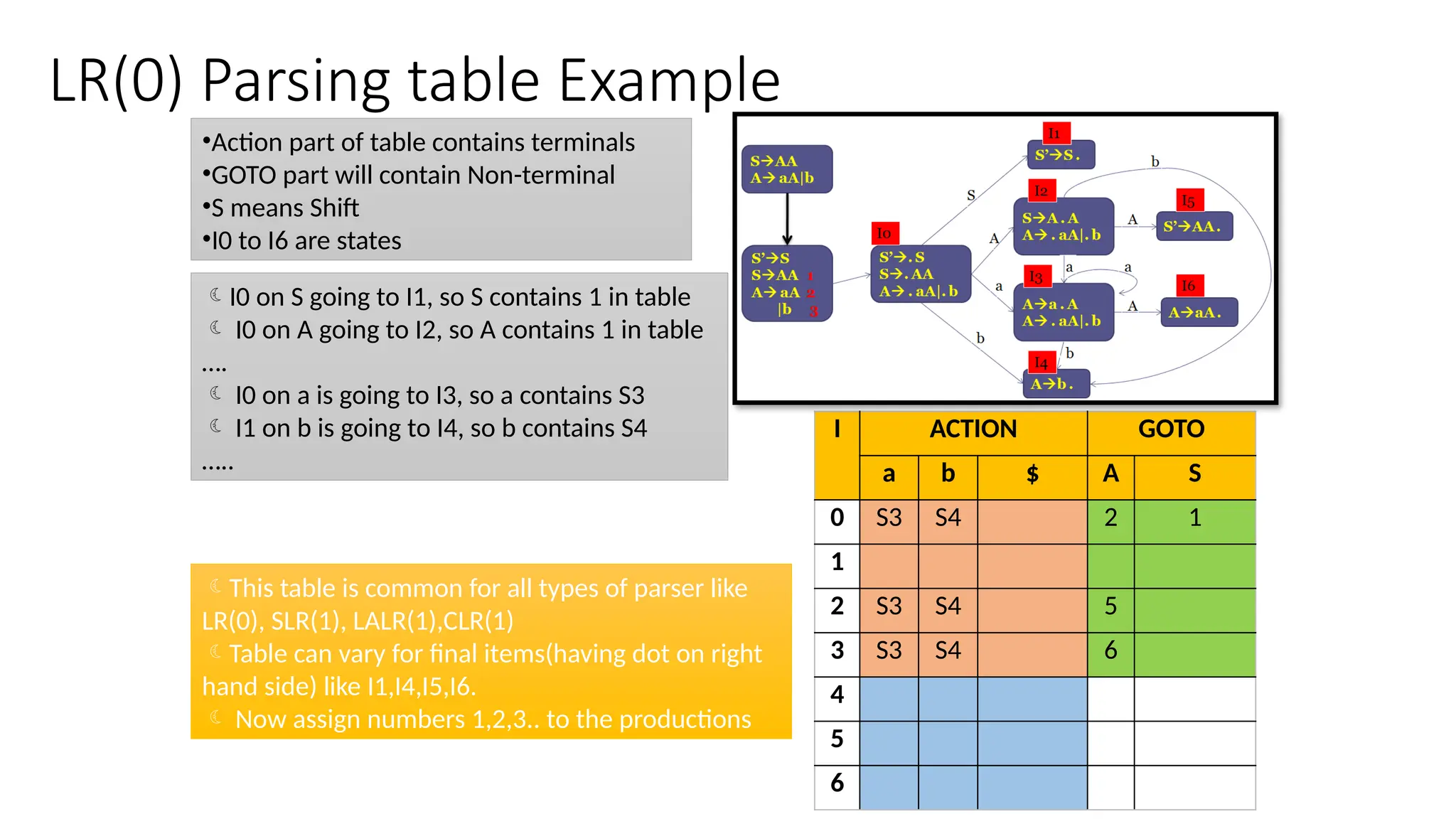
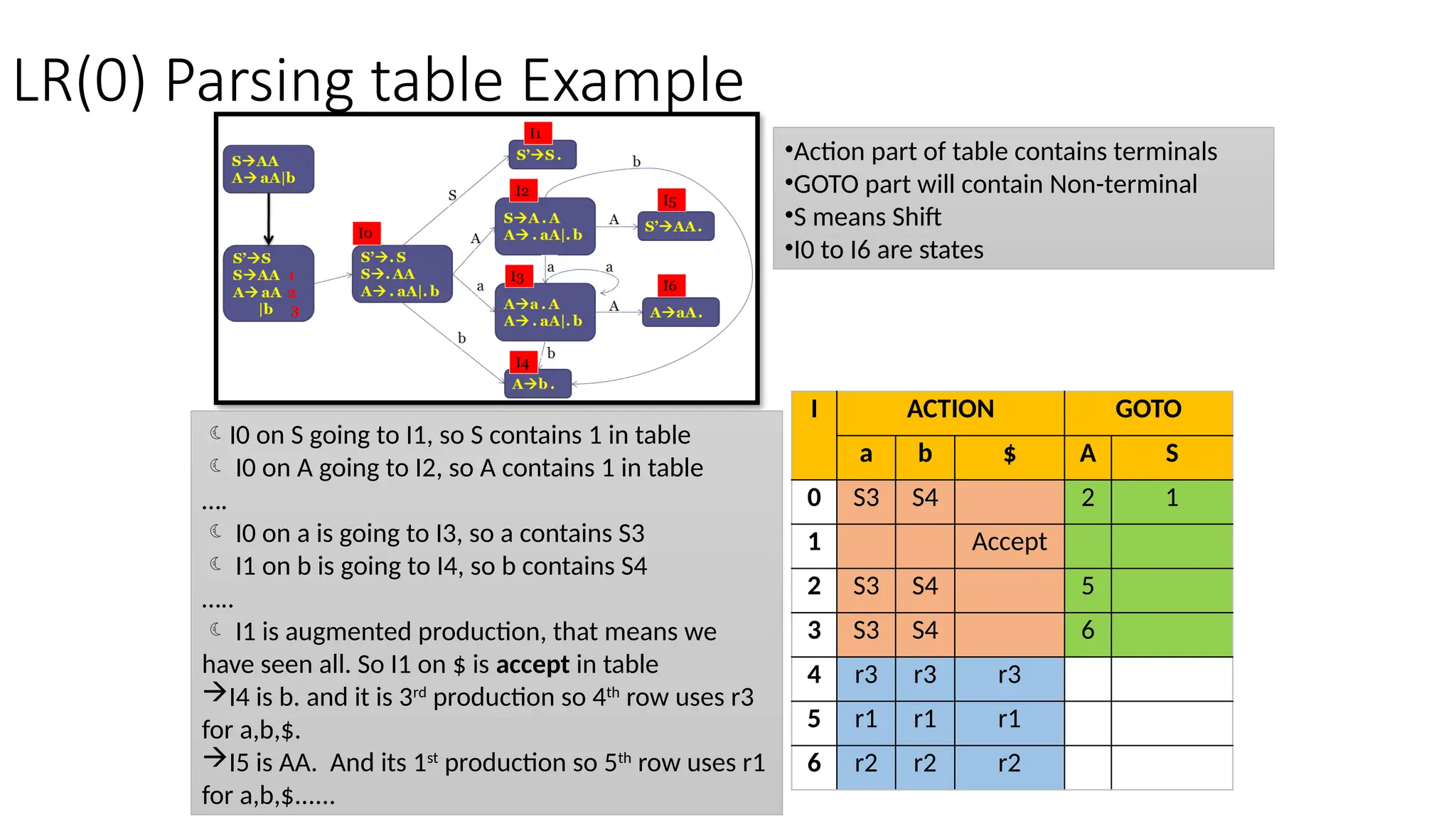
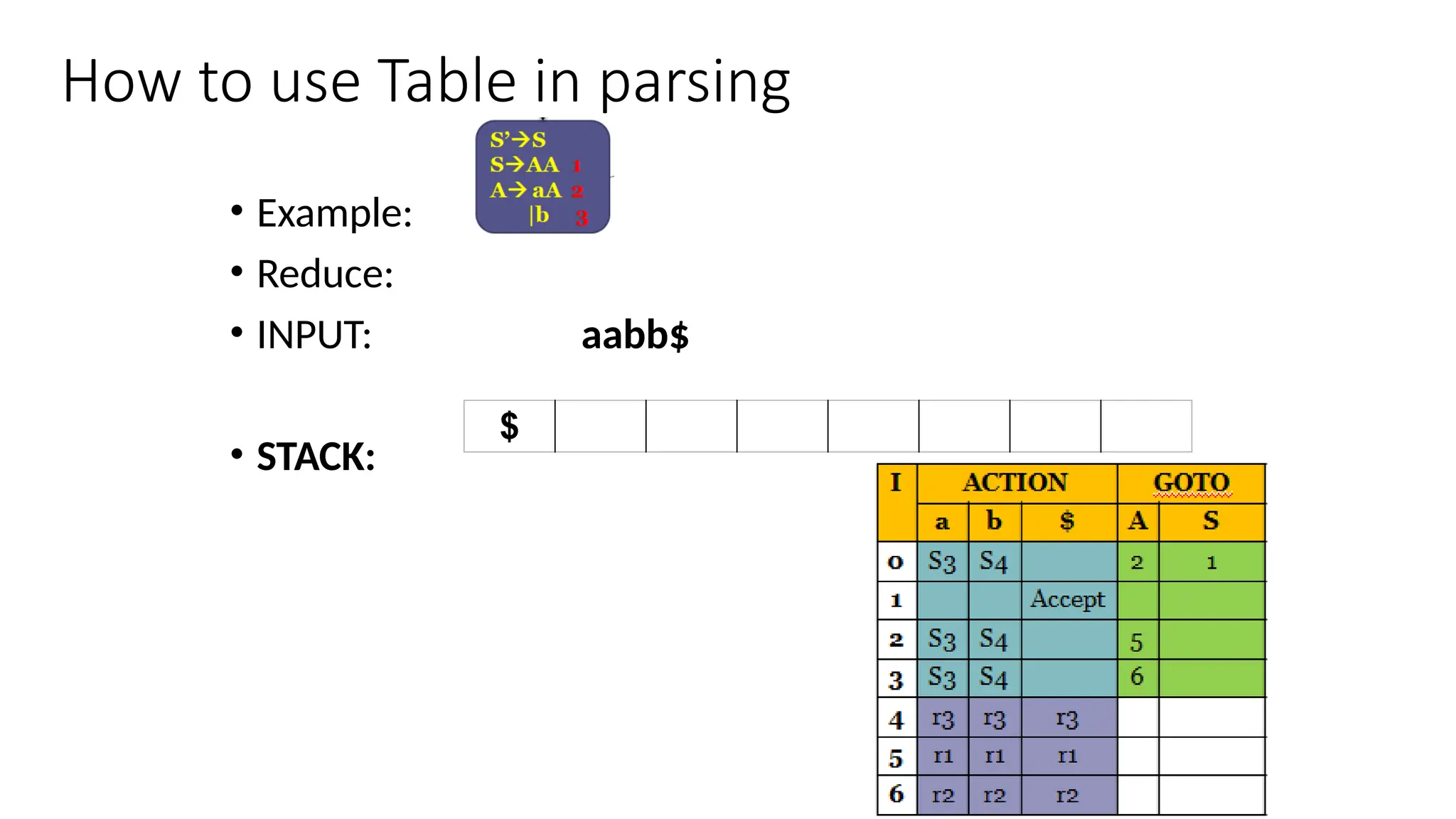
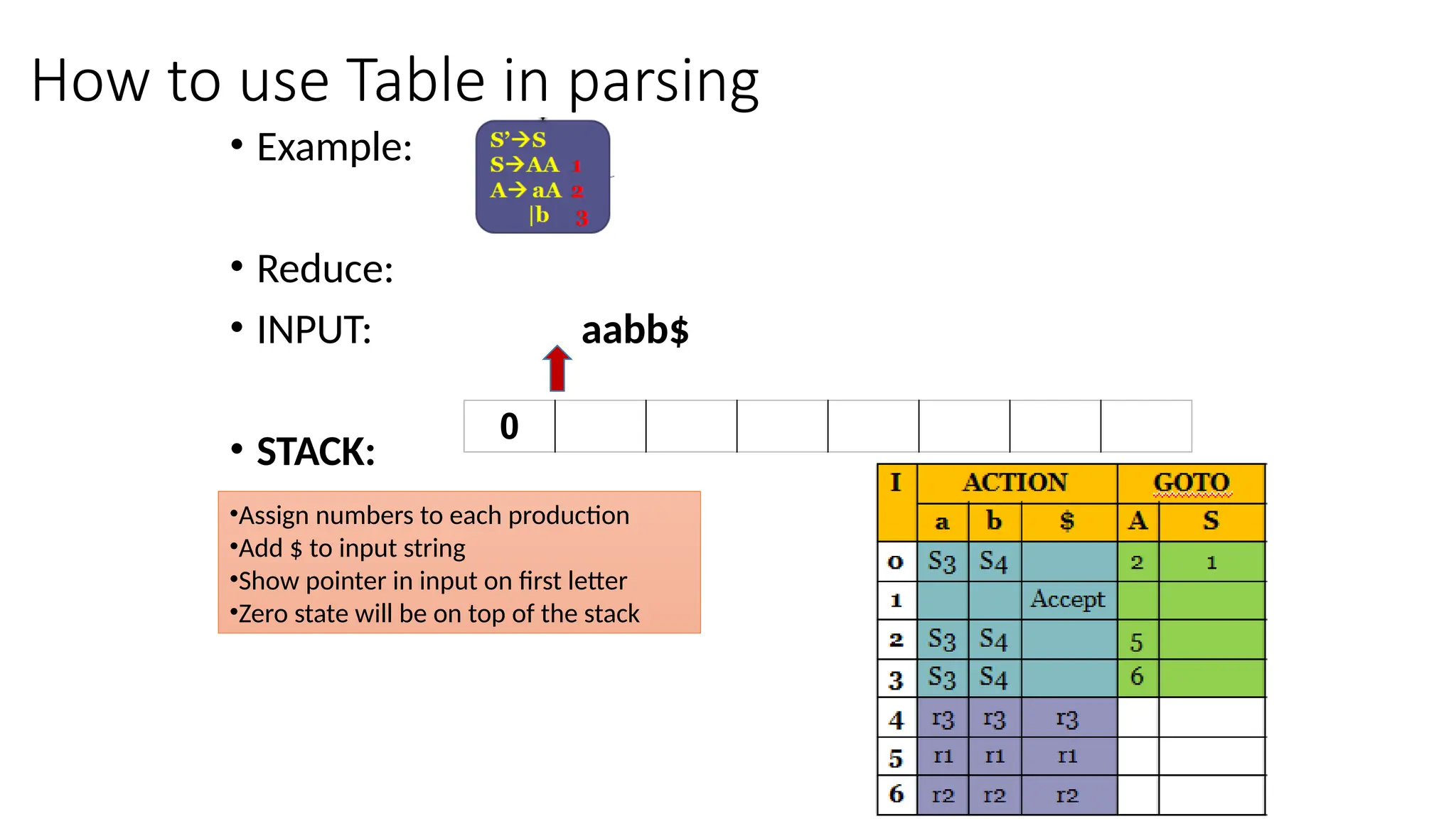
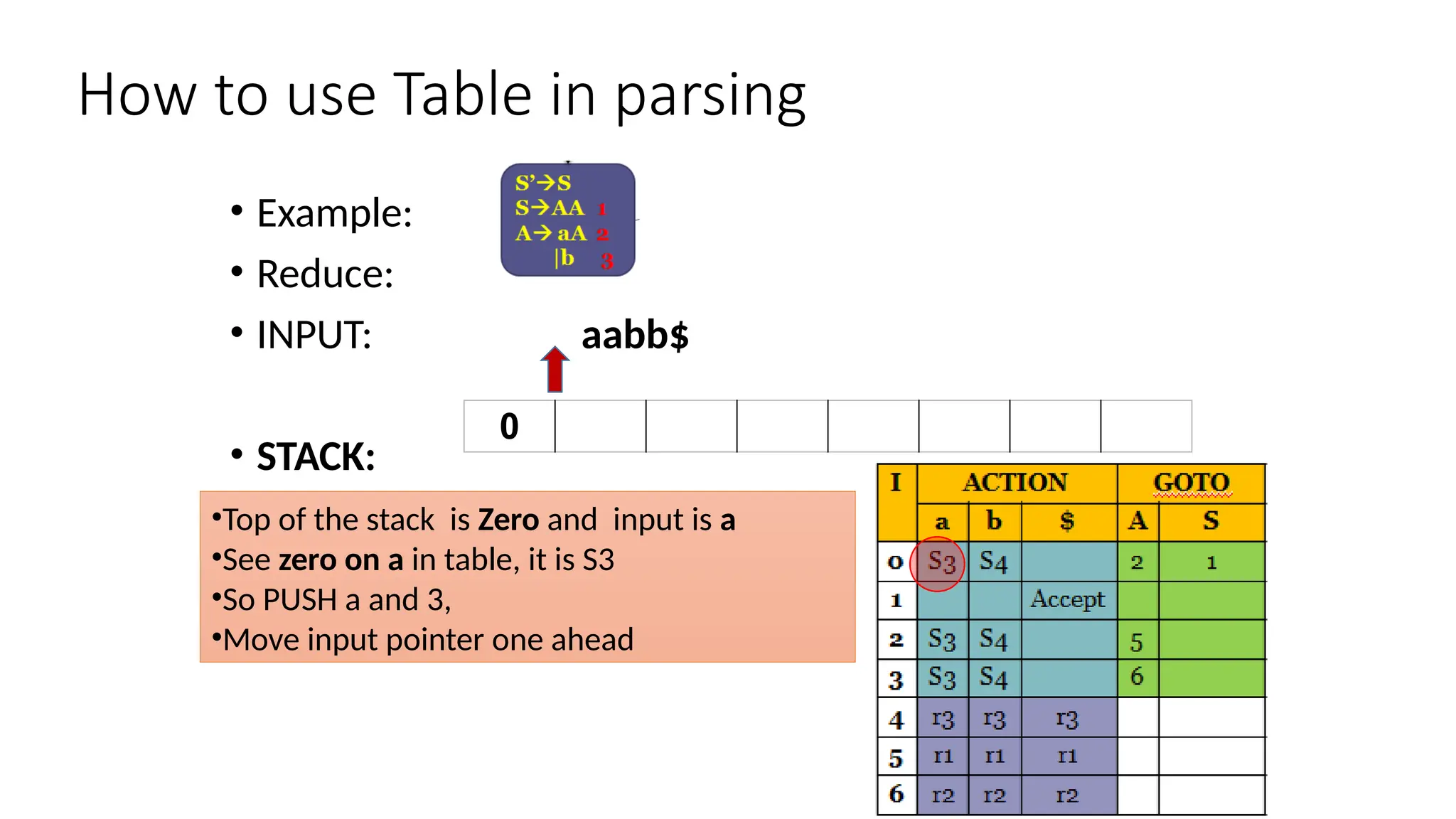
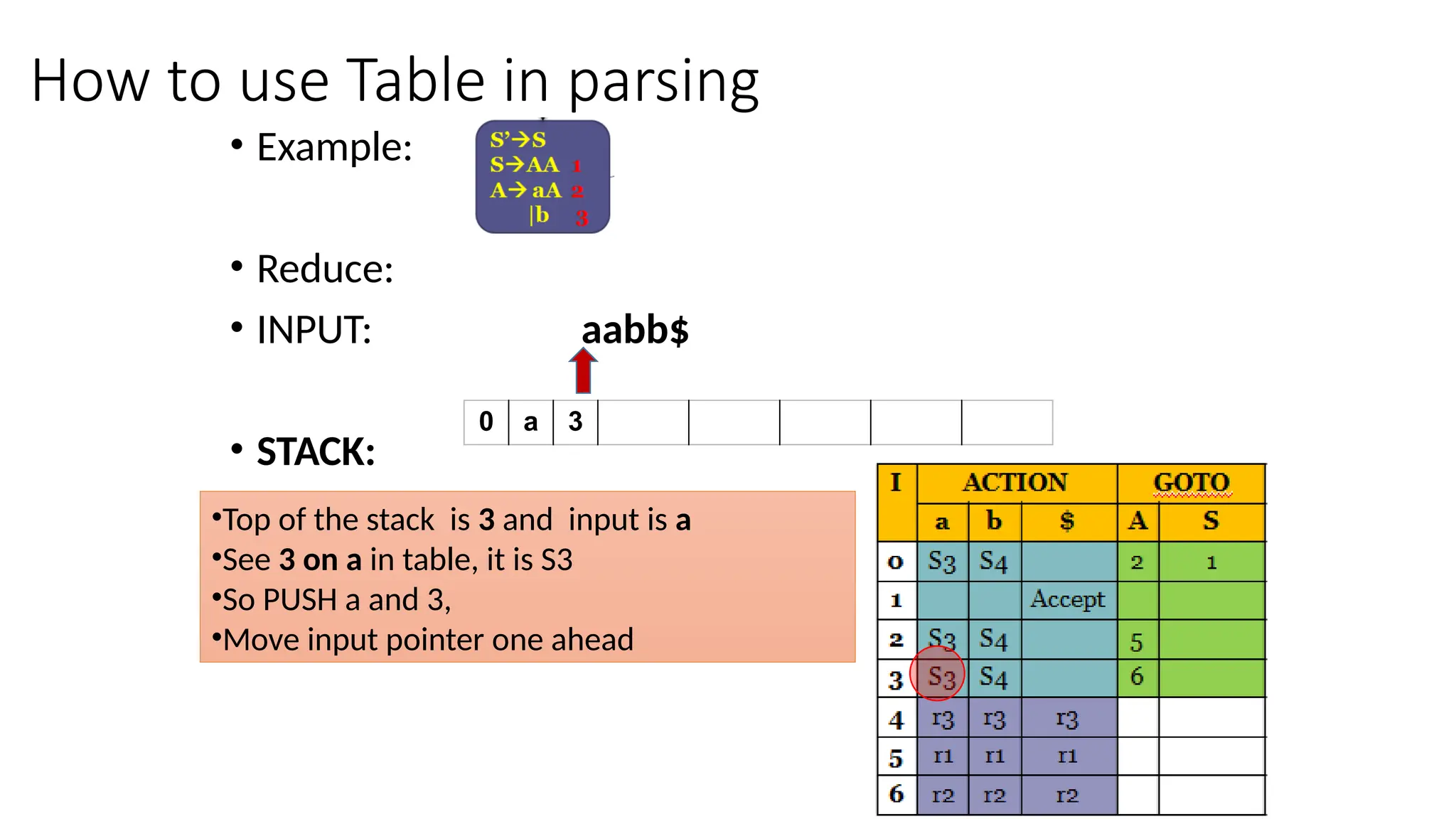
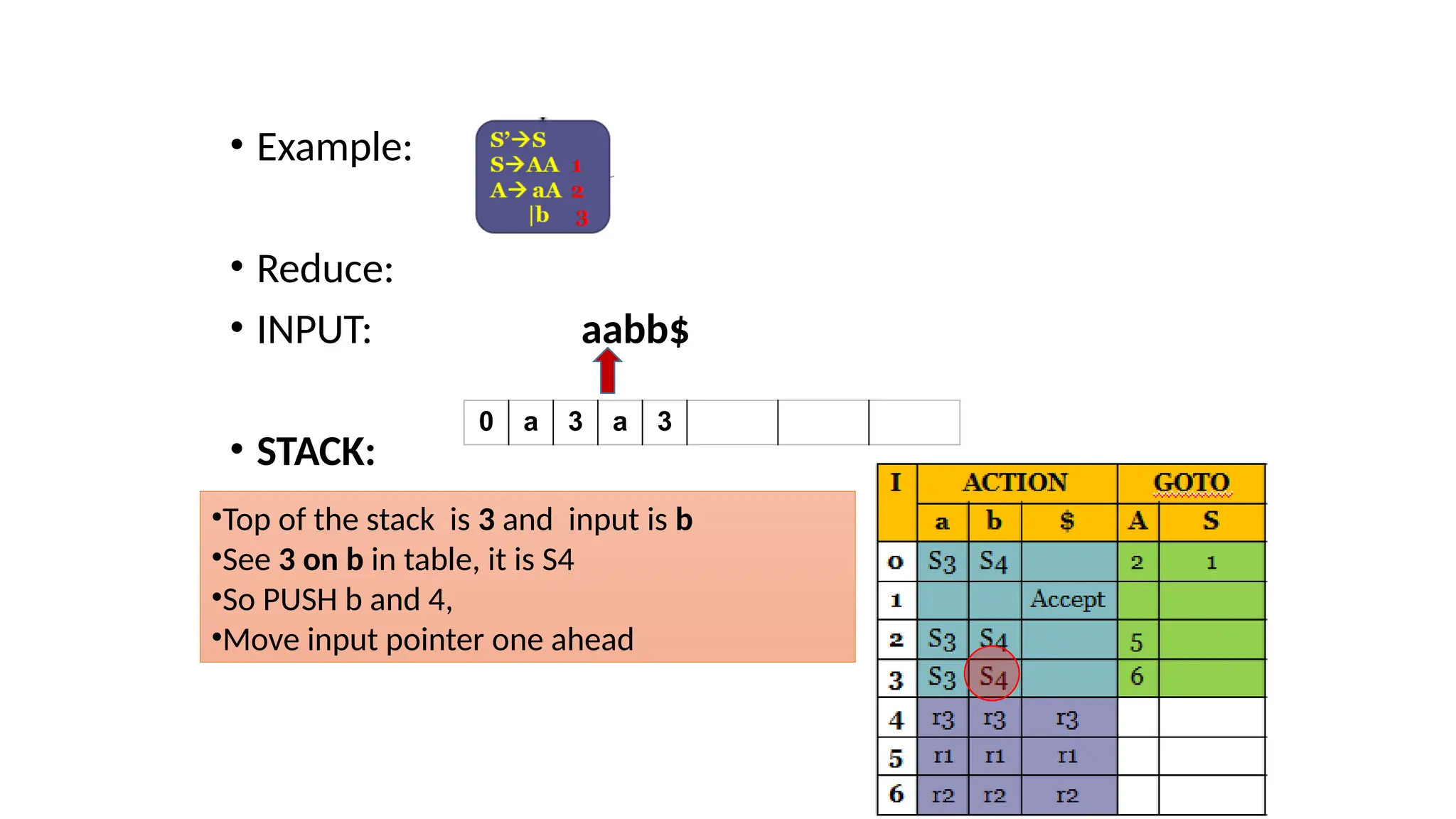
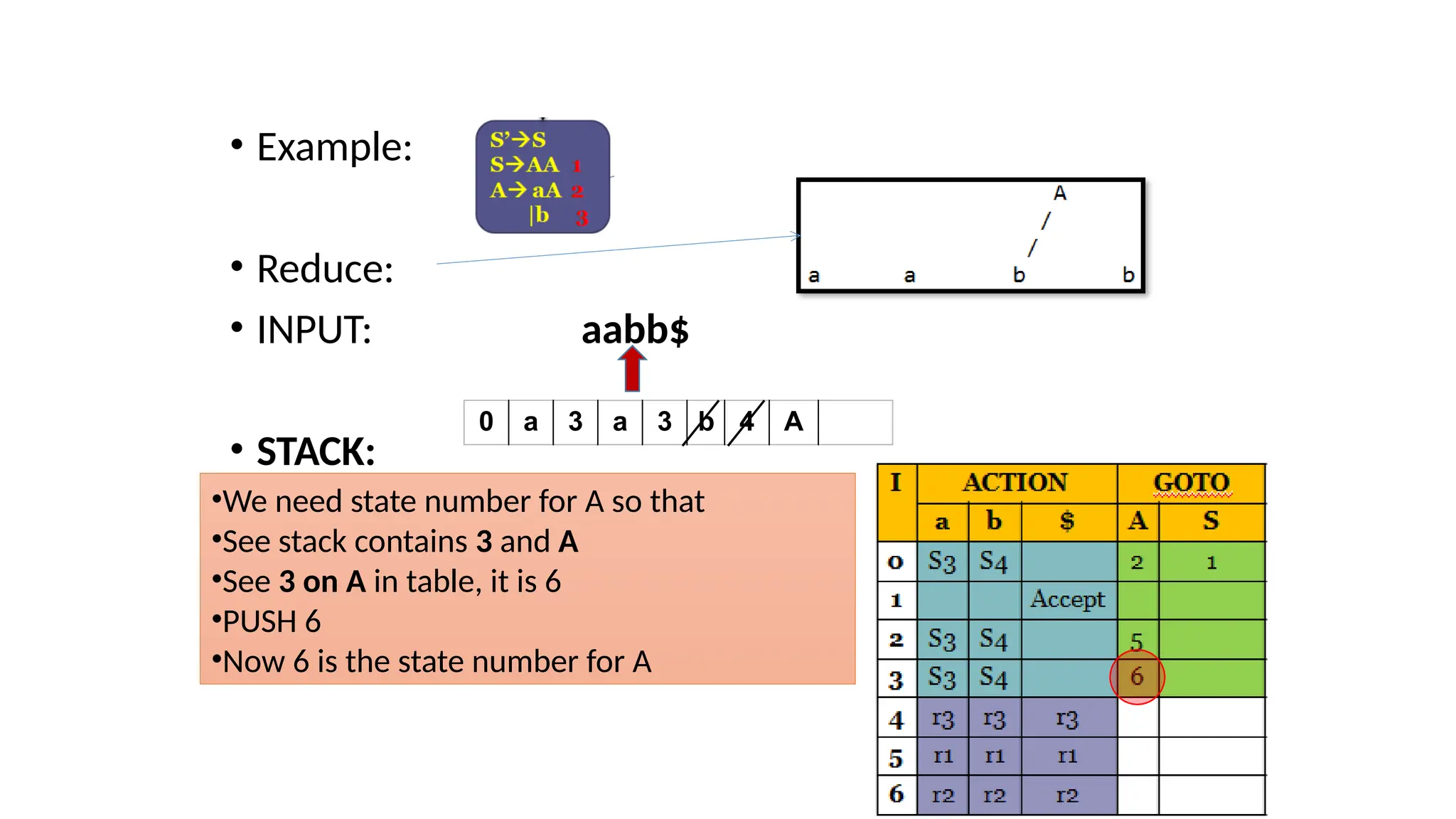
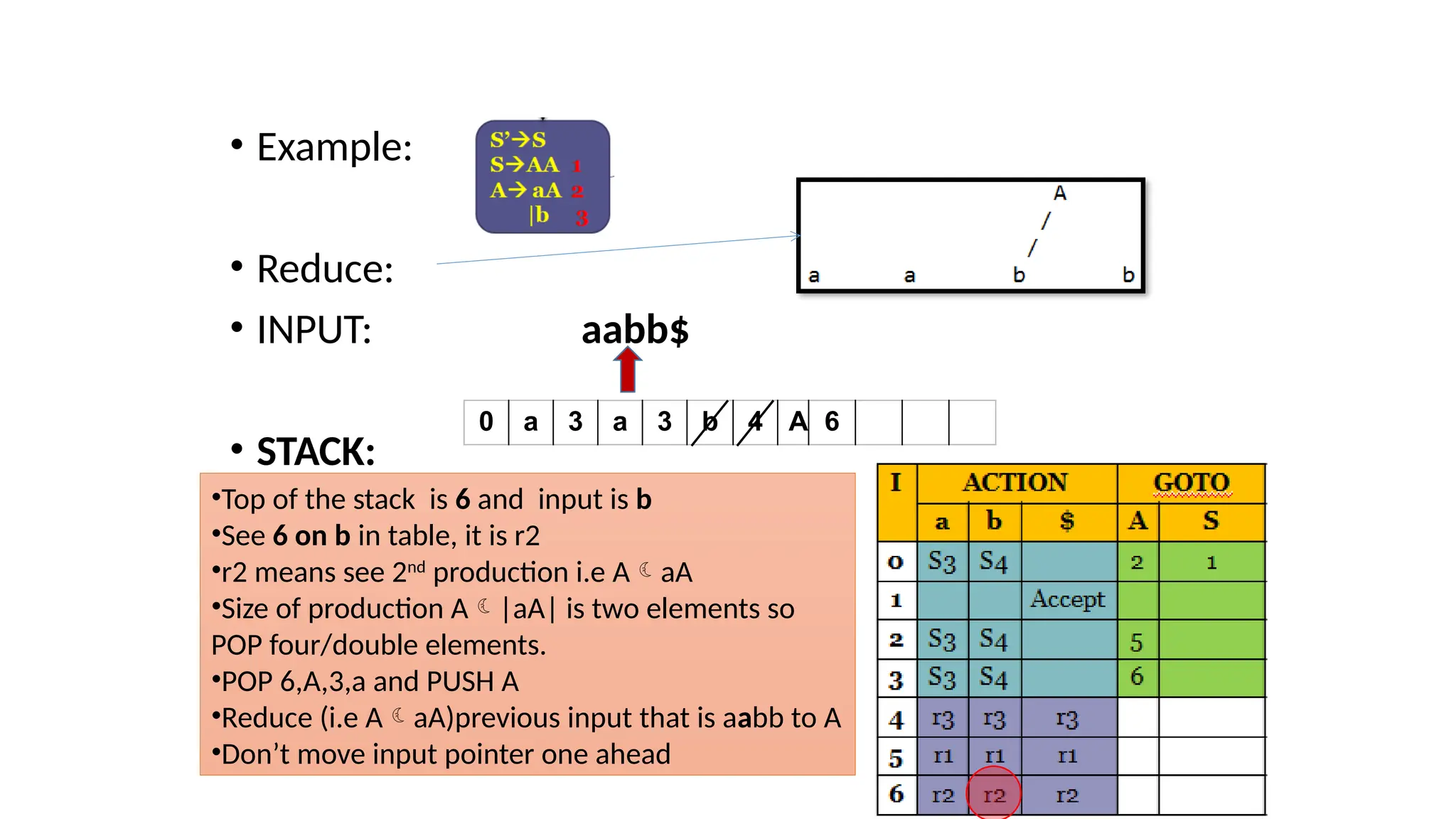
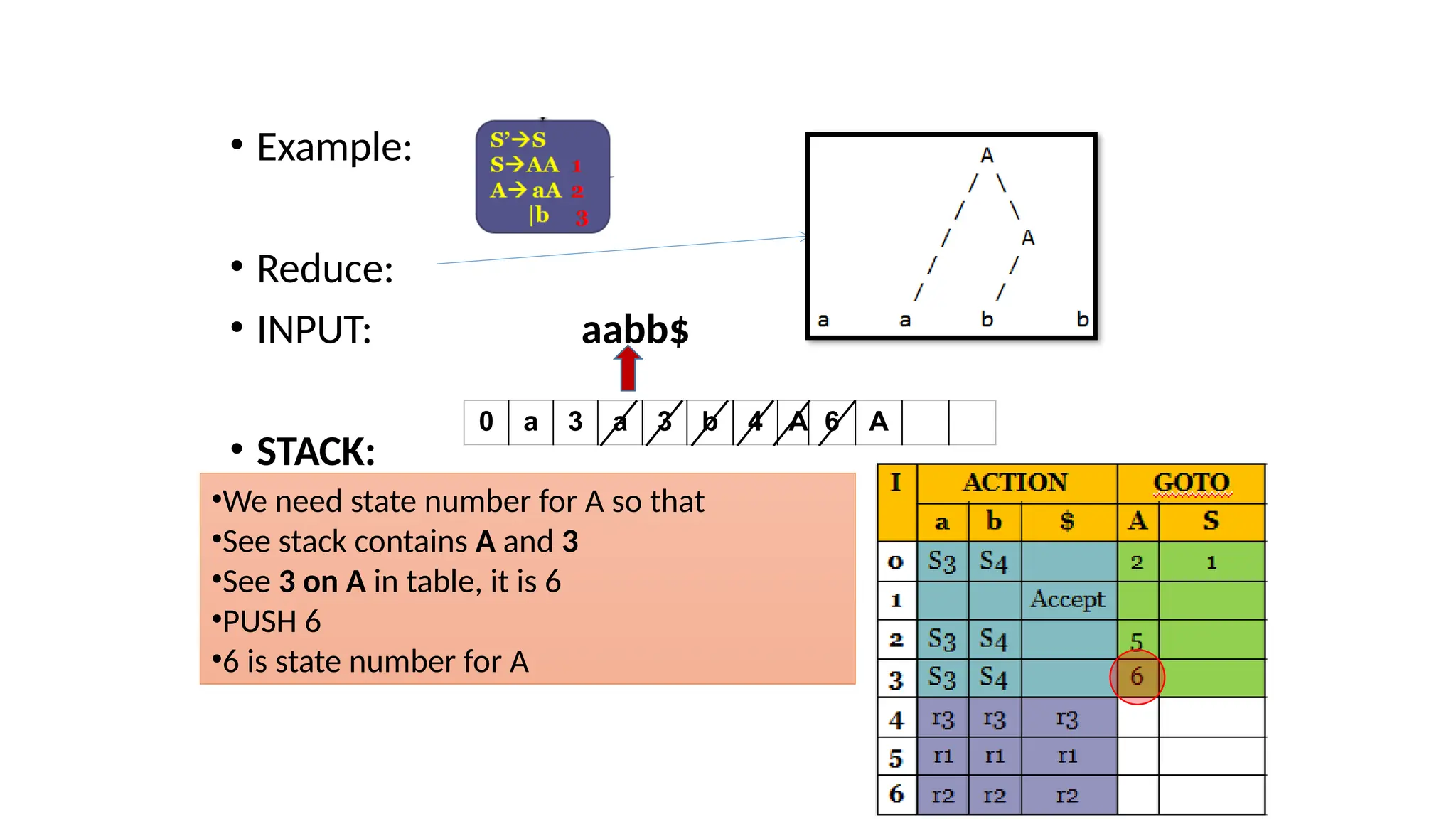
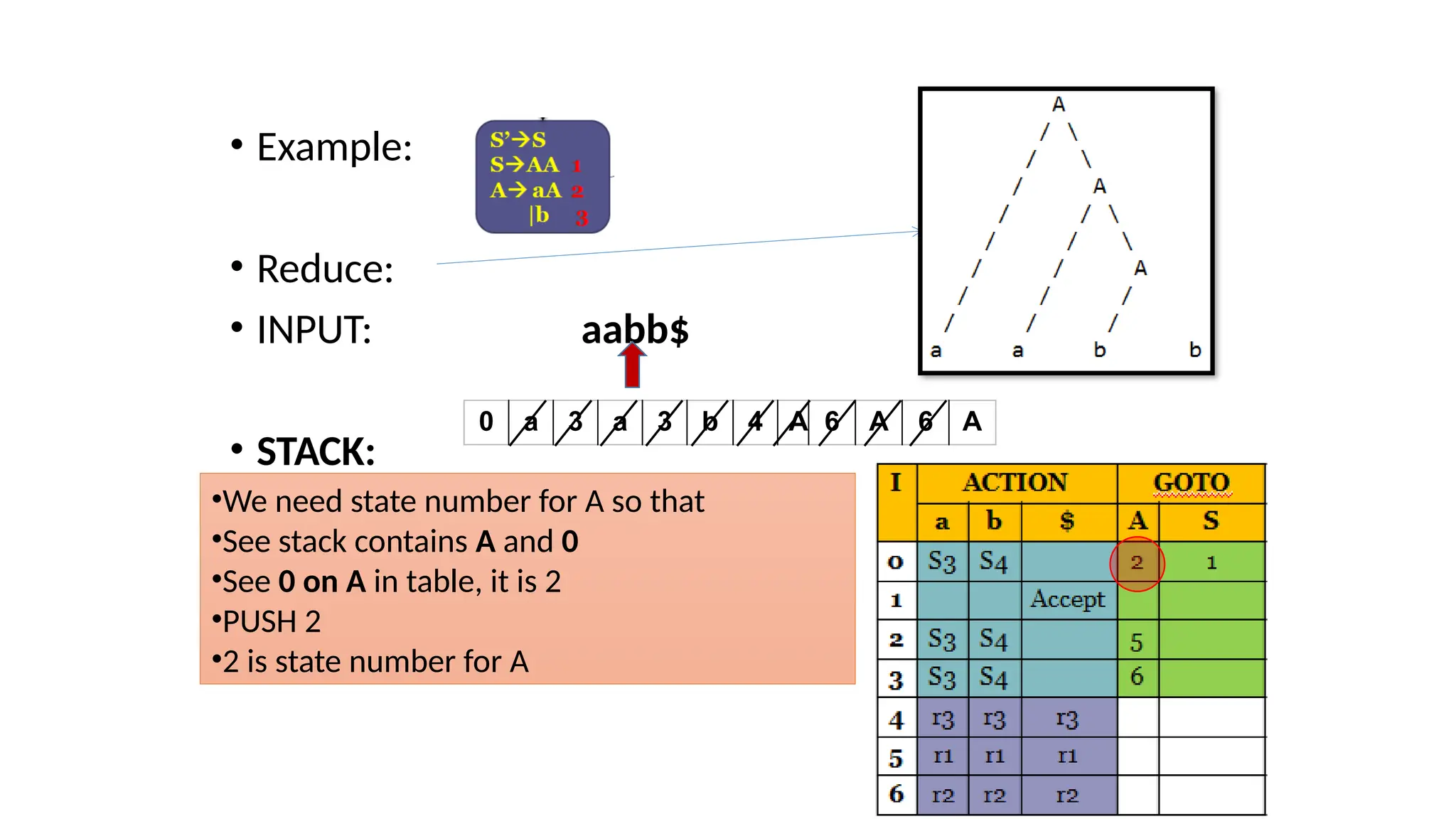
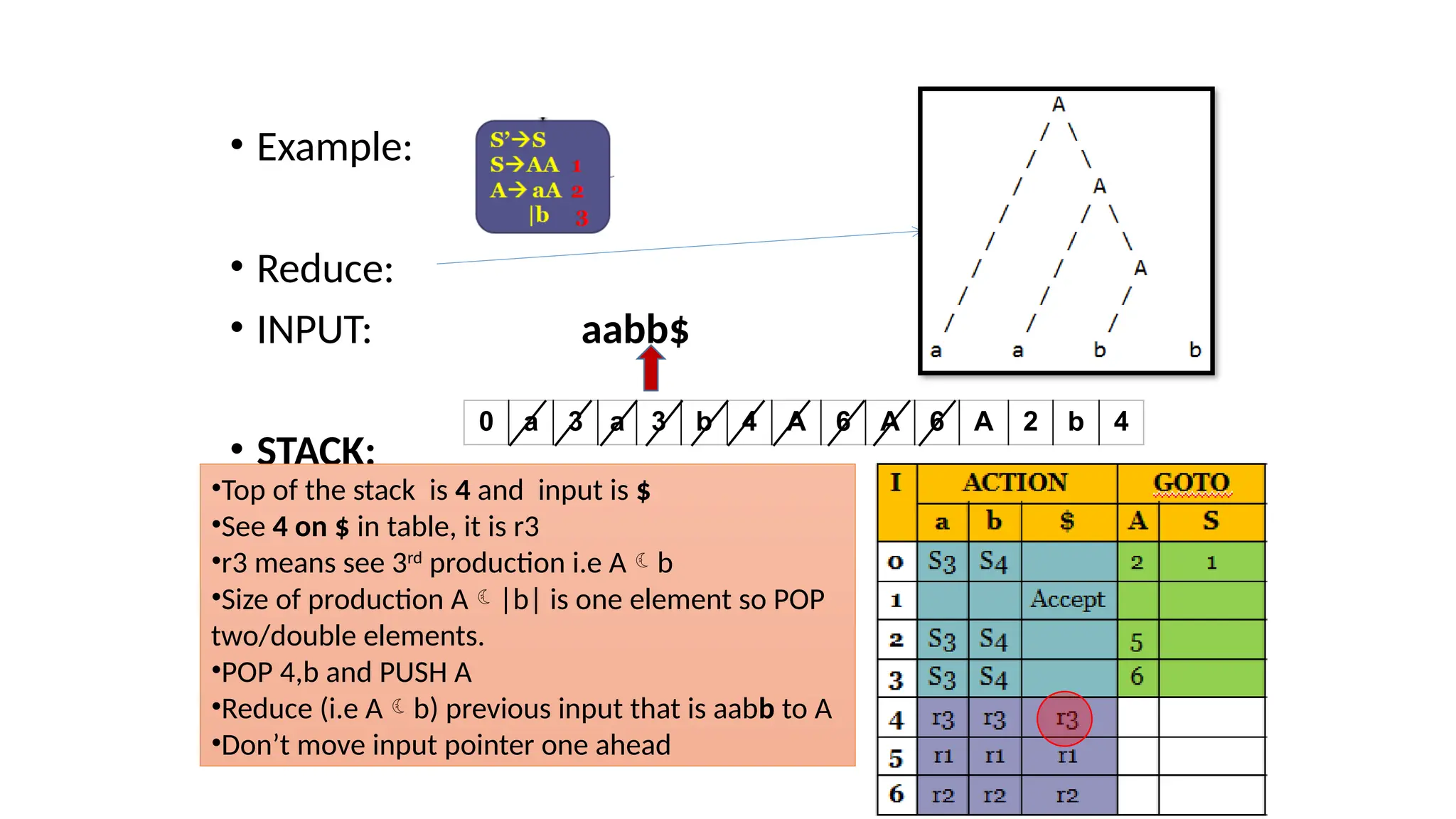
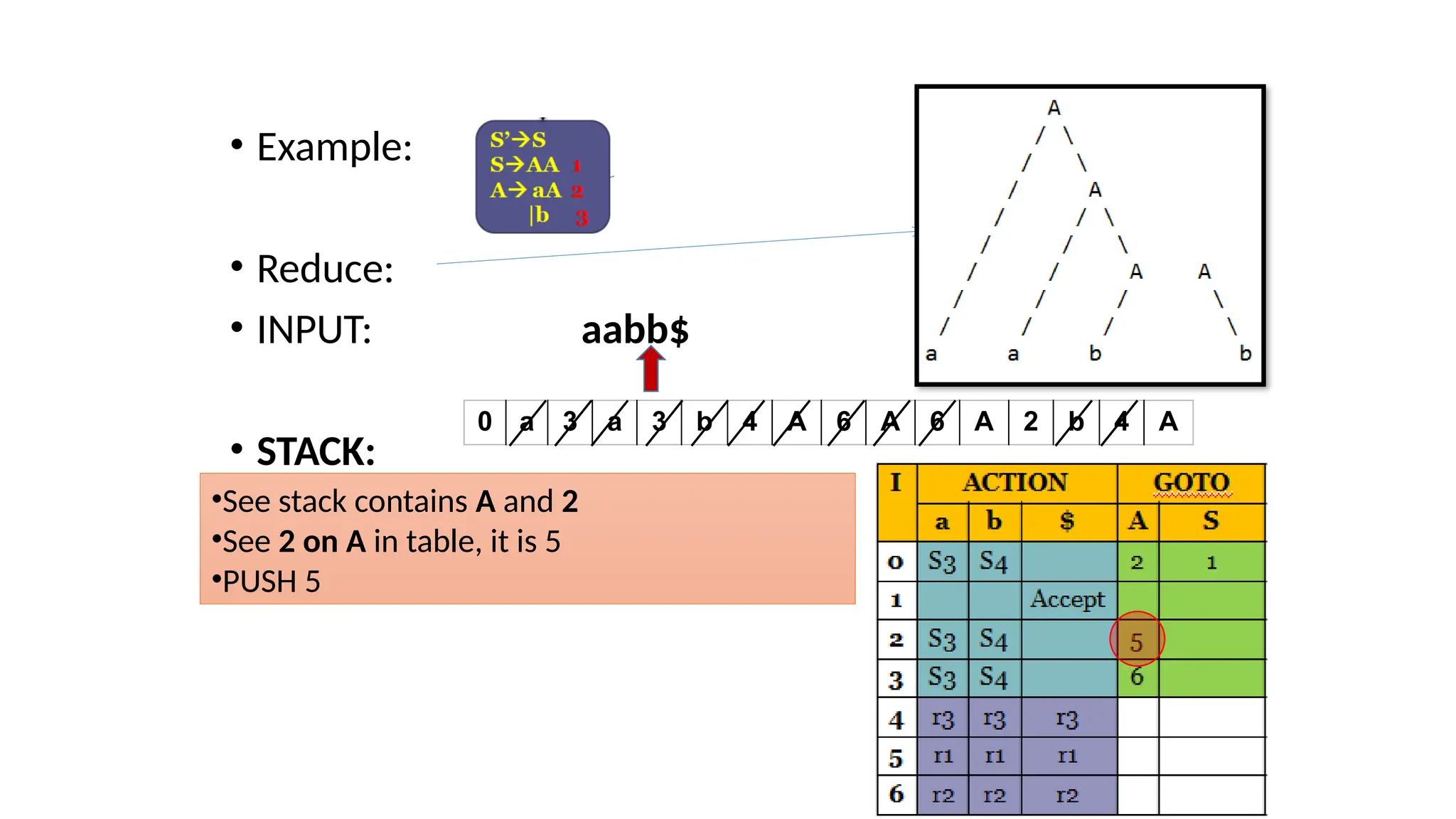
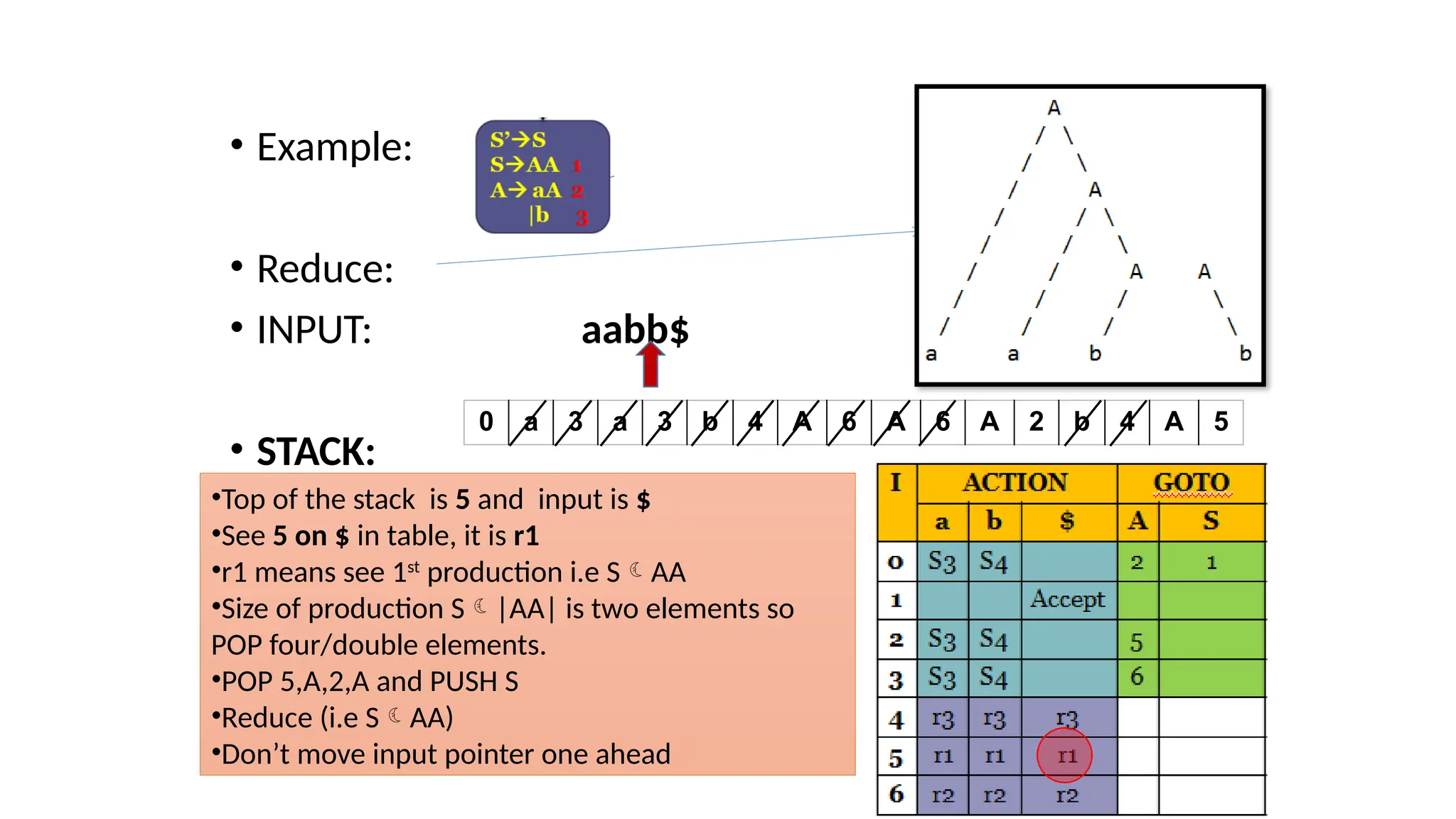
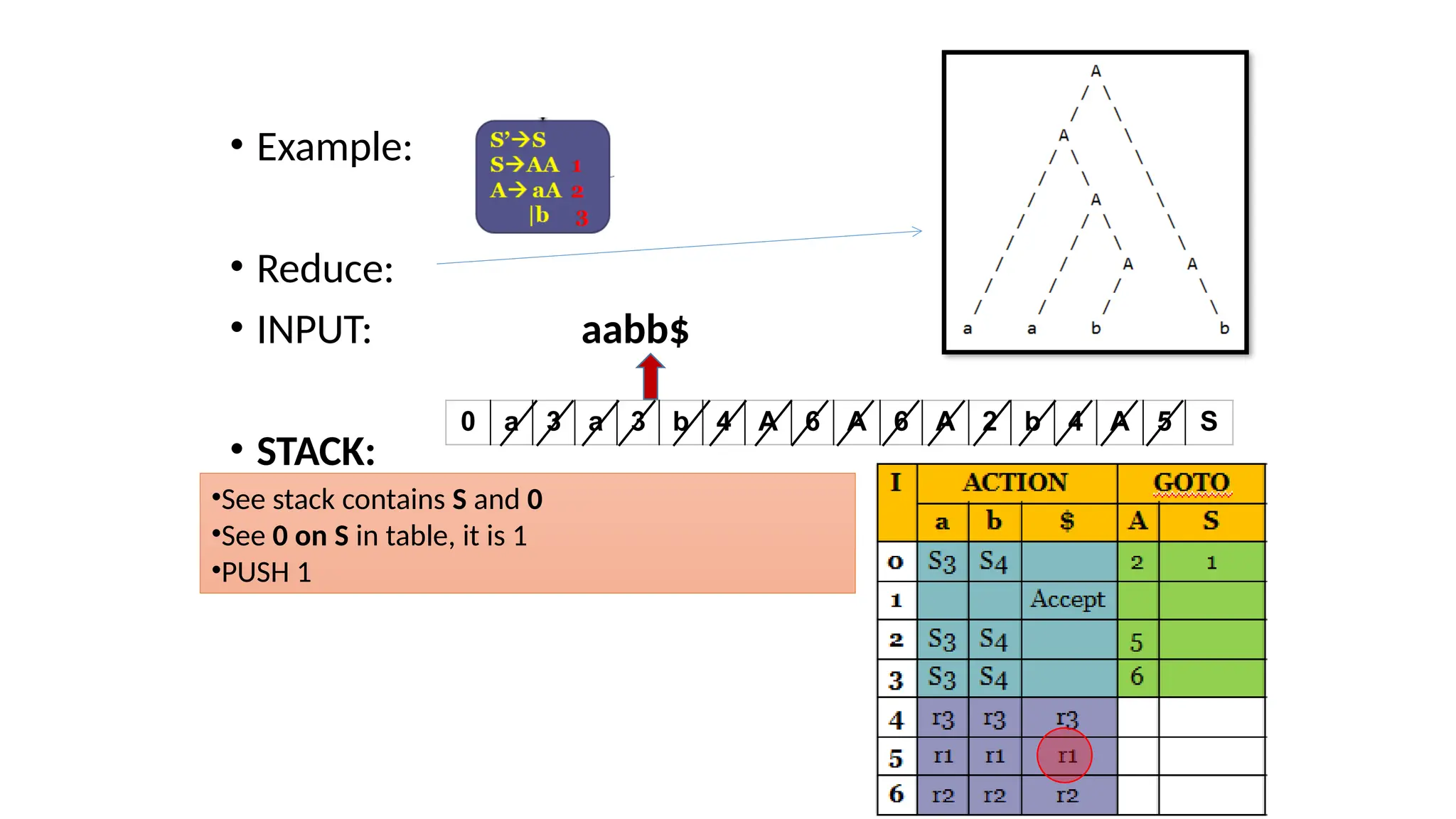
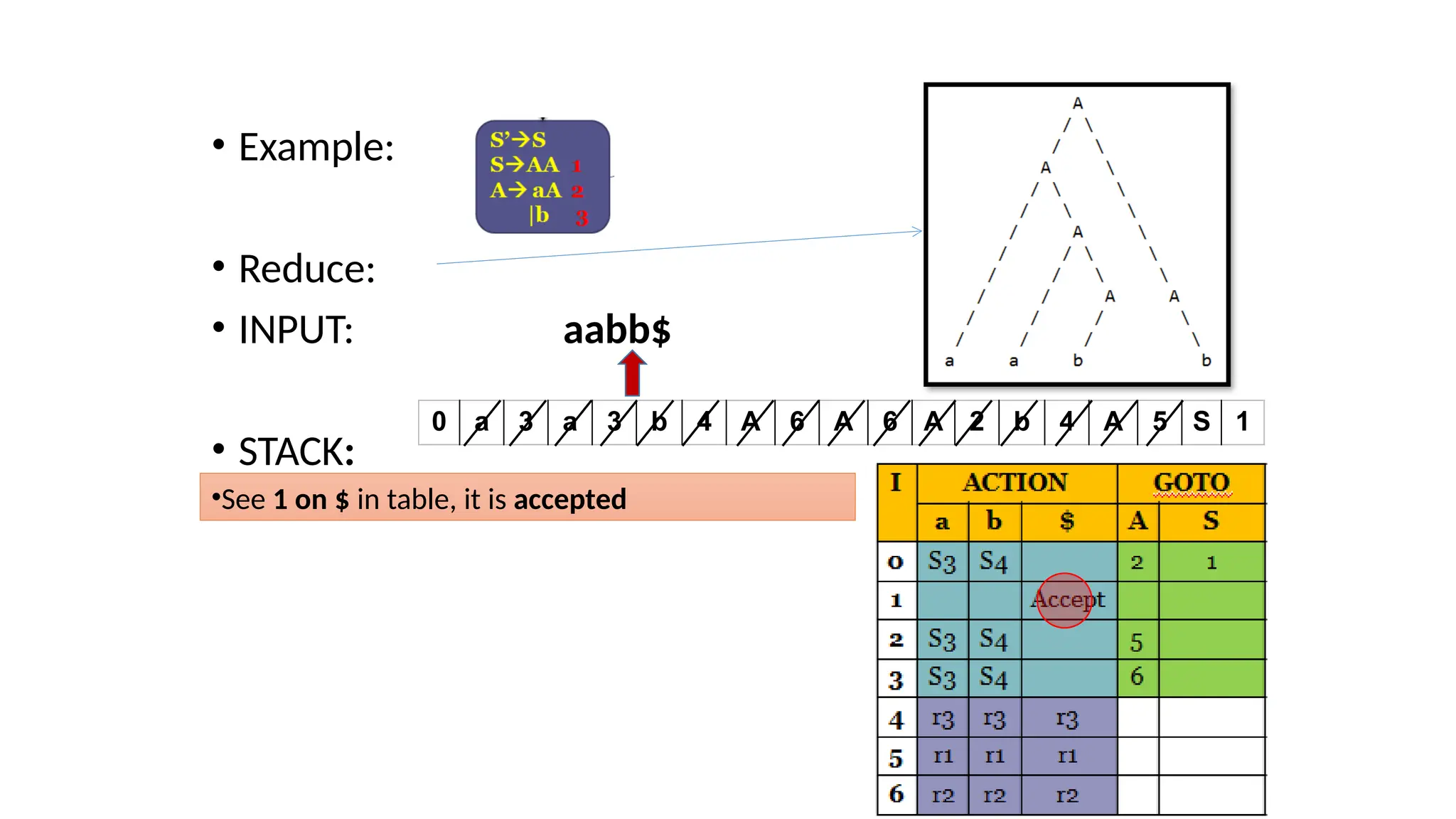
This document discusses bottom-up parsing techniques, particularly LR(0) parsers, which construct parse trees by starting from the leaves of the input string and working upwards. It explains shift-reduce parsing actions, potential conflicts during parsing, and different types of LR parsers and their efficiencies. The text also provides examples of LR(0) parsing tables and parsing processes, highlighting the challenges and methods for constructing these parsers.