Study on Adaptive PID Control Algorithm Based on RBF Neural Network

Study on Adaptive PID Control Algorithm Based on RBF Neural Network

• 1.
  TELKOMNIKA Indonesian Journalof Electrical Engineering Vol. 13, No. 2, February 2015, pp. 287 ~ 291 DOI: 10.11591/telkomnika.v13i2.6958  287 Received November 3, 2014; Revised December 19, 2014; Accepted January 2, 2015 Study on Adaptive PID Control Algorithm Based on RBF Neural Network Qi Xuemei，Zhang Jingdong School of Transportation and Automobile Engineering, Panzhihua University, Panzhihua, 617000, China Abstract Aim at the limitation of traditional PID controller has certain limitation, the traditionalPID control is often difficult to obtain satisfactory control performance, and the RBF neural networkis difficult to meet the requirement ofreal-time control system.To overcome it, an adaptive PID control strategy based on (RBF) neural network isproposed in this paper. The resultsshow that the proposed controller is practical and effective, because of the adaptability, strong robustness and satisfactory controlperformance.It is also revealed from simulation results that the proposed control algorithm is valid for DC motor and also provides the theoretical and experimental basis. Keywords: adaptive PID controller, RBF neural network, DC motor Copyright © 2015 Institute of Advanced Engineering and Science. All rights reserved. 1. Introduction PID controllers are the most common industrial process controller, its structure is simple, good robustness and high reliability, and the PID controller is widely used industrial process control [1]. However, the conventional PID controller has a certain limiting, especially the controlled object contains a nonlinear and time-varying characteristics,the traditionalPID control is often difficult to obtain satisfactory control performance [2]. Since the parameters empirical formula of PID controller is proposed by the Ziegler andNiehols, and the many methods have been used for the parameter setting of the PID controller. With the development of intelligent control theory, the intelligent control technology was introduced in PID control by many scholars, and provided new method means for the PID controltechnology.In recent years, the artificial neural network has been used in complex process control, and has attracted widespread attention [3, 4]. Because the neural network has adaptive learning, parallel processing and the strong ability of fault tolerance.The neural network adaptivePID control scheme which is locally approximated by the RBFnetworkis adopted in this paper, and in order to improve the system accuracy, robustness and adaptiveness [5]. 2. RBF function The Radial Basis Function (RBF) is a neural network which was put forward by J.Moodyand C.Darken in the late 1980s, it is a three layer feed forward network with single hidden layer (Figure 1), is a kind of local approximation of the neural network. The RBFis a kind of three layer forward network. The mapping which is from the input to the output is nonlinear, and the mapping which is from hidden layer space to the output space is linear [6]. It simulates the neural network structure for the partial adjustment of the human brain and each receiving domain. RBF is a kind of local approximation network, which has been proved that the any precision approximates any continuous function. This kind of network characteristics is that it onlyhas a few output of connection power influence aim at local input space, so that local approximation network has the advantages of fasterlearning speed [7]. Therefore, the RBF network can significantly accelerate the learning speed and avoid local minimum problem, which is suitable for the real-time control.
• 2.
   ISSN: 2302-4046 TELKOMNIKAVol. 13, No. 2, February 2015 : 287 – 291 288 Figure 1. Three layer feed forward network with single hidden layer In the structure of RBF network, 1 2[ , , ]T nX x x x  is the input vector of network. Assuming the radial basis vectors of the RBF network is 1 2[ , , ]T nH h h h  . Where jh isgaussian basis function: 2 2 exp( ), 1, 2, . 2 j j j X C h j m b      (1) The j network node of center vector is , 1 2 , ,[ , , ]T i j j j i j n jC c c c c   . Assuming the basis width vector of network is 1 2[ , , ]T mB b b b  , jb is the basis width parameter of node, and is greater than zero. The weight vector of network is 1 2[ , , ]mW w w w  .The output of the network is given as: 1 1 2 2( )m m my k wh w h w h w h     (2) Assuming the ideal output is ( )y k , the performance index function is: 21 ( ) ( ( ) ( )) 2 mE k y k y k  (3) Based on the gradient descent method, the iterative algorithm of output power, node center and base width parameterare: ( ) ( 1) ( ( ) ( )) ( ( 1) ( 2))j j m j j jw k w k y k y k h w k w k         (4) 2 3 ( ( ) ( )) j j m j j j X C b y k y k w h b     (5) ( ) ( 1) ( ( 1) ( 2))j j j j jb k b k b b k b k         (6) , 2 ( ( ) ( )) j ji j i m j j x c c y k y k w b     (7) ( ) ( 1) ( ( 1) ( 2))ij ij ij ij ijc k c k c c k c k         (8) Where  is learning rate, is momentum factor.
• 3.
  TELKOMNIKA ISSN: 2302-4046 Study on Adaptive PID Control Algorithm Based on RBF Neural Network (Qi Xuemei) 289 Jacobian matrix algorithm is as follows: 1 1 2 1 ( )( ) ( ) ( ) m jm j j j j c xy ky k w h u k u k b       (10) Where 1 ( )x u k . 3. Design of Adaptive PID Controller Based on the BRF Neural Network There are many function form of RBF neural network, Gauss function was selected inthis article as the hidden layer node function according to its unique advantages [8]. Based on the RBF neural network, the adaptive PID control system structure is as shown in Figure 2. Neural network adaptive PID controller adjusts the connection weights of neural network NN and the three parameters of PID according to the square error of the given input and system outputas the objective function [9]. The PID controller is applied to the controlled object, and makes the system output close to the given input of system. Figure 2. Adaptive PID Controller based on the BRF neural network The control error of PID controlleris given as following: ( ) ( ) ( )error k rin k yout k  (11) The three inputs of PID is given following as: (1) ( ) ( 1)xc error k error k   (12) (2) ( )xc error k (13) (3) ( ) 2 ( 1) ( 2)xc error k error k error k     (14) Control algorithm is given as: ( ) ( 1) ( )u k u k u k    (15) ( ) ( ( ) ( 1)) ( ) ( ( ) 2 ( 1) ( 2)) p i d u k k error k error k k error k k error k error k error k          (16) Where , ,p i dk k k arethe proportion, integral and differential parameters respectively. The tuning index of neural network is selected as: 21 ( ) ( ) 2 E k error k (17) The gradient descent method is used for adjustment of , ,p i dk k k .
• 4.
   ISSN: 2302-4046 TELKOMNIKAVol. 13, No. 2, February 2015 : 287 – 291 290 ( ) (1)p p p E E y u y k error k xc k y u k u                    (18) ( ) (2)i i i E E y u y k error k xc k y u k u                    (19) ( ) (3)d d d E E y u y k error k xc k y u k u                    (20) The y u   can be obtained by the identification of neural network. 4. Simulation In this section, using the PID control principle based onRBF neural networkmakes simulationfor DC motor in MATLAB. Parameters of the system for simulation are:KP=0.3, KD=0.3, KI=0.1,the transfer function of the DC motor is: 2 103 ( ) 15 G s s s   (21) Where the sampling time is 2ms, the input signal is step signal, network hidden layer neurons number is m = 6.The Figure 3 shows the square wave response curve without the adaptive setting PID control strategy based on RBF neural network. The Figure 4 shows the square wave response curve with the adaptive setting PID control strategy based on RBF neural network. The Figure 5, Figure 6 and Figure 7 reflect the process of PID parameter adjustment. From the simulation curve we can see that the adjusted online PID controller based on the RBF neural network has good control effect, and the control effect comparing simple PIDis greatly improved. This shows that aim at the controlled object which has nonlinear and time-varying parameter, the algorithm has trace ability and anti-interference ability. Figure 3. The step signal without the adaptive settingPID based on RBF NN Figure 4. The step signal with the adaptive setting PID based on RBF NN
• 5.
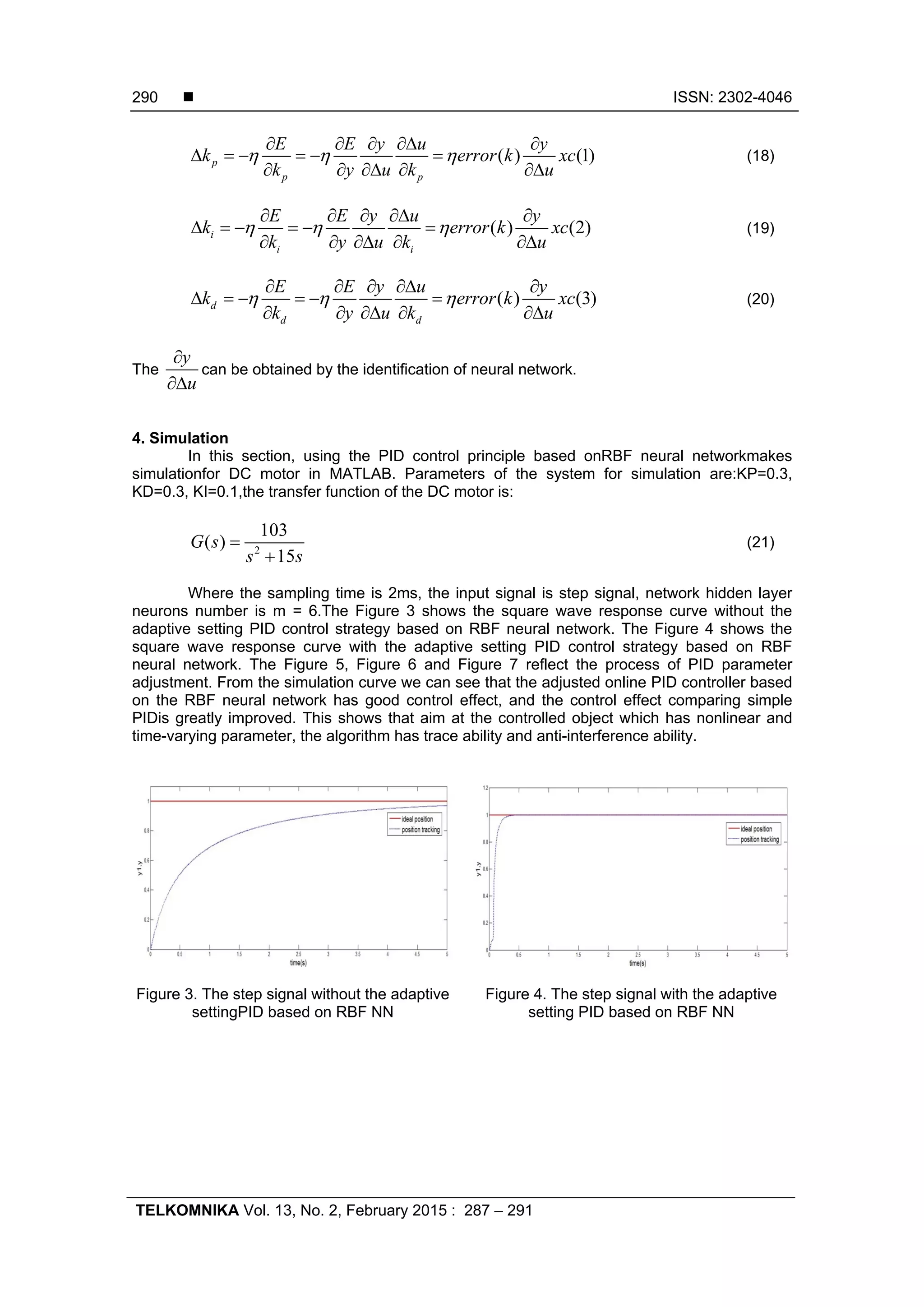
  TELKOMNIKA ISSN: 2302-4046 Study on Adaptive PID Control Algorithm Based on RBF Neural Network (Qi Xuemei) 291 Figure 5. The adaptive setting curve of ki Figure 6. The adaptive setting curve of kp Figure 7. The adaptive setting curve of kd 5. Conclusion In this paper, based on RBF neural network adaptive PID control strategyis proposed for the DC motor. The results show that the proposed controller is practical and effective, because of the adaptability, strong robustness and satisfactory control performance. RBFNeural network adaptive PID controller achieved good control effect. It is also revealed from simulation results that the proposed control algorithm is valid for DC motor and also provides the theoretical and experimental basis, and the controller is a kind of practical engineering. References [1] Li Lixiang, Peng Haipeng, Wang Xiangdong. PID parametertuning based on chaotic ant swarm. Chinese Journal ofScientific Instrument. 2006; 27(9): 1104-1106. [2] KH Ang, G Chong, Y Li. PID Control System Analysis, Design and Technology. IEEE Trans. on Control SystemTechnology. 2005; 13(4): 559-576. [3] Li Yuying, Wen Qiaoyan, Li Lixiang, Peng Haipeng, Zhu Hui. Improved chaotic ant swarm algorithm. Chinese Journal of Scientific Instrument. 2009; 30(4): 733-737. [4] ZHI Hui-qiang, YANG Zeng-jun, TIAN Liang. AComparative Study on BP Network and RBF Networkin Function Approximation. Bulletin of Science andTechnology. 2005; 21(2):193-196. [5] Xia Hong. A fast identification algorithm for box-coxtransformation based radial basis function neural network. IEEE Transactions on Neural Networks. 2006; 17(4): 1064-1069 [6] ZHAN Li, SUN Peng, CHEN Wen-bai. Control of SwingUp and Stabilization of an Inverted Pendulum System. Computer Simulation. 2006; 23(8): 289-292 [7] CONG Shuang, ZHANG Dong-jun, WEI Heng-hua.Comparative Study on Three Control Methods of theSingle Inverted-Pendulum System. SystemsEngineering and Electronics. 2001; 23(11): 47－49 [8] Zhang Jingdong, Wen Guang, Wei Yongqiao, Yin Guofu. RBF Neural Network PID for Bilateral Servo ControlSystem. TELKOMNIKA. 2013; 11(9): 5200-5209 [9] Liu Jinkun. MATLAB Simulation with Advanced PID Control. Publishing House of Electronics Industry, Beijing. 2011.