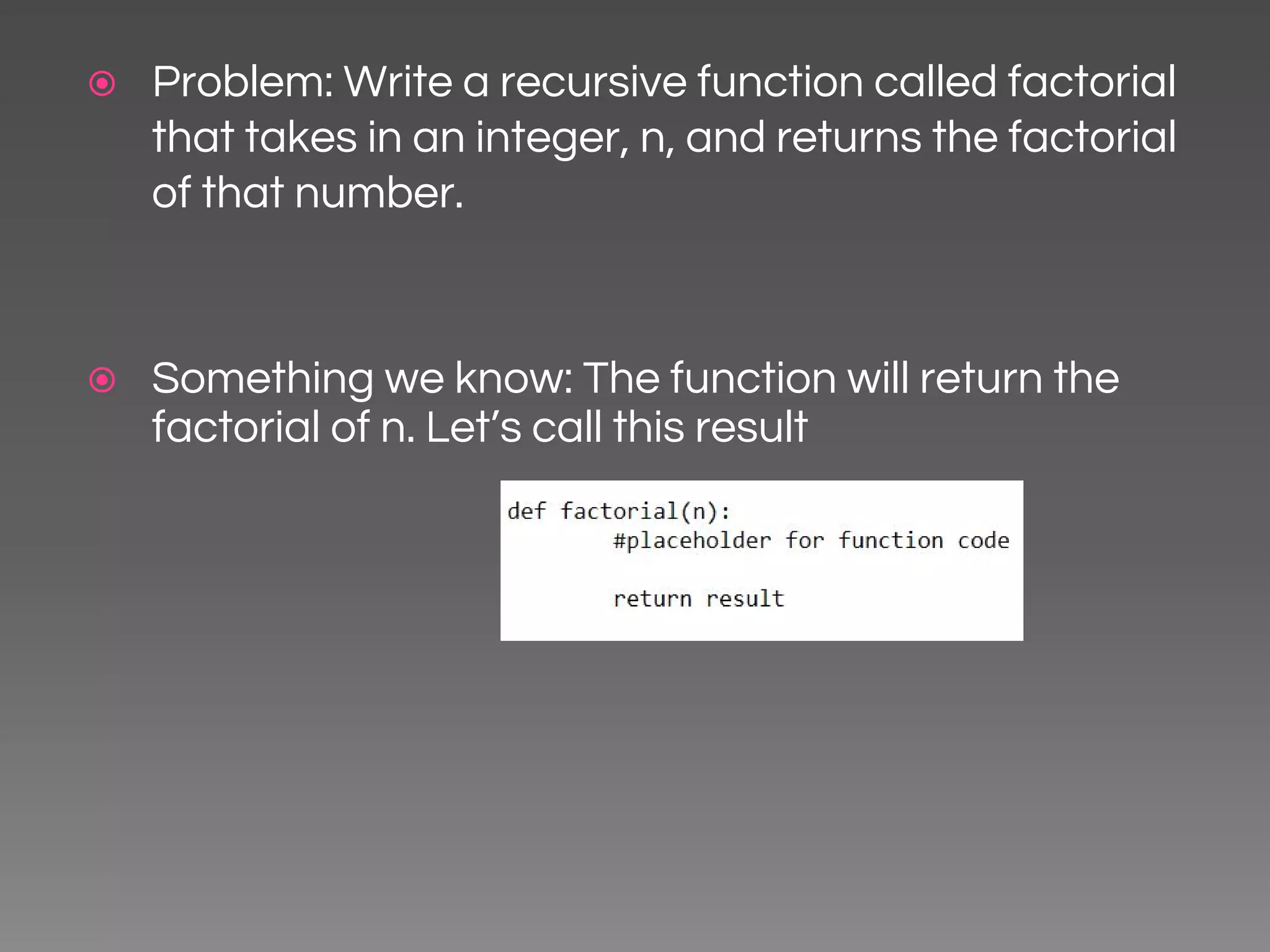
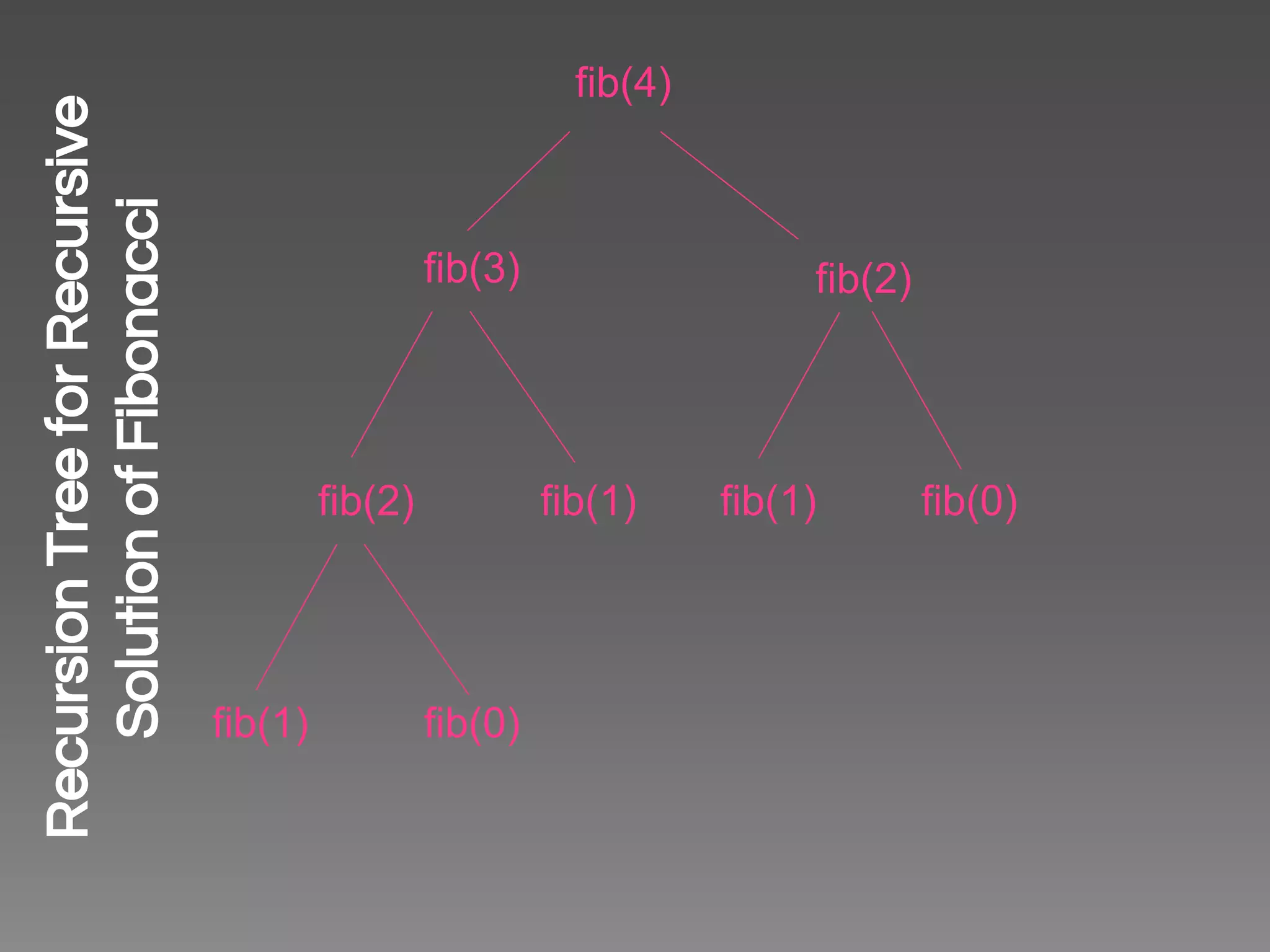
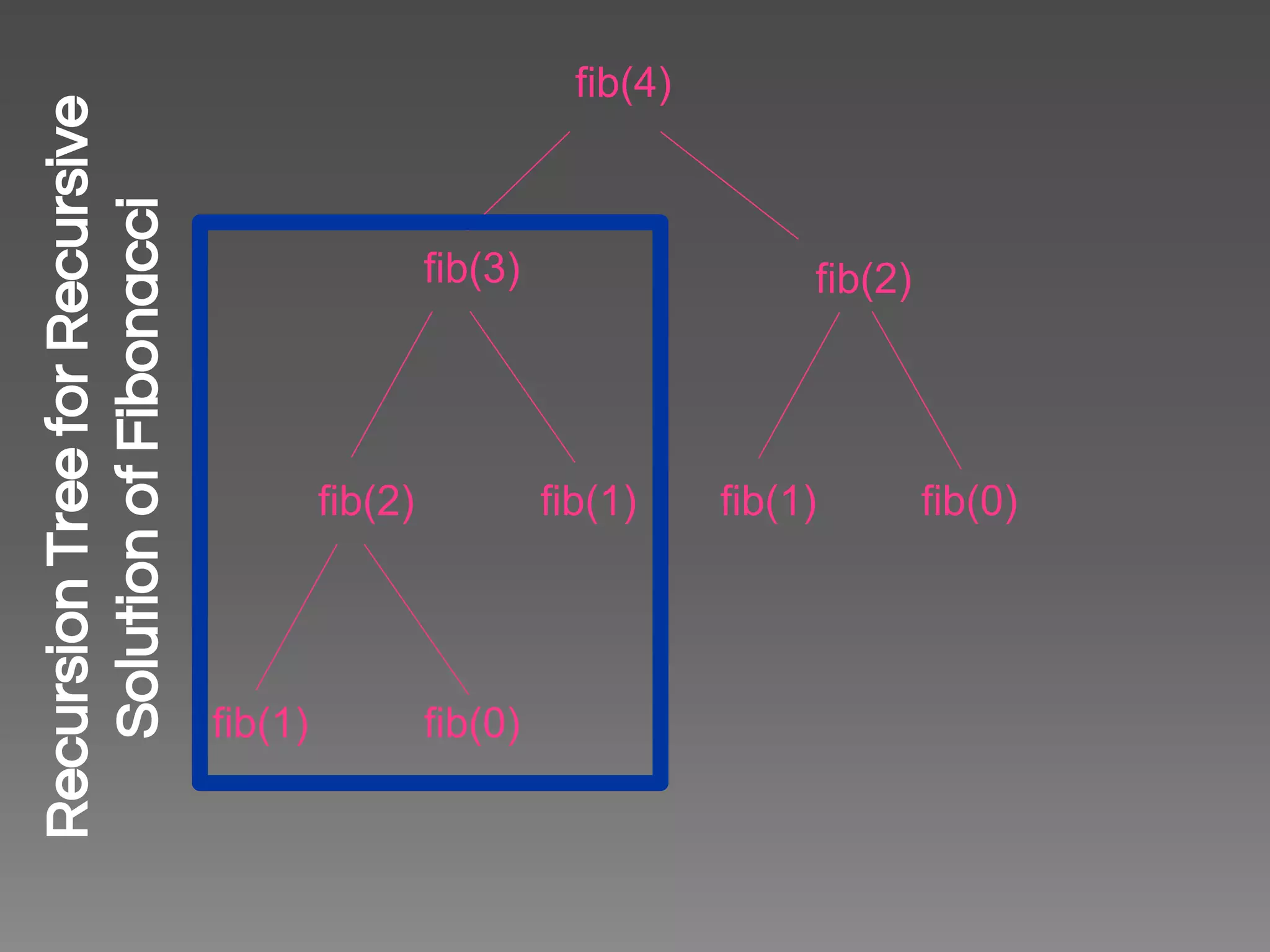
The document provides an introduction to recursion through a presentation on defining the factorial function recursively. It begins by explaining why recursion is an important concept for technical interviews. It then defines recursion conceptually, using the factorial function to illustrate a recursive definition. It emphasizes the need for a base case to terminate the recursion. The presentation walks through defining the factorial function recursively step-by-step and translates the definition into code. It concludes by providing tips for approaching recursive problems in general.