Andrea Tassi, profile picture
Uploaded byAndrea Tassi
371 views

On Optimization of Network-coded Scalable Multimedia Service Multicasting

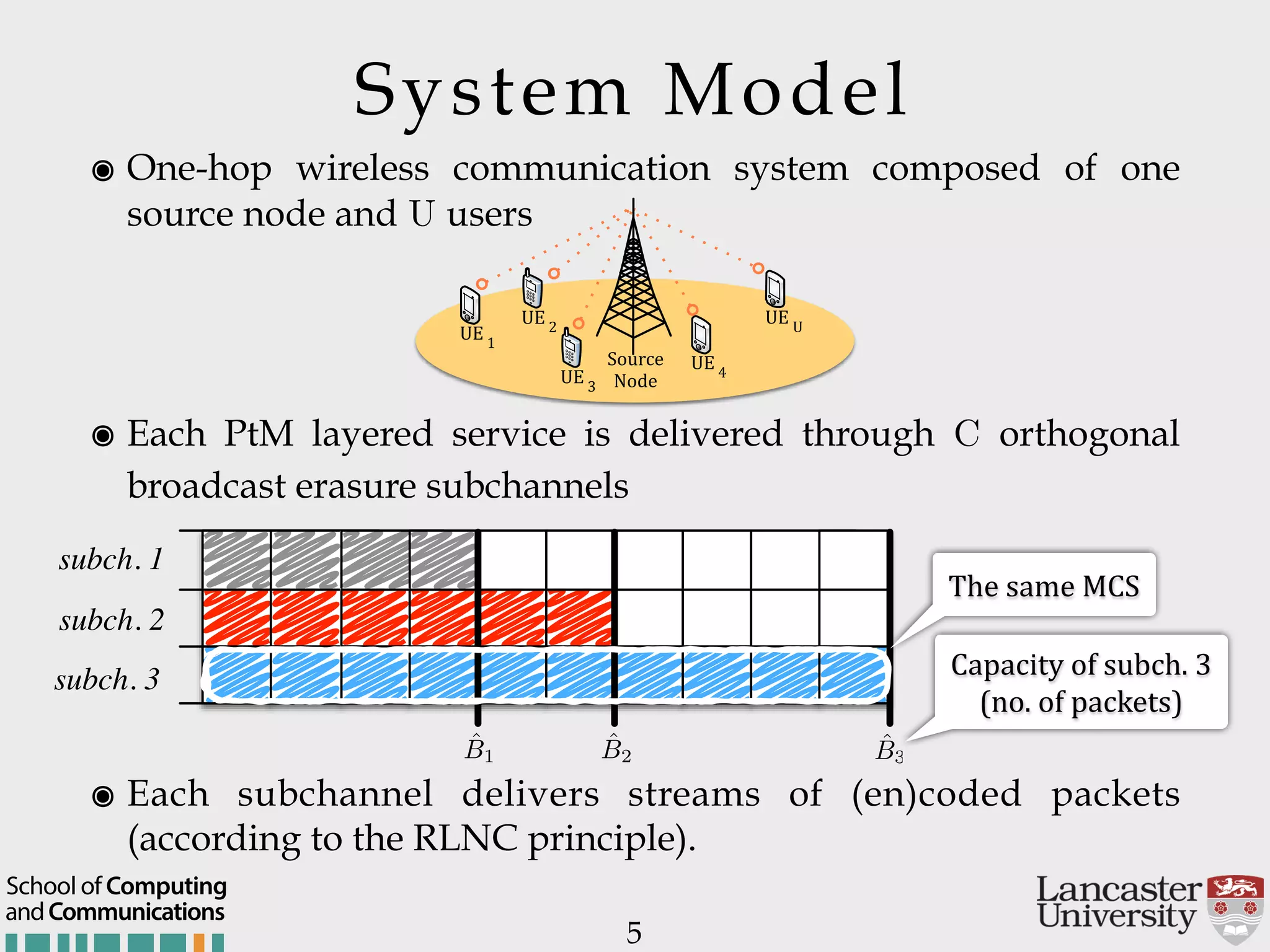
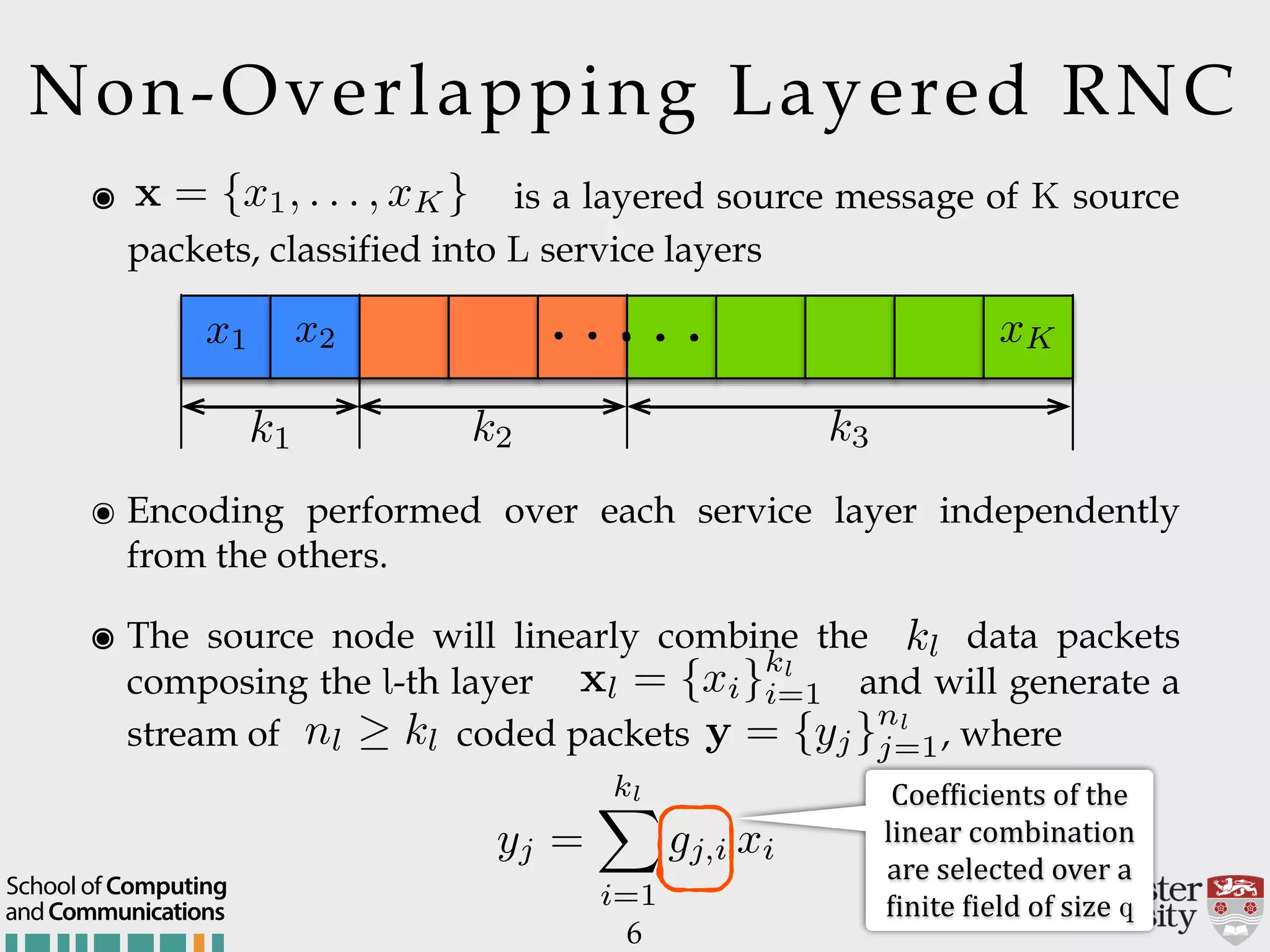
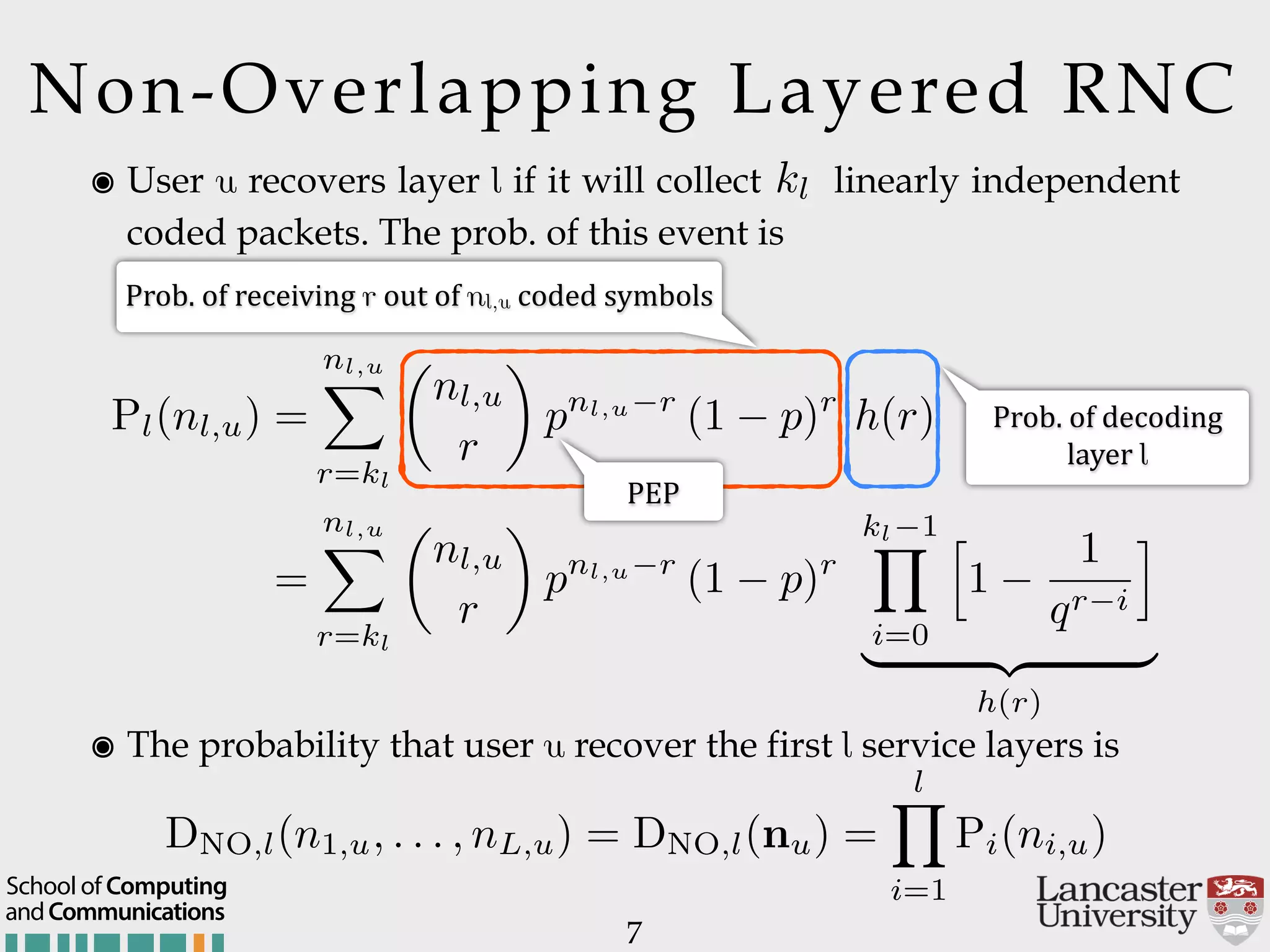
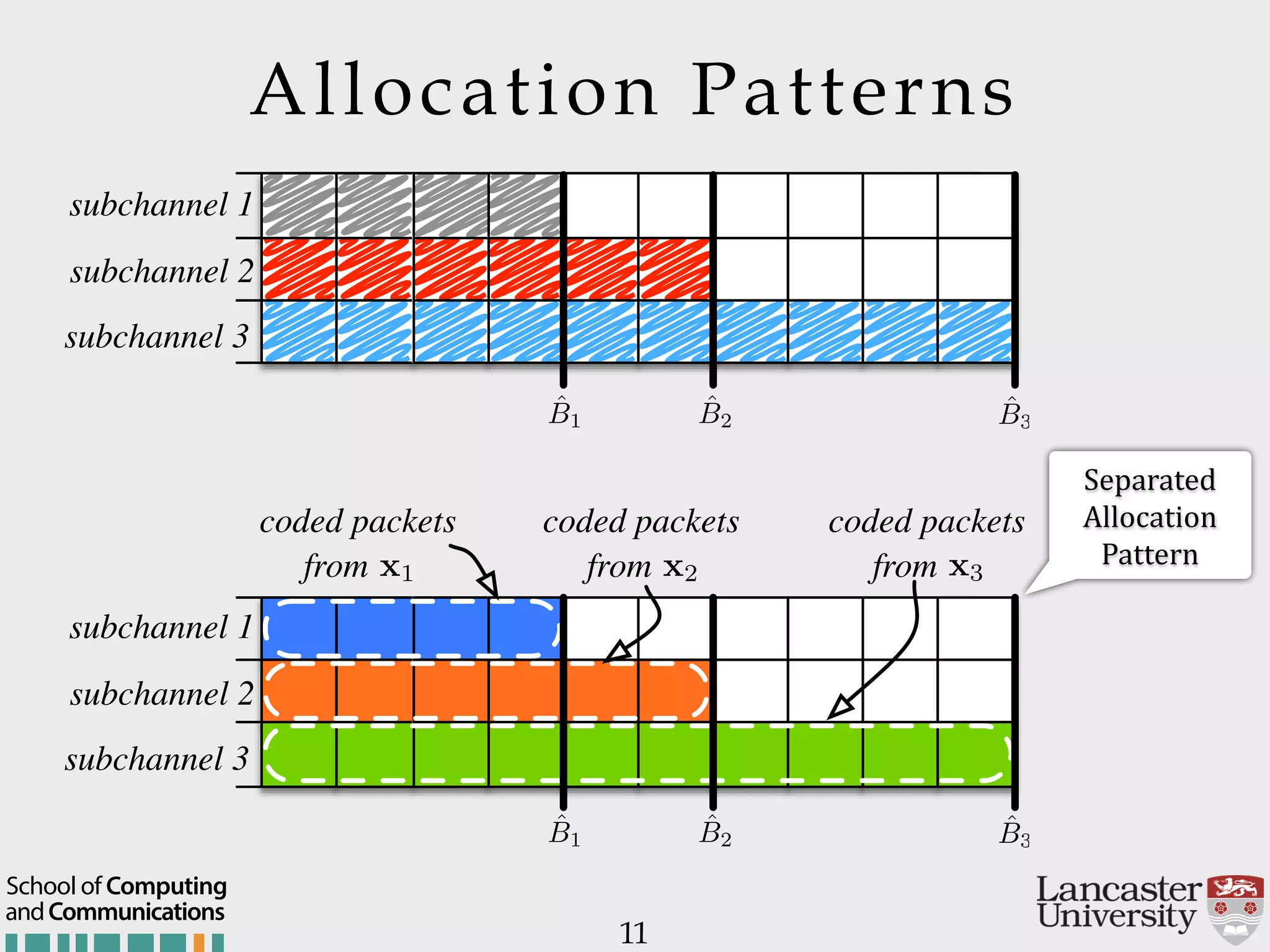
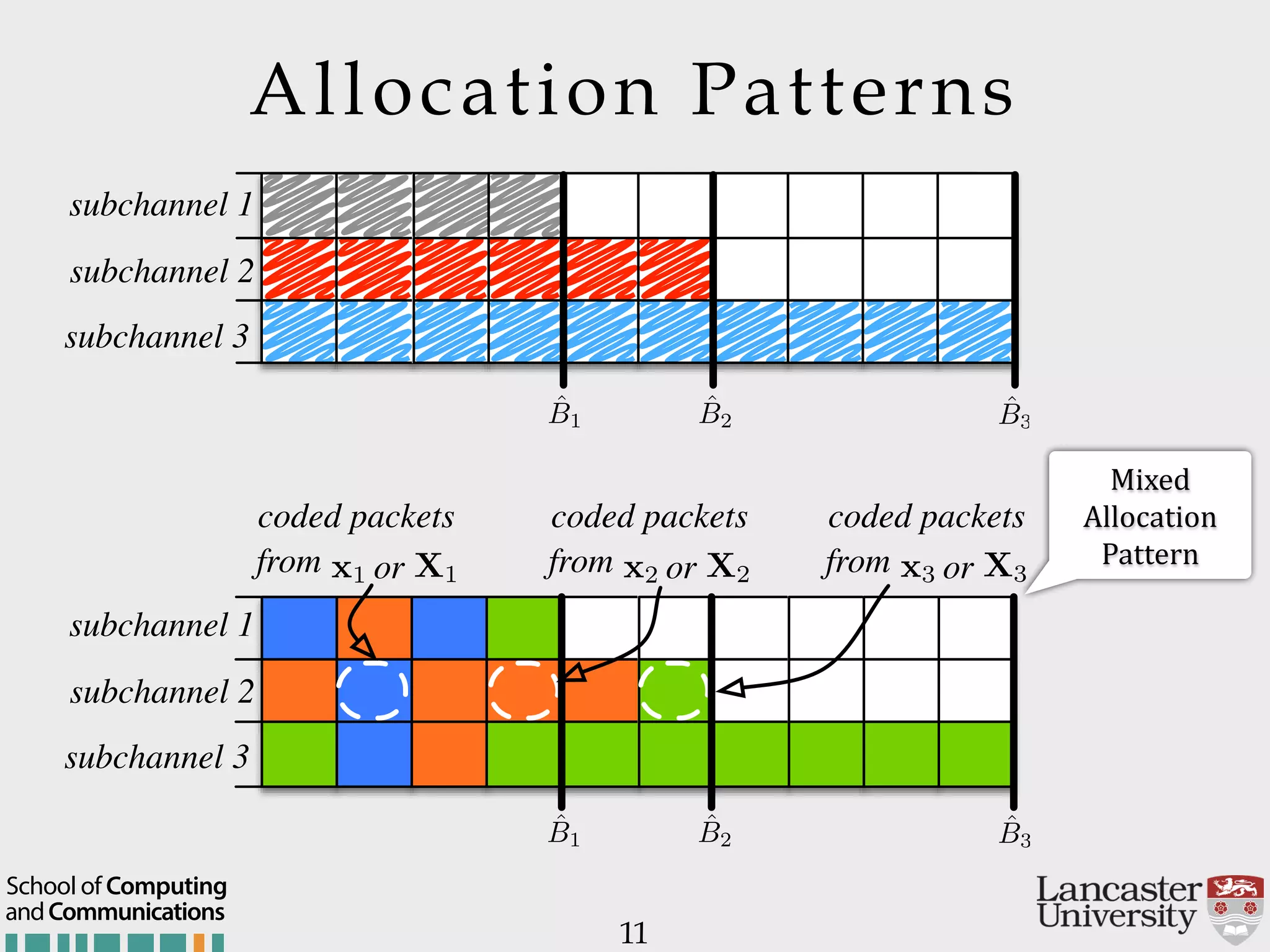
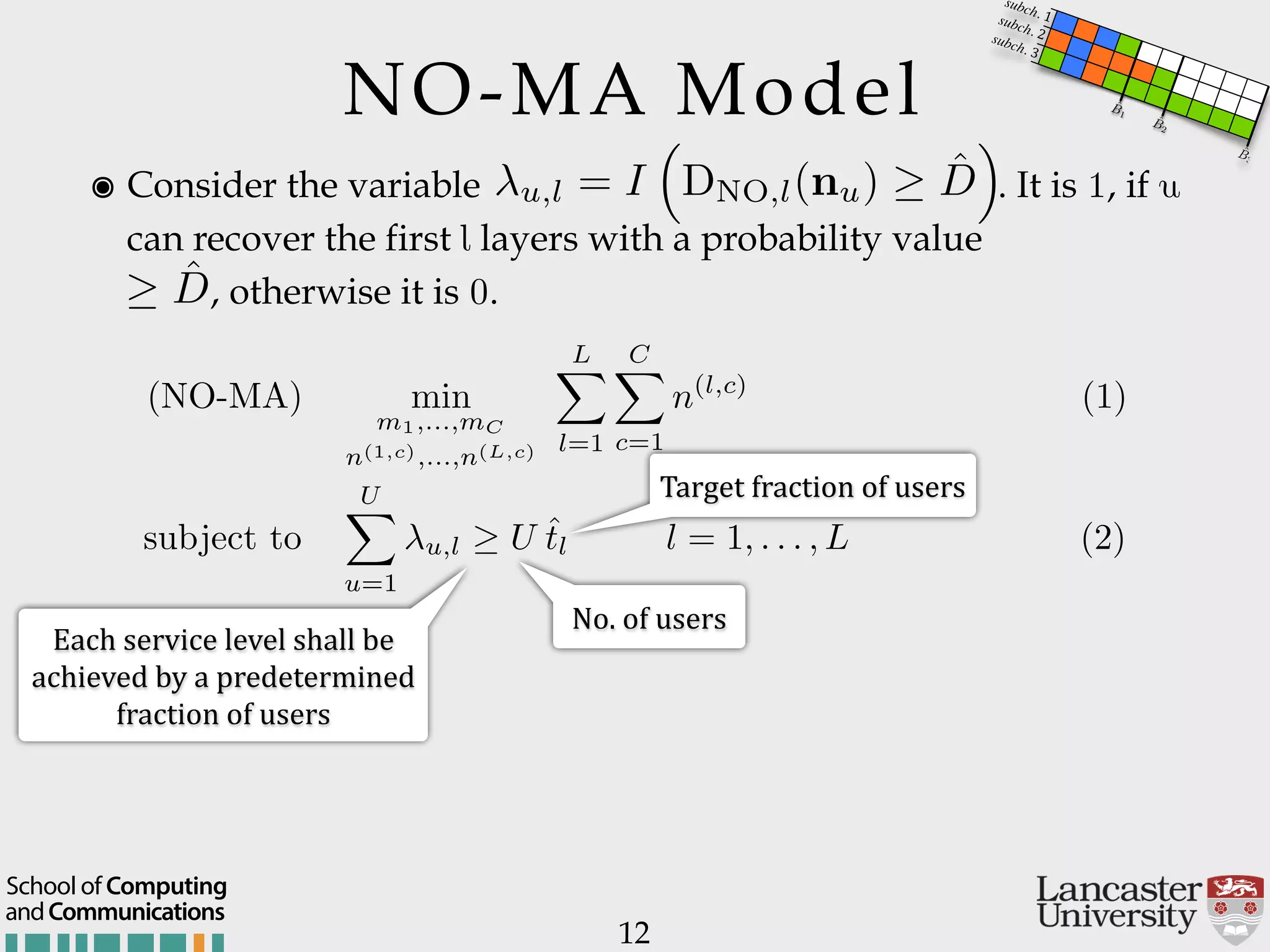
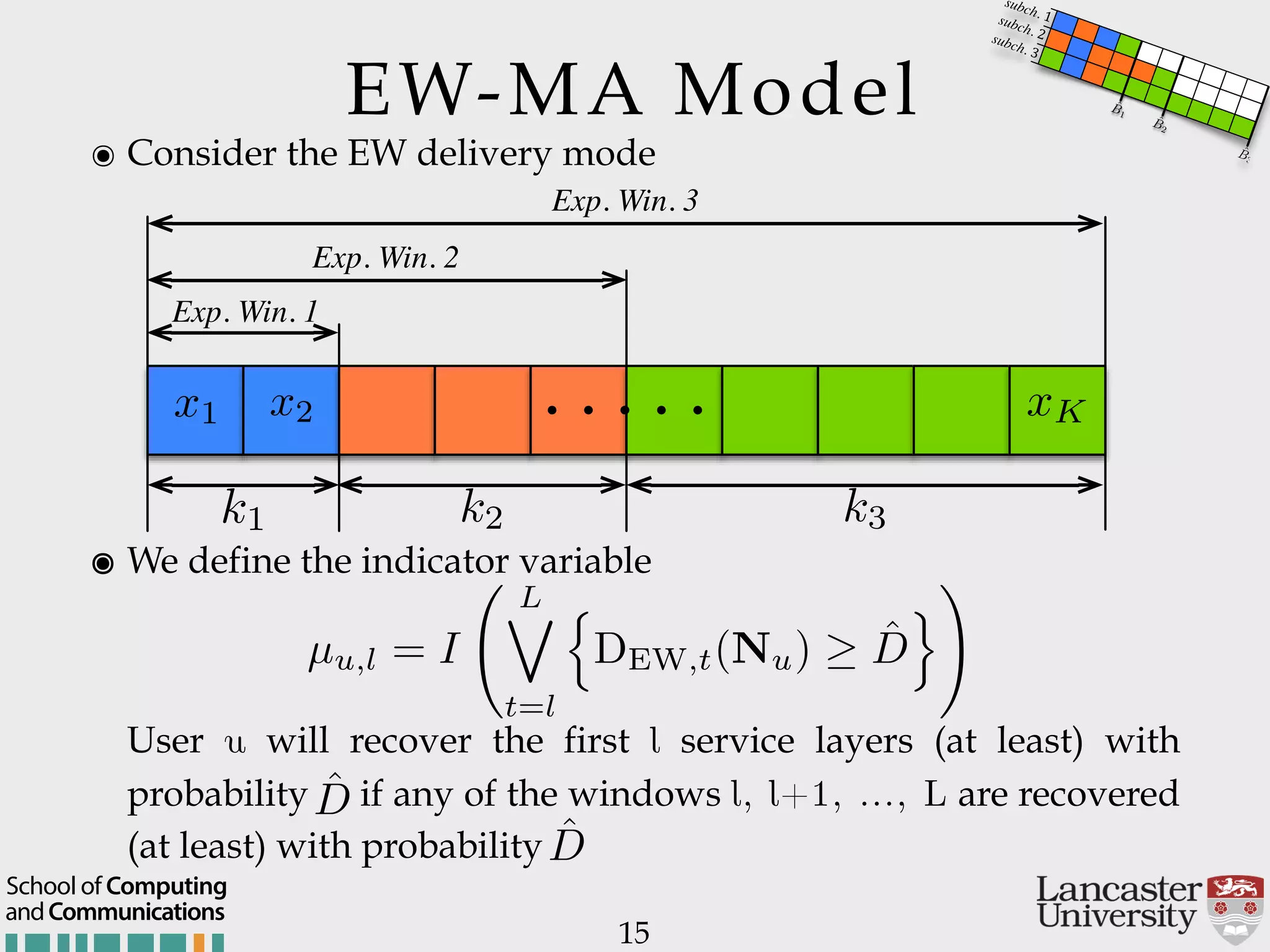
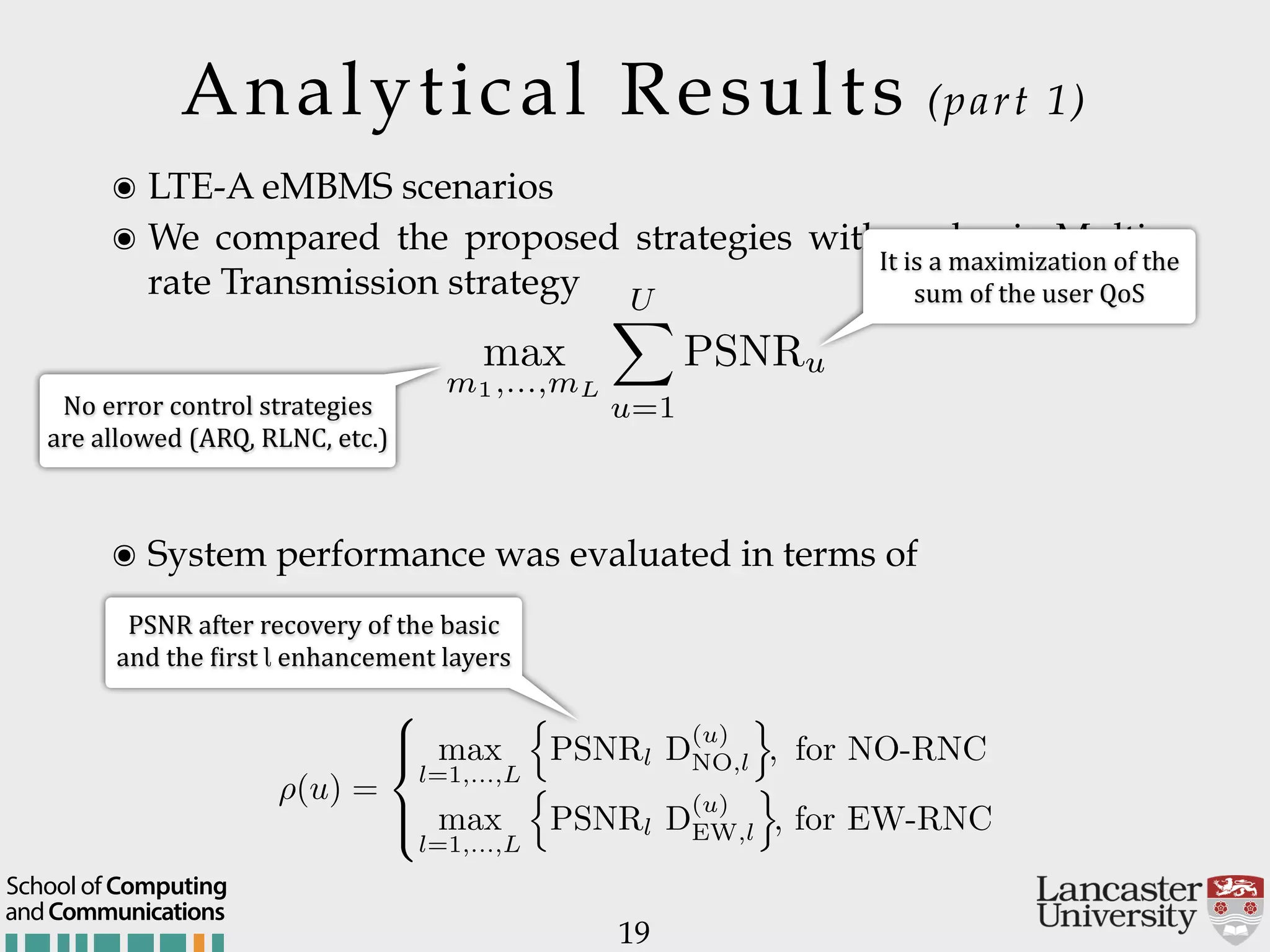
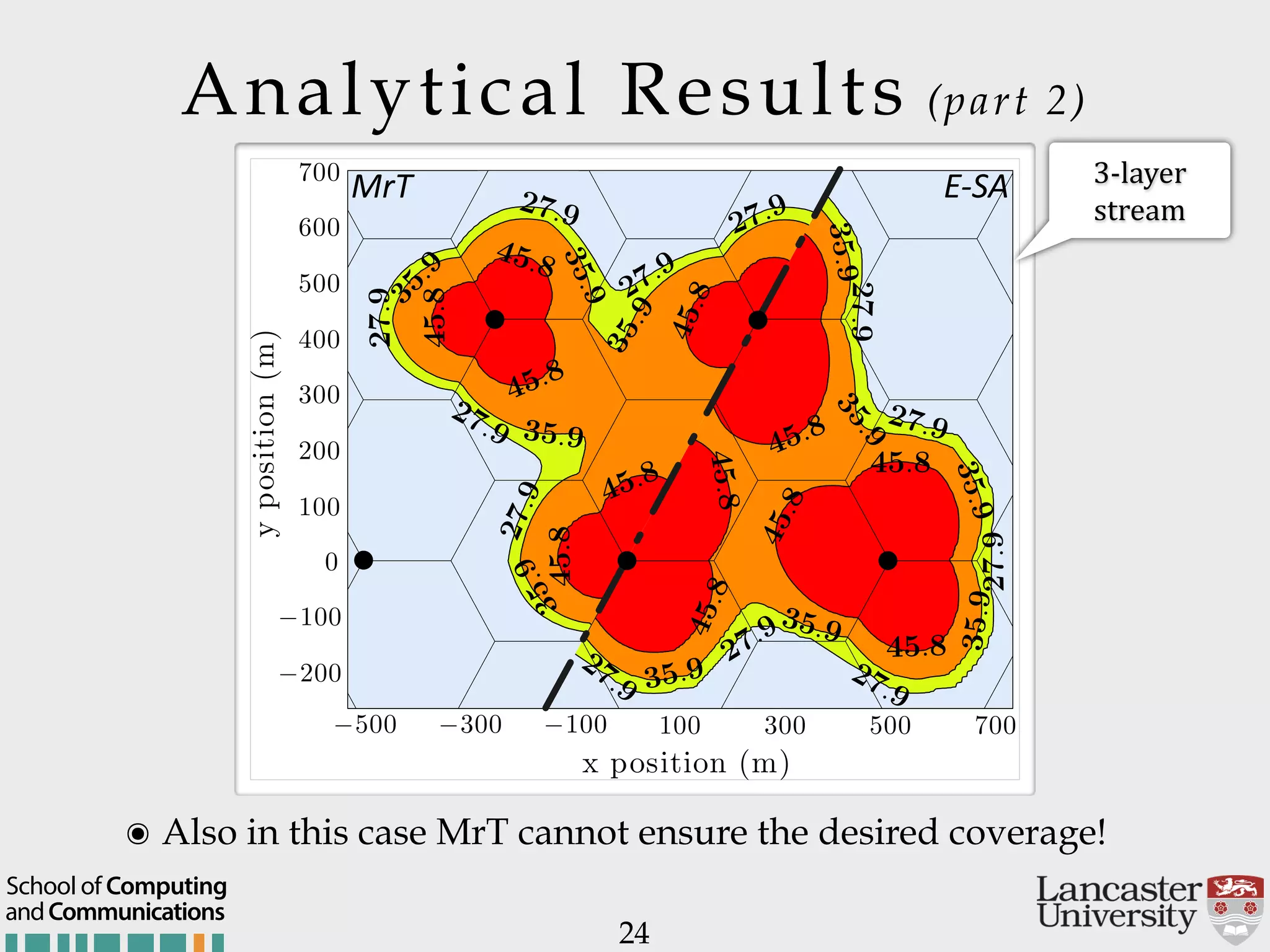
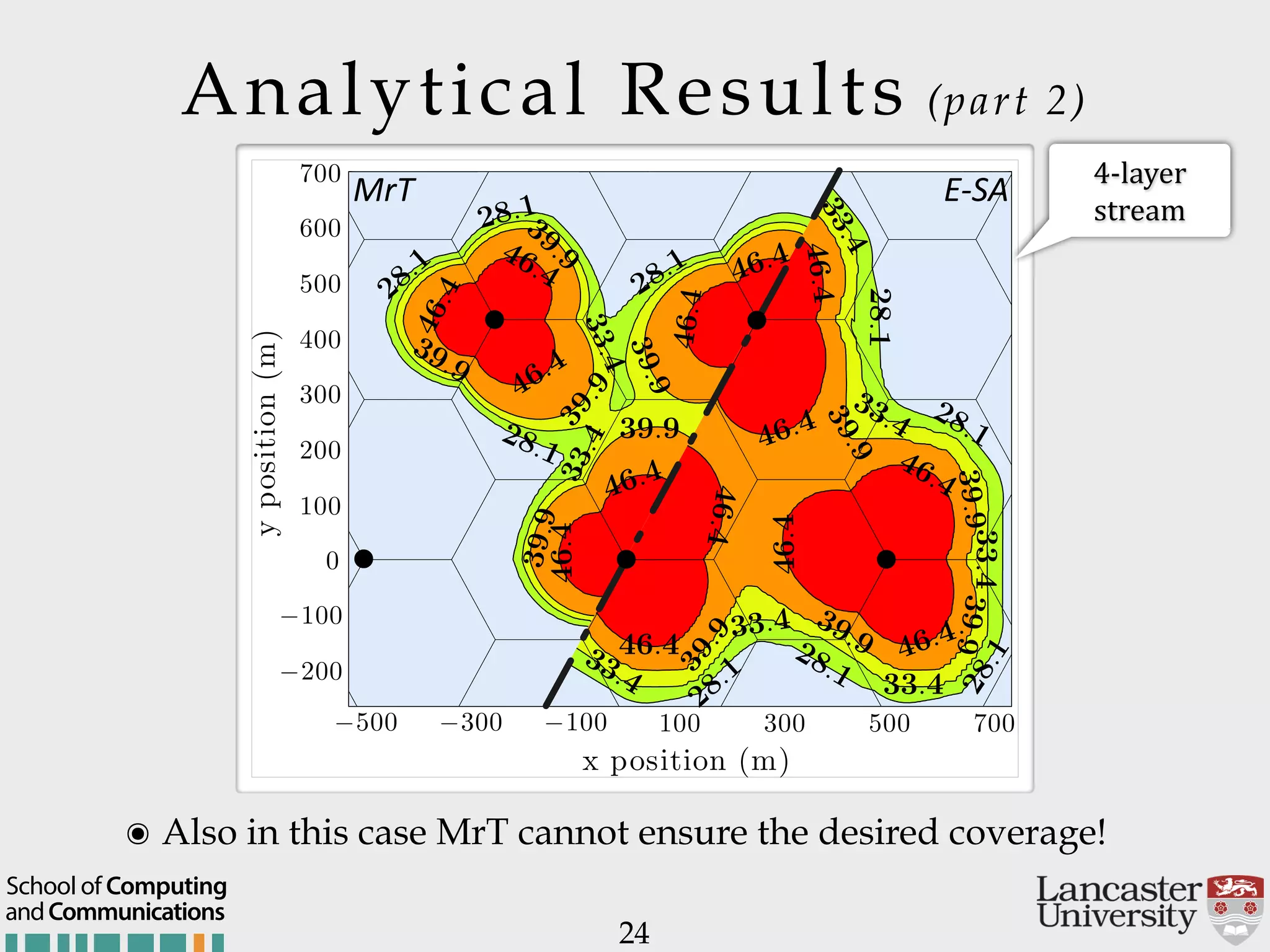
The document outlines the R2D2 project focused on optimizing data delivery for multimedia broadcasting over 4G/5G networks, particularly through error control and resource optimization strategies. It discusses a multi-rate transmission system that delivers layered services to users based on their channel conditions, utilizing techniques like Random Linear Network Coding (RLNC). Additionally, various resource allocation models and heuristic strategies are proposed to enhance the efficient delivery of service levels while minimizing radio resource usage.

Internet◦
Related topics:
Resource Allocation•
Download to read offline
Bristol, 5th February 2015 R2D2: Network error control for Rapid and Reliable Data Delivery Project supported by EPSRC under the First Grant scheme (EP/L006251/1) On Optimization of Network-coded Scalable Multimedia Service Multicasting University of Bristol Andrea Tassi and Ioannis Chatzigeorgiou {a.tassi, i.chatzigeorgiou}@lancaster.ac.uk andCommunications School of Computing
Starting Point and Goals ๏ Delivery of multimedia broadcast/multicast services over 
 4G/5G networks is a challenging task. This has propelled research into delivery schemes. ๏ Multi-rate Transmission (MrT) strategies have been proposed as a means of delivering layered services to users experiencing different downlink channel conditions. ๏ Layered service consists of a basic layer and multiple enhancement layers. Goals ๏ Error control - Ensure that a predetermined fraction of users achieves a certain service level with at least a given probability ๏ Resource optimisation - Reduce the total amount of radio resources needed to deliver a layered service. 2 andCommunications School of Computing
Index 1. System Parameters and Performance Analysis 2. Multi-Channel Resource Allocation Models and Heuristic Strategies 3. Analytical Results 4. Concluding Remarks 3 andCommunications School of Computing
1. System Parameters and Performance Analysis andCommunications School of Computing
System Model ๏ One-hop wireless communication system composed of one source node and U users 5 UE 1 UE 3 UE 2 UE 4 UE U Source Node ˆB3 ˆB2 ˆB1 subch. 1 subch. 2 subch. 3 ๏ Each PtM layered service is delivered through C orthogonal broadcast erasure subchannels The$same$MCS Capacity$of$subch.$3$ (no.$of$packets) ๏ Each subchannel delivers streams of (en)coded packets (according to the RLNC principle). andCommunications School of Computing
6 ๏ Encoding performed over each service layer independently from the others. ๏ The source node will linearly combine the data packets composing the l-th layer and will generate a stream of coded packets , where k1 k2 k3 x1 x2 xK. . .. . . ๏ is a layered source message of K source packets, classified into L service layers x = {x1, . . . , xK} Non-Overlapping Layered RNC andCommunications School of Computing kl xl = {xi}kl i=1 nl kl y = {yj}nl j=1 yj = klX i=1 gj,i xi Coef:icients$of$the$ linear$combination$ are$selected$over$a$ :inite$:ield$of$size$q
Non-Overlapping Layered RNC ๏ User u recovers layer l if it will collect k_l linearly independent coded packets. The prob. of this event is 7 kl Pl(nl,u) = nl,u X r=kl ✓ nl,u r ◆ pnl,u r (1 p)r h(r) = nl,u X r=kl ✓ nl,u r ◆ pnl,u r (1 p)r kl 1Y i=0 h 1 1 qr i i | {z } h(r) Prob.$of$receiving$r$out$of$nl,u$coded$symbols Prob.$of$decoding$
 layer$l ๏ The probability that user u recover the first l service layers is DNO,l(n1,u, . . . , nL,u) = DNO,l(nu) = lY i=1 Pi(ni,u) PEP andCommunications School of Computing
8 ๏ The source node (i) linearly combines data packets belonging to the same window, (ii) repeats this process for all windows, and (iii) broadcasts each stream of coded packets over one or more subchannels Expanding Window Layered RNC ๏ We define the l-th window as the set of source packets belonging to the first l service layers. Namely, 
 where Xl Xl ={xj}Kl j=1 Kl = Pl i=1 ki k1 k2 k3 x1 x2 xK. . .. . . Exp. Win. 3 Exp. Win. 2 Exp. Win. 1 andCommunications School of Computing
Expanding Window Layered RNC ๏ Sums allow us to consider all the possible combinations of received coded packets 9 ๏ The probability of user u recovering the first l layers (namely, the l-th window) can be written as DEW,l L,u) = =DEW,l(Nu) = N1,u X r1=0 · · · Nl 1,u X rl 1=0 Nl,u X rl=rmin,l ✓ N1,u r1 ◆ · · · ✓ Nl,u rl ◆ p Pl i=1(Ni,u ri) (1 p) Pl i=1 ri gl(r) Prob.$of$receiving $out$ of$ coded$symbols Prob.$of$decoding$
 window$l DEW,l(Nu) DEW,l(N1,u, . . . , NL,u) = =DEW,l(Nu) = N1,u X r1=0 · · · Nl 1,u X rl 1=0 Nl,u X rl=rmin,l ✓ N1,u r1 ◆ · · · ✓ Nl,u rl ◆ p Pl i=1(Ni,u ri) ( r = {r1, . . . , rl} andCommunications School of Computing
2. Multi-Channel Resource Allocation Models andCommunications School of Computing
Allocation Patterns 11 ˆB3 ˆB2 ˆB1 subchannel 1 subchannel 2 subchannel 3 coded packets from x1 coded packets from x2 coded packets from x3 ˆB3 ˆB2 ˆB1 subchannel 1 subchannel 2 subchannel 3 Separated$ Allocation$ Pattern andCommunications School of Computing
Mixed$ Allocation$ Pattern ˆB3 ˆB2 ˆB1 coded packets from x3 or X3 coded packets from x2 or X2 coded packets from x1 or X1 subchannel 1 subchannel 2 subchannel 3 Allocation Patterns 11 ˆB3 ˆB2 ˆB1 subchannel 1 subchannel 2 subchannel 3 andCommunications School of Computing
NO-MA Model 12 andCommunications School of Computing ๏ Consider the variable . It is 1, if u can recover the first l layers with a probability value 
 , otherwise it is 0. u,l = I ⇣ DNO,l(nu) ˆD ⌘ ˆD (NO-MA) min m1,...,mC n(1,c),...,n(L,c) LX l=1 CX c=1 n(l,c) (1) subject to UX u=1 u,l U ˆtl l = 1, . . . , L (2) mc 1 < mc c = 2, . . . , L (3) 0  LX l=1 n(l,c)  ˆBc c = 1, . . . , C (4) No.$of$packets$of$layer$l$ delivered$over$cMinimization$of$ resource$footprint ˆB3 ˆB2 ˆB1 subch. 1subch. 2subch. 3
NO-MA Model 12 andCommunications School of Computing ๏ Consider the variable . It is 1, if u can recover the first l layers with a probability value 
 , otherwise it is 0. u,l = I ⇣ DNO,l(nu) ˆD ⌘ ˆD (NO-MA) min m1,...,mC n(1,c),...,n(L,c) LX l=1 CX c=1 n(l,c) (1) subject to UX u=1 u,l U ˆtl l = 1, . . . , L (2) mc 1 < mc c = 2, . . . , L (3) 0  LX l=1 n(l,c)  ˆBc c = 1, . . . , C (4) Each$service$level$shall$be$ achieved$by$a$predetermined$ fraction$of$users No.$of$users Target$fraction$of$users (NO-MA) min m1,...,mC n(1,c),...,n(L,c) LX l=1 CX c=1 n(l,c) (1) subject to UX u=1 u,l U ˆtl l = 1, . . . , L (2) mc 1 < mc c = 2, . . . , L (3) 0  LX l=1 n(l,c)  ˆBc c = 1, . . . , C (4) ˆB3 ˆB2 ˆB1 subch. 1subch. 2subch. 3
NO-MA Model 12 andCommunications School of Computing ๏ Consider the variable . It is 1, if u can recover the first l layers with a probability value 
 , otherwise it is 0. u,l = I ⇣ DNO,l(nu) ˆD ⌘ ˆD (NO-MA) min m1,...,mC n(1,c),...,n(L,c) LX l=1 CX c=1 n(l,c) (1) subject to UX u=1 u,l U ˆtl l = 1, . . . , L (2) mc 1 < mc c = 2, . . . , L (3) 0  LX l=1 n(l,c)  ˆBc c = 1, . . . , C (4) DynamicH$and$ systemHrelated$ constraints (NO-MA) min m1,...,mC n(1,c),...,n(L,c) LX l=1 CX c=1 n(l,c) (1) subject to UX u=1 u,l U ˆtl l = 1, . . . , L (2) mc 1 < mc c = 2, . . . , L (3) 0  LX l=1 n(l,c)  ˆBc c = 1, . . . , C (4) (NO-MA) min m1,...,mC n(1,c),...,n(L,c) LX l=1 CX c=1 n(l,c) (1) subject to UX u=1 u,l U ˆtl l = 1, . . . , L (2) mc 1 < mc c = 2, . . . , L (3) 0  LX l=1 n(l,c)  ˆBc c = 1, . . . , C (4) ˆB3 ˆB2 ˆB1 subch. 1subch. 2subch. 3
NO-MA Heuristic ๏ The NO-MA is an hard integer optimisation problem because of the coupling constraints among variables ๏ We propose a two-step heuristic strategy i. MCSs optimisation ( ) ii. No. of coded packet per-subchannel optimization
 ( ) 13 m1, . . . , mC n(1,c) , . . . , n(L,c) ๏ The first step selects the 
 value of such that packets delivered through subch. c are received (at least with a target prob.) by users. mc |U(mc) | U · ˆtc apping Resource Allocation Strategies system where the source node delivers the by means of the NO RNC principle. From (??), indication variable u,l as follows: u,l = I ⇣ DNO,l(nu) ˆD ⌘ . (13) s, u,l = 1, if u can recover the first l layers ity value that is equal to or greater than a target wise u,l = 0. e allocation model that we propose for the Step 1 Subchannel MCSs optimization. 1: c C 2: v mMAX and 3: while c 1 do 4: repeat 5: mc v 6: v v 1 7: until |U(mc) | U · ˆtc or v < mmin 8: c c 1 9: end while because of the nature of the considered a andCommunications School of Computing
NO-MA Heuristic ๏ The idea behind the second step can be summarised as follows 14 ˆB3 ˆB2 ˆB1 subchannel 1 subchannel 2 subchannel 3 DNO,1(n(1) ) ˆD DNO,2(n(1) , n(2) ) ˆD DNO,3(n(1) , n(2) , n(3) ) ˆD andCommunications School of Computing
NO-MA Heuristic ๏ The idea behind the second step can be summarised as follows 14 e node delivers the principle. From (6), follows: ˆD ⌘ . (13) ver the first l layers greater than a target we propose for the A (NO-SA) can be (l,c) (14) = 1, . . . , L (15) = 2, . . . , L (16) = 1, . . . , C (17) or l 6= c (18) nts the overall num- d to deliver all the L 1: c C 2: v mMAX and 3: while c 1 do 4: repeat 5: mc v 6: v v 1 7: until |U(mc) | U · ˆtc or v < mmin 8: c c 1 9: end while Step 2 Coded packet allocation for a the NO-MA case. 1: c 1 2: n(l,c) 1 for any l = 1, . . . , L and c = 1, . . . , C 3: n = {n(l) }L l=1, where n(l) 1 for any l = 1, . . . , L 4: for l 1, . . . , L do 5: while DNO,l(n) < ˆD and c  C do 6: n(l,c) n(l,c) + 1 7: n(l) PC t=1 n(l,t) for any l = 1, . . . , L 8: if PL t=1 n(t,c) = ˆBc then 9: c c + 1 10: end if 11: end while 12: if DNO,l(n) < ˆD and c > C then 13: no solution can be found. 14: end if 15: end for because of the nature of the considered allocation pattern. Furthermore, without loss of generality, we assume that coded Requires$a$no.$of$steps
  PC t=1 ˆBt andCommunications School of Computing
EW-MA Model ๏ We define the indicator variable
 
 
 
 User u will recover the first l service layers (at least) with probability if any of the windows l, l+1, …, L are recovered (at least) with probability 15 µu,l = I L_ t=l n DEW,t(Nu) ˆD o ! ˆD ˆD ๏ Consider the EW delivery mode andCommunications School of Computing k1 k2 k3 x1 x2 xK. . .. . . Exp. Win. 3 Exp. Win. 2 Exp. Win. 1 ˆB3 ˆB2 ˆB1 subch. 1subch. 2subch. 3
EW-MA Model ๏ The RA problem for the EW-MA case is 16 (EW-MA) min m1,...,mC N(1,c),...,N(L,c) LX l=1 CX c=1 N(l,c) (1) subject to UX u=1 µu,l U ˆtl l = 1, . . . , L (2) mc 1 < mc c = 2, . . . , L (3) 0  LX l=1 N(l,c)  ˆBc c = 1, . . . , C (4) No.$of$packets$of$ window$l$delivered$ over$c ๏ It is still an hard integer optimisation problem but the previously proposed heuristic strategy can be still applied. andCommunications School of Computing ˆB3 ˆB2 ˆB1 subch. 1subch. 2subch. 3
“Egalitarian” Model 17 andCommunications School of Computing ๏ Previous strategies ensure minimum SLA and minimize the resource footprint. Point of view of the ISP… ๏ Best practice for burglars - To still object with the maximum value and the minimum weight. The profit-cost ratio is maximized. ๏ We define the model for a SA pattern as: (E-SA) maximize m1,...,mL N(1),...,N(L) UX u=1 LX l=1 Qu,l , LX l=1 N(l) (1) subject to UX u=1 Qu,l U ˆtl l = 1, . . . , L (2) 0  N(l)  ˆBl l = 1, . . . , L. (3) Pro(it$H$No.$of$video$layers$ recovered$by$any$of$the$users Cost$H$No.$of$ transmissions$needed SLAHrelated$constraint ๏ We can refer to the previous heuristics. ˆB3 ˆB2 ˆB1 subch. 1subch. 2subch. 3
3. Analytical Results andCommunications School of Computing
Analytical Results (part 1) 19 ๏ LTE-A eMBMS scenarios ๏ We compared the proposed strategies with a classic Multi- rate Transmission strategy ๏ System performance was evaluated in terms of It$is$a$maximization$of$the$ sum$of$the$user$QoS Resource$footprint = 8 >>>>< >>>>: LX l=1 CX c=1 n(l,c) , for NO-RNC LX l=1 CX c=1 N(l,c) , for EW-RNC. max m1,...,mL UX u=1 PSNRu No$error$control$strategies$ are$allowed$(ARQ,$RLNC,$etc.) andCommunications School of Computing
Analytical Results (part 1) 19 ๏ LTE-A eMBMS scenarios ๏ We compared the proposed strategies with a classic Multi- rate Transmission strategy ๏ System performance was evaluated in terms of It$is$a$maximization$of$the$ sum$of$the$user$QoS PSNR$after$recovery$of$the$basic$ and$the$:irst$l$enhancement$layers ⇢(u) = 8 >< >: max l=1,...,L n PSNRl D (u) NO,l o , for NO-RNC max l=1,...,L n PSNRl D (u) EW,l o , for EW-RNC max m1,...,mL UX u=1 PSNRu No$error$control$strategies$ are$allowed$(ARQ,$RLNC,$etc.) andCommunications School of Computing
Target cellTarget MG eNB Scenario$with$a$high$heterogeneity.$80$ UEs$equally$spaced$and$$placed$along$the$ radial$line$representing$the$symmetry$ axis$of$one$sector$of$the$target$cell Analytical Results (part 1) 20 We$considered$Stream$A$and$B$ which$have$3$layers,$bitrate$of$ A$is$smaller$than$that$of$B andCommunications School of Computing
Distance (m) MaximumPSNRρ(dB) 90 110 130 150 170 190 210 230 250 270 290 0 5 15 25 35 45 55 ˆt1ˆt2ˆt3 MrT Heu. NOW−MA Heu. EW−MA ⌧ = 60 ⌧ = 43 Analytical Results (part 1) 21 Stream$A andCommunications School of Computing All$the$proposed$ strategies$meet$ the$coverage$ constraints EWHMA NOHMA MrT PSNR
 layers$1+2+3 PSNR
 layers$1+2 PSNR
 layers$1
Distance (m) MaximumPSNRρ(dB) 90 110 130 150 170 190 210 230 250 270 290 0 5 15 25 35 45 55 ˆt1ˆt2ˆt3 MrT Heu. NOW−MA Heu. EW−MA ⌧ = 73 ⌧ = 88 Analytical Results (part 1) 22 andCommunications School of Computing All$the$proposed$ strategies$meet$ the$coverage$ constraints MrT EWHMA NOHMA PSNR
 layers$1+2+3 PSNR
 layers$1+2 PSNR
 layers$1 Stream$B
Analytical Results (part 2) 23 andCommunications School of Computing ๏ LTE-A allows multiple contiguous BS to deliver (in a synchronous fashion) the same services by means of the same signals eNB eNB eNB eNB M1/M2 MCE / MBMS-GW SFN 3 2 1 B UE3 UEMUE2 UE1 UE4 −400 −200 0 200 400 600 −200 −100 0 100 200 300 400 500 600 700 0 5 10 15 Spacial$SINR$distribution Single$Frequency$Network 4HBS$SFN,$1700$users$placed$at$ the$vertices$of$a$regular$square$ grid$placed$on$the$playground.$
Analytical Results (part 2) 24 andCommunications School of Computing x position (m) yposition(m) −500 −300 −100 100 300 500 700 −200 −100 0 100 200 300 400 500 600 700 x position (m) yposition(m) −500 −300 −100 100 300 500 700 −200 −100 0 100 200 300 400 500 600 700 45.8 45.8 45.8 45.8 45.8 45.845.8 45.8 45.8 45.8 35.9 35.9 35.9 35.9 35.9 35.9 35.9 35.9 35.9 35.9 35.9 27.9 27.9 27.9 27.9 27.9 27.9 27.9 27.9 27.9 27.9 27.9 27.9 E"SAMrT 45.8 45.8 3Hlayer$ stream ๏ Also in this case MrT cannot ensure the desired coverage!
x position (m) yposition(m) −500 −300 −100 100 300 500 700 −200 −100 0 100 200 300 400 500 600 700 x position (m) yposition(m) −500 −300 −100 100 300 500 700 −200 −100 0 100 200 300 400 500 600 700 46.4 46.4 46.4 46.4 46.4 46.4 46.4 46.4 46.4 46.4 46.4 46.4 39.9 39.9 39.9 39.9 39.9 39.9 39.9 39.9 39.939.9 39.9 33.4 33.4 33.4 33.4 33.4 33.4 33.4 33.4 28.1 28.1 28.1 28.1 28.1 28.1 28.1 28.1 28.1 46.4 46.4 E"SAMrT 4Hlayer$ stream Analytical Results (part 2) 24 andCommunications School of Computing ๏ Also in this case MrT cannot ensure the desired coverage!
4. Concluding Remarks andCommunications School of Computing
Concluding Remarks 26 ๏ Definition of a generic system model that can be easily adapted to practical scenarios and different viewpoints (ISP vs users). ๏ Derivation of the theoretical framework to assess user QoS ๏ Definition of efficient resource allocation frameworks, that can jointly optimise both system parameters and the error control strategy in use ๏ Development of efficient heuristic strategies that can derive good quality solutions in a finite number of steps. andCommunications School of Computing
Thank you for your attention andCommunications School of Computing For more information
 http://arxiv.org/abs/1411.5547 or http://goo.gl/Z4Y9YF A. Tassi, I. Chatzigeorgiou, and D. Vukobratović, “Resource Allocation Frameworks for Network-coded Layered Multimedia Multicast Services”, IEEE Journal on Selected Areas in Communications, Special Issue on “Fundamental Approaches to Network Coding in Wireless Communication Systems”, in press.
Bristol, 5th February 2015 R2D2: Network error control for Rapid and Reliable Data Delivery Project supported by EPSRC under the First Grant scheme (EP/L006251/1) On Optimization of Network-coded Scalable Multimedia Service Multicasting University of Bristol Andrea Tassi and Ioannis Chatzigeorgiou {a.tassi, i.chatzigeorgiou}@lancaster.ac.uk andCommunications School of Computing

More Related Content

PDF
nn network
byShivashankar Hiremath
 
PDF
2014 vulnerability assesment of spatial network - models and solutions
byFrancisco Pérez
 
PPTX
Error correction using redundant residue number system
byNimi T
 
PDF
Perceptron
byVARUN KUMAR
 
PDF
A robust blind and secure watermarking scheme using positive semi definite ma...
byijcsit
 
PDF
The Perceptron - Xavier Giro-i-Nieto - UPC Barcelona 2018
byUniversitat Politècnica de Catalunya
 
PDF
Subproblem-Tree Calibration: A Unified Approach to Max-Product Message Passin...
byVarad Meru
 
PDF
P5 - Routing Protocols
byKurniawan Dwi Irianto
 
nn network
byShivashankar Hiremath
 
2014 vulnerability assesment of spatial network - models and solutions
byFrancisco Pérez
 
Error correction using redundant residue number system
byNimi T
 
Perceptron
byVARUN KUMAR
 
A robust blind and secure watermarking scheme using positive semi definite ma...
byijcsit
 
The Perceptron - Xavier Giro-i-Nieto - UPC Barcelona 2018
byUniversitat Politècnica de Catalunya
 
Subproblem-Tree Calibration: A Unified Approach to Max-Product Message Passin...
byVarad Meru
 
P5 - Routing Protocols
byKurniawan Dwi Irianto
 

What's hot

PDF
The Perceptron (D1L2 Deep Learning for Speech and Language)
byUniversitat Politècnica de Catalunya
 
PDF
Gate Computer Science Solved Paper 2007
byRohit Garg
 
PDF
1508.07756v1
bySamir Crypticus
 
PPTX
Programacion Cuadratica
bypaquitootd
 
PDF
Weight enumerators of block codes and the mc williams
byMadhumita Tamhane
 
KEY
P2P Supernodes
byKevin Regan
 
PDF
Novel Performance Analysis of Network Coded Communications in Single-Relay Ne...
byEvgeny Tsimbalo
 
PDF
CINAF protocol
bySreekanth Vp
 
PPTX
A general multiobjective clustering approach based on multiple distance measures
byMehran Mesbahzadeh
 
PDF
Word Embeddings (D2L4 Deep Learning for Speech and Language UPC 2017)
byUniversitat Politècnica de Catalunya
 
PDF
GATE Computer Science Solved Paper 2004
byRohit Garg
 
PPTX
Deep Learning: R with Keras and TensorFlow
byOswald Campesato
 
DOC
algorithm Unit 3
byMonika Choudhery
 
PPTX
Deep Learning, Scala, and Spark
byOswald Campesato
 
PDF
Support Vector Machines for Classification
byPrakash Pimpale
 
PPTX
C++ and Deep Learning
byOswald Campesato
 
PDF
Ma2520962099
byIJERA Editor
 
DOC
algorithm Unit 2
byMonika Choudhery
 
PDF
Learning multifractal structure in large networks (KDD 2014)
byAustin Benson
 
PDF
Laboratory 7
byShafiul Omam
 
The Perceptron (D1L2 Deep Learning for Speech and Language)
byUniversitat Politècnica de Catalunya
 
Gate Computer Science Solved Paper 2007
byRohit Garg
 
1508.07756v1
bySamir Crypticus
 
Programacion Cuadratica
bypaquitootd
 
Weight enumerators of block codes and the mc williams
byMadhumita Tamhane
 
P2P Supernodes
byKevin Regan
 
Novel Performance Analysis of Network Coded Communications in Single-Relay Ne...
byEvgeny Tsimbalo
 
CINAF protocol
bySreekanth Vp
 
A general multiobjective clustering approach based on multiple distance measures
byMehran Mesbahzadeh
 
Word Embeddings (D2L4 Deep Learning for Speech and Language UPC 2017)
byUniversitat Politècnica de Catalunya
 
GATE Computer Science Solved Paper 2004
byRohit Garg
 
Deep Learning: R with Keras and TensorFlow
byOswald Campesato
 
algorithm Unit 3
byMonika Choudhery
 
Deep Learning, Scala, and Spark
byOswald Campesato
 
Support Vector Machines for Classification
byPrakash Pimpale
 
C++ and Deep Learning
byOswald Campesato
 
Ma2520962099
byIJERA Editor
 
algorithm Unit 2
byMonika Choudhery
 
Learning multifractal structure in large networks (KDD 2014)
byAustin Benson
 
Laboratory 7
byShafiul Omam
 

Viewers also liked

PDF
Sleep Period Optimization Model For Layered Video Service Delivery Over eMBMS...
byAndrea Tassi
 
PDF
Parte 1 - Linux ed i sistemi embedded per le reti (di Andrea Tassi)
byAndrea Tassi
 
PDF
Lecture
bysaeed alqhtany
 
PDF
Silicon Cluster Optimization Using Extended Compact Genetic Algorithm
bykknsastry
 
PDF
On Extended Compact Genetic Algorithm
bykknsastry
 
PDF
Real-Coded Extended Compact Genetic Algorithm based on Mixtures of Models
byPier Luca Lanzi
 
PDF
Parte 2 - Linux ed i sistemi embedded per le reti (di Massimiliano Toce)
byAndrea Tassi
 
PDF
Presentation of 'A Novel Convex Power Adaptation Strategy for Multicast Commu...
byAndrea Tassi
 
PDF
RLNC
byAndrea Tassi
 
DOCX
Research techniques
byMia Buckley
 
PDF
PRINCE2 Practitioner
byMd. Shahed Rahman (ISMS Lead Auditor, CEH v8)
 
PDF
Optimized Network-coded Scalable Video Multicasting over eMBMS Networks
byAndrea Tassi
 
PDF
Sparse Random Network Coding for Reliable Multicast Services
byAndrea Tassi
 
PDF
R2D2 Project (EP/L006251/1) - Research Objectives & Outcomes
byAndrea Tassi
 
PDF
Parte 3 - Linux ed i sistemi embedded per le reti (di Riccardo Coppola)
byAndrea Tassi
 
PDF
Talk on Resource Allocation Strategies for Layered Multimedia Multicast Services
byAndrea Tassi
 
PPTX
A short introduction to Network coding
byArash Pourdamghani
 
PDF
Presentation of 'Reliable Rate-Optimized Video Multicasting Services over LTE...
byAndrea Tassi
 
PDF
Introduction to Network Coding
byElectronics & Communication Staff SCU Suez Canal University
 
PPTX
Simple regenerating codes: Network Coding for Cloud Storage
byKevin Tong
 
Sleep Period Optimization Model For Layered Video Service Delivery Over eMBMS...
byAndrea Tassi
 
Parte 1 - Linux ed i sistemi embedded per le reti (di Andrea Tassi)
byAndrea Tassi
 
Lecture
bysaeed alqhtany
 
Silicon Cluster Optimization Using Extended Compact Genetic Algorithm
bykknsastry
 
On Extended Compact Genetic Algorithm
bykknsastry
 
Real-Coded Extended Compact Genetic Algorithm based on Mixtures of Models
byPier Luca Lanzi
 
Parte 2 - Linux ed i sistemi embedded per le reti (di Massimiliano Toce)
byAndrea Tassi
 
Presentation of 'A Novel Convex Power Adaptation Strategy for Multicast Commu...
byAndrea Tassi
 
RLNC
byAndrea Tassi
 
Research techniques
byMia Buckley
 
PRINCE2 Practitioner
byMd. Shahed Rahman (ISMS Lead Auditor, CEH v8)
 
Optimized Network-coded Scalable Video Multicasting over eMBMS Networks
byAndrea Tassi
 
Sparse Random Network Coding for Reliable Multicast Services
byAndrea Tassi
 
R2D2 Project (EP/L006251/1) - Research Objectives & Outcomes
byAndrea Tassi
 
Parte 3 - Linux ed i sistemi embedded per le reti (di Riccardo Coppola)
byAndrea Tassi
 
Talk on Resource Allocation Strategies for Layered Multimedia Multicast Services
byAndrea Tassi
 
A short introduction to Network coding
byArash Pourdamghani
 
Presentation of 'Reliable Rate-Optimized Video Multicasting Services over LTE...
byAndrea Tassi
 
Introduction to Network Coding
byElectronics & Communication Staff SCU Suez Canal University
 
Simple regenerating codes: Network Coding for Cloud Storage
byKevin Tong
 

Similar to On Optimization of Network-coded Scalable Multimedia Service Multicasting

PDF
Fair channel allocation and access design for cognitive ad hoc networks
byPolytechnique Montreal
 
PDF
Tech report: Fair Channel Allocation and Access Design for Cognitive Ad Hoc N...
byPolytechnique Montreal
 
PDF
Tech report
byPolytechnique Montreal
 
PDF
M1802037781
byIOSR Journals
 
PPT
wireless communication :channel capacity
byLTMECEPSGCT
 
PDF
Localized Algorithm for Channel Assignment in Cognitive Radio Networks
byIJERA Editor
 
PDF
Bu4301411416
byIJERA Editor
 
PDF
Cross layer design of congestion control and power control in fast-fading wir...
byEcwayt
 
PDF
Dotnet cross-layer design of congestion control and power control in fast-fa...
byEcwayt
 
PDF
Dotnet cross-layer design of congestion control and power control in fast-fa...
byEcwaytech
 
PDF
Cross layer design of congestion control and power control in fast-fading wir...
byEcwayt
 
PDF
Cross layer design of congestion control and power control in fast-fading wir...
byEcwaytech
 
PDF
Cross layer design of congestion control and power control in fast-fading wir...
byecwayprojects
 
PPTX
Information Theory and Coding - Lecture 5
byAref35
 
PDF
Flexible channel allocation using best Secondary user detection algorithm
byijsrd.com
 
PDF
QCon London 2015 Protocols of Interaction
byTodd Montgomery
 
PPTX
The Stochastic Network Calculus: A Modern Approach.pptx
byManiMaran230751
 
DOCX
Power allocation for statistical qo s provisioning in
byIEEEFINALYEARPROJECTS
 
PDF
PARTIAL HARQ RETRANSMISSION FOR BROADCAST IN FADING CHANNELS
bycsandit
 
PDF
Channel quality
bySaraswathi Venkataraman
 
Fair channel allocation and access design for cognitive ad hoc networks
byPolytechnique Montreal
 
Tech report: Fair Channel Allocation and Access Design for Cognitive Ad Hoc N...
byPolytechnique Montreal
 
Tech report
byPolytechnique Montreal
 
M1802037781
byIOSR Journals
 
wireless communication :channel capacity
byLTMECEPSGCT
 
Localized Algorithm for Channel Assignment in Cognitive Radio Networks
byIJERA Editor
 
Bu4301411416
byIJERA Editor
 
Cross layer design of congestion control and power control in fast-fading wir...
byEcwayt
 
Dotnet cross-layer design of congestion control and power control in fast-fa...
byEcwayt
 
Dotnet cross-layer design of congestion control and power control in fast-fa...
byEcwaytech
 
Cross layer design of congestion control and power control in fast-fading wir...
byEcwayt
 
Cross layer design of congestion control and power control in fast-fading wir...
byEcwaytech
 
Cross layer design of congestion control and power control in fast-fading wir...
byecwayprojects
 
Information Theory and Coding - Lecture 5
byAref35
 
Flexible channel allocation using best Secondary user detection algorithm
byijsrd.com
 
QCon London 2015 Protocols of Interaction
byTodd Montgomery
 
The Stochastic Network Calculus: A Modern Approach.pptx
byManiMaran230751
 
Power allocation for statistical qo s provisioning in
byIEEEFINALYEARPROJECTS
 
PARTIAL HARQ RETRANSMISSION FOR BROADCAST IN FADING CHANNELS
bycsandit
 
Channel quality
bySaraswathi Venkataraman
 

Recently uploaded

PPT
C++ Chapter 6-pointers about pointers in programming
byfirehiwot8
 
PDF
Paper: World Game (s) Great Redesign.pdf
bySteven McGee
 
PDF
Unit 1 Introduction To Computer Networks.pdf
byaida818570
 
PPT
Tools in communication technologies - CT
byswisssom2025
 
PDF
Articulo aobre los ladrillos y como se fabrican
byDiegoAlexanderGarcia12
 
PDF
Slides: The World Game (s) Great Redesign: Eco Economic Epochs pdf
bySteven McGee
 
PPTX
Information Assurance and Security chapter two-part 1.pptx
byfirehiwot8
 
PPT
CHAPTER 2 RISK MANAGEMENT and security.ppt
byfirehiwot8
 
PDF
Comprehensive IT Infrastructure Solutions.pdf
byDurocorre
 
PPTX
Information comiunication technology HNDIT1212 Lecture 01.pptx
bynmziyard
 
PPTX
Powerpoint slides Eco Economic Epochs.pptx
bySteven McGee
 
PDF
Tamagui: Bridging Web and Mobile Development
byEugene Zharkov
 
PDF
Top 10 Countries to Hire Remote Developers in 2025 copy.pdf
byOuranos Technologies Pvt Ltd
 
PPTX
Intellectual Property Code of the Philippines_20251030_085011_0000.pptx
byronthefourth
 
PPTX
C++ Chapter about pointers in programming
byfirehiwot8
 
PPT
Web Service Security note for teaching.ppt
byfirehiwot8
 
PDF
Unit 2 Local Area Networks (LANs) Networking.pdf
byaida818570
 
PDF
Empower Your Brand with YouRefresh’s Online Hub Builder
byyourefreshdm
 
PPTX
Python Oops concepts of power point presentation
bySwapnitaKendre
 
C++ Chapter 6-pointers about pointers in programming
byfirehiwot8
 
Paper: World Game (s) Great Redesign.pdf
bySteven McGee
 
Unit 1 Introduction To Computer Networks.pdf
byaida818570
 
Tools in communication technologies - CT
byswisssom2025
 
Articulo aobre los ladrillos y como se fabrican
byDiegoAlexanderGarcia12
 
Slides: The World Game (s) Great Redesign: Eco Economic Epochs pdf
bySteven McGee
 
Information Assurance and Security chapter two-part 1.pptx
byfirehiwot8
 
CHAPTER 2 RISK MANAGEMENT and security.ppt
byfirehiwot8
 
Comprehensive IT Infrastructure Solutions.pdf
byDurocorre
 
Information comiunication technology HNDIT1212 Lecture 01.pptx
bynmziyard
 
Powerpoint slides Eco Economic Epochs.pptx
bySteven McGee
 
Tamagui: Bridging Web and Mobile Development
byEugene Zharkov
 
Top 10 Countries to Hire Remote Developers in 2025 copy.pdf
byOuranos Technologies Pvt Ltd
 
Intellectual Property Code of the Philippines_20251030_085011_0000.pptx
byronthefourth
 
C++ Chapter about pointers in programming
byfirehiwot8
 
Web Service Security note for teaching.ppt
byfirehiwot8
 
Unit 2 Local Area Networks (LANs) Networking.pdf
byaida818570
 
Empower Your Brand with YouRefresh’s Online Hub Builder
byyourefreshdm
 
Python Oops concepts of power point presentation
bySwapnitaKendre
 

On Optimization of Network-coded Scalable Multimedia Service Multicasting

  • 1.
    Bristol, 5th February2015 R2D2: Network error control for Rapid and Reliable Data Delivery Project supported by EPSRC under the First Grant scheme (EP/L006251/1) On Optimization of Network-coded Scalable Multimedia Service Multicasting University of Bristol Andrea Tassi and Ioannis Chatzigeorgiou {a.tassi, i.chatzigeorgiou}@lancaster.ac.uk andCommunications School of Computing
  • 2.
    Starting Point andGoals ๏ Delivery of multimedia broadcast/multicast services over 
 4G/5G networks is a challenging task. This has propelled research into delivery schemes. ๏ Multi-rate Transmission (MrT) strategies have been proposed as a means of delivering layered services to users experiencing different downlink channel conditions. ๏ Layered service consists of a basic layer and multiple enhancement layers. Goals ๏ Error control - Ensure that a predetermined fraction of users achieves a certain service level with at least a given probability ๏ Resource optimisation - Reduce the total amount of radio resources needed to deliver a layered service. 2 andCommunications School of Computing
  • 3.
    Index 1. System Parametersand Performance Analysis 2. Multi-Channel Resource Allocation Models and Heuristic Strategies 3. Analytical Results 4. Concluding Remarks 3 andCommunications School of Computing
  • 4.
    1. System Parametersand Performance Analysis andCommunications School of Computing
  • 5.
    System Model ๏ One-hopwireless communication system composed of one source node and U users 5 UE 1 UE 3 UE 2 UE 4 UE U Source Node ˆB3 ˆB2 ˆB1 subch. 1 subch. 2 subch. 3 ๏ Each PtM layered service is delivered through C orthogonal broadcast erasure subchannels The$same$MCS Capacity$of$subch.$3$ (no.$of$packets) ๏ Each subchannel delivers streams of (en)coded packets (according to the RLNC principle). andCommunications School of Computing
  • 6.
    6 ๏ Encoding performedover each service layer independently from the others. ๏ The source node will linearly combine the data packets composing the l-th layer and will generate a stream of coded packets , where k1 k2 k3 x1 x2 xK. . .. . . ๏ is a layered source message of K source packets, classified into L service layers x = {x1, . . . , xK} Non-Overlapping Layered RNC andCommunications School of Computing kl xl = {xi}kl i=1 nl kl y = {yj}nl j=1 yj = klX i=1 gj,i xi Coef:icients$of$the$ linear$combination$ are$selected$over$a$ :inite$:ield$of$size$q
  • 7.
    Non-Overlapping Layered RNC ๏User u recovers layer l if it will collect k_l linearly independent coded packets. The prob. of this event is 7 kl Pl(nl,u) = nl,u X r=kl ✓ nl,u r ◆ pnl,u r (1 p)r h(r) = nl,u X r=kl ✓ nl,u r ◆ pnl,u r (1 p)r kl 1Y i=0 h 1 1 qr i i | {z } h(r) Prob.$of$receiving$r$out$of$nl,u$coded$symbols Prob.$of$decoding$
 layer$l ๏ The probability that user u recover the first l service layers is DNO,l(n1,u, . . . , nL,u) = DNO,l(nu) = lY i=1 Pi(ni,u) PEP andCommunications School of Computing
  • 8.
    8 ๏ The sourcenode (i) linearly combines data packets belonging to the same window, (ii) repeats this process for all windows, and (iii) broadcasts each stream of coded packets over one or more subchannels Expanding Window Layered RNC ๏ We define the l-th window as the set of source packets belonging to the first l service layers. Namely, 
 where Xl Xl ={xj}Kl j=1 Kl = Pl i=1 ki k1 k2 k3 x1 x2 xK. . .. . . Exp. Win. 3 Exp. Win. 2 Exp. Win. 1 andCommunications School of Computing
  • 9.
    Expanding Window LayeredRNC ๏ Sums allow us to consider all the possible combinations of received coded packets 9 ๏ The probability of user u recovering the first l layers (namely, the l-th window) can be written as DEW,l L,u) = =DEW,l(Nu) = N1,u X r1=0 · · · Nl 1,u X rl 1=0 Nl,u X rl=rmin,l ✓ N1,u r1 ◆ · · · ✓ Nl,u rl ◆ p Pl i=1(Ni,u ri) (1 p) Pl i=1 ri gl(r) Prob.$of$receiving $out$ of$ coded$symbols Prob.$of$decoding$
 window$l DEW,l(Nu) DEW,l(N1,u, . . . , NL,u) = =DEW,l(Nu) = N1,u X r1=0 · · · Nl 1,u X rl 1=0 Nl,u X rl=rmin,l ✓ N1,u r1 ◆ · · · ✓ Nl,u rl ◆ p Pl i=1(Ni,u ri) ( r = {r1, . . . , rl} andCommunications School of Computing
  • 10.
    2. Multi-Channel ResourceAllocation Models andCommunications School of Computing
  • 11.
    Allocation Patterns 11 ˆB3 ˆB2 ˆB1 subchannel 1 subchannel2 subchannel 3 coded packets from x1 coded packets from x2 coded packets from x3 ˆB3 ˆB2 ˆB1 subchannel 1 subchannel 2 subchannel 3 Separated$ Allocation$ Pattern andCommunications School of Computing
  • 12.
    Mixed$ Allocation$ Pattern ˆB3 ˆB2 ˆB1 coded packets from x3or X3 coded packets from x2 or X2 coded packets from x1 or X1 subchannel 1 subchannel 2 subchannel 3 Allocation Patterns 11 ˆB3 ˆB2 ˆB1 subchannel 1 subchannel 2 subchannel 3 andCommunications School of Computing
  • 13.
    NO-MA Model 12 andCommunications School ofComputing ๏ Consider the variable . It is 1, if u can recover the first l layers with a probability value 
 , otherwise it is 0. u,l = I ⇣ DNO,l(nu) ˆD ⌘ ˆD (NO-MA) min m1,...,mC n(1,c),...,n(L,c) LX l=1 CX c=1 n(l,c) (1) subject to UX u=1 u,l U ˆtl l = 1, . . . , L (2) mc 1 < mc c = 2, . . . , L (3) 0  LX l=1 n(l,c)  ˆBc c = 1, . . . , C (4) No.$of$packets$of$layer$l$ delivered$over$cMinimization$of$ resource$footprint ˆB3 ˆB2 ˆB1 subch. 1subch. 2subch. 3
  • 14.
    NO-MA Model 12 andCommunications School ofComputing ๏ Consider the variable . It is 1, if u can recover the first l layers with a probability value 
 , otherwise it is 0. u,l = I ⇣ DNO,l(nu) ˆD ⌘ ˆD (NO-MA) min m1,...,mC n(1,c),...,n(L,c) LX l=1 CX c=1 n(l,c) (1) subject to UX u=1 u,l U ˆtl l = 1, . . . , L (2) mc 1 < mc c = 2, . . . , L (3) 0  LX l=1 n(l,c)  ˆBc c = 1, . . . , C (4) Each$service$level$shall$be$ achieved$by$a$predetermined$ fraction$of$users No.$of$users Target$fraction$of$users (NO-MA) min m1,...,mC n(1,c),...,n(L,c) LX l=1 CX c=1 n(l,c) (1) subject to UX u=1 u,l U ˆtl l = 1, . . . , L (2) mc 1 < mc c = 2, . . . , L (3) 0  LX l=1 n(l,c)  ˆBc c = 1, . . . , C (4) ˆB3 ˆB2 ˆB1 subch. 1subch. 2subch. 3
  • 15.
    NO-MA Model 12 andCommunications School ofComputing ๏ Consider the variable . It is 1, if u can recover the first l layers with a probability value 
 , otherwise it is 0. u,l = I ⇣ DNO,l(nu) ˆD ⌘ ˆD (NO-MA) min m1,...,mC n(1,c),...,n(L,c) LX l=1 CX c=1 n(l,c) (1) subject to UX u=1 u,l U ˆtl l = 1, . . . , L (2) mc 1 < mc c = 2, . . . , L (3) 0  LX l=1 n(l,c)  ˆBc c = 1, . . . , C (4) DynamicH$and$ systemHrelated$ constraints (NO-MA) min m1,...,mC n(1,c),...,n(L,c) LX l=1 CX c=1 n(l,c) (1) subject to UX u=1 u,l U ˆtl l = 1, . . . , L (2) mc 1 < mc c = 2, . . . , L (3) 0  LX l=1 n(l,c)  ˆBc c = 1, . . . , C (4) (NO-MA) min m1,...,mC n(1,c),...,n(L,c) LX l=1 CX c=1 n(l,c) (1) subject to UX u=1 u,l U ˆtl l = 1, . . . , L (2) mc 1 < mc c = 2, . . . , L (3) 0  LX l=1 n(l,c)  ˆBc c = 1, . . . , C (4) ˆB3 ˆB2 ˆB1 subch. 1subch. 2subch. 3
  • 16.
    NO-MA Heuristic ๏ TheNO-MA is an hard integer optimisation problem because of the coupling constraints among variables ๏ We propose a two-step heuristic strategy i. MCSs optimisation ( ) ii. No. of coded packet per-subchannel optimization
 ( ) 13 m1, . . . , mC n(1,c) , . . . , n(L,c) ๏ The first step selects the 
 value of such that packets delivered through subch. c are received (at least with a target prob.) by users. mc |U(mc) | U · ˆtc apping Resource Allocation Strategies system where the source node delivers the by means of the NO RNC principle. From (??), indication variable u,l as follows: u,l = I ⇣ DNO,l(nu) ˆD ⌘ . (13) s, u,l = 1, if u can recover the first l layers ity value that is equal to or greater than a target wise u,l = 0. e allocation model that we propose for the Step 1 Subchannel MCSs optimization. 1: c C 2: v mMAX and 3: while c 1 do 4: repeat 5: mc v 6: v v 1 7: until |U(mc) | U · ˆtc or v < mmin 8: c c 1 9: end while because of the nature of the considered a andCommunications School of Computing
  • 17.
    NO-MA Heuristic ๏ Theidea behind the second step can be summarised as follows 14 ˆB3 ˆB2 ˆB1 subchannel 1 subchannel 2 subchannel 3 DNO,1(n(1) ) ˆD DNO,2(n(1) , n(2) ) ˆD DNO,3(n(1) , n(2) , n(3) ) ˆD andCommunications School of Computing
  • 18.
    NO-MA Heuristic ๏ Theidea behind the second step can be summarised as follows 14 e node delivers the principle. From (6), follows: ˆD ⌘ . (13) ver the first l layers greater than a target we propose for the A (NO-SA) can be (l,c) (14) = 1, . . . , L (15) = 2, . . . , L (16) = 1, . . . , C (17) or l 6= c (18) nts the overall num- d to deliver all the L 1: c C 2: v mMAX and 3: while c 1 do 4: repeat 5: mc v 6: v v 1 7: until |U(mc) | U · ˆtc or v < mmin 8: c c 1 9: end while Step 2 Coded packet allocation for a the NO-MA case. 1: c 1 2: n(l,c) 1 for any l = 1, . . . , L and c = 1, . . . , C 3: n = {n(l) }L l=1, where n(l) 1 for any l = 1, . . . , L 4: for l 1, . . . , L do 5: while DNO,l(n) < ˆD and c  C do 6: n(l,c) n(l,c) + 1 7: n(l) PC t=1 n(l,t) for any l = 1, . . . , L 8: if PL t=1 n(t,c) = ˆBc then 9: c c + 1 10: end if 11: end while 12: if DNO,l(n) < ˆD and c > C then 13: no solution can be found. 14: end if 15: end for because of the nature of the considered allocation pattern. Furthermore, without loss of generality, we assume that coded Requires$a$no.$of$steps
  PC t=1 ˆBt andCommunications School of Computing
  • 19.
    EW-MA Model ๏ Wedefine the indicator variable
 
 
 
 User u will recover the first l service layers (at least) with probability if any of the windows l, l+1, …, L are recovered (at least) with probability 15 µu,l = I L_ t=l n DEW,t(Nu) ˆD o ! ˆD ˆD ๏ Consider the EW delivery mode andCommunications School of Computing k1 k2 k3 x1 x2 xK. . .. . . Exp. Win. 3 Exp. Win. 2 Exp. Win. 1 ˆB3 ˆB2 ˆB1 subch. 1subch. 2subch. 3
  • 20.
    EW-MA Model ๏ TheRA problem for the EW-MA case is 16 (EW-MA) min m1,...,mC N(1,c),...,N(L,c) LX l=1 CX c=1 N(l,c) (1) subject to UX u=1 µu,l U ˆtl l = 1, . . . , L (2) mc 1 < mc c = 2, . . . , L (3) 0  LX l=1 N(l,c)  ˆBc c = 1, . . . , C (4) No.$of$packets$of$ window$l$delivered$ over$c ๏ It is still an hard integer optimisation problem but the previously proposed heuristic strategy can be still applied. andCommunications School of Computing ˆB3 ˆB2 ˆB1 subch. 1subch. 2subch. 3
  • 21.
    “Egalitarian” Model 17 andCommunications School ofComputing ๏ Previous strategies ensure minimum SLA and minimize the resource footprint. Point of view of the ISP… ๏ Best practice for burglars - To still object with the maximum value and the minimum weight. The profit-cost ratio is maximized. ๏ We define the model for a SA pattern as: (E-SA) maximize m1,...,mL N(1),...,N(L) UX u=1 LX l=1 Qu,l , LX l=1 N(l) (1) subject to UX u=1 Qu,l U ˆtl l = 1, . . . , L (2) 0  N(l)  ˆBl l = 1, . . . , L. (3) Pro(it$H$No.$of$video$layers$ recovered$by$any$of$the$users Cost$H$No.$of$ transmissions$needed SLAHrelated$constraint ๏ We can refer to the previous heuristics. ˆB3 ˆB2 ˆB1 subch. 1subch. 2subch. 3
  • 22.
  • 23.
    Analytical Results (part1) 19 ๏ LTE-A eMBMS scenarios ๏ We compared the proposed strategies with a classic Multi- rate Transmission strategy ๏ System performance was evaluated in terms of It$is$a$maximization$of$the$ sum$of$the$user$QoS Resource$footprint = 8 >>>>< >>>>: LX l=1 CX c=1 n(l,c) , for NO-RNC LX l=1 CX c=1 N(l,c) , for EW-RNC. max m1,...,mL UX u=1 PSNRu No$error$control$strategies$ are$allowed$(ARQ,$RLNC,$etc.) andCommunications School of Computing
  • 24.
    Analytical Results (part1) 19 ๏ LTE-A eMBMS scenarios ๏ We compared the proposed strategies with a classic Multi- rate Transmission strategy ๏ System performance was evaluated in terms of It$is$a$maximization$of$the$ sum$of$the$user$QoS PSNR$after$recovery$of$the$basic$ and$the$:irst$l$enhancement$layers ⇢(u) = 8 >< >: max l=1,...,L n PSNRl D (u) NO,l o , for NO-RNC max l=1,...,L n PSNRl D (u) EW,l o , for EW-RNC max m1,...,mL UX u=1 PSNRu No$error$control$strategies$ are$allowed$(ARQ,$RLNC,$etc.) andCommunications School of Computing
  • 25.
    Target cellTarget MG eNB Scenario$with$a$high$heterogeneity.$80$ UEs$equally$spaced$and$$placed$along$the$ radial$line$representing$the$symmetry$ axis$of$one$sector$of$the$target$cell AnalyticalResults (part 1) 20 We$considered$Stream$A$and$B$ which$have$3$layers,$bitrate$of$ A$is$smaller$than$that$of$B andCommunications School of Computing
  • 26.
    Distance (m) MaximumPSNRρ(dB) 90 110130 150 170 190 210 230 250 270 290 0 5 15 25 35 45 55 ˆt1ˆt2ˆt3 MrT Heu. NOW−MA Heu. EW−MA ⌧ = 60 ⌧ = 43 Analytical Results (part 1) 21 Stream$A andCommunications School of Computing All$the$proposed$ strategies$meet$ the$coverage$ constraints EWHMA NOHMA MrT PSNR
 layers$1+2+3 PSNR
 layers$1+2 PSNR
 layers$1
  • 27.
    Distance (m) MaximumPSNRρ(dB) 90 110130 150 170 190 210 230 250 270 290 0 5 15 25 35 45 55 ˆt1ˆt2ˆt3 MrT Heu. NOW−MA Heu. EW−MA ⌧ = 73 ⌧ = 88 Analytical Results (part 1) 22 andCommunications School of Computing All$the$proposed$ strategies$meet$ the$coverage$ constraints MrT EWHMA NOHMA PSNR
 layers$1+2+3 PSNR
 layers$1+2 PSNR
 layers$1 Stream$B
  • 28.
    Analytical Results (part2) 23 andCommunications School of Computing ๏ LTE-A allows multiple contiguous BS to deliver (in a synchronous fashion) the same services by means of the same signals eNB eNB eNB eNB M1/M2 MCE / MBMS-GW SFN 3 2 1 B UE3 UEMUE2 UE1 UE4 −400 −200 0 200 400 600 −200 −100 0 100 200 300 400 500 600 700 0 5 10 15 Spacial$SINR$distribution Single$Frequency$Network 4HBS$SFN,$1700$users$placed$at$ the$vertices$of$a$regular$square$ grid$placed$on$the$playground.$
  • 29.
    Analytical Results (part2) 24 andCommunications School of Computing x position (m) yposition(m) −500 −300 −100 100 300 500 700 −200 −100 0 100 200 300 400 500 600 700 x position (m) yposition(m) −500 −300 −100 100 300 500 700 −200 −100 0 100 200 300 400 500 600 700 45.8 45.8 45.8 45.8 45.8 45.845.8 45.8 45.8 45.8 35.9 35.9 35.9 35.9 35.9 35.9 35.9 35.9 35.9 35.9 35.9 27.9 27.9 27.9 27.9 27.9 27.9 27.9 27.9 27.9 27.9 27.9 27.9 E"SAMrT 45.8 45.8 3Hlayer$ stream ๏ Also in this case MrT cannot ensure the desired coverage!
  • 30.
    x position (m) yposition(m) −500−300 −100 100 300 500 700 −200 −100 0 100 200 300 400 500 600 700 x position (m) yposition(m) −500 −300 −100 100 300 500 700 −200 −100 0 100 200 300 400 500 600 700 46.4 46.4 46.4 46.4 46.4 46.4 46.4 46.4 46.4 46.4 46.4 46.4 39.9 39.9 39.9 39.9 39.9 39.9 39.9 39.9 39.939.9 39.9 33.4 33.4 33.4 33.4 33.4 33.4 33.4 33.4 28.1 28.1 28.1 28.1 28.1 28.1 28.1 28.1 28.1 46.4 46.4 E"SAMrT 4Hlayer$ stream Analytical Results (part 2) 24 andCommunications School of Computing ๏ Also in this case MrT cannot ensure the desired coverage!
  • 31.
  • 32.
    Concluding Remarks 26 ๏ Definitionof a generic system model that can be easily adapted to practical scenarios and different viewpoints (ISP vs users). ๏ Derivation of the theoretical framework to assess user QoS ๏ Definition of efficient resource allocation frameworks, that can jointly optimise both system parameters and the error control strategy in use ๏ Development of efficient heuristic strategies that can derive good quality solutions in a finite number of steps. andCommunications School of Computing
  • 33.
    Thank you for yourattention andCommunications School of Computing For more information
 http://arxiv.org/abs/1411.5547 or http://goo.gl/Z4Y9YF A. Tassi, I. Chatzigeorgiou, and D. Vukobratović, “Resource Allocation Frameworks for Network-coded Layered Multimedia Multicast Services”, IEEE Journal on Selected Areas in Communications, Special Issue on “Fundamental Approaches to Network Coding in Wireless Communication Systems”, in press.
  • 34.
    Bristol, 5th February2015 R2D2: Network error control for Rapid and Reliable Data Delivery Project supported by EPSRC under the First Grant scheme (EP/L006251/1) On Optimization of Network-coded Scalable Multimedia Service Multicasting University of Bristol Andrea Tassi and Ioannis Chatzigeorgiou {a.tassi, i.chatzigeorgiou}@lancaster.ac.uk andCommunications School of Computing