Albert Bifet, profile picture
Uploaded byAlbert Bifet
1,032 views

Mining Frequent Closed Graphs on Evolving Data Streams

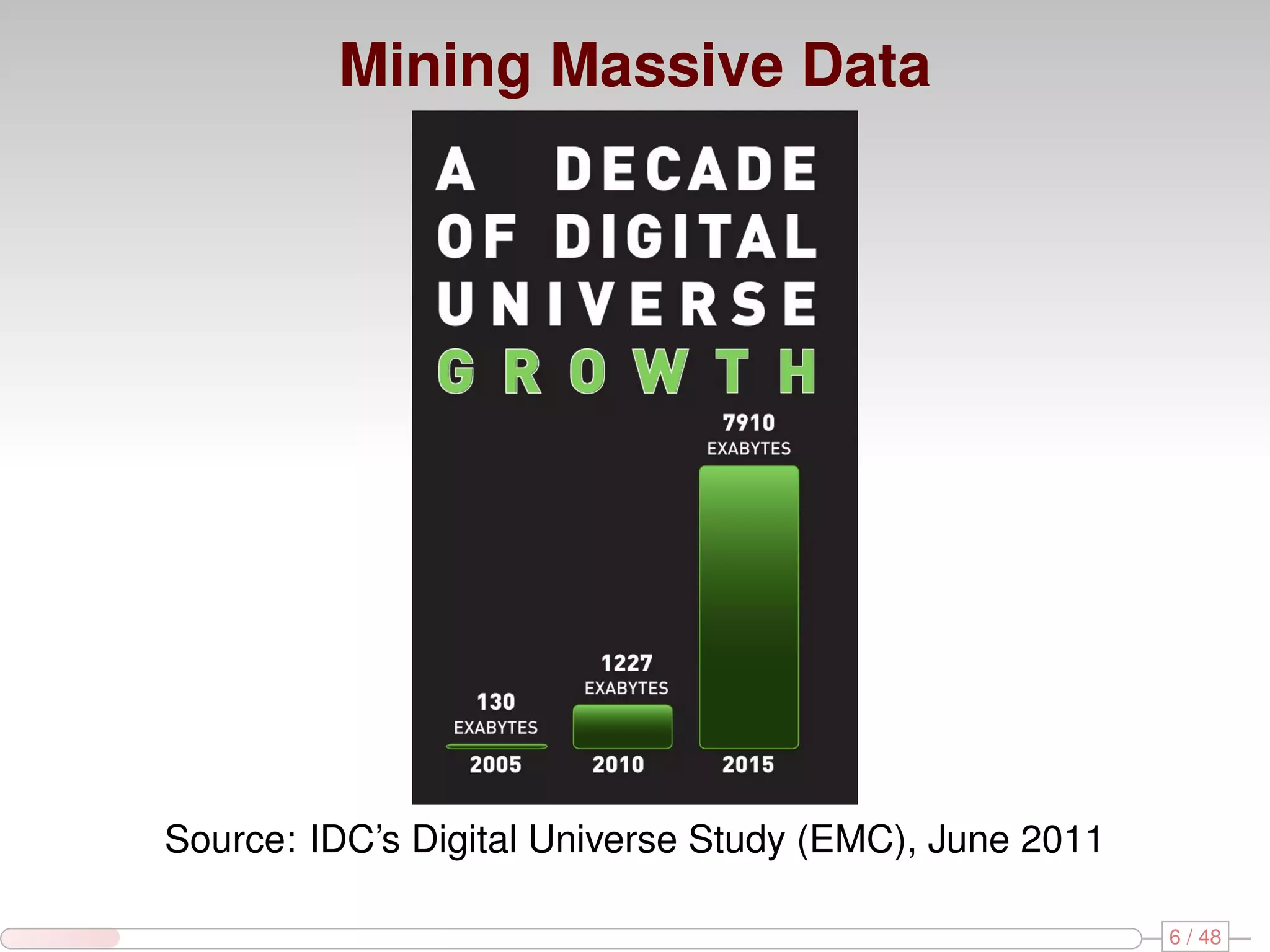
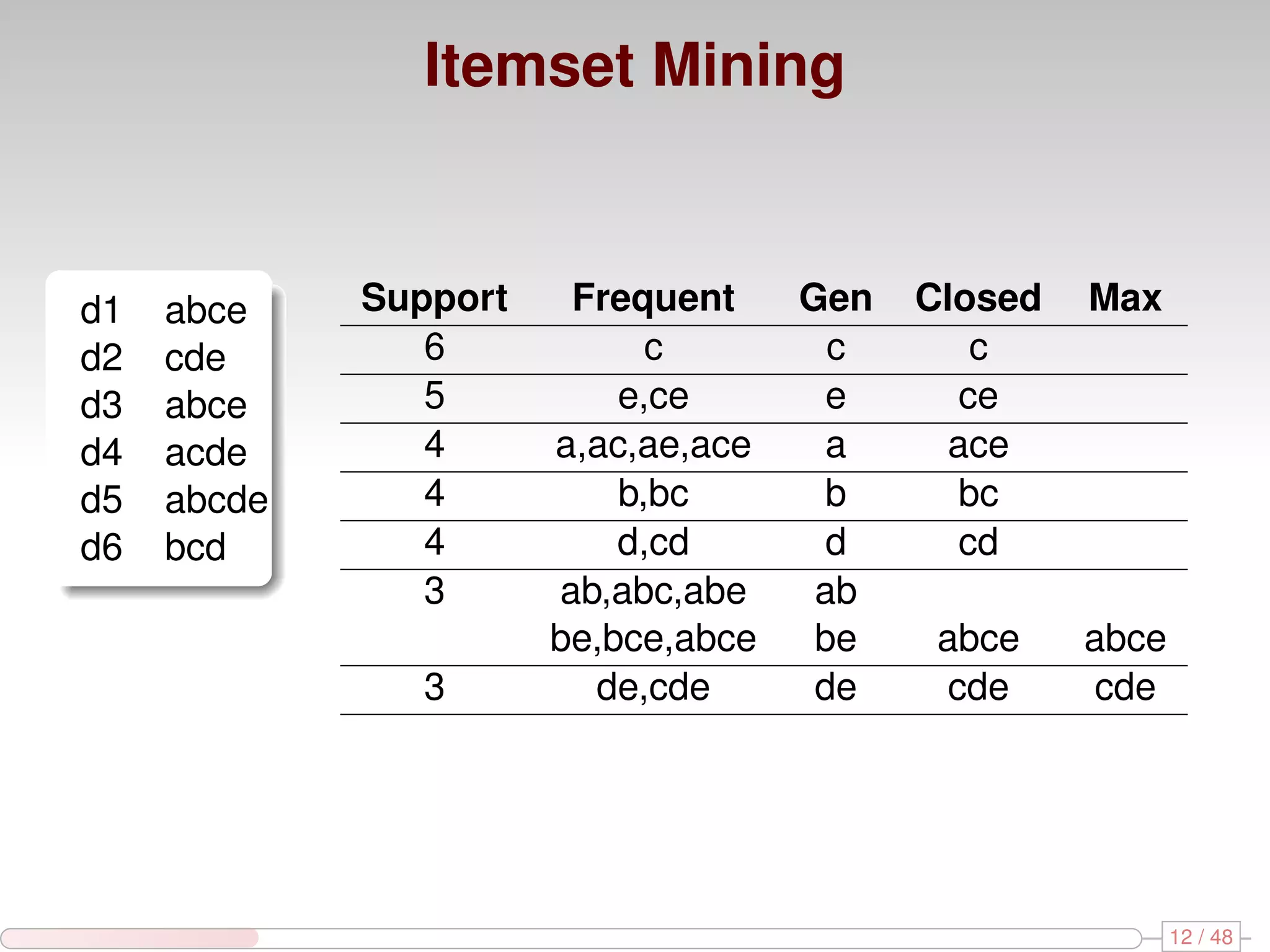
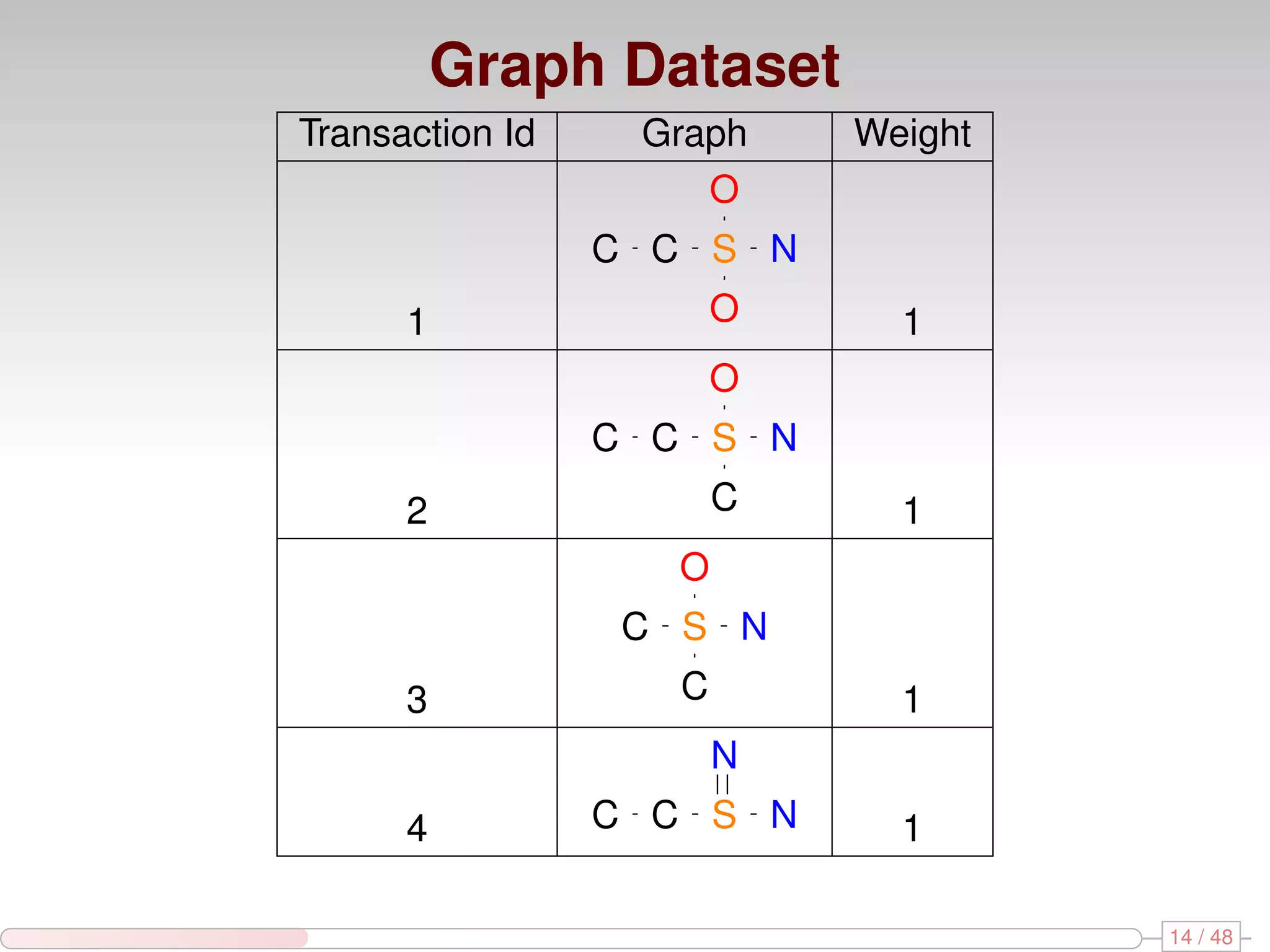
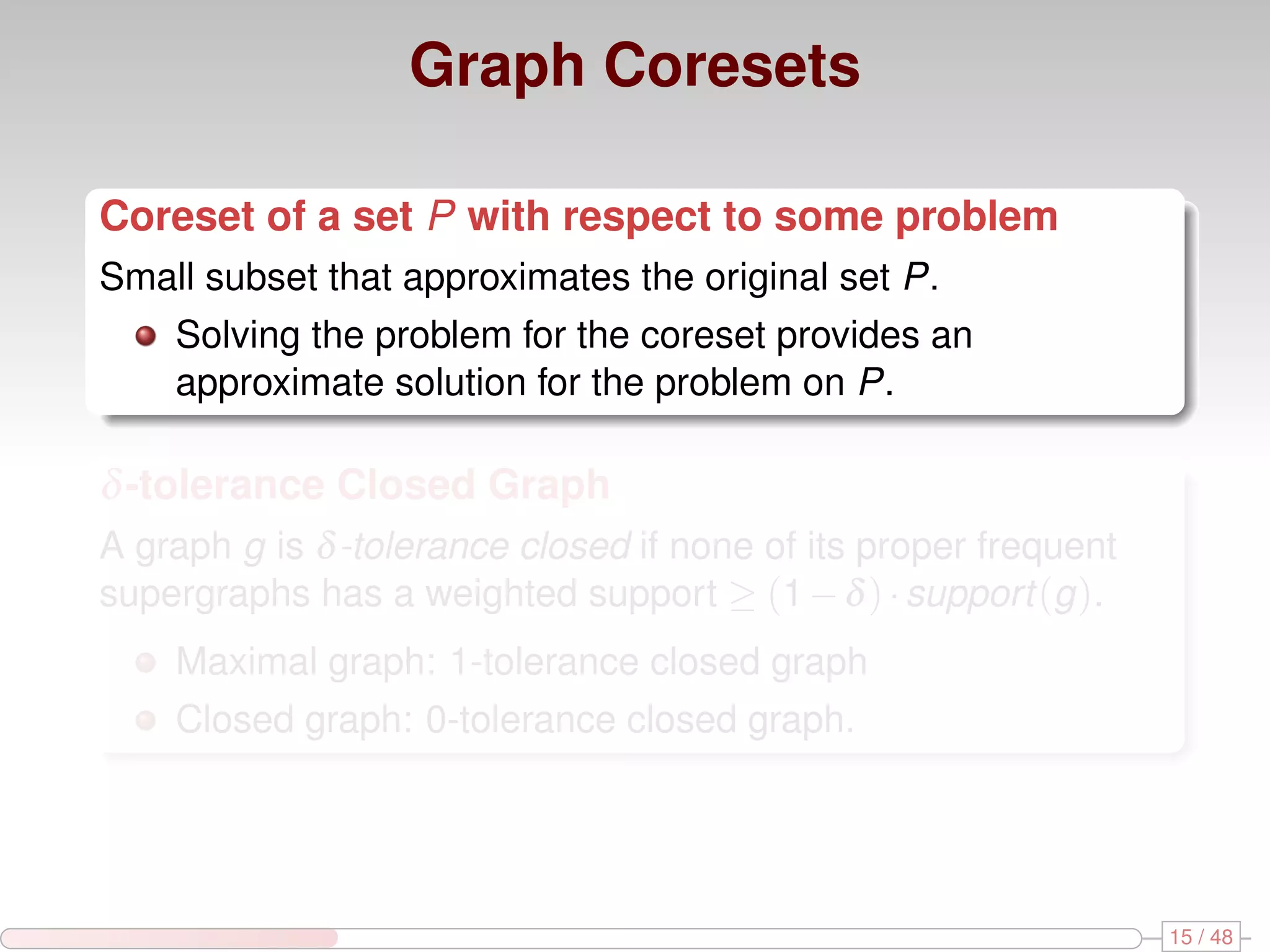
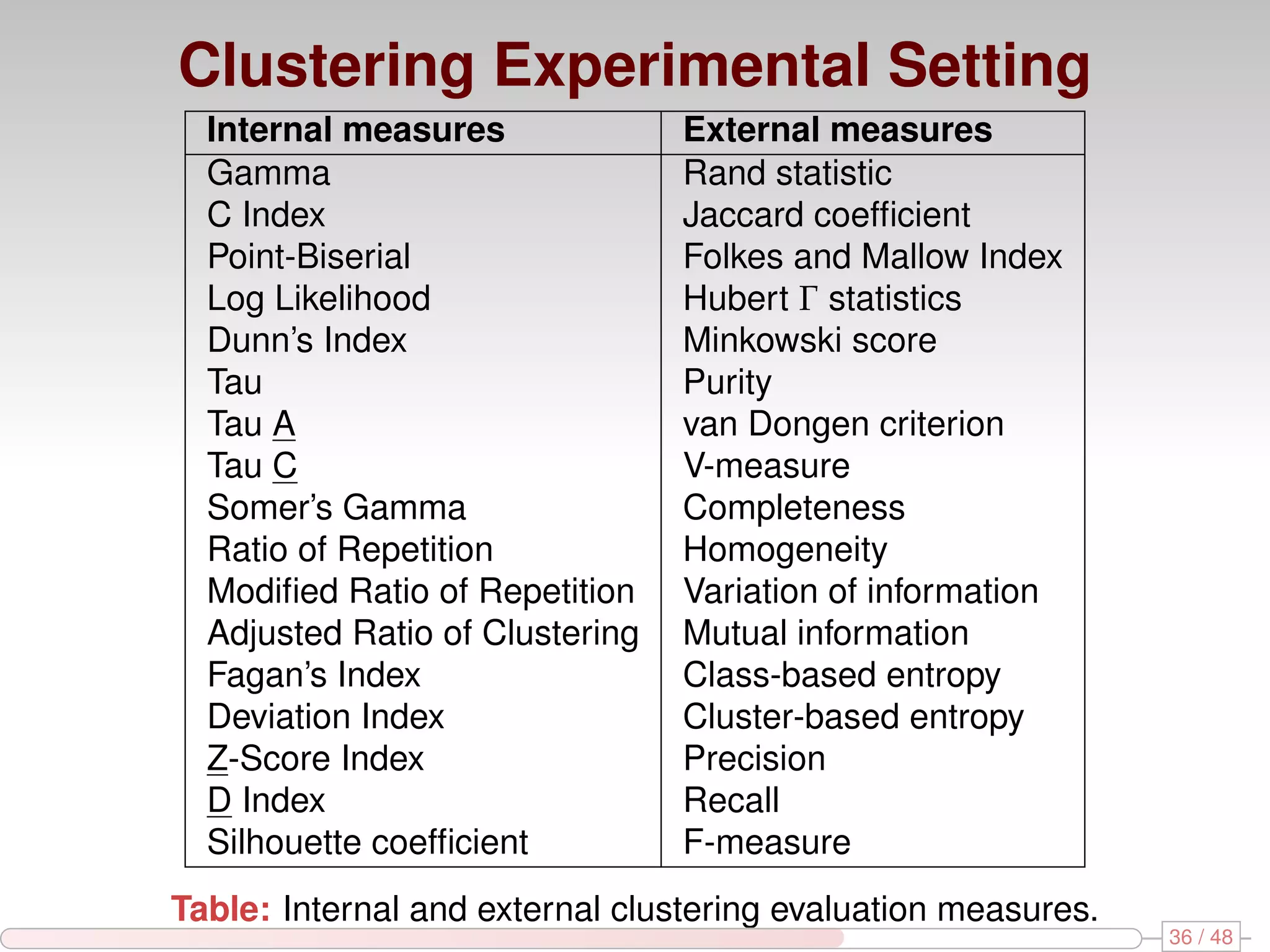
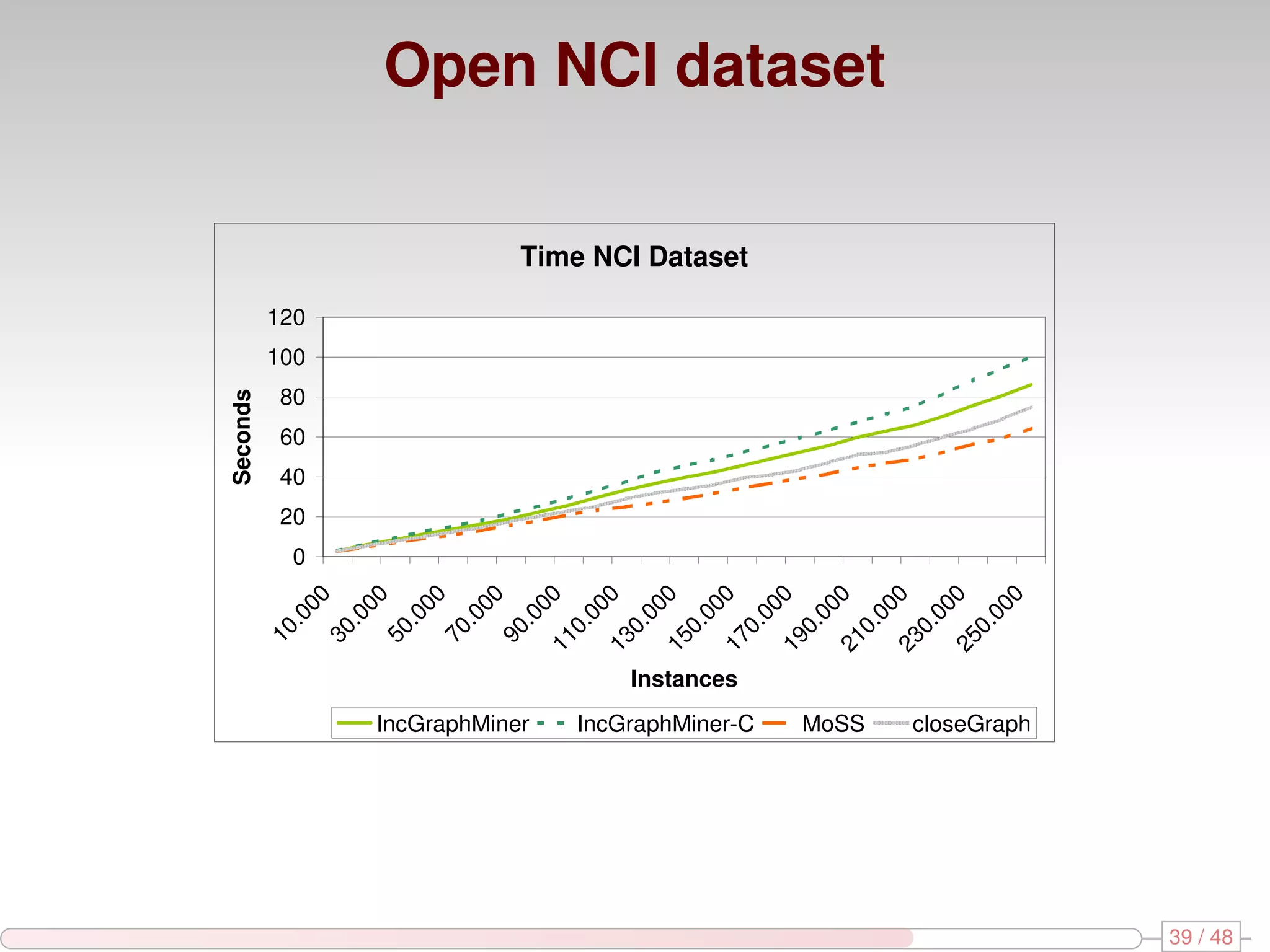
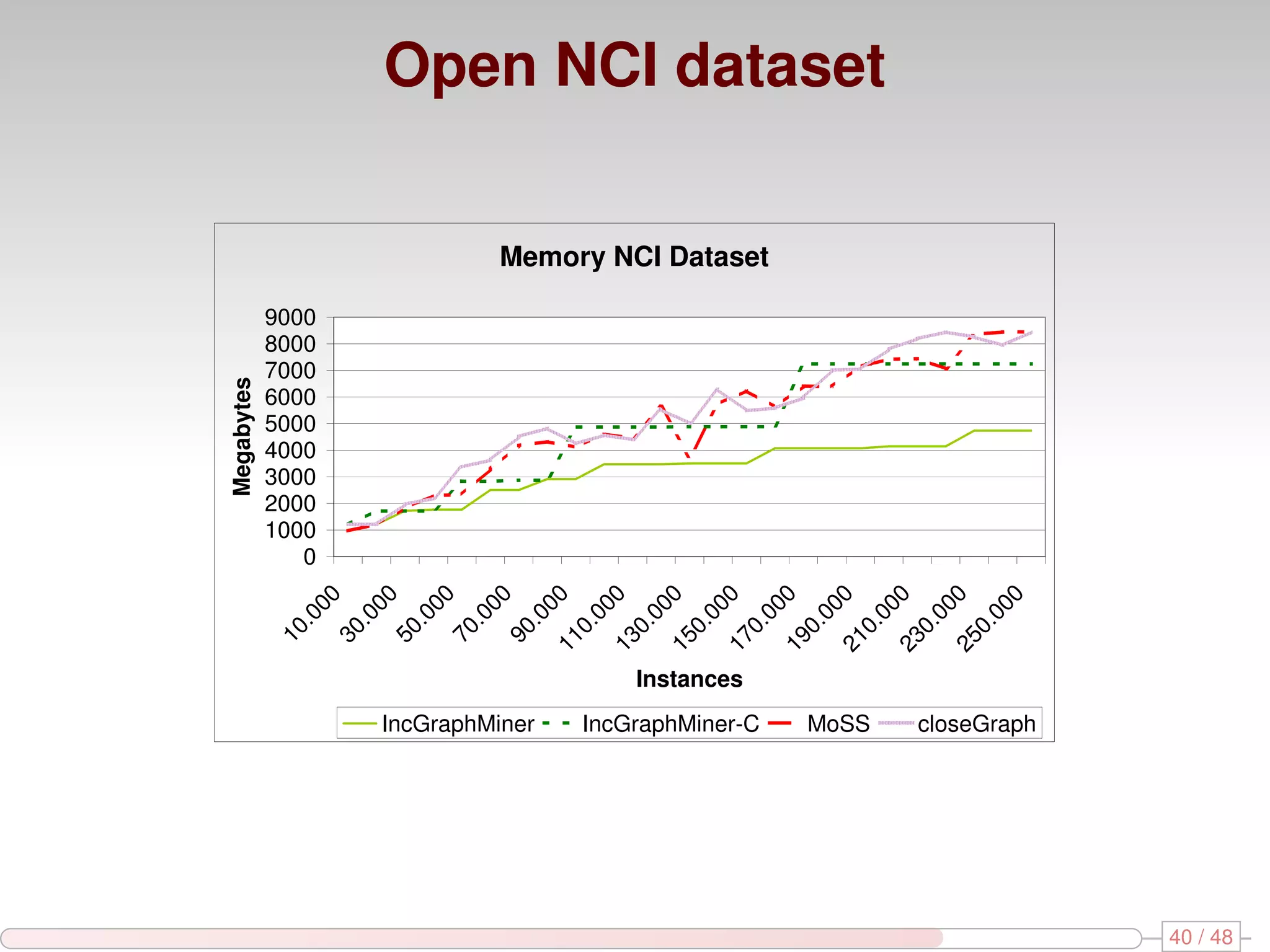
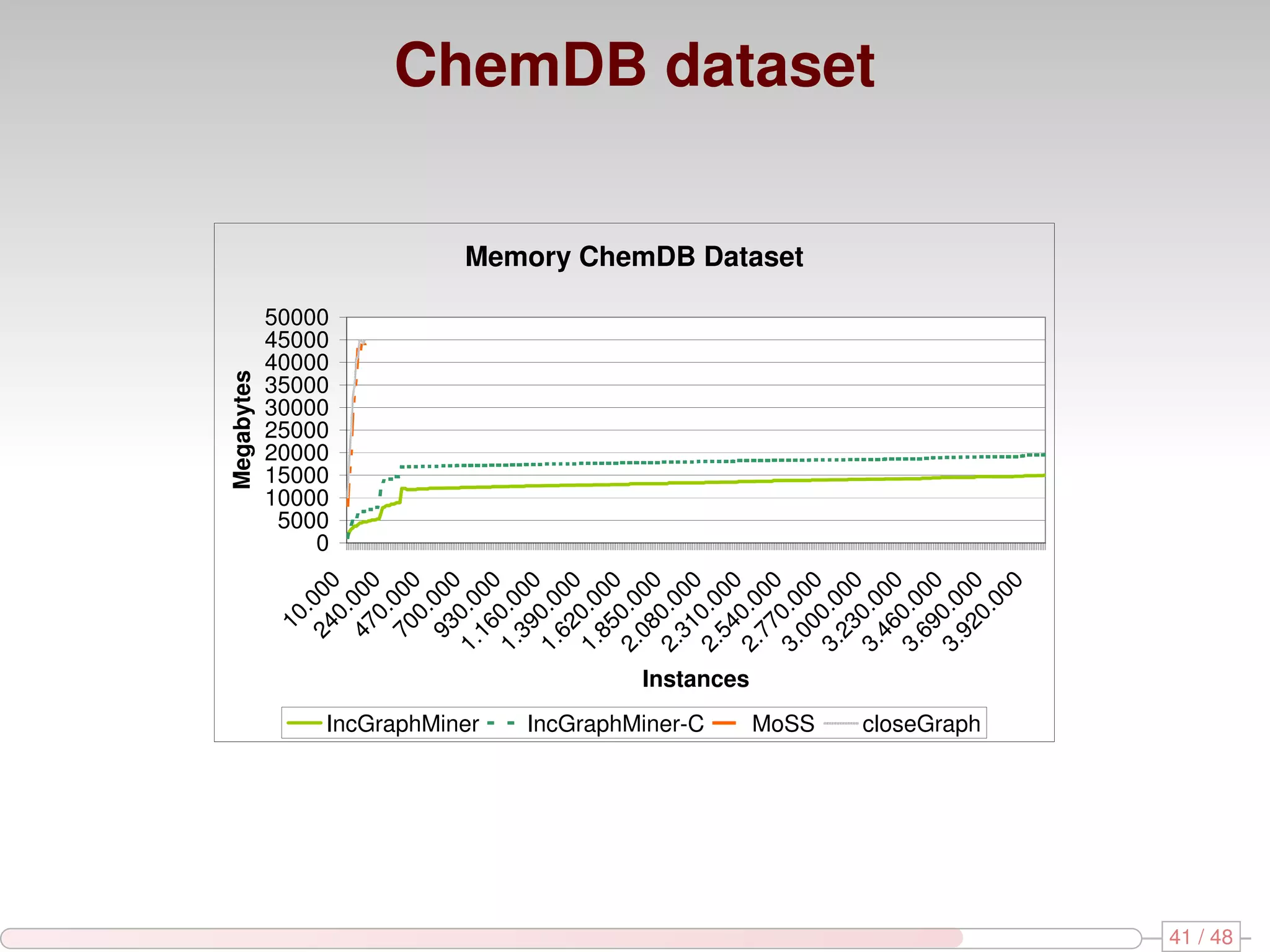
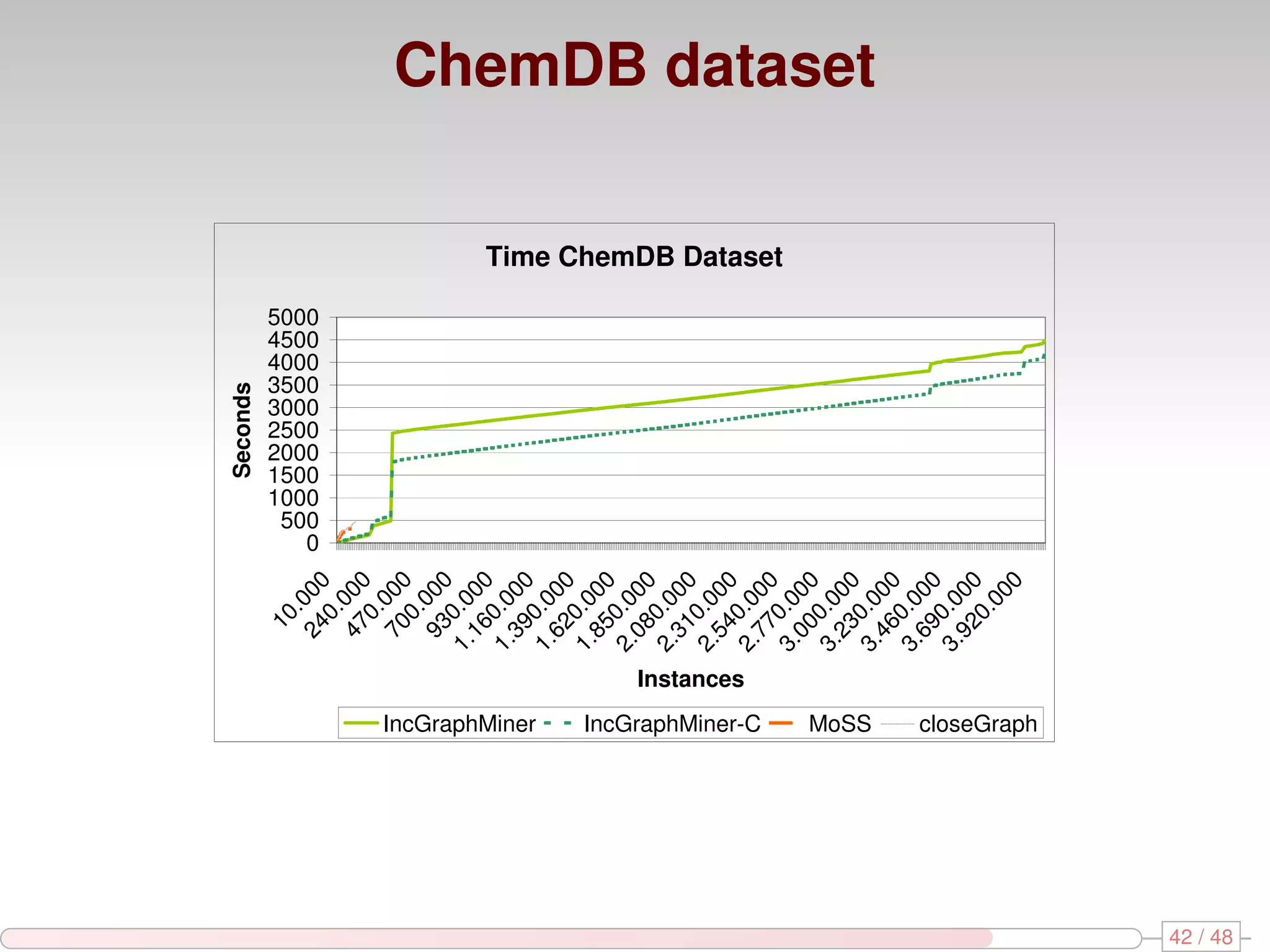
The document discusses algorithms for mining frequent closed graphs from evolving data streams, particularly focusing on incremental and non-incremental approaches. It reviews techniques such as sliding windows and adaptive algorithms for maintaining statistics over graph datasets while highlighting experimental evaluations. The research aims to improve methods for handling large and dynamic data sources in graph mining.

Downloaded 72 times
Mining Frequent Closed Graphs on Evolving Data Streams ` A. Bifet, G. Holmes, B. Pfahringer and R. Gavalda University of Waikato Hamilton, New Zealand Laboratory for Relational Algorithmics, Complexity and Learning LARCA UPC-Barcelona Tech, Catalonia San Diego, 24 August 2011 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 2011
Mining Evolving Graph Data Streams Problem Given a data stream D of graphs, find frequent closed graphs. Transaction Id Graph We provide three algorithms, O of increasing power C C S N Incremental 1 O Sliding Window O Adaptive C C S N 2 C N 3 C C S N 2 / 48
Non-incremental Frequent Closed Graph Mining CloseGraph: Xifeng Yan, Jiawei Han right-most extension based on depth-first search based on gSpan ICDM’02 MoSS: Christian Borgelt, Michael R. Berthold breadth-first search based on MoFa ICDM’02 3 / 48
Outline 1 Streaming Data 2 Frequent Pattern Mining Mining Evolving Graph Streams A DAG RAPH M INER 3 Experimental Evaluation 4 Summary and Future Work 4 / 48
Outline 1 Streaming Data 2 Frequent Pattern Mining Mining Evolving Graph Streams A DAG RAPH M INER 3 Experimental Evaluation 4 Summary and Future Work 5 / 48
Mining Massive Data Source: IDC’s Digital Universe Study (EMC), June 2011 6 / 48
Data Streams Data Streams Sequence is potentially infinite High amount of data High speed of arrival Once an element from a data stream has been processed it is discarded or archived Tools: approximation randomization, sampling sketching 7 / 48
Data Streams Approximation Algorithms 1011000111 1010101 Sliding Window We can maintain simple statistics over sliding windows, using O ( 1 log2 N ) space, where ε N is the length of the sliding window ε is the accuracy parameter M. Datar, A. Gionis, P. Indyk, and R. Motwani. Maintaining stream statistics over sliding windows. 2002 8 / 48
Data Streams Approximation Algorithms 10110001111 0101011 Sliding Window We can maintain simple statistics over sliding windows, using O ( 1 log2 N ) space, where ε N is the length of the sliding window ε is the accuracy parameter M. Datar, A. Gionis, P. Indyk, and R. Motwani. Maintaining stream statistics over sliding windows. 2002 8 / 48
Data Streams Approximation Algorithms 101100011110 1010111 Sliding Window We can maintain simple statistics over sliding windows, using O ( 1 log2 N ) space, where ε N is the length of the sliding window ε is the accuracy parameter M. Datar, A. Gionis, P. Indyk, and R. Motwani. Maintaining stream statistics over sliding windows. 2002 8 / 48
Data Streams Approximation Algorithms 1011000111101 0101110 Sliding Window We can maintain simple statistics over sliding windows, using O ( 1 log2 N ) space, where ε N is the length of the sliding window ε is the accuracy parameter M. Datar, A. Gionis, P. Indyk, and R. Motwani. Maintaining stream statistics over sliding windows. 2002 8 / 48
Data Streams Approximation Algorithms 10110001111010 1011101 Sliding Window We can maintain simple statistics over sliding windows, using O ( 1 log2 N ) space, where ε N is the length of the sliding window ε is the accuracy parameter M. Datar, A. Gionis, P. Indyk, and R. Motwani. Maintaining stream statistics over sliding windows. 2002 8 / 48
Data Streams Approximation Algorithms 101100011110101 0111010 Sliding Window We can maintain simple statistics over sliding windows, using O ( 1 log2 N ) space, where ε N is the length of the sliding window ε is the accuracy parameter M. Datar, A. Gionis, P. Indyk, and R. Motwani. Maintaining stream statistics over sliding windows. 2002 8 / 48
Outline 1 Streaming Data 2 Frequent Pattern Mining Mining Evolving Graph Streams A DAG RAPH M INER 3 Experimental Evaluation 4 Summary and Future Work 9 / 48
Pattern Mining Dataset Example Document Patterns d1 abce d2 cde d3 abce d4 acde d5 abcde d6 bcd 10 / 48
Itemset Mining d1 abce Support Frequent d2 cde d1,d2,d3,d4,d5,d6 c d3 abce d1,d2,d3,d4,d5 e,ce d4 acde d1,d3,d4,d5 a,ac,ae,ace d5 abcde d1,d3,d5,d6 b,bc d6 bcd d2,d4,d5 d,cd d1,d3,d5 ab,abc,abe be,bce,abce d2,d4,d5 de,cde 11 / 48
Itemset Mining d1 abce Support Frequent d2 cde 6 c d3 abce 5 e,ce d4 acde 4 a,ac,ae,ace d5 abcde 4 b,bc d6 bcd 4 d,cd 3 ab,abc,abe be,bce,abce 3 de,cde 12 / 48
Itemset Mining d1 abce Support Frequent Gen Closed d2 cde 6 c c c d3 abce 5 e,ce e ce d4 acde 4 a,ac,ae,ace a ace d5 abcde 4 b,bc b bc d6 bcd 4 d,cd d cd 3 ab,abc,abe ab be,bce,abce be abce 3 de,cde de cde 12 / 48
Itemset Mining d1 abce Support Frequent Gen Closed Max d2 cde 6 c c c d3 abce 5 e,ce e ce d4 acde 4 a,ac,ae,ace a ace d5 abcde 4 b,bc b bc d6 bcd 4 d,cd d cd 3 ab,abc,abe ab be,bce,abce be abce abce 3 de,cde de cde cde 12 / 48
Outline 1 Streaming Data 2 Frequent Pattern Mining Mining Evolving Graph Streams A DAG RAPH M INER 3 Experimental Evaluation 4 Summary and Future Work 13 / 48
Graph Dataset Transaction Id Graph Weight O C C S N 1 O 1 O C C S N 2 C 1 O C S N 3 C 1 N 4 C C S N 1 14 / 48
Graph Coresets Coreset of a set P with respect to some problem Small subset that approximates the original set P. Solving the problem for the coreset provides an approximate solution for the problem on P. δ -tolerance Closed Graph A graph g is δ -tolerance closed if none of its proper frequent supergraphs has a weighted support ≥ (1 − δ ) · support (g ). Maximal graph: 1-tolerance closed graph Closed graph: 0-tolerance closed graph. 15 / 48
Graph Coresets Coreset of a set P with respect to some problem Small subset that approximates the original set P. Solving the problem for the coreset provides an approximate solution for the problem on P. δ -tolerance Closed Graph A graph g is δ -tolerance closed if none of its proper frequent supergraphs has a weighted support ≥ (1 − δ ) · support (g ). Maximal graph: 1-tolerance closed graph Closed graph: 0-tolerance closed graph. 15 / 48
Graph Coresets Relative support of a closed graph Support of a graph minus the relative support of its closed supergraphs. The sum of the closed supergraphs’ relative supports of a graph and its relative support is equal to its own support. (s, δ )-coreset for the problem of computing closed graphs Weighted multiset of frequent δ -tolerance closed graphs with minimum support s using their relative support as a weight. 16 / 48
Graph Coresets Relative support of a closed graph Support of a graph minus the relative support of its closed supergraphs. The sum of the closed supergraphs’ relative supports of a graph and its relative support is equal to its own support. (s, δ )-coreset for the problem of computing closed graphs Weighted multiset of frequent δ -tolerance closed graphs with minimum support s using their relative support as a weight. 16 / 48
Graph Dataset Transaction Id Graph Weight O C C S N 1 O 1 O C C S N 2 C 1 O C S N 3 C 1 N 4 C C S N 1 17 / 48
Graph Coresets Graph Relative Support Support C C S N 3 3 O C S N 3 3 N C S 3 3 Table: Example of a coreset with minimum support 50% and δ = 1 18 / 48
Graph Coresets Figure: Number of graphs in a (40%, δ )-coreset for NCI. 19 / 48
Outline 1 Streaming Data 2 Frequent Pattern Mining Mining Evolving Graph Streams A DAG RAPH M INER 3 Experimental Evaluation 4 Summary and Future Work 20 / 48
I NC G RAPH M INER I NC G RAPH M INER (D, min sup ) Input: A graph dataset D, and min sup. Output: The frequent graph set G. 1 G←0 / 2 for every batch bt of graphs in D 3 do C ← C ORESET (bt , min sup ) 4 G ← C ORESET (G ∪ C, min sup ) 5 return G 21 / 48
W IN G RAPH M INER W IN G RAPH M INER (D, W , min sup ) Input: A graph dataset D, a size window W and min sup. Output: The frequent graph set G. 1 G←0 / 2 for every batch bt of graphs in D 3 do C ← C ORESET (bt , min sup ) 4 Store C in sliding window 5 if sliding window is full 6 then R ← Oldest C stored in sliding window, negate all support values 7 else R ← 0 / 8 G ← C ORESET (G ∪ C ∪ R, min sup ) 9 return G 22 / 48
Algorithm ADaptive Sliding WINdow Example W = 101010110111111 W0 = 1 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
Algorithm ADaptive Sliding WINdow Example W = 101010110111111 W0 = 1 W1 = 01010110111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
Algorithm ADaptive Sliding WINdow Example W = 101010110111111 W0 = 10 W1 = 1010110111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
Algorithm ADaptive Sliding WINdow Example W = 101010110111111 W0 = 101 W1 = 010110111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
Algorithm ADaptive Sliding WINdow Example W = 101010110111111 W0 = 1010 W1 = 10110111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
Algorithm ADaptive Sliding WINdow Example W = 101010110111111 W0 = 10101 W1 = 0110111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
Algorithm ADaptive Sliding WINdow Example W = 101010110111111 W0 = 101010 W1 = 110111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
Algorithm ADaptive Sliding WINdow Example W = 101010110111111 W0 = 1010101 W1 = 10111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
Algorithm ADaptive Sliding WINdow Example W = 101010110111111 W0 = 10101011 W1 = 0111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
Algorithm ADaptive Sliding WINdow Example W = 101010110111111 |µW0 − µW1 | ≥ εc : CHANGE DET.! ˆ ˆ W0 = 101010110 W1 = 111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
Algorithm ADaptive Sliding WINdow Example W = 101010110111111 Drop elements from the tail of W W0 = 101010110 W1 = 111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
Algorithm ADaptive Sliding WINdow Example W = 01010110111111 Drop elements from the tail of W W0 = 101010110 W1 = 111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
Algorithm ADaptive Sliding WINdow Theorem At every time step we have: 1 (False positive rate bound). If µt remains constant within W , the probability that ADWIN shrinks the window at this step is at most δ . 2 (False negative rate bound). Suppose that for some partition of W in two parts W0 W1 (where W1 contains the most recent items) we have |µW0 − µW1 | > 2εc . Then with probability 1 − δ ADWIN shrinks W to W1 , or shorter. ADWIN tunes itself to the data stream at hand, with no need for the user to hardwire or precompute parameters. 24 / 48
Algorithm ADaptive Sliding WINdow ADWIN using a Data Stream Sliding Window Model, can provide the exact counts of 1’s in O (1) time per point. tries O (log W ) cutpoints uses O ( 1 log W ) memory words ε the processing time per example is O (log W ) (amortized and worst-case). Sliding Window Model 1010101 101 11 1 1 Content: 4 2 2 1 1 Capacity: 7 3 2 1 1 25 / 48
A DAG RAPH M INER A DAG RAPH M INER (D, Mode, min sup ) 1 G←0 / 2 Init ADWIN 3 for every batch bt of graphs in D 4 do C ← C ORESET (bt , min sup ) 5 R←0 / 6 if Mode is Sliding Window 7 then Store C in sliding window 8 if ADWIN detected change 9 then R ← Batches to remove in sliding window with negative support 10 G ← C ORESET (G ∪ C ∪ R, min sup ) 11 if Mode is Sliding Window 12 then Insert # closed graphs into ADWIN 13 else for every g in G update g’s ADWIN 14 return G 26 / 48
A DAG RAPH M INER A DAG RAPH M INER (D, Mode, min sup ) 1 G←0 / 2 Init ADWIN 3 for every batch bt of graphs in D 4 do C ← C ORESET (bt , min sup ) 5 R←0 / 6 7 8 9 10 G ← C ORESET (G ∪ C ∪ R, min sup ) 11 12 13 for every g in G update g’s ADWIN 14 return G 26 / 48
A DAG RAPH M INER A DAG RAPH M INER (D, Mode, min sup ) 1 G←0 / 2 Init ADWIN 3 for every batch bt of graphs in D 4 do C ← C ORESET (bt , min sup ) 5 R←0 / 6 if Mode is Sliding Window 7 then Store C in sliding window 8 if ADWIN detected change 9 then R ← Batches to remove in sliding window with negative support 10 G ← C ORESET (G ∪ C ∪ R, min sup ) 11 if Mode is Sliding Window 12 then Insert # closed graphs into ADWIN 13 14 return G 26 / 48
Outline 1 Streaming Data 2 Frequent Pattern Mining Mining Evolving Graph Streams A DAG RAPH M INER 3 Experimental Evaluation 4 Summary and Future Work 27 / 48
Experimental Evaluation ChemDB dataset Public dataset 4 million molecules Institute for Genomics and Bioinformatics at the University of California, Irvine Open NCI Database Public domain 250,000 structures National Cancer Institute 28 / 48
What is MOA? {M}assive {O}nline {A}nalysis is a framework for online learning from data streams. It is closely related to WEKA It includes a collection of offline and online as well as tools for evaluation: classification clustering Easy to extend Easy to design and run experiments 29 / 48
WEKA: the bird 30 / 48
MOA: the bird The Moa (another native NZ bird) is not only flightless, like the Weka, but also extinct. 31 / 48
MOA: the bird The Moa (another native NZ bird) is not only flightless, like the Weka, but also extinct. 31 / 48
MOA: the bird The Moa (another native NZ bird) is not only flightless, like the Weka, but also extinct. 31 / 48
Classification Experimental Setting 32 / 48
Classification Experimental Setting Classifiers Naive Bayes Decision stumps Hoeffding Tree Hoeffding Option Tree Bagging and Boosting ADWIN Bagging and Leveraging Bagging Prediction strategies Majority class Naive Bayes Leaves Adaptive Hybrid 33 / 48
Clustering Experimental Setting 34 / 48
Clustering Experimental Setting Clusterers StreamKM++ CluStream ClusTree Den-Stream CobWeb 35 / 48
Clustering Experimental Setting Internal measures External measures Gamma Rand statistic C Index Jaccard coefficient Point-Biserial Folkes and Mallow Index Log Likelihood Hubert Γ statistics Dunn’s Index Minkowski score Tau Purity Tau A van Dongen criterion Tau C V-measure Somer’s Gamma Completeness Ratio of Repetition Homogeneity Modified Ratio of Repetition Variation of information Adjusted Ratio of Clustering Mutual information Fagan’s Index Class-based entropy Deviation Index Cluster-based entropy Z-Score Index Precision D Index Recall Silhouette coefficient F-measure Table: Internal and external clustering evaluation measures. 36 / 48
Cluster Mapping Measure Hardy Kremer, Philipp Kranen, Timm Jansen, Thomas Seidl, Albert Bifet, Geoff Holmes and Bernhard Pfahringer. An Effective Evaluation Measure for Clustering on Evolving Data Stream KDD’11 CMM: Cluster Mapping Measure A novel evaluation measure for stream clustering on evolving streams ∑o∈F w (o ) · pen(o, C ) CMM (C , C L ) = 1 − ∑o∈F w (o ) · con(o, Cl (o )) 37 / 48
Extensions of MOA Multi-label Classification Active Learning Regression Closed Frequent Graph Mining Twitter Sentiment Analysis Challenges for bigger data streams Sampling and distributed systems (Map-Reduce, Hadoop, S4) 38 / 48
Open NCI dataset Time NCI Dataset 120 100 80 Seconds 60 40 20 0 00 00 00 00 00 0 0 0 0 0 0 0 0 00 00 00 00 00 00 00 00 .0 .0 .0 .0 .0 0. 0. 0. 0. 0. 0. 0. 0. 10 30 50 70 90 11 13 15 17 19 21 23 25 Instances IncGraphMiner IncGraphMiner-C MoSS closeGraph 39 / 48
Open NCI dataset Memory NCI Dataset 9000 8000 7000 Megabytes 6000 5000 4000 3000 2000 1000 0 00 00 00 00 00 0 0 0 0 0 0 0 0 00 00 00 00 00 00 00 00 .0 .0 .0 .0 .0 0. 0. 0. 0. 0. 0. 0. 0. 10 30 50 70 90 11 13 15 17 19 21 23 25 Instances IncGraphMiner IncGraphMiner-C MoSS closeGraph 40 / 48
Megabytes 10 . 0 5000 10000 15000 20000 25000 30000 35000 40000 45000 24 000 50000 0. 47 000 0. 70 000 0. 93 000 IncGraphMiner 1. 0. 0 16 00 1. 0.0 39 00 1. 0.0 62 00 1. 0.0 85 00 2. 0.0 08 00 2. 0.0 31 00 IncGraphMiner-C 2. 0.0 54 00 Instances 2. 0.0 77 00 Memory ChemDB Dataset 3. 0.0 MoSS 00 00 3. 0.0 23 00 ChemDB dataset 3. 0.0 46 00 3. 0.0 69 00 3. 0.0 92 00 closeGraph 0. 00 0 41 / 48
Seconds 10 . 0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000 24 000 0. 47 000 0. 70 000 0. 93 000 1. 0. 0 16 00 1. 0.0 39 00 IncGraphMiner 1. 0.0 62 00 1. 0.0 85 00 2. 0.0 08 00 2. 0.0 31 00 2. 0.0 54 00 Instances IncGraphMiner-C 2. 0.0 77 00 Time ChemDB Dataset 3. 0.0 00 00 3. 0.0 23 00 MoSS ChemDB dataset 3. 0.0 46 00 3. 0.0 69 00 3. 0.0 92 00 0. 00 0 closeGraph 42 / 48
Number of Closed Graphs 10 .0 0 10 20 30 40 50 60 0 60 0 .0 11 00 0. 0 16 00 0. 00 21 0 0. 0 26 00 0. 0 31 00 0. 0 36 00 0. 0 ADAGRAPHMINER 41 00 0. 0 46 00 0. 0 51 00 0. 0 56 00 0. 00 Instances 61 0 0. 0 66 00 0. 0 71 00 0. 0 76 00 ADAGRAPHMINER-Window 0. 0 81 00 0. A DAG RAPH M INER 0 86 00 0. 0 91 00 0. 0 96 00 0. 00 IncGraphMiner 0 43 / 48
Outline 1 Streaming Data 2 Frequent Pattern Mining Mining Evolving Graph Streams A DAG RAPH M INER 3 Experimental Evaluation 4 Summary and Future Work 44 / 48
Summary Mining Evolving Graph Data Streams Given a data stream D of graphs, find frequent closed graphs. Transaction Id Graph We provide three algorithms, O of increasing power C C S N Incremental 1 O Sliding Window O Adaptive C C S N 2 C N 3 C C S N 45 / 48
Summary {M}assive {O}nline {A}nalysis is a framework for online learning from data streams. http://moa.cs.waikato.ac.nz It is closely related to WEKA It includes a collection of offline and online as well as tools for evaluation: classification clustering frequent pattern mining MOA deals with evolving data streams MOA is easy to use and extend 46 / 48
Future work Structured massive data mining sampling, sketching parallel techniques 47 / 48
Thanks! 48 / 48

More Related Content

PDF
Internet of Things Data Science
byAlbert Bifet
 
PDF
A Short Course in Data Stream Mining
byAlbert Bifet
 
PDF
Real-Time Big Data Stream Analytics
byAlbert Bifet
 
PPTX
STRIP: stream learning of influence probabilities.
byAlbert Bifet
 
PDF
Mining Adaptively Frequent Closed Unlabeled Rooted Trees in Data Streams
byAlbert Bifet
 
PDF
Efficient Data Stream Classification via Probabilistic Adaptive Windows
byAlbert Bifet
 
PDF
Introduction to Big Data Science
byAlbert Bifet
 
PDF
Real Time Big Data Management
byAlbert Bifet
 
Internet of Things Data Science
byAlbert Bifet
 
A Short Course in Data Stream Mining
byAlbert Bifet
 
Real-Time Big Data Stream Analytics
byAlbert Bifet
 
STRIP: stream learning of influence probabilities.
byAlbert Bifet
 
Mining Adaptively Frequent Closed Unlabeled Rooted Trees in Data Streams
byAlbert Bifet
 
Efficient Data Stream Classification via Probabilistic Adaptive Windows
byAlbert Bifet
 
Introduction to Big Data Science
byAlbert Bifet
 
Real Time Big Data Management
byAlbert Bifet
 

What's hot

PDF
Parallel Optimization in Machine Learning
byFabian Pedregosa
 
PDF
Distance oracle - Truy vấn nhanh khoảng cách giữa hai điểm bất kỳ trên đồ thị
byHong Ong
 
PDF
Codes and Isogenies
byPriyanka Aash
 
PDF
Text classification in scikit-learn
byJimmy Lai
 
PDF
Scaling Deep Learning with MXNet
byAI Frontiers
 
PDF
Sebastian Schelter – Distributed Machine Learing with the Samsara DSL
byFlink Forward
 
PPTX
Distributed GLM with H2O - Atlanta Meetup
bySri Ambati
 
PDF
Speaker Diarization
byHONGJOO LEE
 
PPT
Processing Reachability Queries with Realistic Constraints on Massive Network...
byBigMine
 
PDF
Sea Amsterdam 2014 November 19
byGoDataDriven
 
PDF
Accelerating Metropolis Hastings with Lightweight Inference Compilation
byFeynman Liang
 
PDF
Leveraging Bagging for Evolving Data Streams
byAlbert Bifet
 
PPT
Accelerating Collapsed Variational Bayesian Inference for Latent Dirichlet Al...
byTomonari Masada
 
PDF
EuroPython 2017 - PyData - Deep Learning your Broadband Network @ HOME
byHONGJOO LEE
 
PPT
Python classes in mumbai
byVibrant Technologies & Computers
 
PDF
Sergei Vassilvitskii, Research Scientist, Google at MLconf NYC - 4/15/16
byMLconf
 
Parallel Optimization in Machine Learning
byFabian Pedregosa
 
Distance oracle - Truy vấn nhanh khoảng cách giữa hai điểm bất kỳ trên đồ thị
byHong Ong
 
Codes and Isogenies
byPriyanka Aash
 
Text classification in scikit-learn
byJimmy Lai
 
Scaling Deep Learning with MXNet
byAI Frontiers
 
Sebastian Schelter – Distributed Machine Learing with the Samsara DSL
byFlink Forward
 
Distributed GLM with H2O - Atlanta Meetup
bySri Ambati
 
Speaker Diarization
byHONGJOO LEE
 
Processing Reachability Queries with Realistic Constraints on Massive Network...
byBigMine
 
Sea Amsterdam 2014 November 19
byGoDataDriven
 
Accelerating Metropolis Hastings with Lightweight Inference Compilation
byFeynman Liang
 
Leveraging Bagging for Evolving Data Streams
byAlbert Bifet
 
Accelerating Collapsed Variational Bayesian Inference for Latent Dirichlet Al...
byTomonari Masada
 
EuroPython 2017 - PyData - Deep Learning your Broadband Network @ HOME
byHONGJOO LEE
 
Python classes in mumbai
byVibrant Technologies & Computers
 
Sergei Vassilvitskii, Research Scientist, Google at MLconf NYC - 4/15/16
byMLconf
 

Viewers also liked

PDF
Frequent Pattern Mining - Krishna Sridhar, Feb 2016
bySeattle DAML meetup
 
PPT
Data Mining: Concepts and Techniques chapter 07 : Advanced Frequent Pattern M...
bySalah Amean
 
PPSX
Frequent itemset mining methods
byProf.Nilesh Magar
 
PPTX
Frequent Itemset Mining(FIM) on BigData
byRaju Gupta
 
PDF
Data Mining: Association Rules Basics
byBenazir Income Support Program (BISP)
 
PPTX
9 Data Mining Challenges From Data Scientists Like You
bySalford Systems
 
PDF
Lecture13 - Association Rules
byAlbert Orriols-Puig
 
PDF
Comunicación en Redes Sociales y Políticas Corporativas por IBM México en 5° ...
byPRORP México
 
PPT
Survey on Frequent Pattern Mining on Graph Data - Slides
byKasun Gajasinghe
 
PPTX
New opportunities for connected data : Neo4j the graph database
byCédric Fauvet
 
Frequent Pattern Mining - Krishna Sridhar, Feb 2016
bySeattle DAML meetup
 
Data Mining: Concepts and Techniques chapter 07 : Advanced Frequent Pattern M...
bySalah Amean
 
Frequent itemset mining methods
byProf.Nilesh Magar
 
Frequent Itemset Mining(FIM) on BigData
byRaju Gupta
 
Data Mining: Association Rules Basics
byBenazir Income Support Program (BISP)
 
9 Data Mining Challenges From Data Scientists Like You
bySalford Systems
 
Lecture13 - Association Rules
byAlbert Orriols-Puig
 
Comunicación en Redes Sociales y Políticas Corporativas por IBM México en 5° ...
byPRORP México
 
Survey on Frequent Pattern Mining on Graph Data - Slides
byKasun Gajasinghe
 
New opportunities for connected data : Neo4j the graph database
byCédric Fauvet
 

Similar to Mining Frequent Closed Graphs on Evolving Data Streams

PDF
Feequent Item Mining - Data Mining - Pattern Mining
byJason J Pulikkottil
 
PDF
Approximation Data Structures for Streaming Applications
byDebasish Ghosh
 
PPTX
Data streaming algorithms
bySandeep Joshi
 
PDF
Delay A Lazy Approach for Mining Frequent Patterns over High Speed Data Strea...
bykuskuslijj46
 
PPT
Chapter - 8.3 Data Mining Concepts and Techniques 2nd Ed slides Han & Kamber
byerror007
 
PPT
Graph mining seminar_2009
byHouw Liong The
 
PDF
Adaptive Learning and Mining for Data Streams and Frequent Patterns
byAlbert Bifet
 
PPTX
Frequent Itemset Mining on BigData
byRaju Gupta
 
PPT
Lecture20
bymattriley
 
PPT
graph_mining_seminar_2009.ppt
byVenkateswara Rao Katevarapu
 
PDF
Db2425082511
byIJMER
 
PPT
Cs501 mining frequentpatterns
byKamal Singh Lodhi
 
PDF
386 390
byEditor IJARCET
 
PDF
386 390
byEditor IJARCET
 
PDF
An Efficient Algorithm for Mining Frequent Itemsets within Large Windows over...
byWaqas Tariq
 
PPTX
2013 py con awesome big data algorithms
byc.titus.brown
 
PDF
Graph based Approach and Clustering of Patterns (GACP) for Sequential Pattern...
byAshishDPatel1
 
PDF
A New Data Stream Mining Algorithm for Interestingness-rich Association Rules
byVenu Madhav
 
PDF
Literature Survey of modern frequent item set mining methods
byijsrd.com
 
PDF
Usage and Research Challenges in the Area of Frequent Pattern in Data Mining
byIOSR Journals
 
Feequent Item Mining - Data Mining - Pattern Mining
byJason J Pulikkottil
 
Approximation Data Structures for Streaming Applications
byDebasish Ghosh
 
Data streaming algorithms
bySandeep Joshi
 
Delay A Lazy Approach for Mining Frequent Patterns over High Speed Data Strea...
bykuskuslijj46
 
Chapter - 8.3 Data Mining Concepts and Techniques 2nd Ed slides Han & Kamber
byerror007
 
Graph mining seminar_2009
byHouw Liong The
 
Adaptive Learning and Mining for Data Streams and Frequent Patterns
byAlbert Bifet
 
Frequent Itemset Mining on BigData
byRaju Gupta
 
Lecture20
bymattriley
 
graph_mining_seminar_2009.ppt
byVenkateswara Rao Katevarapu
 
Db2425082511
byIJMER
 
Cs501 mining frequentpatterns
byKamal Singh Lodhi
 
386 390
byEditor IJARCET
 
386 390
byEditor IJARCET
 
An Efficient Algorithm for Mining Frequent Itemsets within Large Windows over...
byWaqas Tariq
 
2013 py con awesome big data algorithms
byc.titus.brown
 
Graph based Approach and Clustering of Patterns (GACP) for Sequential Pattern...
byAshishDPatel1
 
A New Data Stream Mining Algorithm for Interestingness-rich Association Rules
byVenu Madhav
 
Literature Survey of modern frequent item set mining methods
byijsrd.com
 
Usage and Research Challenges in the Area of Frequent Pattern in Data Mining
byIOSR Journals
 

More from Albert Bifet

PDF
MOA for the IoT at ACML 2016
byAlbert Bifet
 
PDF
Introduction to Big Data
byAlbert Bifet
 
PDF
Artificial intelligence and data stream mining
byAlbert Bifet
 
PDF
Kalman Filters and Adaptive Windows for Learning in Data Streams
byAlbert Bifet
 
PDF
Pitfalls in benchmarking data stream classification and how to avoid them
byAlbert Bifet
 
PDF
MOA : Massive Online Analysis
byAlbert Bifet
 
PDF
Multi-label Classification with Meta-labels
byAlbert Bifet
 
PDF
PAKDD 2011 TUTORIAL Handling Concept Drift: Importance, Challenges and Solutions
byAlbert Bifet
 
PDF
Fast Perceptron Decision Tree Learning from Evolving Data Streams
byAlbert Bifet
 
PDF
Moa: Real Time Analytics for Data Streams
byAlbert Bifet
 
PDF
Métodos Adaptativos de Minería de Datos y Aprendizaje para Flujos de Datos.
byAlbert Bifet
 
PDF
Mining Big Data in Real Time
byAlbert Bifet
 
PDF
Efficient Online Evaluation of Big Data Stream Classifiers
byAlbert Bifet
 
PDF
Sentiment Knowledge Discovery in Twitter Streaming Data
byAlbert Bifet
 
PDF
Mining Big Data Streams with APACHE SAMOA
byAlbert Bifet
 
PDF
New ensemble methods for evolving data streams
byAlbert Bifet
 
PDF
Apache Samoa: Mining Big Data Streams with Apache Flink
byAlbert Bifet
 
PDF
Adaptive XML Tree Mining on Evolving Data Streams
byAlbert Bifet
 
PDF
Mining Implications from Lattices of Closed Trees
byAlbert Bifet
 
PPTX
Mining Big Data in Real Time
byAlbert Bifet
 
MOA for the IoT at ACML 2016
byAlbert Bifet
 
Introduction to Big Data
byAlbert Bifet
 
Artificial intelligence and data stream mining
byAlbert Bifet
 
Kalman Filters and Adaptive Windows for Learning in Data Streams
byAlbert Bifet
 
Pitfalls in benchmarking data stream classification and how to avoid them
byAlbert Bifet
 
MOA : Massive Online Analysis
byAlbert Bifet
 
Multi-label Classification with Meta-labels
byAlbert Bifet
 
PAKDD 2011 TUTORIAL Handling Concept Drift: Importance, Challenges and Solutions
byAlbert Bifet
 
Fast Perceptron Decision Tree Learning from Evolving Data Streams
byAlbert Bifet
 
Moa: Real Time Analytics for Data Streams
byAlbert Bifet
 
Métodos Adaptativos de Minería de Datos y Aprendizaje para Flujos de Datos.
byAlbert Bifet
 
Mining Big Data in Real Time
byAlbert Bifet
 
Efficient Online Evaluation of Big Data Stream Classifiers
byAlbert Bifet
 
Sentiment Knowledge Discovery in Twitter Streaming Data
byAlbert Bifet
 
Mining Big Data Streams with APACHE SAMOA
byAlbert Bifet
 
New ensemble methods for evolving data streams
byAlbert Bifet
 
Apache Samoa: Mining Big Data Streams with Apache Flink
byAlbert Bifet
 
Adaptive XML Tree Mining on Evolving Data Streams
byAlbert Bifet
 
Mining Implications from Lattices of Closed Trees
byAlbert Bifet
 
Mining Big Data in Real Time
byAlbert Bifet
 

Recently uploaded

PPTX
Your First Deep Learning project With CNN (workshop).pptx
byMuhammad Fahad Bashir
 
PDF
MicroPython presentation - PyConFr Lyon 2025 - Amine Bendahmane
byAmine Bendahmane
 
PDF
How to not make bugs (in JSC), and the future of 32-bits
byIgalia
 
PDF
WebXR in Android and Linux with OpenXR
byIgalia
 
PDF
Supercharge Your JVM with Project Leyden
byAna-Maria Mihalceanu
 
PDF
How Tridens DevSecOps Ensures Compliance, Security, and Agility
byTridens
 
PDF
Wrapping up unowned UTF8 C strings: CStringView
byIgalia
 
PDF
GDG Boise - Innovating with Google Cloud Artificial Intelligence
byJoey Brown
 
PDF
Data Center Exit to Cloud _ Managed Datacenter Migration.pdf
byAstuteBusiness
 
PDF
The Future-Ready PMO: Unlocking Project Success with Copilot and AI Innovatio...
byWellingtone
 
PPTX
A GREEN BUSINESS TOOLKIT FOR EARLY-STAGE ENTREPRENEURS (1).pptx.pptx
bylearnskillsofficial1
 
PDF
Transform Your Online Store with AltiusNxt AI Enriched data
byAltiusNxt Technologies
 
PPTX
Sephora UAE API Service Real-Time Product & Price Data Access.pptx
bycreativeclicks1733
 
PDF
Exclusive Hands-On Workshop: Agentic Automation with UiPath (First Edition)
byanabulhac
 
PDF
Virtualization and Container Technologies in Cloud Security - ISC2 Certificate
byVICTOR MAESTRE RAMIREZ
 
PPTX
GenAI GraphTalk - Kuala Lumpur - 4 Nov 2025
bygourisachdeva2
 
PDF
Revolutionizing SQL Database Design for the Modern Era.pdf
bySQL DBM
 
PDF
ENTSO-E's Response to the European Commission Call for Evidence on the Strate...
byReynir Orn Bachmann Gudmundsson
 
PDF
The Complete Crypto Airdrop Playbook: Strategies, Scams & Success Stories | 3...
by3verseTV
 
PDF
Private Governance: How Decentralized Mechanisms Can Regulate the Crypto Economy
byFederico Ast
 
Your First Deep Learning project With CNN (workshop).pptx
byMuhammad Fahad Bashir
 
MicroPython presentation - PyConFr Lyon 2025 - Amine Bendahmane
byAmine Bendahmane
 
How to not make bugs (in JSC), and the future of 32-bits
byIgalia
 
WebXR in Android and Linux with OpenXR
byIgalia
 
Supercharge Your JVM with Project Leyden
byAna-Maria Mihalceanu
 
How Tridens DevSecOps Ensures Compliance, Security, and Agility
byTridens
 
Wrapping up unowned UTF8 C strings: CStringView
byIgalia
 
GDG Boise - Innovating with Google Cloud Artificial Intelligence
byJoey Brown
 
Data Center Exit to Cloud _ Managed Datacenter Migration.pdf
byAstuteBusiness
 
The Future-Ready PMO: Unlocking Project Success with Copilot and AI Innovatio...
byWellingtone
 
A GREEN BUSINESS TOOLKIT FOR EARLY-STAGE ENTREPRENEURS (1).pptx.pptx
bylearnskillsofficial1
 
Transform Your Online Store with AltiusNxt AI Enriched data
byAltiusNxt Technologies
 
Sephora UAE API Service Real-Time Product & Price Data Access.pptx
bycreativeclicks1733
 
Exclusive Hands-On Workshop: Agentic Automation with UiPath (First Edition)
byanabulhac
 
Virtualization and Container Technologies in Cloud Security - ISC2 Certificate
byVICTOR MAESTRE RAMIREZ
 
GenAI GraphTalk - Kuala Lumpur - 4 Nov 2025
bygourisachdeva2
 
Revolutionizing SQL Database Design for the Modern Era.pdf
bySQL DBM
 
ENTSO-E's Response to the European Commission Call for Evidence on the Strate...
byReynir Orn Bachmann Gudmundsson
 
The Complete Crypto Airdrop Playbook: Strategies, Scams & Success Stories | 3...
by3verseTV
 
Private Governance: How Decentralized Mechanisms Can Regulate the Crypto Economy
byFederico Ast
 

Mining Frequent Closed Graphs on Evolving Data Streams

  • 1.
    Mining Frequent ClosedGraphs on Evolving Data Streams ` A. Bifet, G. Holmes, B. Pfahringer and R. Gavalda University of Waikato Hamilton, New Zealand Laboratory for Relational Algorithmics, Complexity and Learning LARCA UPC-Barcelona Tech, Catalonia San Diego, 24 August 2011 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 2011
  • 2.
    Mining Evolving GraphData Streams Problem Given a data stream D of graphs, find frequent closed graphs. Transaction Id Graph We provide three algorithms, O of increasing power C C S N Incremental 1 O Sliding Window O Adaptive C C S N 2 C N 3 C C S N 2 / 48
  • 3.
    Non-incremental Frequent Closed Graph Mining CloseGraph: Xifeng Yan, Jiawei Han right-most extension based on depth-first search based on gSpan ICDM’02 MoSS: Christian Borgelt, Michael R. Berthold breadth-first search based on MoFa ICDM’02 3 / 48
  • 4.
    Outline 1 Streaming Data 2 Frequent Pattern Mining Mining Evolving Graph Streams A DAG RAPH M INER 3 Experimental Evaluation 4 Summary and Future Work 4 / 48
  • 5.
    Outline 1 Streaming Data 2 Frequent Pattern Mining Mining Evolving Graph Streams A DAG RAPH M INER 3 Experimental Evaluation 4 Summary and Future Work 5 / 48
  • 6.
    Mining Massive Data Source:IDC’s Digital Universe Study (EMC), June 2011 6 / 48
  • 7.
    Data Streams Data Streams Sequence is potentially infinite High amount of data High speed of arrival Once an element from a data stream has been processed it is discarded or archived Tools: approximation randomization, sampling sketching 7 / 48
  • 8.
    Data Streams ApproximationAlgorithms 1011000111 1010101 Sliding Window We can maintain simple statistics over sliding windows, using O ( 1 log2 N ) space, where ε N is the length of the sliding window ε is the accuracy parameter M. Datar, A. Gionis, P. Indyk, and R. Motwani. Maintaining stream statistics over sliding windows. 2002 8 / 48
  • 9.
    Data Streams ApproximationAlgorithms 10110001111 0101011 Sliding Window We can maintain simple statistics over sliding windows, using O ( 1 log2 N ) space, where ε N is the length of the sliding window ε is the accuracy parameter M. Datar, A. Gionis, P. Indyk, and R. Motwani. Maintaining stream statistics over sliding windows. 2002 8 / 48
  • 10.
    Data Streams ApproximationAlgorithms 101100011110 1010111 Sliding Window We can maintain simple statistics over sliding windows, using O ( 1 log2 N ) space, where ε N is the length of the sliding window ε is the accuracy parameter M. Datar, A. Gionis, P. Indyk, and R. Motwani. Maintaining stream statistics over sliding windows. 2002 8 / 48
  • 11.
    Data Streams ApproximationAlgorithms 1011000111101 0101110 Sliding Window We can maintain simple statistics over sliding windows, using O ( 1 log2 N ) space, where ε N is the length of the sliding window ε is the accuracy parameter M. Datar, A. Gionis, P. Indyk, and R. Motwani. Maintaining stream statistics over sliding windows. 2002 8 / 48
  • 12.
    Data Streams ApproximationAlgorithms 10110001111010 1011101 Sliding Window We can maintain simple statistics over sliding windows, using O ( 1 log2 N ) space, where ε N is the length of the sliding window ε is the accuracy parameter M. Datar, A. Gionis, P. Indyk, and R. Motwani. Maintaining stream statistics over sliding windows. 2002 8 / 48
  • 13.
    Data Streams ApproximationAlgorithms 101100011110101 0111010 Sliding Window We can maintain simple statistics over sliding windows, using O ( 1 log2 N ) space, where ε N is the length of the sliding window ε is the accuracy parameter M. Datar, A. Gionis, P. Indyk, and R. Motwani. Maintaining stream statistics over sliding windows. 2002 8 / 48
  • 14.
    Outline 1 Streaming Data 2 Frequent Pattern Mining Mining Evolving Graph Streams A DAG RAPH M INER 3 Experimental Evaluation 4 Summary and Future Work 9 / 48
  • 15.
    Pattern Mining Dataset Example Document Patterns d1 abce d2 cde d3 abce d4 acde d5 abcde d6 bcd 10 / 48
  • 16.
    Itemset Mining d1 abce Support Frequent d2 cde d1,d2,d3,d4,d5,d6 c d3 abce d1,d2,d3,d4,d5 e,ce d4 acde d1,d3,d4,d5 a,ac,ae,ace d5 abcde d1,d3,d5,d6 b,bc d6 bcd d2,d4,d5 d,cd d1,d3,d5 ab,abc,abe be,bce,abce d2,d4,d5 de,cde 11 / 48
  • 17.
    Itemset Mining d1 abce Support Frequent d2 cde 6 c d3 abce 5 e,ce d4 acde 4 a,ac,ae,ace d5 abcde 4 b,bc d6 bcd 4 d,cd 3 ab,abc,abe be,bce,abce 3 de,cde 12 / 48
  • 18.
    Itemset Mining d1 abce Support Frequent Gen Closed d2 cde 6 c c c d3 abce 5 e,ce e ce d4 acde 4 a,ac,ae,ace a ace d5 abcde 4 b,bc b bc d6 bcd 4 d,cd d cd 3 ab,abc,abe ab be,bce,abce be abce 3 de,cde de cde 12 / 48
  • 19.
    Itemset Mining d1 abce Support Frequent Gen Closed Max d2 cde 6 c c c d3 abce 5 e,ce e ce d4 acde 4 a,ac,ae,ace a ace d5 abcde 4 b,bc b bc d6 bcd 4 d,cd d cd 3 ab,abc,abe ab be,bce,abce be abce abce 3 de,cde de cde cde 12 / 48
  • 20.
    Outline 1 Streaming Data 2 Frequent Pattern Mining Mining Evolving Graph Streams A DAG RAPH M INER 3 Experimental Evaluation 4 Summary and Future Work 13 / 48
  • 21.
    Graph Dataset Transaction Id Graph Weight O C C S N 1 O 1 O C C S N 2 C 1 O C S N 3 C 1 N 4 C C S N 1 14 / 48
  • 22.
    Graph Coresets Coreset ofa set P with respect to some problem Small subset that approximates the original set P. Solving the problem for the coreset provides an approximate solution for the problem on P. δ -tolerance Closed Graph A graph g is δ -tolerance closed if none of its proper frequent supergraphs has a weighted support ≥ (1 − δ ) · support (g ). Maximal graph: 1-tolerance closed graph Closed graph: 0-tolerance closed graph. 15 / 48
  • 23.
    Graph Coresets Coreset ofa set P with respect to some problem Small subset that approximates the original set P. Solving the problem for the coreset provides an approximate solution for the problem on P. δ -tolerance Closed Graph A graph g is δ -tolerance closed if none of its proper frequent supergraphs has a weighted support ≥ (1 − δ ) · support (g ). Maximal graph: 1-tolerance closed graph Closed graph: 0-tolerance closed graph. 15 / 48
  • 24.
    Graph Coresets Relative supportof a closed graph Support of a graph minus the relative support of its closed supergraphs. The sum of the closed supergraphs’ relative supports of a graph and its relative support is equal to its own support. (s, δ )-coreset for the problem of computing closed graphs Weighted multiset of frequent δ -tolerance closed graphs with minimum support s using their relative support as a weight. 16 / 48
  • 25.
    Graph Coresets Relative supportof a closed graph Support of a graph minus the relative support of its closed supergraphs. The sum of the closed supergraphs’ relative supports of a graph and its relative support is equal to its own support. (s, δ )-coreset for the problem of computing closed graphs Weighted multiset of frequent δ -tolerance closed graphs with minimum support s using their relative support as a weight. 16 / 48
  • 26.
    Graph Dataset Transaction Id Graph Weight O C C S N 1 O 1 O C C S N 2 C 1 O C S N 3 C 1 N 4 C C S N 1 17 / 48
  • 27.
    Graph Coresets Graph Relative Support Support C C S N 3 3 O C S N 3 3 N C S 3 3 Table: Example of a coreset with minimum support 50% and δ = 1 18 / 48
  • 28.
    Graph Coresets Figure: Numberof graphs in a (40%, δ )-coreset for NCI. 19 / 48
  • 29.
    Outline 1 Streaming Data 2 Frequent Pattern Mining Mining Evolving Graph Streams A DAG RAPH M INER 3 Experimental Evaluation 4 Summary and Future Work 20 / 48
  • 30.
    I NC GRAPH M INER I NC G RAPH M INER (D, min sup ) Input: A graph dataset D, and min sup. Output: The frequent graph set G. 1 G←0 / 2 for every batch bt of graphs in D 3 do C ← C ORESET (bt , min sup ) 4 G ← C ORESET (G ∪ C, min sup ) 5 return G 21 / 48
  • 31.
    W IN GRAPH M INER W IN G RAPH M INER (D, W , min sup ) Input: A graph dataset D, a size window W and min sup. Output: The frequent graph set G. 1 G←0 / 2 for every batch bt of graphs in D 3 do C ← C ORESET (bt , min sup ) 4 Store C in sliding window 5 if sliding window is full 6 then R ← Oldest C stored in sliding window, negate all support values 7 else R ← 0 / 8 G ← C ORESET (G ∪ C ∪ R, min sup ) 9 return G 22 / 48
  • 32.
    Algorithm ADaptive SlidingWINdow Example W = 101010110111111 W0 = 1 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
  • 33.
    Algorithm ADaptive SlidingWINdow Example W = 101010110111111 W0 = 1 W1 = 01010110111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
  • 34.
    Algorithm ADaptive SlidingWINdow Example W = 101010110111111 W0 = 10 W1 = 1010110111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
  • 35.
    Algorithm ADaptive SlidingWINdow Example W = 101010110111111 W0 = 101 W1 = 010110111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
  • 36.
    Algorithm ADaptive SlidingWINdow Example W = 101010110111111 W0 = 1010 W1 = 10110111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
  • 37.
    Algorithm ADaptive SlidingWINdow Example W = 101010110111111 W0 = 10101 W1 = 0110111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
  • 38.
    Algorithm ADaptive SlidingWINdow Example W = 101010110111111 W0 = 101010 W1 = 110111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
  • 39.
    Algorithm ADaptive SlidingWINdow Example W = 101010110111111 W0 = 1010101 W1 = 10111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
  • 40.
    Algorithm ADaptive SlidingWINdow Example W = 101010110111111 W0 = 10101011 W1 = 0111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
  • 41.
    Algorithm ADaptive SlidingWINdow Example W = 101010110111111 |µW0 − µW1 | ≥ εc : CHANGE DET.! ˆ ˆ W0 = 101010110 W1 = 111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
  • 42.
    Algorithm ADaptive SlidingWINdow Example W = 101010110111111 Drop elements from the tail of W W0 = 101010110 W1 = 111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
  • 43.
    Algorithm ADaptive SlidingWINdow Example W = 01010110111111 Drop elements from the tail of W W0 = 101010110 W1 = 111111 ADWIN: A DAPTIVE W INDOWING A LGORITHM 1 Initialize Window W 2 for each t > 0 3 do W ← W ∪ {xt } (i.e., add xt to the head of W ) 4 repeat Drop elements from the tail of W 5 until |µW0 − µW1 | ≥ εc holds ˆ ˆ 6 for every split of W into W = W0 · W1 7 Output µWˆ 23 / 48
  • 44.
    Algorithm ADaptive SlidingWINdow Theorem At every time step we have: 1 (False positive rate bound). If µt remains constant within W , the probability that ADWIN shrinks the window at this step is at most δ . 2 (False negative rate bound). Suppose that for some partition of W in two parts W0 W1 (where W1 contains the most recent items) we have |µW0 − µW1 | > 2εc . Then with probability 1 − δ ADWIN shrinks W to W1 , or shorter. ADWIN tunes itself to the data stream at hand, with no need for the user to hardwire or precompute parameters. 24 / 48
  • 45.
    Algorithm ADaptive SlidingWINdow ADWIN using a Data Stream Sliding Window Model, can provide the exact counts of 1’s in O (1) time per point. tries O (log W ) cutpoints uses O ( 1 log W ) memory words ε the processing time per example is O (log W ) (amortized and worst-case). Sliding Window Model 1010101 101 11 1 1 Content: 4 2 2 1 1 Capacity: 7 3 2 1 1 25 / 48
  • 46.
    A DAG RAPHM INER A DAG RAPH M INER (D, Mode, min sup ) 1 G←0 / 2 Init ADWIN 3 for every batch bt of graphs in D 4 do C ← C ORESET (bt , min sup ) 5 R←0 / 6 if Mode is Sliding Window 7 then Store C in sliding window 8 if ADWIN detected change 9 then R ← Batches to remove in sliding window with negative support 10 G ← C ORESET (G ∪ C ∪ R, min sup ) 11 if Mode is Sliding Window 12 then Insert # closed graphs into ADWIN 13 else for every g in G update g’s ADWIN 14 return G 26 / 48
  • 47.
    A DAG RAPHM INER A DAG RAPH M INER (D, Mode, min sup ) 1 G←0 / 2 Init ADWIN 3 for every batch bt of graphs in D 4 do C ← C ORESET (bt , min sup ) 5 R←0 / 6 7 8 9 10 G ← C ORESET (G ∪ C ∪ R, min sup ) 11 12 13 for every g in G update g’s ADWIN 14 return G 26 / 48
  • 48.
    A DAG RAPHM INER A DAG RAPH M INER (D, Mode, min sup ) 1 G←0 / 2 Init ADWIN 3 for every batch bt of graphs in D 4 do C ← C ORESET (bt , min sup ) 5 R←0 / 6 if Mode is Sliding Window 7 then Store C in sliding window 8 if ADWIN detected change 9 then R ← Batches to remove in sliding window with negative support 10 G ← C ORESET (G ∪ C ∪ R, min sup ) 11 if Mode is Sliding Window 12 then Insert # closed graphs into ADWIN 13 14 return G 26 / 48
  • 49.
    Outline 1 Streaming Data 2 Frequent Pattern Mining Mining Evolving Graph Streams A DAG RAPH M INER 3 Experimental Evaluation 4 Summary and Future Work 27 / 48
  • 50.
    Experimental Evaluation ChemDB dataset Public dataset 4 million molecules Institute for Genomics and Bioinformatics at the University of California, Irvine Open NCI Database Public domain 250,000 structures National Cancer Institute 28 / 48
  • 51.
    What is MOA? {M}assive{O}nline {A}nalysis is a framework for online learning from data streams. It is closely related to WEKA It includes a collection of offline and online as well as tools for evaluation: classification clustering Easy to extend Easy to design and run experiments 29 / 48
  • 52.
  • 53.
    MOA: the bird TheMoa (another native NZ bird) is not only flightless, like the Weka, but also extinct. 31 / 48
  • 54.
    MOA: the bird TheMoa (another native NZ bird) is not only flightless, like the Weka, but also extinct. 31 / 48
  • 55.
    MOA: the bird TheMoa (another native NZ bird) is not only flightless, like the Weka, but also extinct. 31 / 48
  • 56.
  • 57.
    Classification Experimental Setting Classifiers Naive Bayes Decision stumps Hoeffding Tree Hoeffding Option Tree Bagging and Boosting ADWIN Bagging and Leveraging Bagging Prediction strategies Majority class Naive Bayes Leaves Adaptive Hybrid 33 / 48
  • 58.
  • 59.
    Clustering Experimental Setting Clusterers StreamKM++ CluStream ClusTree Den-Stream CobWeb 35 / 48
  • 60.
    Clustering Experimental Setting Internal measures External measures Gamma Rand statistic C Index Jaccard coefficient Point-Biserial Folkes and Mallow Index Log Likelihood Hubert Γ statistics Dunn’s Index Minkowski score Tau Purity Tau A van Dongen criterion Tau C V-measure Somer’s Gamma Completeness Ratio of Repetition Homogeneity Modified Ratio of Repetition Variation of information Adjusted Ratio of Clustering Mutual information Fagan’s Index Class-based entropy Deviation Index Cluster-based entropy Z-Score Index Precision D Index Recall Silhouette coefficient F-measure Table: Internal and external clustering evaluation measures. 36 / 48
  • 61.
    Cluster Mapping Measure Hardy Kremer, Philipp Kranen, Timm Jansen, Thomas Seidl, Albert Bifet, Geoff Holmes and Bernhard Pfahringer. An Effective Evaluation Measure for Clustering on Evolving Data Stream KDD’11 CMM: Cluster Mapping Measure A novel evaluation measure for stream clustering on evolving streams ∑o∈F w (o ) · pen(o, C ) CMM (C , C L ) = 1 − ∑o∈F w (o ) · con(o, Cl (o )) 37 / 48
  • 62.
    Extensions of MOA Multi-label Classification Active Learning Regression Closed Frequent Graph Mining Twitter Sentiment Analysis Challenges for bigger data streams Sampling and distributed systems (Map-Reduce, Hadoop, S4) 38 / 48
  • 63.
    Open NCI dataset Time NCI Dataset 120 100 80 Seconds 60 40 20 0 00 00 00 00 00 0 0 0 0 0 0 0 0 00 00 00 00 00 00 00 00 .0 .0 .0 .0 .0 0. 0. 0. 0. 0. 0. 0. 0. 10 30 50 70 90 11 13 15 17 19 21 23 25 Instances IncGraphMiner IncGraphMiner-C MoSS closeGraph 39 / 48
  • 64.
    Open NCI dataset Memory NCI Dataset 9000 8000 7000 Megabytes 6000 5000 4000 3000 2000 1000 0 00 00 00 00 00 0 0 0 0 0 0 0 0 00 00 00 00 00 00 00 00 .0 .0 .0 .0 .0 0. 0. 0. 0. 0. 0. 0. 0. 10 30 50 70 90 11 13 15 17 19 21 23 25 Instances IncGraphMiner IncGraphMiner-C MoSS closeGraph 40 / 48
  • 65.
    Megabytes 10 . 0 5000 10000 15000 20000 25000 30000 35000 40000 45000 24 000 50000 0. 47 000 0. 70 000 0. 93 000 IncGraphMiner 1. 0. 0 16 00 1. 0.0 39 00 1. 0.0 62 00 1. 0.0 85 00 2. 0.0 08 00 2. 0.0 31 00 IncGraphMiner-C 2. 0.0 54 00 Instances 2. 0.0 77 00 Memory ChemDB Dataset 3. 0.0 MoSS 00 00 3. 0.0 23 00 ChemDB dataset 3. 0.0 46 00 3. 0.0 69 00 3. 0.0 92 00 closeGraph 0. 00 0 41 / 48
  • 66.
    Seconds 10 . 0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000 24 000 0. 47 000 0. 70 000 0. 93 000 1. 0. 0 16 00 1. 0.0 39 00 IncGraphMiner 1. 0.0 62 00 1. 0.0 85 00 2. 0.0 08 00 2. 0.0 31 00 2. 0.0 54 00 Instances IncGraphMiner-C 2. 0.0 77 00 Time ChemDB Dataset 3. 0.0 00 00 3. 0.0 23 00 MoSS ChemDB dataset 3. 0.0 46 00 3. 0.0 69 00 3. 0.0 92 00 0. 00 0 closeGraph 42 / 48
  • 67.
    Number of ClosedGraphs 10 .0 0 10 20 30 40 50 60 0 60 0 .0 11 00 0. 0 16 00 0. 00 21 0 0. 0 26 00 0. 0 31 00 0. 0 36 00 0. 0 ADAGRAPHMINER 41 00 0. 0 46 00 0. 0 51 00 0. 0 56 00 0. 00 Instances 61 0 0. 0 66 00 0. 0 71 00 0. 0 76 00 ADAGRAPHMINER-Window 0. 0 81 00 0. A DAG RAPH M INER 0 86 00 0. 0 91 00 0. 0 96 00 0. 00 IncGraphMiner 0 43 / 48
  • 68.
    Outline 1 Streaming Data 2 Frequent Pattern Mining Mining Evolving Graph Streams A DAG RAPH M INER 3 Experimental Evaluation 4 Summary and Future Work 44 / 48
  • 69.
    Summary Mining Evolving GraphData Streams Given a data stream D of graphs, find frequent closed graphs. Transaction Id Graph We provide three algorithms, O of increasing power C C S N Incremental 1 O Sliding Window O Adaptive C C S N 2 C N 3 C C S N 45 / 48
  • 70.
    Summary {M}assive {O}nline {A}nalysisis a framework for online learning from data streams. http://moa.cs.waikato.ac.nz It is closely related to WEKA It includes a collection of offline and online as well as tools for evaluation: classification clustering frequent pattern mining MOA deals with evolving data streams MOA is easy to use and extend 46 / 48
  • 71.
    Future work Structured massivedata mining sampling, sketching parallel techniques 47 / 48
  • 72.
    Thanks! 48 / 48