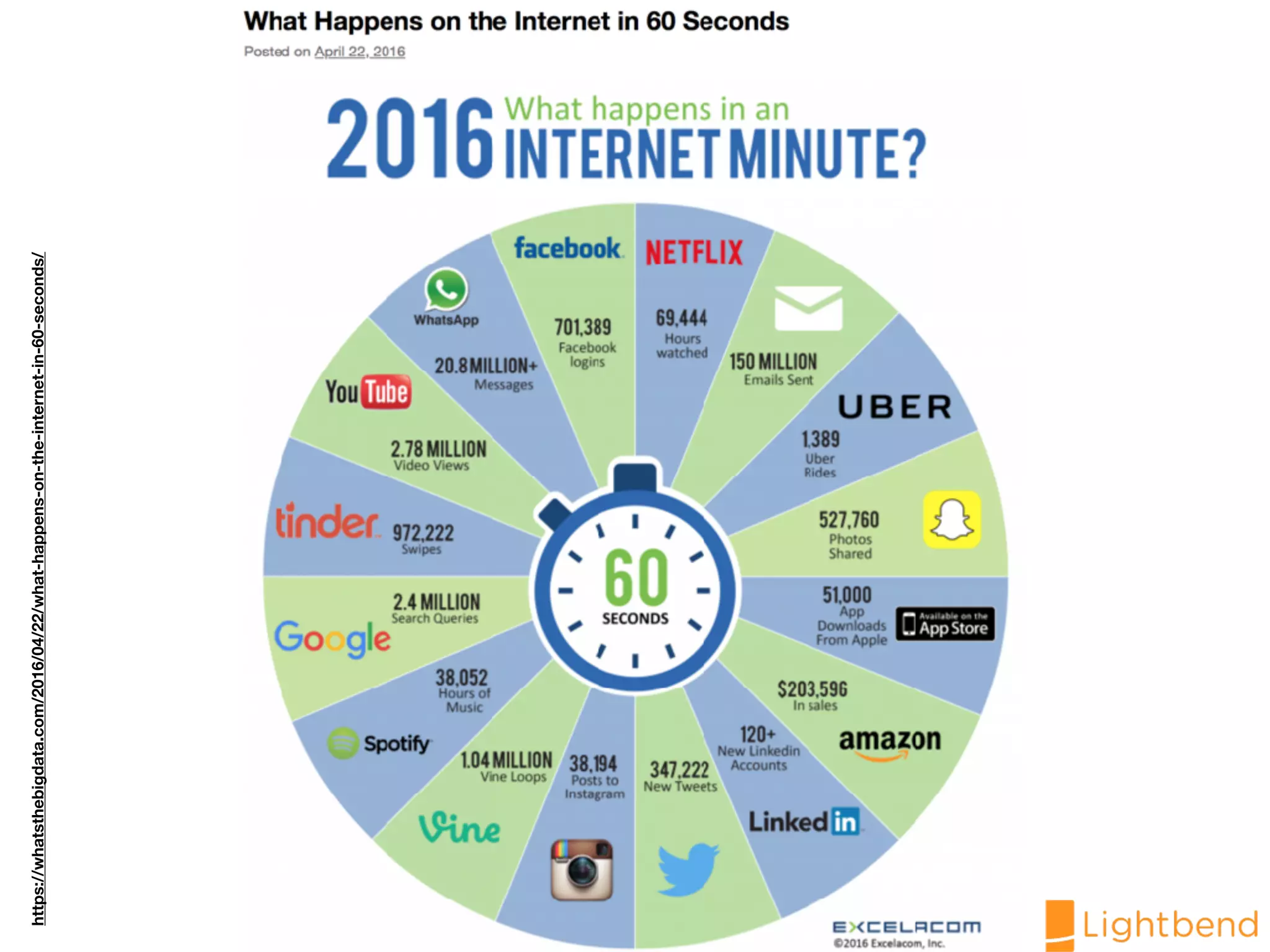
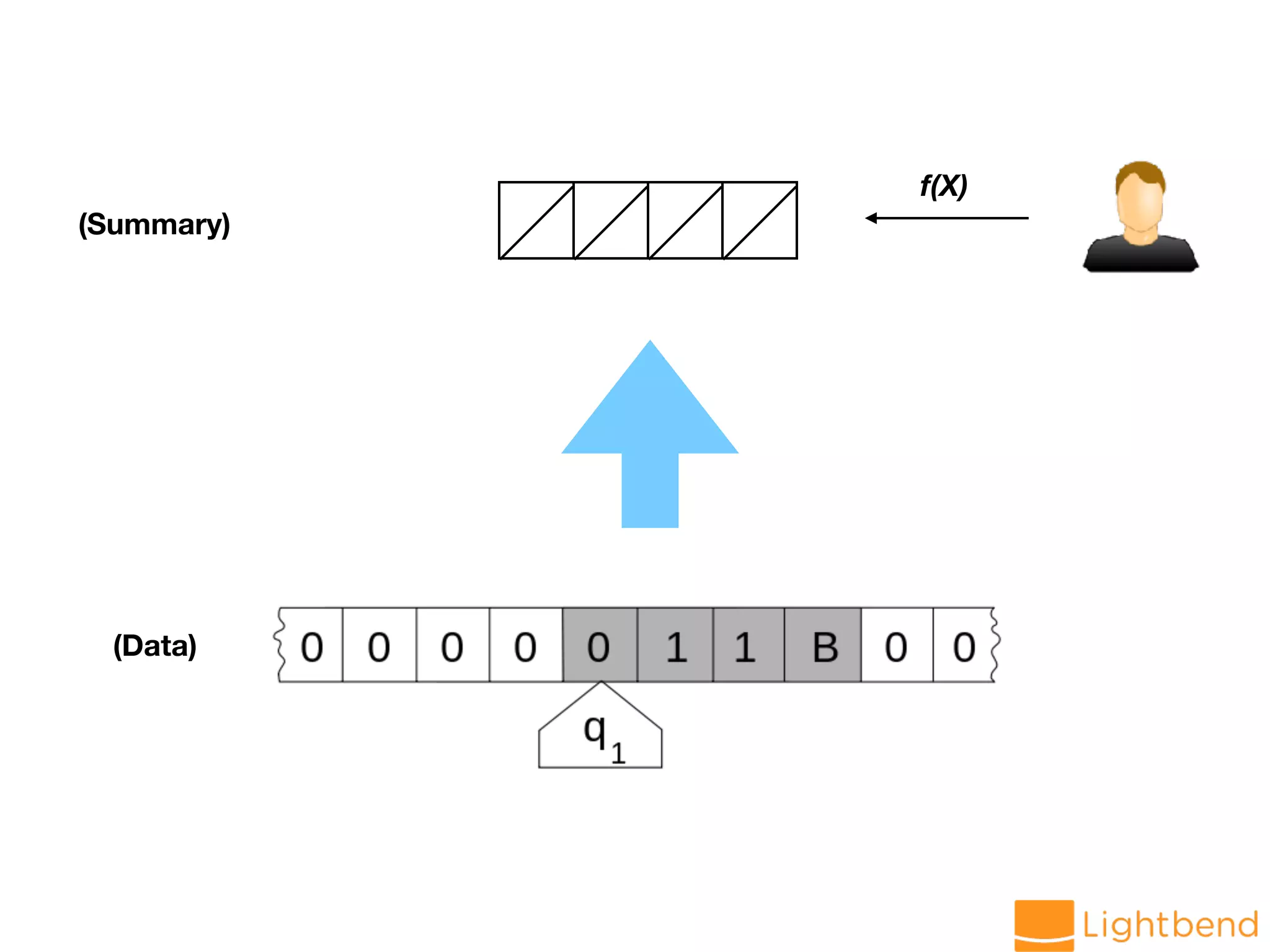
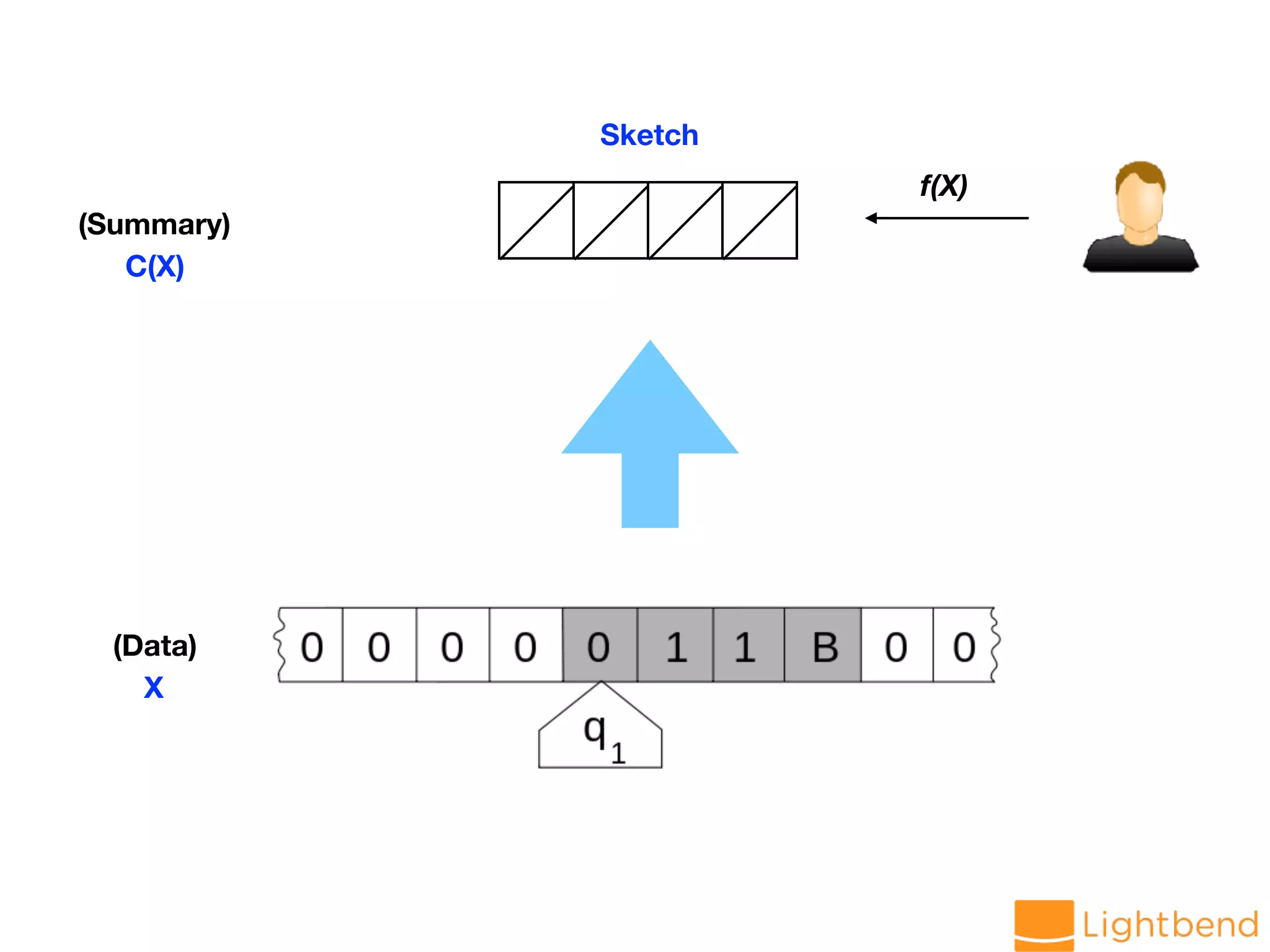
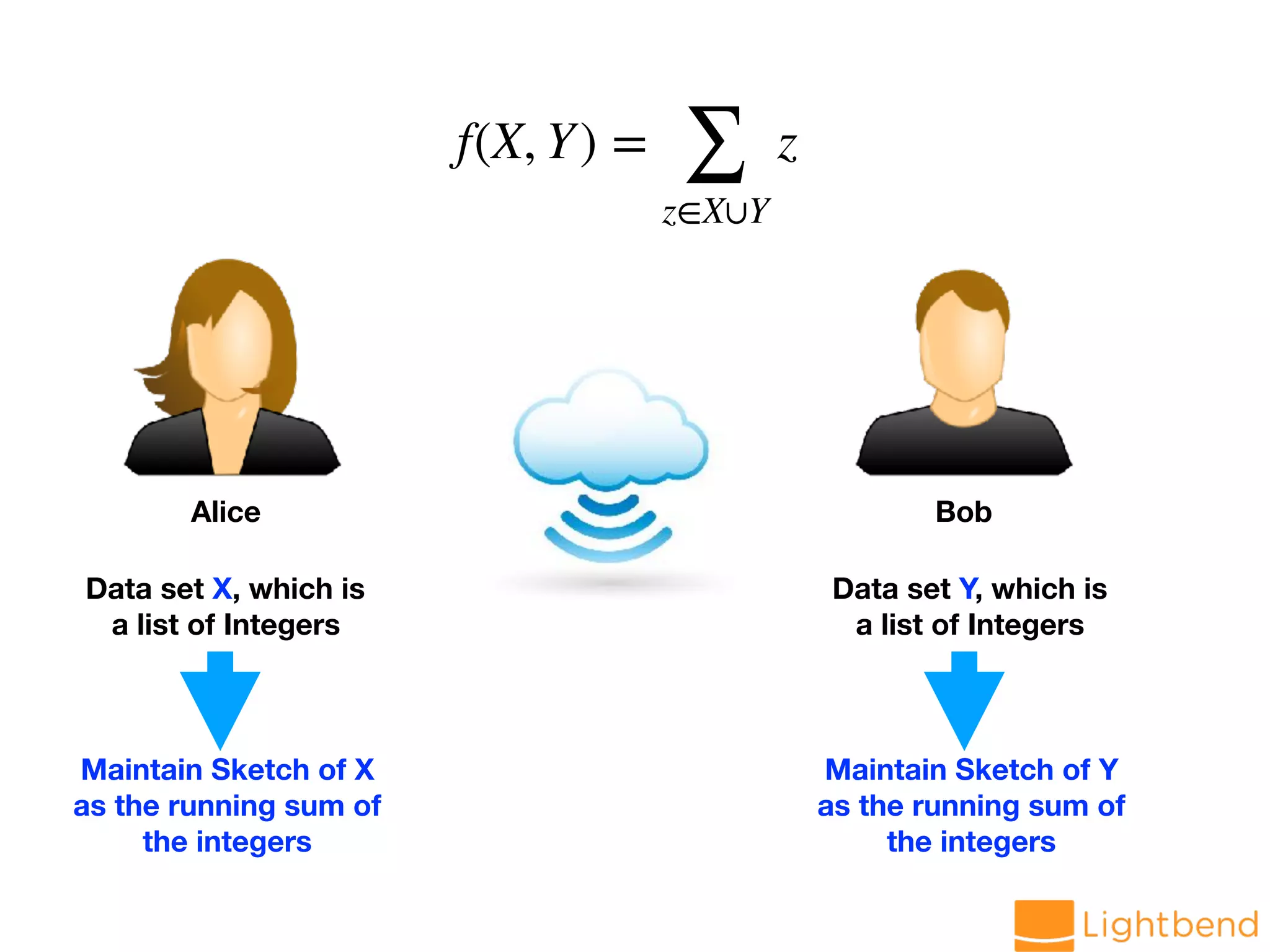
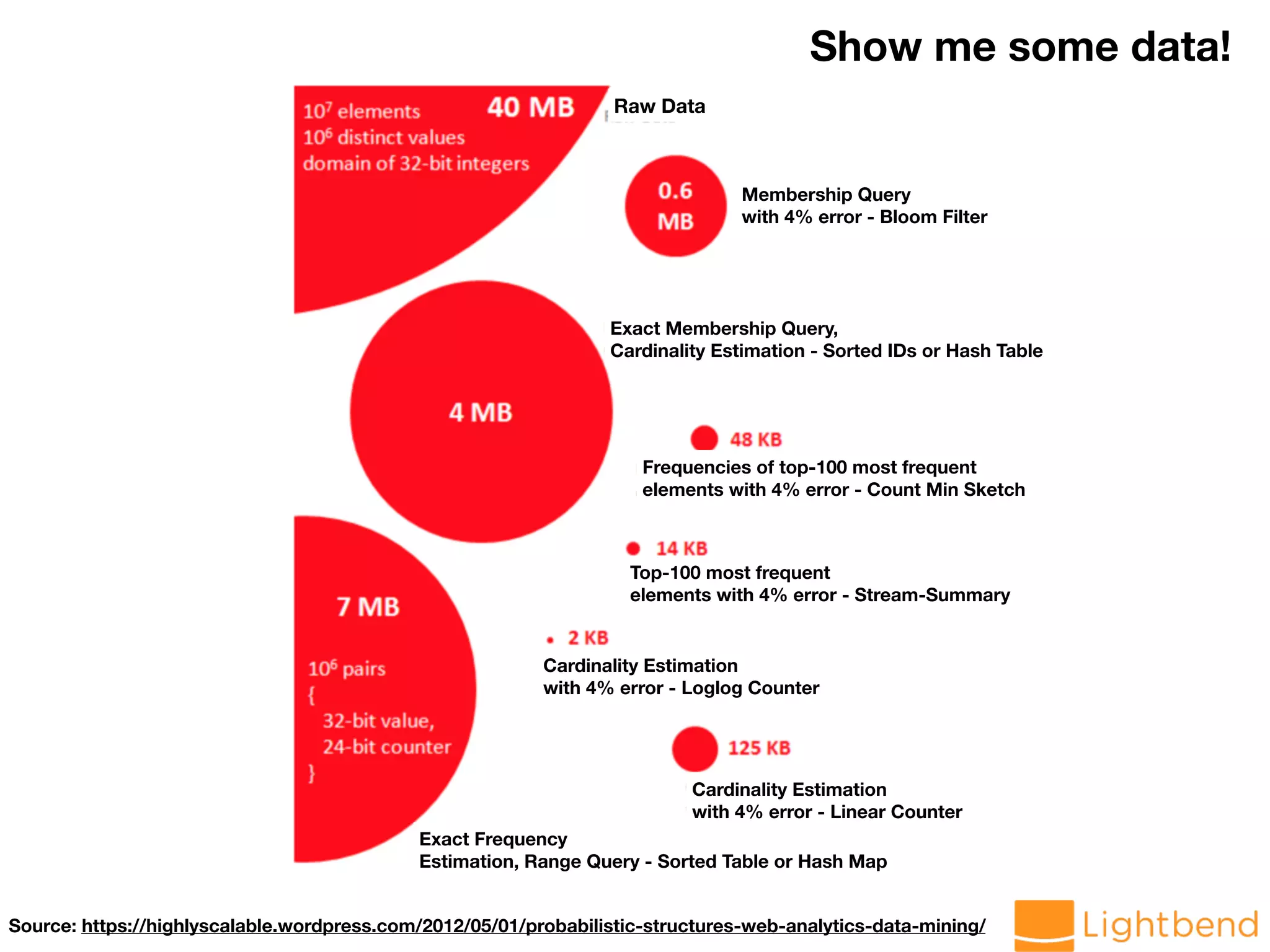
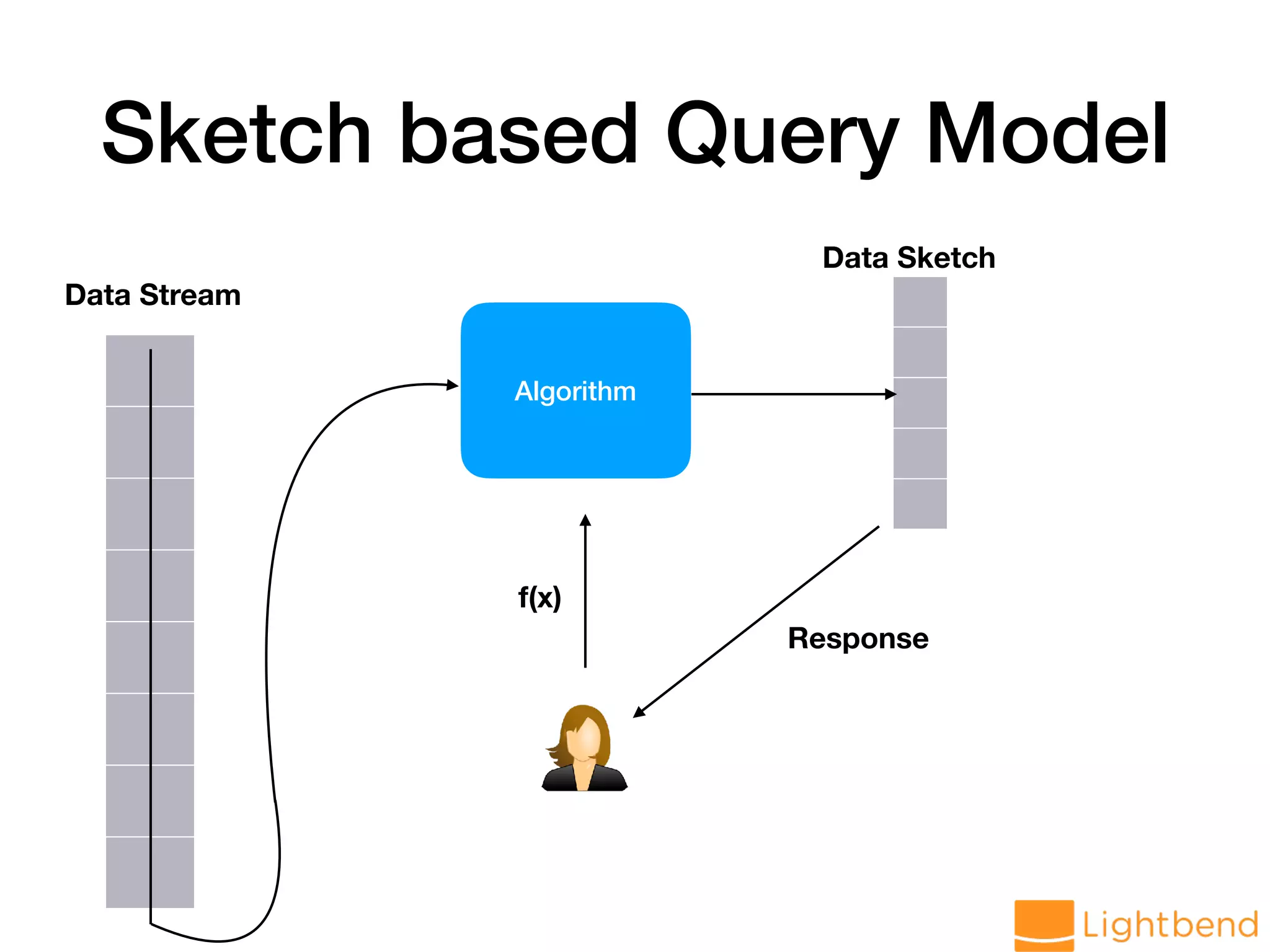
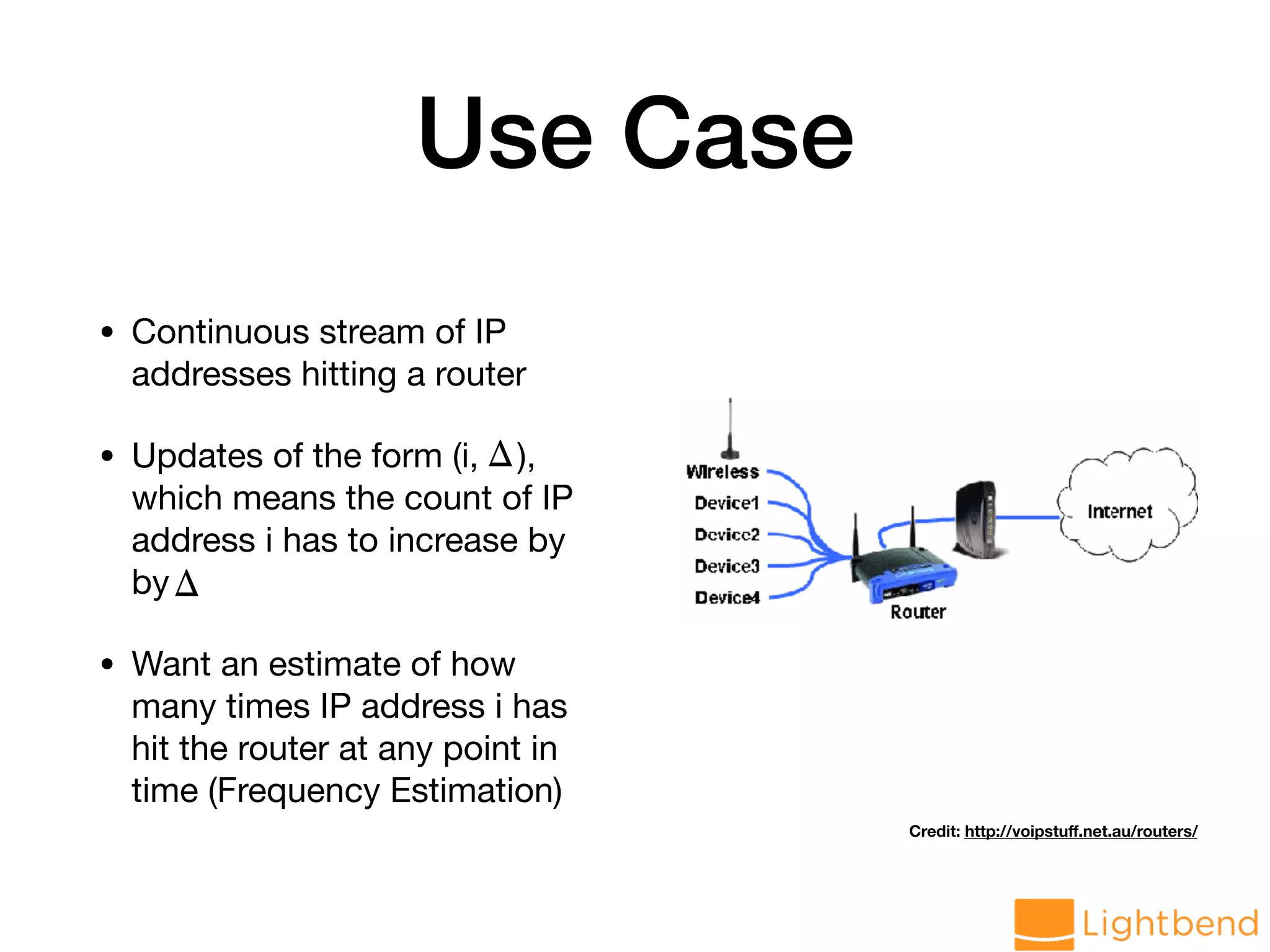
The document discusses approximation data structures for handling streaming data applications, emphasizing the challenges posed by unbounded data streams that require low-latency processing. It explores various algorithms and structures, such as count-min sketch and Bloom filters, to perform tasks like distinct element counting, frequency estimation, and heavy hitter identification with limited memory usage. The document also highlights the necessity of randomized and approximate methods to achieve efficient data processing under the constraints of space and accuracy.












![Distinct Elements Problem • Input: Stream of integers • Where: [n] denotes the Set { 1, 2, .. , n } • Output: The number of distinct elements seen in the stream • Goal: Minimize space consumption i1, . . . , im ∈ [n]](https://image.slidesharecdn.com/approx-pdf-180307224918/75/Approximation-Data-Structures-for-Streaming-Applications-14-2048.jpg)



















![Generalization steps .. • Compute the expected value of the estimator. In [Morris ’78] we have • Compute the variance of the estimator. In [Morris ’78] we have • Using median trick, establish 𝔼[2X − 1] = n var[2X − 1] = O(n2 ) ϵ − δ Approximation](https://image.slidesharecdn.com/approx-pdf-180307224918/75/Approximation-Data-Structures-for-Streaming-Applications-38-2048.jpg)






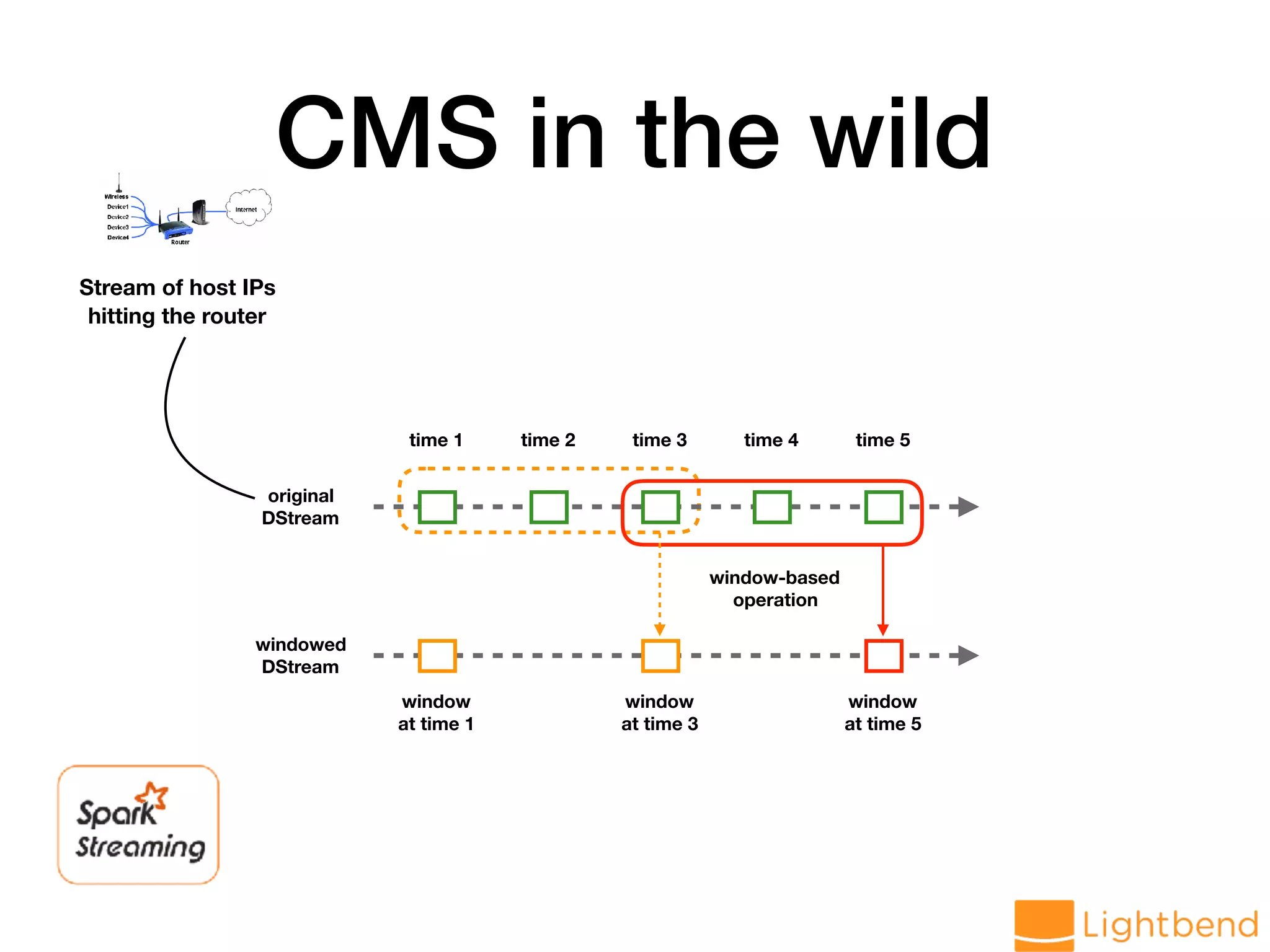
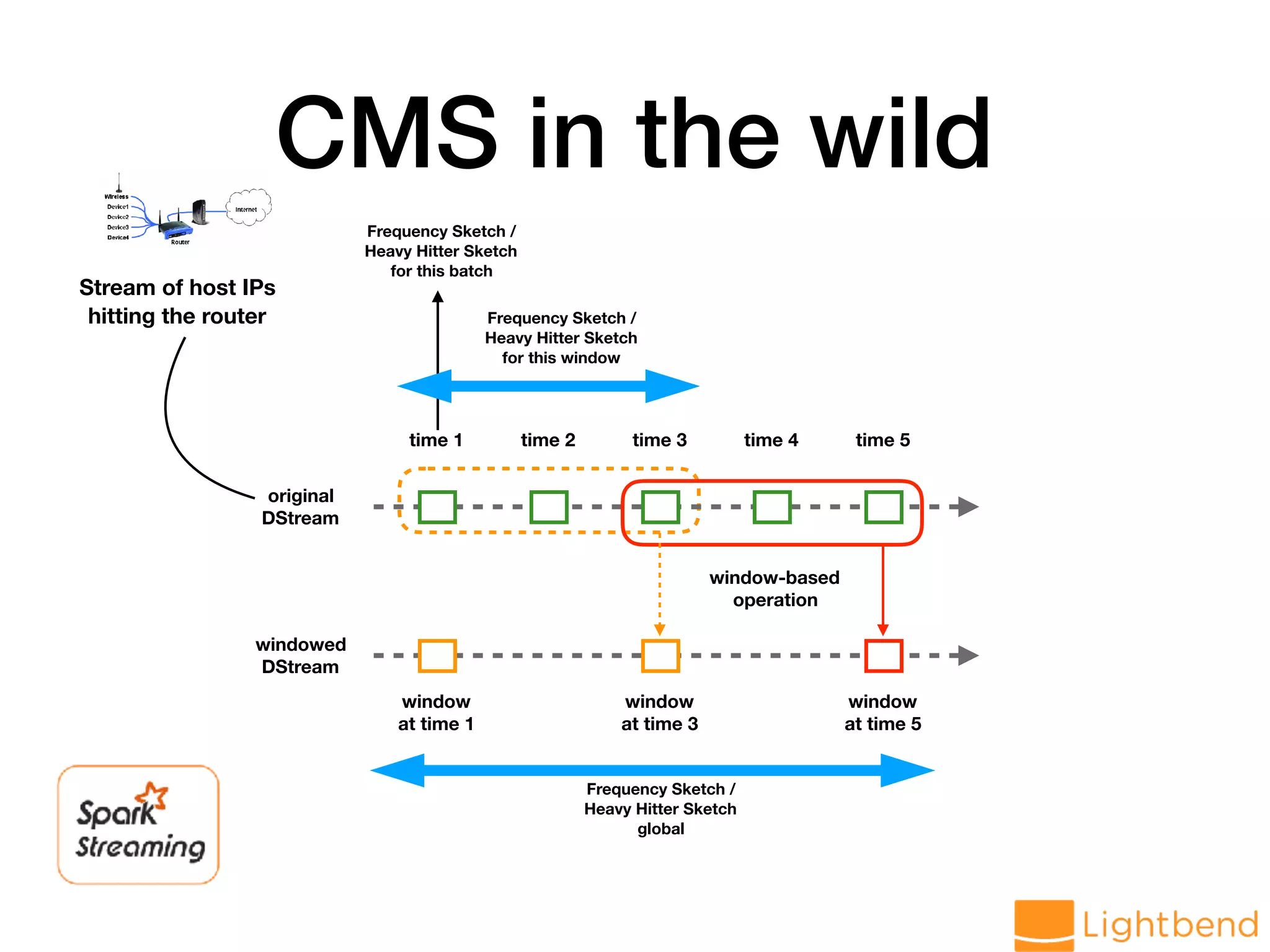
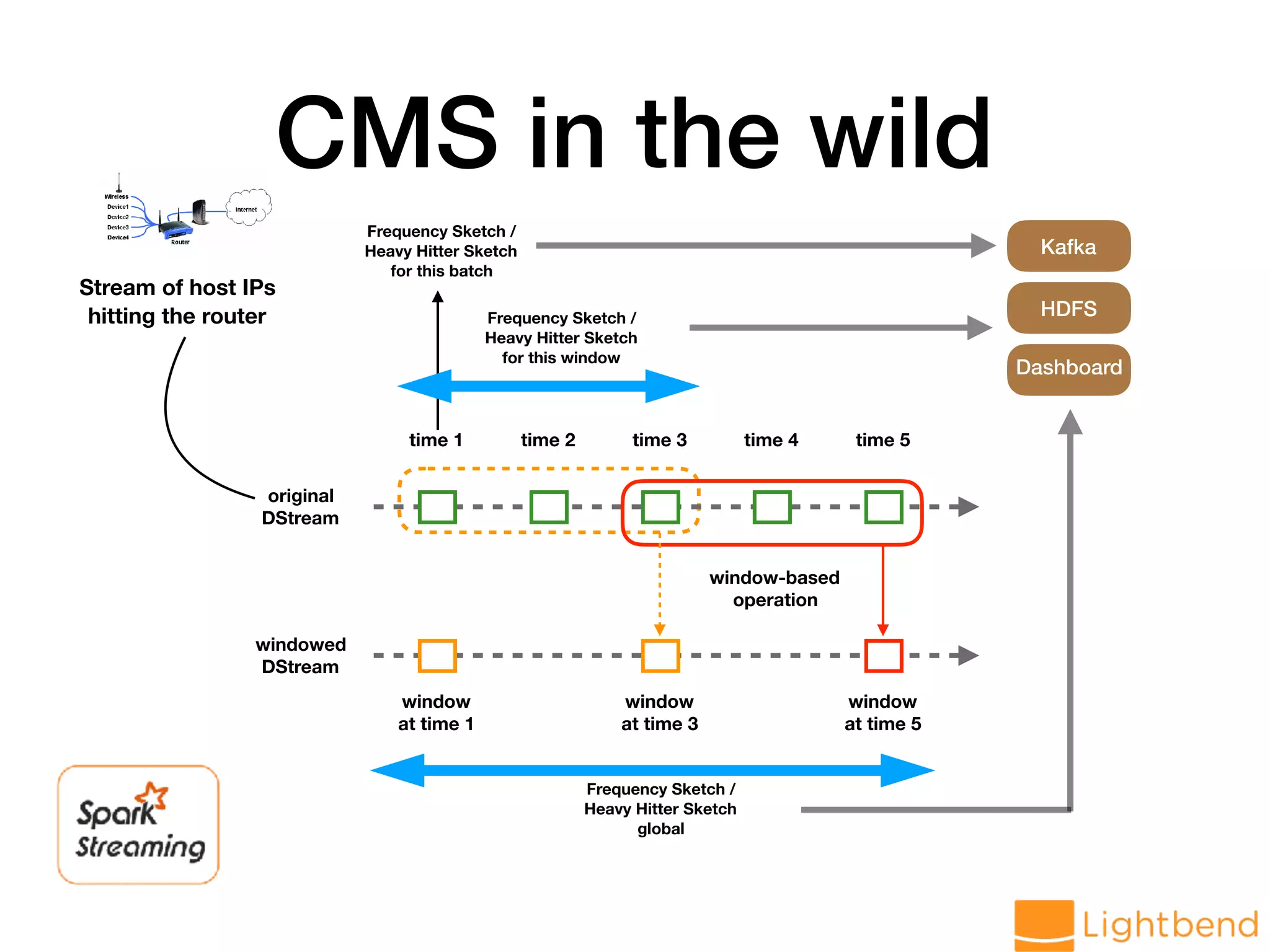
 var globalCMS = cmsMonoid.zero // Generate data stream val hosts: DStream[String] = lines.flatMap(r => LogParseUtil.parseHost(r.value).toOption) // load data into CMS val approxHosts: DStream[CMS[String]] = hosts.mapPartitions(ids => { val cms = CMS.monoid[String](DELTA, EPS, SEED) ids.map(cms.create) }).reduce(_ ++ _)](https://image.slidesharecdn.com/approx-pdf-180307224918/75/Approximation-Data-Structures-for-Streaming-Applications-53-2048.jpg)
![Streaming CMS approxHosts.foreachRDD(rdd => { if (rdd.count() != 0) { val cmsThisBatch: CMS[String] = rdd.first globalCMS ++= cmsThisBatch val f1ThisBatch = cmsThisBatch.f1 val freqThisBatch = cmsThisBatch.frequency("world.std.com") val f1Overall = globalCMS.f1 val freqOverall = globalCMS.frequency("world.std.com") // .. } })](https://image.slidesharecdn.com/approx-pdf-180307224918/75/Approximation-Data-Structures-for-Streaming-Applications-54-2048.jpg)

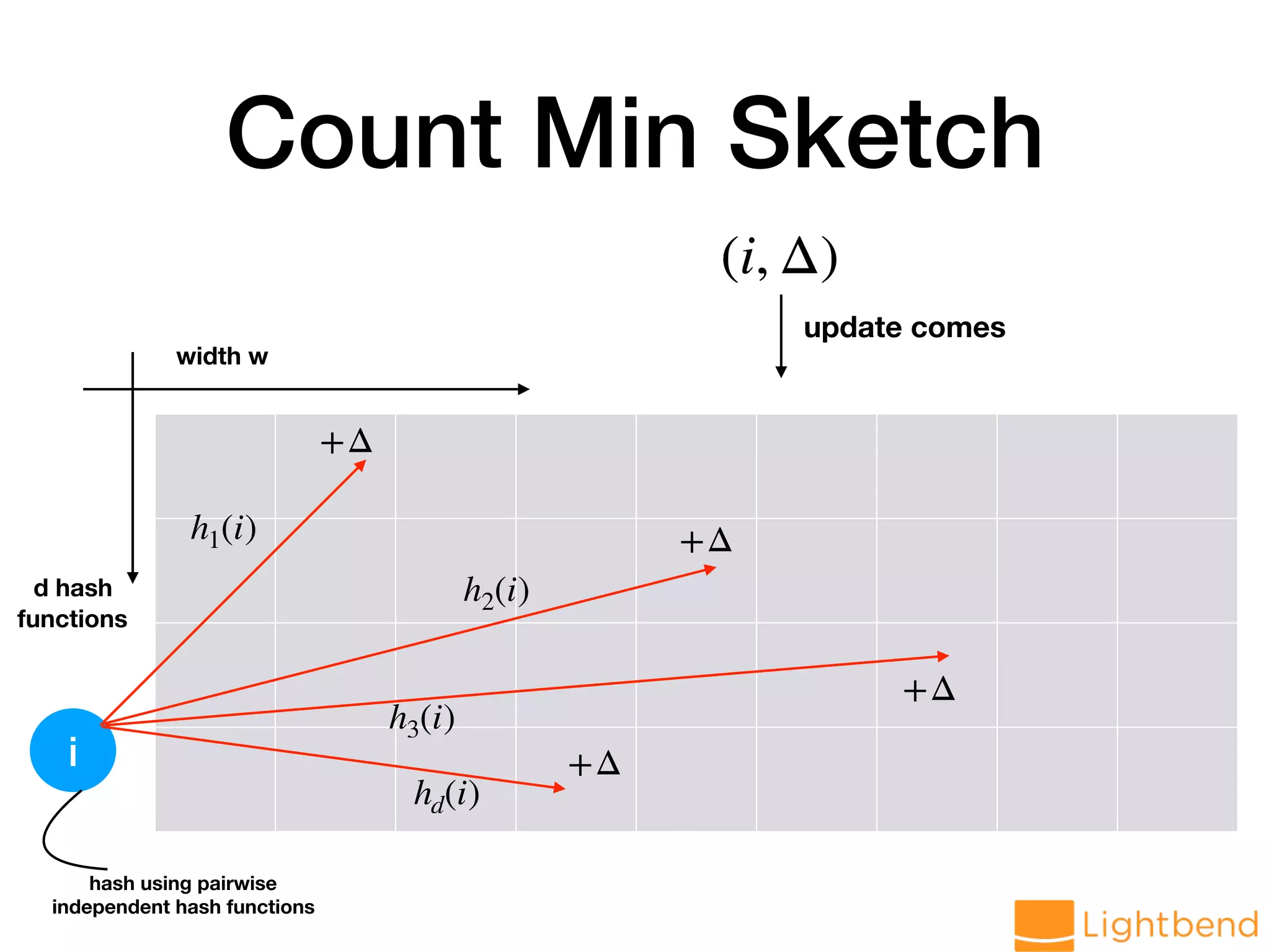
![Count Min Sketch - Applications • AT&T has used it in network switches to perform network analyses on streaming network traffic with limited memory [1]. • Streaming log analysis • Join size estimation for database query planners • Heavy hitters - • Top-k active users on Twitter • Popular products - most viewed products page • Compute frequent search queries • Identify heavy TCP flow • Identify volatile stocks [1] G. Cormode, T. Johnson, F. Korn, S. Muthukrishnan, O. Spatscheck, and D. Srivastava. Holistic UDAFs at streaming speeds. In Proceedings of the 2004 ACM SIGMOD International Conference on Management of Data, pages 35–46, 2004.](https://image.slidesharecdn.com/approx-pdf-180307224918/75/Approximation-Data-Structures-for-Streaming-Applications-56-2048.jpg)

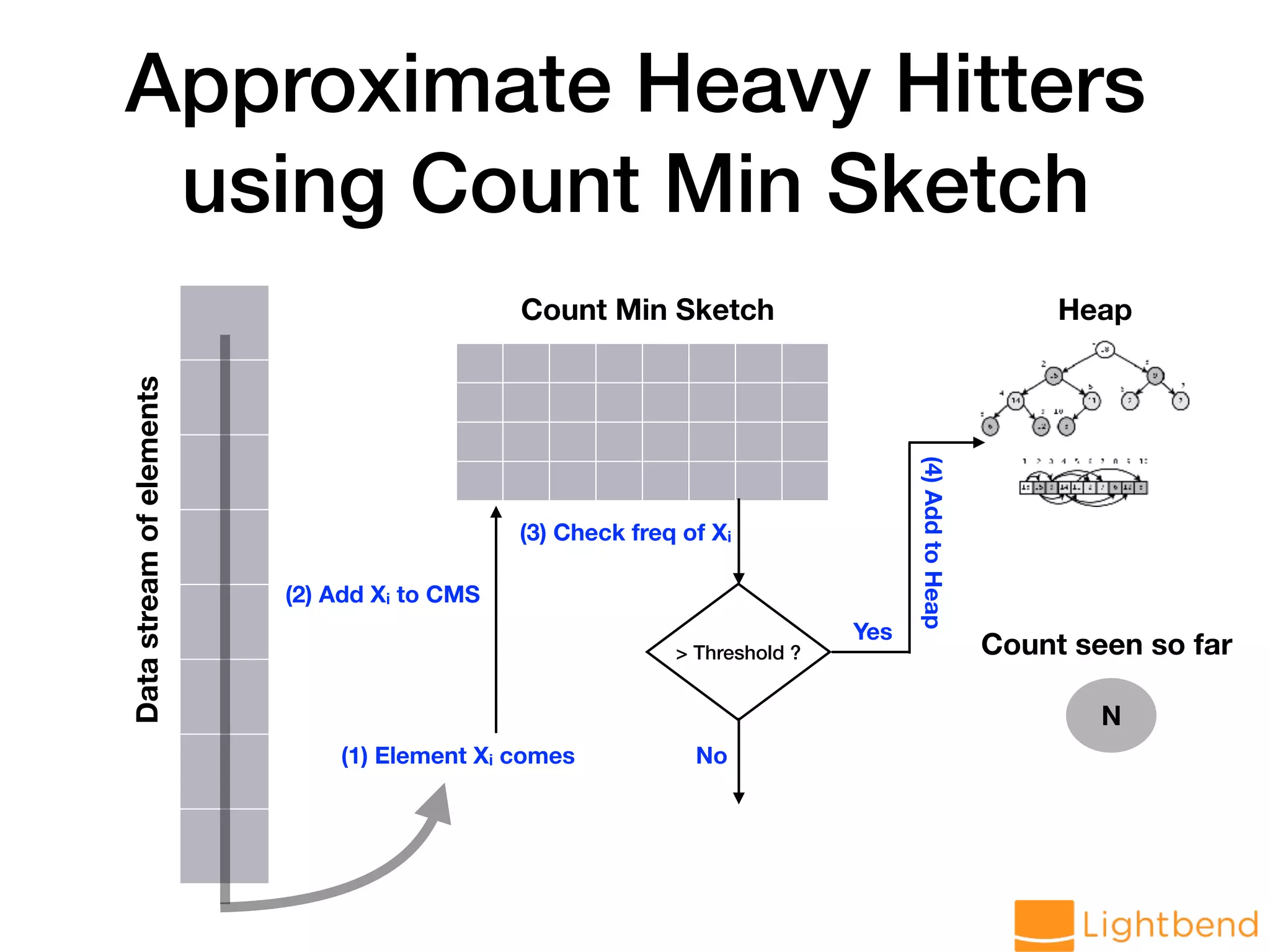
![Streaming Approximate Heavy Hitters // create heavy hitter CMS val approxHH: DStream[TopCMS[String]] = hosts.mapPartitions(ids => { val cms = TopPctCMS.monoid[String](DELTA, EPS, SEED, 0.15) ids.map(cms.create(_)) }).reduce(_ ++ _) // analyze in microbatch approxHH.foreachRDD(rdd => { if (rdd.count() != 0) { val hhThisBatch: TopCMS[String] = rdd.first hhThisBatch.heavyHitters.foreach(println) } })](https://image.slidesharecdn.com/approx-pdf-180307224918/75/Approximation-Data-Structures-for-Streaming-Applications-59-2048.jpg)

![Bloom Filter - Under the Hood • Ingredients • Array A of n bits. If we store a dataset S, then number of bits used per object = n/|S| • k hash functions (h1,h2, ..,hk) (usually k is small) • Insert(x) • For i=1,2, ..,k set A[hi(x)]=1 irrespective of what the previous values of those bits were • Query(x) • if for every i=1,2, ..,k A[hi(x)]=1 return true • No false negatives • Can have false positives Space/time trade-offs in hash coding with allowable errors - B. H. Bloom. Communications of the ACM 13(7): 422-426. 1970. ByDavidEppstein-self-made,originallyforatalkatWADS2007,PublicDomain,https://commons.wikimedia.org/w/index.p](https://image.slidesharecdn.com/approx-pdf-180307224918/75/Approximation-Data-Structures-for-Streaming-Applications-61-2048.jpg)
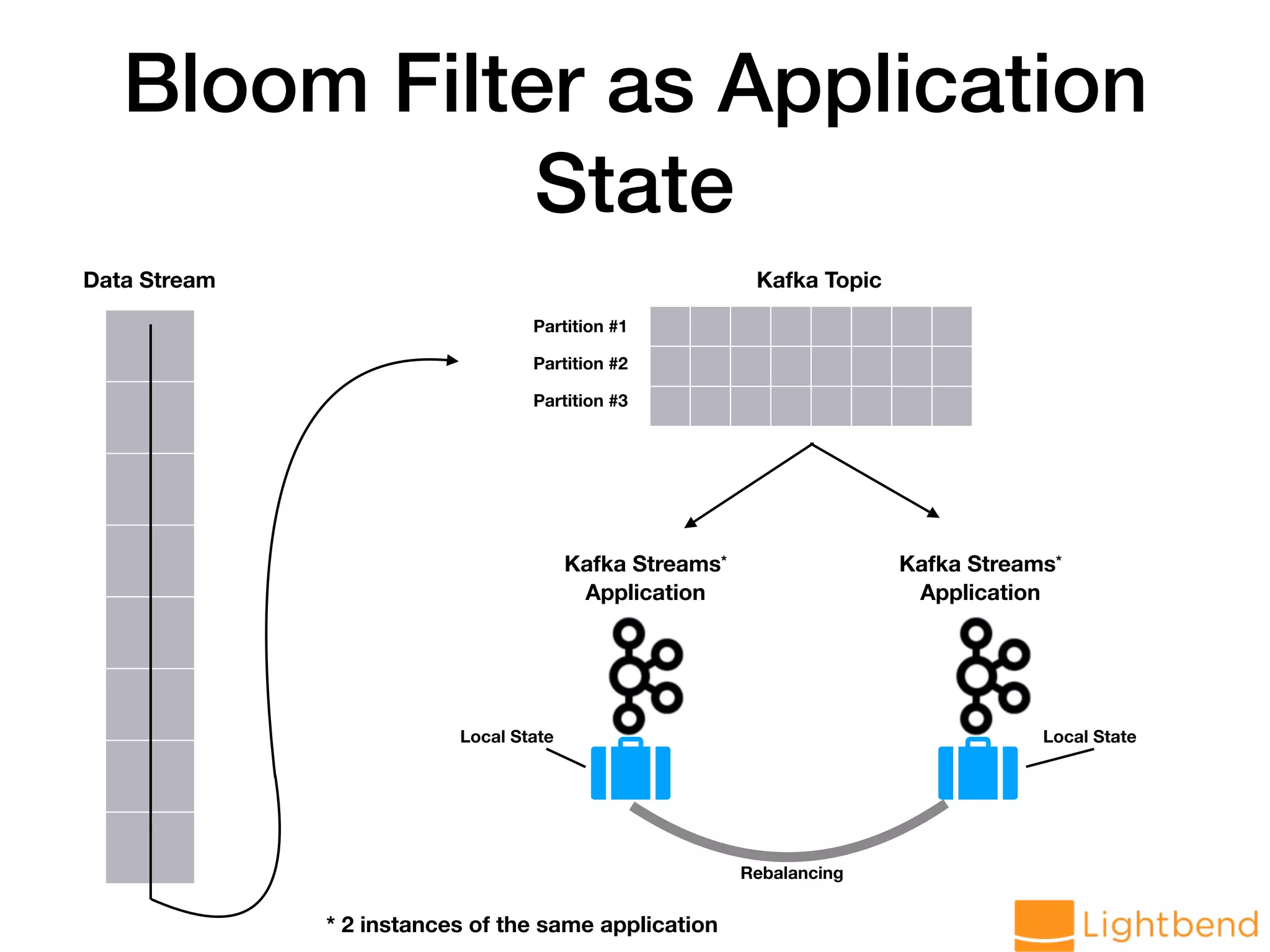
 extends WriteableBFStore[T] with StateStore { // monoid! private val bfMonoid = new BloomFilterMonoid[T](numHashes, width) // initialize private[processor] var bf: BF[T] = bfMonoid.zero // .. }](https://image.slidesharecdn.com/approx-pdf-180307224918/75/Approximation-Data-Structures-for-Streaming-Applications-63-2048.jpg)
 extends WriteableBFStore[T] with StateStore { // .. def +(item: T): Unit = bf = bf + item def contains(item: T): Boolean = { val v = bf.contains(item) v.isTrue && v.withProb > ACCEPTABLE_PROBABILITY } def maybeContains(item: T): Boolean = bf.maybeContains(item) def size: Approximate[Long] = bf.size }](https://image.slidesharecdn.com/approx-pdf-180307224918/75/Approximation-Data-Structures-for-Streaming-Applications-64-2048.jpg)
![BF Store with Kafka Streams Processor // the Kafka Streams processor that will be part of the topology class WeblogProcessor extends AbstractProcessor[String, String] // the store instance private var bfStore: BFStore[String] = _ override def init(context: ProcessorContext): Unit = { super.init(context) // .. bfStore = this.context.getStateStore( WeblogDriver.LOG_COUNT_STATE_STORE).asInstanceOf[BFStore[String]] } override def process(dummy: String, record: String): Unit = LogParseUtil.parseLine(record) match { case Success(r) => { bfStore + r.host bfStore.changeLogger.logChange(bfStore.changelogKey, bfStore.bf) } case Failure(ex) => // .. } // .. }](https://image.slidesharecdn.com/approx-pdf-180307224918/75/Approximation-Data-Structures-for-Streaming-Applications-65-2048.jpg)

