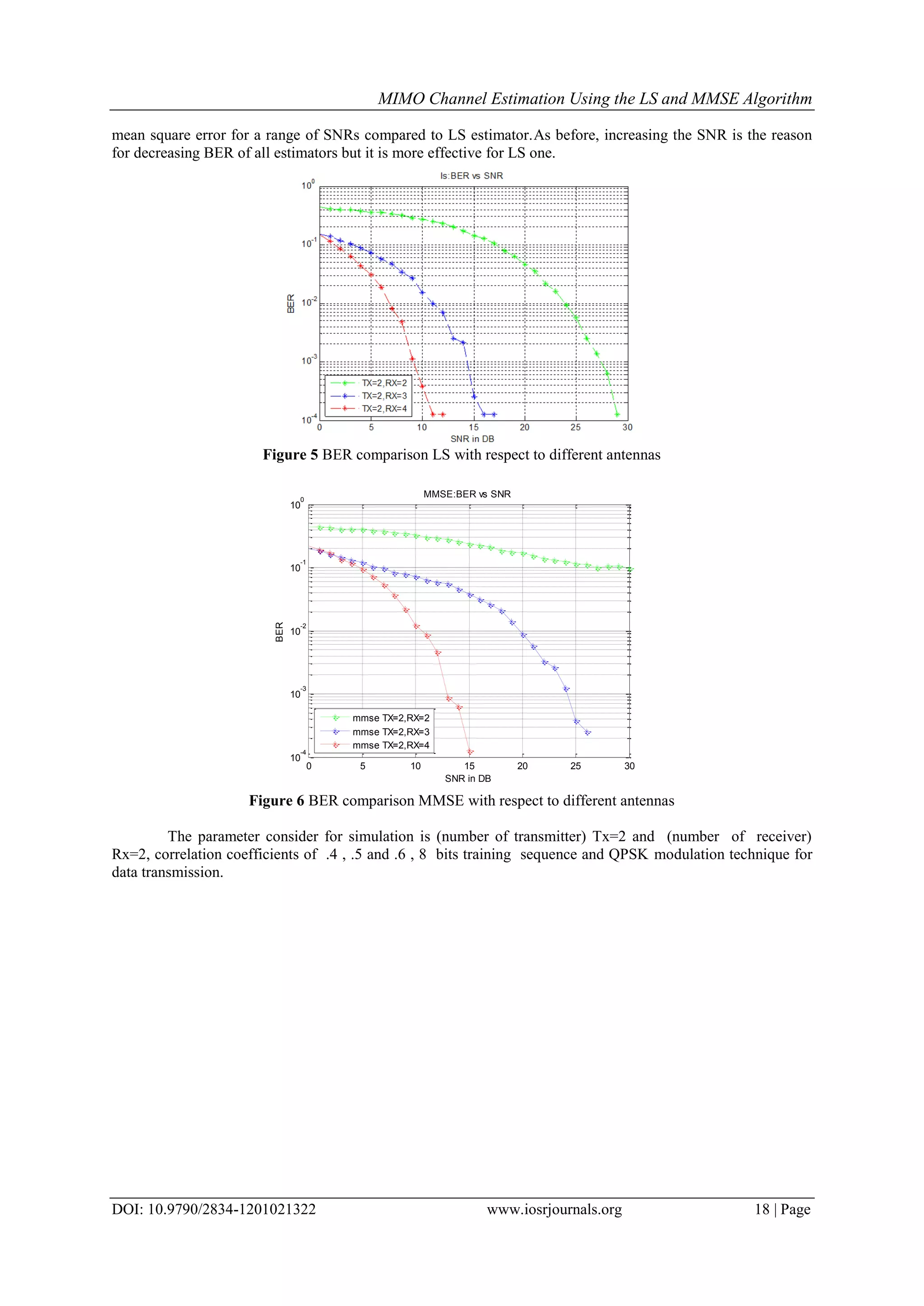
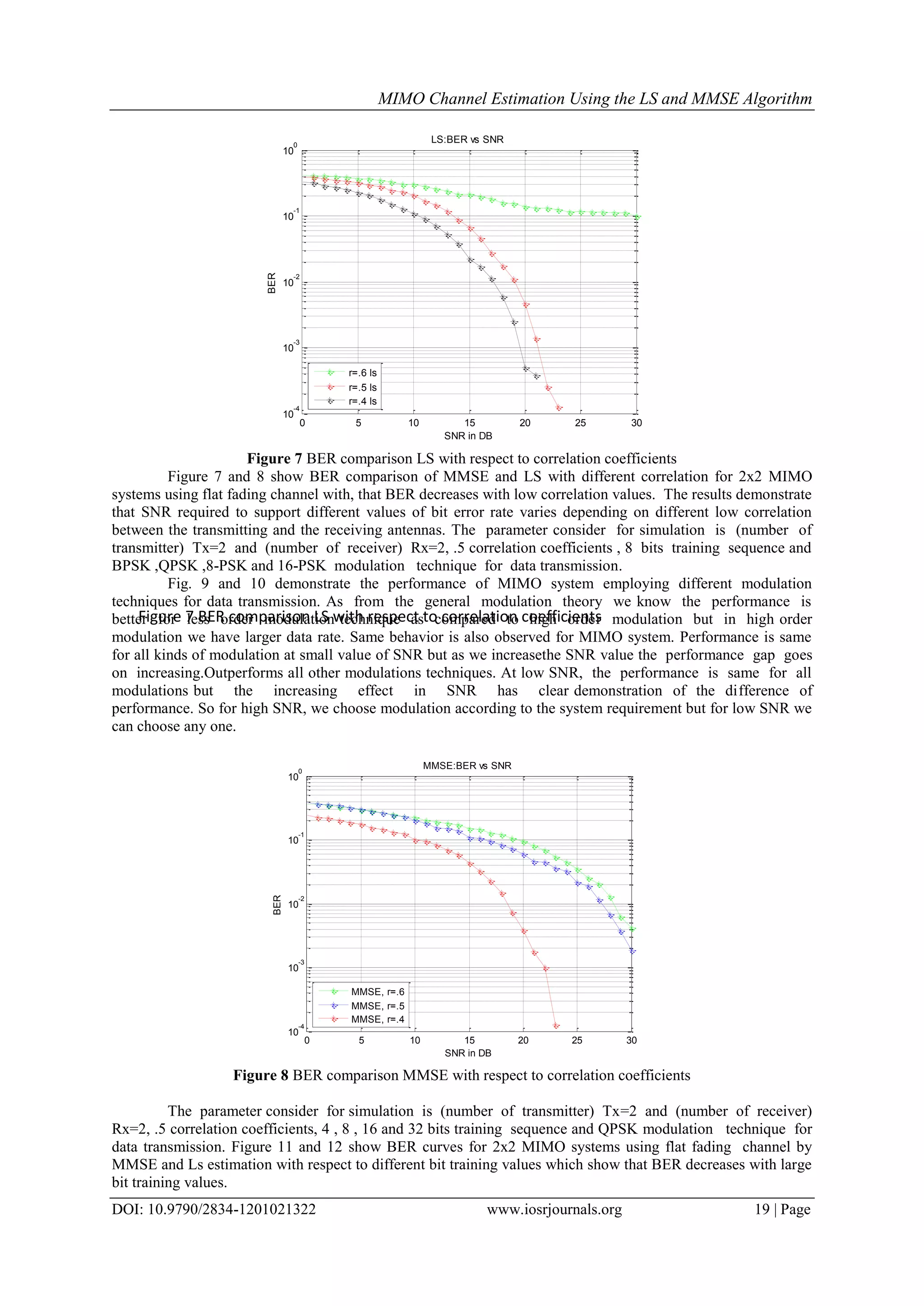
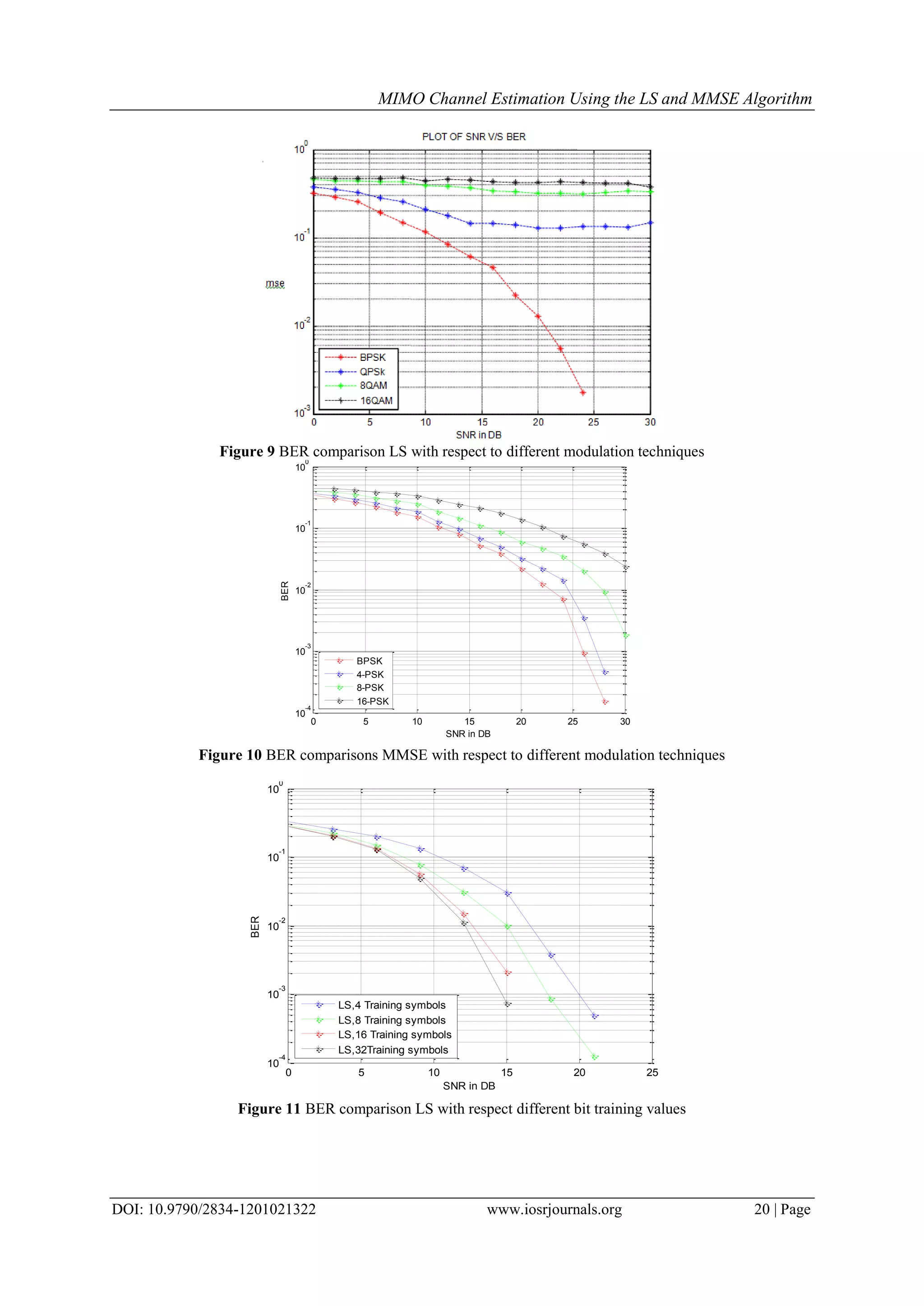
This document discusses the implementation and comparison of channel estimation techniques in MIMO systems using Least Squares (LS) and Minimum Mean Square Error (MMSE) algorithms. It highlights the importance of accurate channel state information for improved wireless communication performance and presents simulation results showing that MMSE outperforms LS, particularly at higher Signal-to-Noise Ratios (SNRs). The efficiency of these algorithms is validated through simulations demonstrating Bit Error Rate (BER) and Mean Square Error (MSE) under various conditions.
![IOSR Journal of Electronics and Communication Engineering (IOSR-JECE) e-ISSN: 2278-2834,p- ISSN: 2278-8735.Volume 12, Issue 1, Ver. II (Jan.-Feb. 2017), PP 13-22 www.iosrjournals.org DOI: 10.9790/2834-1201021322 www.iosrjournals.org 13 | Page MIMO Channel Estimation Using the LS and MMSE Algorithm *Mohammed Ali Mohammed MOQBEL1 , Wangdong2 , Al-marhabi Zaid Ali3 1,2 Hunan University, Changsha, Hunan, China 3 Hajjah University, Hajjah, Yemen Abstract: Wireless Communication Technology has developed over the past few yearsfor other objectives.The Multiple InputMultiple Output (MIMO) is one of techniques that is used to enhancethe data rates, in which multiple antennas are employed both the transmitter and receiver. Multiple signals are transmitted from different antennas at the transmitter using the same frequency and separated space. Various channel estimation techniques are employed in order to judge the physical effects of the medium present. In this paper, we analyze and implementvarious estimation techniques for MIMO Systems such as Least Squares (LS), Minimum Mean Square Error (MMSE),these techniques are therefore compared to effectively estimate the channel in MIMO System. The results demonstrate that SNR required to support different values of bit error rate varies depending on different low correlation between the transmitting and the receiving antennas .In addition, it is illustrated that when the number of transmitter and receiver antennas increases, the performance of TBCE schemes significantly improves. The Same behavior isalso observed for MIMO system. Performance of both MMSE and LSestimation are the same for allkinds of modulation at small value of SNR but the more we increase the SNR value the more performance gap goes on increasing. Keywords: Channel estimation, Minimum mean square error (MMSE), Least square (LS), Kalman filter, Orthogonal frequency division multiplexing. I. Introduction In recent years, Multi-Input Multi-Output (MIMO) communications are introduced as an emerging technology to offer significant promise for high data rates and mobility required by the next generation wireless communication systems. Using multiple transmit as well as receive antennas, a MIMO system exploits spatial diversity, higher data rate, greater coverage and improved link robustness without increasing total transmission power or bandwidth. However, MIMO relies upon the knowledge of Channel State Information (CSI) at the receiver for data detection and decoding [1] [2]. It has been proved that when the channel is flat fading and perfectly known to the receiver, the performance of a MIMO system grows linearlywith the number of transmit or receive antennas, whichever less is [3]. Therefore, an accurate and robust channel estimation is of crucial importance for coherent demodulation in wireless MIMO systems [7]. Use of MIMO channels, when bandwidth is limited, has much higher spectral efficiency versus Single- Input Single-Output (SISO), Single-Input Multi-Output (SIMO), and Multi Input Single-Output (MISO) channels [4]. It is shown that the maximum achievable diversity gain of MIMO channels is the product of the number of transmitter and receiver antennas. Therefore, by employing MIMO channels not only the mobility of wireless communications can be increased, but also its robustness [6].Mobile communication systems transmit information by changing the amplitude or phase of radio waves. In the receiving side of mobile system, amplitude or phase can vary widely [11]. This causes degradation in the quality of system since the performance of receiver is highly dependent on the accuracy of estimated instantaneous channelHowever; these detectors require knowledge on the channel impulse response (CIR), which can be provided by a separate channel estimator to minimize the error probability [5]. In this paper, we analyze aLS and MMSE channel estimators, in MIMO system, that signal detector needs to know channel impulse response (CIR) characteristics to ensure minimum Mean Square Error of the Channel Estimation and to minimize the error probability. We present an efficient MIMOchannel estimation with training sequences.The proposed algorithms has been designed and simulated usingMatlab Program then tested and evaluated the efficiency of the proposed algorithms. Outlines ….. The rest of this paper is organized as follows. We present the system description Sect. 2. Section 3 introduces the basics of a phrase-based SMT system, which is regarded as the basis of our experiments. Section 4 will illustrate the feature factors (POS and CCG) that parse the tag and supertag of the corpus. In Sect. 5, we will explain how n-gram LM was included in the translation process. Section 6 will introduce the basis of factored translation model and show its similarity to phrase-based SMT models. In Sect. 7, we will explore our experiments and results on the four models with BLEU scores in the presence of various high n-gram language models. Section 8 will comprehensively conclude the work.](https://image.slidesharecdn.com/b1201021322-170704045109/75/MIMO-Channel-Estimation-Using-the-LS-and-MMSE-Algorithm-1-2048.jpg)
![MIMO Channel Estimation Using the LS and MMSE Algorithm DOI: 10.9790/2834-1201021322 www.iosrjournals.org 14 | Page II. System Description Consider a MIMO system equipped with Nttransmit antennas and Nrreceive antennas. The block diagram of a typical MIMO 2×2 is shown in Figure. 1. Figure.1 General Architecture of a MIMO It is assumed that the channel coherence bandwidth is larger than the transmitted signal bandwidth so that the channel can be considered as narrowband or flat fading [10]. Furthermore, the channel is assumed to be stationary during the communication process of a block. Hence, by assuming the block Rayleigh fading model for flat MIMO channels, the channel response is fixed within one block and changes from one block to another one randomly. During the training period, the received signal in such a system can be written as (1) where Y, S and N are the complex NR -vector of received signals on theNR receive antennas, the possibly complex NTvector of transmitted signals on theNTtransmit antennas, and the complex NR -vector of additive receiver noise, respectively. The elements of the noise matrix are independent and identically distributed complex Gaussian random variables with zero-mean and variance, and the correlation matrix ofN is then given by [8]: where (.)H is reserved for the matrix hermitian, E(.) is the mathematical expectation,andINpdenotes the ܰNpxNpidentity matrix. Np the number of transmitted training symbols by each transmitter antenna. The matrixHin the model (3.1) is theܰNR x Ntmatrix of complex fading coefficients. The (m,n)-th element of the matrixH denoted byhm,nrepresents the fading coefficient value between the m-th receiver antenna and the n-th transmitter antenna. Here, it is assumed that the MIMOsystem has equal transmit and receive antennas. The elements of H and noise are independent of each other. In order to estimate the channelmatrix, it is required that ܰ training symbols are transmitted by each transmitter antenna. The function of a channel estimation algorithm is to recover the channel matrixH based on the knowledge of Y andS. Output (received) signals in locationsCanare as follow: 2.1 Signal Model: We consider a flat fading MIMO wireless system with NT transmit and NR receive antennas. The symbol transmitted by antenna m at time instant k is denoted by Sm(k). The transmitted symbols are arranged in the vector of length NT , where (·)T denotes the transpose operation. Between every transmit antenna m and every receive antenna n there is a complex single-input single-output (SISO) channel impulse response hn,m(k) of length L+1, described by the vector Assuming the same channel order L for all channels, theMIMO channel can be described by L+1complex channel matrices of the dimension NR×NT .The symbol received by antenna n at time instant k is denoted](https://image.slidesharecdn.com/b1201021322-170704045109/75/MIMO-Channel-Estimation-Using-the-LS-and-MMSE-Algorithm-2-2048.jpg)
![MIMO Channel Estimation Using the LS and MMSE Algorithm DOI: 10.9790/2834-1201021322 www.iosrjournals.org 15 | Page byYn(k). The symbols received by the NR antennas are arranged in a vector of length NR, which can be expressed with (3.1), (3.3) and n(k)as noise vector of length NR as We assume additive white Gaussian noise (AWGN) with zero mean and variance per receive antenna, i.e. the spatial correlation matrix of the noise is given by where is the identity matrix and (·)H denotes the complex conjugate(Hermitian) transpose. The receive vector yNfollows to 2.2 QPSK Modulator/ Demodulator PSK is a digital modulation technique which is most commonly used modulation technique in present digital communication systems [12]. In PSK modulation, the phase of the carrier is altered in accordance with the input binary coded information [9]. The PSK is further subdivided into BPSK,8-PSK, 16-PSK, QPSK, DPSK. In binary phase shifting keying the transmitted signal is sinusoid of fixed amplitude, has fixed phase as shown in Figure.2. Figure.2 Phase Shift Keying QPSK [4] is a phase modulation scheme, used in constellation mapping. Here the input bits stream is converted into complex stream using equation 10 and where the I and Q both are in phase with I-out and Q-out respectively. QPSK modulator accepts the binary bits as inputs taken as a symbol and converts them into complex value. QPSK takes only 4 symbols and generate its complex value in this fashion. Where =1/1.414 III. Perfect Channel Estimation Perfect estimator is the simplest algorithm to estimate the channel matrix. By setting the noise equal to zero in (1), the perfect approach estimates the channel matrix as In this way the channel matrix is simply will be obtained by inverse matrix of S/Y. Least Square Algorithm: In this case we estimate the free noise MIMO channel perfectly. Perfect estimation will be used as a lower bound. Consider a Rayleigh flat-fading MIMO channel characterized by H, S as the training sequence, Y as related received signal. N represents Additive White Gaussian Noise. If we assume that: Y = SH + N (12) LS estimator finds Hˆ that SHˆ ≈ Y .[6],[7]LS Algorithm, minimizes the Euclidian distance of SHˆ −Y . Table 3.1 Table 3.1 Show the Input and the Output of QPSK modulator Input Bits I-Out Q-Out 00 01 10 -1 -1 +1 -1 +1 -1](https://image.slidesharecdn.com/b1201021322-170704045109/75/MIMO-Channel-Estimation-Using-the-LS-and-MMSE-Algorithm-3-2048.jpg)
![MIMO Channel Estimation Using the LS and MMSE Algorithm DOI: 10.9790/2834-1201021322 www.iosrjournals.org 16 | Page 11 +1 +1 For this minimization we do following steps: (13) After derivation in respect to Hˆ and to put the equation equal the zero: And so we will have: We use formula (3.15), as the LS channel estimation algorithm. Minimum Mean Square Error Channel Estimation: The Minimum Mean Square Error (MMSE) channel estimates given by [5] Where and in the case of additive white noise the MMSE channel estimate follows to Setting the term in (3.18) to zero yields the Least Square channel estimate in the case of additive white noise. Meansquareerrorofthechannelestimation: The correlation matrix of the error of the channel estimations given by For the Minimum Mean Square Error channel estimation itfollows to [5] (19) The Mean Square Error (MSE) of a MIMO channel is the trace of the error correlation matrix Ree. The trace of amatrix denoted bytr (·) is the sum of the diagonal elements.For additive white noise theMean Square Error follows to (21) For the Least Square channel estimation the term hasto be set to zero. IV. Simulation Results In this work the Simulation Results of the channel estimation are presented. The chosen network simulate or, c Matlab. The simulation results that are collected from the implementation of both the LS and MMSE using the Matlab simulation are presented. 4.1 Simulation Model And Results It will be useful to provide a simple Matlab example simulating a QPSK transmission and reception in Flat MIMO channel. The script performs the following 1- Generate random binary sequence of 1′s and 0′s. 2- Mapping the binary sequence using QPSK. 3- Multiply the symbols with the channel and then add white Gaussian noise. 4- At the receiver, equalize (divide) the received symbols with the known channel. 5- Perform hard decision demapping and count the bit errors. 6- Repeat for multiple values of SNR and plot the simulation Here, simulation results and derived performance metrics of before mentioned algorithms will be explained. flat fading MIMO channel used for training-based estimating channel After , random data is generated in the transmitter and modulated signal will be sent through the channel. By counting number of errors, BER will be extracted. In the perfect channel estimation, we haven’t used the AWGN in estimating process, but it is used in calculating the error. 8 bits training sequence for a MIMO 2×2 system has been considered. We also used a QPSk modulator for modulation data in transmitter. In addition, 100 iterations for calculating BER and MSE which each contains 400 bits have been used. In this section, we evaluate the BER to estimate the channel conditions. Figure 3shows BER comparison of MMSE and LS with respect perfect channel. Here we consider MIMO based system for high multimedia communication system. The parameter](https://image.slidesharecdn.com/b1201021322-170704045109/75/MIMO-Channel-Estimation-Using-the-LS-and-MMSE-Algorithm-4-2048.jpg)

![MIMO Channel Estimation Using the LS and MMSE Algorithm DOI: 10.9790/2834-1201021322 www.iosrjournals.org 21 | Page Figure 12 BER comparison MMSE with respect different bit training values V. Conclusion MIMO systems play a vital role in fourth generation wireless systems to provide advanced data rate. In order to attain the advantages of MIMO systems, it is necessary that the receiver and/or transmitter have access CSI. The time-varying nature of the channel typically requires the use of frequent channel retraining, which in turn increases the data overhead due to training signals, thus reducing the system’s overall spectral efficiency. Hence, effective channel estimation algorithms are needed to guarantee the performance of communication. In this project, a number of channel estimation algorithms have been implemented and evaluated. In this chapter, training based channel estimation schemes in flat fading MIMO systems are investigated. After introducing LS and MMSE estimators, they are simulated in a flat fading MIMO channel considering AWGN. Simulation results show that The algorithm of LS estimator is very simple, As LS algorithm does not require correlation function calculation nor does it require matrix inversion. MMSE estimator is complex; As MMSE algorithm requires both correlation function calculation and matrix inversion. From the Simulation results it is clear that MMSE estimator provides better performance than LS estimator in terms of mean square error (MSE) and Bit error rate (BER) whereas implementation of LS algorithm is much easier than MMSE algorithm Also Simulation results show that the BER for 2x2 MIMO systems using flat fading channel with different correlation values decreases with low correlation values. The results demonstrate that SNR required to support different values of bit error rate varies depending on different low correlation between the transmitting and the receiving antennas. In addition, it is illustrated that when the number of and receiver antennas increases, the performance of TBCE schemes significantly improves. Also The results show BER curves for 2x2 MIMO systems using flat fading channel by MMSE and Ls estimation with different bit training values which show that BER decreases with large bit training values.As from the general modulation theory weknow the performance is better for less order modulation technique as compared to high order modulation but in highorder modulation we have larger data rate. Same behavior isalso observed for MIMO system. Performance both MMSE and LS estimation are same for allkinds of modulation at small value of SNR but as we increase the SNR value the performance gap goes on increasing. References [1]. Joseph, W. Reynders, W. Debruyne, J. and Martens, L., “Influence of Channel Models and MIMO on the Performance of a System based on IEEE 802.16”,Wireless Communications and Networking Conference, ISBN 1-4244-0659-5, pp.1826-1830, 11-15March, 2007. [2]. George Tsoulos, “MIMO System Technology For Wireless Communications”, Revised Edition, CRC Publisher, 2006. [3]. Yan taoQiao, Songyu Yu, Pengcheng Su and Lijun Zhang, “Research on an IterativeAlgorithm of LS Channel Estimation in MIMO OFDM Systems”, IEEE Transactions on Broadcasting, vol. 51, no. 1, pp. (149-153), March 2005. [4]. BPSK/QPSK Modulation and Demodulation.Retrieved February 11, 2010, from Free Online Course Materials — USU Open Course Ware. [5]. C.R. Murthy, A.K. Jagannatham, and B.D. Rao,"Training-Based and Semi-Blind Channel Estimation for MIMO Systems with Maximum Ratio Transmission", IEEE Transactions on Signal Processing, Vol. 54, No. 7, 2006. [6]. M. Pukkila, "Channel Estimation Modeling", Postgraduate Course in Radio-Communications, Nokia Research Center, Fall 2000. [7]. TianbinWo, Peter Adam Hoeher, AnsgarScherb, Karl-Dirk Kammeyer, "Analysis of Semiblind Channel Estimation for FIR-MIMO Systems", German Research Foundation (DFG), October 2005. 0 2 4 6 8 10 12 14 16 18 20 10 -4 10 -3 10 -2 10 -1 10 0 SNR in DB BER MMSE:BER vs SNR MMSE,4 Training symbols MMSE,8 Training symbols MMSE,16 Training symbols MMSE,32 Training symbols](https://image.slidesharecdn.com/b1201021322-170704045109/75/MIMO-Channel-Estimation-Using-the-LS-and-MMSE-Algorithm-9-2048.jpg)
![MIMO Channel Estimation Using the LS and MMSE Algorithm DOI: 10.9790/2834-1201021322 www.iosrjournals.org 22 | Page [8]. XiaoyunHou, BaoyaXeng, HanwenLuo, Wenato Song, Hong-Bin, "Channel Estimation for MIMO- OFDM based Wireless Networks", IEEE Vehicular Technology Conference, VTC, Vol. 4,pp.1883-1887. [9]. Chia-Liang Lui, “Impacts of I/Q Imbalance on QPSK –OFDM-QAM Detection”, IEEE Transactions on Consumer Electronics, vol. 44, no. 3, pp. (984-989), August, 1998. [10]. A.J. Paulraj, R.U. Nabar and D.A. Gore, "Introduction to Space Time Wireless Communication, Cambridge, UK: Cambridge University Press, 2003.Mertins, Signal Analysis. Wiley,1999. [11]. Zelst and J.S. Hammerschmidt. 2002. “A single coefficient spatial correlation [12]. models for multiple-input multiple output (MIMO) radio channels,” in Proc.URSIXXVIIth General Assembly, 2002. [13]. Comparison of different models for the analysis of Rayleigh fading channels.” -- PDF article. [14]. D.S. Shiu, G. Foschini, M. Gans and J. Kahn, “Fading correlation and effect on the capacity of multielement antenna systems”, IEEE Trans. Commun., vol. 48, no. 3, [15]. March 2000, pp. 502–512. [16]. D. Chizhik, G. Foschini, M. Gans and R. Valenzuela, “Keyholes, correlations and capacities of multielement transmit and receive antennas”, Proc. Vehicular TechnologyConf., VTC’2001, May 2001, Rhodes, Greece.](https://image.slidesharecdn.com/b1201021322-170704045109/75/MIMO-Channel-Estimation-Using-the-LS-and-MMSE-Algorithm-10-2048.jpg)