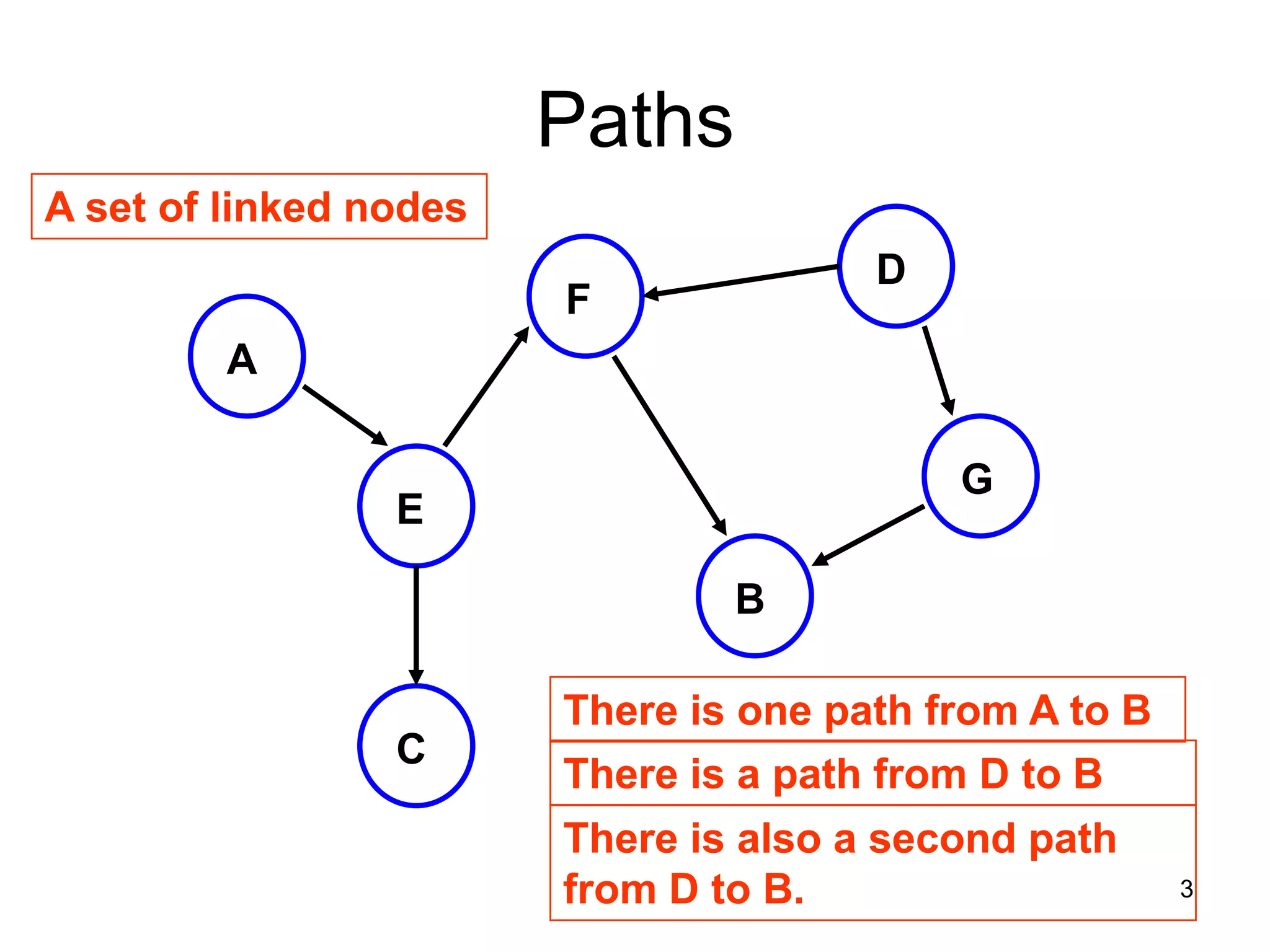
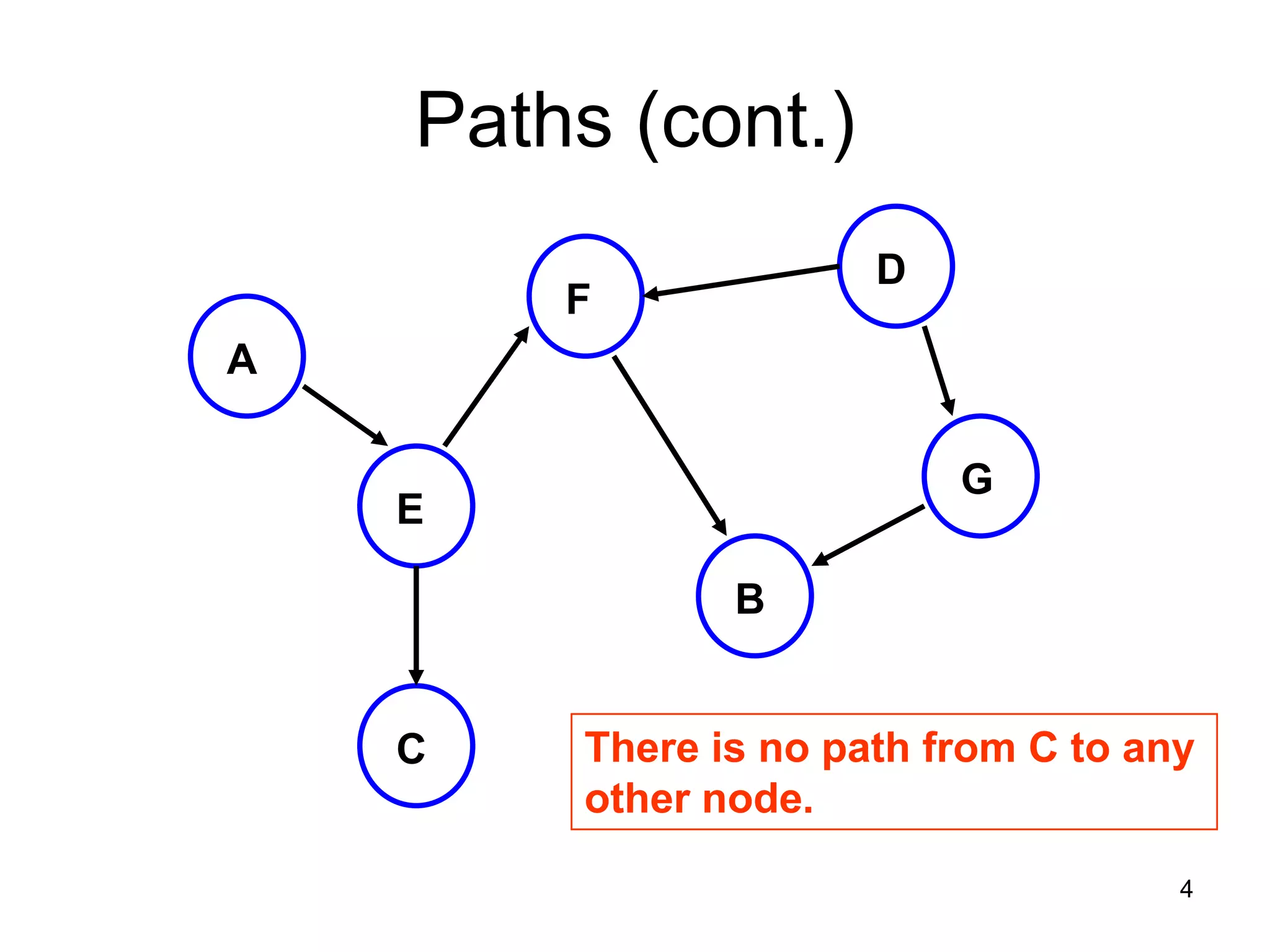
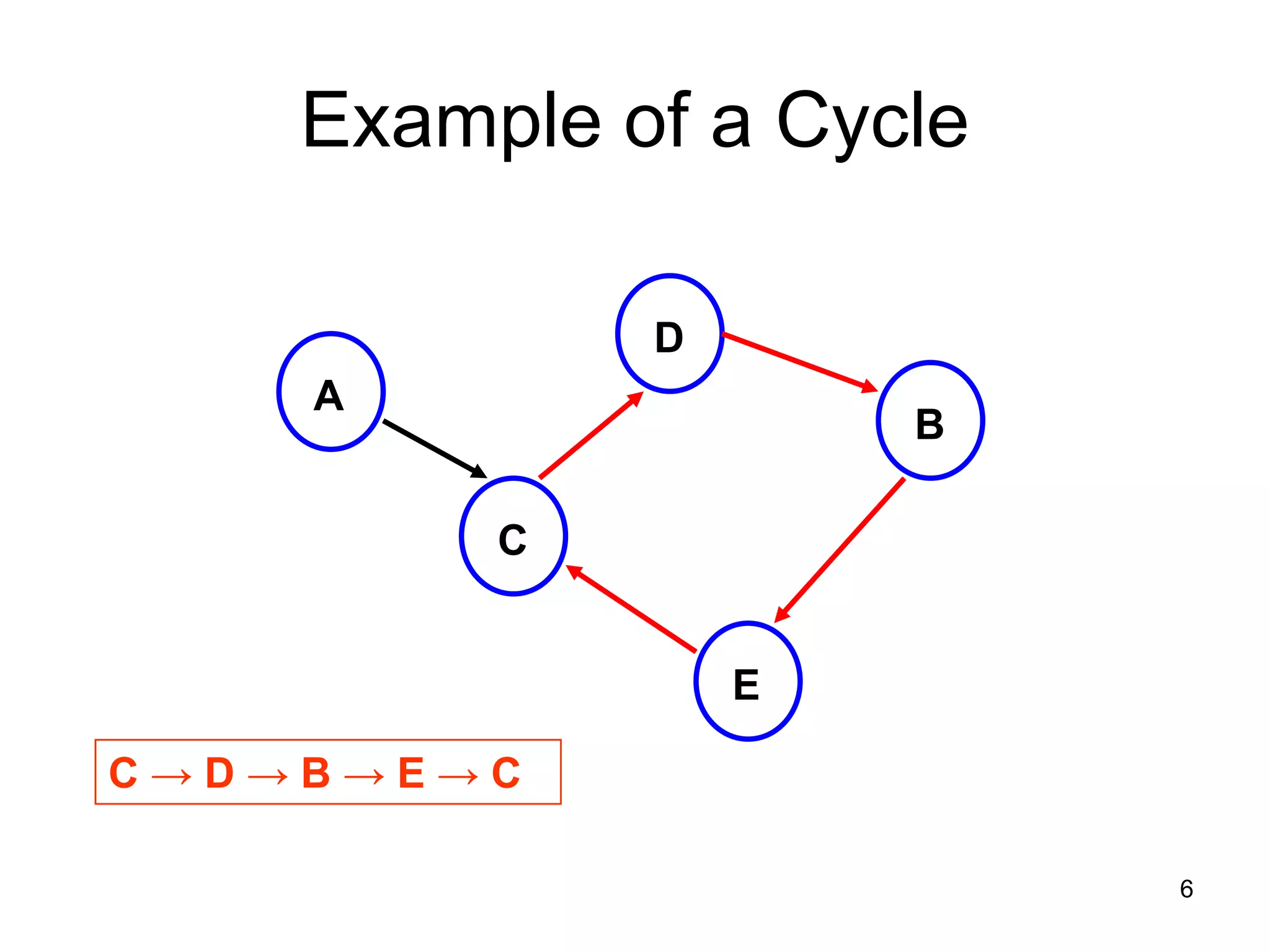
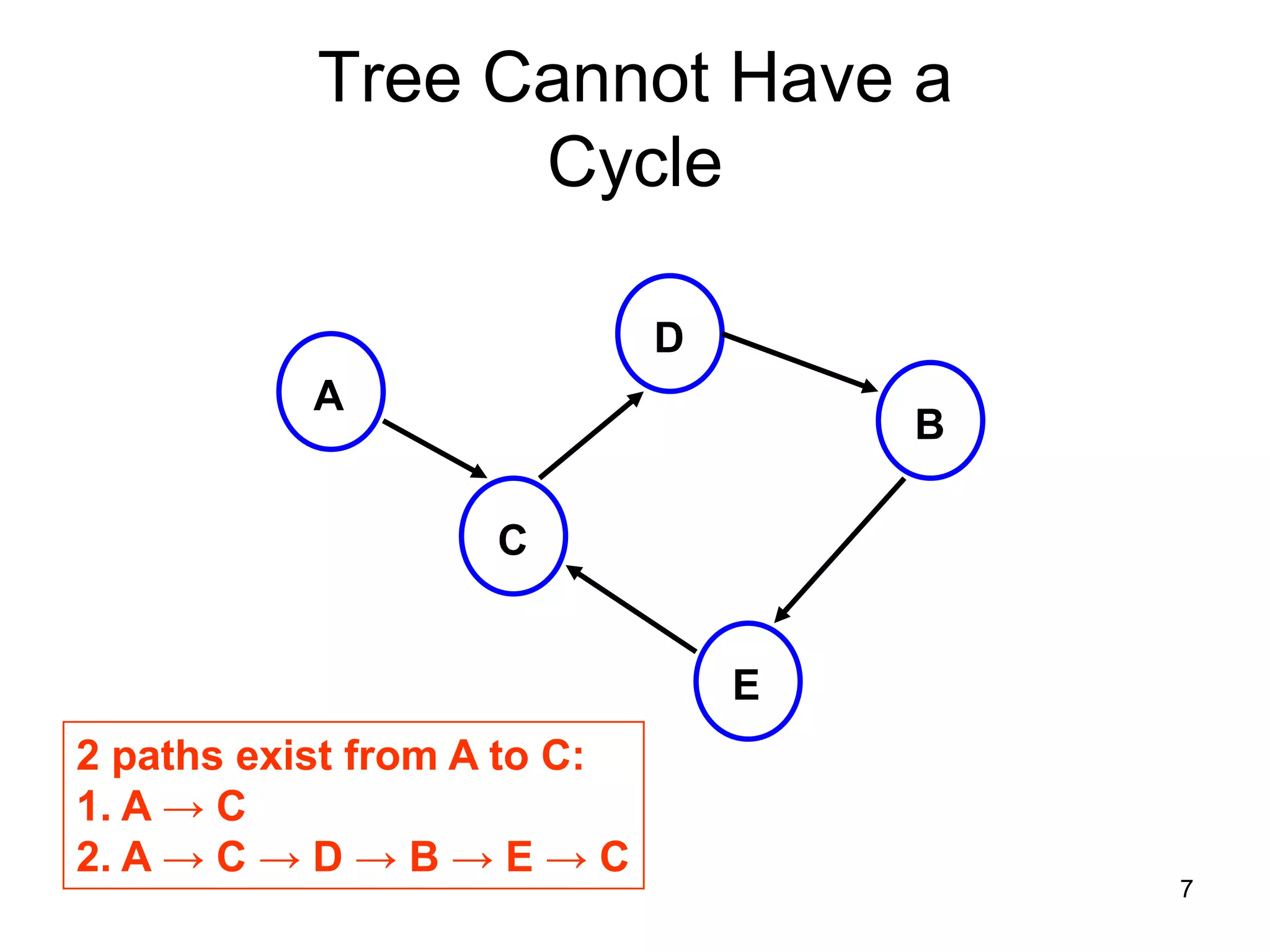
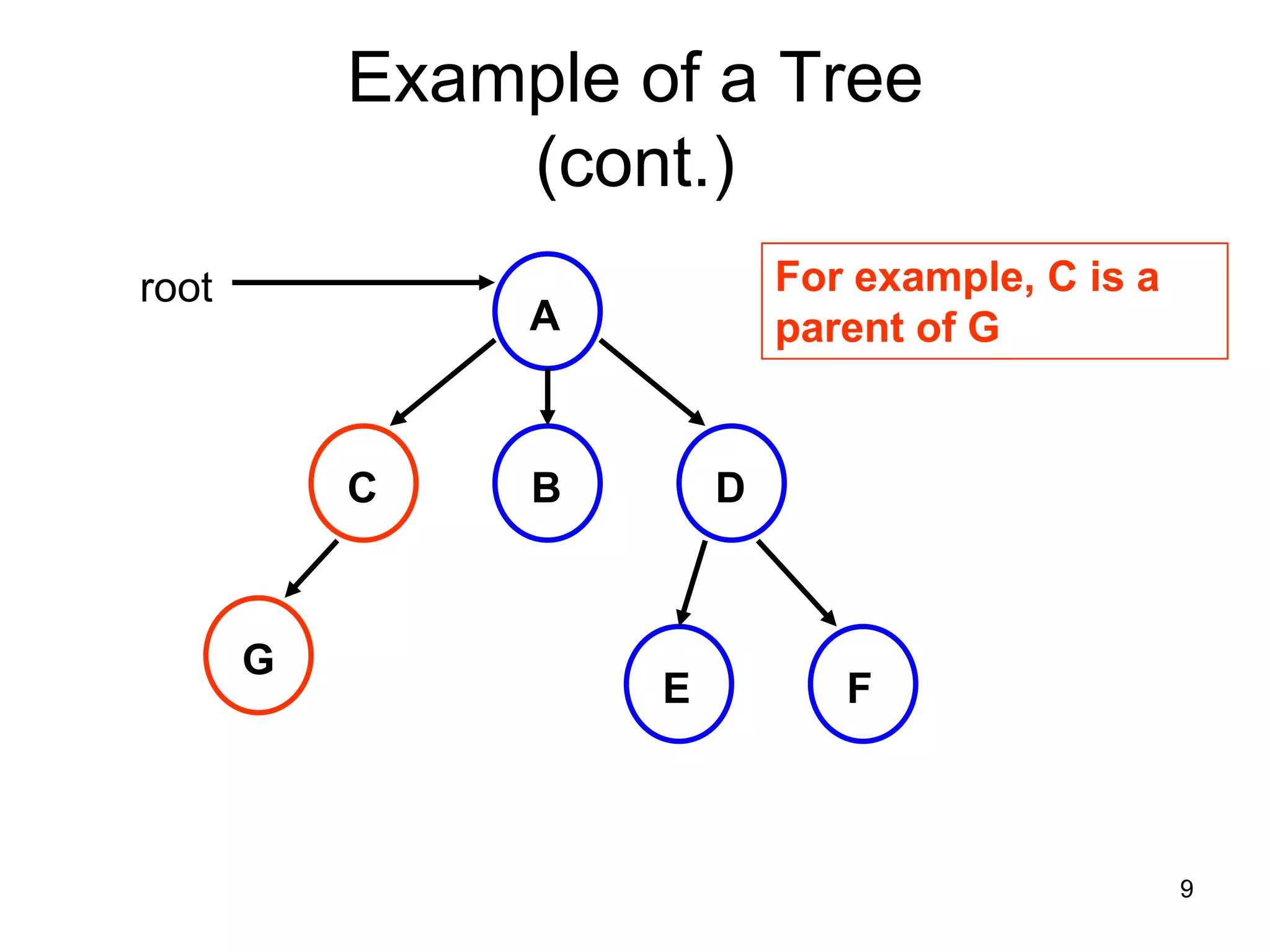
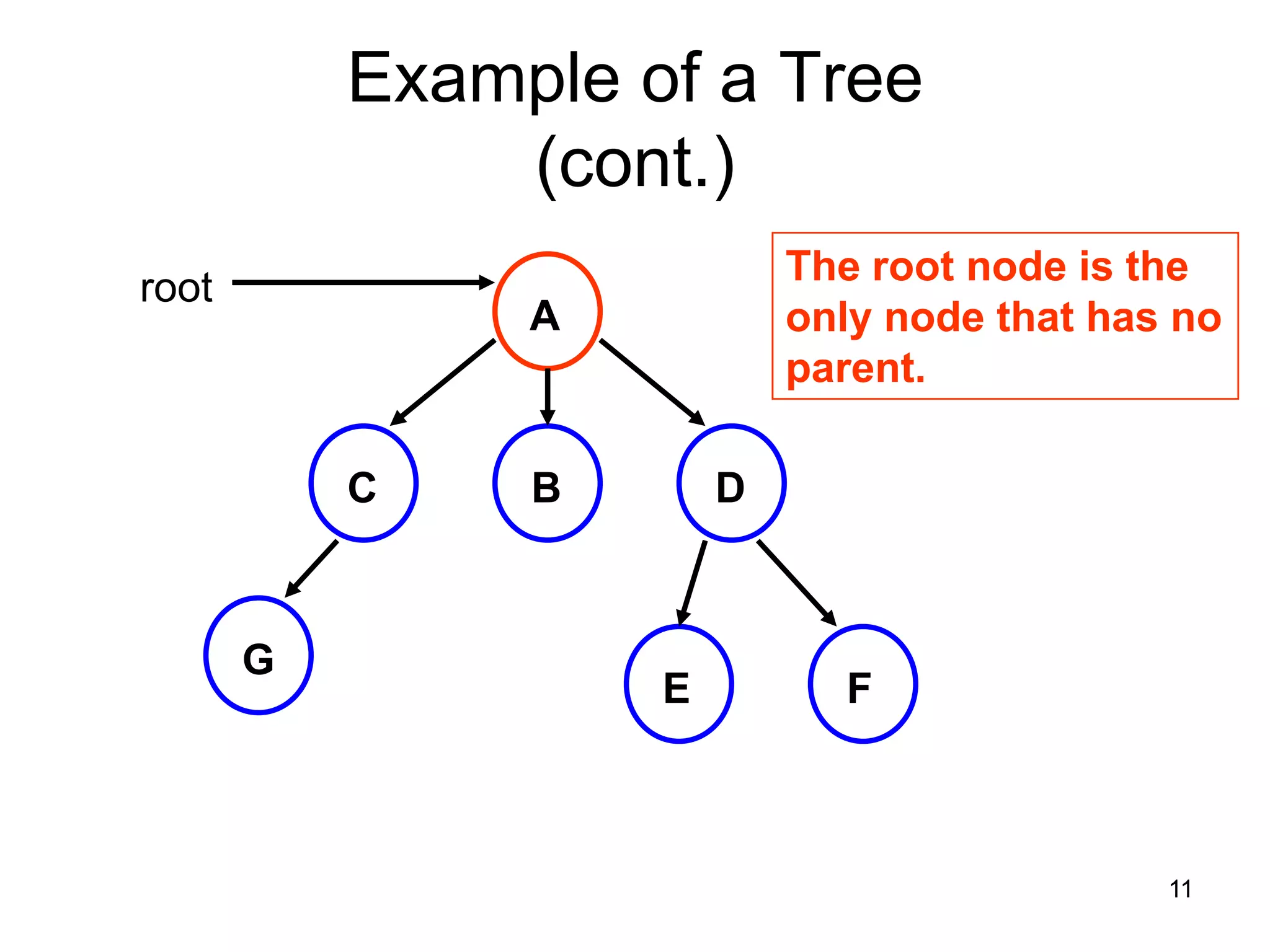
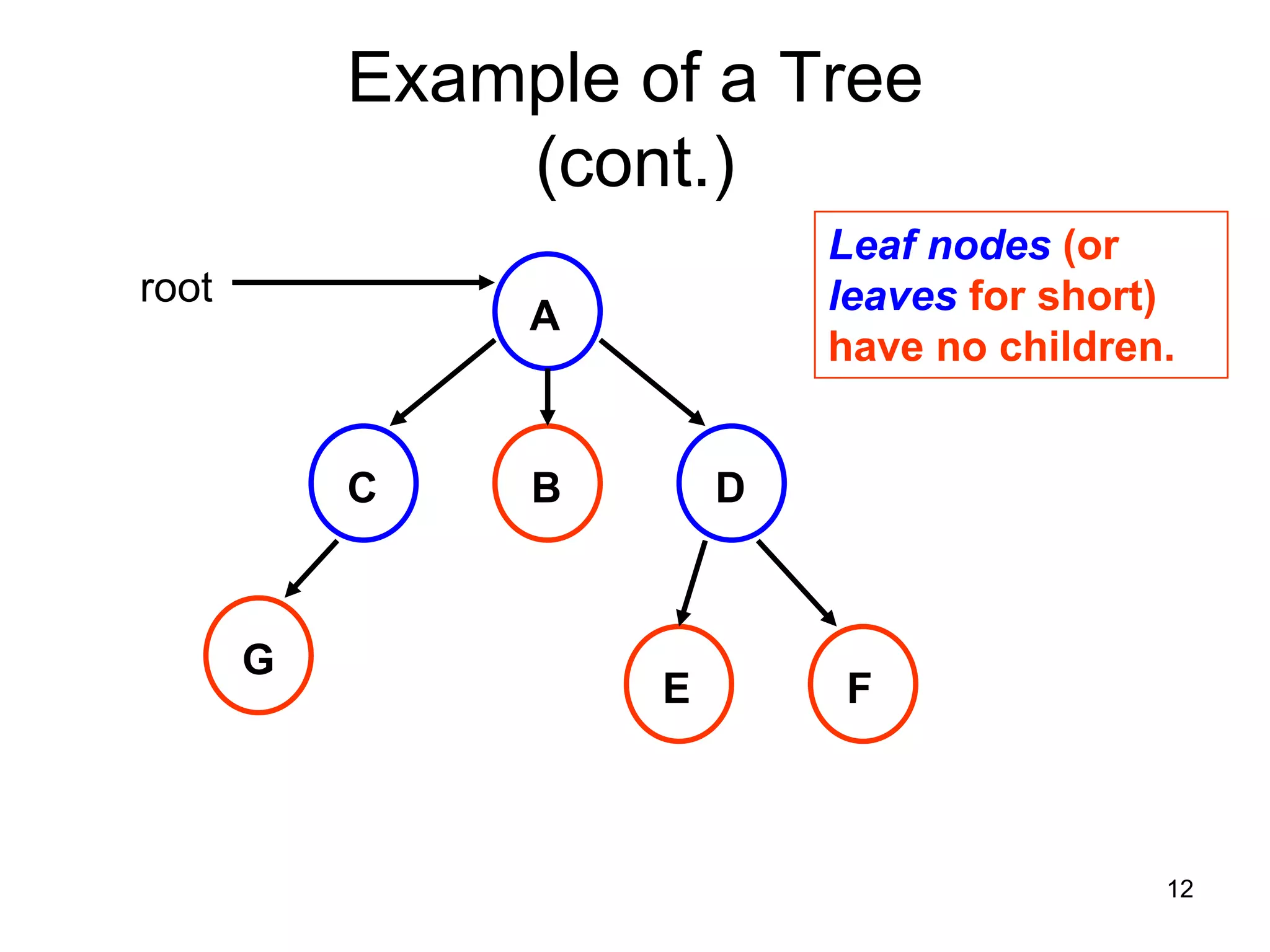
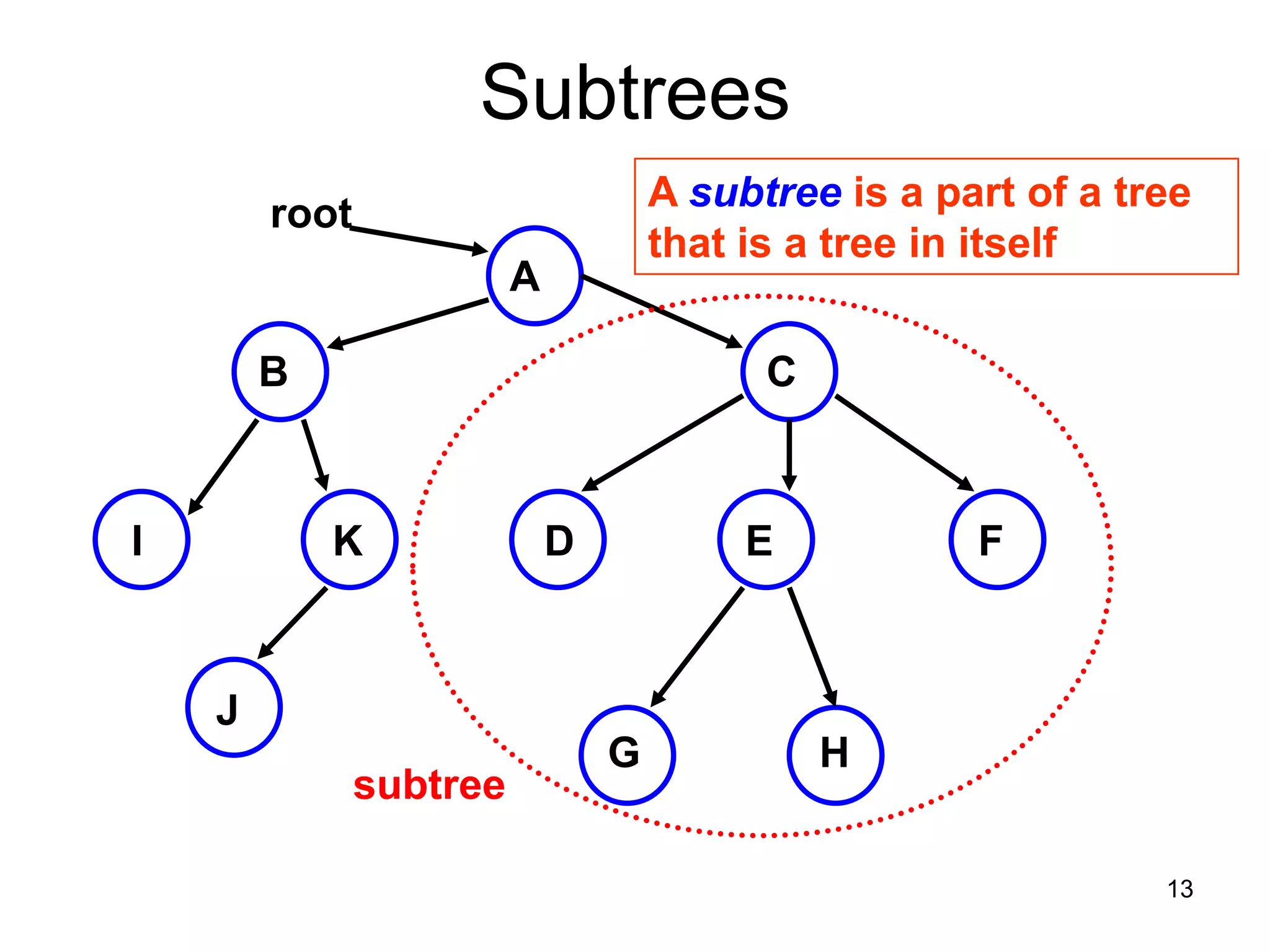
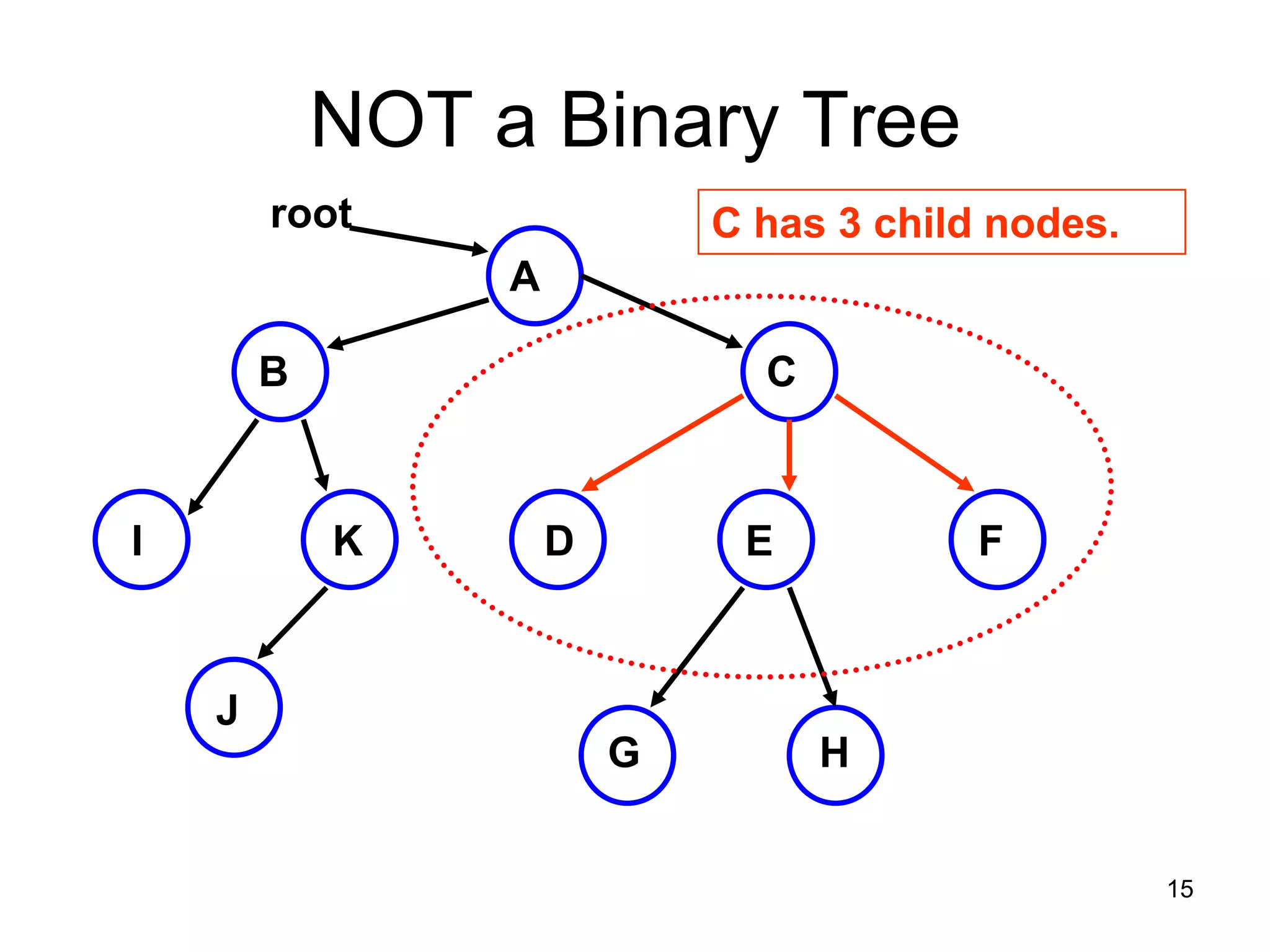
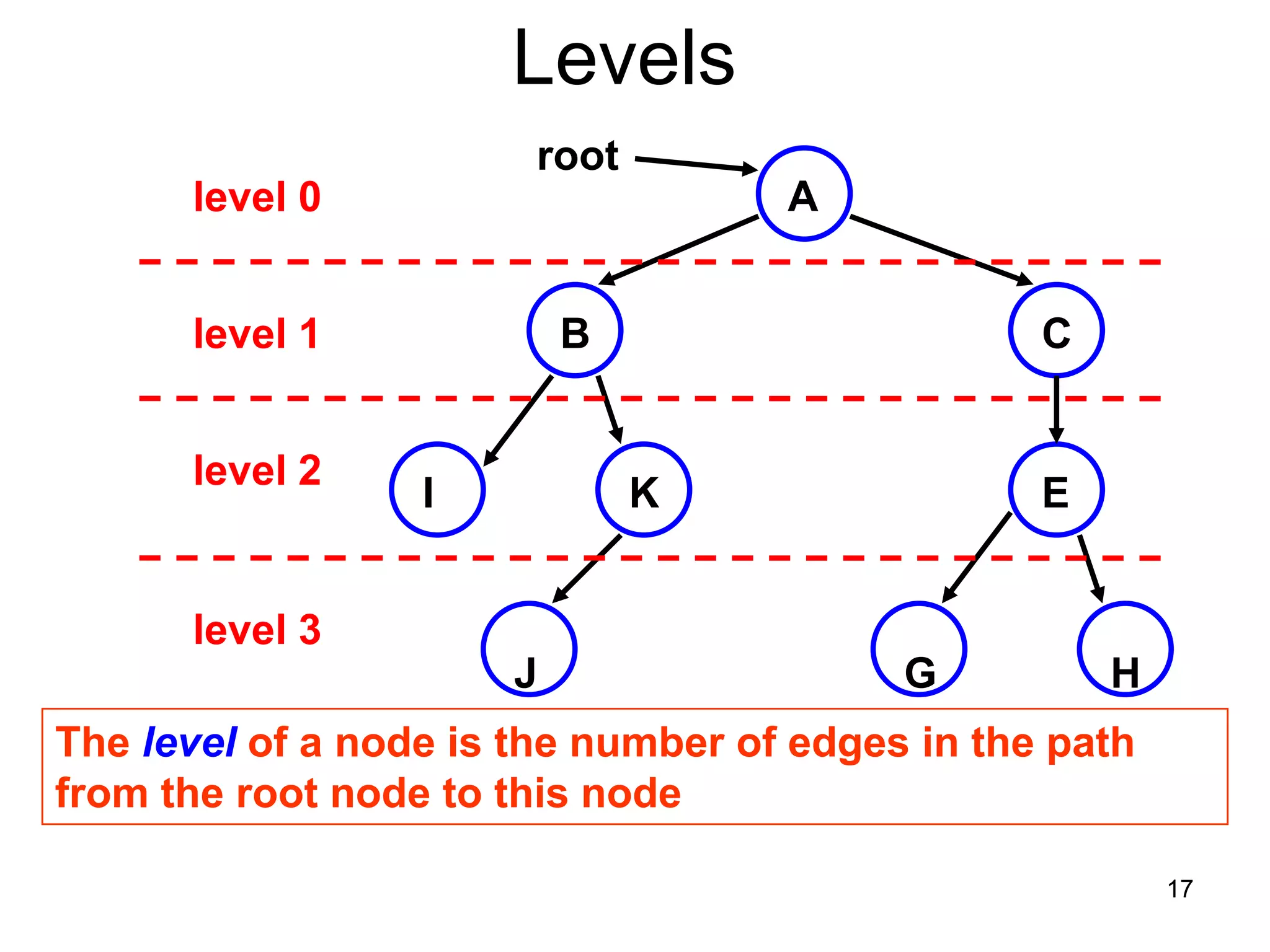
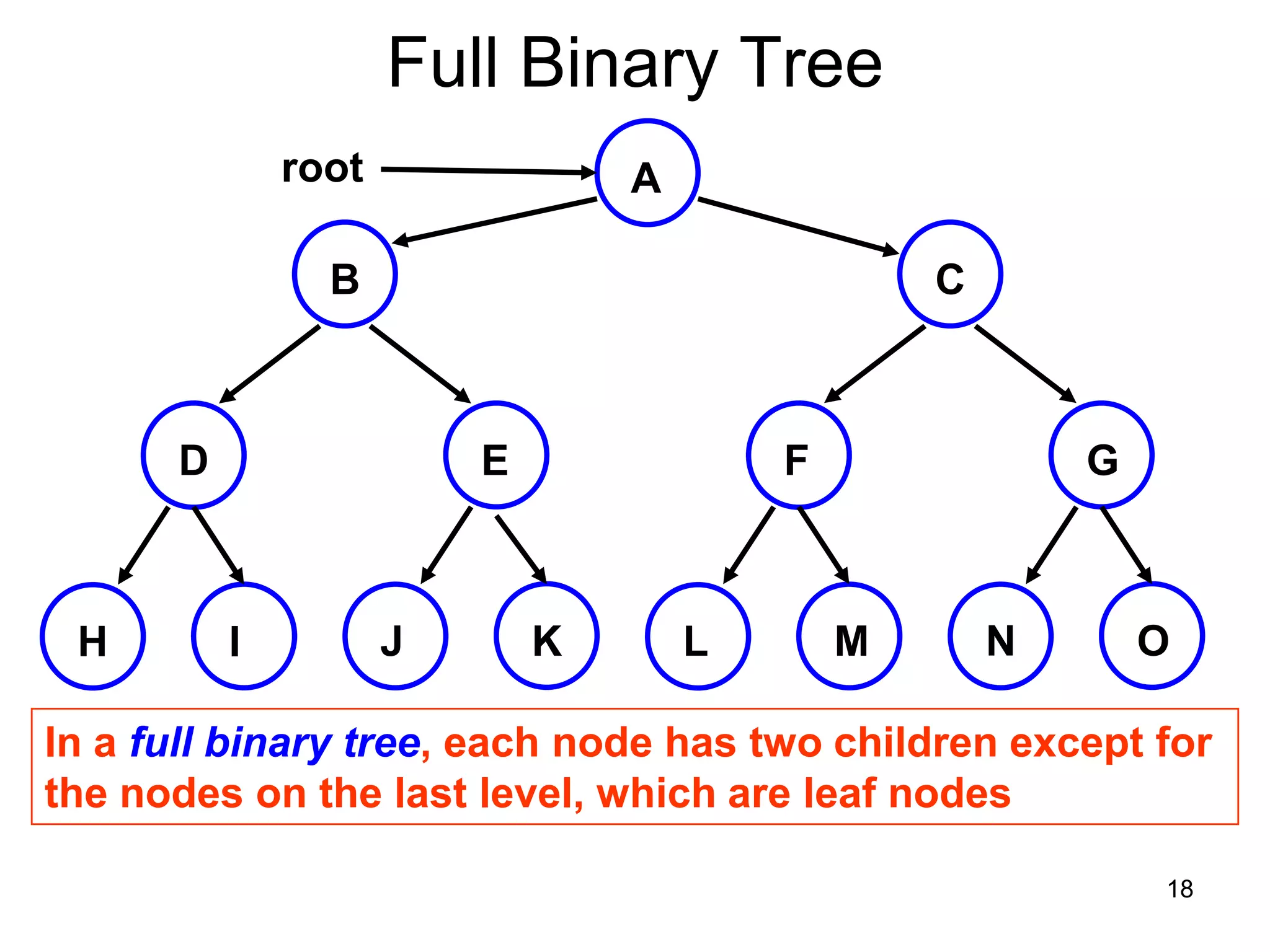
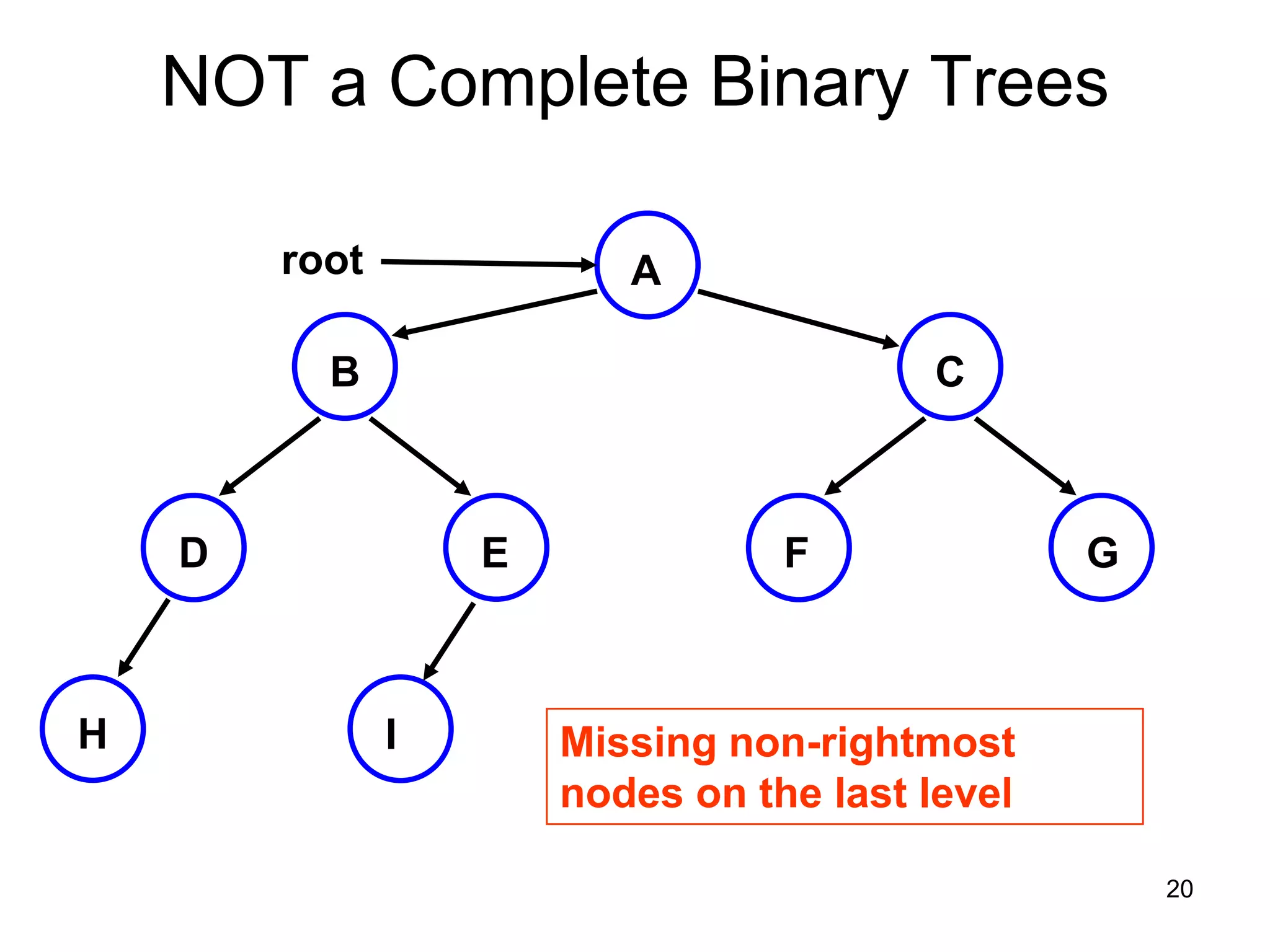
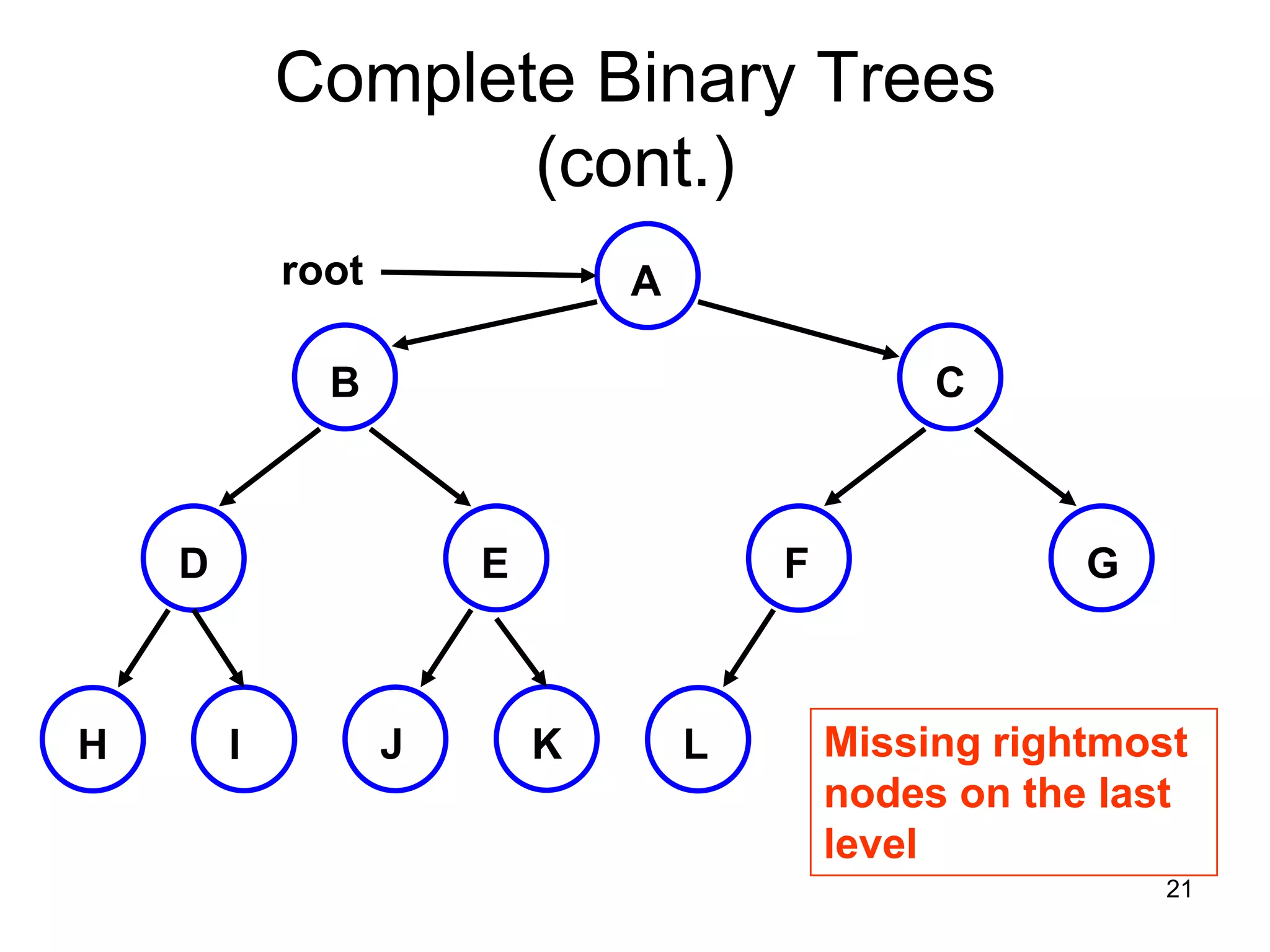
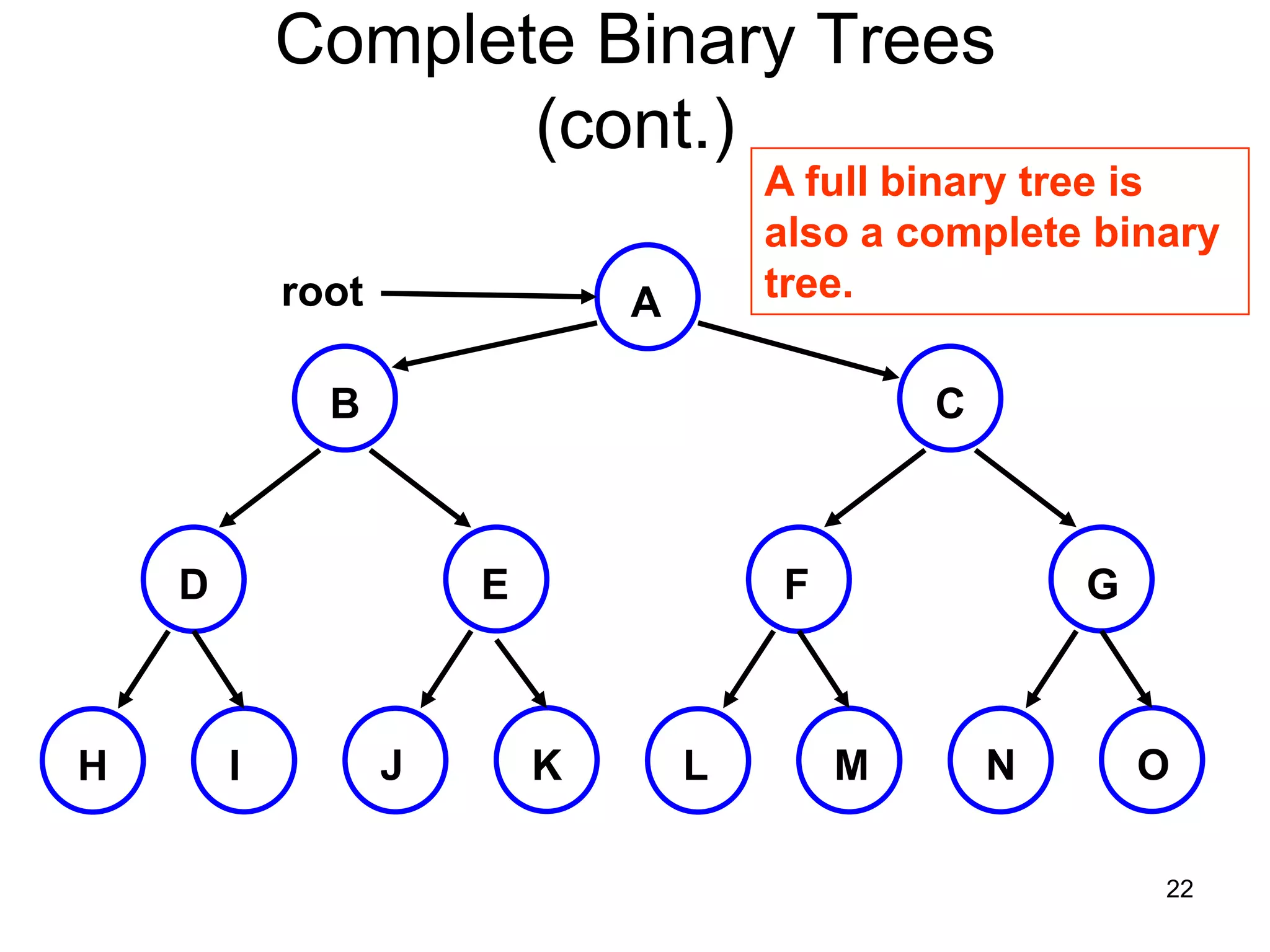
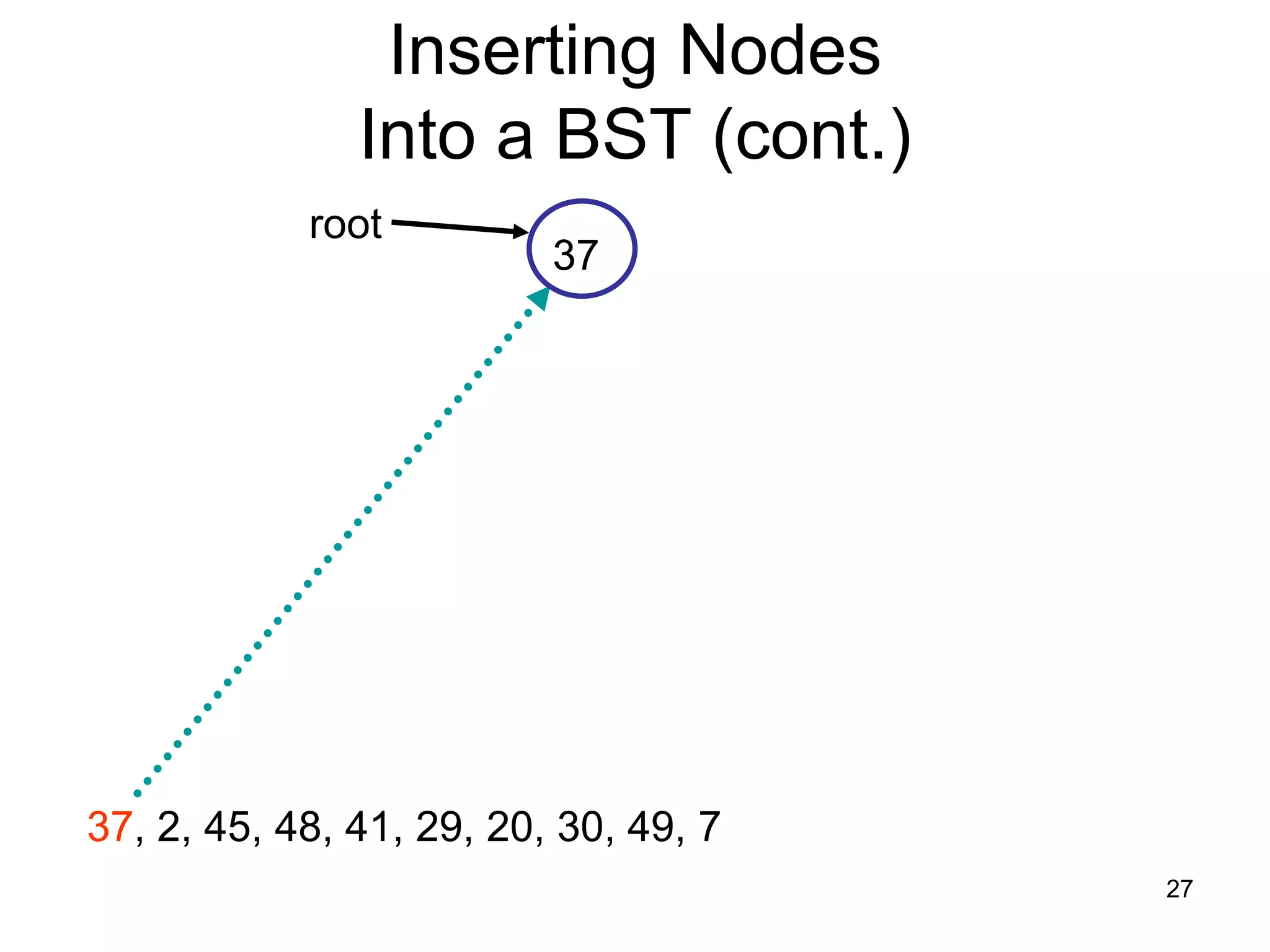
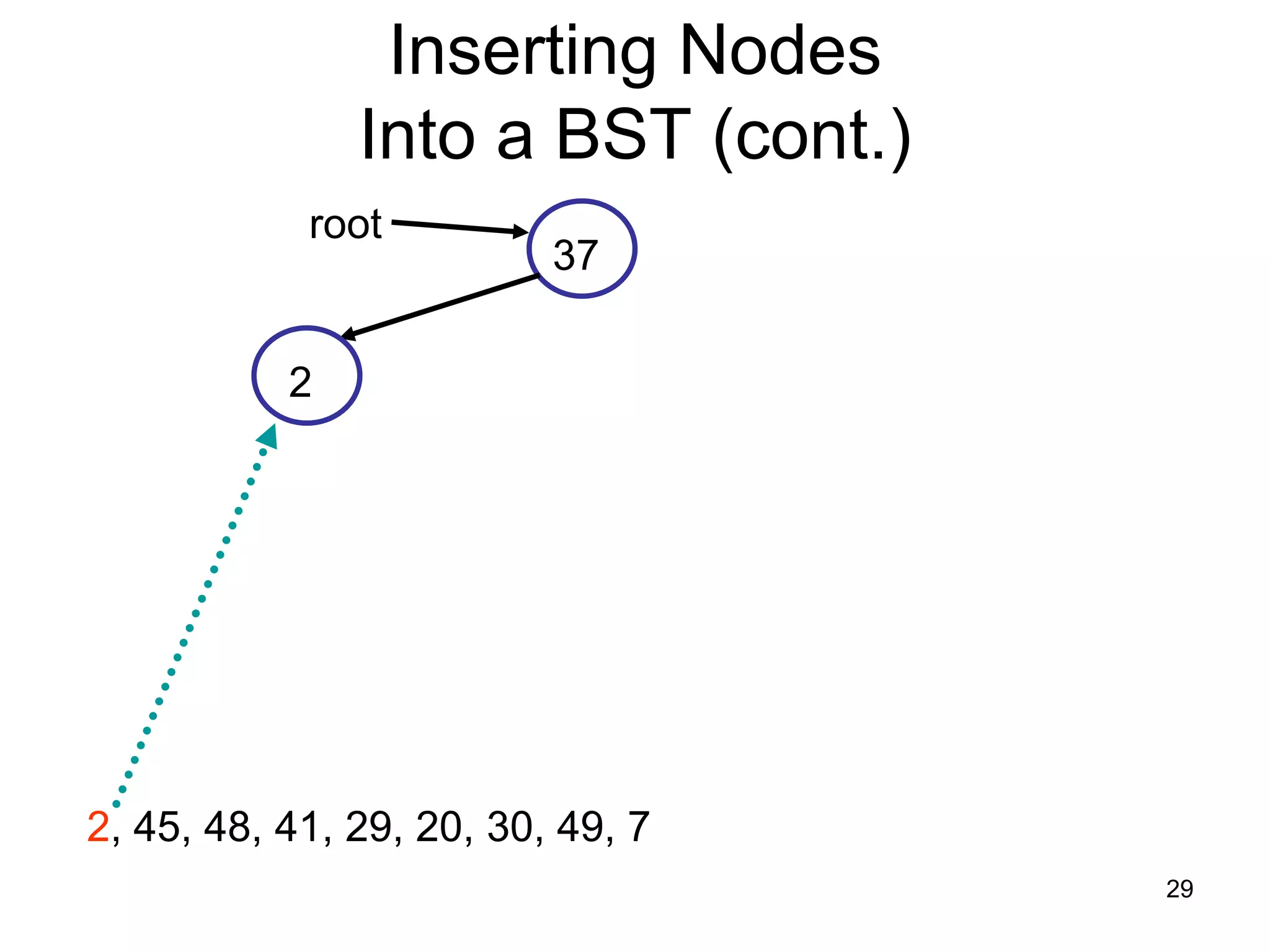
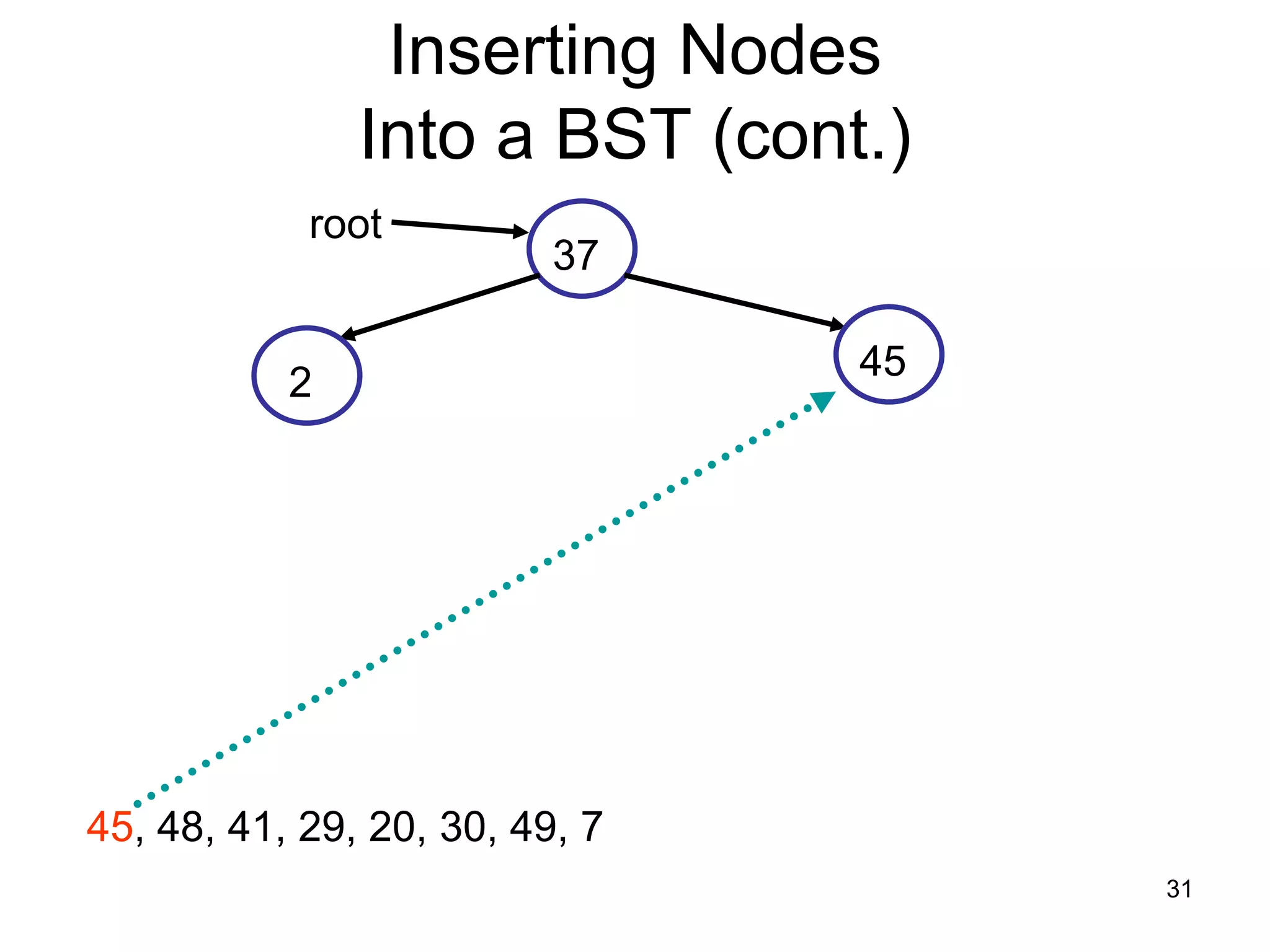
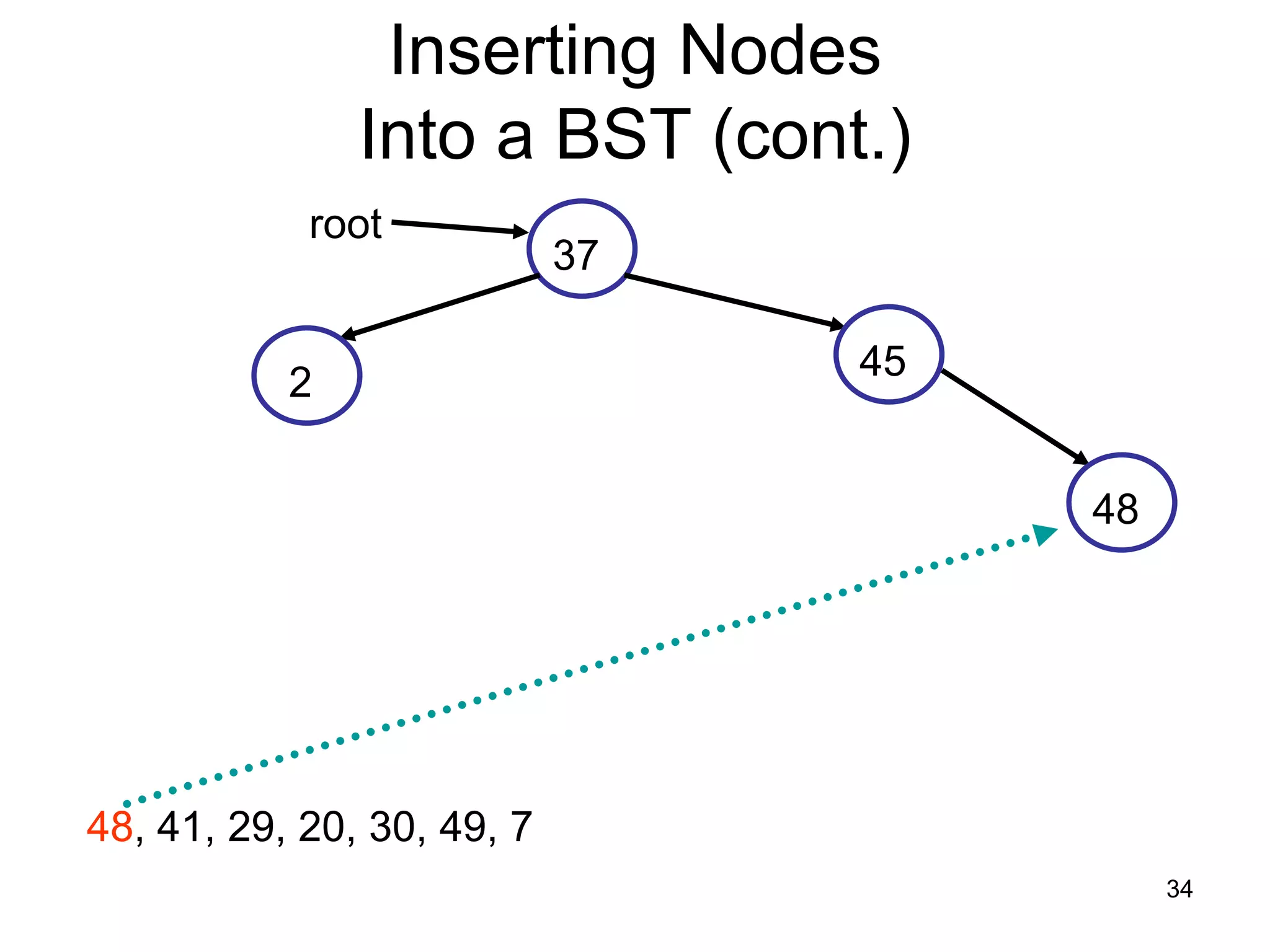
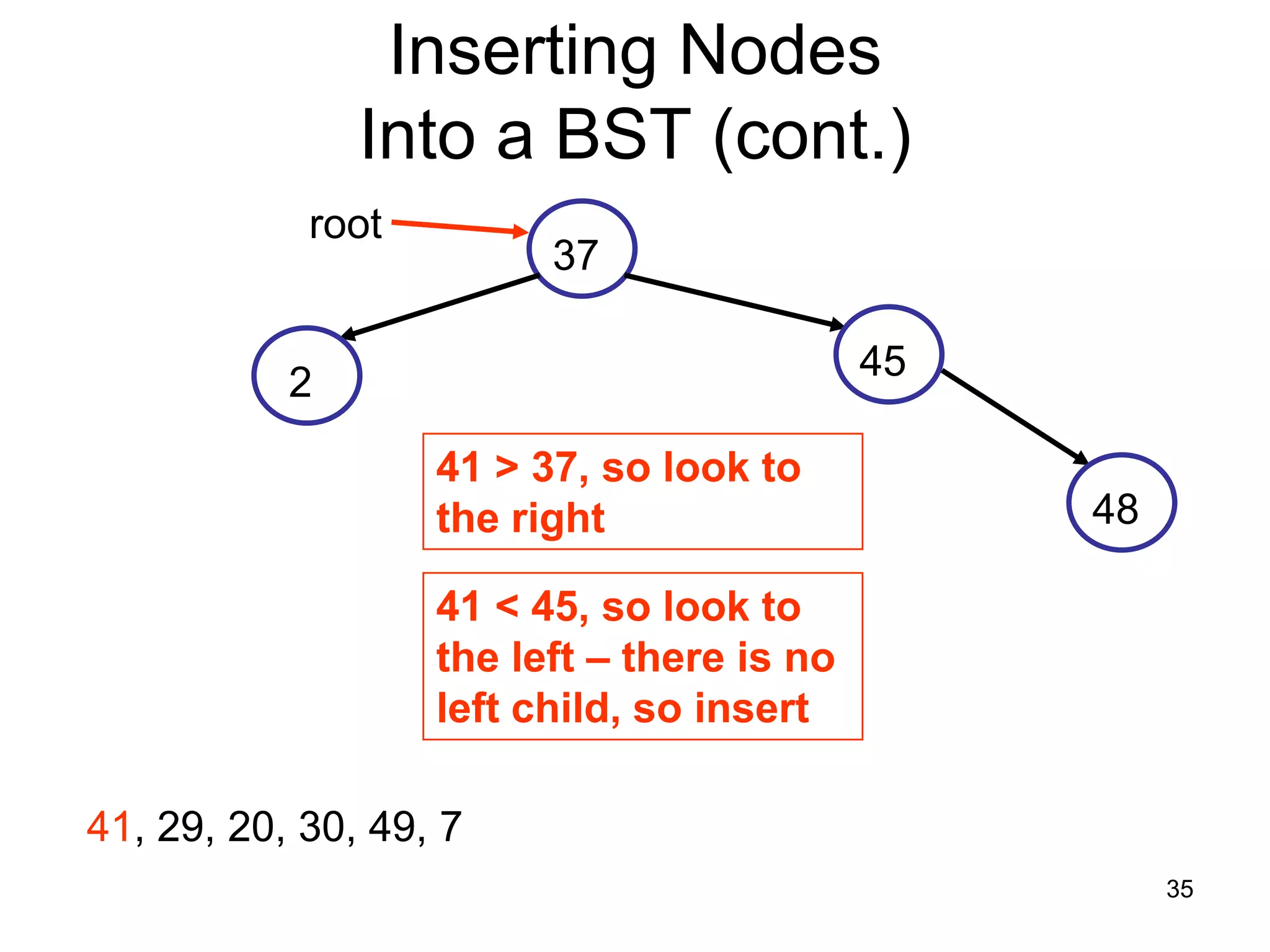
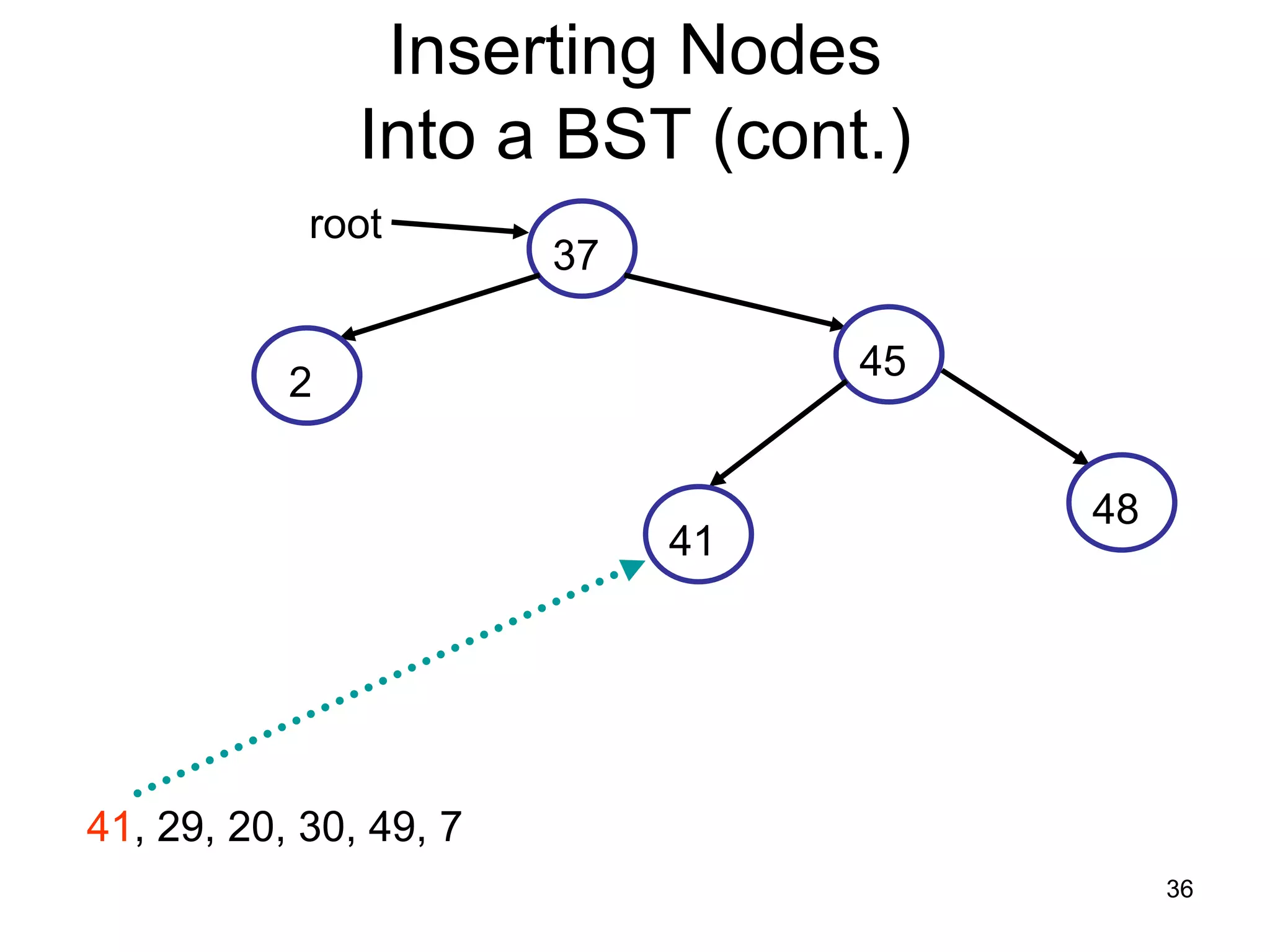
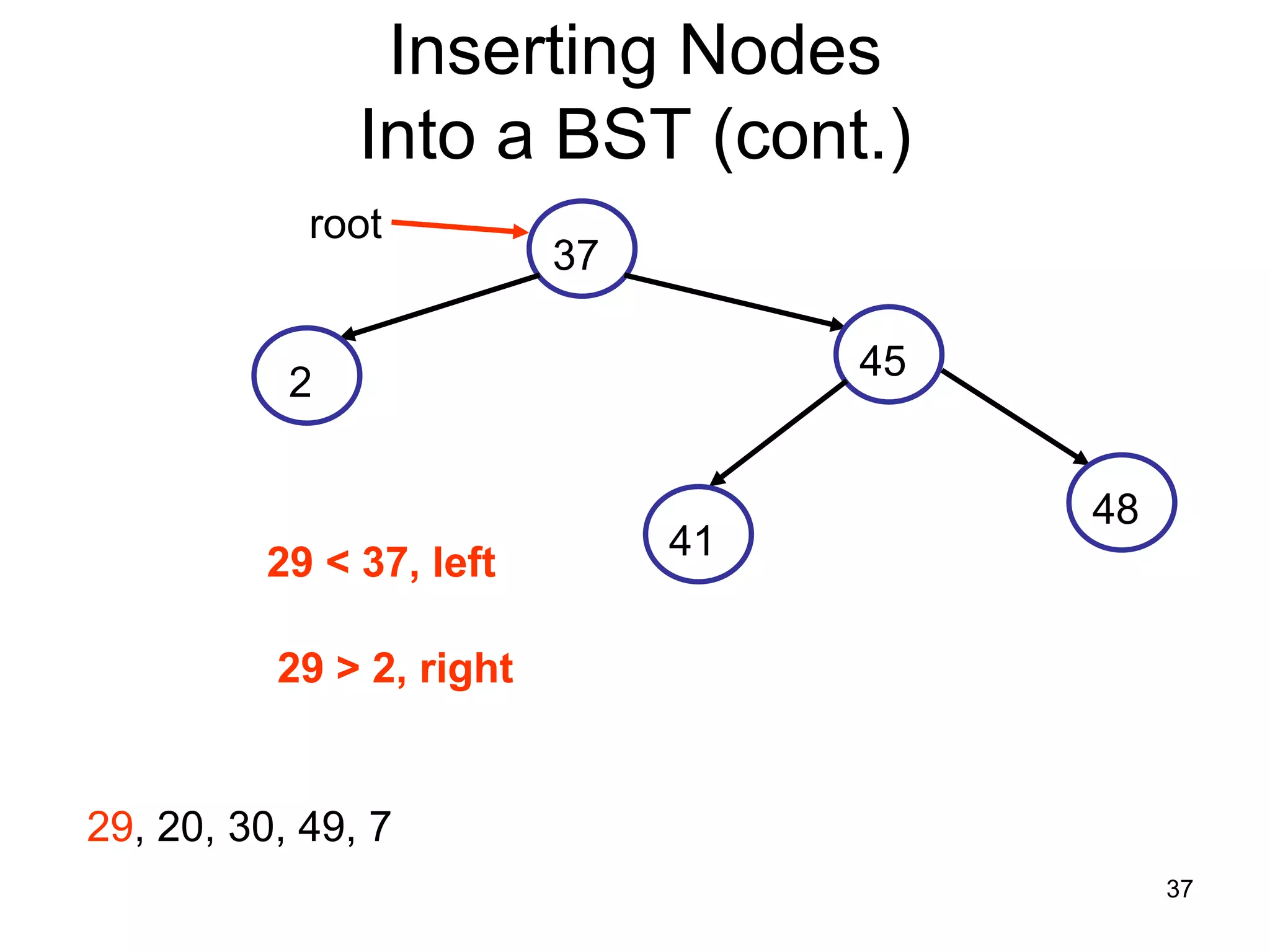
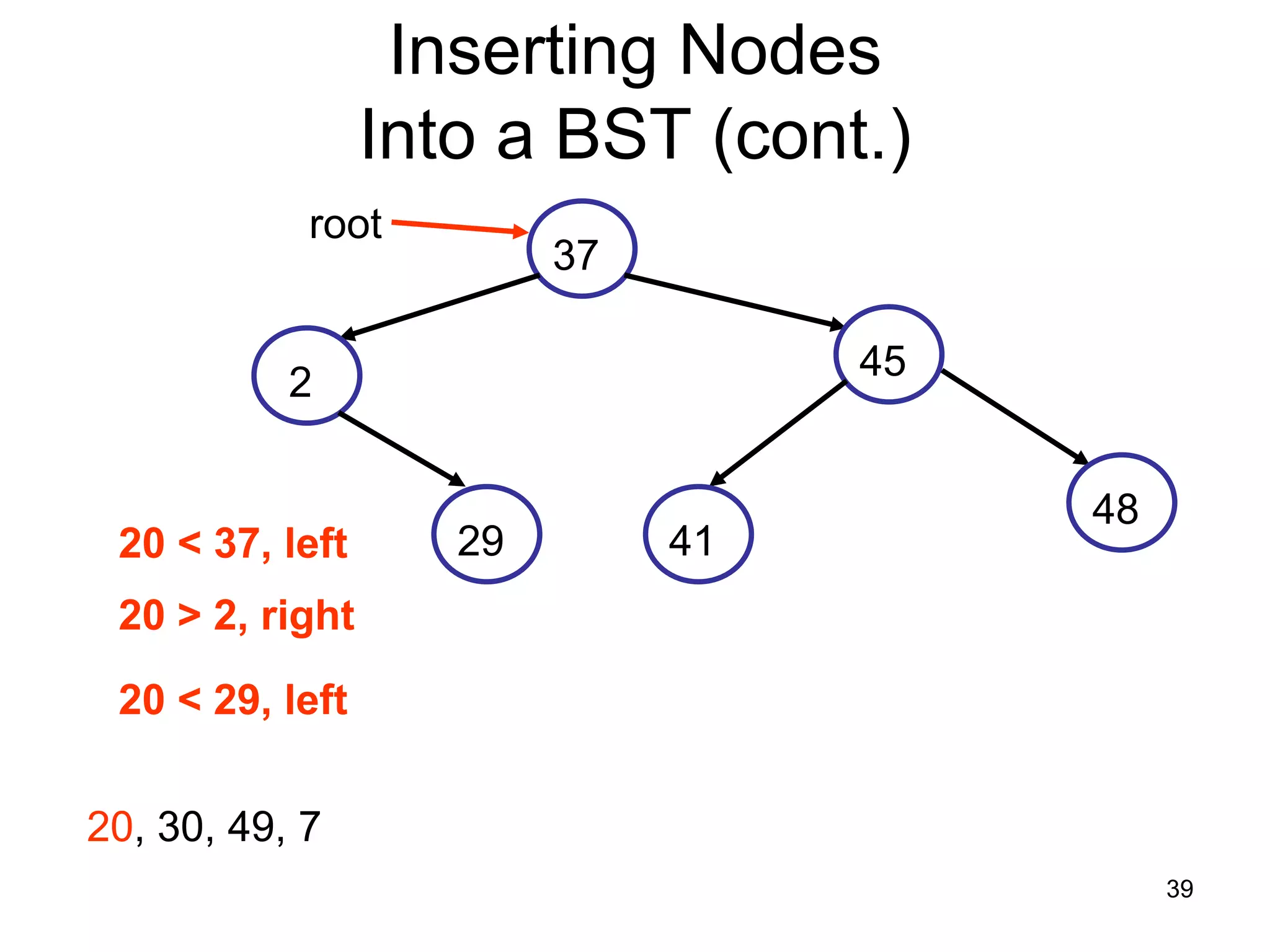
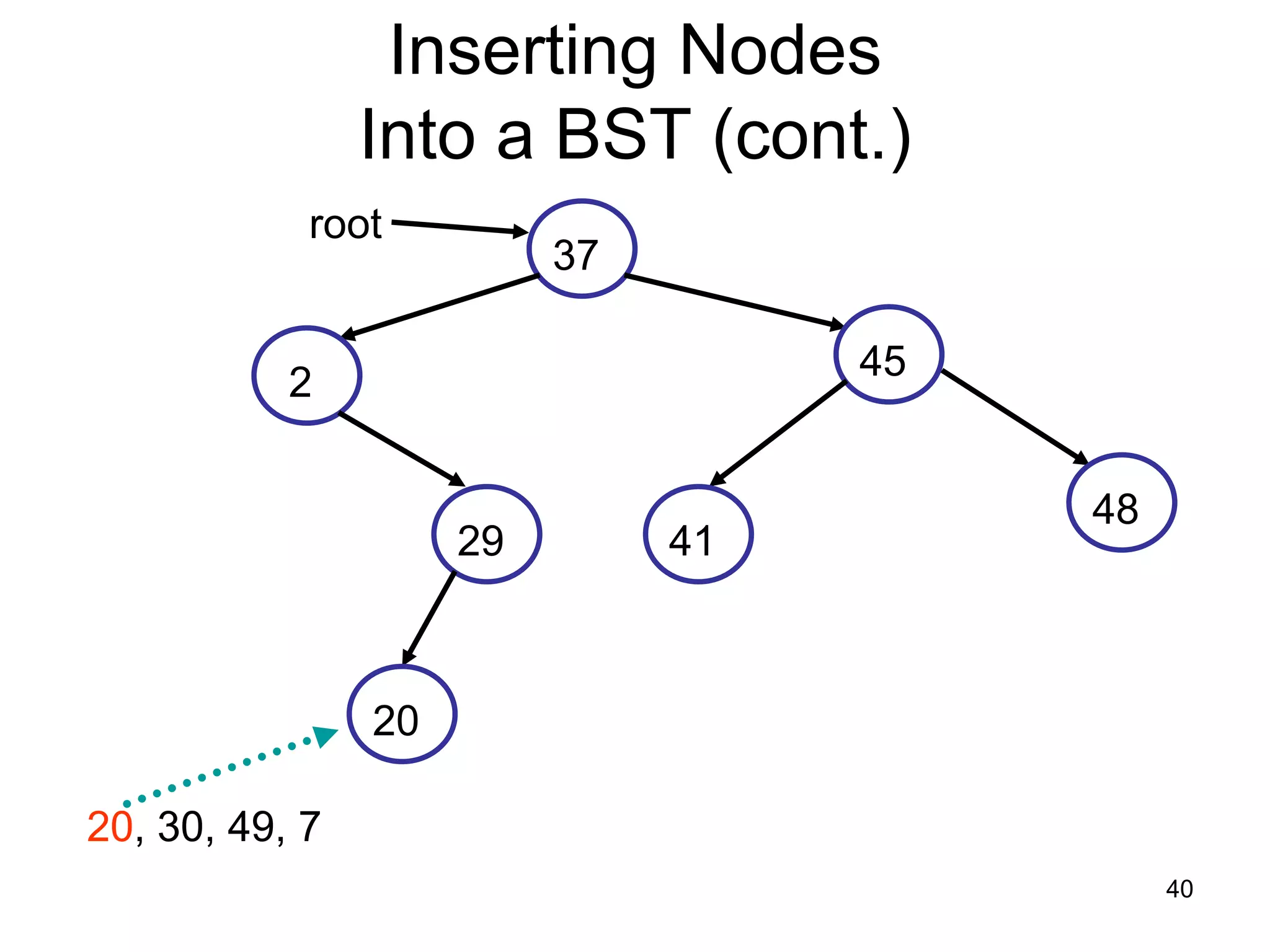
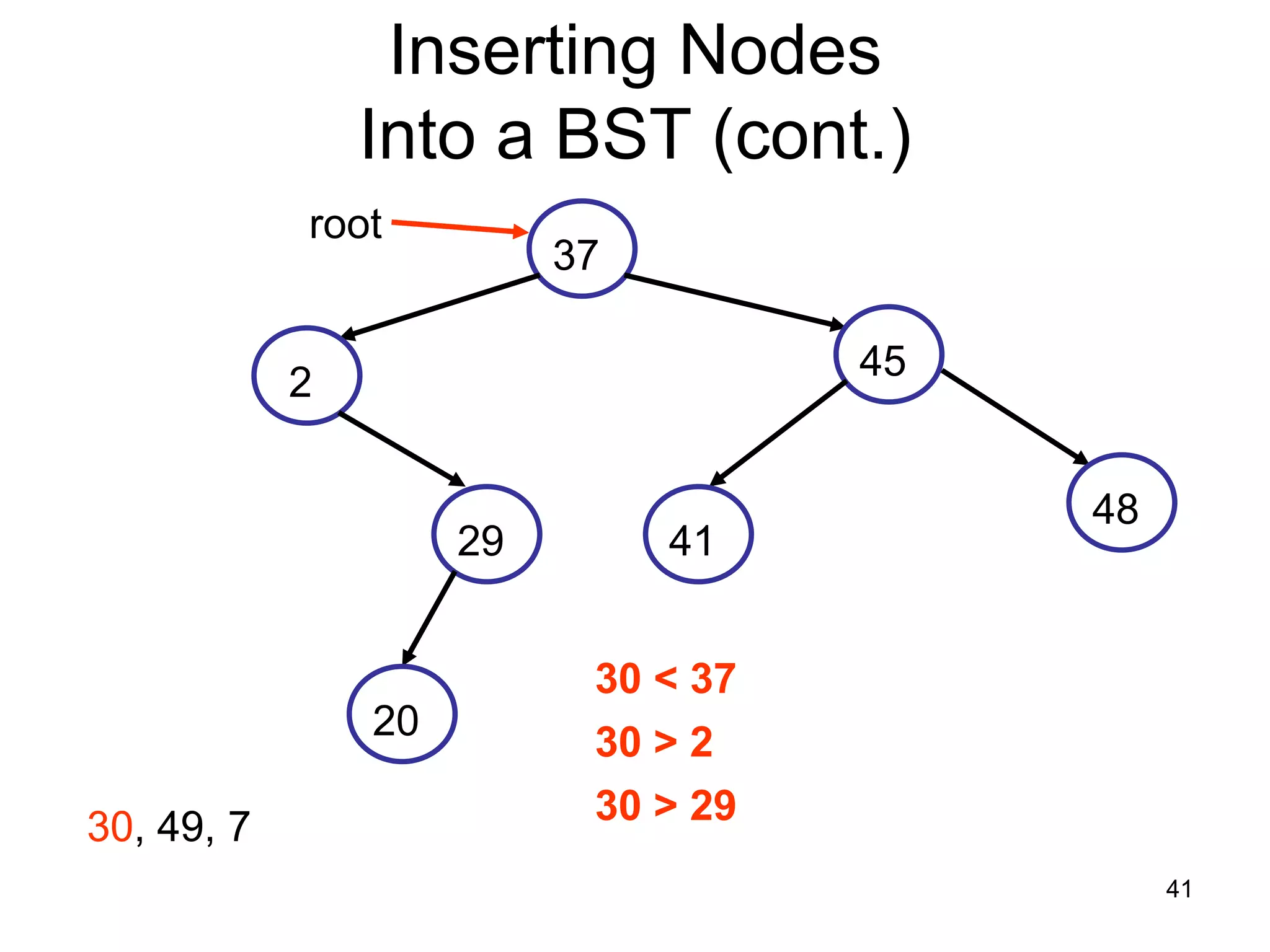
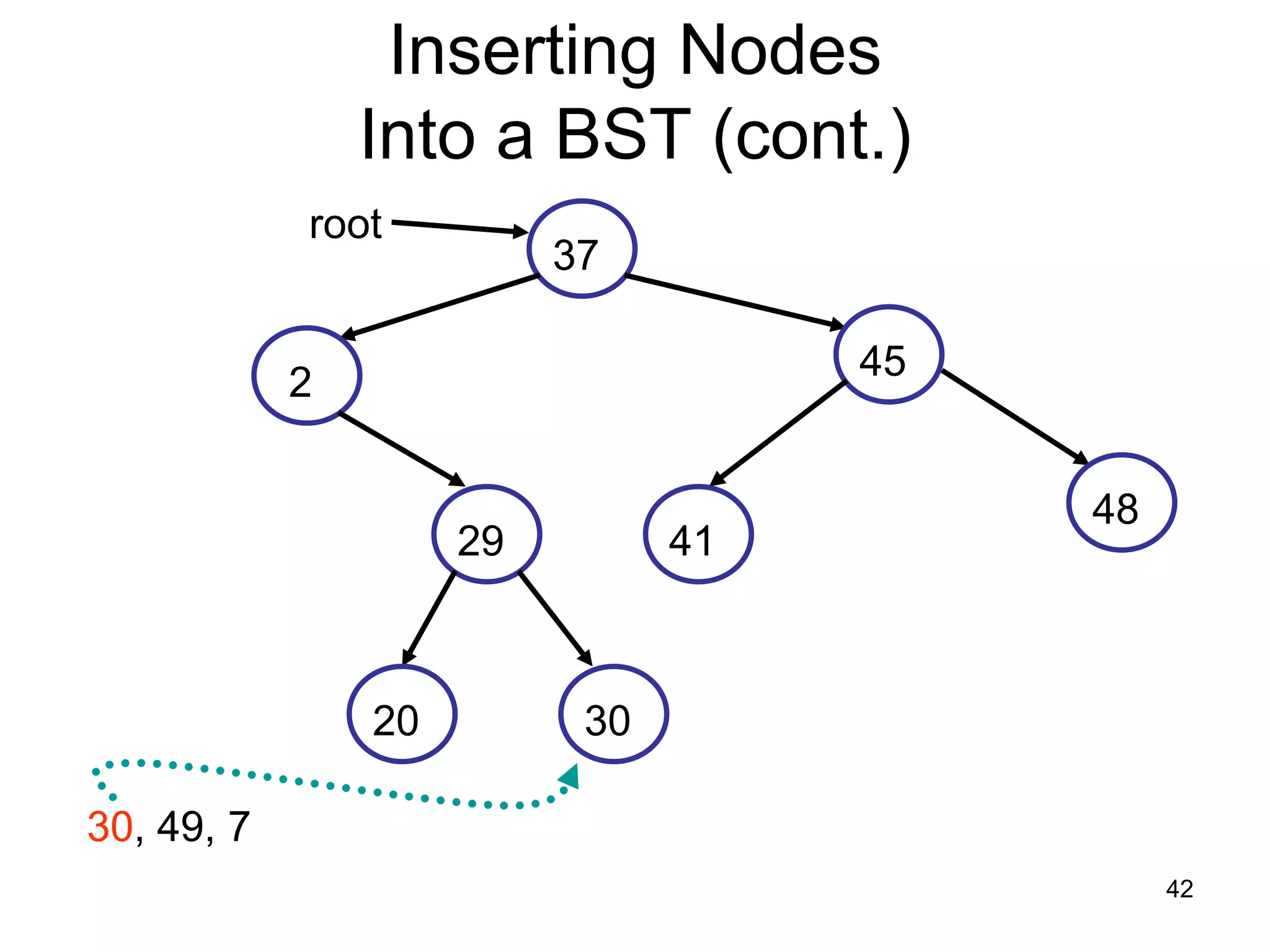
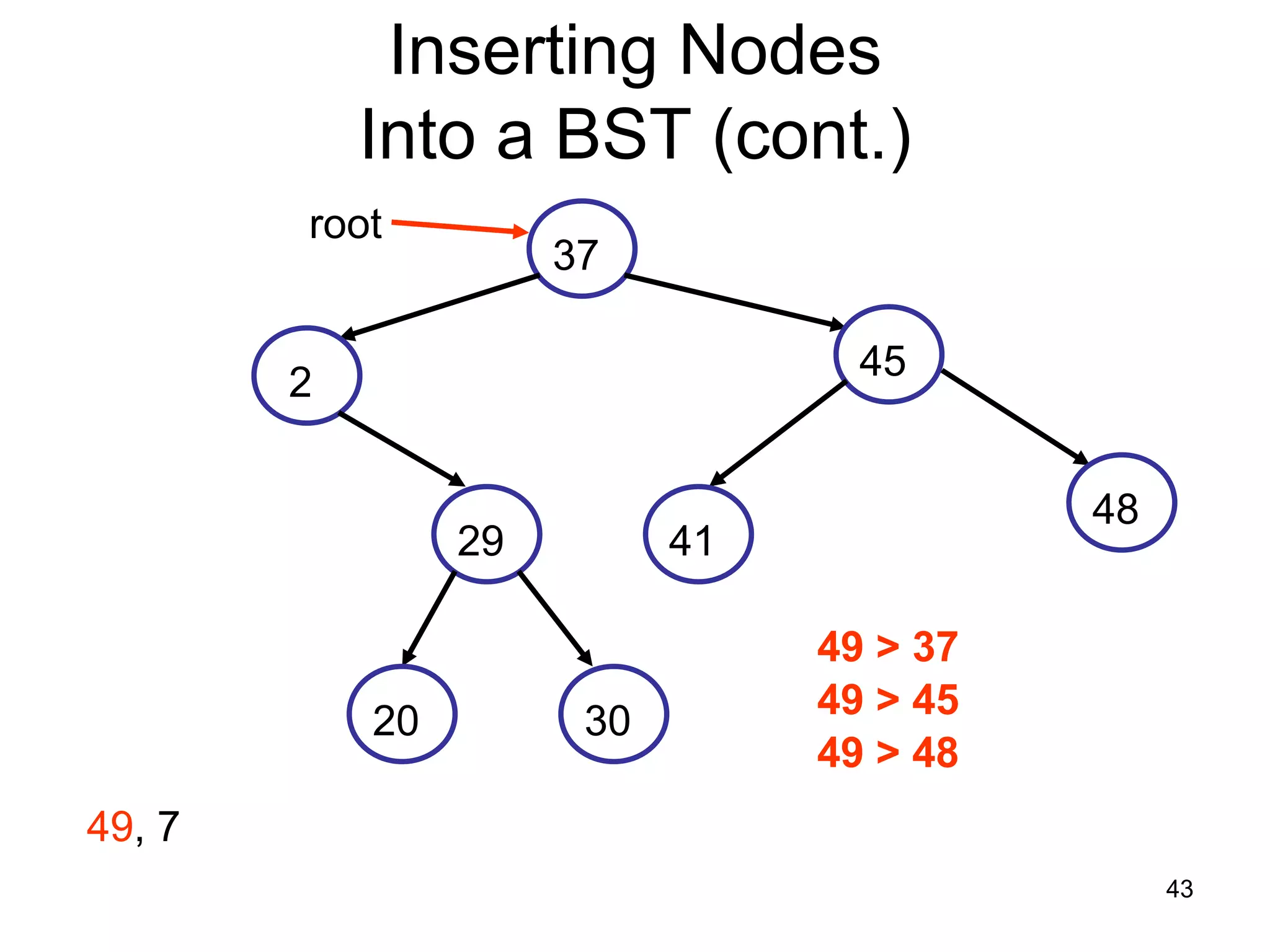
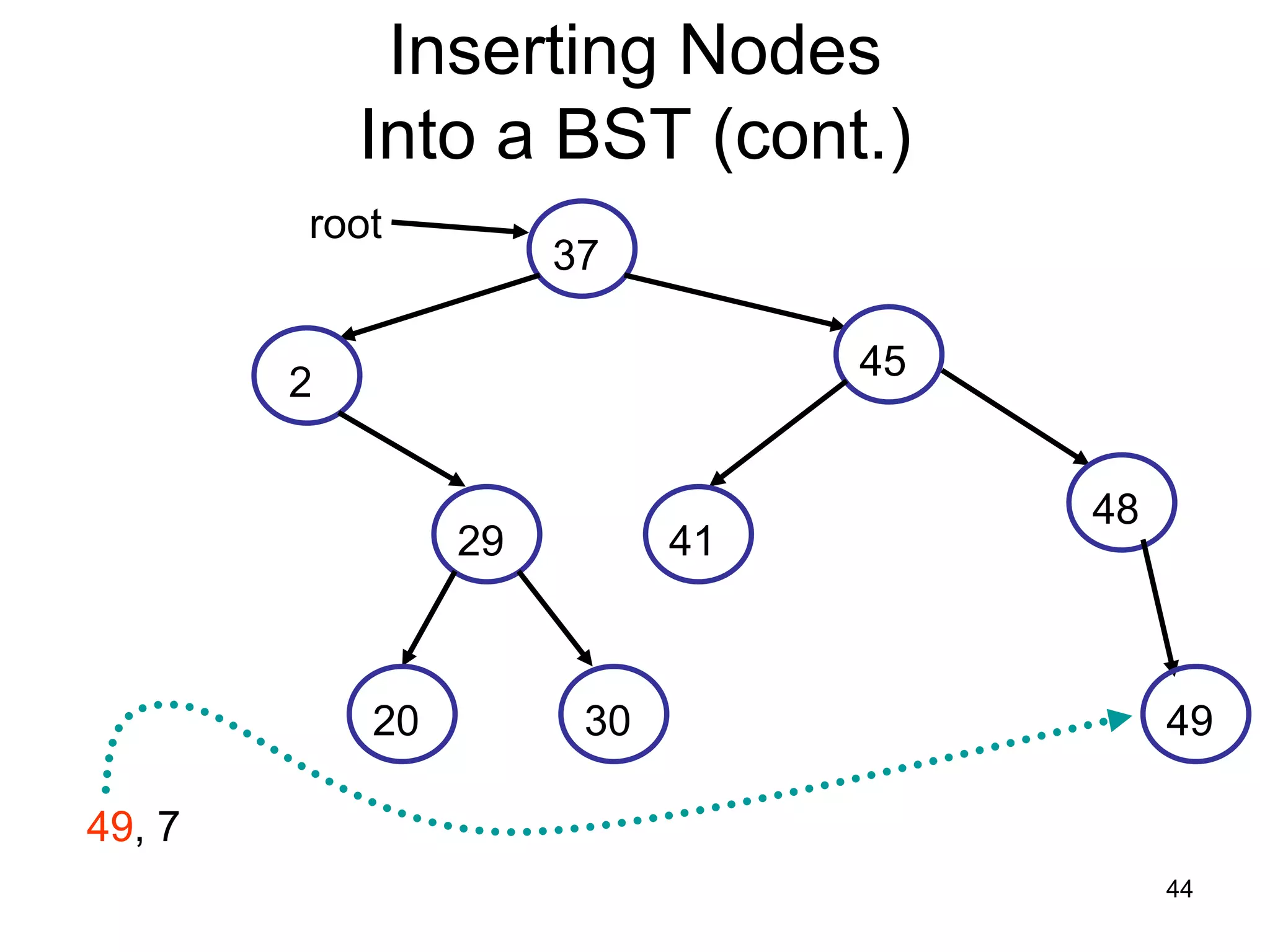
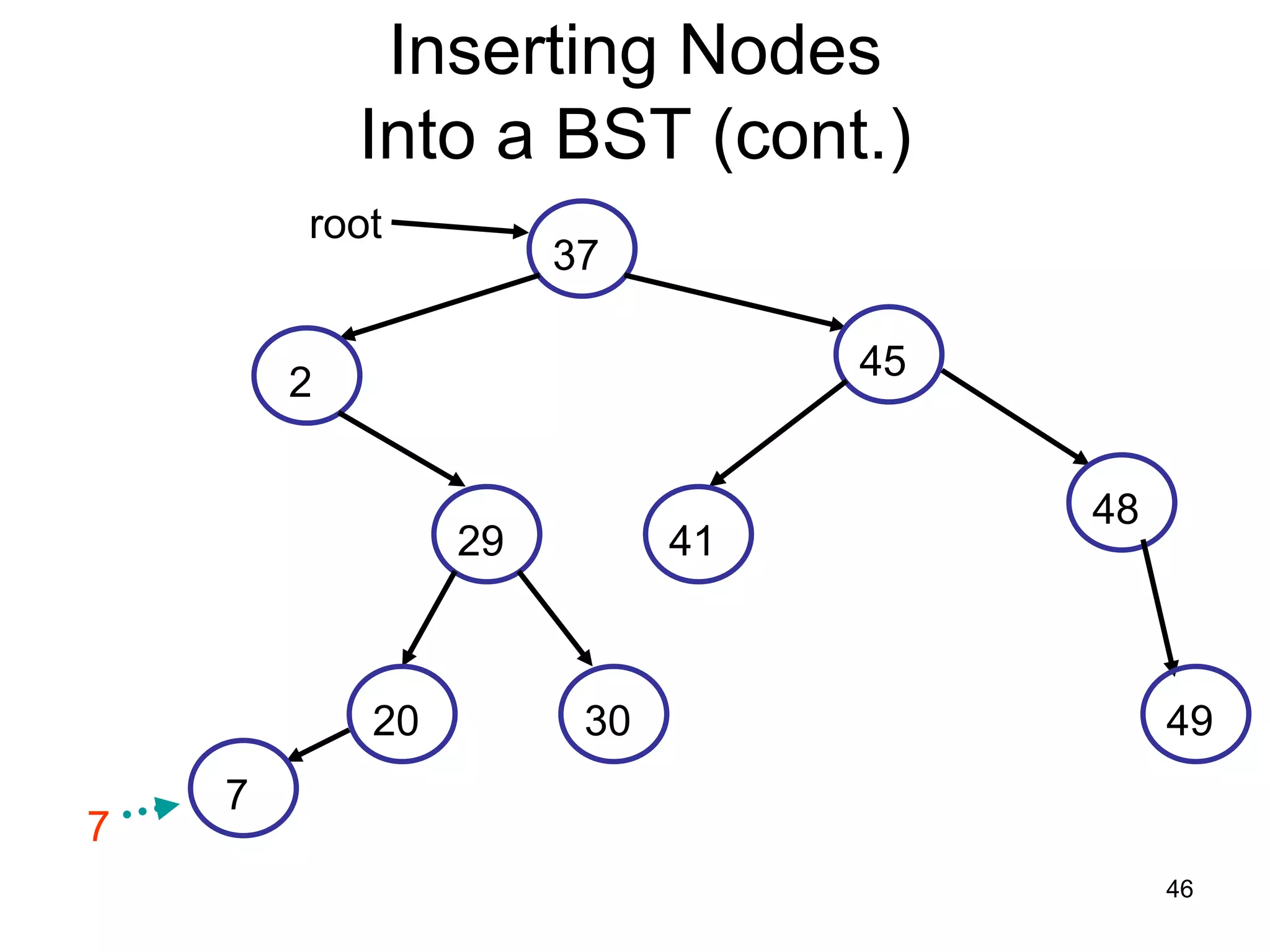
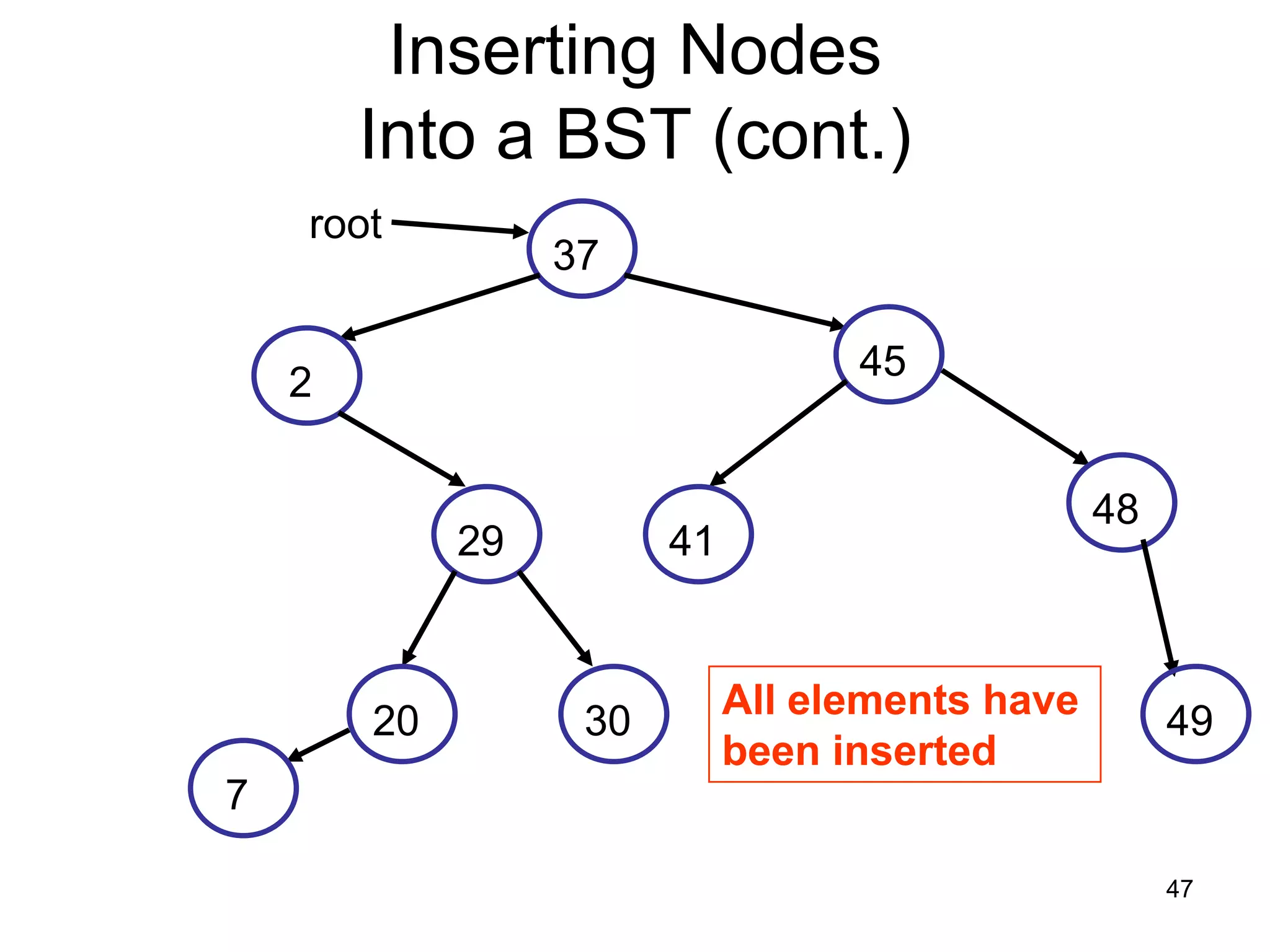
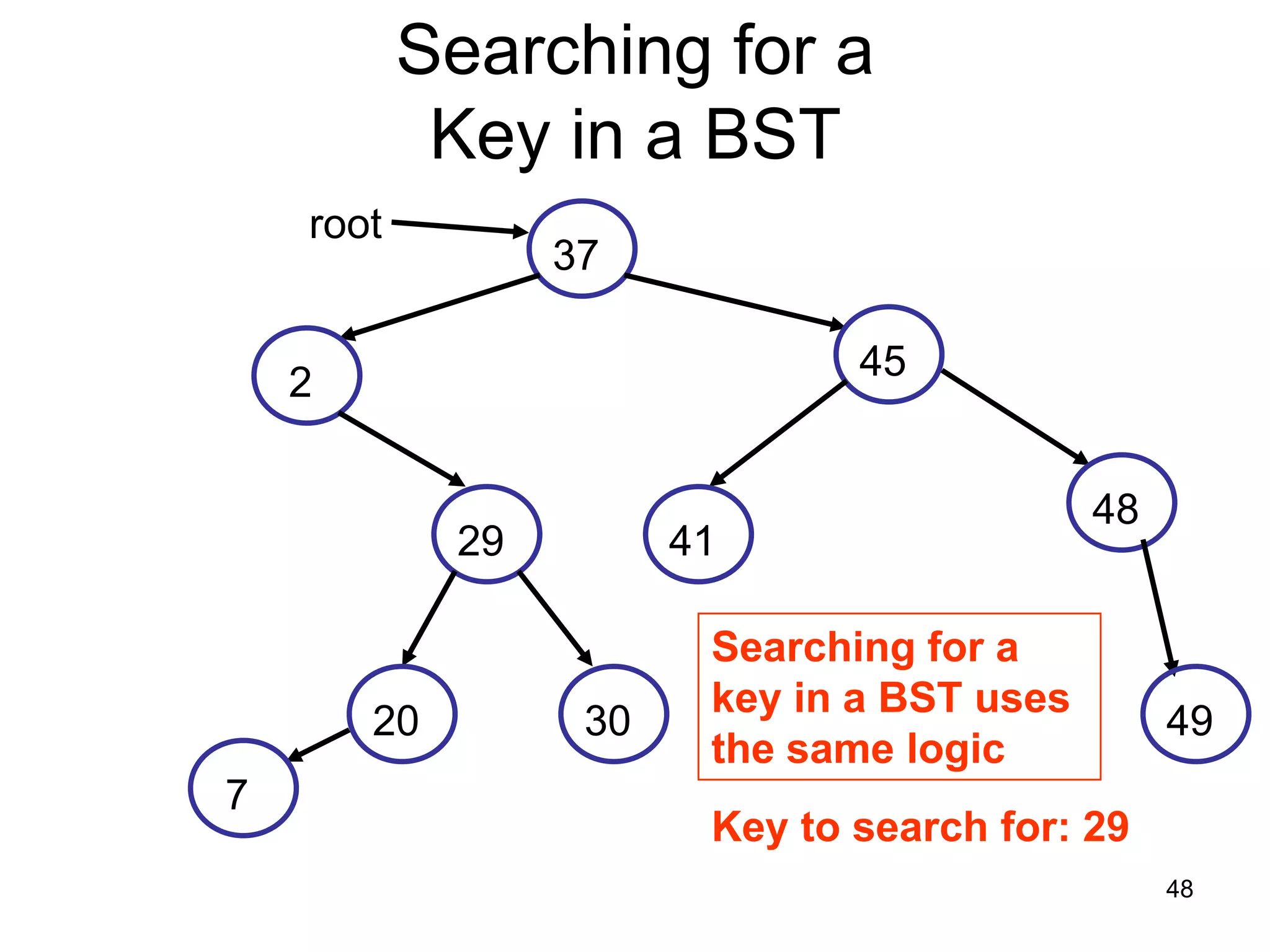
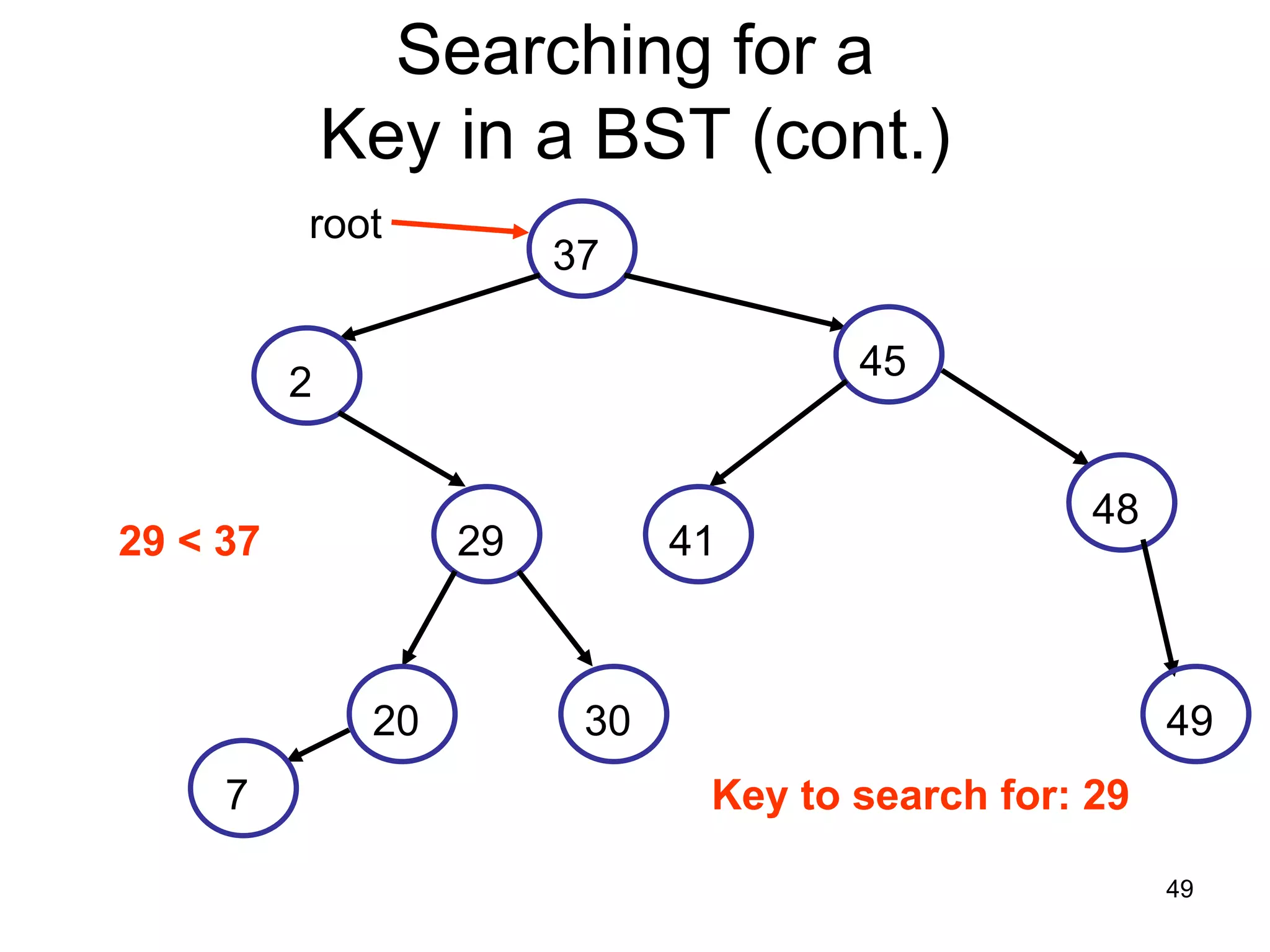
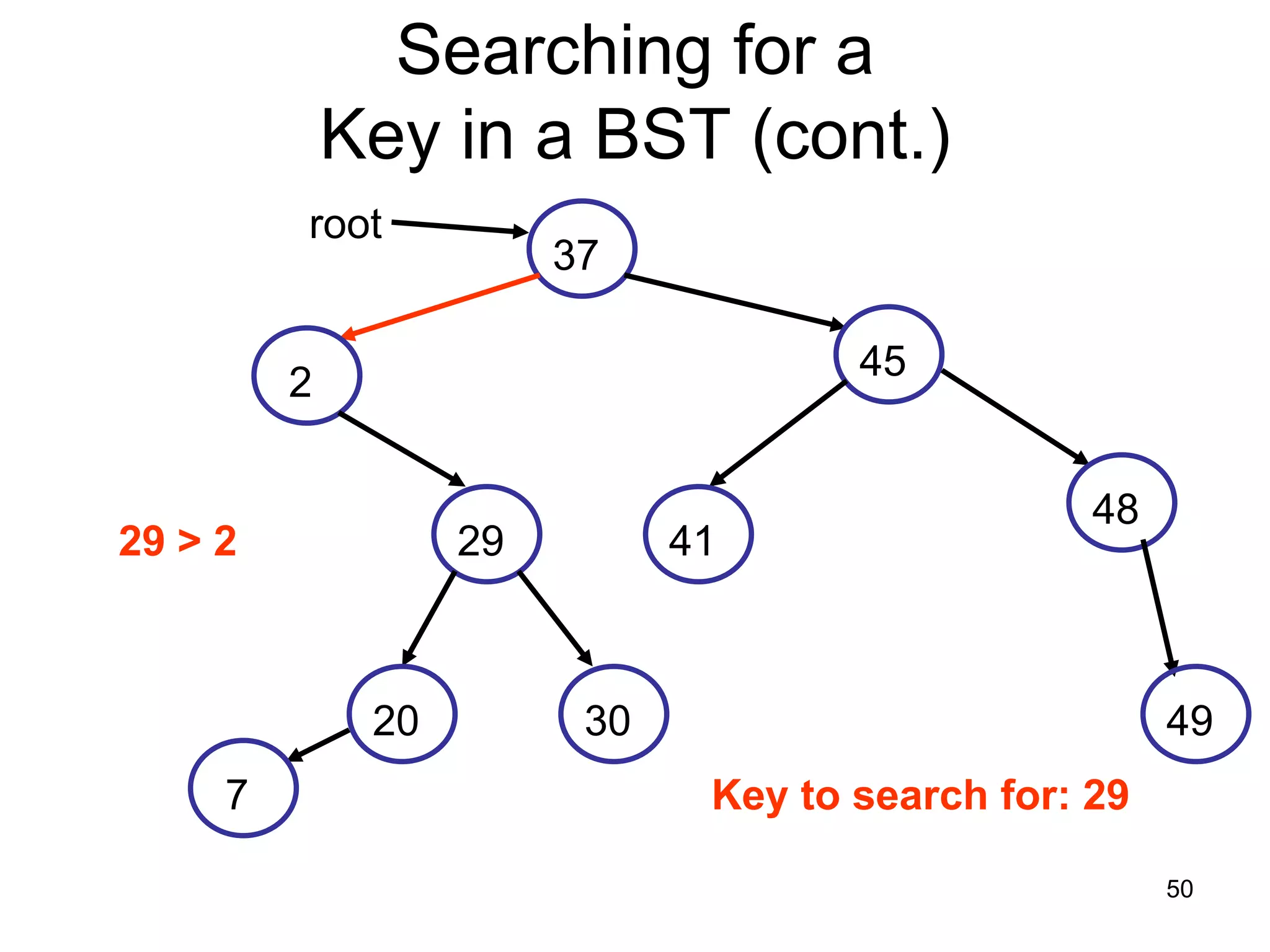
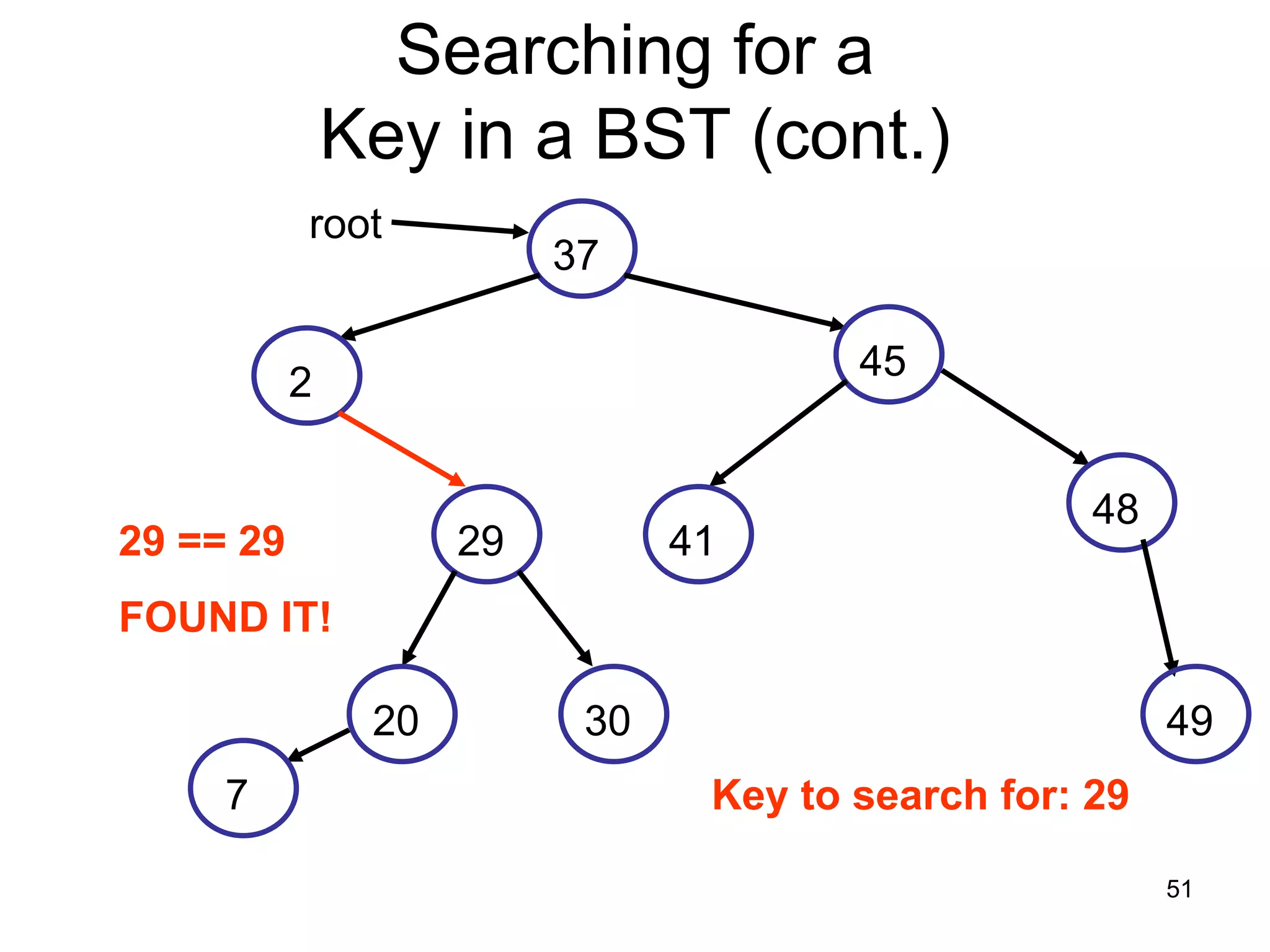
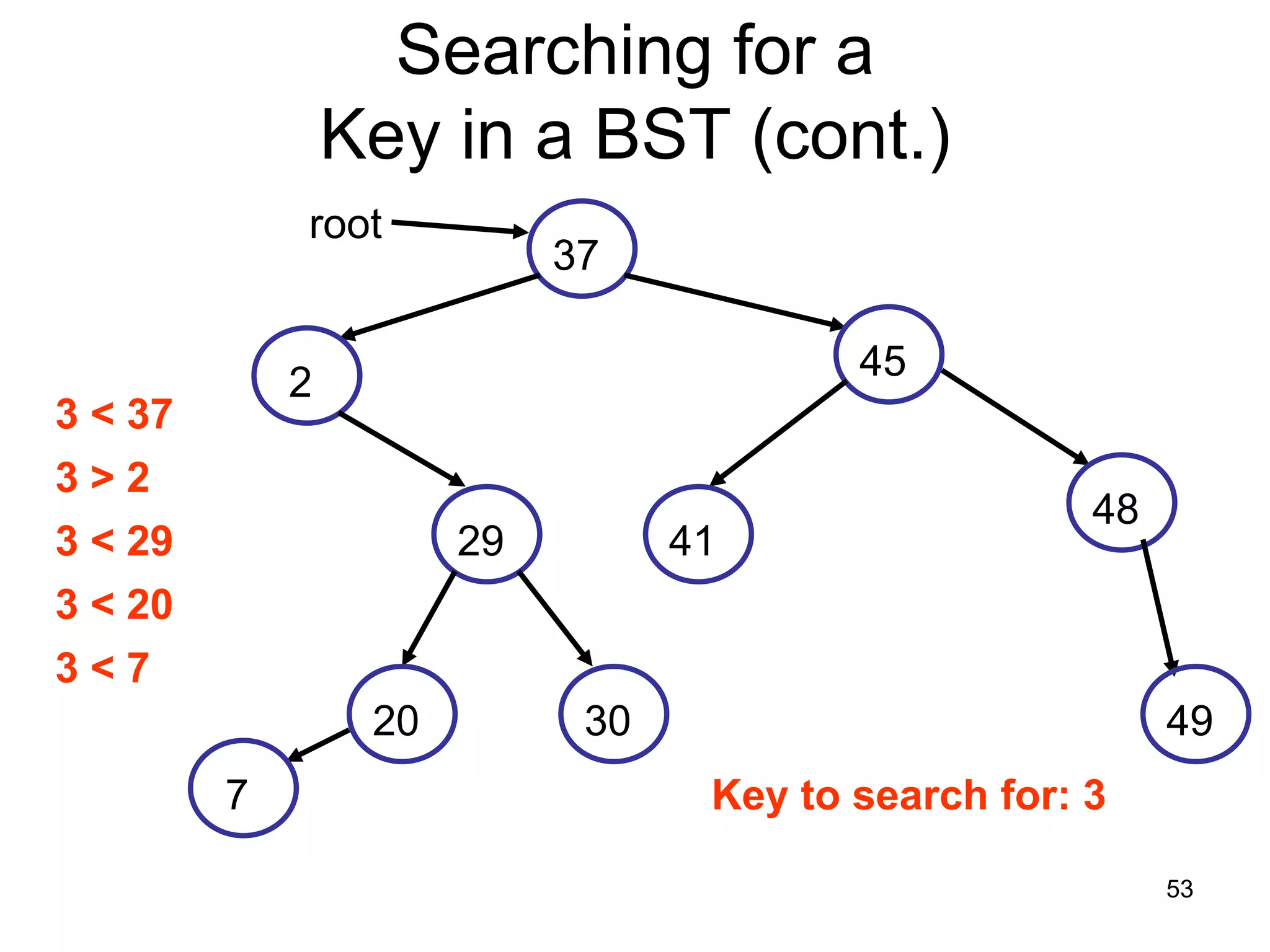
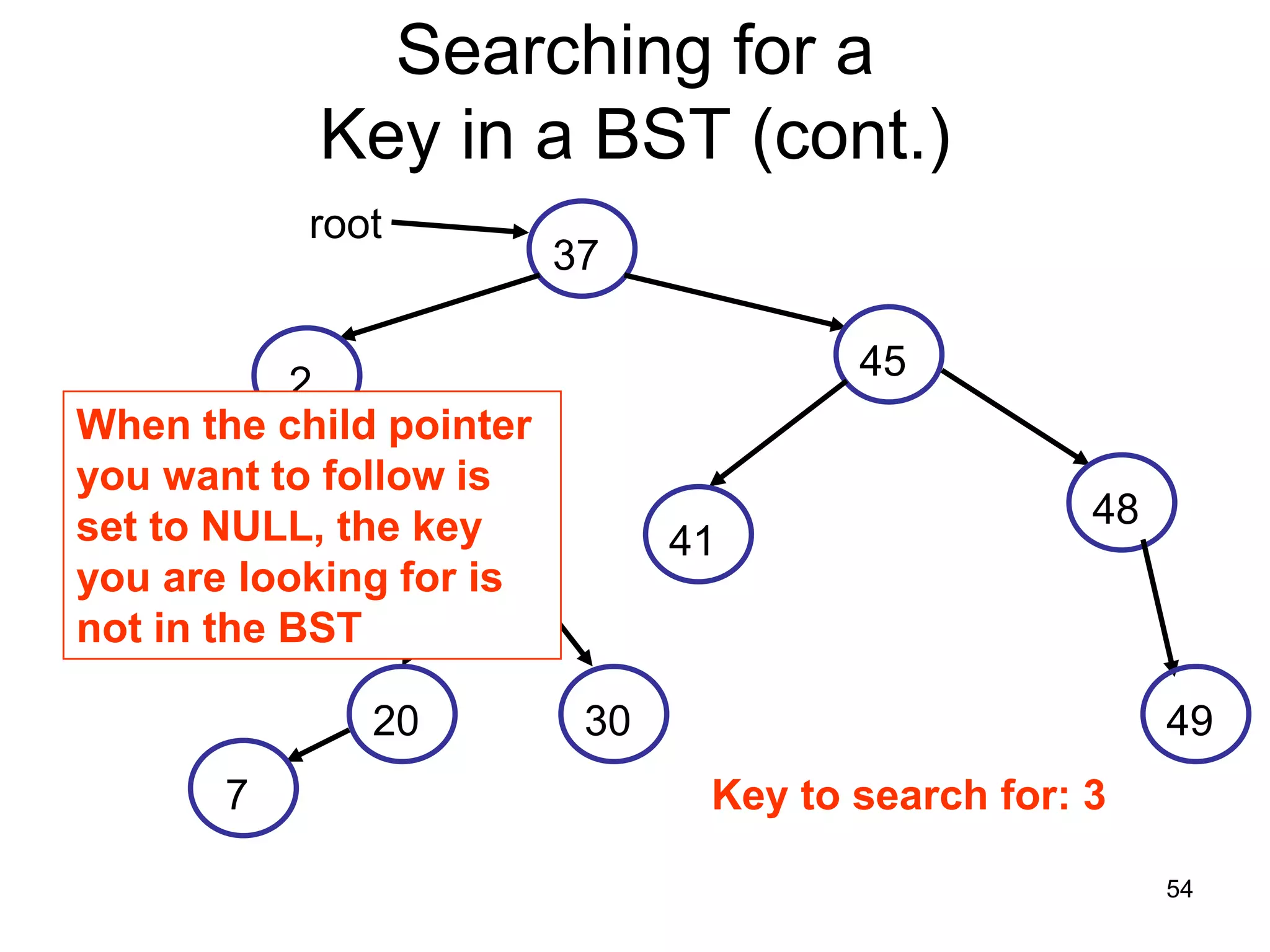
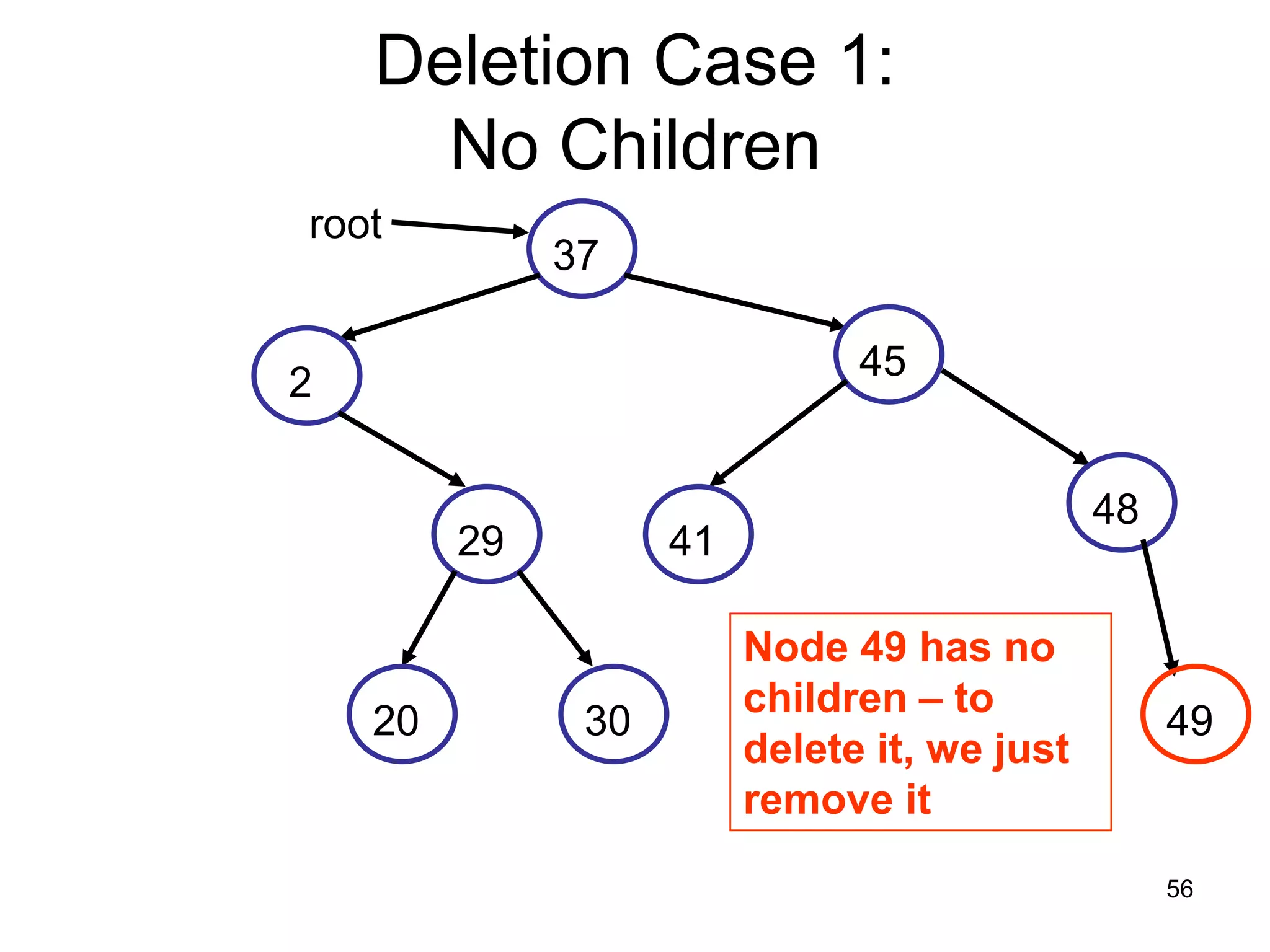
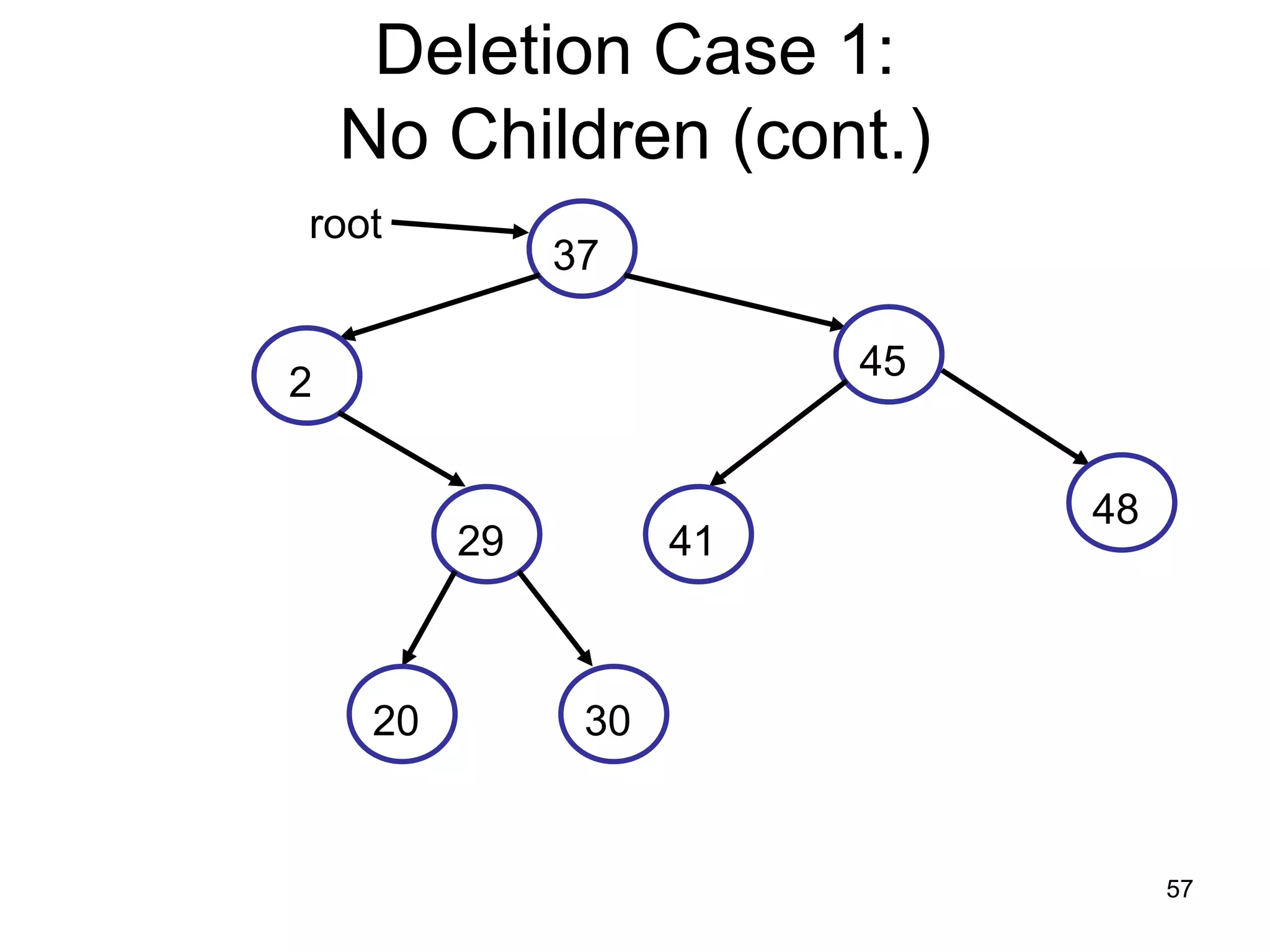
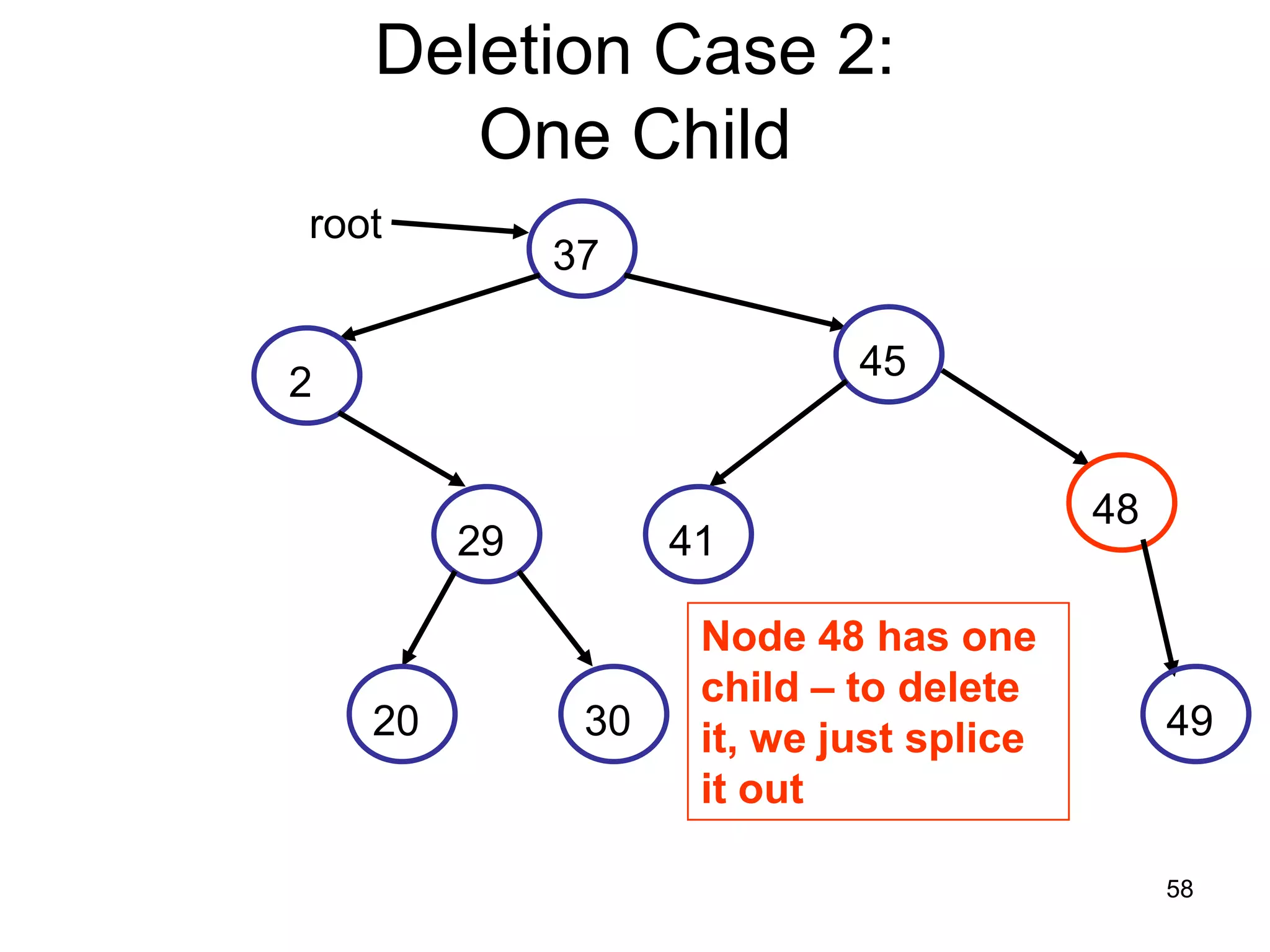
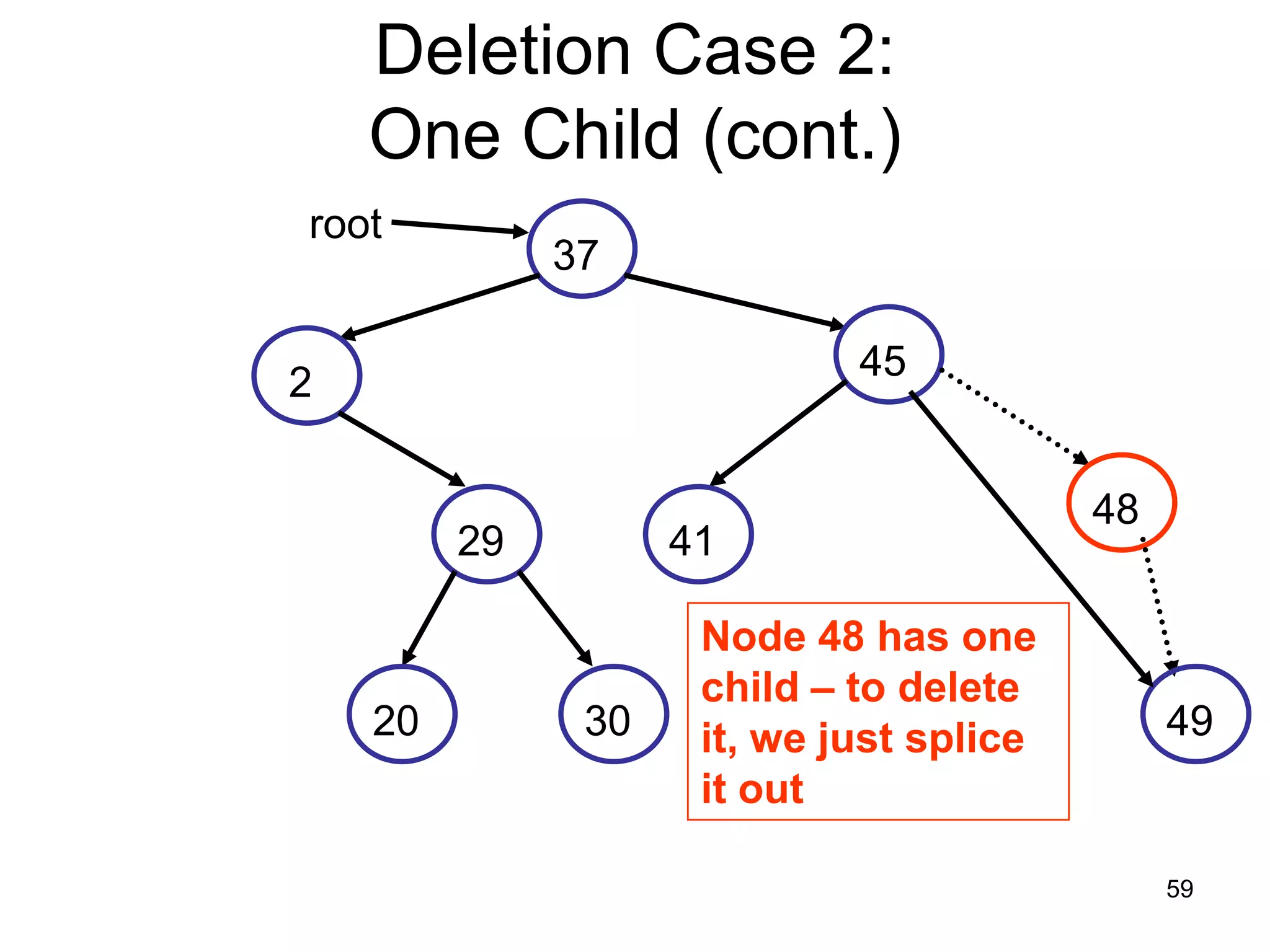
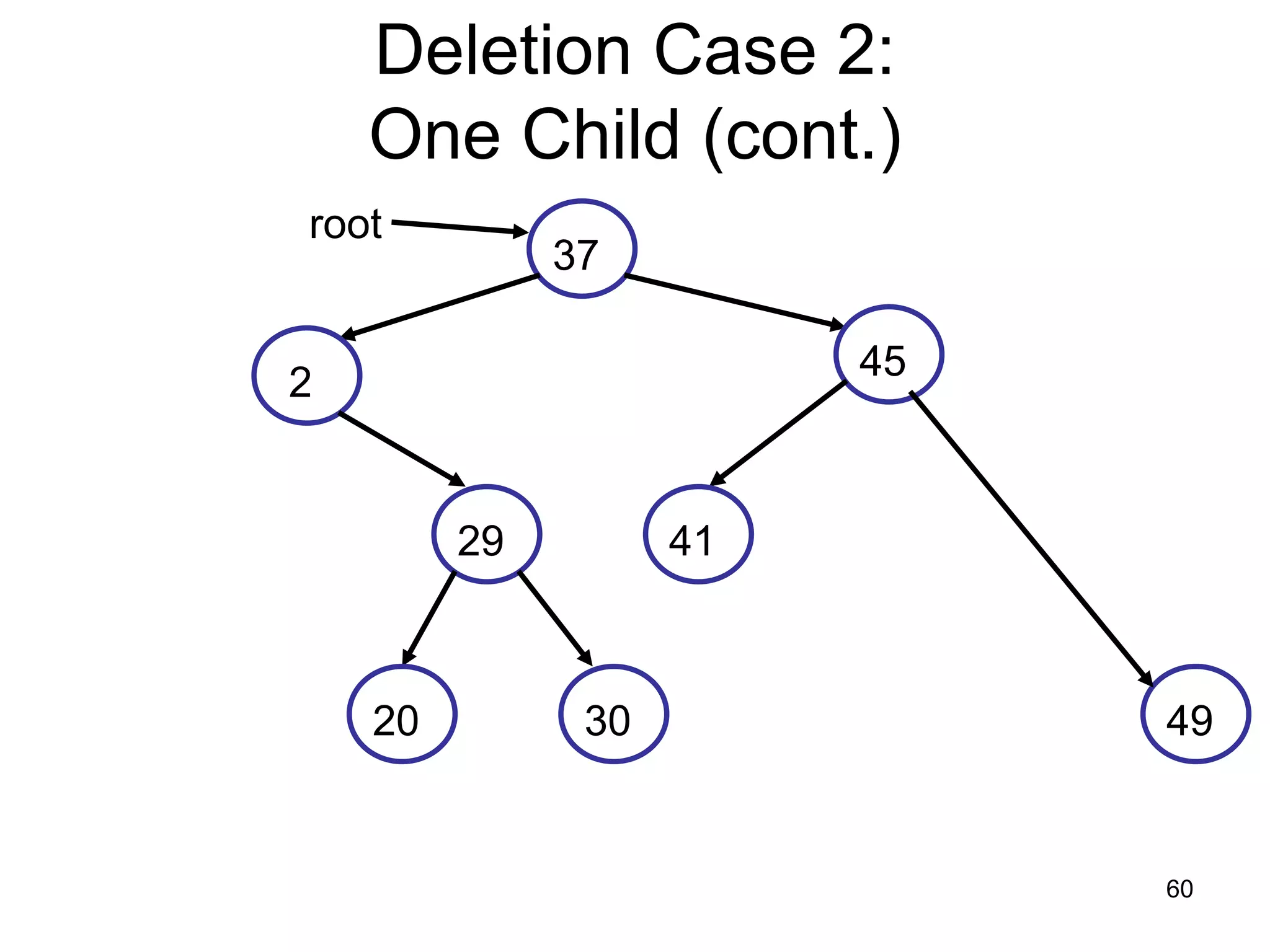
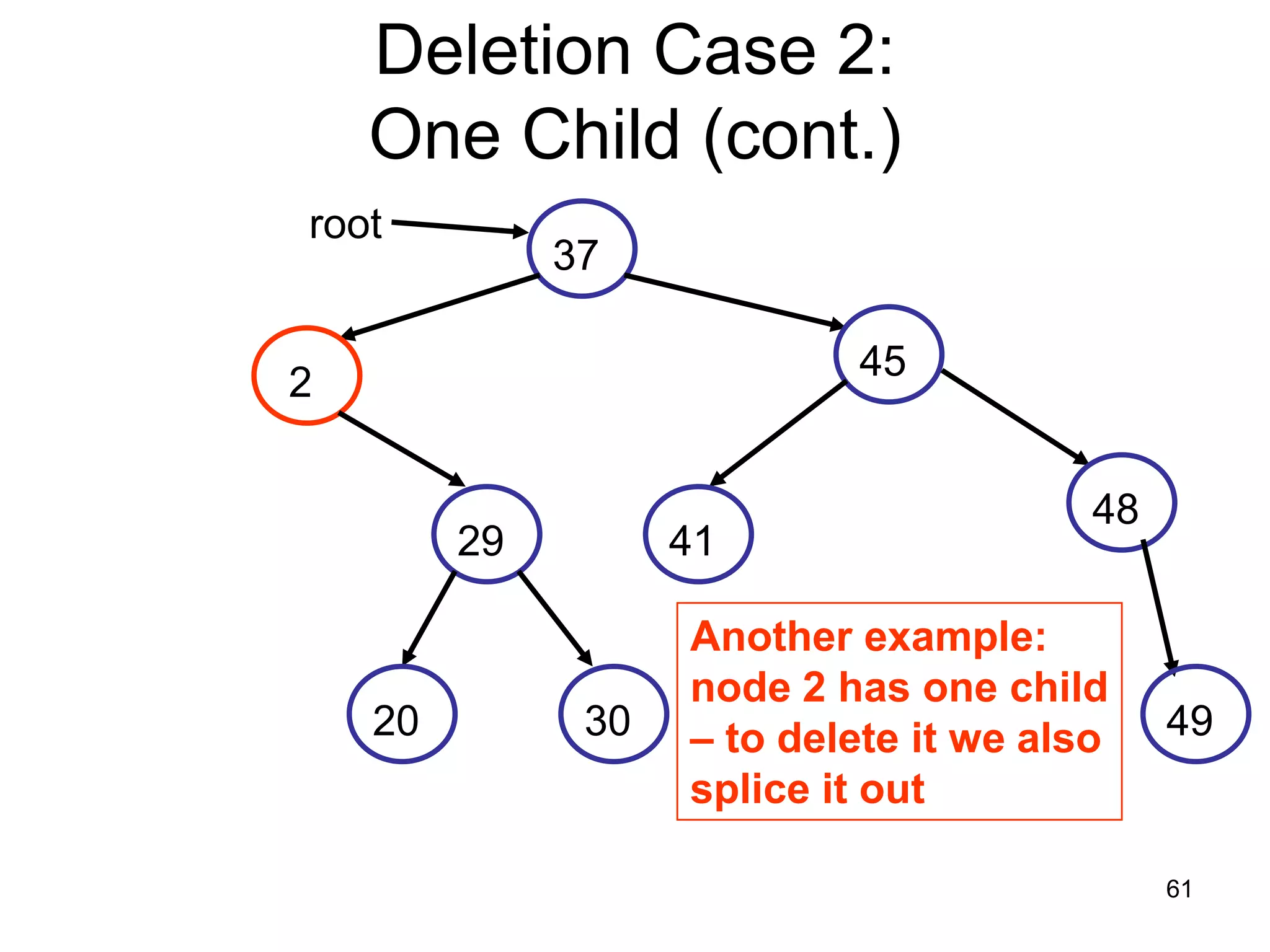
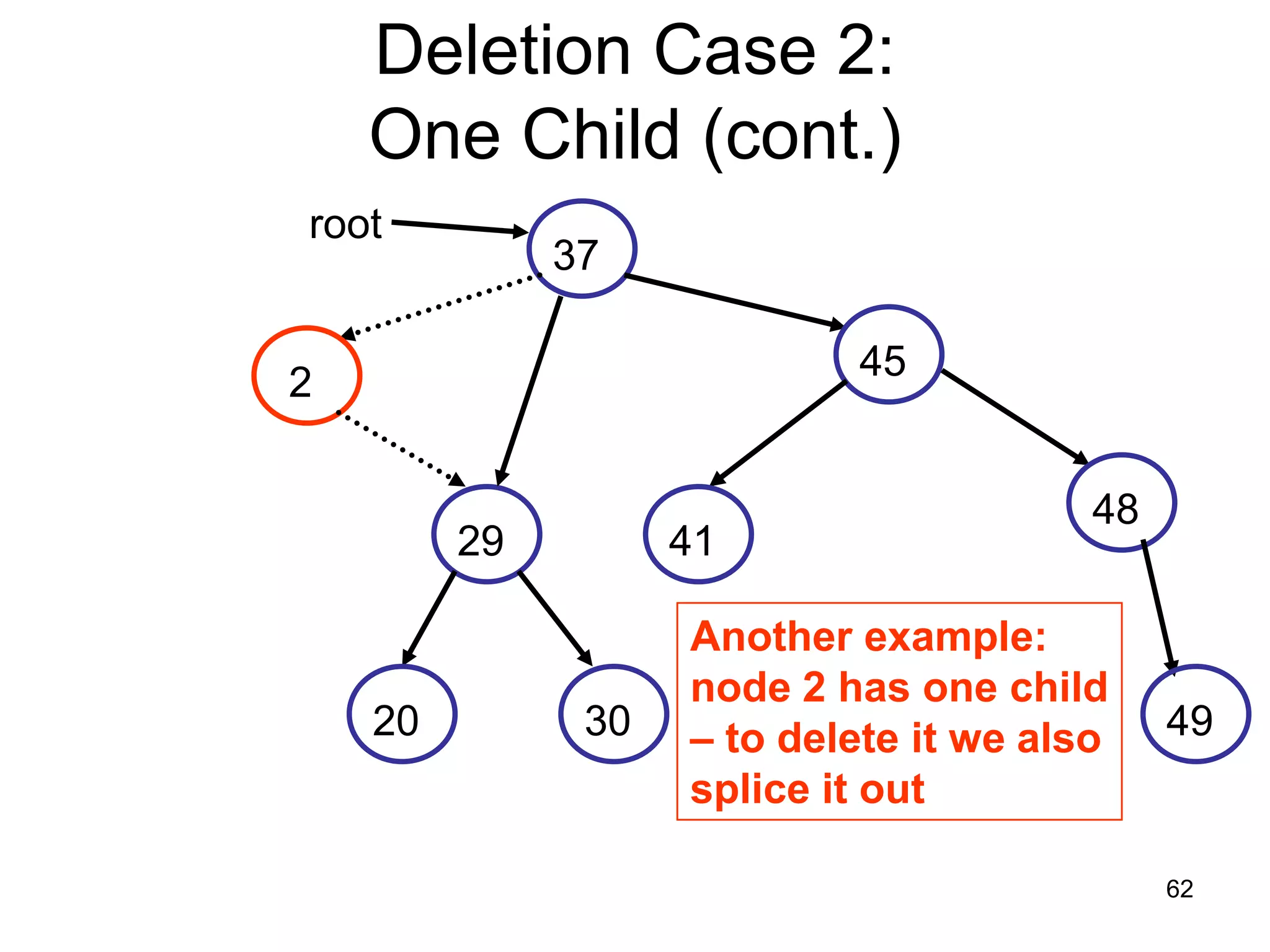
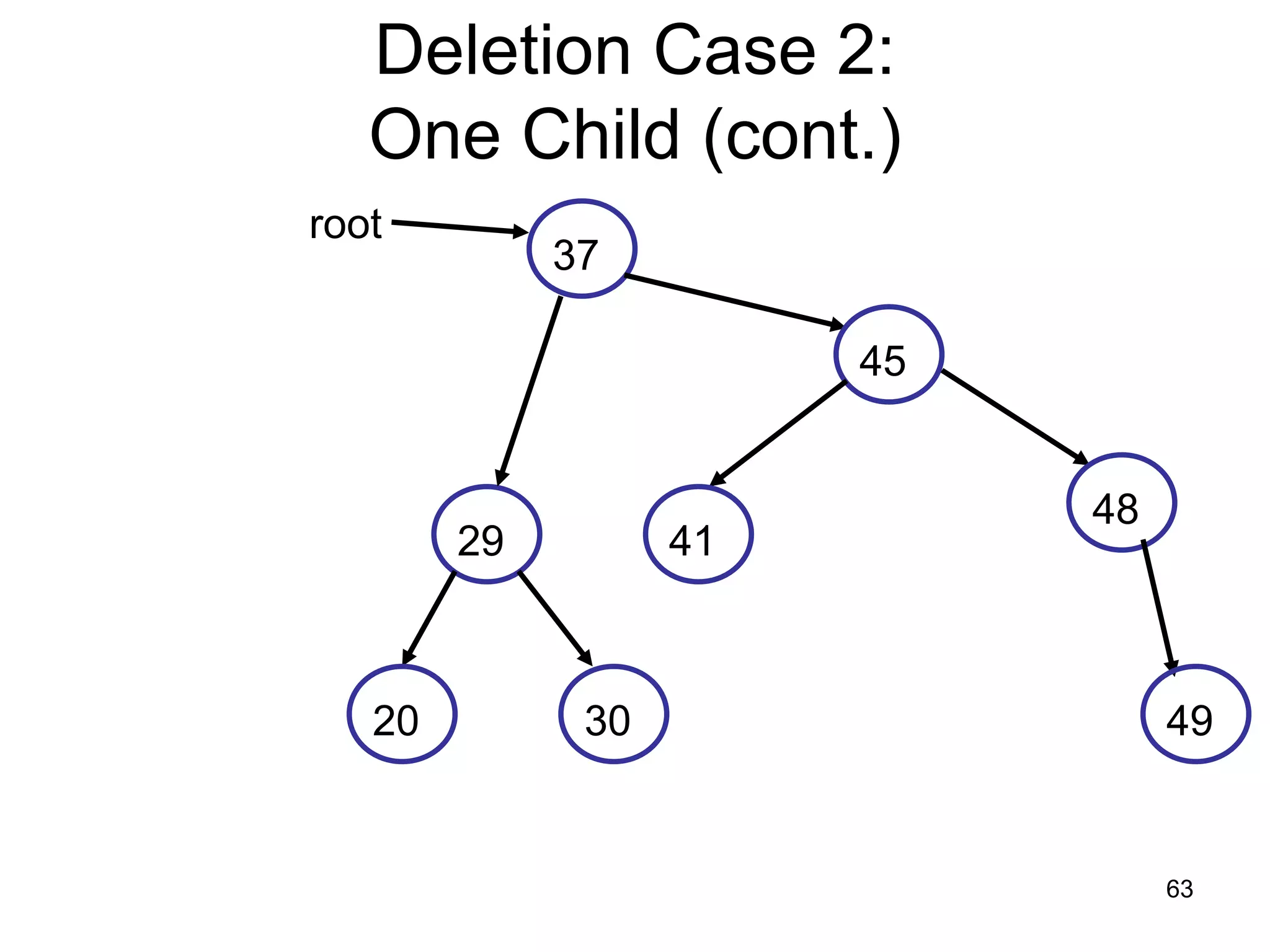
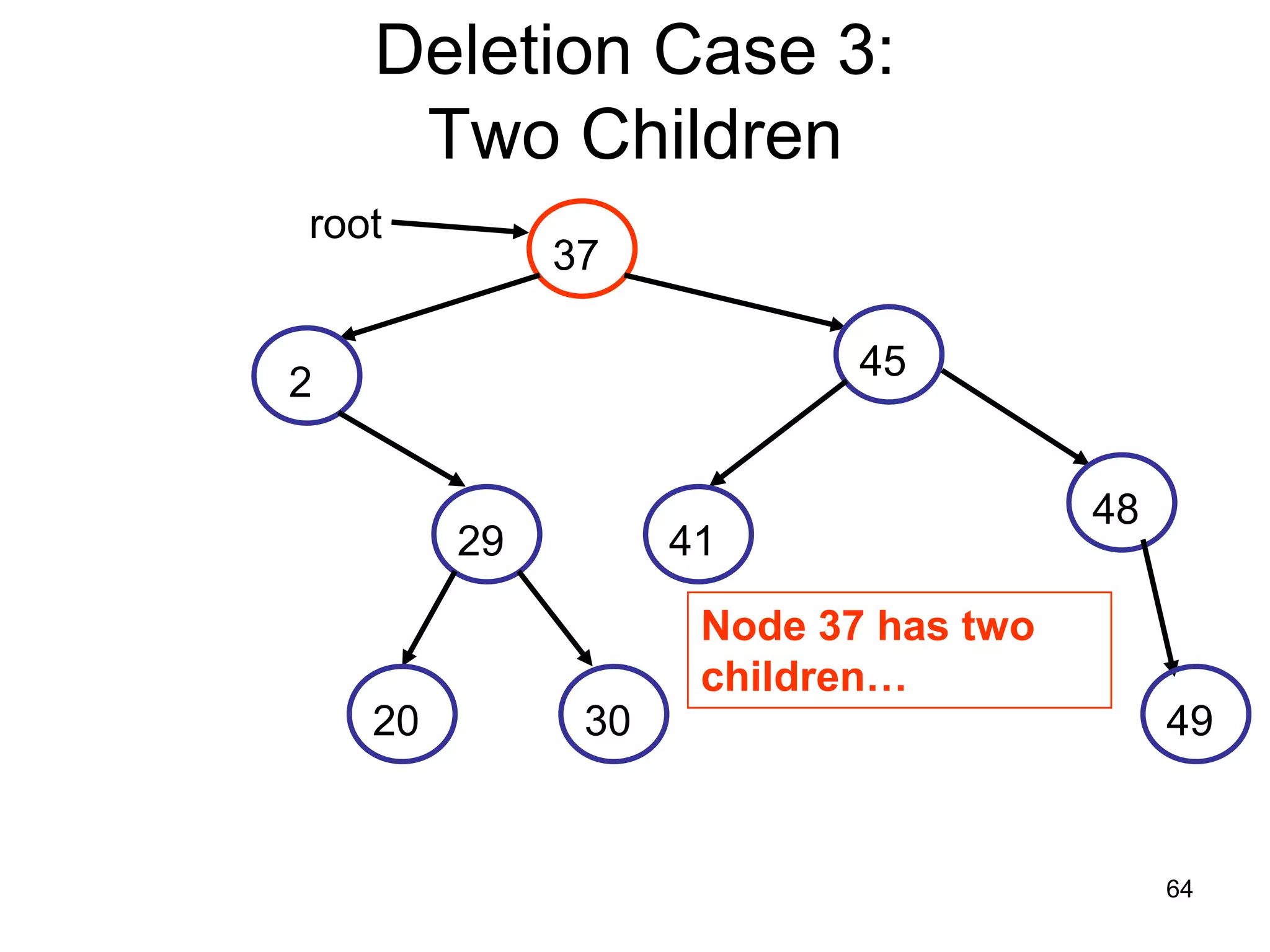
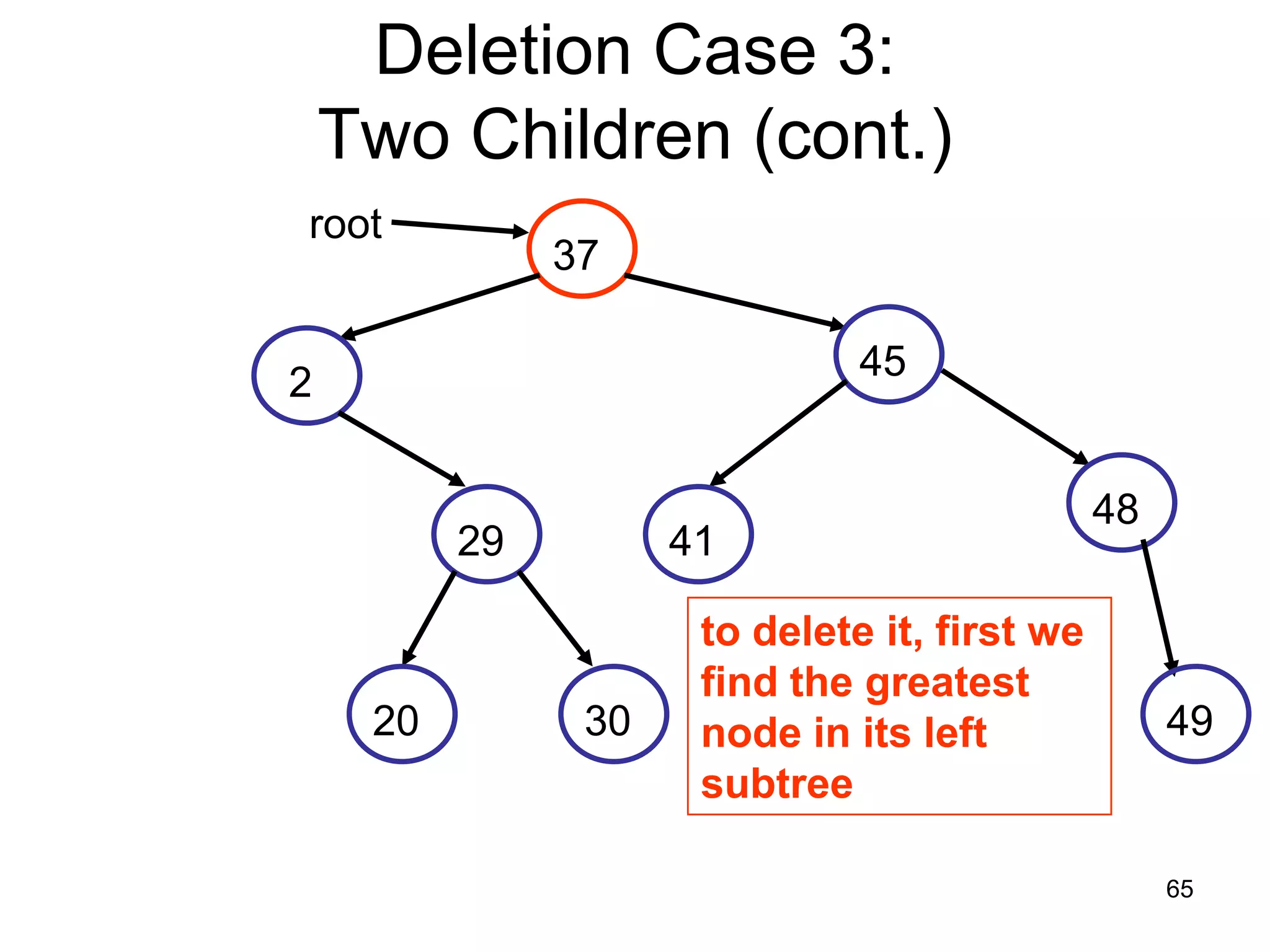
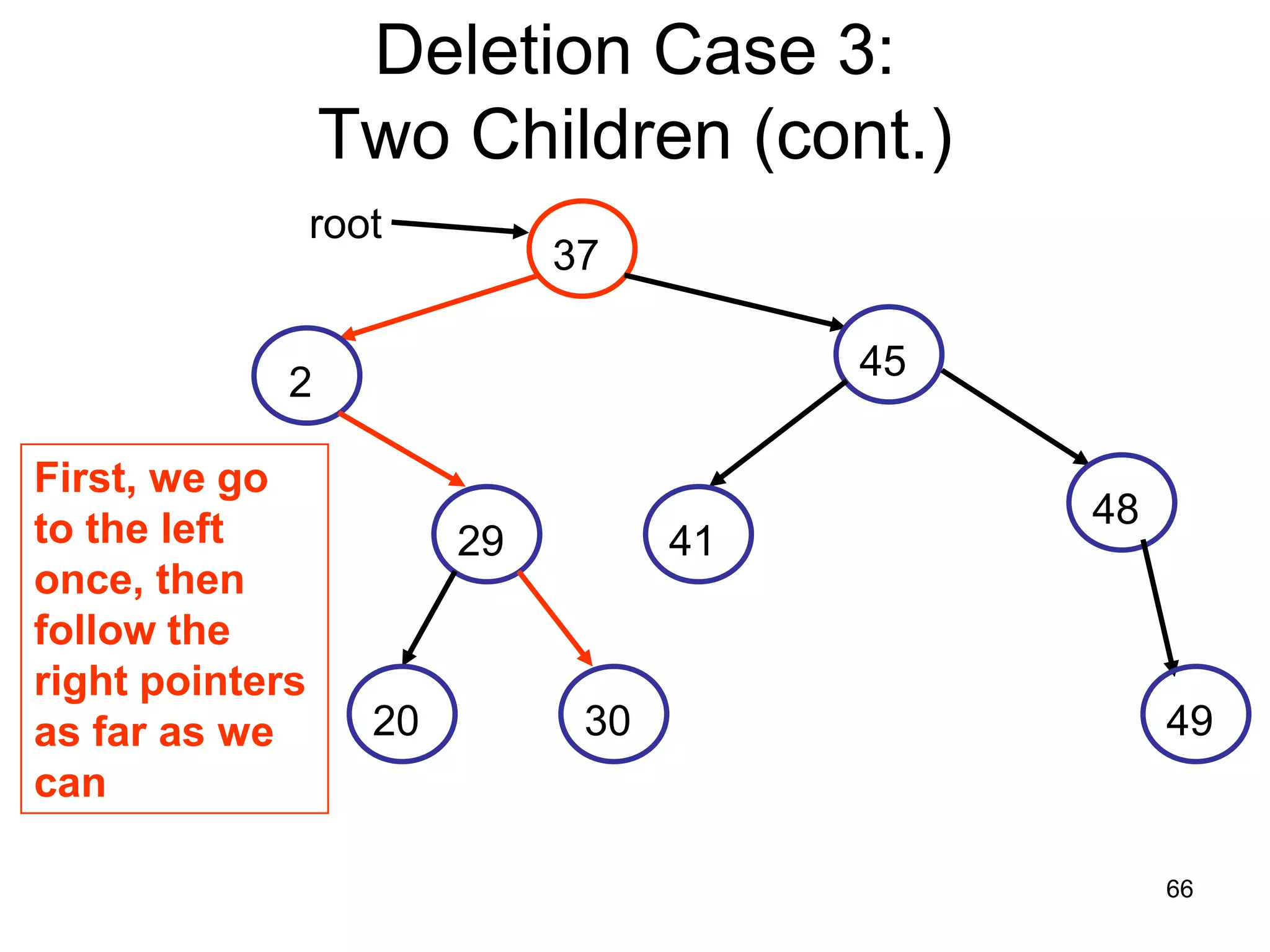
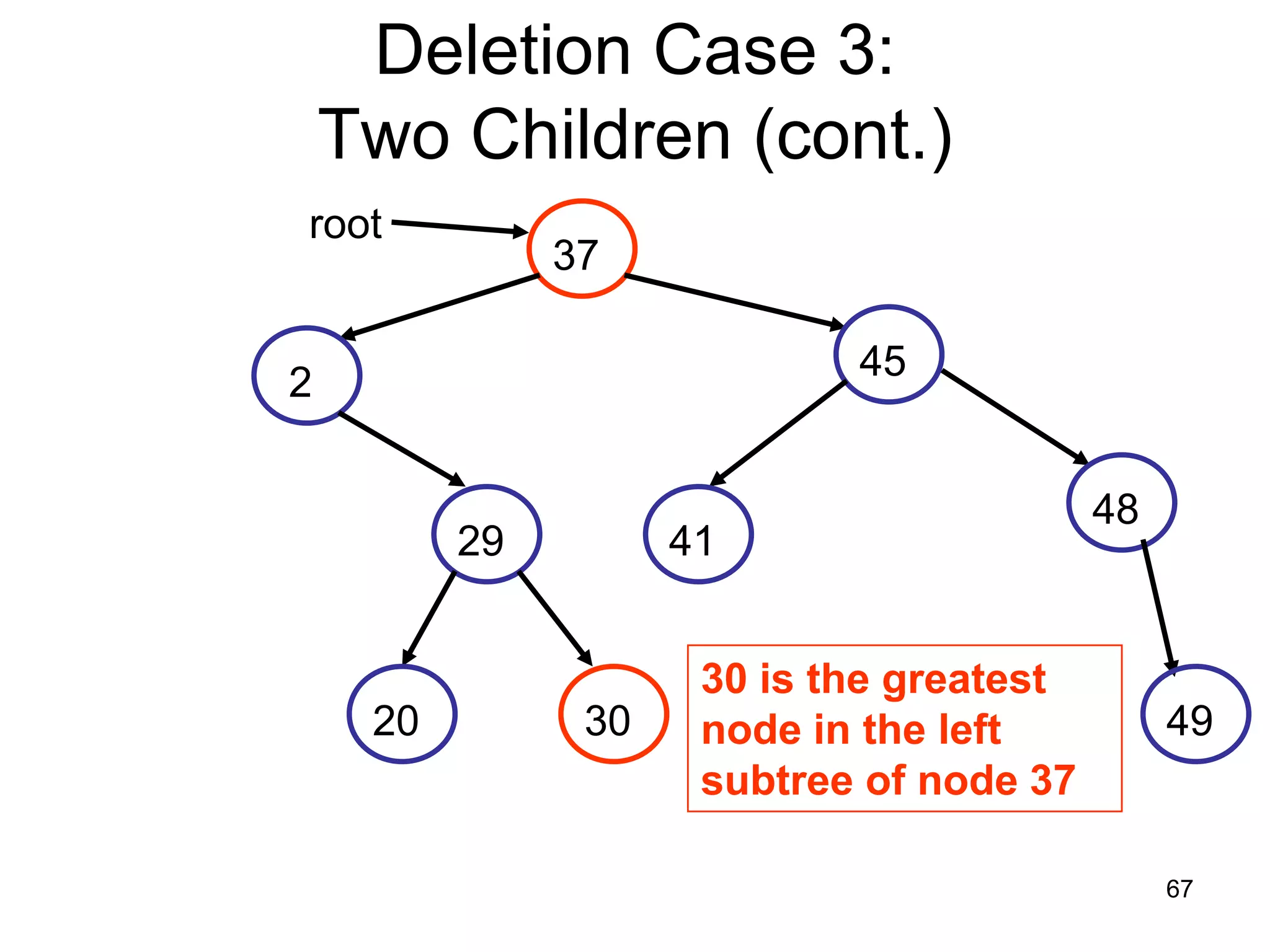
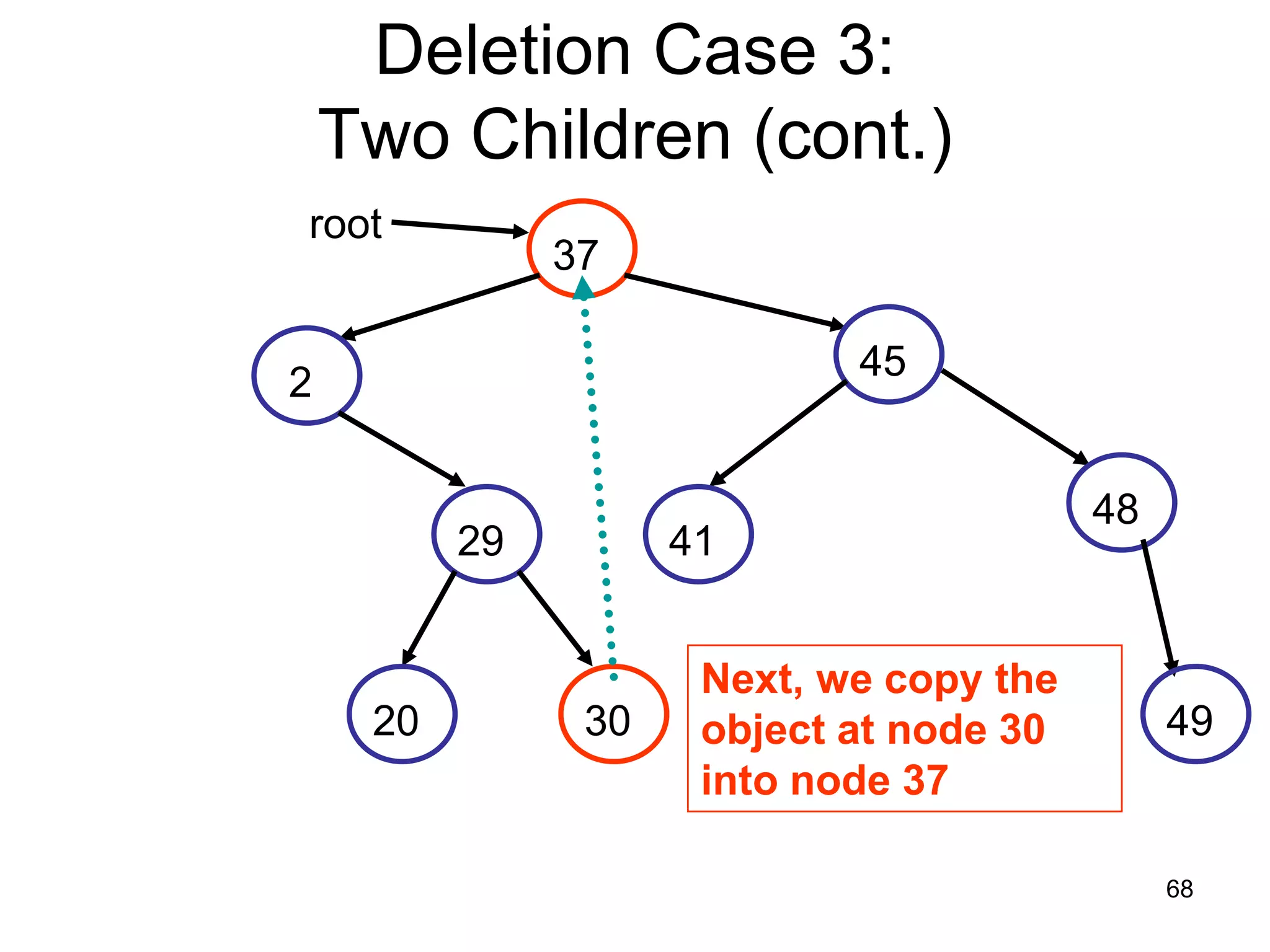
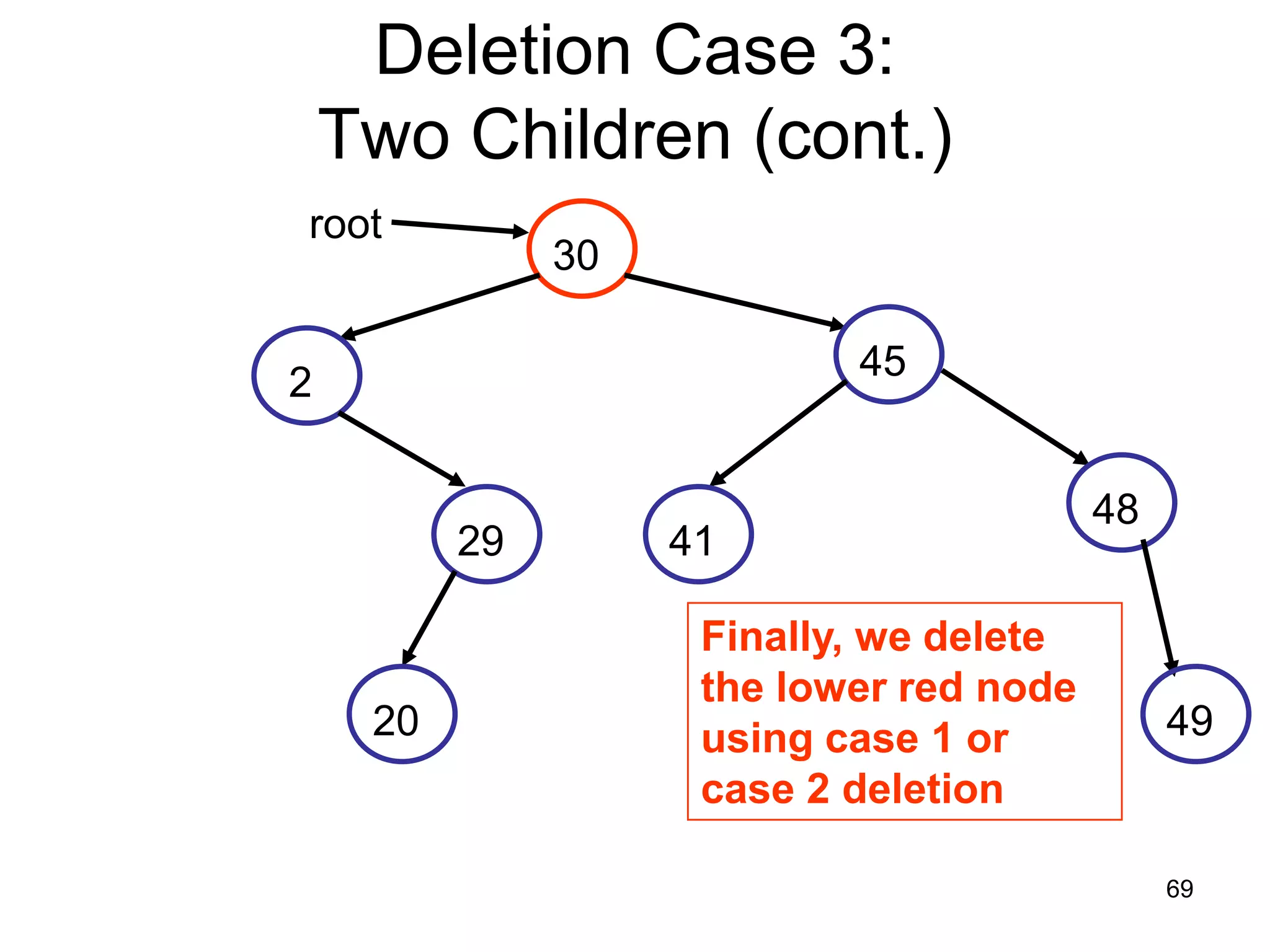
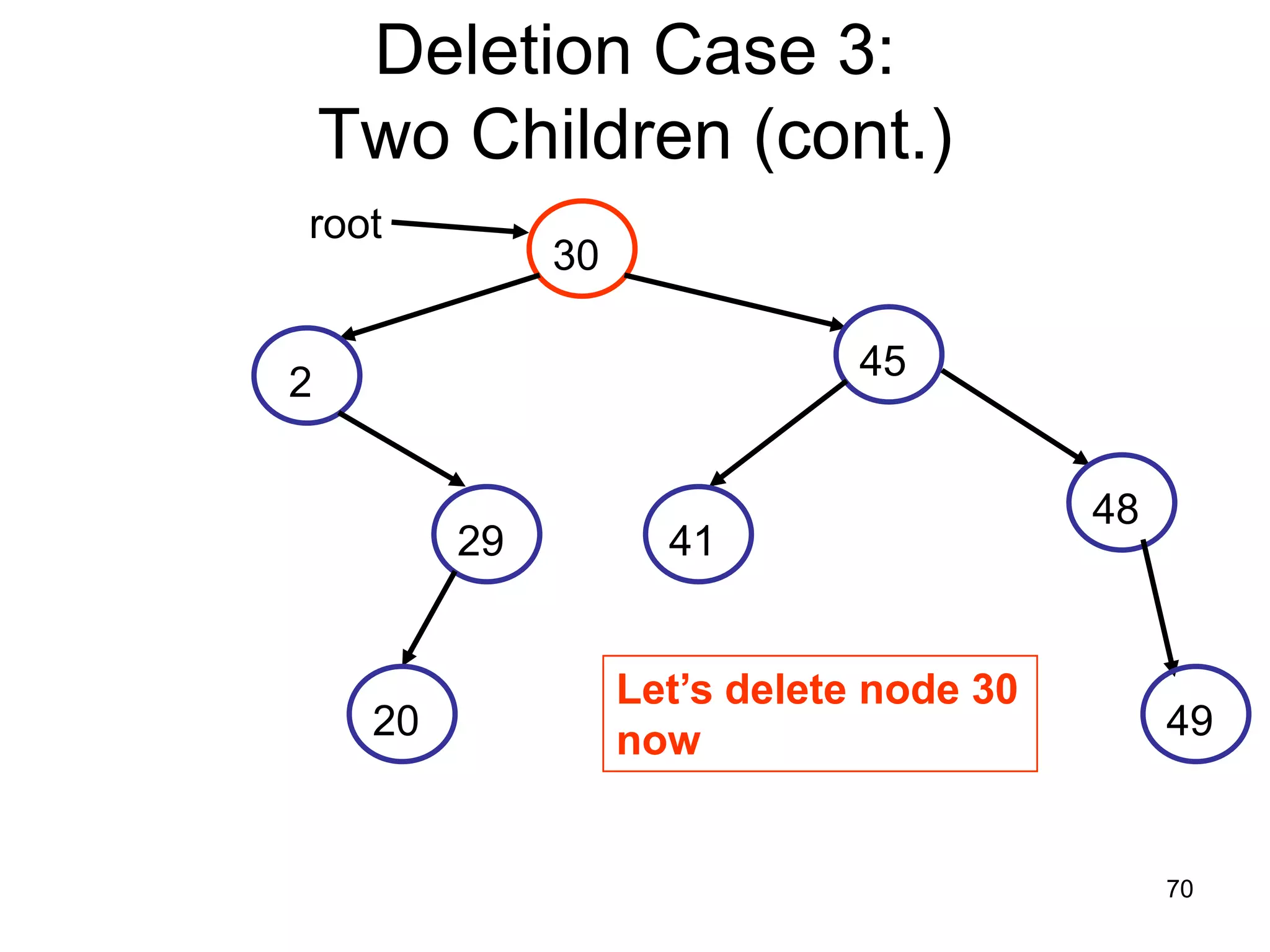
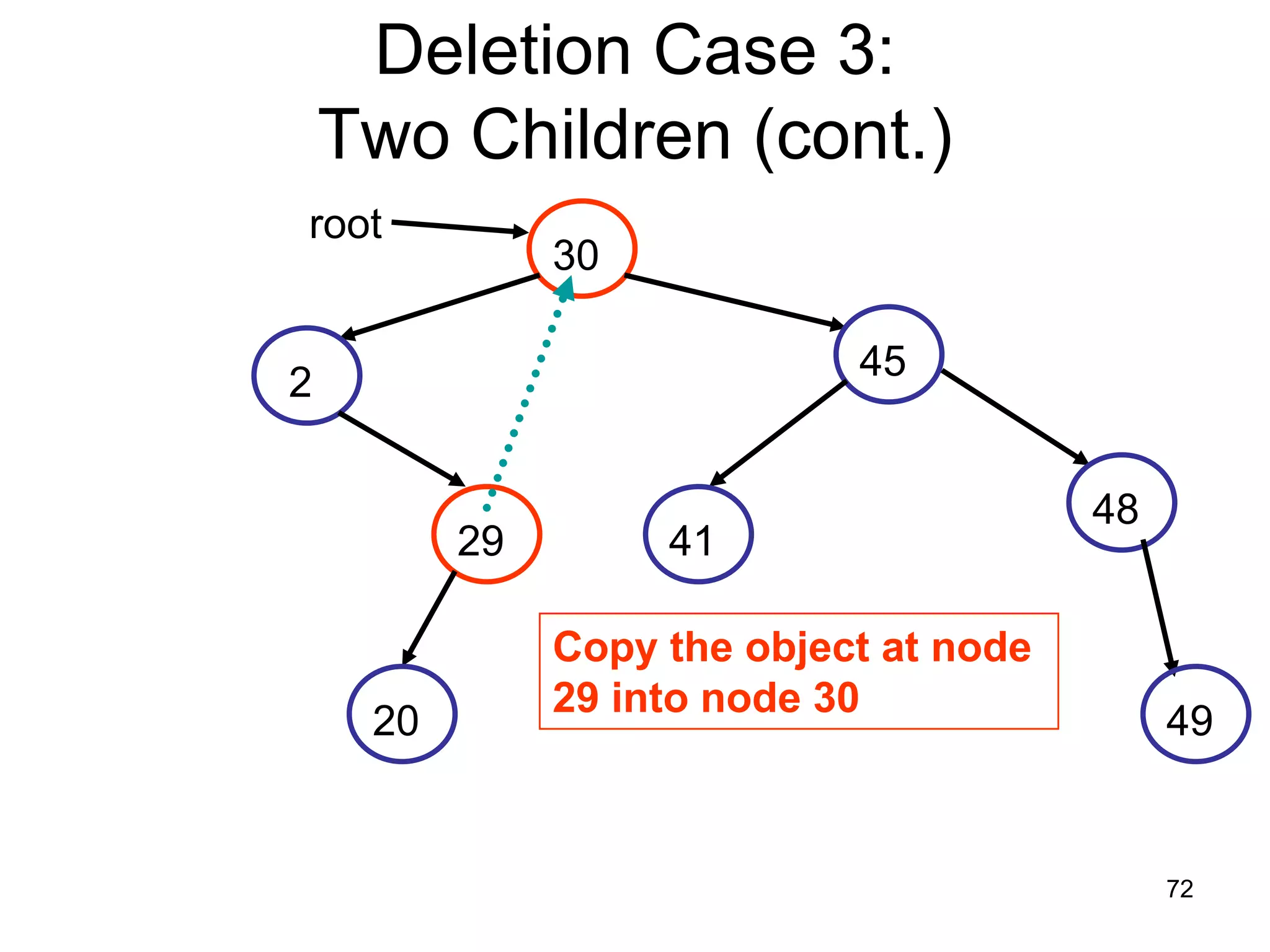
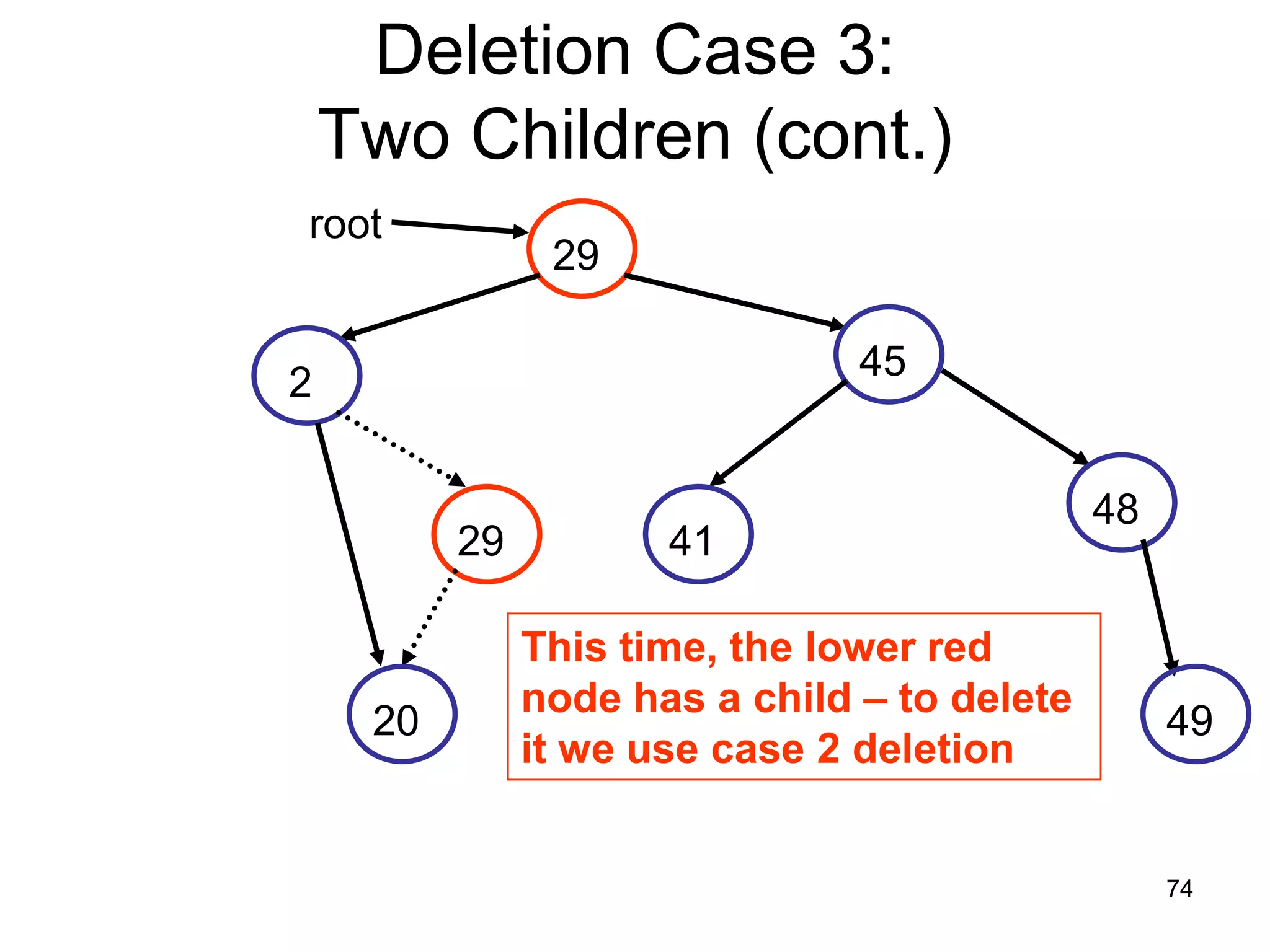
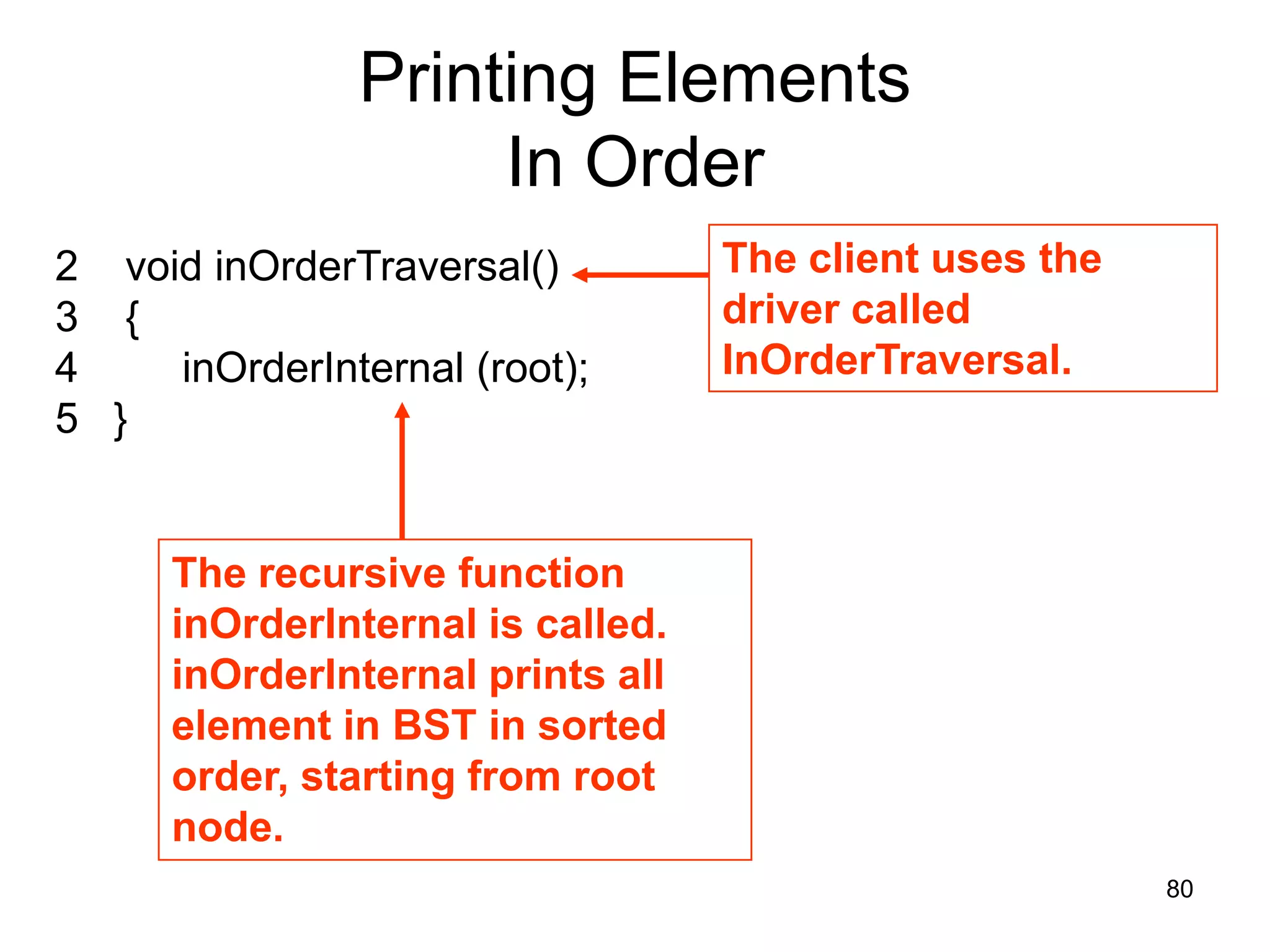
There are three key points about trees: 1) A tree is a set of linked nodes with a unique path from a root node to every other node. There can be no cycles in a tree. 2) Binary trees restrict nodes to having at most two children. Binary search trees order nodes so that all left children are less than the parent and all right children are greater. 3) Insertion into a binary search tree involves recursively comparing the key of the node to be inserted with the key of each parent node until a suitable position is found.