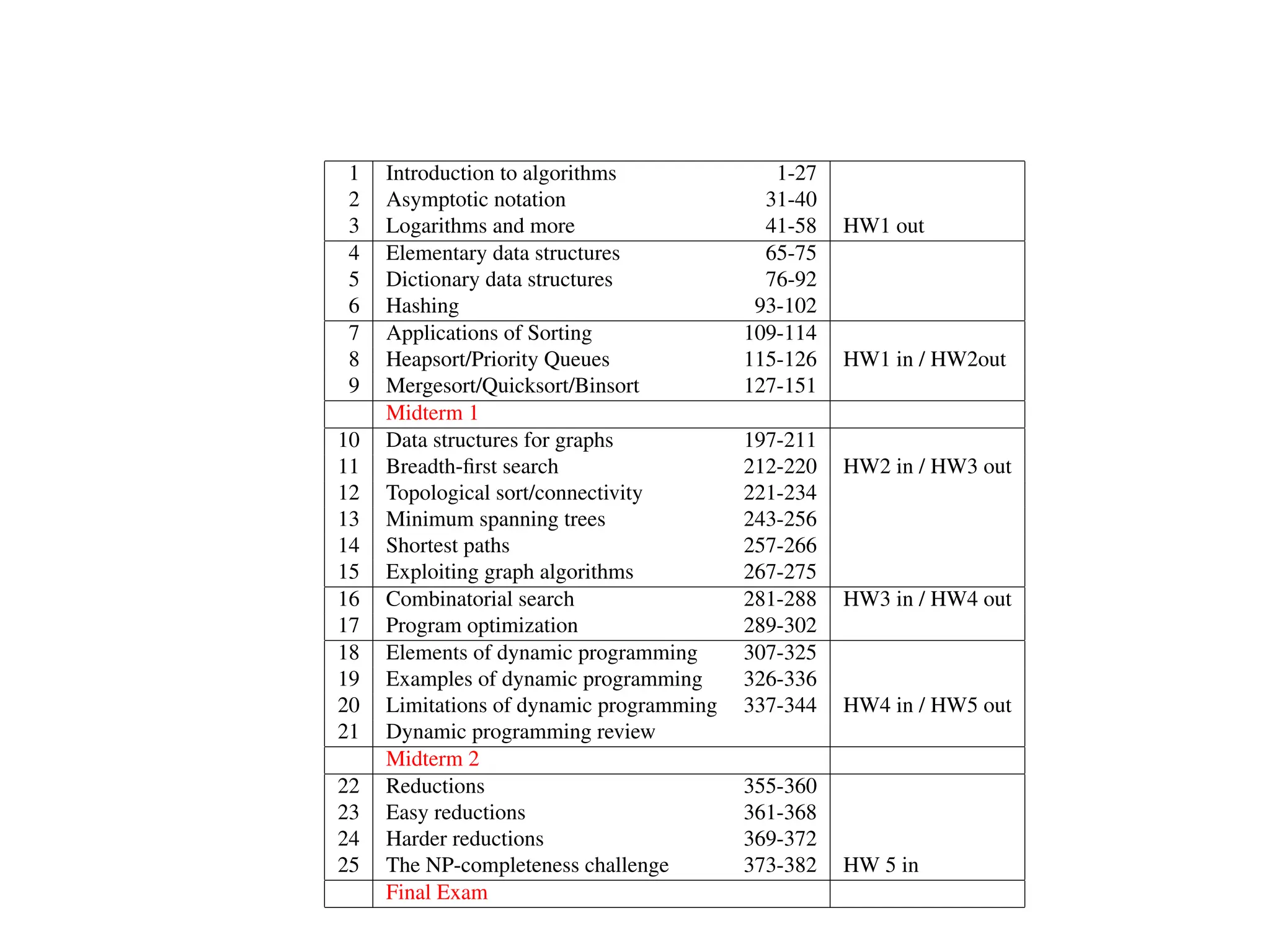
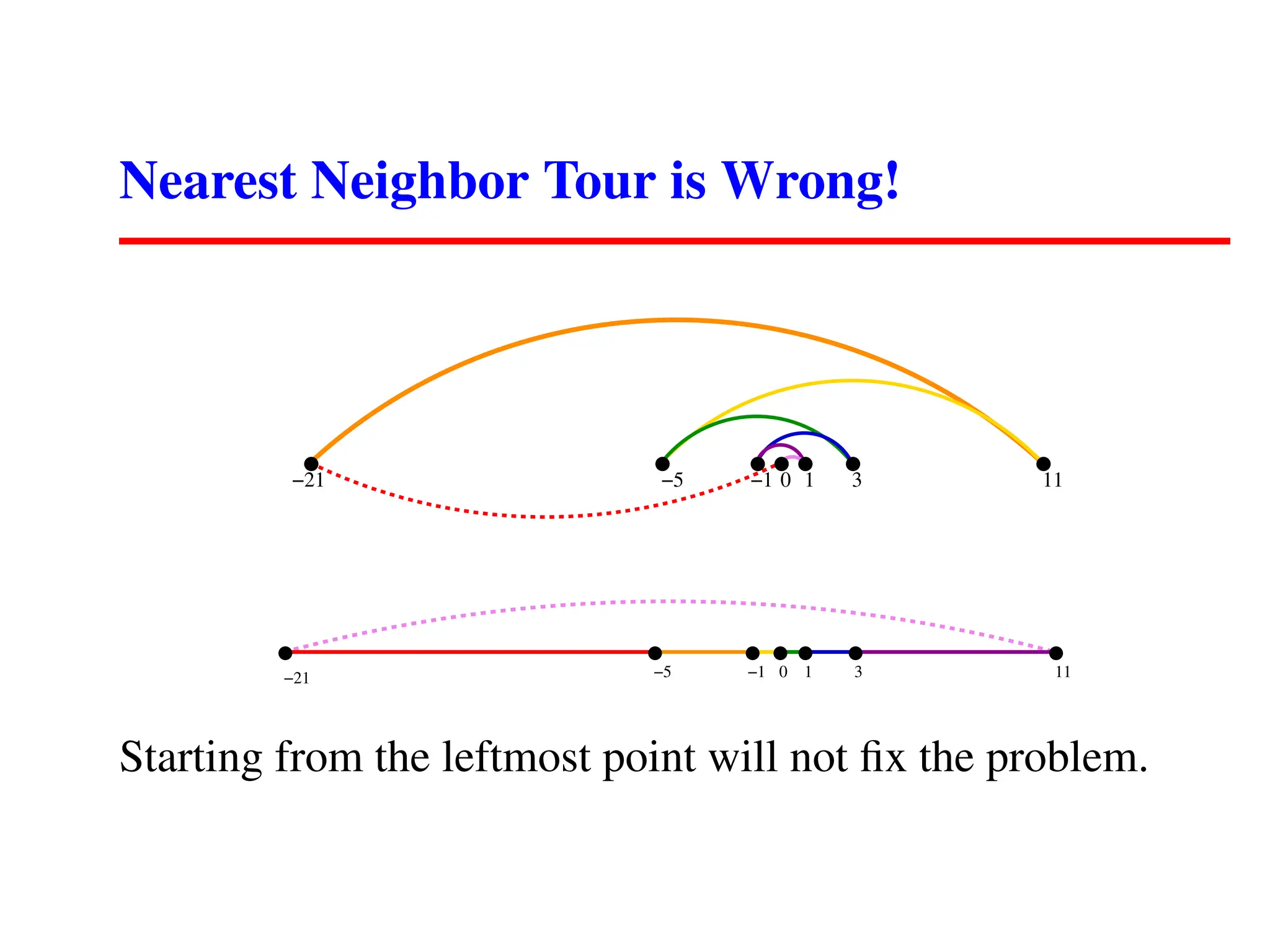
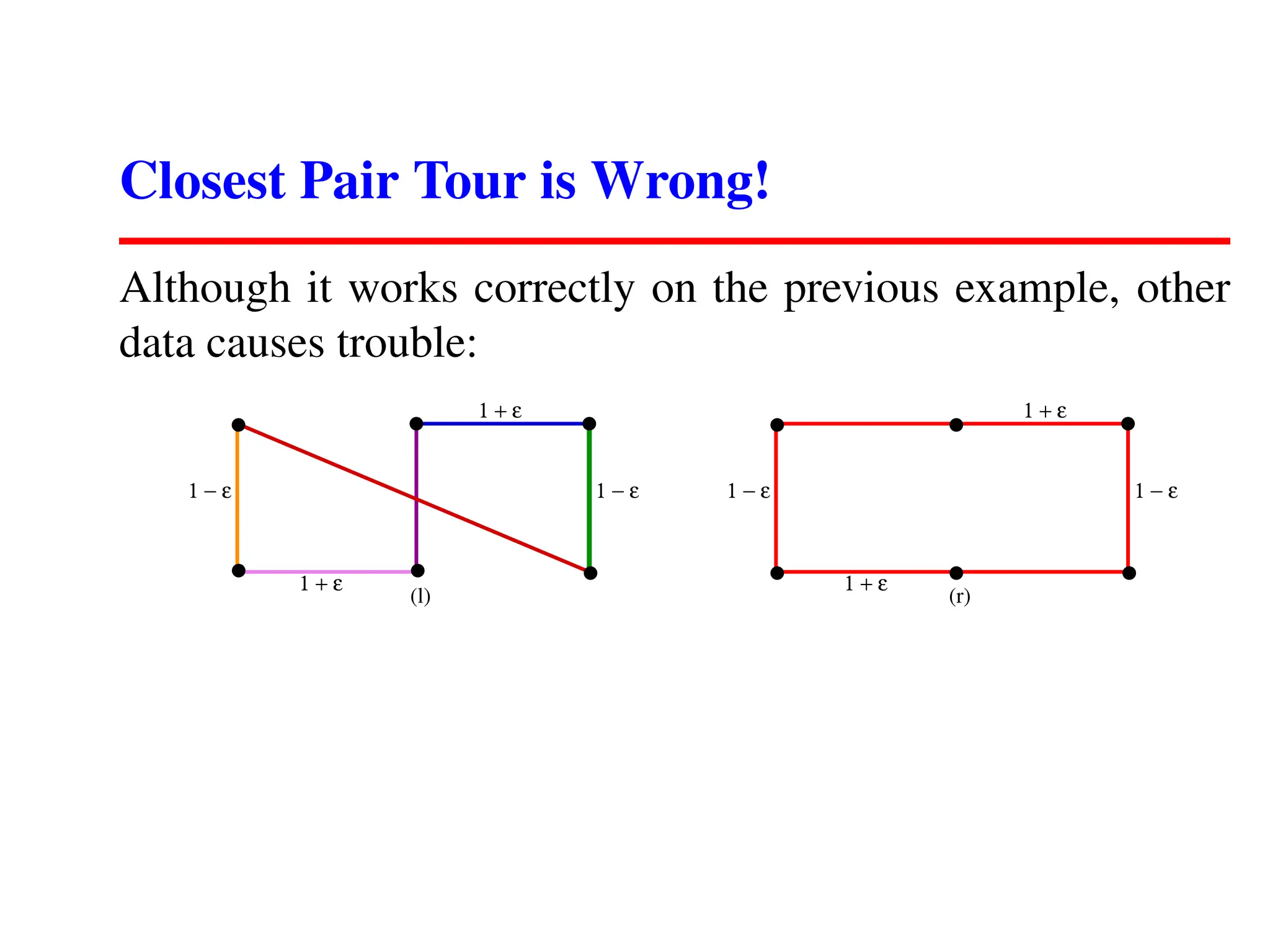
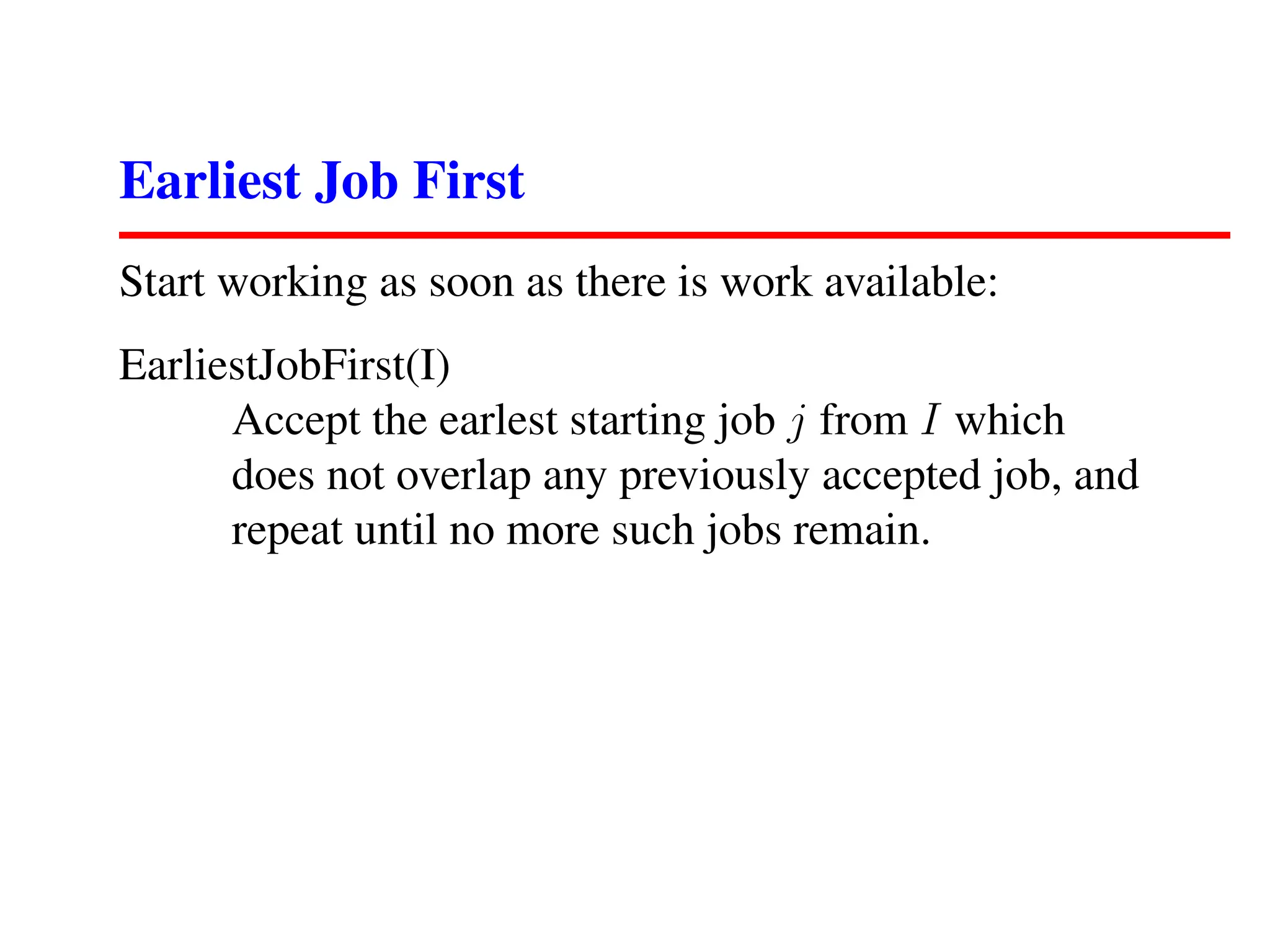
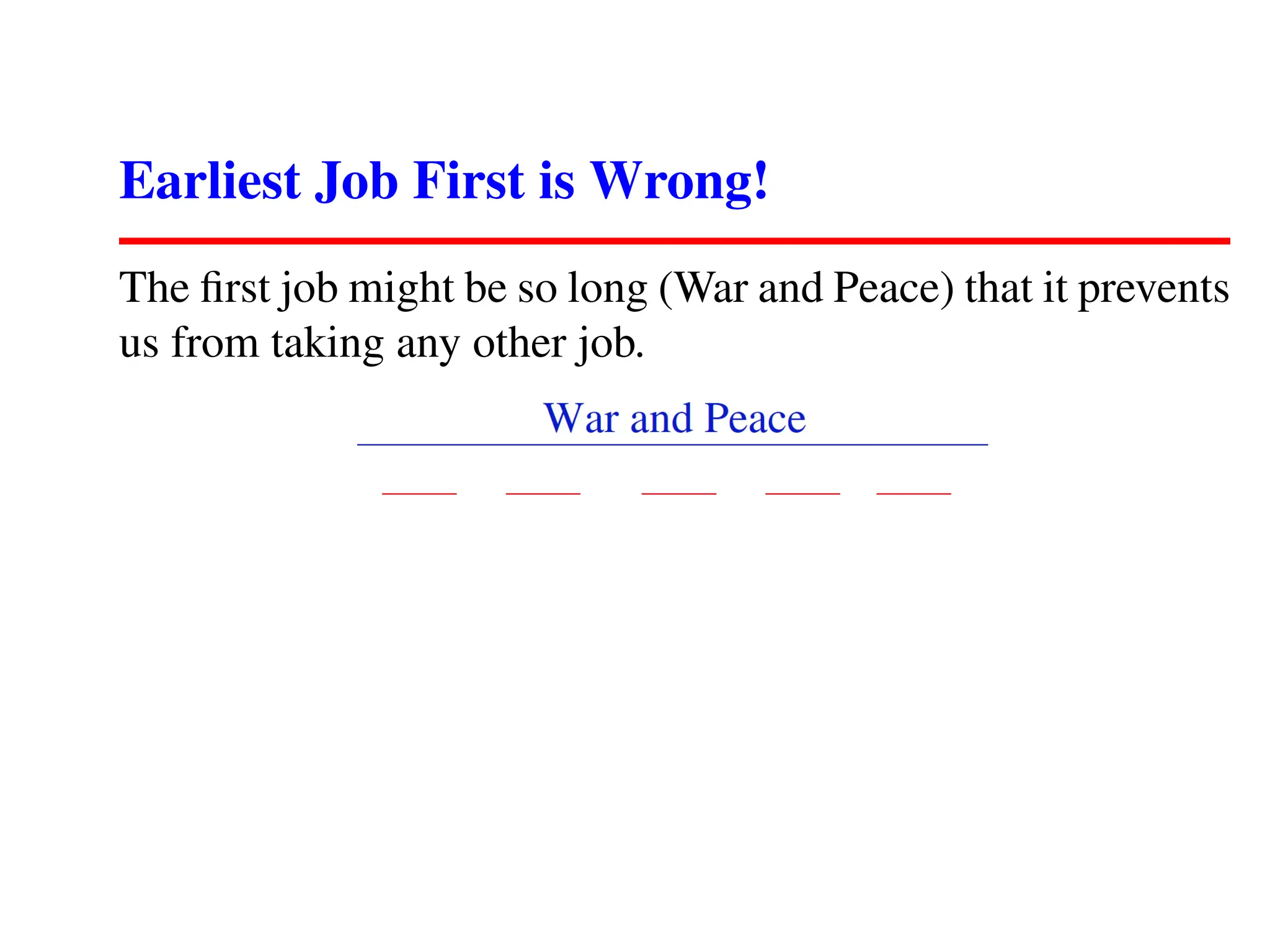
The document outlines an introductory lecture on algorithms, covering course mechanics, key topics including algorithm correctness, optimization problems, and specific examples like sorting, the traveling salesman problem, and scheduling jobs. It emphasizes the importance of correctly defining algorithmic problems and presents several flawed algorithm strategies alongside more viable approaches. A central theme is that no efficient, correct algorithm exists for some problems, highlighting challenges in algorithm design.