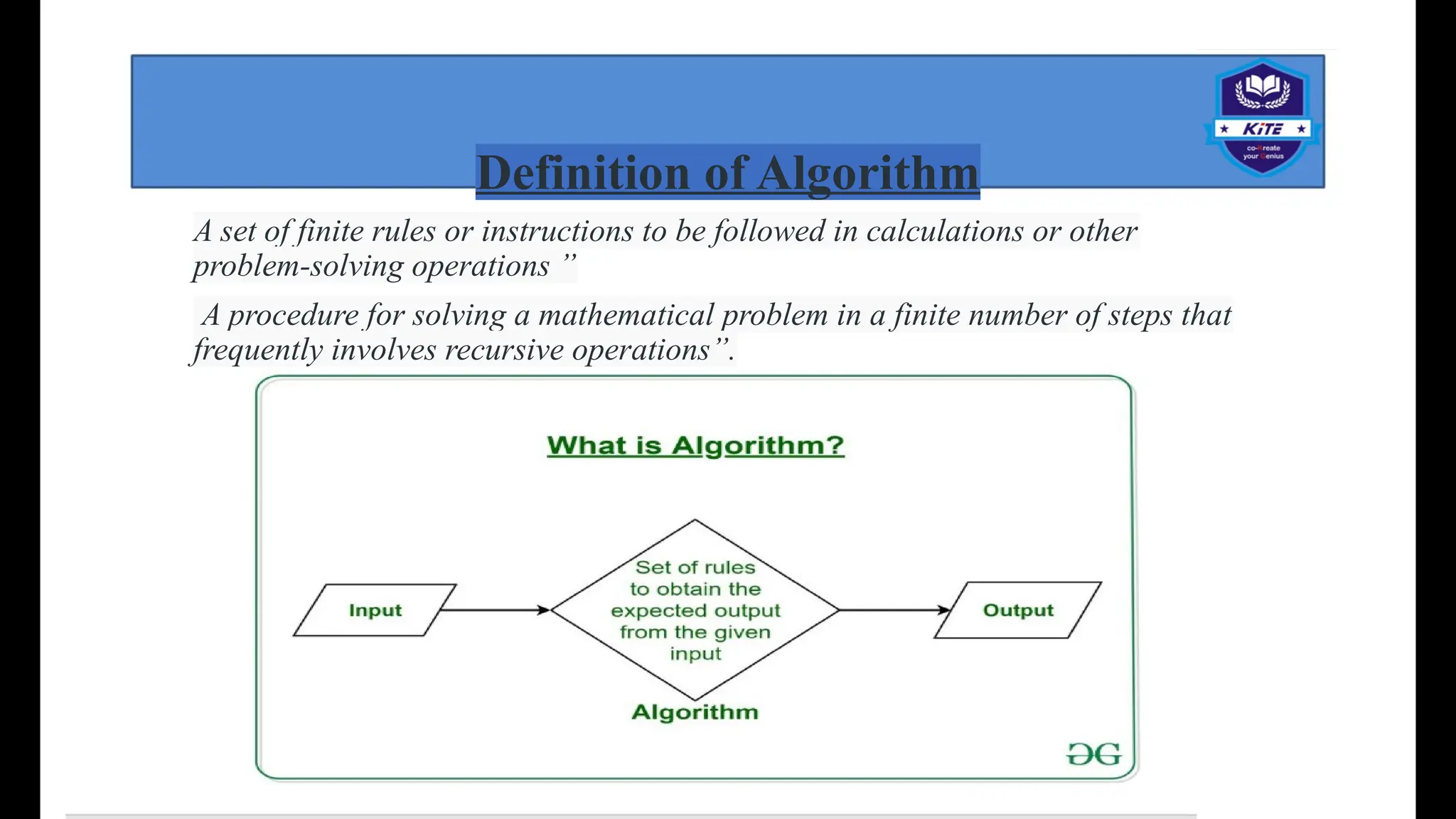
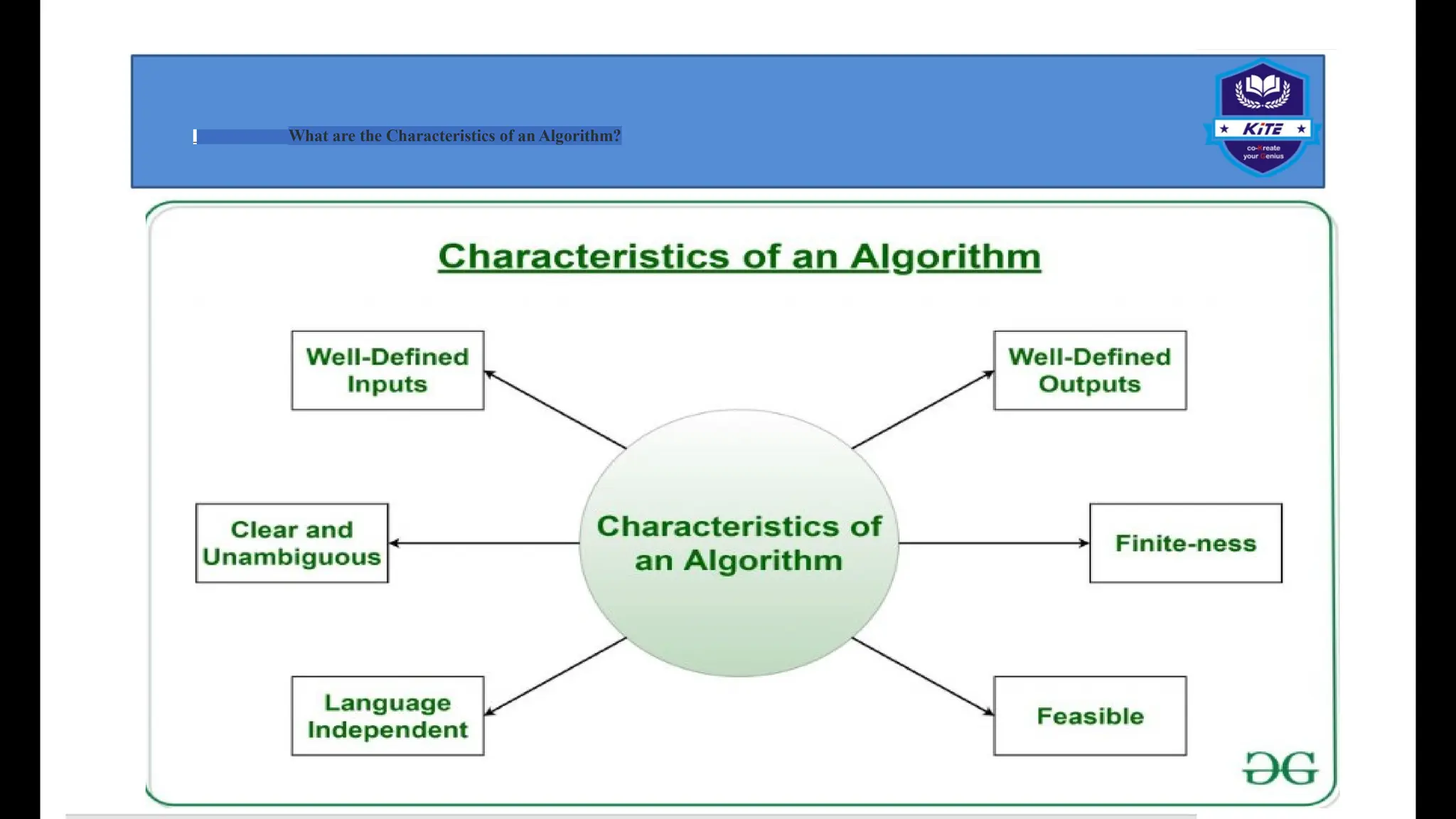
Data structures and ALGORITHMS methd binary SEARCH

Department of Computer Science and Engineering Name of the Faculty : Ms. Dhamayanthi P Subject Name & Code : CS3401 & ALGORITHMS Branch & Department : Computer Science and Engineering Year & Semester : II / IV Academic Year :2023-24 CS8691/AI/IIICSE/VISEM/KG-KiTE KGiSL Institute of Technology (Approved by AICTE, New Delhi; Affiliated to Anna University, Chennai) Recognized by UGC, Accredited by NBA (IT) 365, KGiSL Campus, Thudiyalur Road, Saravanampatti, Coimbatore – 641035.

CS3401 & ALGORITHMS UNIT I INTRODUCTION Algorithm analysis: Time and space complexity - Asymptotic Notations and its properties Best case,Worst case and average case analysis – Recurrence relation: substitution method - Lower bounds –searching: linear search, binary search and Interpolation Search, Pattern search: The naïve string- matching algorithm - Rabin-Karp algorithm - Knuth-Morris-Pratt algorithm. Sorting: Insertion sort – heap sort

Definition of Algorithm A set of finite rules or instructions to be followed in calculations or other problem-solving operations ” A procedure for solving a mathematical problem in a finite number of steps that frequently involves recursive operations”.

Use of the Algorithms Use of the Algorithms: Algorithms play a crucial role in various fields and have many applications. Some of the key areas where algorithms are used include: 1. Computer Science: Algorithms form the basis of computer programming and are used to solve problems ranging from simple sorting and searching to complex tasks such as artificial intelligence and machine learning. 2. Mathematics: Algorithms are used to solve mathematical problems, such as finding the optimal solution to a system of linear equations or finding the shortest path in a graph. 3. Operations Research: Algorithms are used to optimize and make decisions in fields such as transportation, logistics, and resource allocation. 4. Artificial Intelligence: Algorithms are the foundation of artificial intelligence and machine learning, and are used to develop intelligent systems that can perform tasks such as image recognition, natural language processing, and decision-making. 5. Data Science: Algorithms are used to analyze, process, and extract insights from large amounts of data in fields such as marketing, finance, and healthcare.

What are the Characteristics of an Algorithm?

What are the Characteristics of an Algorithm? ● Clear and Unambiguous: The algorithm should be unambiguous. Each of its steps should be clear in all aspects and must lead to only one meaning. ● Well-Defined Inputs: If an algorithm says to take inputs, it should be well-defined inputs. It may or may not take input. ● Well-Defined Outputs: The algorithm must clearly define what output will be yielded and it should be well-defined as well. It should produce at least 1 output. ● Finite-ness: The algorithm must be finite, i.e. it should terminate after a finite time. ● Feasible: The algorithm must be simple, generic, and practical, such that it can be executed with the available resources. It must not contain some future technology or anything. ● Language Independent: The Algorithm designed must be language-independent, i.e. it must be just plain instructions that can be implemented in any language, and yet the output will be the same, as expected.

Types of Algorithms: ● Sorting Algorithms ● Searching Algorithms ● Graph Algorithms ● Dynamic Programming ● Divide and Conquer ● Greedy Algorithms ● Backtracking Algorithms ● Randomized Algorithms ● Approximation Algorithms

Time Complexity ● Time complexity Amount of computer time required by an algorithm to run to completion ● It is typically expressed using big O notation, which describes the upper bound on the growth of the time required by the algorithm. ● For example, an algorithm with a time complexity of O(n) takes longer to run as the input size (n)

Properties of Algorithm: ● It should terminate after a finite time. ● It should produce at least one output. ● It should take zero or more input. ● It should be deterministic means giving the same output for the same input case. ● Every step in the algorithm must be effective i.e. every step should do some work.

Time Complexity There are different types of time complexities O(1) or constant time: The algorithm takes the same amount of time to run regardless of the size of the input. Example: Accessing an element in an array by index. O(log n) or logarithmic time: The algorithm's running time increases logarithmically with the size of the input. Example: Binary Search in a sorted array. O(n) or linear time:The algorithm's running time increases linearly with the size of the input. Example: Linear Search in an unsorted array. O(n log n) or linear logarithmic time: The algorithm's running time increases linearly with the size of the input and logarithmically with the size of the input. Example: Merge Sort or Heap Sort. O(n^2) or quadratic time: The algorithm's running time increases quadratically with the size of the input Example: Bubble Sort.

Space complexity ● Space complexity is defined as amount of memory required by an algorithm to run ● Like time complexity, it is typically expressed using big O notation. ● For example, an algorithm with a space complexity of O(n) uses more memory as the input size (n) increases

Space complexity ● O(1) or constant space: the algorithm uses the same amount of memory regardless of the size of the input.Example, a function that sums two numbers and returns the result will only use a fixed amount of memory to store those numbers and the result. ● O(n) or linear space: the algorithm's memory usage increases linearly with the size of the input. Example: Storing elements of an array. ● O(n^2) or quadratic space: the algorithm's memory usage increases quadratically with the size of the input.Example: Creating a 2D array to represent a matrix(n x n matrix) ● O(2^n) or exponential space: the algorithm's memory usage increases exponentially with the size of the input.(Example: Recursive algorithms with exponential branching.)

program Input: Here our input is an integer array of size "n" and we have one integer "k" that we need to search for in that array. Output: If the element "k" is found in the array, then we have return 1, otherwise we have return 0/ for-loop to iterate with each element in the array for (int i = 0; i < n; ++i) { // check if ith element is equal to "k" or not if (arr[i] == k) return 1; // return 1, if you find "k" } return 0; // return 0, if you didn't find "k" }

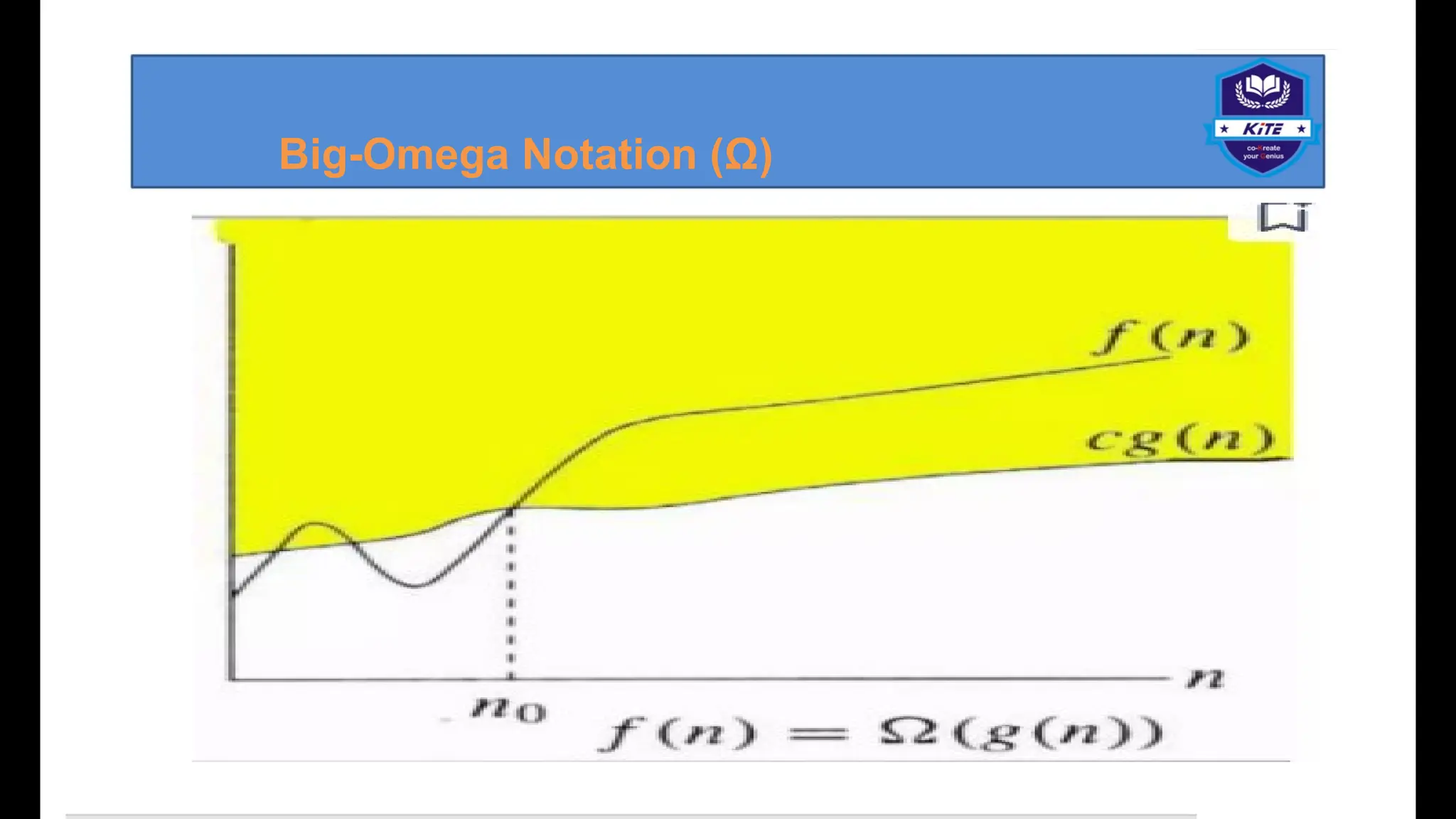
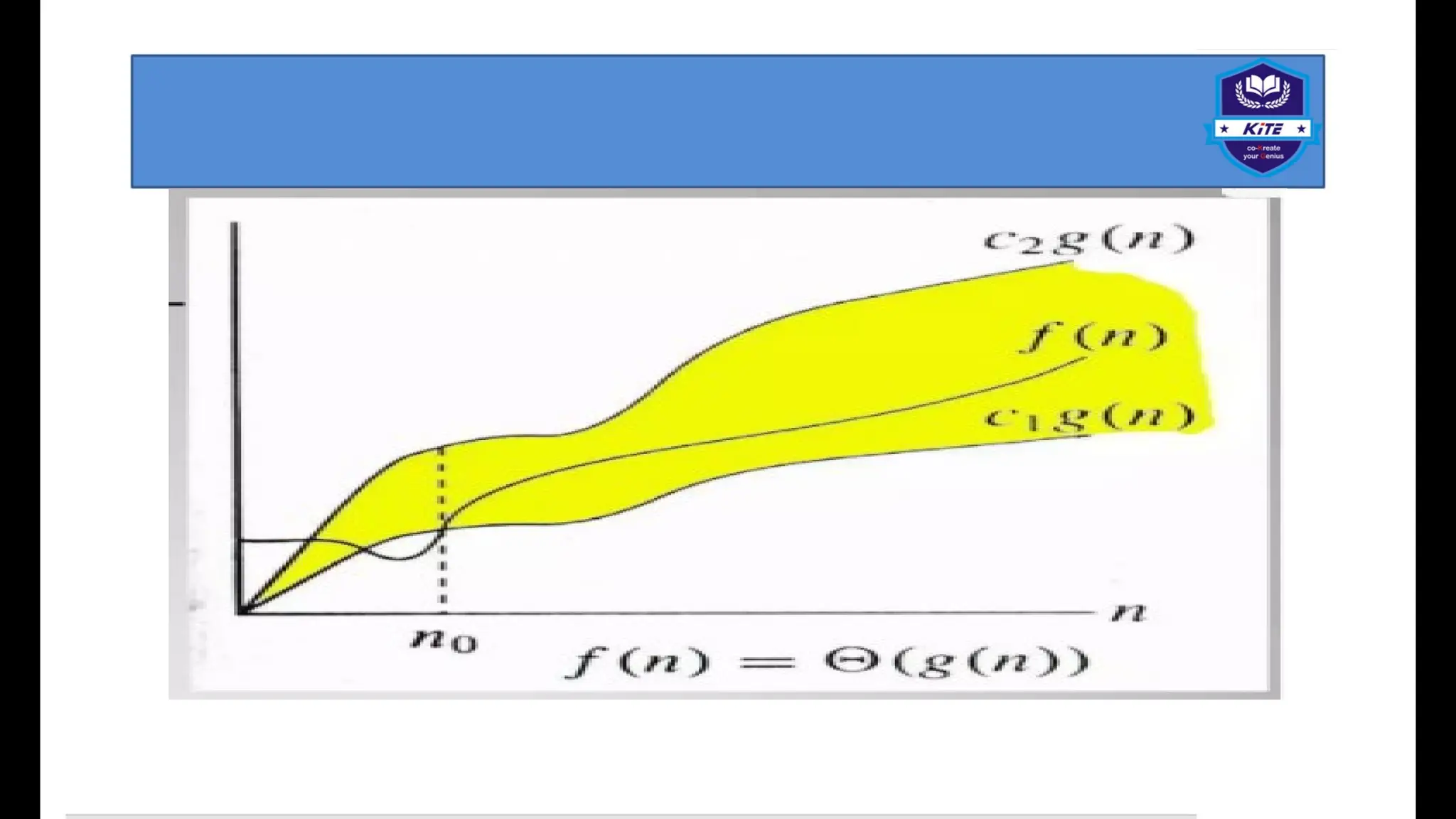
∙ Best case: This is the lower bound on running time of an algorithm. We must knowthecause that causes the minimum number of operations to be executed. In the above example, our array was [1, 2, 3, 4, 5] and we are finding if "1" is present in the array or not. So here, after only one comparison, we will get that element is present in the array. So, this is the best case of our algorithm. Average case: We calculate the running time for all possible inputs, sum all the calculated values and divide the sum by the total number of inputs. We must know(or predict) distribution of cases. ∙ Worst case: This is the upper bound on running time of an algorithm. We must knowthecause that causes the maximum number of operations to be executed. In our example, the worst case can be if the given array is [1, 2, 3, 4, 5] and we try to find if element "6"ispresent in the array or not. Here, the if-condition of our loop will be executed 5 times and then the algorithm will give "0" as output.

Asymptotic Notations and its properties •Asymptotic notation à used to make meaningful statements about the efficiency of a program •To choose the best algorithm, we need to check the efficiency of each algorithm •The efficiency can be measured by computing time complexity of each algorithm •Shorthand way to represent the time complexity •Using asymptotic notation, we can give time complexity as “Fastest possible”, “Slowest possible”, “Average time” •Big-Oh Notation (O) •Big-Omega Notation (Ω) •Big-Theta Notation (Θ)

Big O notation • Denoted as ‘O’ •Upper Bound of algorithm running time •Using Big Oh notation, we can give congest of time taken by the algorithm to complete Definition •A function f(n) is said to be in O(g(n)), denoted as f(n) O(g(n)), if f(n) is bounded ∈ above by some constant multiple of g(n) for all large n. i.e., if there exist some positive constant c and some non-negative integer n0 such that: f(n) ≤ cg(n) for all n ≥ n0

Example Consider function f(n) = 2n+2 and g(n) = n^2. Then we have to find some constant c. So that f(n) ≤ c * g(n). As, f(n) = 2n + 2 and g(n) = n^2, then we find c for n = 1 Given f(n) = 2n + 2, g(n) = n^2 Sub n = 1 f(n) = 2(1) + 2 g(n) = 1^2 f(n) = 4 g(n) = 1 f(n) > g(n) Sub n = 2 f(n) = 2(2) + 2 g(n) = 2^2 f(n) = 6 g(n) = 4 f(n) > g(n)

Example Sub n = 3 f(n) = 2(3) + 2 g(n) = 3^2 f(n) = 8 g(n) = 9 f(n) <g(n) Hence, we can conclude that for n > 2, we obtain f(n) < g(n)

Big-Omega Notation (Ω) •Denoted as Ω •Used to represent the lower bound of algorithms running time •Using Omega notation, we can denote shortest amount of time taken by algorithm Definition A function t(n) is said to be in Ω(g(n)), denoted as t(n) Ω(g(n)), ∈ if t(n) is bounded below by some positive constant multiple of g(n) for all large n. t(n) ≥ cg(n) for all n ≥ n0

Given f(n) = 2n^2+5 , g(n) = 7n Sub n = 1 f(n) = 2〖(1)〗^2+5 g(n) = 7(1) f(n) = 7 g(n) = 7 f(n) =g(n) Sub n = 2 f(n) = 2〖(2)〗^2+5 g(n) = 7(2) f(n) = 13 g(n) = 14 f(n) <g(n) Sub n = 3 f(n) = 2〖(3)〗^2+5 g(n) = 7(3) f(n) = 23 g(n) = 21 f(n) >g(n) Hence, we can conclude that for n > 3, we obtain f(n) > c * g(n)

Big-Theta Notation (Θ) •Denoted as Θ •Running time is between upper bound and lower bound Definition Let f(n) and g(n) à two negative functions C1 and C2 à positive integers C1 ≤ g(n) ≤ c2g(n) Then, f(n) Є (g(n)) Ɵ

Data structures and ALGORITHMS methd binary SEARCH

Data structures and ALGORITHMS methd binary SEARCH

More Related Content

Similar to Data structures and ALGORITHMS methd binary SEARCH

Recently uploaded

Data structures and ALGORITHMS methd binary SEARCH