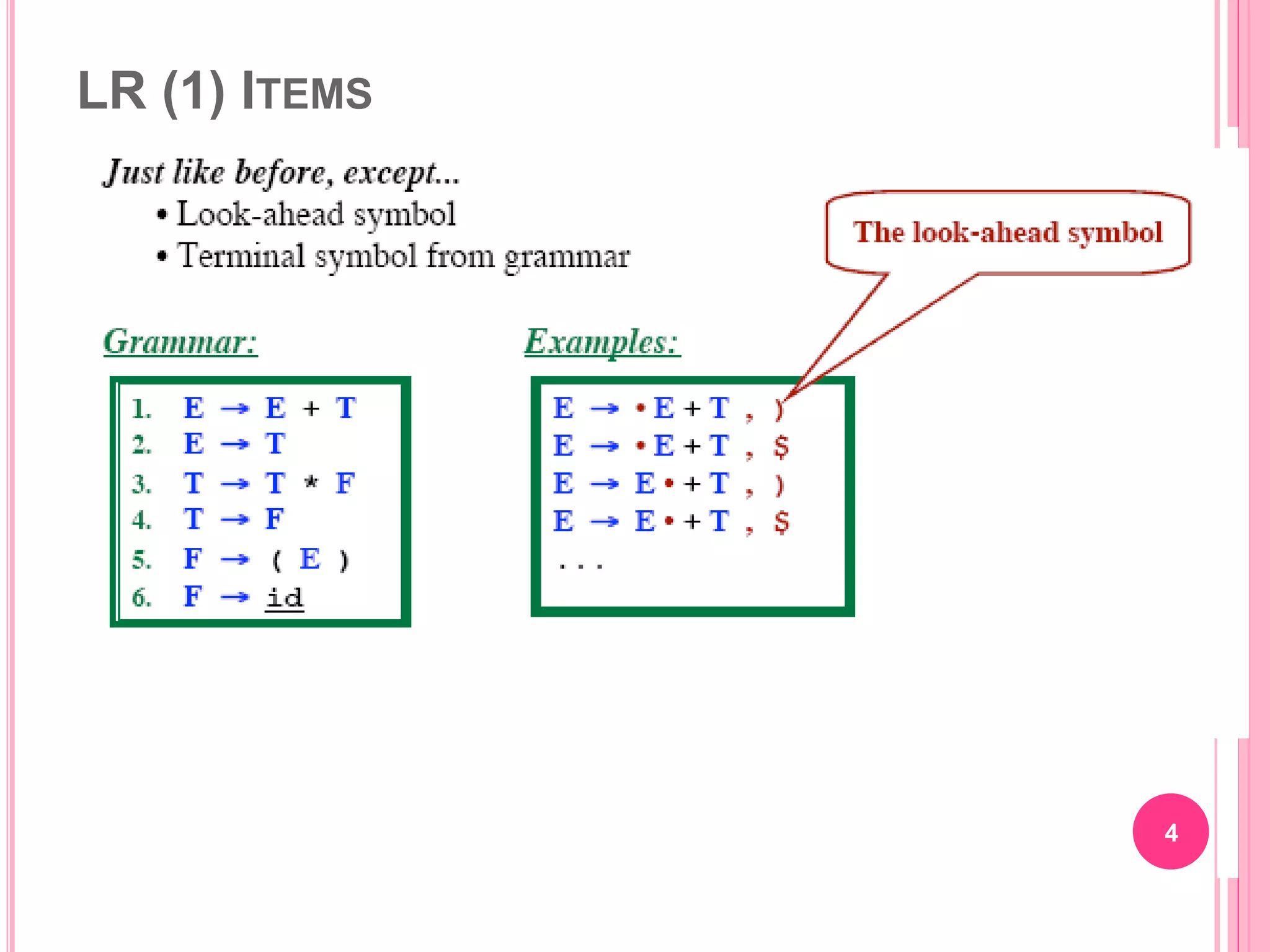
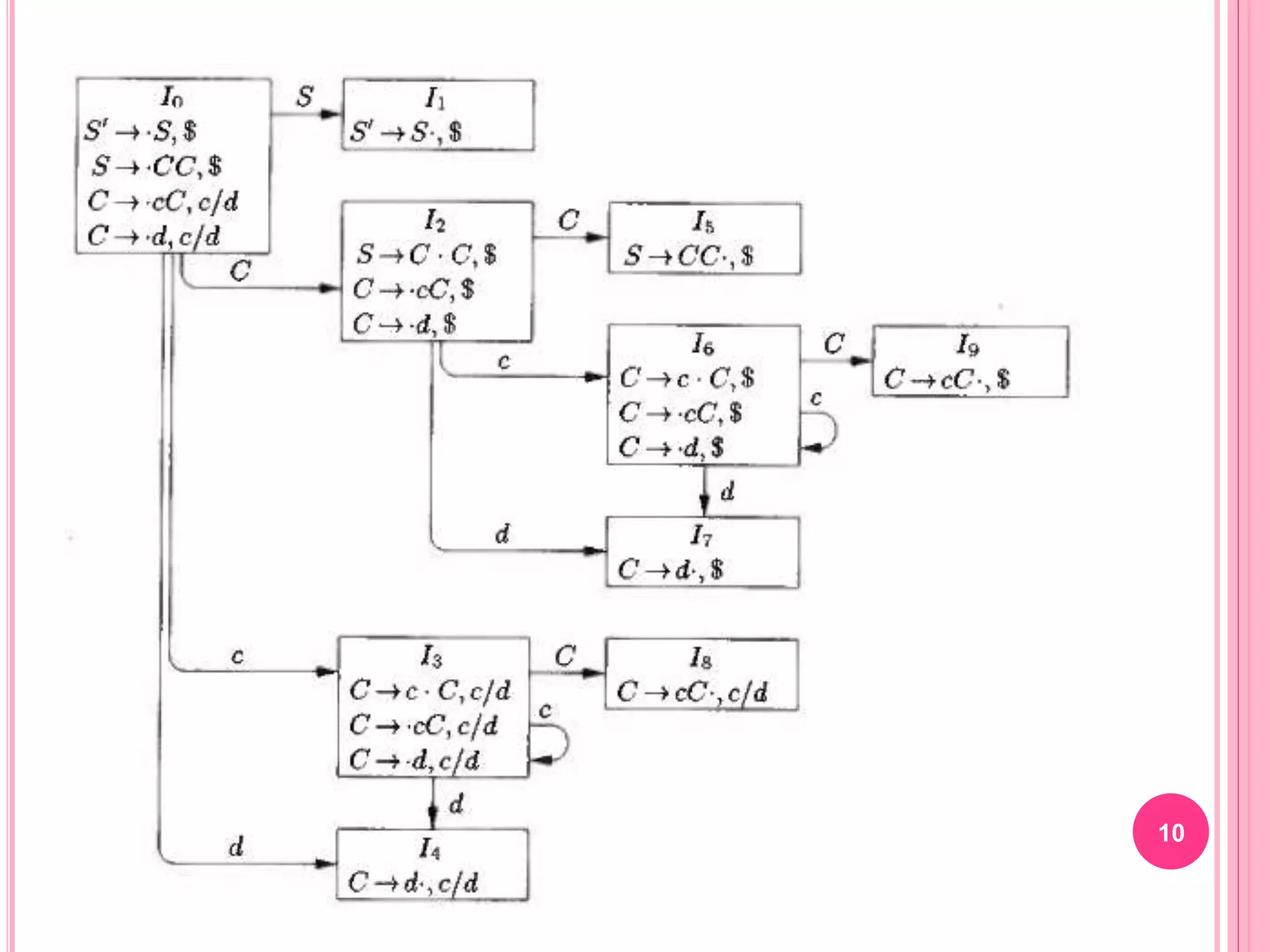
The document discusses LR(1) parsing and the construction of LR(1) parsing tables. It describes how LR(1) items include a lookahead terminal symbol to avoid invalid reductions. The closure and goto functions are used to construct the canonical collection of LR(1) item sets. From this, the action and goto tables of the LR(1) parser are derived. The document also discusses how LALR parsing tables are constructed by merging states that have the same core (first component) of LR(1) items, which can introduce reduce/reduce conflicts but not shift/reduce conflicts.









![CONSTRUCTION OF LR(1) PARSING TABLES 1. Construct the canonical collection of sets of LR(1) items for G’. C{I0,...,In} 2. Create the parsing action table as follows • If a is a terminal, A.a,b in Ii and goto(Ii,a)=Ij then action[i,a] is shift j. • If A.,a is in Ii , then action[i,a] is reduce A where AS’. • If S’S.,$ is in Ii , then action[i,$] is accept. • If any conflicting actions generated by these rules, the grammar is not LR(1). 3. Create the parsing goto table • for all non-terminals A, if goto(Ii,A)=Ij then goto[i,A]=j 4. All entries not defined by (2) and (3) are errors. 5. Initial state of the parser contains S’.S,$ 12](https://image.slidesharecdn.com/lecture09syntaxanalysis05-151020082118-lva1-app6892/75/Lecture-09-syntax-analysis-05-12-2048.jpg)






