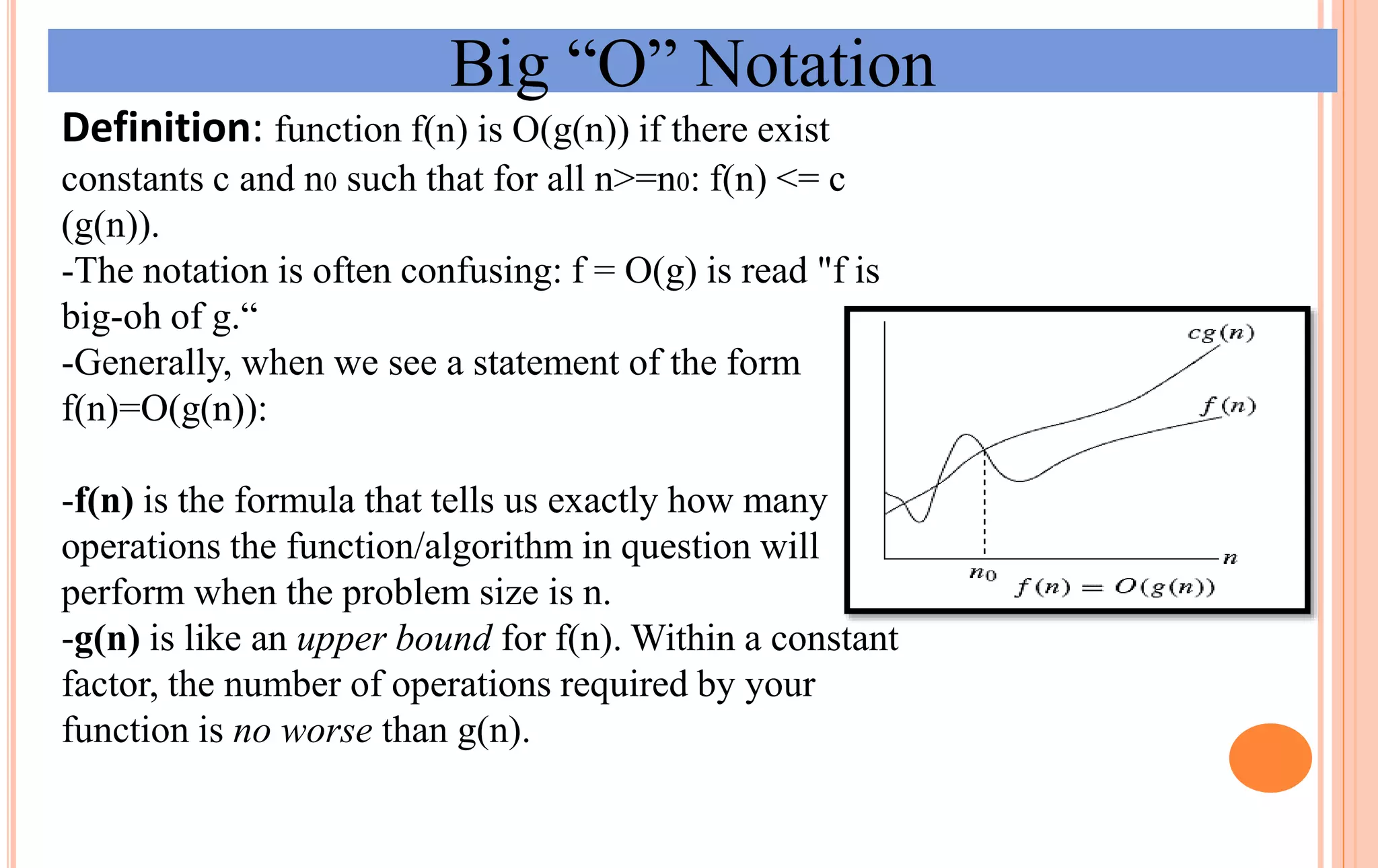
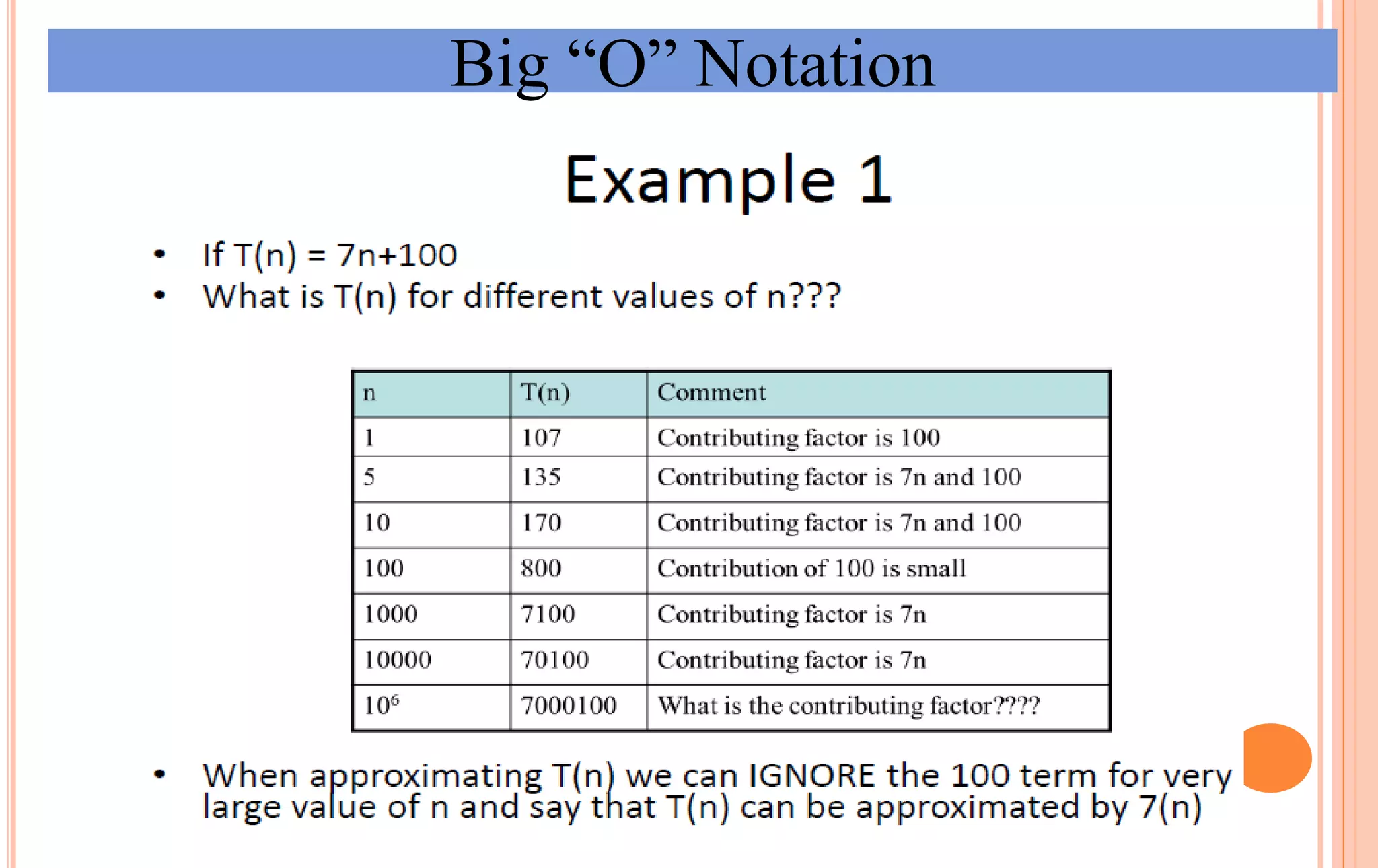
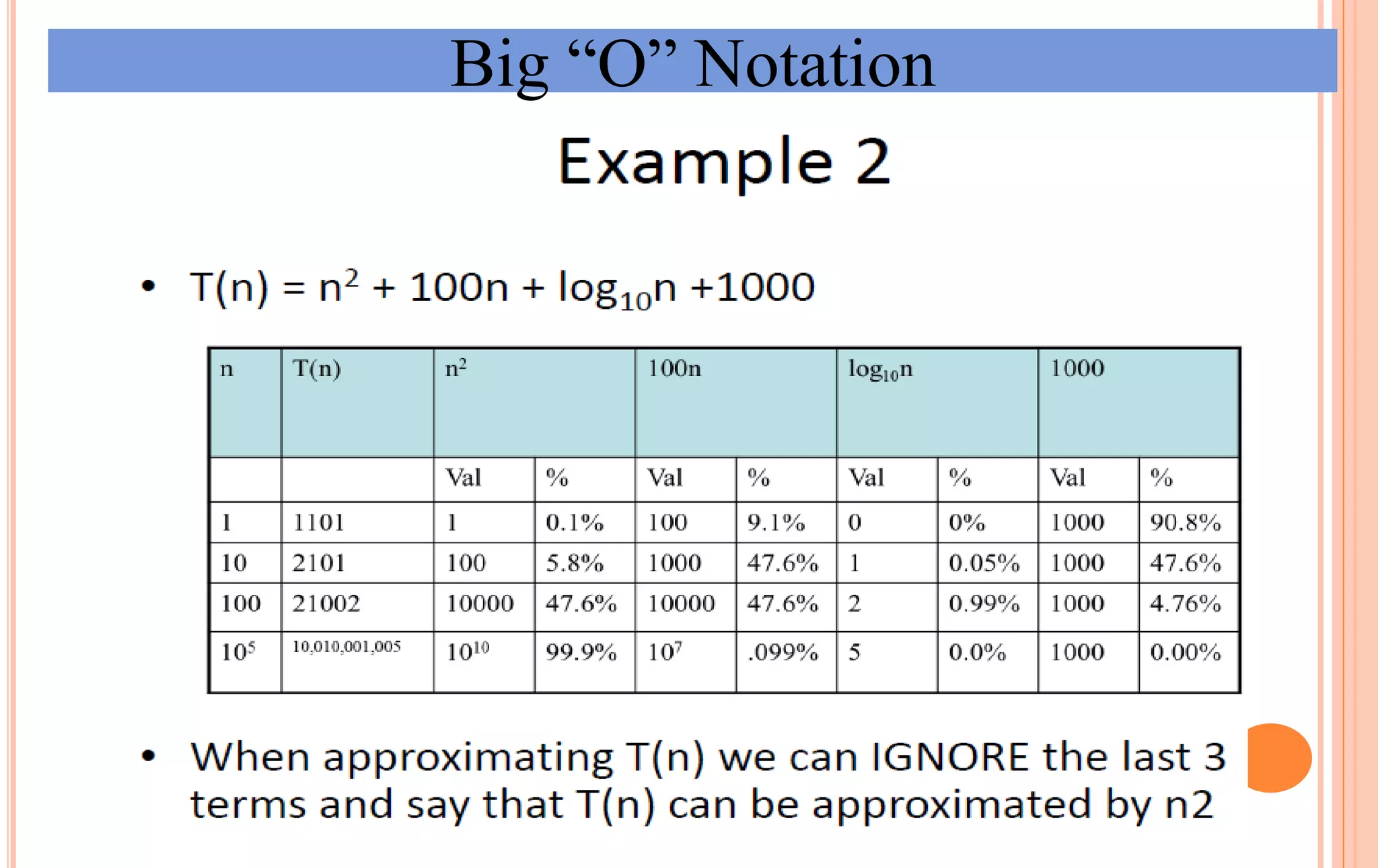
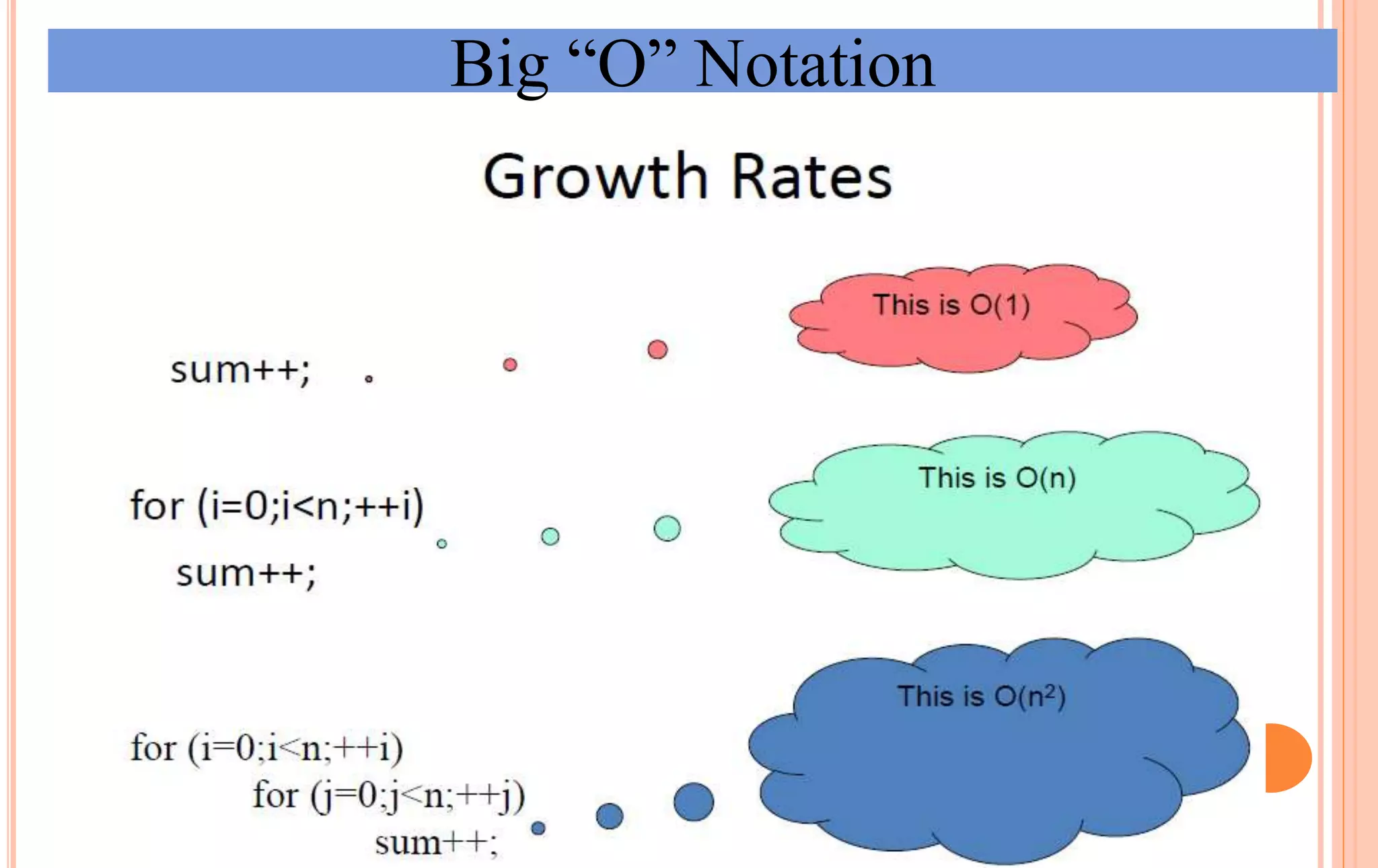
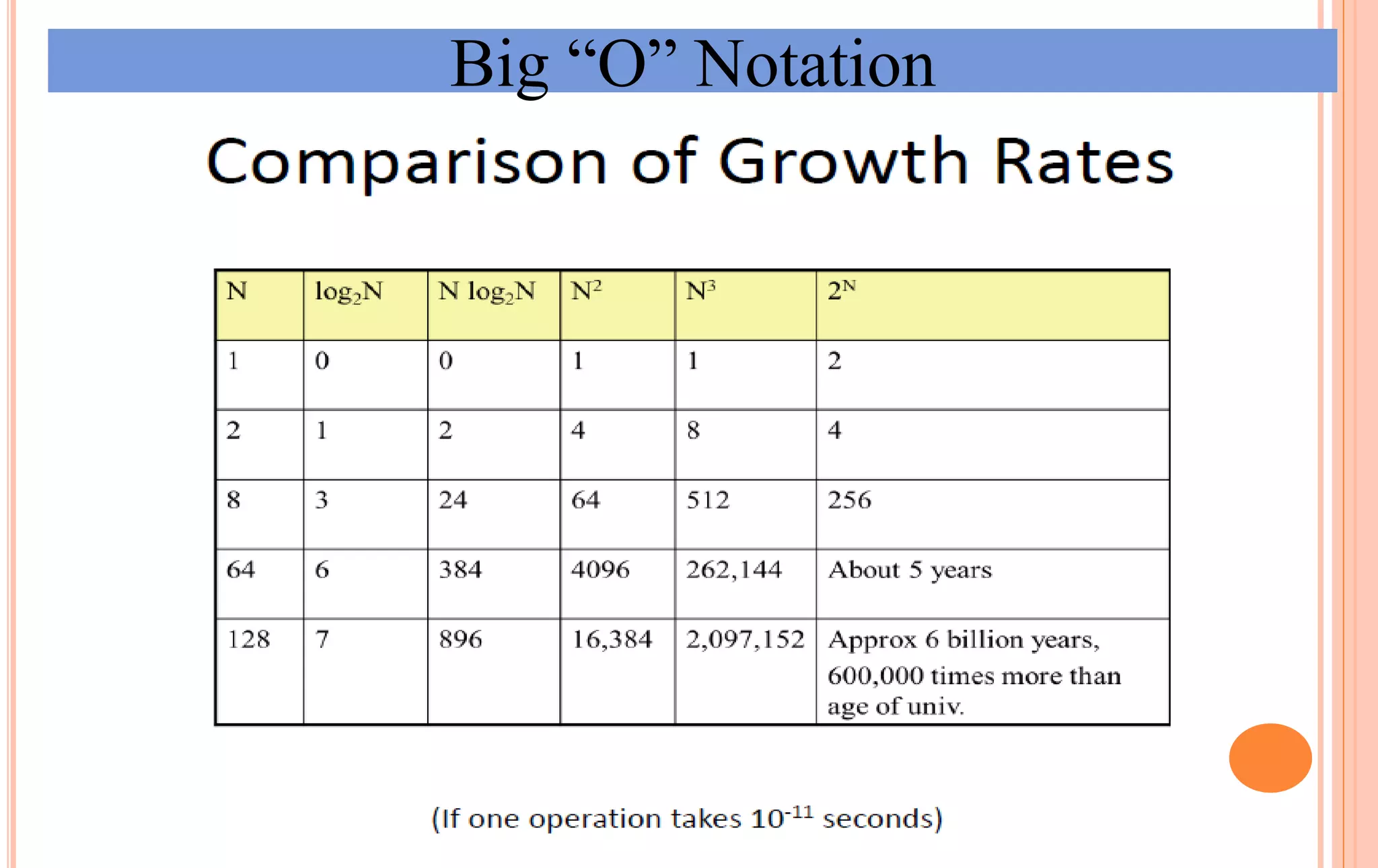
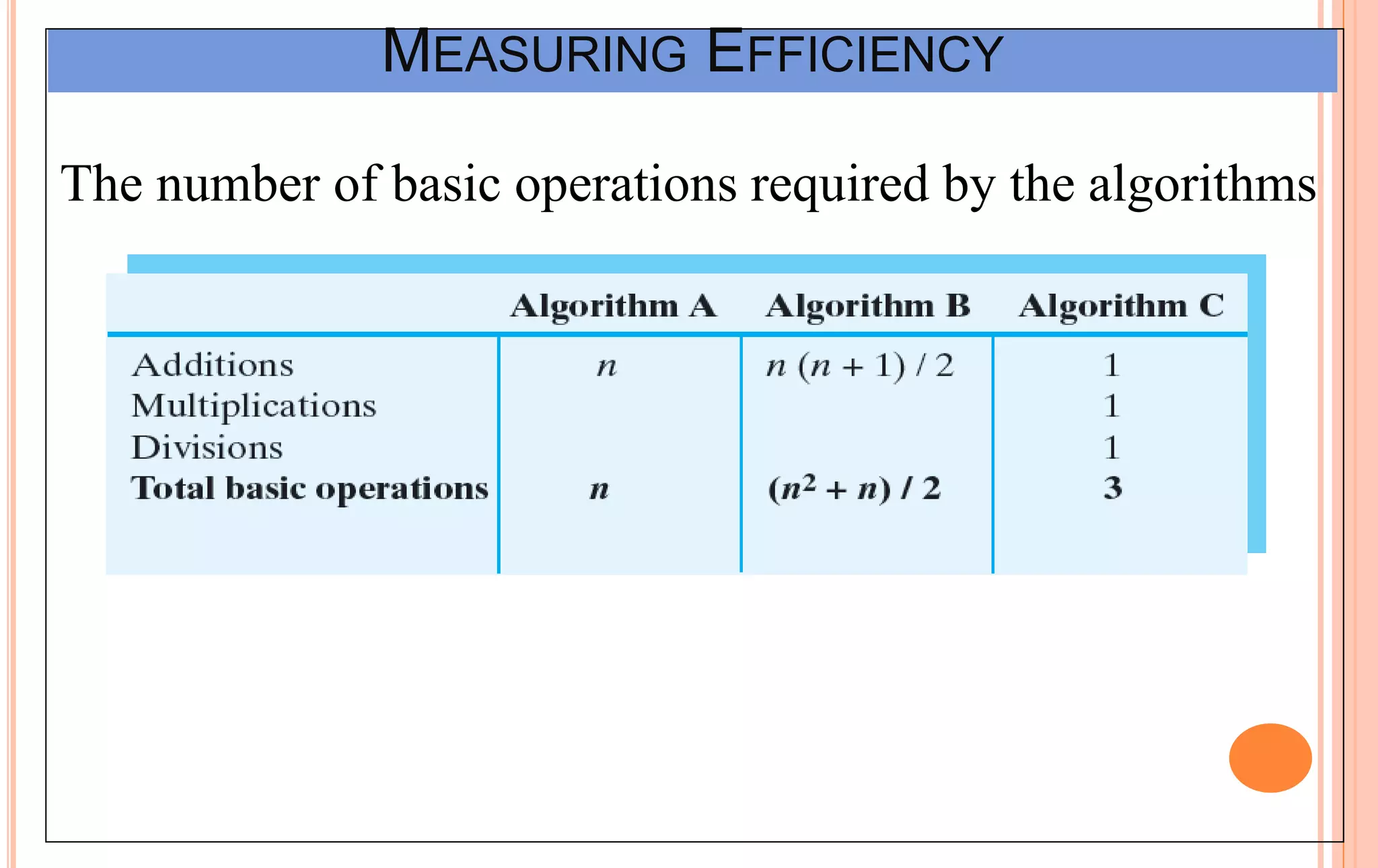
An algorithm is a set of steps to solve a problem. Algorithm efficiency describes how fast an algorithm solves problems of different sizes. Time complexity is the most important measure of efficiency, measuring the number of steps an algorithm takes based on the size of the input. Common techniques to analyze time complexity include calculating the number of operations in loops and recursions. Asymptotic notation like Big-O describes the long-term growth rate of an algorithm's running time as the input size increases.








![ANALYSIS OF SUM (2) // Input: int A[N], array of N integers // Output: Sum of all numbers in array A int Sum(int A[], int N) { int s=0; for (int i=0; i< N; i++ ) { s = s + A[i]; } return s; } 1 2 3 4 5 6 7 8 1,2,8: Once time 3,4,5,6,7: Once per each iteration of for loop, N iteration Total: 5N + 3 The complexity function of the algorithm is : f(N) = 5N +3 A Simple Example](https://image.slidesharecdn.com/lec-2algorithmsefficiencycomplexity-180102151049/75/Lec-2-algorithms-efficiency-complexity-10-2048.jpg)