Identification of unknown parameters and prediction with hierarchical matrices. Comparison with ML methods.

Identification of unknown parameters and prediction with hierarchical matrices. Comparison with ML methods. Alexander Litvinenko1, (joint work with V. Berikov2, M. Genton3, D. Keyes3, R. Kriemann4, and Y. Sun3) UNCECOMP 2021 1RWTH Aachen, Germany, 2Novosibirsk Staate University, 3KAUST, Saudi Arabia, 4MPI for Mathematics in the Sciences in Leipzig, Germany

4 * Analysis of large datasets and prediction Goal: analyse a large dataset Need to use a dense cov. matrix C of size 2, 000, 000 × 2, 000, 000 3 2 4 2 9 2 4 2 17 2 2 4 2 7 3 2 18 17 10 10 2 5 2 8 2 4 2 10 3 3 2 32 14 10 18 10 36 28 3 6 2 4 2 14 2 4 2 5 2 4 2 14 18 14 18 2 4 2 8 2 5 3 19 2 4 2 6 3 6 3 65 32 19 21 18 18 29 29 61 61 2 5 3 7 3 2 5 2 18 3 6 3 6 3 17 17 12 12 3 2 7 2 4 2 2 12 3 2 4 2 32 17 12 12 12 29 29 2 5 3 2 7 2 4 2 12 2 5 3 10 10 19 12 3 3 2 10 2 5 2 5 2 4 2 119 65 32 10 15 10 19 27 27 54 54 118 118 2 5 3 4 2 15 2 5 3 11 3 6 3 15 17 10 10 2 4 2 8 2 4 2 10 3 2 3 21 14 10 7 7 33 27 2 4 3 3 2 7 3 8 7 14 7 2 3 8 2 4 2 7 3 2 10 2 5 2 59 21 8 18 8 12 21 29 59 54 3 6 3 2 5 2 12 2 5 3 2 18 12 11 11 3 2 7 3 5 2 11 2 5 3 25 9 9 16 11 30 29 3 3 9 3 4 2 6 3 9 16 9 16 3 2 4 2 7 3 2 16 3 2 7 2 4 2 121 119 59 25 18 16 10 10 25 34 59 59 119 118 80 119 2 4 2 4 2 9 2 4 2 10 3 4 2 19 10 15 10 2 5 3 2 7 3 2 15 3 4 2 5 2 31 15 15 16 15 32 34 3 2 4 2 4 2 15 2 4 3 2 5 2 15 16 15 16 2 5 3 2 12 3 6 3 20 3 2 7 3 2 6 3 58 27 18 18 9 9 31 31 66 67 2 5 3 2 6 3 9 2 4 2 12 9 18 9 3 6 3 12 3 4 2 9 2 4 2 27 12 16 12 19 27 31 3 2 3 6 3 16 2 5 2 4 2 6 3 16 20 8 8 2 4 2 7 3 2 7 3 2 8 2 3 115 58 30 15 8 15 8 28 28 57 57 119 119 2 5 2 4 2 2 15 2 4 2 6 3 9 9 15 15 3 3 9 2 5 3 2 7 3 2 27 9 16 9 11 30 28 3 5 2 5 2 11 2 5 2 16 11 13 11 3 3 2 7 3 2 13 2 5 2 4 2 48 25 5 5 17 13 23 23 58 57 2 5 2 4 2 5 2 6 3 5 8 5 15 2 3 8 3 2 2 6 3 25 8 15 8 9 25 23 2 5 3 6 3 7 3 2 9 2 4 2 15 9 23 9 3 3 6 3 15 2 4 2 5 2 10 2 5 2 90 122 115 48 32 15 15 15 17 33 33 48 60 115 119 81 234 56 89 3 2 7 2 4 2 15 3 4 2 7 3 2 15 17 6 6 2 5 2 5 3 11 2 5 3 6 3 30 11 6 19 6 30 30 3 5 2 11 3 2 7 3 2 5 2 11 13 11 17 2 4 2 5 2 13 3 5 2 6 3 65 30 13 17 13 17 30 30 61 60 2 4 3 6 3 5 2 21 2 4 2 4 2 12 3 6 3 20 20 14 14 2 4 2 8 2 4 2 3 14 2 5 2 4 2 32 17 14 15 14 29 29 2 4 2 8 2 4 2 15 2 5 2 5 2 10 10 17 15 2 5 2 10 3 6 2 4 2 5 2 125 75 32 10 18 10 19 32 29 69 61 125 134 2 5 3 2 6 3 18 3 2 6 3 8 2 4 2 17 17 18 19 2 4 2 8 2 4 2 17 3 6 3 2 6 3 39 17 19 17 18 25 25 3 2 7 2 4 2 11 2 4 3 2 18 3 6 3 6 3 10 10 15 15 3 2 3 10 2 4 3 5 2 65 30 10 15 10 12 35 25 69 69 2 4 2 9 2 4 2 12 2 2 5 2 18 12 14 12 2 5 2 10 2 4 3 2 14 3 6 2 4 2 30 15 14 16 14 30 35 2 4 2 6 3 15 3 2 4 2 5 2 15 15 15 16 2 4 2 5 2 2 15 3 6 3 8 2 4 2 3 227 111 61 31 15 21 15 16 24 24 50 50 116 116 81 224 3 6 3 9 2 4 2 16 2 5 2 6 2 19 16 5 5 2 5 3 8 2 4 2 5 2 23 16 5 7 5 27 24 3 6 2 5 2 7 2 3 10 7 16 7 3 4 2 10 3 6 3 5 2 54 23 10 17 10 11 23 25 61 50 2 2 7 2 5 3 11 2 5 2 13 11 12 11 3 2 5 2 12 2 4 2 4 2 29 13 12 13 12 27 25 2 5 2 5 2 15 2 5 3 2 7 2 4 2 15 18 9 9 2 5 2 5 2 3 9 2 4 2 111 54 33 18 9 12 9 22 22 54 59 110 110 3 2 7 2 4 2 6 3 12 2 5 3 2 9 9 13 12 2 4 2 9 3 2 6 3 33 9 13 9 13 22 22 3 2 6 3 9 2 4 2 15 2 4 2 6 3 12 12 10 10 2 2 6 3 10 2 4 2 49 23 7 7 12 10 26 22 55 59 3 7 3 2 4 2 4 2 7 8 7 16 3 2 8 3 6 3 6 3 23 8 15 8 11 23 26 3 2 7 3 2 11 2 4 2 3 12 11 15 11 3 2 5 2 12 2 4 2 6 3 8 2 4 2 We show how to: 1. reduce storage cost from 32TB to 16 GB 2. approximate Cholesky factorisation of C, its determinant, inverse in 8 minutes on modern desktop computer. 3. make prediction 2

4 * The structure of the talk 1. Motivation: improve statistical models, data analysis, prediction 2. Identification of unknown parameters via maximizing Gaussian log-likelihood (MLE) 3. Tools: Hierarchical matrices [Hackbusch 1999] 4. Matérn covariance function, joint Gaussian log-likelihood 5. Error analysis 6. Prediction at new locations 7. Comparison with machine learning methods 3

4 * Identifying unknown parameters Given: Let s1, . . . , sn be locations. Z = {Z(s1), . . . , Z(sn)}>, where Z(s) is a Gaussian random field indexed by a spatial location s ∈ Rd , d ≥ 1. Assumption: Z has mean zero and stationary parametric covariance function, e.g. Matérn: C(θ) = 2σ2 Γ(ν) r 2` ν Kν r ` + τ2 I, θ = (σ2 , ν, `, τ2 ). To identify: unknown parameters θ := (σ2, ν, `, τ2). 4

4 * Identifying unknown parameters Statistical inference about θ is then based on the Gaussian log-likelihood function: L(C(θ)) = L(θ) = − n 2 log(2π) − 1 2 log|C(θ)| − 1 2 Z C(θ)−1 Z, (1) where the covariance matrix C(θ) has entries C(si − sj ; θ), i, j = 1, . . . , n. The maximum likelihood estimator of θ is the value b θ that maximizes (1). 5

4 * H-matrix approximations of C, L and C−1 43 13 28 14 34 10 5 9 15 44 13 29 13 35 14 7 5 14 50 14 62 15 6 6 15 60 15 31 17 44 13 14 6 7 14 3 13 6 5 16 12 8 7 15 3 15 34 11 31 16 59 13 6 7 12 58 15 51 16 7 6 16 31 15 39 12 36 14 40 15 6 6 17 32 14 40 10 7 7 10 41 16 35 5 13 8 6 9 10 7 7 9 3 10 1 5 6 6 6 8 8 7 8 8 3 9 7 7 9 8 6 7 7 3 9 1 6 47 12 51 15 7 7 15 38 17 34 17 34 15 32 13 7 7 10 9 7 6 9 3 10 56 14 46 14 7 8 12 64 15 57 9 6 6 8 16 8 7 14 3 9 5 5 9 9 7 15 16 6 5 14 2 9 6 6 8 54 16 30 10 5 7 8 32 15 33 14 5 8 16 34 14 35 9 6 7 9 34 15 31 17 6 7 15 60 15 34 14 28 15 6 7 13 29 13 35 16 54 2 1 1 2 14 12 6 9 12 2 12 6 9 8 6 6 8 16 9 6 13 3 16 1 1 1 2 1 1 2 1 6 1 1 1 6 1 1 2 1 1 3 7 6 6 9 15 6 7 14 2 9 6 6 8 8 5 8 5 7 9 14 6 8 15 2 14 1 1 1 1 3 1 1 2 56 16 31 12 32 12 6 10 14 55 16 35 14 43 15 8 7 9 5 8 4 9 3 10 41 16 28 15 30 16 38 14 7 6 17 36 11 38 8 8 6 9 40 17 36 13 13 7 7 15 3 14 8 6 12 16 6 6 13 2 16 60 17 29 14 35 11 6 6 17 54 15 67 14 6 6 16 36 14 39 18 59 14 6 7 17 52 14 58 6 9 9 8 6 8 3 10 7 8 17 1 5 5 7 6 15 7 9 13 1 5 61 13 59 13 6 6 13 37 16 38 15 58 13 5 4 16 31 13 33 18 59 12 6 7 12 74 15 63 15 15 7 7 17 3 9 6 6 9 7 7 9 6 6 8 15 7 7 14 1 14 51 15 42 13 37 13 7 6 14 59 16 54 14 8 6 16 36 14 37 19 57 14 7 6 10 52 13 65 43 13 28 13 34 10 5 9 15 44 13 29 13 35 14 7 5 14 50 14 62 14 6 6 14 60 15 31 16 44 13 14 8 7 14 3 13 5 5 17 11 7 7 15 2 15 34 11 31 16 59 13 6 7 12 58 15 51 16 7 6 16 31 15 39 12 36 14 40 15 5 6 17 32 14 40 10 7 7 10 41 17 35 5 13 8 6 9 10 7 7 9 3 10 1 5 5 6 5 9 8 7 8 8 3 9 7 7 10 8 5 7 7 4 9 1 5 47 12 51 15 7 7 15 38 16 34 16 34 15 32 13 8 7 12 8 6 6 9 3 10 56 14 46 14 8 8 12 64 15 57 11 6 6 8 15 9 7 14 3 10 5 5 9 7 7 16 16 7 5 15 2 9 6 6 9 54 15 30 10 5 7 8 32 14 33 13 5 8 16 34 14 35 9 6 7 9 34 15 31 17 5 7 15 60 15 34 13 28 14 5 7 13 29 13 35 15 54 1 1 1 2 14 12 6 9 11 2 12 5 9 9 5 6 8 16 10 6 13 3 16 1 2 1 1 2 1 6 1 1 6 1 1 2 1 1 2 8 5 6 9 15 8 7 14 3 9 6 6 8 8 5 9 5 7 9 14 7 8 15 2 14 1 1 1 2 1 1 1 56 15 31 12 32 12 6 10 13 55 16 35 14 43 15 8 7 10 5 9 4 9 3 10 41 16 28 9 4 8 7 30 16 38 14 7 6 17 36 11 38 8 8 6 9 40 17 36 13 13 6 7 15 3 14 8 6 13 16 6 6 13 1 16 60 16 29 14 35 11 8 6 17 54 15 67 13 5 6 16 36 14 39 17 59 14 6 7 17 52 14 58 6 10 9 8 6 8 3 10 7 8 16 1 4 5 7 5 15 6 9 13 1 5 61 13 59 12 6 6 13 37 16 38 15 58 13 5 4 16 31 12 33 18 59 12 5 7 12 74 14 63 14 15 8 7 18 2 10 6 6 8 5 7 11 6 6 8 15 6 7 14 2 14 51 15 42 13 37 12 8 6 14 59 15 54 13 8 6 15 36 13 37 19 57 15 6 6 10 52 13 65 H-matrix approximations of the exponential covariance matrix (left), its hierarchical Cholesky factor L̃ (middle), and the zoomed upper-left corner of the matrix (right), n = 4000, ` = 0.09, ν = 0.5, σ2 = 1. 6

4 * What will change after H-matrix approximation? Approximate C by CH 1. How the eigenvalues of C and CH differ ? 2. How det(C) differs from det(CH) ? 3. How L differs from LH ? [Mario Bebendorf et al] 4. How C−1 differs from (CH)−1 ? [Mario Bebendorf et al] 5. How L̃(θ, k) differs from L(θ)? 6. What is optimal H-matrix rank? 7. How θH differs from θ? For theory, estimates for the rank and accuracy see works of Bebendorf, Grasedyck, Le Borne, Hackbusch,... 7

4 * Details of the parameter identification To maximize the log-likelihood function we use the Brent’s method (combining bisection method, secant method and inverse quadratic interpolation) or any other. 1. C(θ) ≈ e C(θ, ε). 2. e C(θ, k) = e L(θ, k)e L(θ, k)T 3. ZT e C−1Z = ZT (e Le LT )−1Z = vT · v, where v is a solution of e L(θ, k)v(θ) := Z. log det{e C} = log det{e Le LT } = log det{ n Y i=1 λ2 i } = 2 n X i=1 logλi , e L(θ, k) = − n 2 log(2π) − n X i=1 log{e Lii (θ, k)} − 1 2 (v(θ)T · v(θ)). (2) 8

Dependence of log-likelihood ingredients on parameters, n = 4225. k = 8 in the first row and k = 16 in the second. 9

4 * Remark: stabilization with nugget To avoid instability in computing Cholesky, we add: e Cm = e C + τ2I. Let λi be eigenvalues of e C, then eigenvalues of e Cm will be λi + τ2, log det(e Cm) = log Qn i=1(λi + τ2) = Pn i=1 log(λi + τ2). (left) Dependence of the negative log-likelihood on parameter ` with nuggets {0.01, 0.005, 0.001} for the Gaussian covariance. (right) Zoom of the left figure near minimum; n = 2000 random points from moisture example, rank k = 14, τ2 = 1, ν = 0.5. 10

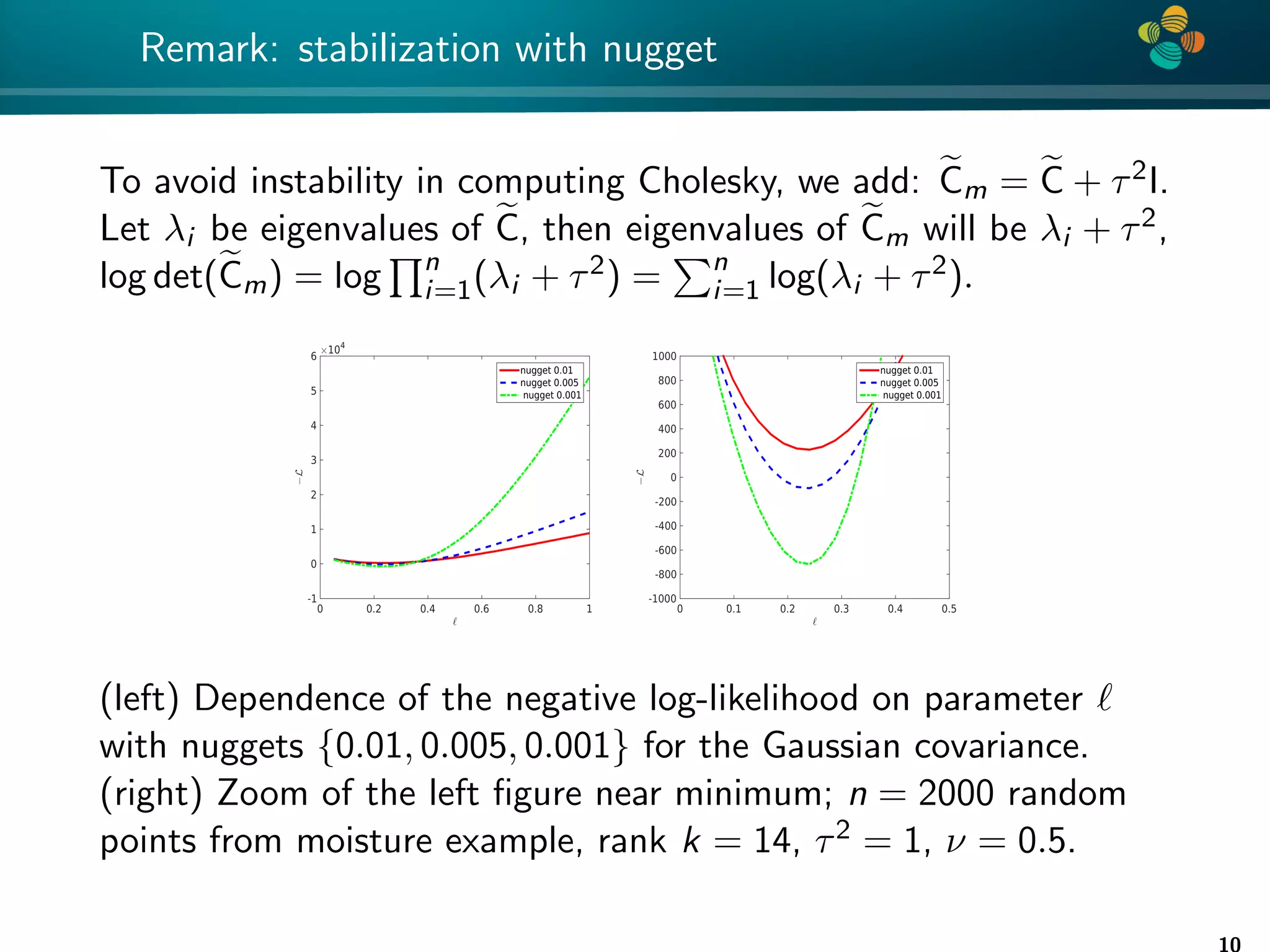
4 * Error analysis Theorem (1) Let e C be an H-matrix approximation of matrix C ∈ Rn×n such that ρ(e C−1 C − I) ≤ ε 1. Then |log det C − log det e C| ≤ −nlog(1 − ε), (3) Proof: See [Ballani, Kressner 14] and [Ipsen 05]. Remark: factor n is pessimistic and is not really observed numerically. 11

4 * Error in the log-likelihood Theorem (2) Let e C ≈ C ∈ Rn×n and Z be a vector, kZk ≤ c0 and kC−1k ≤ c1. Let ρ(e C−1C − I) ≤ ε 1. Then it holds | e L(θ) − L(θ)| = 1 2 (log|C| − log|e C|) + 1 2 |ZT C−1 − e C−1 Z| ≤ − 1 2 · nlog(1 − ε) + 1 2 |ZT C−1 C − e C−1 C C−1 Z| ≤ − 1 2 · nlog(1 − ε) + 1 2 c2 0 · c1 · ε. 12

4 * H-matrix approximation ε accuracy in each sub-block, n = 16641, ν = 0.5, c.r.=compression ratio. ε |log|C| − log|e C|| | log|C|−log|e C| log|e C| | kC − e CkF kC−e Ck2 kCk2 kI − (e Le L )−1 Ck2 c.r. in % ` = 0.0334 1e-1 3.2e-4 1.2e-4 7.0e-3 7.6e-3 2.9 9.16 1e-2 1.6e-6 6.0e-7 1.0e-3 6.7e-4 9.9e-2 9.4 1e-4 1.8e-9 7.0e-10 1.0e-5 7.3e-6 2.0e-3 10.2 1e-8 4.7e-13 1.8e-13 1.3e-9 6e-10 2.1e-7 12.7 ` = 0.2337 1e-4 9.8e-5 1.5e-5 8.1e-5 1.4e-5 2.5e-1 9.5 1e-8 1.45e-9 2.3e-10 1.1e-8 1.5e-9 4e-5 11.3 log|C| = 2.63 for ` = 0.0334 and log|C| = 6.36 for ` = 0.2337. 13

4 * Boxplots for unknown parameters Moisture data example. Boxplots for the 100 estimates of (`, ν, σ2), respectively, when n = 32K, 16K, 8K, 4K, 2K. H-matrix with a fixed rank k = 11. Green horizontal lines denote 25% and 75% quantiles for n = 32K. 14

4 * How much memory is needed? 0 0.5 1 1.5 2 2.5 ℓ, ν = 0.325, σ2 = 0.98 5 5.5 6 6.5 size, in bytes ×10 6 1e-4 1e-6 0.2 0.4 0.6 0.8 1 1.2 1.4 ν, ℓ = 0.58, σ2 = 0.98 5.2 5.4 5.6 5.8 6 6.2 6.4 6.6 size, in bytes ×10 6 1e-4 1e-6 (left) Dependence of the matrix size on the covariance length `, and (right) the smoothness ν for two different H-accuracies ε = {10−4, 10−6} 15

4 * Error convergence 0 10 20 30 40 50 60 70 80 90 100 −25 −20 −15 −10 −5 0 rank k log(rel. error) Spectral norm, L=0.1, nu=1 Frob. norm, L=0.1 Spectral norm, L=0.2 Frob. norm, L=0.2 Spectral norm, L=0.5 Frob. norm, L=0.5 0 10 20 30 40 50 60 70 80 90 100 −16 −14 −12 −10 −8 −6 −4 −2 0 rank k log(rel. error) Spectral norm, L=0.1, nu=0.5 Frob. norm, L=0.1 Spectral norm, L=0.2 Frob. norm, L=0.2 Spectral norm, L=0.5 Frob. norm, L=0.5 Convergence of the H-matrix approximation errors for covariance lengths {0.1, 0.2, 0.5}; (left) ν = 1 and (right) ν = 0.5, computational domain [0, 1]2. 16

4 * How log-likelihood depends on n? ν 0 0.1 0.2 0.3 0.4 0.5 0.6 −L 10 3 10 4 10 5 2000 4000 8000 16000 32000 Figure: Dependence of negative log-likelihood function on different number of locations n = {2000, 4000, 8000, 16000, 32000} in log-scale. 17

4 * Time and memory for parallel H-matrix approximation Maximal # cores is 40, ν = 0.325, ` = 0.64, σ2 = 0.98 n C̃ L̃L̃ time size kB/dof time size kI − (L̃L̃ )−1 C̃k2 sec. MB sec. MB 32.000 3.3 162 5.1 2.4 172.7 2.4 · 10−3 128.000 13.3 776 6.1 13.9 881.2 1.1 · 10−2 512.000 52.8 3420 6.7 77.6 4150 3.5 · 10−2 2.000.000 229 14790 7.4 473 18970 1.4 · 10−1 Dell Station, 20 × 2 cores, 128 GB RAM, bought in 2013 for 10.000 USD. 18

4 * Prediction Let Z = (Z1, Z2) has mean zero and a stationary covariance, Z1 - known, Z2 unknown. C = C11 C12 C21 C22, We compute predicted values Z2 = C21C−1 11 Z1 Z2 has the conditional distribution with the mean value C21C−1 11 Z1 and the covariance matrix C22 − C21C−1 11 C12. 19

4 * 2021 KAUST Competition We participated in 2021 KAUST Competition on Spatial Statistics for Large Datasets. You can download the datasets and look the final results here https://cemse.kaust.edu.sa/stsds/ 2021-kaust-competition-spatial-statistics-large-datasets 20

4 * Prediction Prediction for two datasets. The yellow points at 900.000 locations were used for training and the blue points were predicted at 100.000 new locations. 21

4 * Machine learning methods to make prediction k-nearest neighbours (kNN): For each point x find its k nearest neighbors x1, . . . , xk, and set: ŷ(x) = 1 k Pk i=1 yi . Random Forest (RF): a large number of decision (or regression) trees are generated independently on random sub-samples of data. The final decision for x is calculated over the ensemble of trees by averaging the predicted outcomes. Deep Neural Network (DNN): fully connected neural network Input layer consists of two neurons (input feature dimensionality), and output layer consists of one neuron (predicted feature dimensionality). 22

4 * Prediction by kNN Prediction obtained by the kNN method. The yellow points at 900.000 locations were used for training and the blue points were predicted at 100.000 new locations. One can see a very well alignment of both. 23

4 * Conclusion I With H-matrices you can approximate Matérn covariance matrices, Gaussian log-likelihoods, identify unknown parameters and make predictions I MLE estimate and predictions depend on H-matrix accuracy I parameter identification problem has multiple solutions I Investigated dependence of H-matrix approximation error on the estimated parameters I Each of ML methods needs fine-tuning stage to optimize its hyperparameters or architecture. 24

4 * Open questions and TODOs I The Gaussian log-likelihood function has some drawbacks for very large matrices I How to skip/avoid redundant data? I A good starting point for optimization is needed I a “preconditioner” (a simple cov. matrix) is needed I H-matrices become expensive for large number of parameters to be identified I error estimates are needed

4 * Literature All tests are reproducible https://github.com/litvinen/large_random_fields.git 1. A. Litvinenko, R. Kriemann, M.G. Genton, Y. Sun, D.E. Keyes, HLIBCov: Parallel hierarchical matrix approximation of large covariance matrices and likelihoods with applications in parameter identification, MethodsX 7, 100600, 2020 2. A. Litvinenko, Y. Sun, M.G. Genton, D.E. Keyes, Likelihood approximation with hierarchical matrices for large spatial datasets, Computational Statistics Data Analysis 137, 115-132, 2019 3. A. Litvinenko, R. Kriemann, V. Berikov, Identification of unknown parameters and prediction with hierarchical matrices, look arXiv and ResearchGate, March 2021 4. M. Espig, W. Hackbusch, A. Litvinenko, H.G. Matthies, E. Zander, Iterative algorithms for the post-processing of high-dimensional data, Journal of Computational Physics 410, 109396, 2020 26

4 * Literature 5. A. Litvinenko, D. Keyes, V. Khoromskaia, B.N. Khoromskij, H.G. Matthies, Tucker tensor analysis of Matérn functions in spatial statistics, Computational Methods in Applied Mathematics 19 (1), 101-122, 2019 6. B. N. Khoromskij, A. Litvinenko, H.G. Matthies, Application of hierarchical matrices for computing the Karhunen-Loéve expansion, Computing 84 (1-2), 49-67, 31, 2009 7. W. Nowak, A. Litvinenko, Kriging and spatial design accelerated by orders of magnitude: Combining low-rank covariance approximations with FFT-techniques, Mathematical Geosciences 45 (4), 411-435, 2013 8. M. Espig, W. Hackbusch, A. Litvinenko, H.G. Matthies, E. Zander, Efficient analysis of high dimensional data in tensor formats, Sparse Grids and Applications, 31-56, Springer, Berlin, 2013 27

4 * Acknowledgement V. Berikov was supported by the state contract of the Sobolev Institute of Mathematics (project no 0314-2019-0015), and by RFBR grant 19-29-01175. A. Litvinenko was supported by funding from the Alexander von Humboldt Foundation. 28

Identification of unknown parameters and prediction with hierarchical matrices. Comparison with ML methods.

More Related Content

What's hot

Similar to Identification of unknown parameters and prediction with hierarchical matrices. Comparison with ML methods.

More from Alexander Litvinenko

Recently uploaded

Identification of unknown parameters and prediction with hierarchical matrices. Comparison with ML methods.