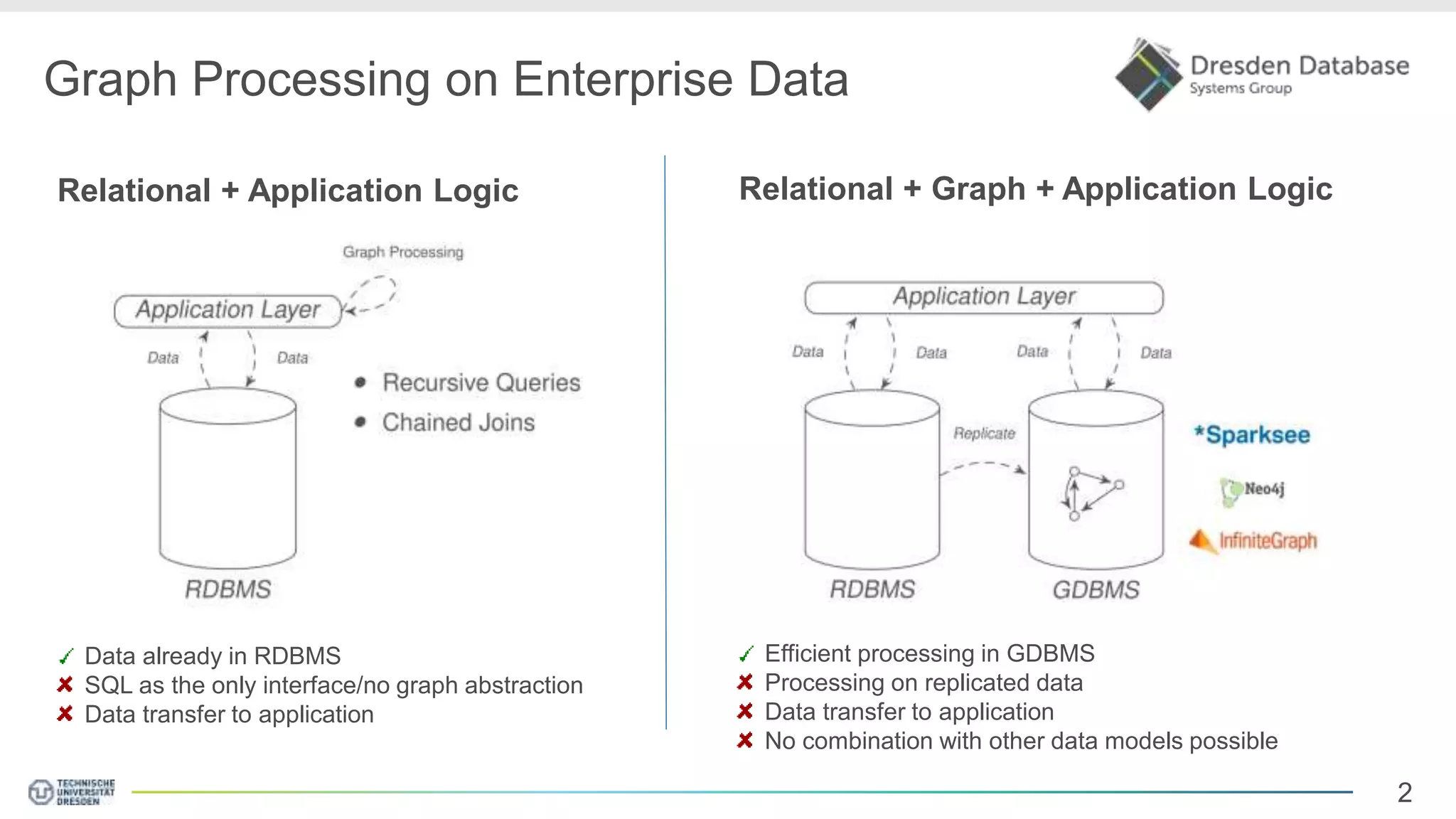
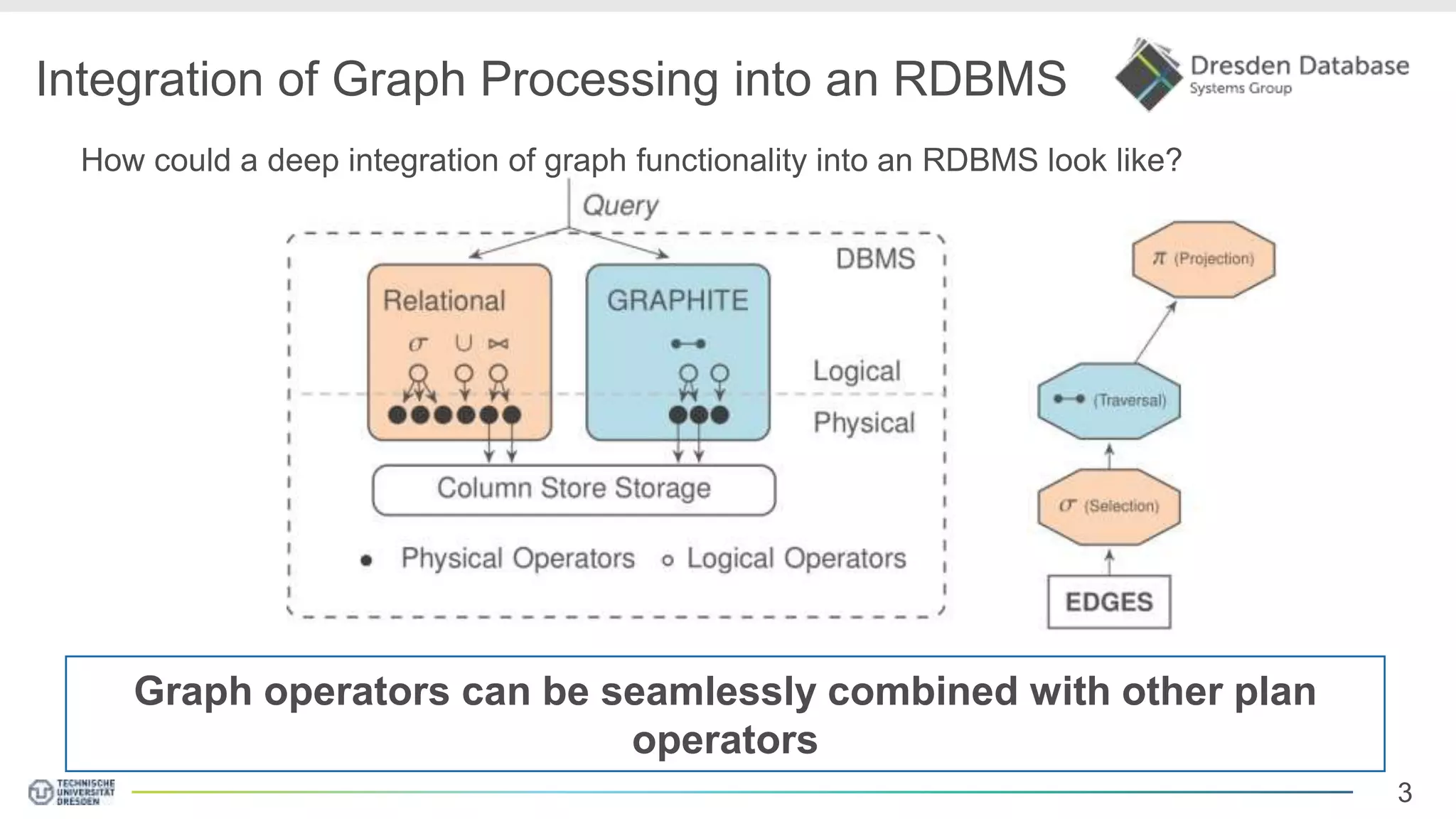
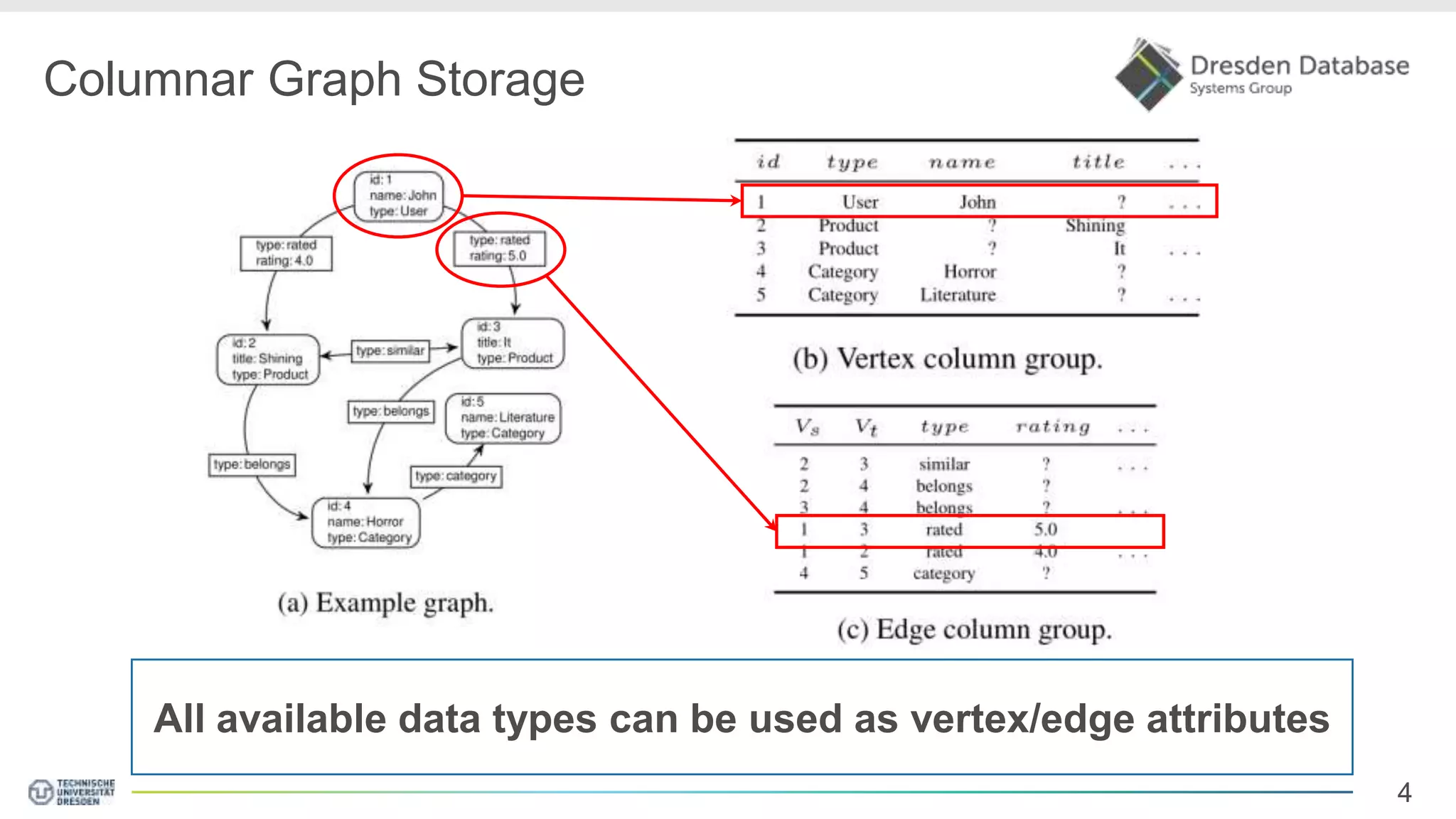
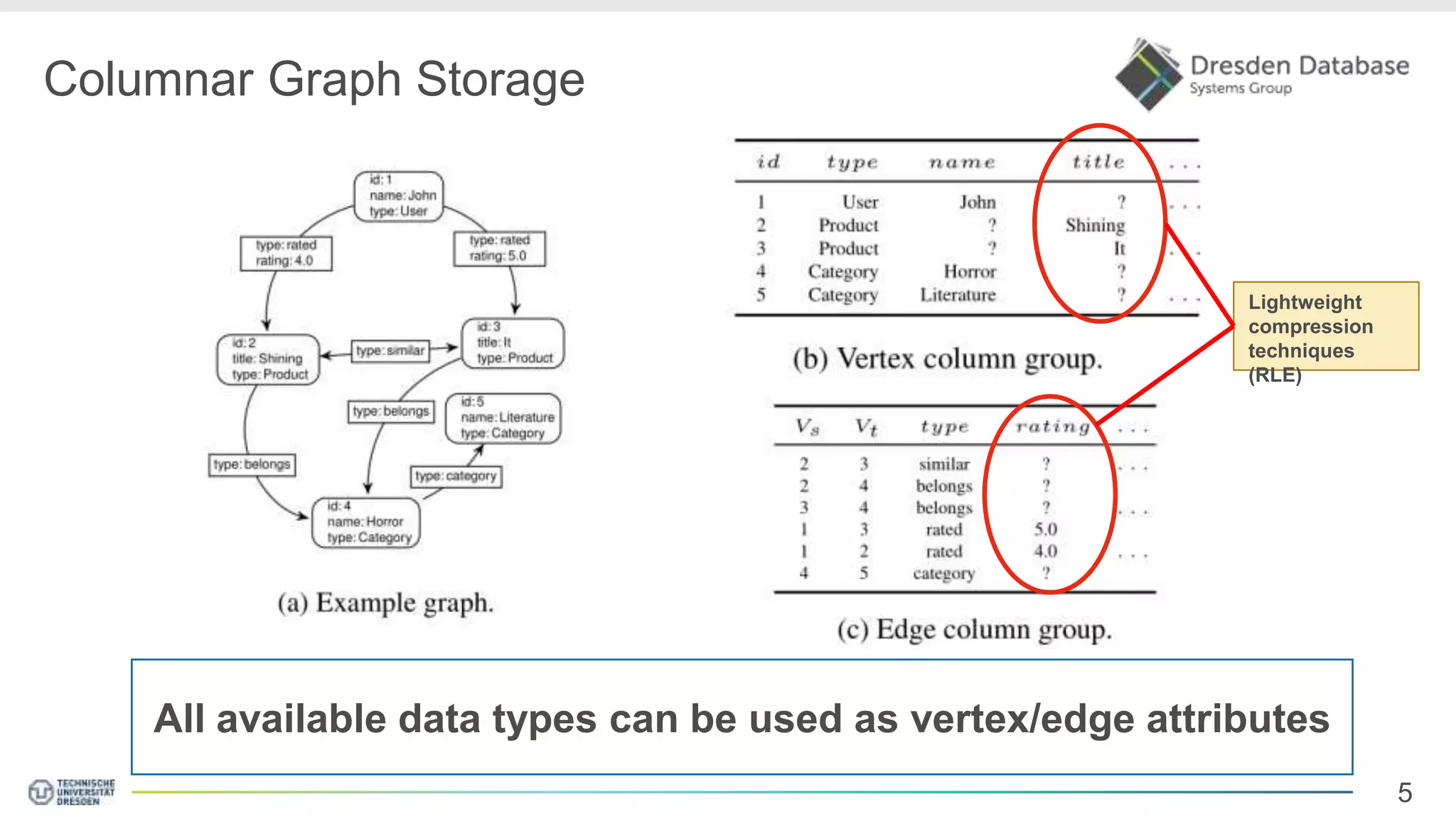
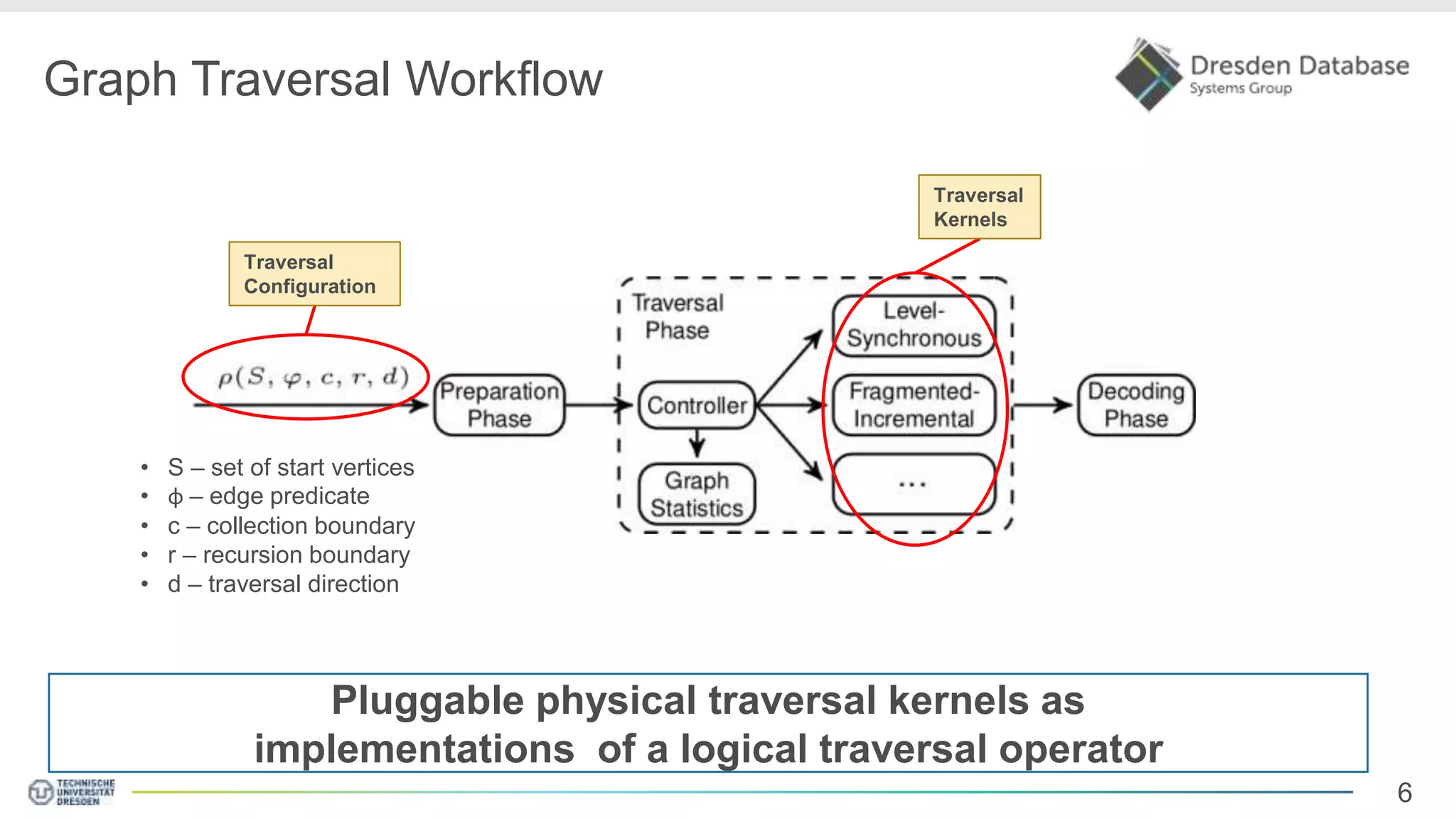
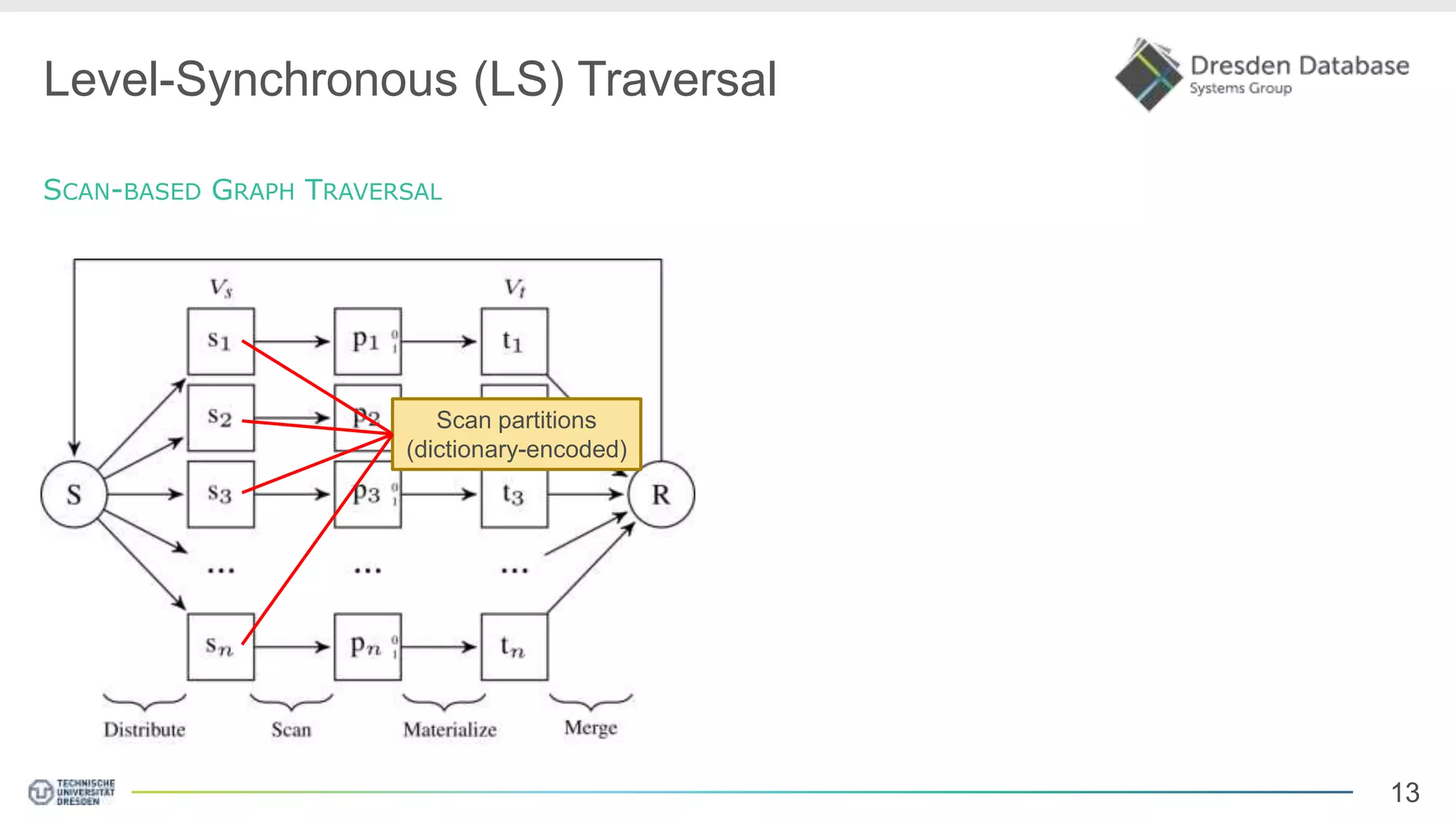
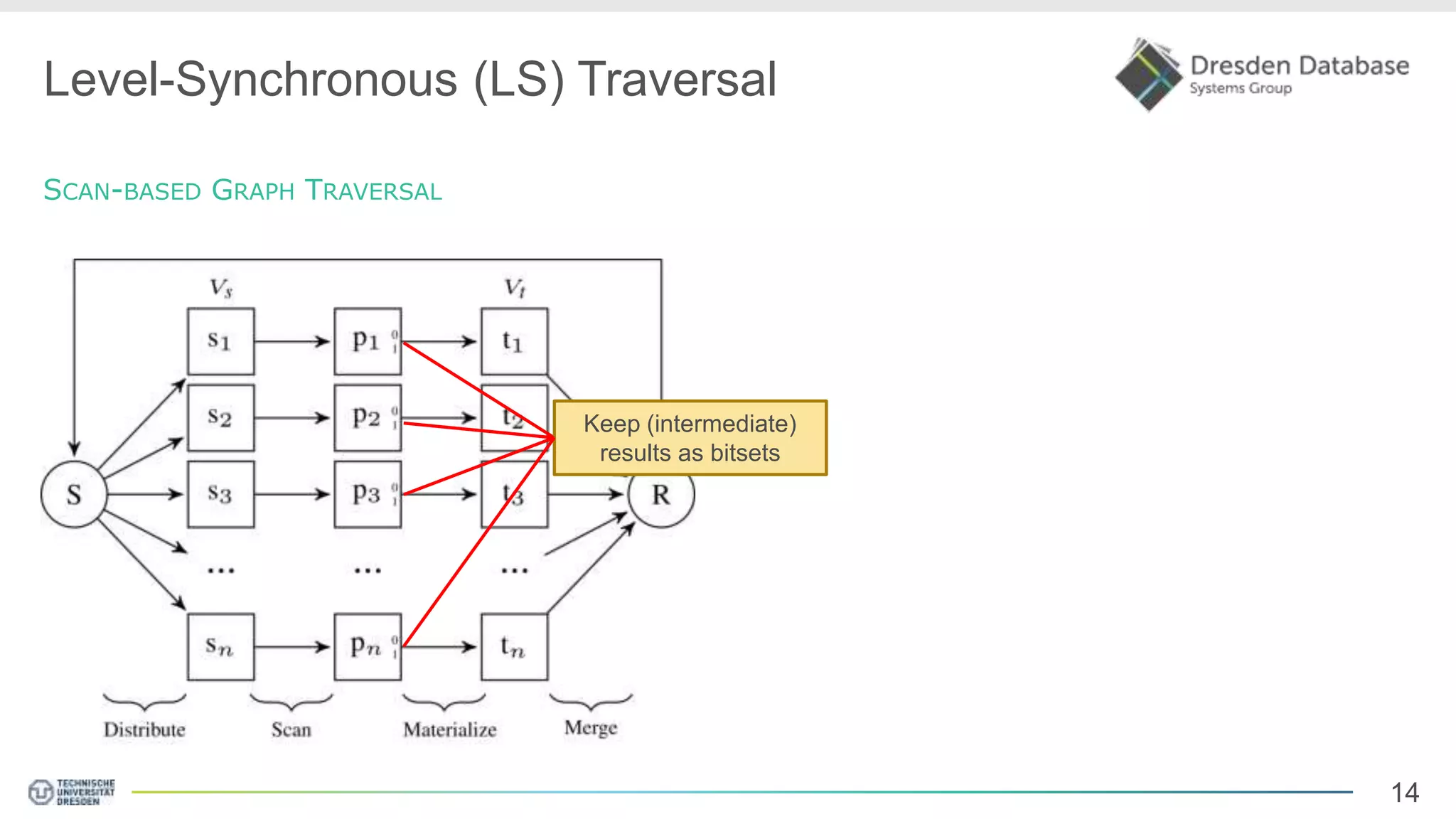
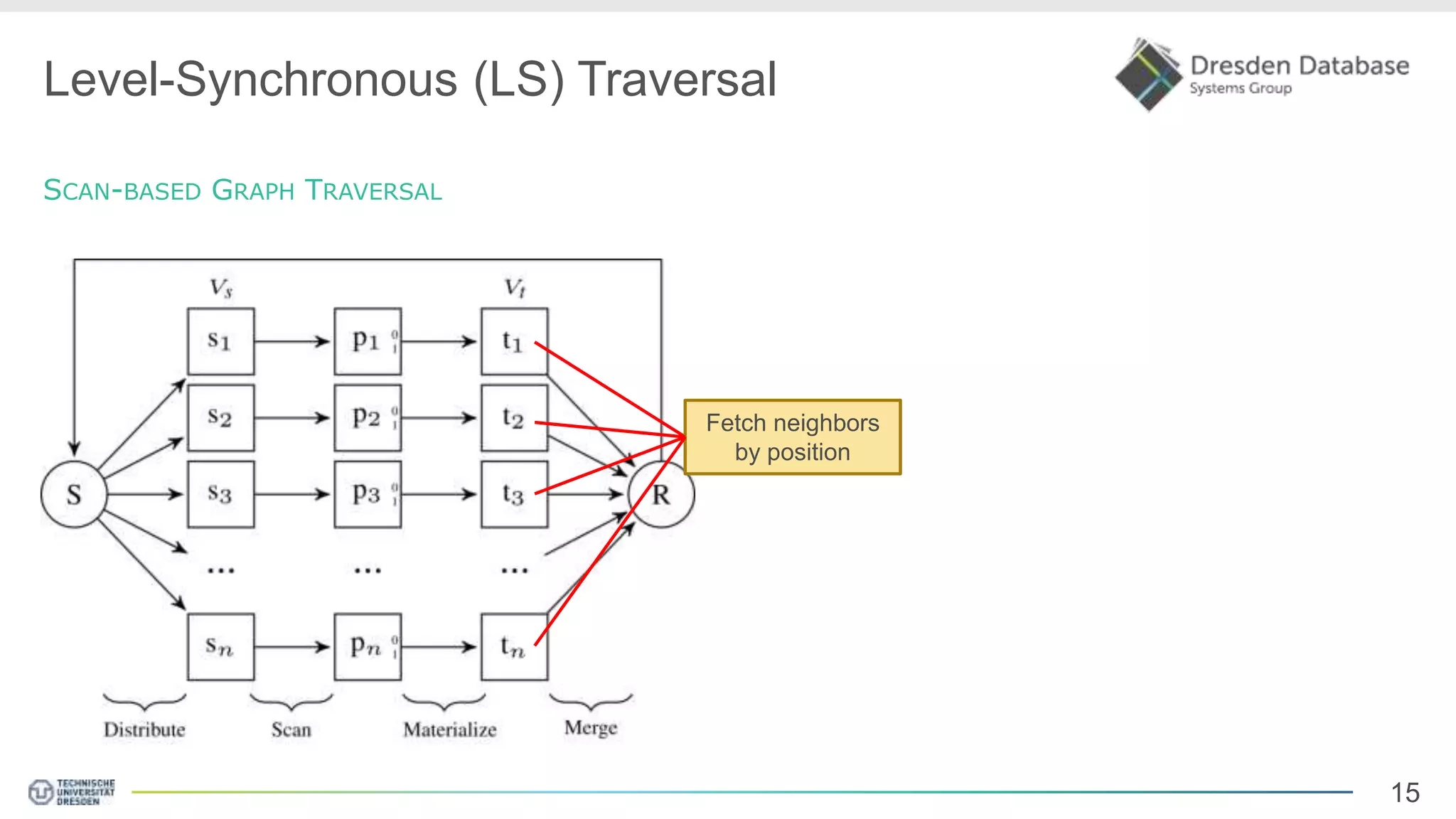
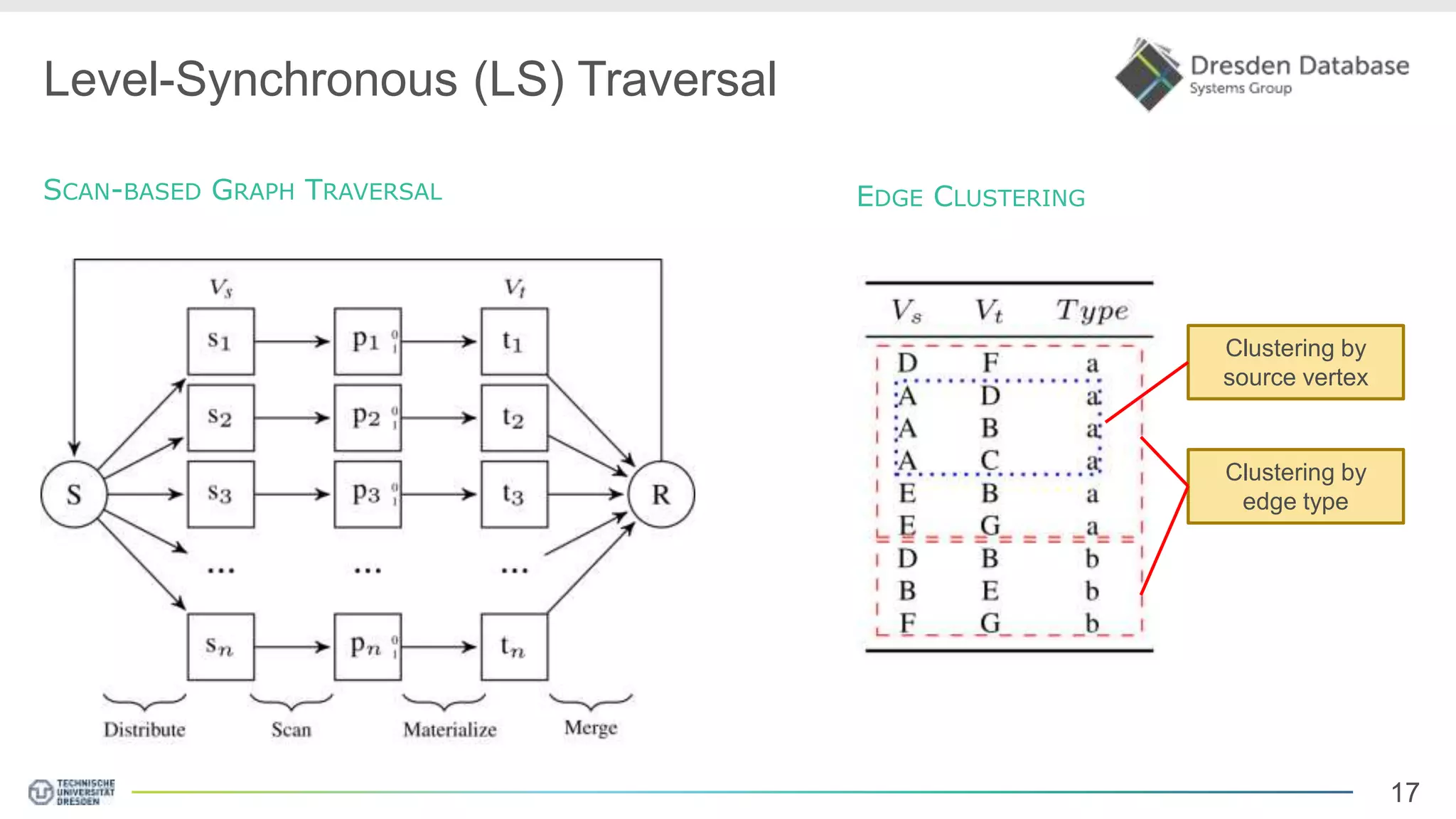
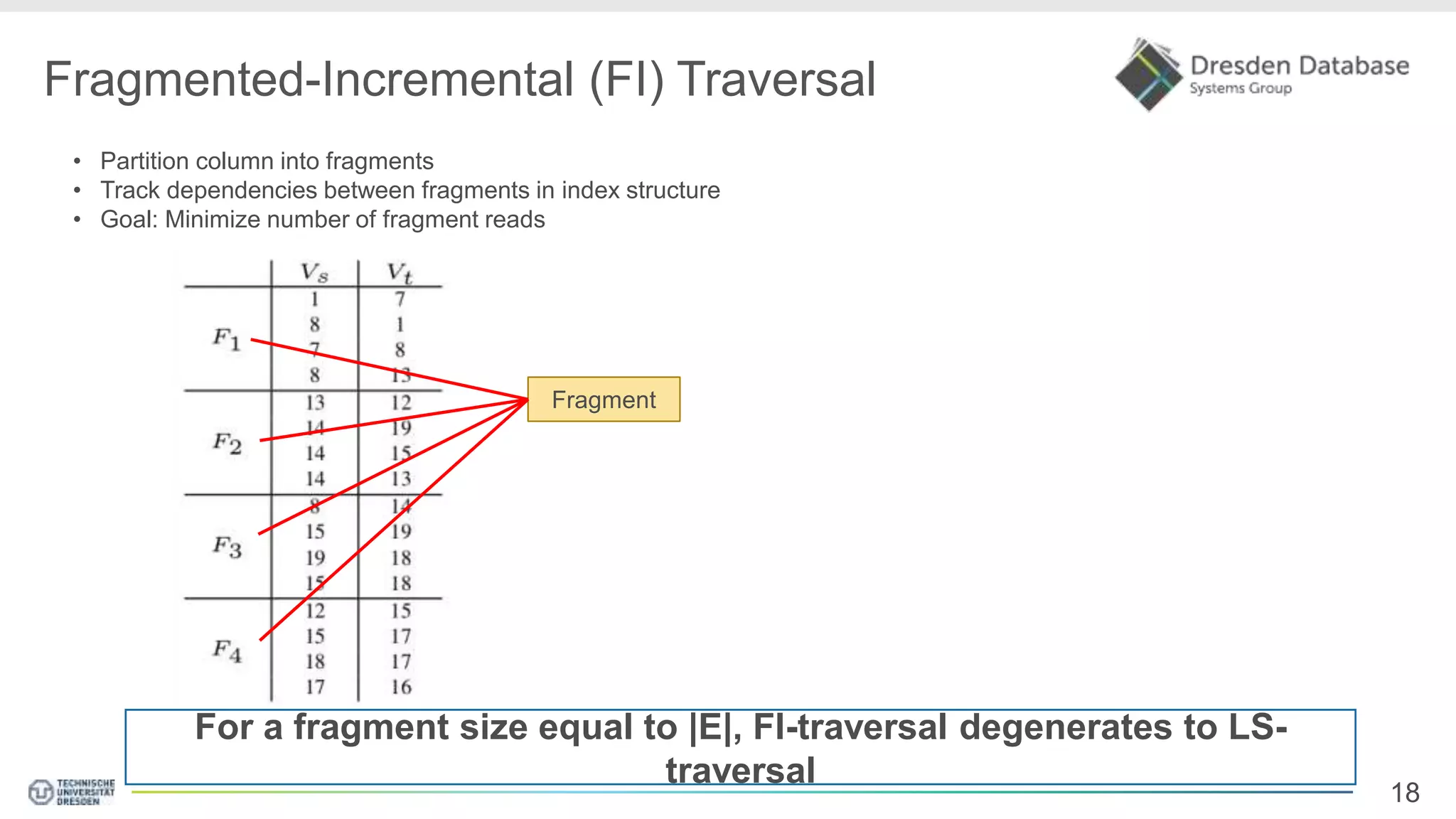
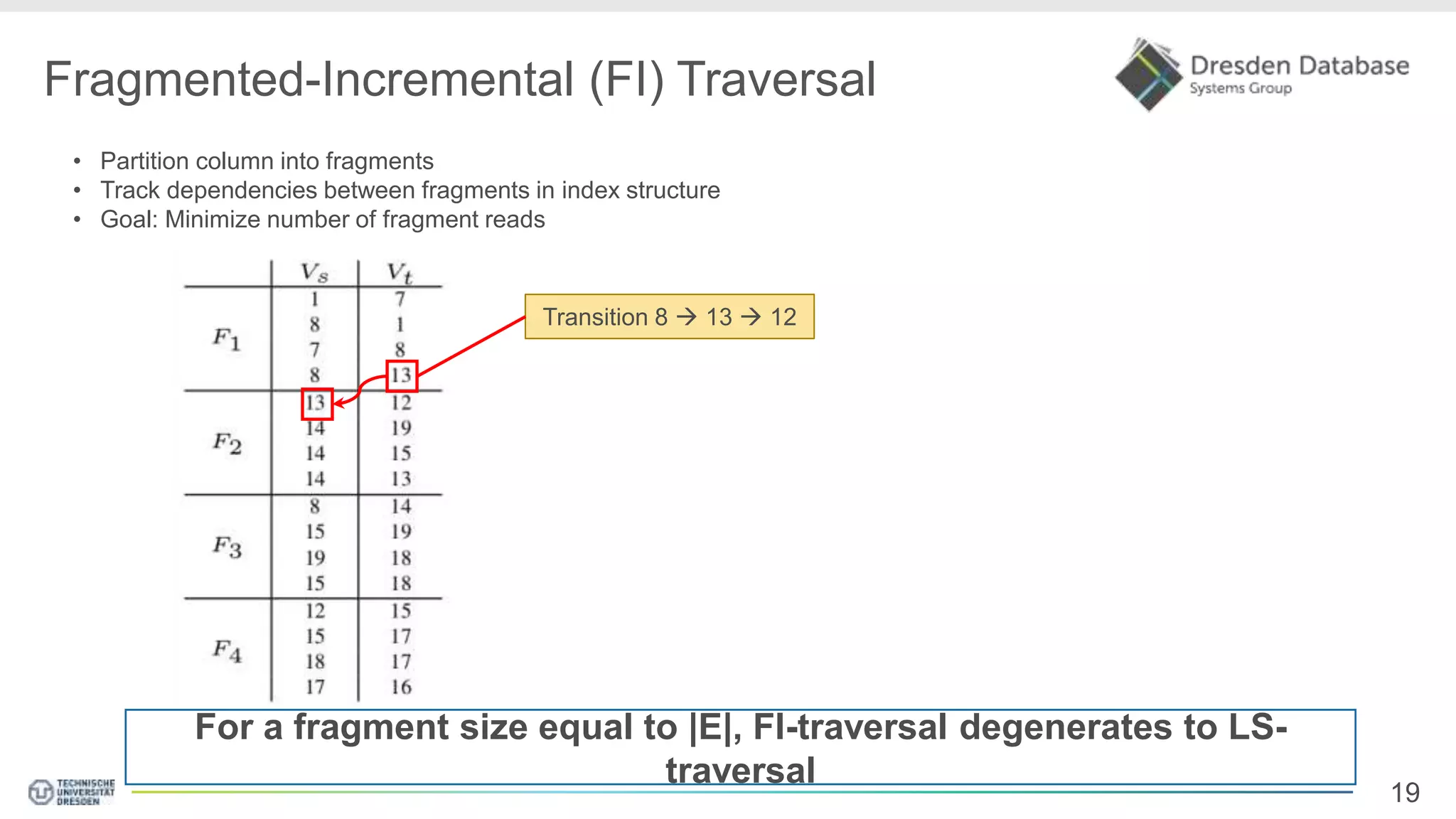
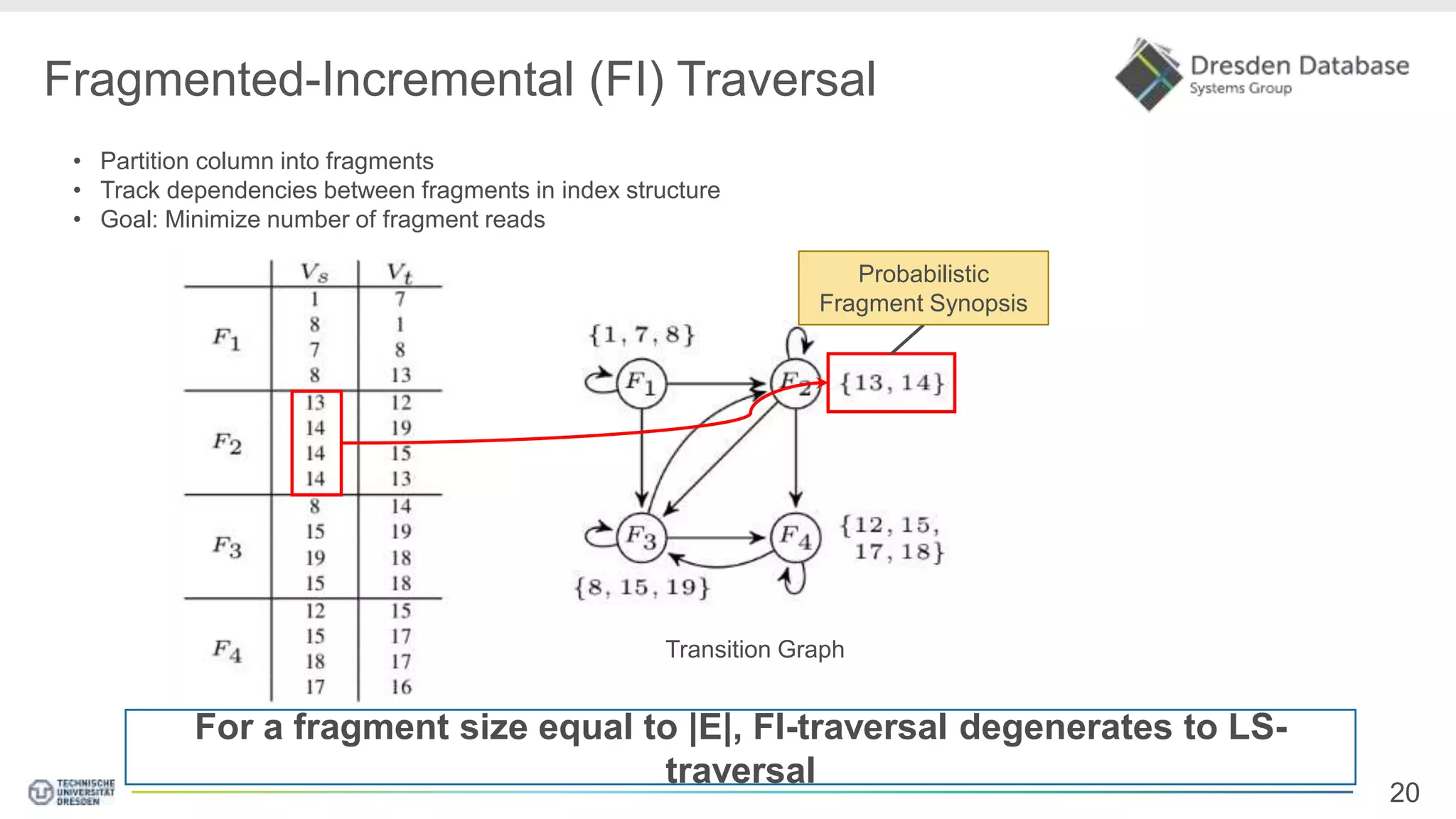
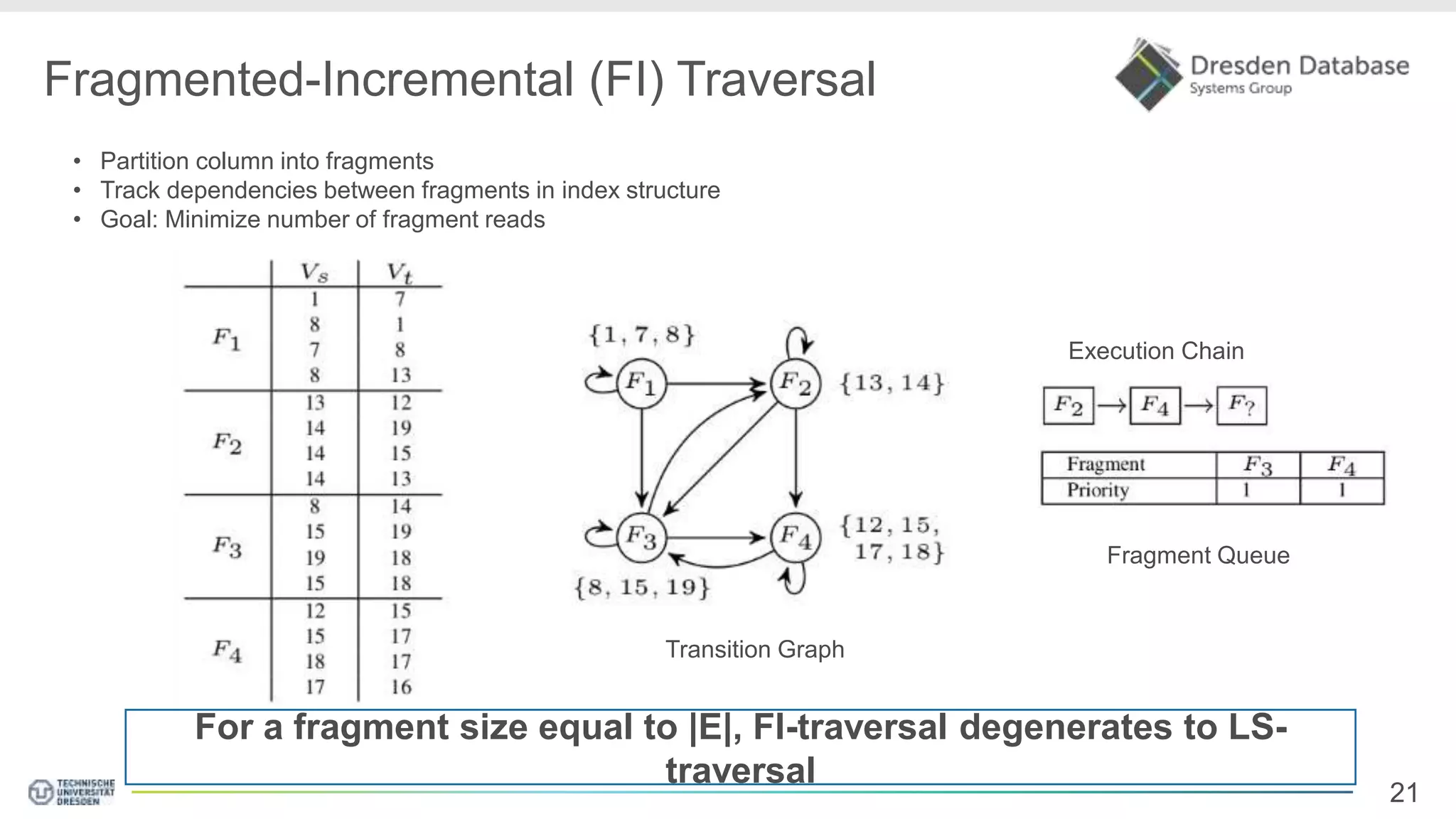
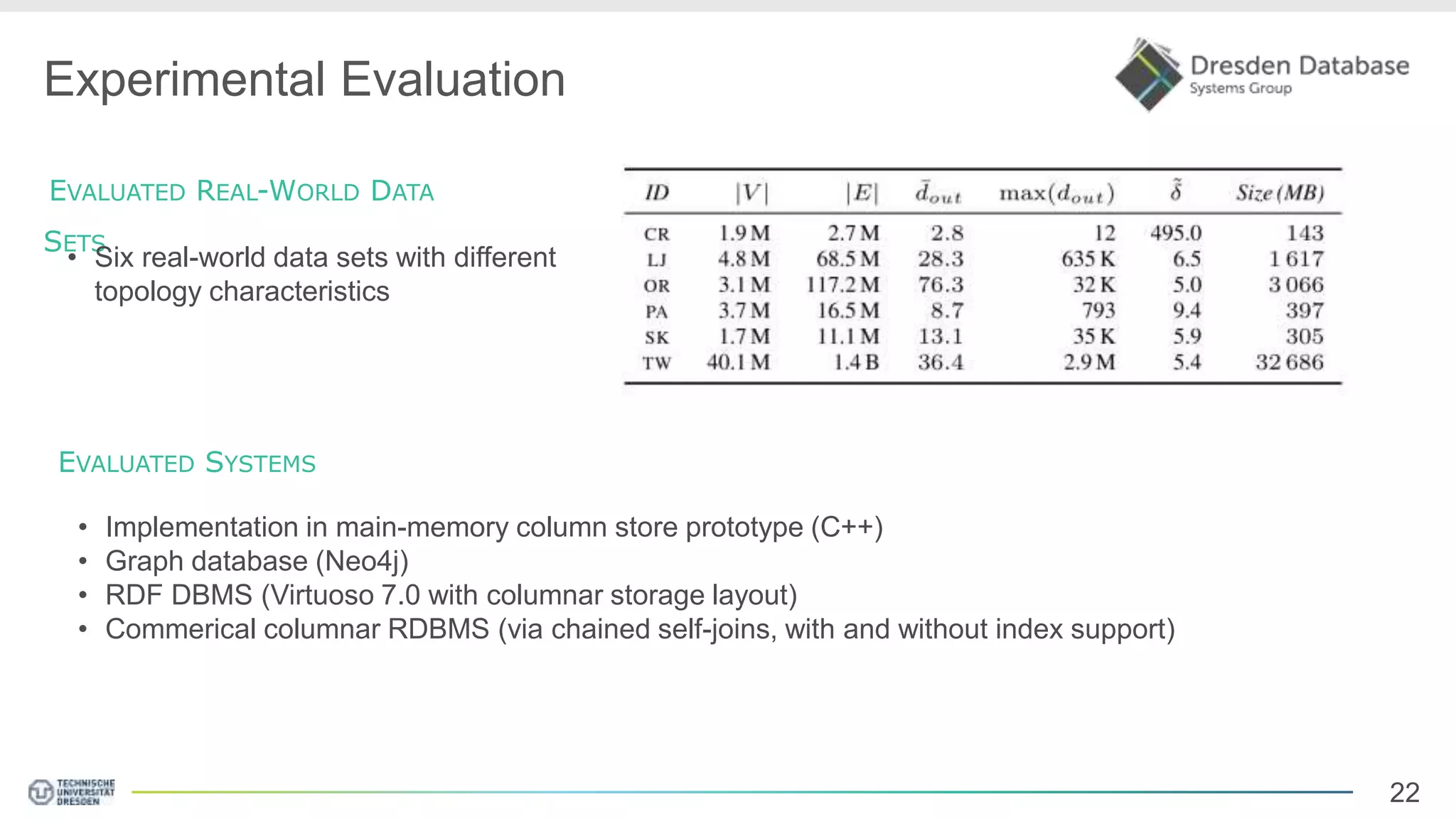
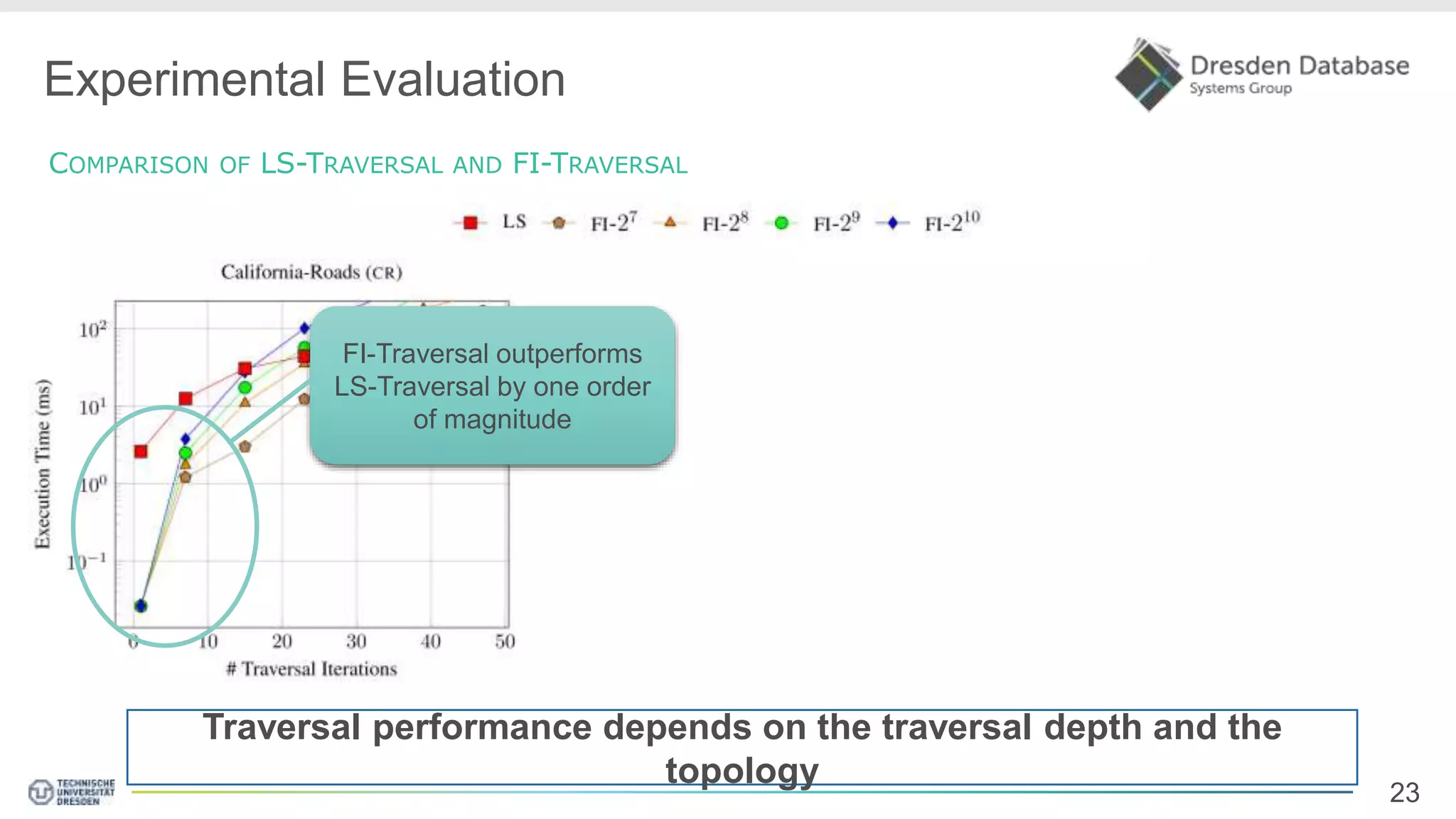
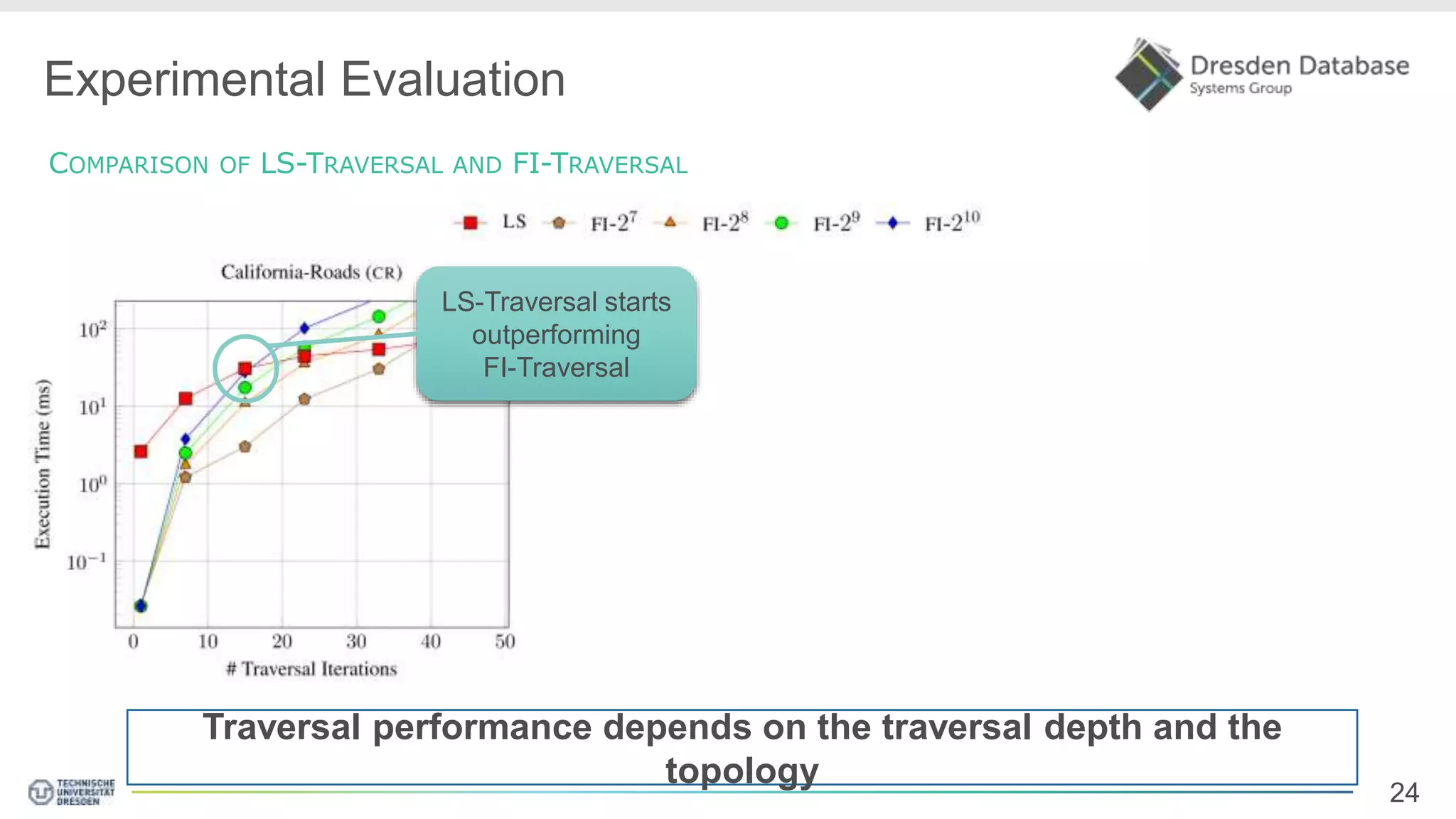
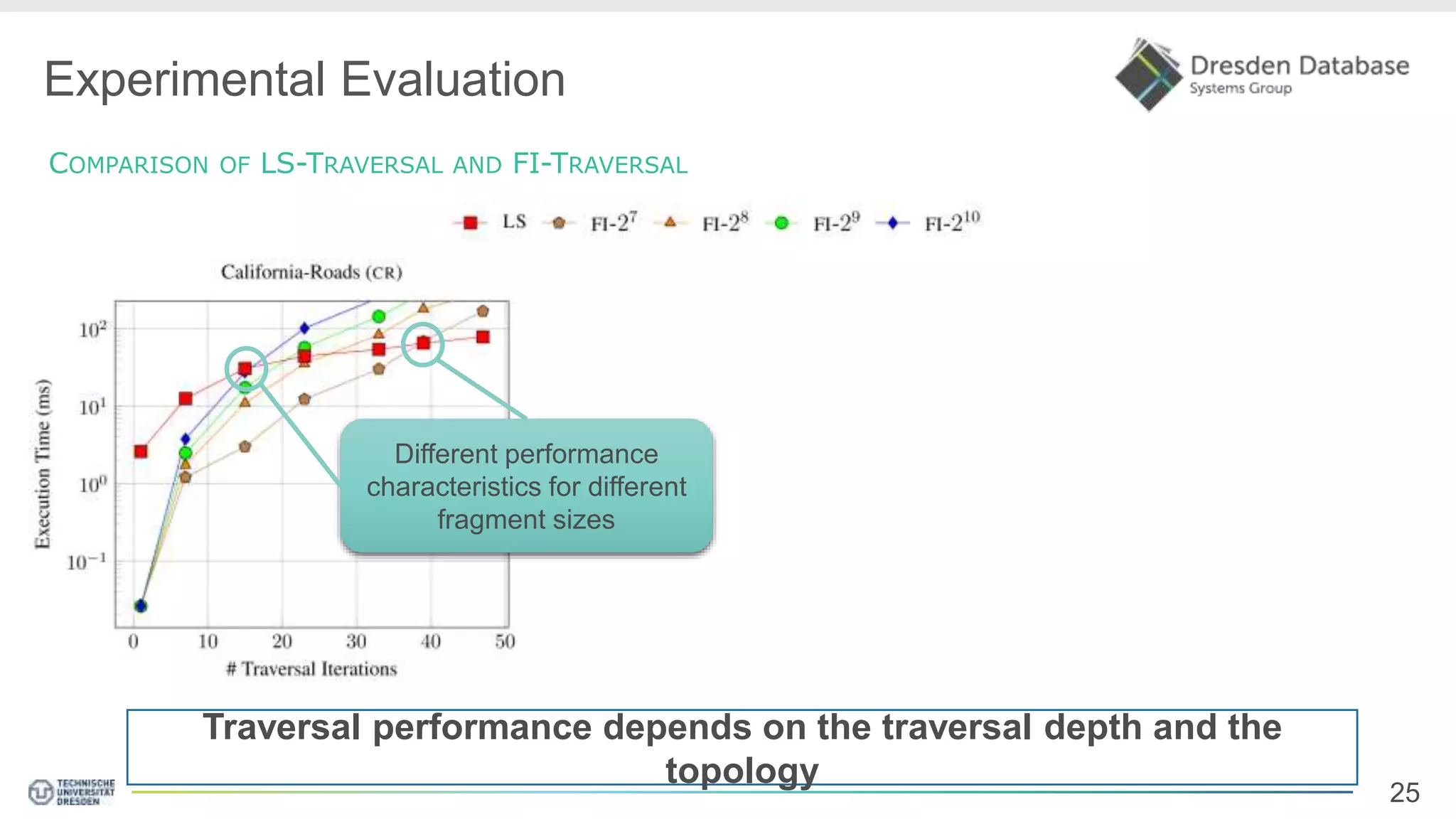
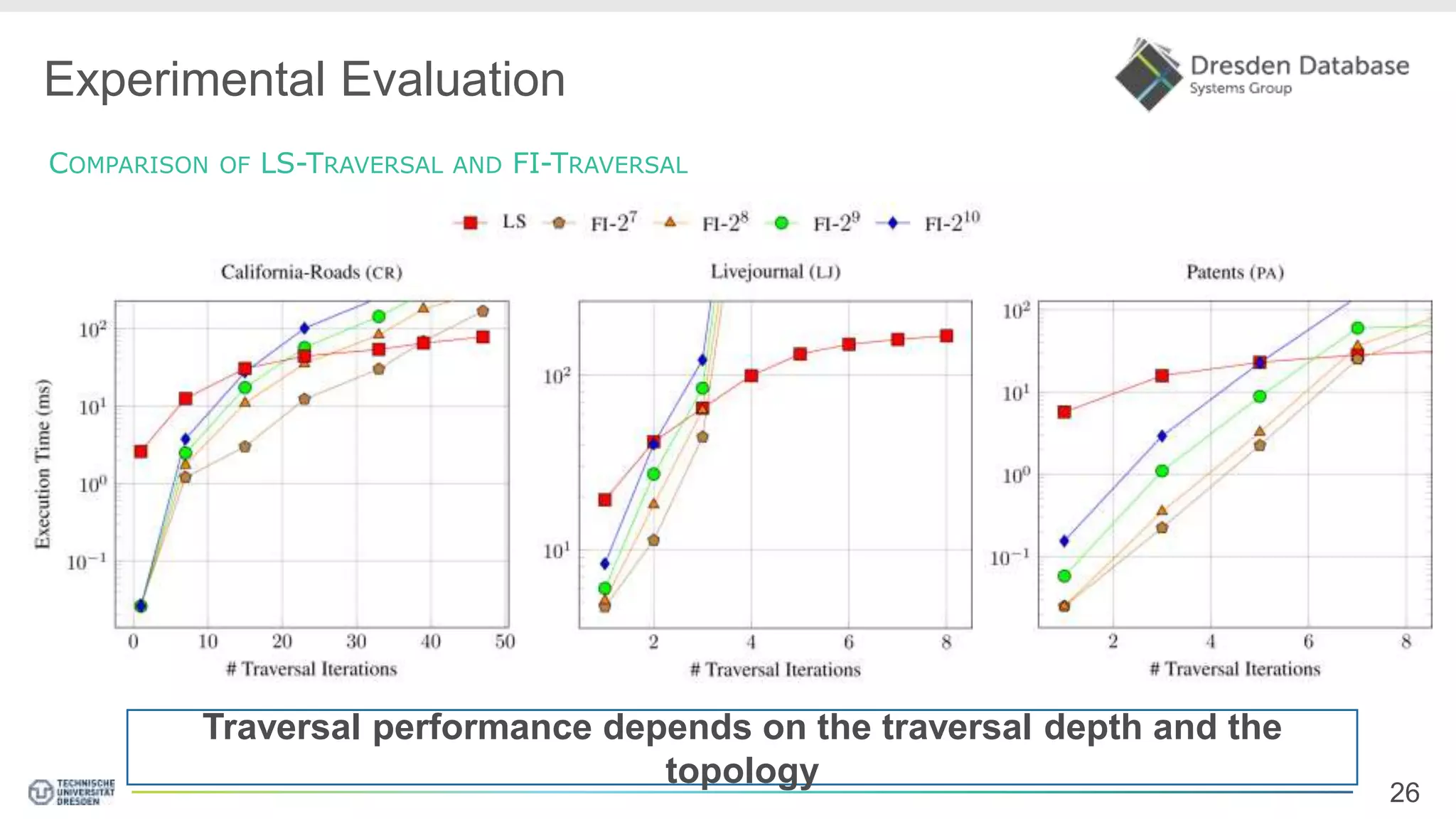
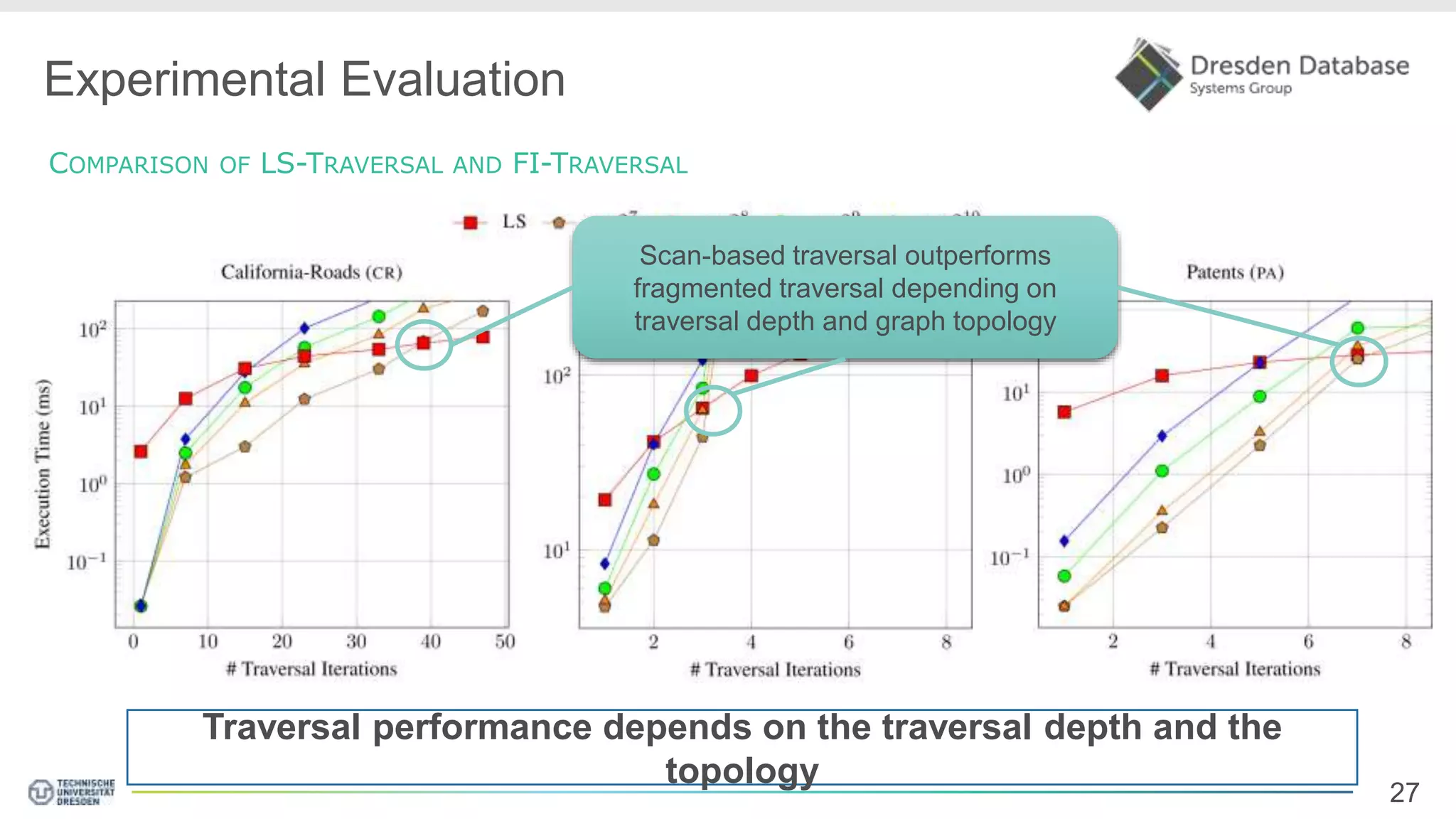
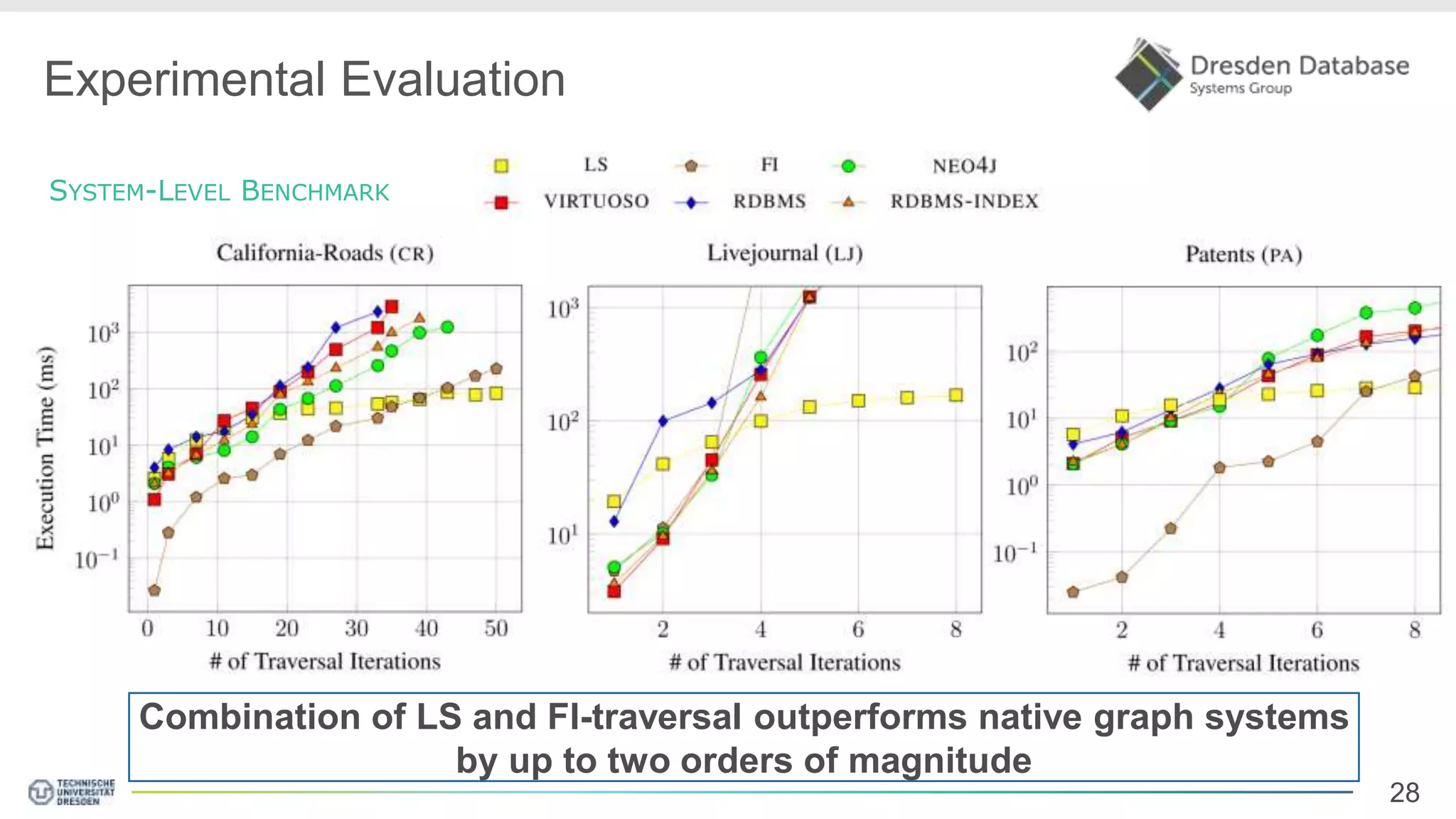
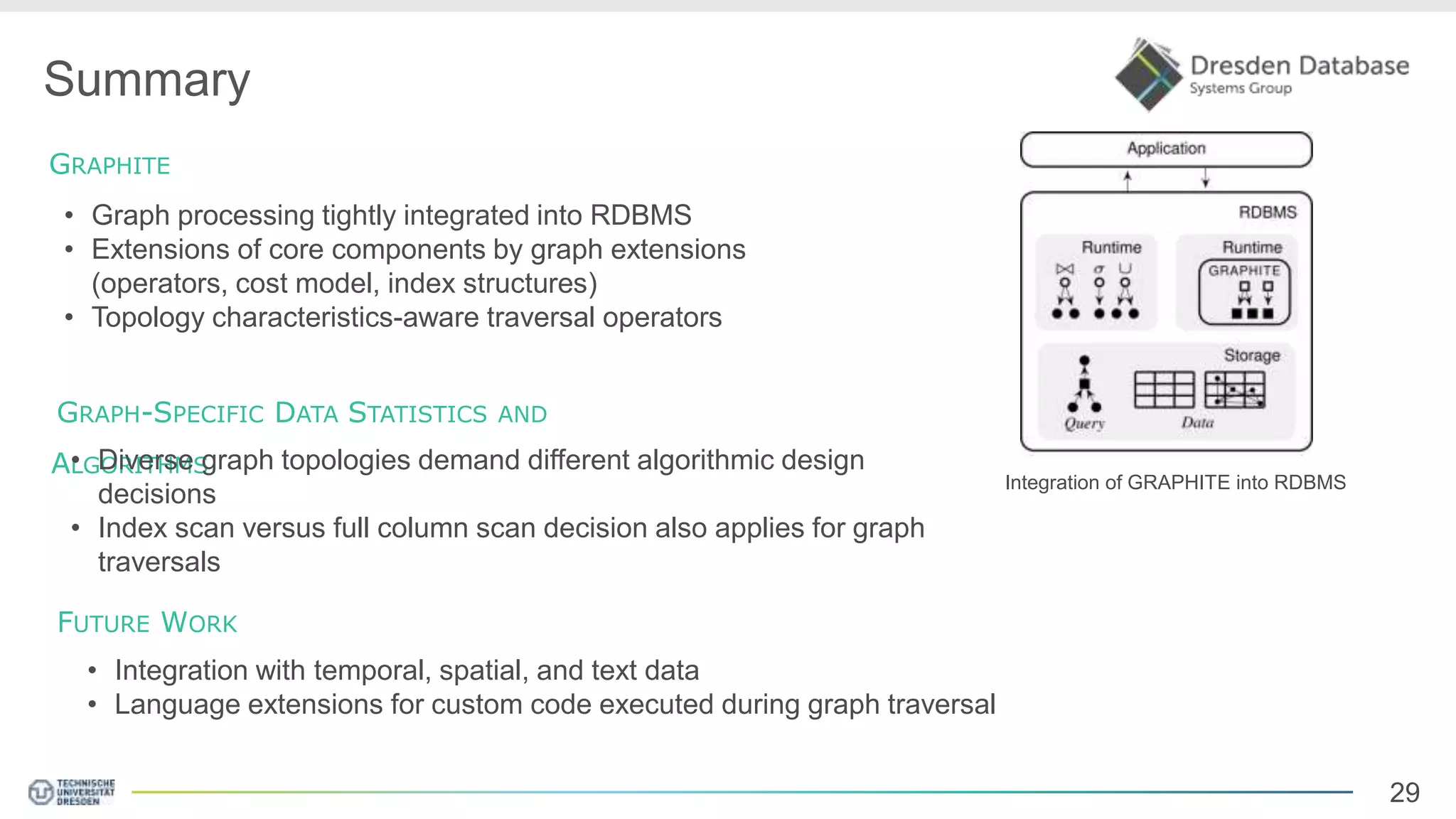
Graphite is a framework that integrates graph processing capabilities into relational database management systems. It allows graph operators to be combined with relational operators. It uses a columnar storage format to efficiently store graph data. The framework includes configurable graph traversal operators that can perform traversals using different algorithms like level-synchronous or fragmented-incremental traversal. An experimental evaluation compares the performance of these traversal algorithms on real-world graph datasets and finds that their performance depends on factors like traversal depth and graph topology. Integrating graph processing tightly into an RDBMS outperformed standalone graph database systems in benchmarks.