Gmdes a graph based modified data encryption standard algorithm with enhanced security

Gmdes a graph based modified data encryption standard algorithm with enhanced security

• 1.
  IJRET: International Journalof Research in Engineering and Technology eISSN: 2319-1163 | pISSN: 2321-7308 __________________________________________________________________________________________ Volume: 03 Issue: 03 | Mar-2014, Available @ http://www.ijret.org 653 GMDES: A GRAPH BASED MODIFIED DATA ENCRYPTION STANDARD ALGORITHM WITH ENHANCED SECURITY Debajit Sensarma1 , Samar Sen Sarma2 1 Department of Computer Science & Engineering, University of Calcutta, Kolkata, West Bengal, India 2 Department of Computer Science & Engineering, University of Calcutta, Kolkata, West Bengal, India Abstract Cryptography is one of the prime techniques of secured symbolic data transmission over any communication channel. Security is the most challenging and essential aspects in today’s internet and network applications. Thus, design of a secure encryption algorithm is very necessary which can protect the unauthorized attacks. An encryption algorithm is computationally secure if it cannot be intruded with the standard resources. The algorithm proposed here is graph based. Its efficiency surpasses the standard DES algorithm in general. Graphs can be used for designing block ciphers, stream ciphers or public-key ciphers. The algorithm is graph automorphism based partial symmetric key algorithm and it is not fully depended on secret key and produces different cipher text by applying same key on the same plain text. Keywords: DES, Graph Automorphism, Hamiltonian Cycle, Encryption, Decryption -----------------------------------------------------------------------***----------------------------------------------------------------------- 1. INTRODUCTION Cryptography is a science which studies the techniques for secure communication in the presence of intruders or unauthenticated access. It is about constructing and analyzing protocols that overcome the influence of intruders. Cryptography converts the original message in a non-readable format and sends the message over an insecure channel. The original message is called plain text. Disguising the plain text to hide its original contents is called encryption. The non- readable format of the plain text after encryption is called cipher text. The process of reverting the cipher text to its corresponding plain text is called decryption process. For both encryption and decryption process key is used. It is used with plain text at the time of encryption and with the cipher text at the time of decryption. Cryptography provides number of security goals to ensure the privacy of the data. The goals of the cryptography are- Confidentiality, Integrity, Availability, Authenticity, Non Repudiation, Access control [2]. In cryptography the encryption algorithms can be classified into two broad categories- Symmetric key and asymmetric key encryption. In Symmetric key cryptography the key used for encryption and decryption is same. Thus, the key must be distributed through the secure channel before transmission started. These types of algorithms are highly depended on the nature of the key. DES, Triple DES, AES, RC4, RC6, BLOWFISH etc are the example of symmetric key algorithms. In asymmetric key cryptography two different keys are used for encryption and decryption, they are private and public key. The public key is available to all in the network. The sender who wants to transmit message, encrypts the message with receiver‟s public key and only the authorized receiver can decrypt the message with its private key. RSA is the example of asymmetric key cryptography. According to [15] symmetric key algorithm is faster than asymmetric key algorithm and also memory requirement of the former is lesser than the later. In this paper a graph based modified DES algorithm is proposed. It is depended on the Hamiltonian cycle and the automorphism [3, 4] property of the 4-cube graph. Here, an arbitrary Hamiltonian cycle of a 4-cube graph is used as a secret key and sixteen different Hamiltonian cycles of the non Automorphic graphs of the given 4-cube graph is used as the sub keys for sixteen rounds like classical DES. It is a partial symmetric key algorithm based on the block cipher. The main advantage of the proposed algorithm is, like other symmetric key algorithms it is not fully depended on the secret key, rather it also depended on the sub keys, which are remain encrypted with the private key of the sender and stored in a secure mapping table. When a receiver wants to decrypt the message, it will send request to the sender. The sender uses Zero Knowledge Protocol [6] to verify the receiver. If the receiver is authorized, then sender will decrypt the sub keys of the secret mapping table with the sender‟s private key. Then only that particular receiver can decrypts the cipher text. Another advantage is that, this algorithm produces different cipher texts for a single key and single pain text, which also decreases the probability of various malicious attacks. The paper is organized as follows- In section 2 some preliminaries are given, Section 3 explain a brief review of related literature, Section 4 illustrates the proposed algorithm, in section 5 a short example is given, section 6 gives some
• 2.
  IJRET: International Journalof Research in Engineering and Technology eISSN: 2319-1163 | pISSN: 2321-7308 __________________________________________________________________________________________ Volume: 03 Issue: 03 | Mar-2014, Available @ http://www.ijret.org 654 experimental results, section 7 explain the strength of the proposed method, Security analysis of proposed method is given in section 8, Concluding remarks and future works are given in Section 9. 2. PRELIMINARIES 2.1 Data Encryption Standard (DES) DES [5] is the most widely used encryption algorithm. It was published by the National Bureau of Standards, now the National Institute of Standards and Technology (NIST), in January 1977 as an algorithm to be used for unclassified data (information not concerned with national security) [16]. According to the specification of FIPS publication 46-3, it is a block cipher operating on 64-bit data blocks. The encryption process depends on 56 bit secret key and sixteen round of Feistel iteration surrounded by two permutation layers, initial bit permutation (IP) at the input and its inverse (IP-1) at the output. The Graphical representation of the encryption process in depicted in fig. 1. The decryption process is same as encryption except the application sub keys used in the Feistel iteration is reversed [1]. The 16-round Feistel cipher is the core of DES. Here at first 64-bit block plain text is divided into two 32-bit words, LPT and RPT. In each iteration, the second word RPT is fed into a function „f‟ and the result is XORed with the left word LPT. Then the both words are swapped and the algorithm continues. The function „f‟ of DES algorithm has following steps: 2.1.1 Key Transformation 64 bit key is the input of the algorithm. Every eighth bit position of the key is ignored to produce 56 bit key. This key is first subjected to a permutation by permuted choice one and the resultant 56 bit key divided into two 28 bit words. They are circularly left shifted according to the number of left shift in the particular round. The resulting shift value serve as the input to permuted choice two to produce 48-bit output. 2.1.2 Expansion Permutation In this phase the 32 bit RPT is expanded to 48 bit and the bits are permuted as well, hence the expansion permutation. 2.1.3 S-box Substitution It is a process that accepts 48 bit input from the XOR operation involving the compressed key and expanded RPT and produces a 32 bit output using the substitution technique. 2.1.4 P-box Permutation The output 32 bit of S-box is permuted using P-box.The modified RPT is XORed with the LPT and the result is fed to the next RPT register. The unmodified RPT is fed to the next LPT register and the same process repeated 15 times. At the end of the 16 rounds the final permutation is performed and the cipher text is produced. Fig- 1: DES Algorithm Fig- 2: Calculation of function „f ‟ 2.2 Hamiltonian Cycle A Hamiltonian cycle, also called Hamiltonian circuit, is a graph cycle (i.e. closed loop) through a graph that visits each vertex exactly once. According to [18], n-cube is Hamiltonian. In the proposed algorithm 4-cube graph is considered and the number of directed Hamiltonian cycle with a marked starting node of 4-cube graph is 43008 [17]. Fig. 3.shows a Hamiltonian cycle of the 4-cube graph.
• 3.
  IJRET: International Journalof Research in Engineering and Technology eISSN: 2319-1163 | pISSN: 2321-7308 __________________________________________________________________________________________ Volume: 03 Issue: 03 | Mar-2014, Available @ http://www.ijret.org 655 Fig- 3: Hamiltonian cycle of 4-cube graph 2.3 Graph Automorphism An automorphism [3, 4, 7, 14] of a graph is a form of symmetry in which graph mapped onto itself while preserving adjacency. Formally, automorphism of a graph G (V, E) is the permutation of the vertex set V, such that vertices u, v  V forms an edge iff ( (u),  (v)) also forms an edge. The automorphism of the graph is isomorphism from the graph to itself. Set of all automorphisms of a graph forms a group under composition. There are various algorithms for computation of automorphism group of a graph namely Nauty [8], Saucy [9, 10], Bliss [11], Conauto 2.0 [13 ], Traces [12 ] etc. According to [14] the order of automorphism group of n-cube is n! 2n. Proposed algorithm is based on 4-cube graph and the fig. 4 shows the Hamiltonian cycle of the automorphic and non-automorphic graph of the given 4-cube graph. To increase strength of the sub keys, Hamiltonian cycle of non Automorphic graph of given 4-cube graph is used. (a) (b) Fig-4: (a) Hamiltonian cycle of the non-automorphic graph of the graph in fig. 3. (b) Hamiltonian cycle of automorphic graph of the graph in fig. 3. 2.4 Zero Knowledge Protocol (ZKP) It is an authentication protocol where user‟s private key is never revealed to the authority. In most traditional authentication scheme the users who wish to gain access to resources reveal their secret to the authority to prove their identity. The drawback of this scheme is that, the authority may be a malicious third party who will gain access to the user‟s private key. Furthermore, even if the authority is trustworthy, revealing a private key is susceptible to eavesdropping, compromising system. The ZKP on other hand effectively removes this problem. Detail description of the ZKP can be found in [6]. The general flow of ZKP is described below. 1) The prover (P) sends the verifier a value that is computed based on his private key. 2) The verifier flips a coin, and asks the prover to answer one of two questions based on the result of the coin flip. Generally the questions are either to answer a question about the value that was sent in step 1, or to answer a question about the secret key. 3) The prover sends the verifier the answer to his question. 4) The verifier checks that the answer is correct. Fig-5: Zero Knowledge Protocol (ZKP) 3. BRIEF REVIEW OF RELATED LITERATURE Over the past few decades DES algorithm has been gone through many enhancements and served as the basis for many other encryption algorithms. At first, Triple DES (3DES or TDES) has been proposed [20]. TDES uses 48 rounds and three 56 bit keys to encrypt data. This algorithm gives three level security to data and high resistant from differential cryptanalysis attacks. But as TDES has to gone through DES algorithm three times, the encryption and decryption time is larger than standard DES algorithm. Next, Advanced
• 4.
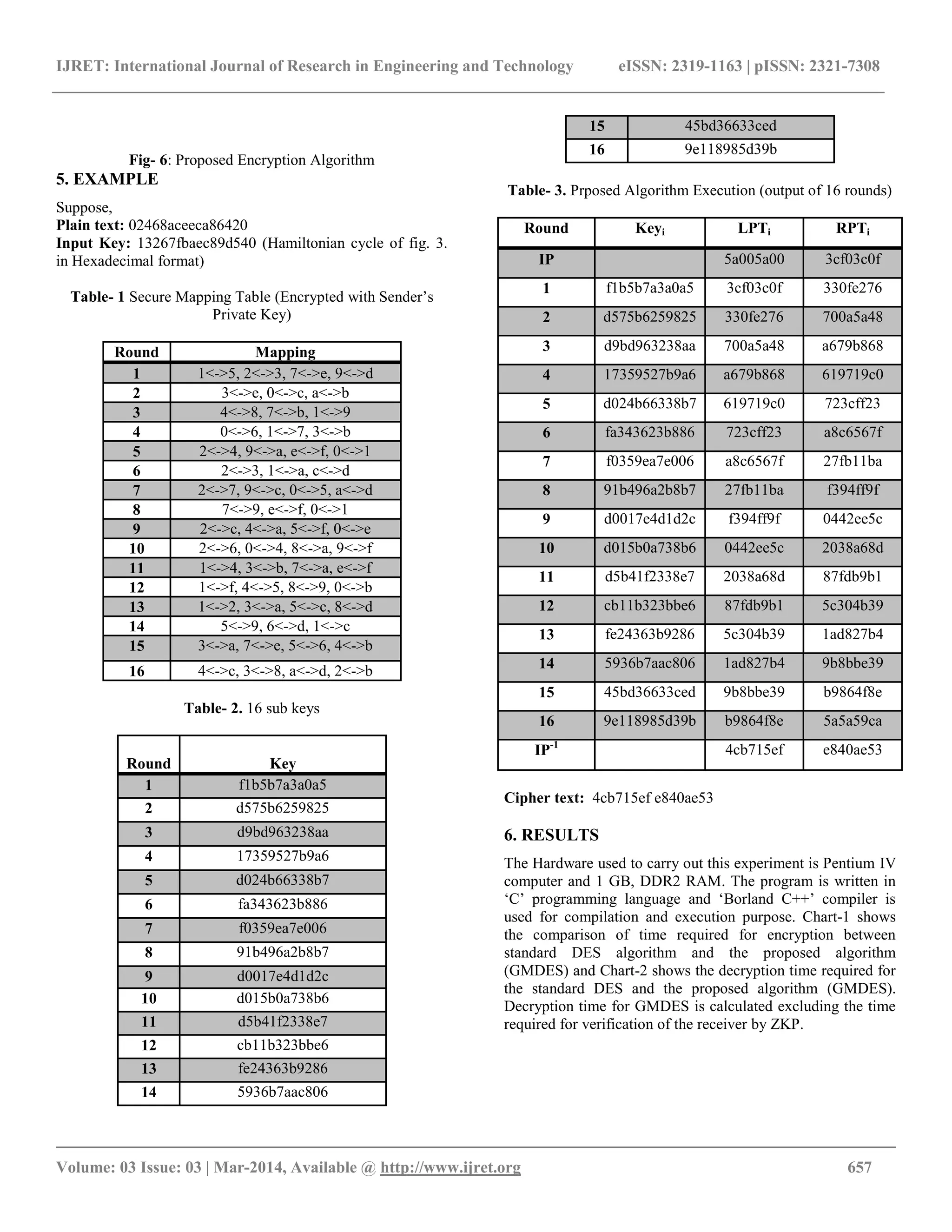
  IJRET: International Journalof Research in Engineering and Technology eISSN: 2319-1163 | pISSN: 2321-7308 __________________________________________________________________________________________ Volume: 03 Issue: 03 | Mar-2014, Available @ http://www.ijret.org 656 Encryption Standard (AES) [21, 22] comes which another encryption standard. It encrypts data blocks of 128 bits using the keys of 128, 192, 256 bits. Although AES has the tighter security compare to DES or TDES, it also has longest encryption time and load, since all variable needed to process encryption. Next, BLOWFISH [23] designed by Bruce Schneier. Blowfish is a 64 bit block cipher with variable length key from 32 bit to 448 bits. The strength of the Blowfish lies in the fact that, in its full round form cryptanalysis techniques have no effect on it. However, anything which is less than four rounds is prone to brute-force attack [24]. Ammar et al. [25] proposed Random Data Encryption Algorithm (RDEA) by extending DES where pseudo randomized cipher key is generated for encryption and embedded with the cipher text. As the length of the cipher text increases and the memory capacity hampered, the overall efficiency of the algorithm also affected poorly. 4. PROPOSED ALGORITHM 4.1 Encryption Process The proposed algorithm is a modified version of DES which uses graph Hamiltonian cycle and the graph automorphism concept for generating keys. The whole process is similar to DES except the key transformation process. The modified key transformation process is depicted below: 4.1.1 Key Transformation Here, the input is an arbitrary Hamiltonian cycle of the 4-cube graph in 64 bit binary format. This is used as the secret key. Here the parity bits are not used because, the sequence is a Gray code and it can support error detection and correction like geometric approach for error detection and correction [26]. In this algorithm a secure mapping table is used which is encrypted with the sender‟s private key and sender can update it dynamically when needed. The secure mapping table consist of mappings between the given 4-cube graph and its non- automorphic graphs. Altogether 16 arbitrary mappings are stored in the secure mapping table for producing sub keys of 16 rounds. The key transformation algorithm for 1st round is given below: Algorithm: Key transformation. Begin Step 1: 64 bit secret key is permuted using the 1st entry of the secure mapping table. Step 2: Every eighth bit position of the sub key is discarded to produce 56 bit sub key. Step 3: 56 bit sub key is permuted using the permuted choice two table used in the standard DES algorithm [1,2] and the sub key for round 1 is produced. End This procedure is continued for remaining 15 rounds. The overall encryption process is given with a graphical representation in fig.6. 4.2 Decryption Process The receiver who wants to decrypt the cipher text with the secret key has to follow the algorithm given below: Algorithm: Decryption. Begin Step 1: Receiver who wants decrypt the cipher text will send a request to the sender for decryption of the encrypted secure mapping table. Step 2: Sender will start Zero Knowledge Protocol (ZKP) to verify if the receiver is authenticated or not. Step 3: If the receiver is authenticated then sender will decrypt the secure mapping table for that particular receiver. Step 4: Receiver will decrypt the cipher text by following the same procedure as encryption except the application of keys in reverse order. Step 5: After successful completion of the decryption, receiver will send a completion message to the sender and the sender will update with secure mapping table and decrypt it with its private key. End
• 5.
  IJRET: International Journalof Research in Engineering and Technology eISSN: 2319-1163 | pISSN: 2321-7308 __________________________________________________________________________________________ Volume: 03 Issue: 03 | Mar-2014, Available @ http://www.ijret.org 657 Fig- 6: Proposed Encryption Algorithm 5. EXAMPLE Suppose, Plain text: 02468aceeca86420 Input Key: 13267fbaec89d540 (Hamiltonian cycle of fig. 3. in Hexadecimal format) Table- 1 Secure Mapping Table (Encrypted with Sender‟s Private Key) Round Mapping 1 1<->5, 2<->3, 7<->e, 9<->d 2 3<->e, 0<->c, a<->b 3 4<->8, 7<->b, 1<->9 4 0<->6, 1<->7, 3<->b 5 2<->4, 9<->a, e<->f, 0<->1 6 2<->3, 1<->a, c<->d 7 2<->7, 9<->c, 0<->5, a<->d 8 7<->9, e<->f, 0<->1 9 2<->c, 4<->a, 5<->f, 0<->e 10 2<->6, 0<->4, 8<->a, 9<->f 11 1<->4, 3<->b, 7<->a, e<->f 12 1<->f, 4<->5, 8<->9, 0<->b 13 1<->2, 3<->a, 5<->c, 8<->d 14 5<->9, 6<->d, 1<->c 15 3<->a, 7<->e, 5<->6, 4<->b 16 4<->c, 3<->8, a<->d, 2<->b Table- 2. 16 sub keys Round Key 1 f1b5b7a3a0a5 2 d575b6259825 3 d9bd963238aa 4 17359527b9a6 5 d024b66338b7 6 fa343623b886 7 f0359ea7e006 8 91b496a2b8b7 9 d0017e4d1d2c 10 d015b0a738b6 11 d5b41f2338e7 12 cb11b323bbe6 13 fe24363b9286 14 5936b7aac806 15 45bd36633ced 16 9e118985d39b Table- 3. Prposed Algorithm Execution (output of 16 rounds) Round Keyi LPTi RPTi IP 5a005a00 3cf03c0f 1 f1b5b7a3a0a5 3cf03c0f 330fe276 2 d575b6259825 330fe276 700a5a48 3 d9bd963238aa 700a5a48 a679b868 4 17359527b9a6 a679b868 619719c0 5 d024b66338b7 619719c0 723cff23 6 fa343623b886 723cff23 a8c6567f 7 f0359ea7e006 a8c6567f 27fb11ba 8 91b496a2b8b7 27fb11ba f394ff9f 9 d0017e4d1d2c f394ff9f 0442ee5c 10 d015b0a738b6 0442ee5c 2038a68d 11 d5b41f2338e7 2038a68d 87fdb9b1 12 cb11b323bbe6 87fdb9b1 5c304b39 13 fe24363b9286 5c304b39 1ad827b4 14 5936b7aac806 1ad827b4 9b8bbe39 15 45bd36633ced 9b8bbe39 b9864f8e 16 9e118985d39b b9864f8e 5a5a59ca IP-1 4cb715ef e840ae53 Cipher text: 4cb715ef e840ae53 6. RESULTS The Hardware used to carry out this experiment is Pentium IV computer and 1 GB, DDR2 RAM. The program is written in „C‟ programming language and „Borland C++‟ compiler is used for compilation and execution purpose. Chart-1 shows the comparison of time required for encryption between standard DES algorithm and the proposed algorithm (GMDES) and Chart-2 shows the decryption time required for the standard DES and the proposed algorithm (GMDES). Decryption time for GMDES is calculated excluding the time required for verification of the receiver by ZKP.
• 6.
  IJRET: International Journalof Research in Engineering and Technology eISSN: 2319-1163 | pISSN: 2321-7308 __________________________________________________________________________________________ Volume: 03 Issue: 03 | Mar-2014, Available @ http://www.ijret.org 658 Chart-1: Time (in seconds) required for encryption of text files Chart-2: Time (in seconds) required for decryption of text files 7. STRENGTH OF THE PROPOSED ALGORITHM 7.1 Key Space The main drawback of standard DES algorithm is that, it can be easily prone to brute-force attack, because of its relatively short key length. In DES there are only 256 possible key combinations which are quite easy to crack. The algorithm proposed here tries to overcome this drawback using the partial symmetric key concept. The advantage is that, the algorithm is not fully depended on the secret key. If the intruder does not know the secret key, the time needed for brute-force attack (if the computation is done in 2.4 GHz processor) = Number of Hamiltonian cycles in 4-cube graph * (All possible permutations of vertices of 4-cube graph – Number of Automorphic graph of given 4-cube graph) number of rounds / (2.4*109 *3600*365*24) =43008* (16!-(4!.24 ))16 / (2.4*109 *3600*365*24) = 5.8005 X 10217 / (2.4*109 *3600*365*24) =7.66 X 10200 years (Theoretically). It is much larger than standard DES which is (256 / (2.4*109 *3600*365*24) = 0.952 years (approx)). Now, if the intruder knows the secret key then the time required for brute-force attack= (16!-(4! 24 ))16 / (2.4*109 *3600*365*24)= 1.77 X 10196 (Theoretically). Chart-3: Comparison of key space of standard DES and Proposed method 7.2 Avalanche Effect (Delta) A change in one bit of the plain text or one bit of the key should produce change in many bits of the cipher text. This effect is known as Avalanche effect. In the example of section 5, if the first bit of the plain text is changed the plain text becomes 12468aceeca86420.The Chart-4 shows the Avalanche effects of both the standard DES and proposed algorithm which shows that Avalanche effect of DES is 50% where in the case of proposed algorithm it is 55%. Chart-4: Avalanche effect of standard DES and Proposed method 8. SECURITY ANALYSIS WITH GMDES Security is a very important aspect of any encryption algorithm. A short discussion about the security issues of the propose algorithm, GMDES from the cryptographic point of view are given below.
• 7.
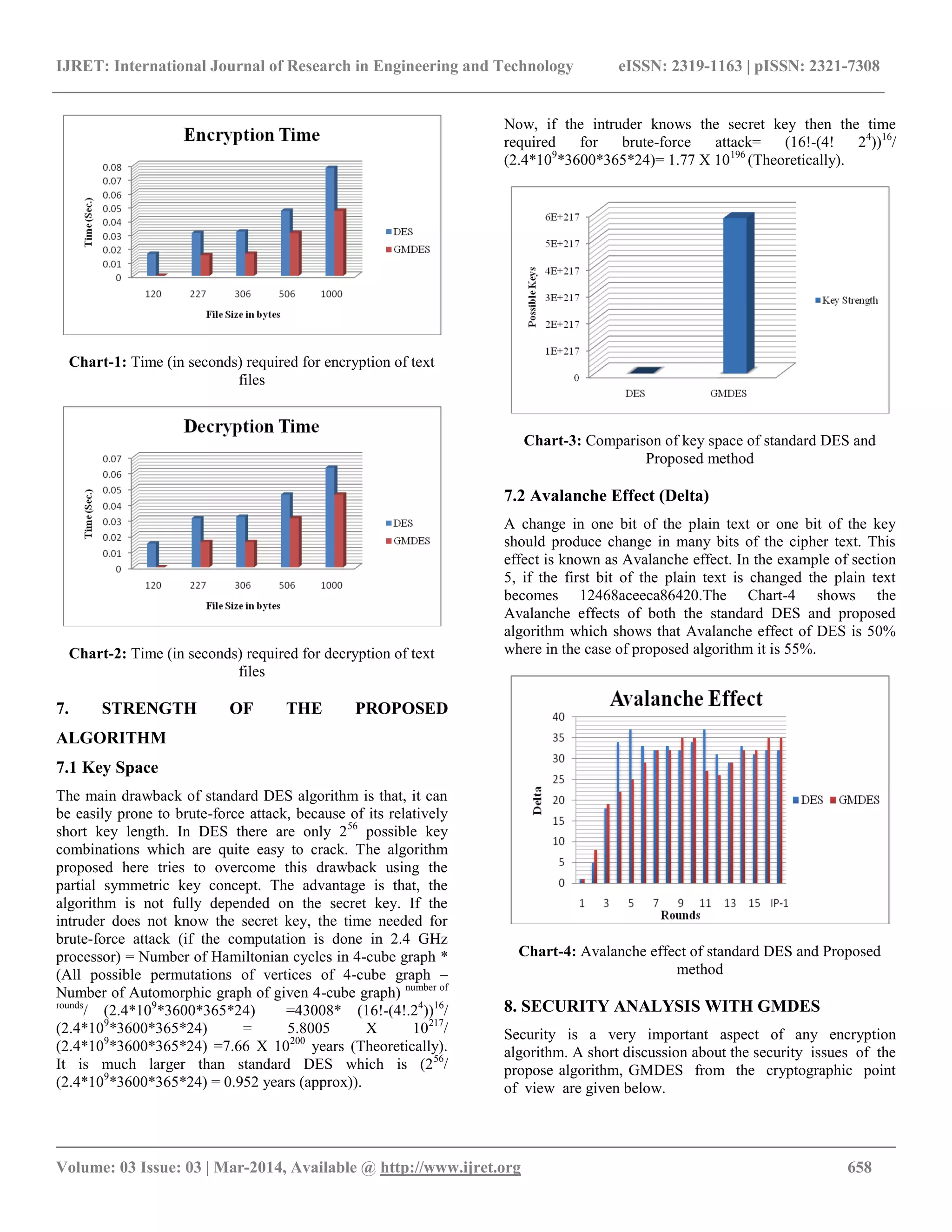
  IJRET: International Journalof Research in Engineering and Technology eISSN: 2319-1163 | pISSN: 2321-7308 __________________________________________________________________________________________ Volume: 03 Issue: 03 | Mar-2014, Available @ http://www.ijret.org 659 8.1 Replay Attack In this attack, an intruder tries to replay the earlier communication and authenticate itself to the sender who is the verifier. But, as Zero Knowledge Protocol is used in this proposed system, the verifier will be sending different challenge values for each communication, replaying earlier communication will not authenticate the receiver. 8.2 Chosen Cipher Text Attack According to this attack model Attacker tries to deduce secret keys by studying various cipher texts and corresponding plain texts. This kind of attack has more chances of success if encryption key size is limited. But in the proposed method, different cipher text is produced for the same key and same plain text and the key space of this algorithm is very large, so deduction of encryption key will not practically possible. 8.3 Cipher Text only Attack It is an attack model for cryptanalysis where the Attacker is assumed to have an access only to a set of cipher texts. The attack is successful if corresponding plain text can be deduced or the key is found. But for the proposed scheme, key space is very large and the algorithm is not fully depended on secret key but also on the protected sub-keys. So possibility of this type of attack is much less. 8.4 Chosen Plain Text Attack In this attack model Attacker chooses an arbitrary plain text to be encrypted and obtain the corresponding cipher text. By comparing this two the Attacker can find his own key. But the proposed method is a partial symmetric key algorithm and is not fully depended on the secret key; rather it also depended on the sub-keys which are protected by sender‟s private key. So, it is not possible for an Attacker to know the sender‟s private key and due to large key space the possibility of this type of attack is very less. 8.5 Brute Force Attack This type of attack consists of systematically checking all possible keys until the correct one is found. In the worst case, this would involve traversing the entire search space. As the key space of this proposed algorithm is very large, so possibility of this type of attack is practically impossible. 8.6 Man-in-the-middle Attack In this attack the cryptanalyst places him in the communication channel between sender and receiver who wish to exchange their data for secure communication and he makes independent connections with the victims by exchanging key with them and relays messages between them, making them believe that they are talking directly to each other over a private connection, when in fact the entire conversation is controlled by the cryptanalyst. So, the cryptanalyst knows the secret key. This type of attack can be defeated by the proposed method as it uses the secure key exchange protocol [27] and Zero Knowledge Protocol for authentication of the receiver. 9. CONCLUSIONS Security is a very complex topic. In this paper a graph based modified DES (GMDES) algorithm is proposed which is more secure than the classical DES algorithm. The proposed algorithm is not fully depended on secret key and for the same plain text it produces different cipher text using the same secret key which reduces the probability of various attacks. Besides this, unauthorized user cannot be able to decrypt the message in a feasible amount of time despite of knowing the secret key. The future depends on detailed simulation and comparison with other encryption algorithm, as well as complete statistical survey and analysis with respect to other attacks. Furthermore, this proposed technique can be implemented in embedded systems, smart card security, cloud computer security etc. ACKNOWLEDGEMENTS The authors would like to thank University Of Calcutta, West Bengal, India, Department of Science & Technology (DST), New Delhi, for financial support and the reviewers for their constructive and helpful comments and specially the Computer without which no work was possible. REFERENCES [1] Stallings, William. Cryptography and Network Security: Principles and Practice. Prentice Hall, 2011. [2] Kahate, Atul. Cryptography & Network Security. Tata McGraw-Hill Education, 2011. [3] Biggs, Norman. Finite groups of automorphisms: course given at the University of Southampton, October-December 1969. Vol. 6. CUP Archive, 1971. [4] Biggs, Norman. Algebraic graph theory. Cambridge University Press, 1993. [5] National Institute of Standards, U.S. Department of Commerce. FIPS 47: Data Encryption Standard, 1977. [6] Hamilton, Wendy L. First Time Authentication for Airborne Networks (FAAN). DISTRIBUTED INFINITY LARKSPUR CO, 2010. [7] Cameron, Peter J., and Queen Mary. Automorphisms of graphs. Topics in algebraic graph theory, 102 (2004): 137-155. [8] McKay, Brendan D. Practical graph isomorphism. Congressus Numerantium, 30:45–87, 1981. [9] Darga, Paul T., Liffiton, Mark H., Sakallah, Karem A. and Markov. Igor L., Exploiting structure in symmetry detection for cnf. DAC, pages 530–534. ACM, 2004. [10] Katebi,H., Sakallah, Karem A. and Markov., Igor L., Symmetry and satisfiability: An update.SAT, of
• 8.
  IJRET: International Journalof Research in Engineering and Technology eISSN: 2319-1163 | pISSN: 2321-7308 __________________________________________________________________________________________ Volume: 03 Issue: 03 | Mar-2014, Available @ http://www.ijret.org 660 Lecture Notes in Computer Science, 6175:113–127. Springer, 2010. [11] Junttila., Tommi and Kaski. Petteri, Conflict propagation and component recursion for canon-ical labeling. Theory and Practice of Algorithms in (Computer) Systems, Lecture Notes in Computer Science, 6595:151–162. Springer Berlin / Heidelberg, 2011. [12] Piperno., Adolfo, Search space contraction in canonical labeling of graphs (preliminary ver-sion).CoRR, abs/0804.4881, 2008. [13] López-Presa, José Luis, Antonio Fernández Anta, and Luis Núñez Chiroque. "Conauto-2.0: Fast Isomorphism Testing and Automorphism Group Computation." arXiv preprint arXiv:1108.1060 (2011). [14] Knuth, D. "The Art of Computer Programming. Volume 4A: Combinatorial Algorithm, Part 1." (2011): 202-208. [15] Agrawal., Monika, Mishra., Pradeep, A Comparative Survey on Symmetric Key Encryption Techniques, International Journal on Computer Science & Engineering; May2012, Vol. 4 Issue 5, p877. [16] Shah Kruti, R., and Gambhava. Bhavika, New Approach of Data Encryption Standard Algorithm., strings. Vol. 1. 2011. [17] Sloane, Neil JA. The on-line encyclopedia of integer sequences. (2010). [18] Ferland, Kevin. Discrete mathematics: an introduction to proofs and combinatorics. CengageBrain. com, 2008. [19] Harary, Frank, John P. Hayes, and Horng-Jyh Wu. A survey of the theory of hypercube graphs. , Computers & Mathematics with Applications 15.4 (1988): 277- 289. [20] American National Standard for Financial Institution Message Authentication (wholesale), ANSI x9.9-1986 (revised), American Bankers Association, X9 Secretariat, American Bankers Association, 1986. [21] National Institute of Standards, U.S. Department of Commerce. FIPS 197: Advanced Encryption Standard, 2001. [22] Alanazi, H., Zaidan, B., Zaidan, A., Jalab, H., Shabbir, M. and Al-Nabhani, Y., New comparative study between DES, 3DESand AES within nine factors, Journal of Computing, Vol. 2, Issue 3, pp. 152- 157,March 2010. [23] Schneier, B., Description of a new variable-length key, 64-bit block cipher (blowfish), Fast Software Encryption, Cambridge Security Workshop, pp. 191- 204,Springer-VerlagLondon, UK, 1994. [24] Sison, Ariel M., Bartolome T. Tanguilig III, Bobby D. Gerardo, and Yung-Cheol Byun. Implementation of Improved DES Algorithm in Securing Smart Card Data. In Computer Applications for Software Engineering, Disaster Recovery, and Business Continuity, pp. 252-263. Springer Berlin Heidelberg, 2012. [25] Ammar, A., El Sherbini, A. , Ashour, I. , Shiple, M., Random data encryption algorithm (RDEA), Radio Science Conference, 2005. NRSC 2005. Proceedings of the Twenty-Second National, 15-17 March 2005. [26] Hamming, Richard W. Coding and information theory. Prentice-Hall, Inc., 1986. [27] Sensarma, D., Banerjee, S., & Basuli, K.. A New Scheme for Key Exchange. International Journal of Modern Engineering Research (IJMER), 2(3), 2012. BIOGRAPHIES Debajit Sensarma is presently pursuing his PhD degree from the department of Computer Science and Engineering, University of Calcutta, Kolkata, India with DST INSPIRE Fellowship. He has published several papers in International journals and conferences. Dr. Samar Sen Sarma is the founder member and senior professor of the Department of Computer Science and Engineering at the University of Calcutta (the first multidisciplinary modern university in South Asia and the oldest institution to have the “University” status), Kolkata, India. He has published several papers in International journals and conferences.