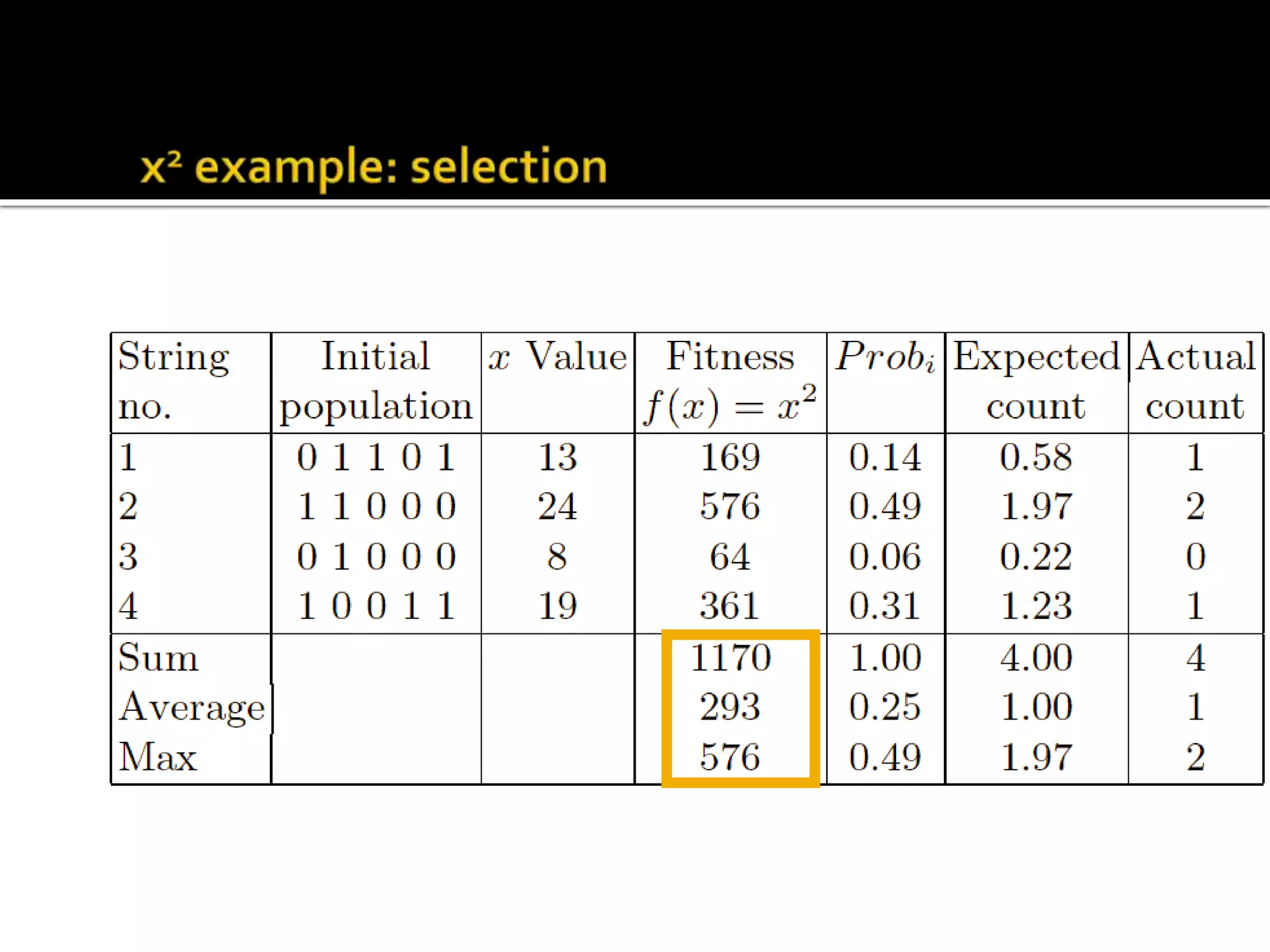
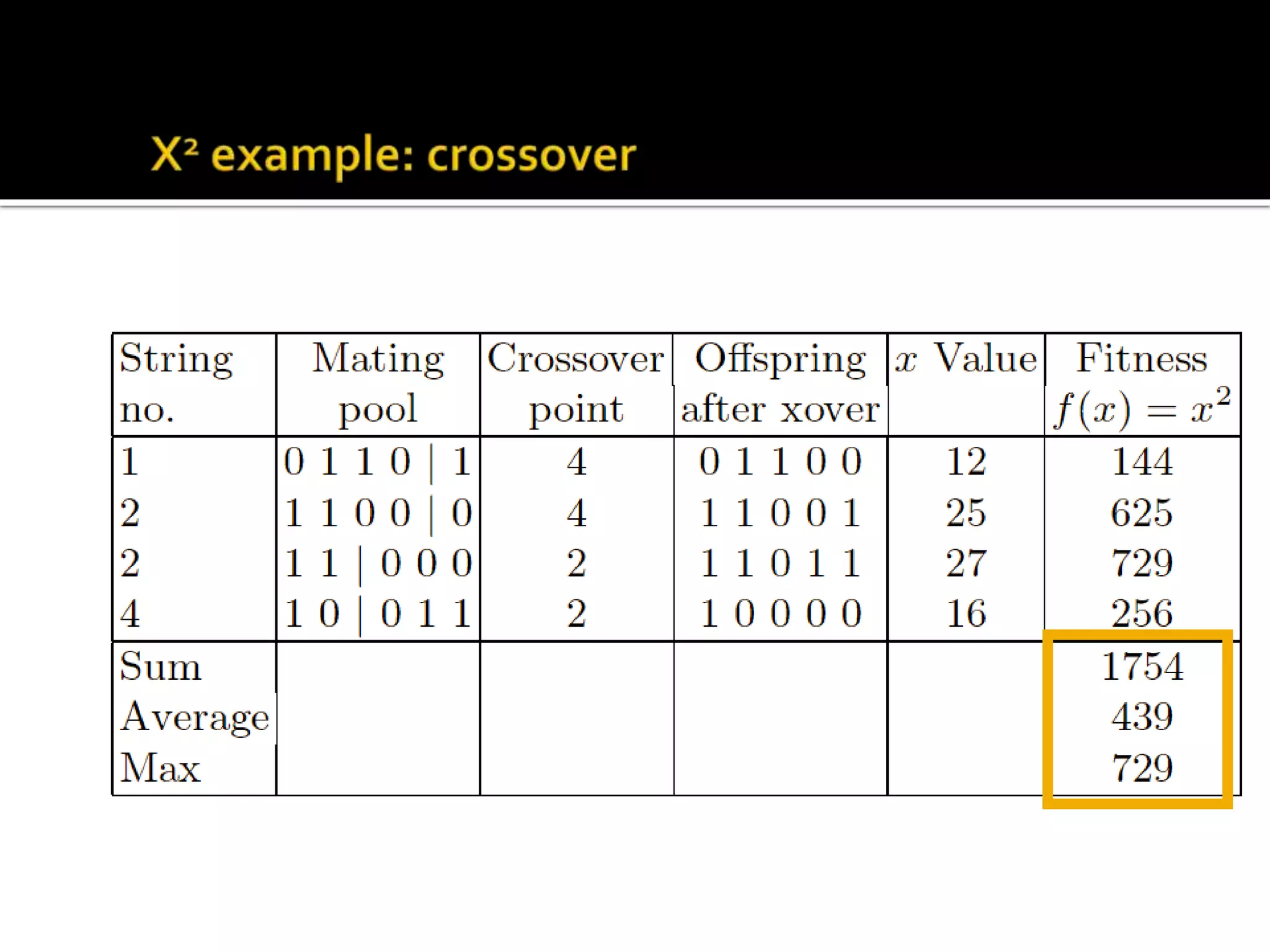
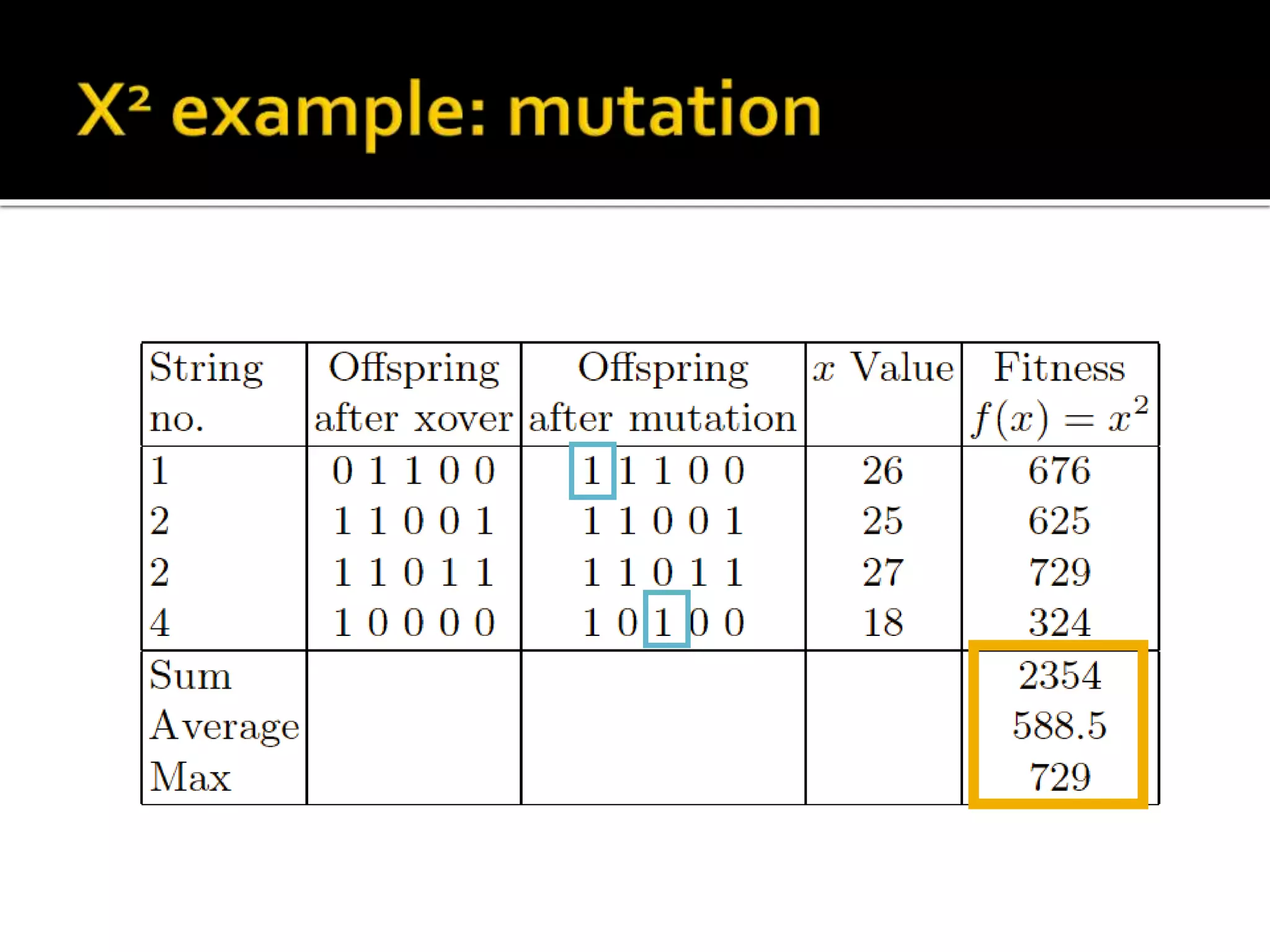
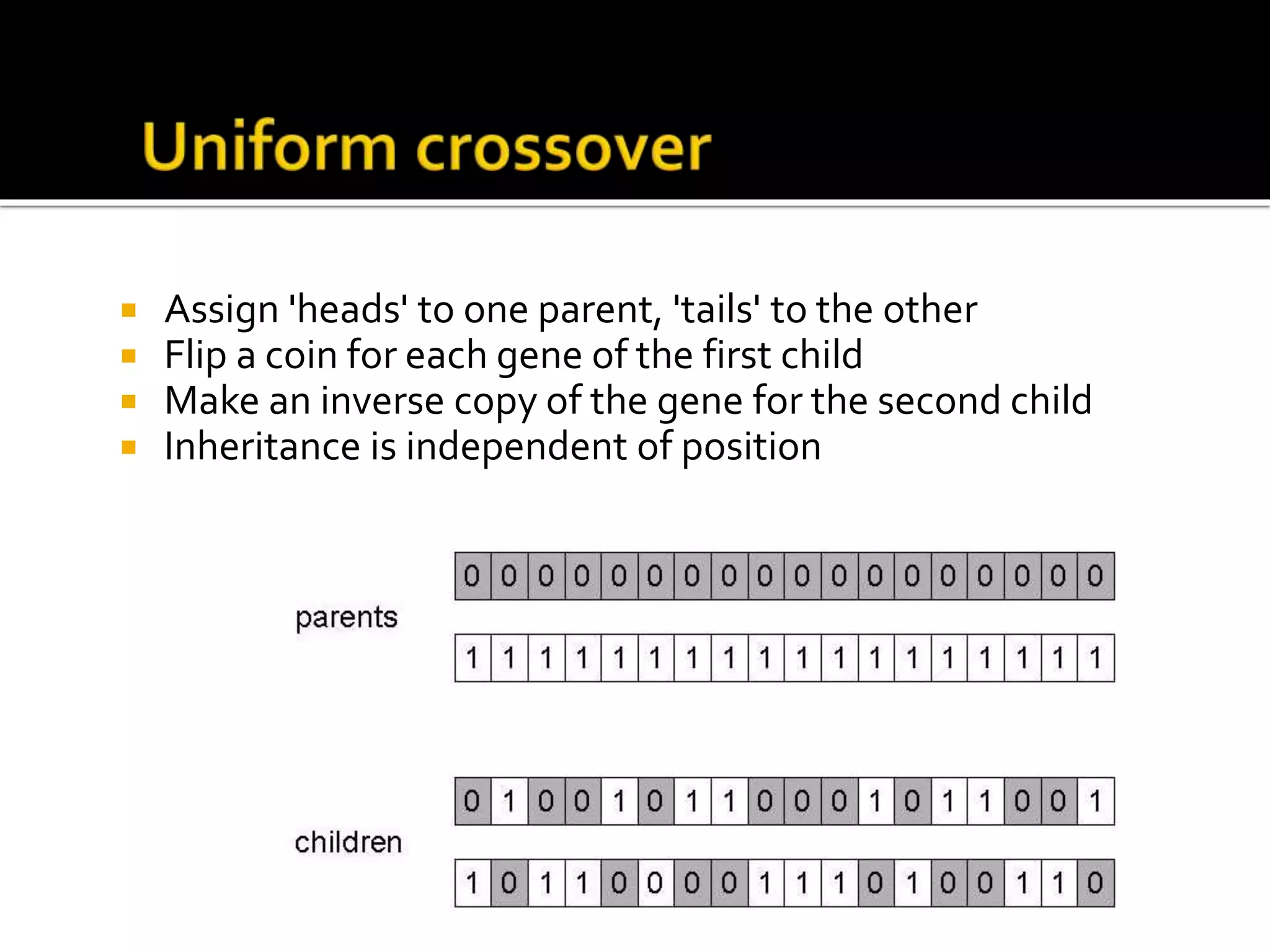
The document describes the process of genetic algorithms using a binary string representation example. It explains the initial population is generated randomly, fitness scores are assigned, and selection, crossover, and mutation are applied to produce the next generation. The roulette wheel selection method is used to probabilistically select individuals for reproduction based on their fitness. Two point crossover and bit mutation are the genetic operators applied, and the process repeats until a stopping criterion is met. Schemata and their order are also introduced to analyze the survival probability of building blocks under genetic operations.




















![Introduction to GeneticAlgorithms 25 {0,1,#} is the symbol alphabet, where # is a special wild card symbol A schema is a template consisting of a string composed of these three symbols Example: the schema [01#1#] matches the strings: [01010], [01011], [01110] and [01111]](https://image.slidesharecdn.com/geneticalgorithmgabinaryandreal-140430213807-phpapp01/75/Genetic-algorithm-ga-binary-and-real-Vijay-Bhaskar-Semwal-25-2048.jpg)
![Introduction to GeneticAlgorithms 26 The order of the schema S (denoted by o(S)) is the number of fixed positions (0 or 1) presented in the schema Example: for S1 = [01#1#], o(S1) = 3 for S2 = [##1#1010], o(S2) = 5 The order of a schema is useful to calculate survival probability of the schema for mutations There are 2 l-o(S) different strings that match S](https://image.slidesharecdn.com/geneticalgorithmgabinaryandreal-140430213807-phpapp01/75/Genetic-algorithm-ga-binary-and-real-Vijay-Bhaskar-Semwal-26-2048.jpg)
