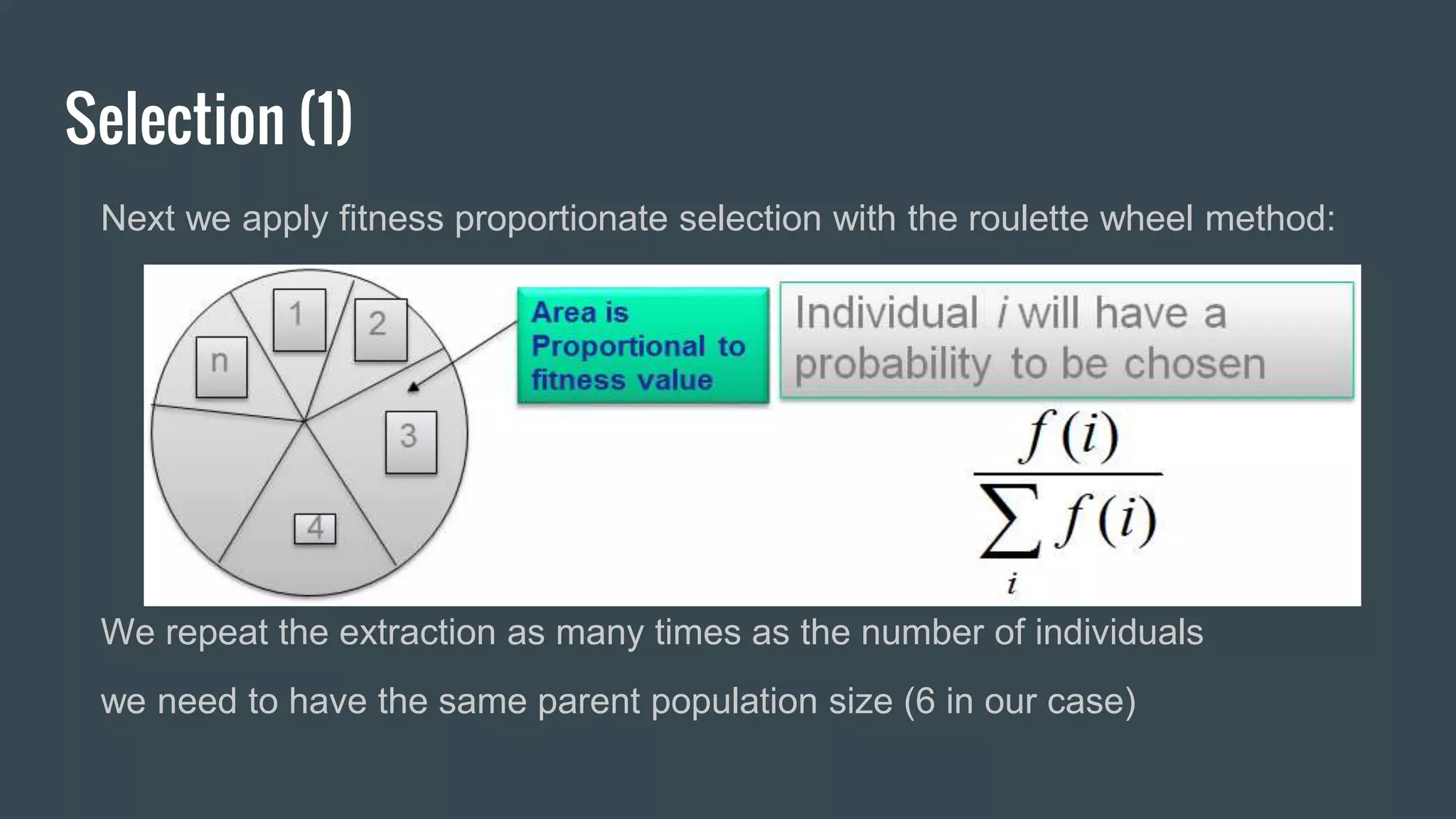
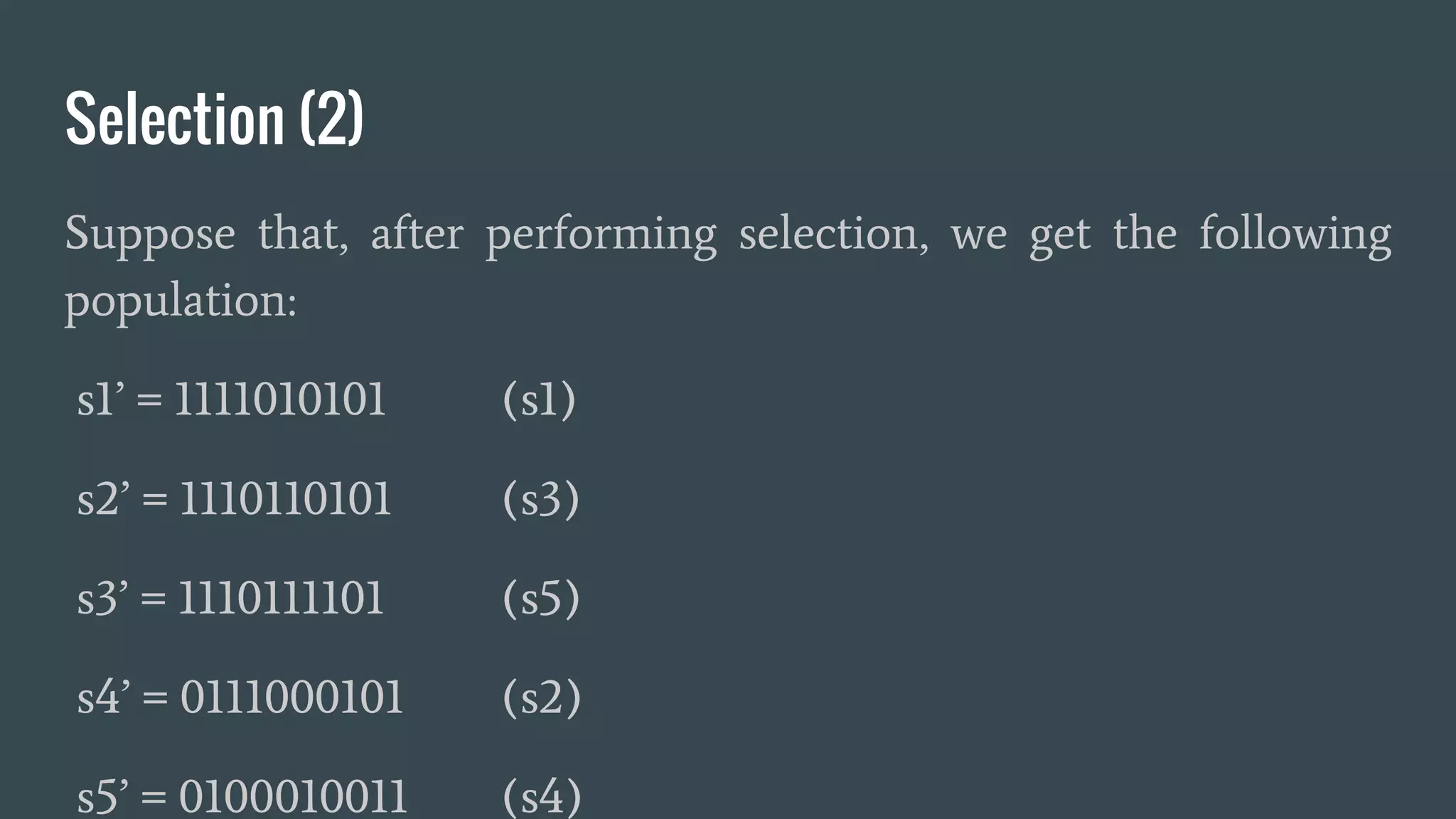
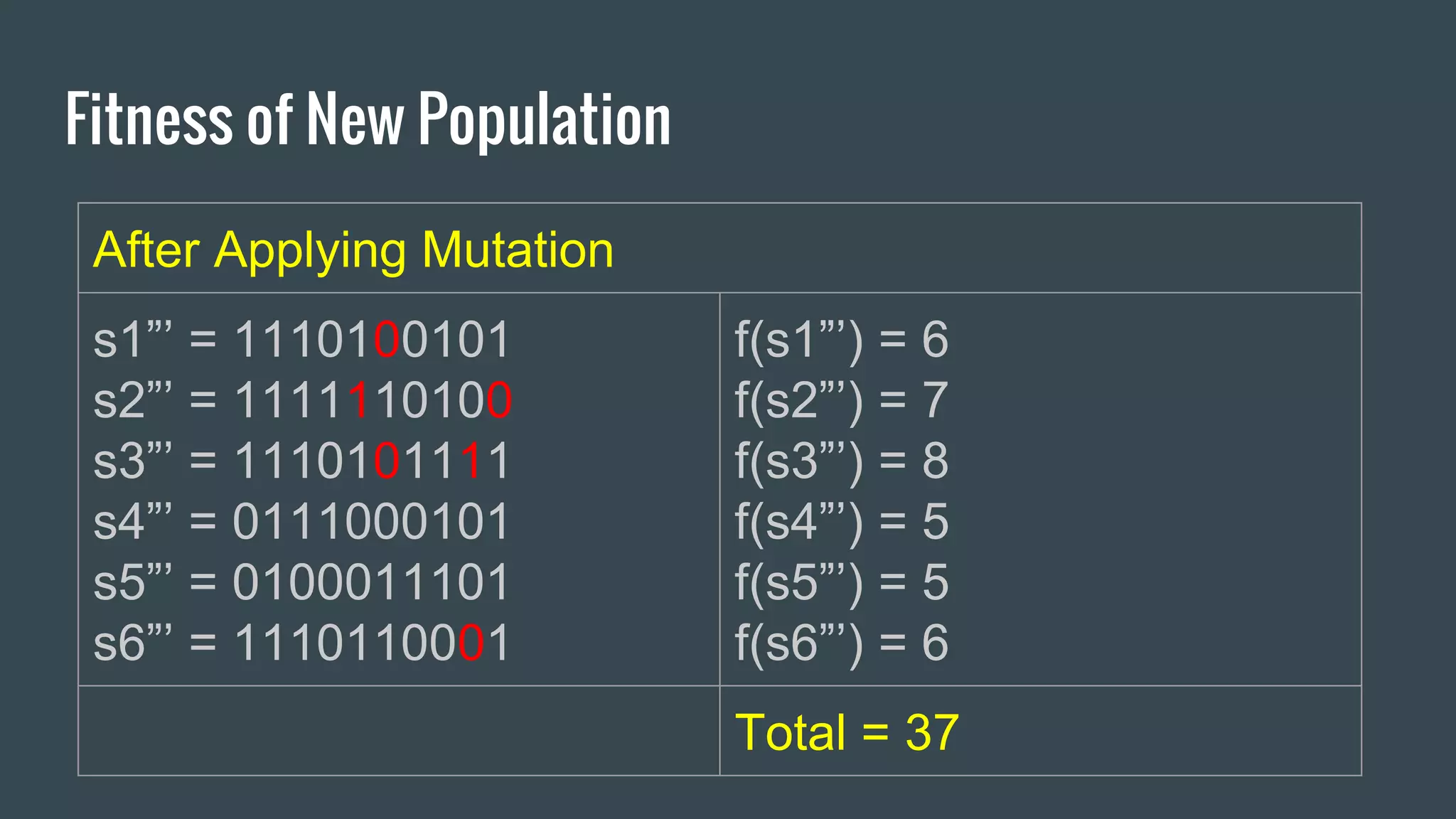
Genetic algorithms are a type of artificial intelligence search technique inspired by natural selection. They work by randomly generating an initial population of solutions, evaluating their fitness, then breeding new solutions through selection, crossover and mutation over many generations until an optimal solution is found. Some key steps include randomly initializing a population, determining fitness, selecting parents, performing crossover on parents to create new solutions, mutating new solutions, determining fitness of new population, and repeating until a stopping criteria is met such as a good enough solution being found. Genetic algorithms have been applied to many optimization and search problems across various domains.




![Outline of the Basic Genetic Algorithm 1. [Start] Generate random population of n chromosomes (suitable solutions for the problem) 2. [Fitness] Evaluate the fitness f(x) of each chromosome x in the population 3. [New population] Create a new population by repeating following steps until the new population is complete 1. [Selection] Select two parent chromosomes from a population according to their fitness (the better fitness, the bigger chance to be selected) 2. [Crossover] With a crossover probability crossover the parents to form a new children. If no crossover was performed, children is an exact copy of parents. 3. [Mutation] With a mutation probability mutate new children at each position in chromosomeNext Page To Continue……](https://image.slidesharecdn.com/geneticalgorithmartificialintelligencepresentation-160406044728/75/Genetic-algorithm-artificial-intelligence-presentation-6-2048.jpg)
![Outline of the Basic Genetic Algorithm 4. [Replace] Use new generated population for a further run of algorithm 5. [Test] If the end condition is satisfied, stop, and return the best solution in current population 6. [Loop] Go to step 2](https://image.slidesharecdn.com/geneticalgorithmartificialintelligencepresentation-160406044728/75/Genetic-algorithm-artificial-intelligence-presentation-7-2048.jpg)