Download as PDF, PPTX
Uploaded byDuyhai Doan
Distributed algorithms for big data @ GeeCon
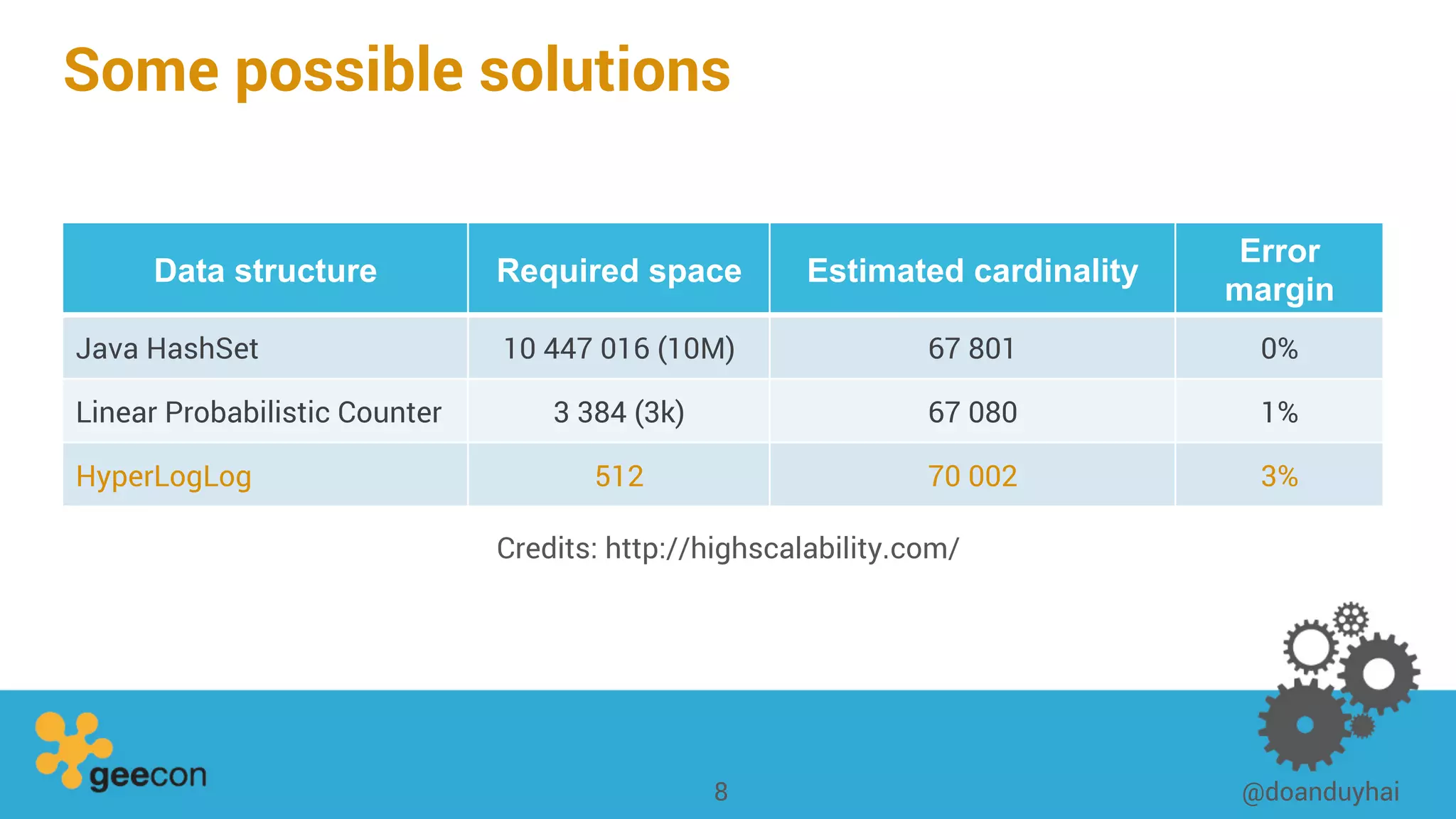
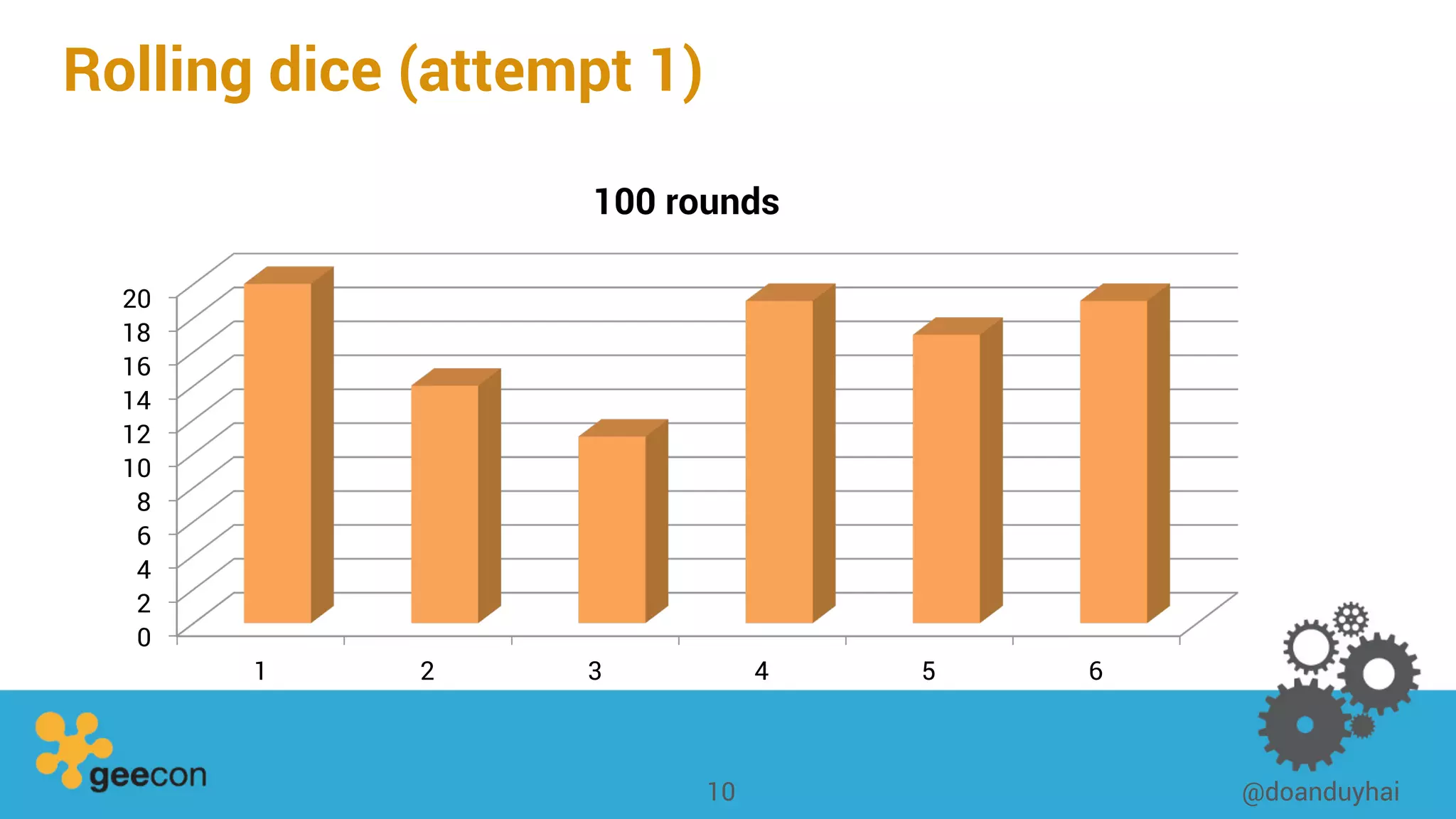
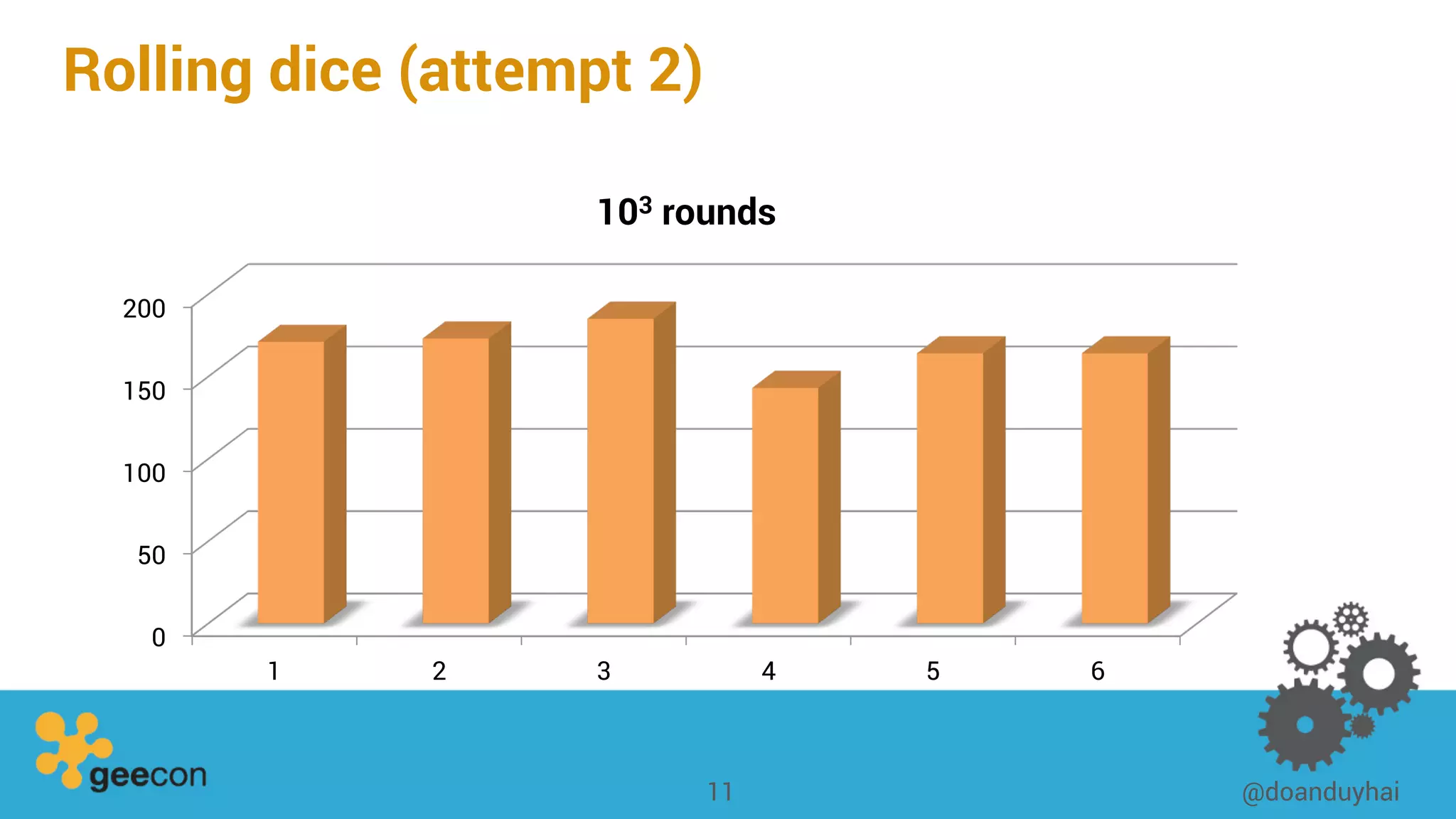
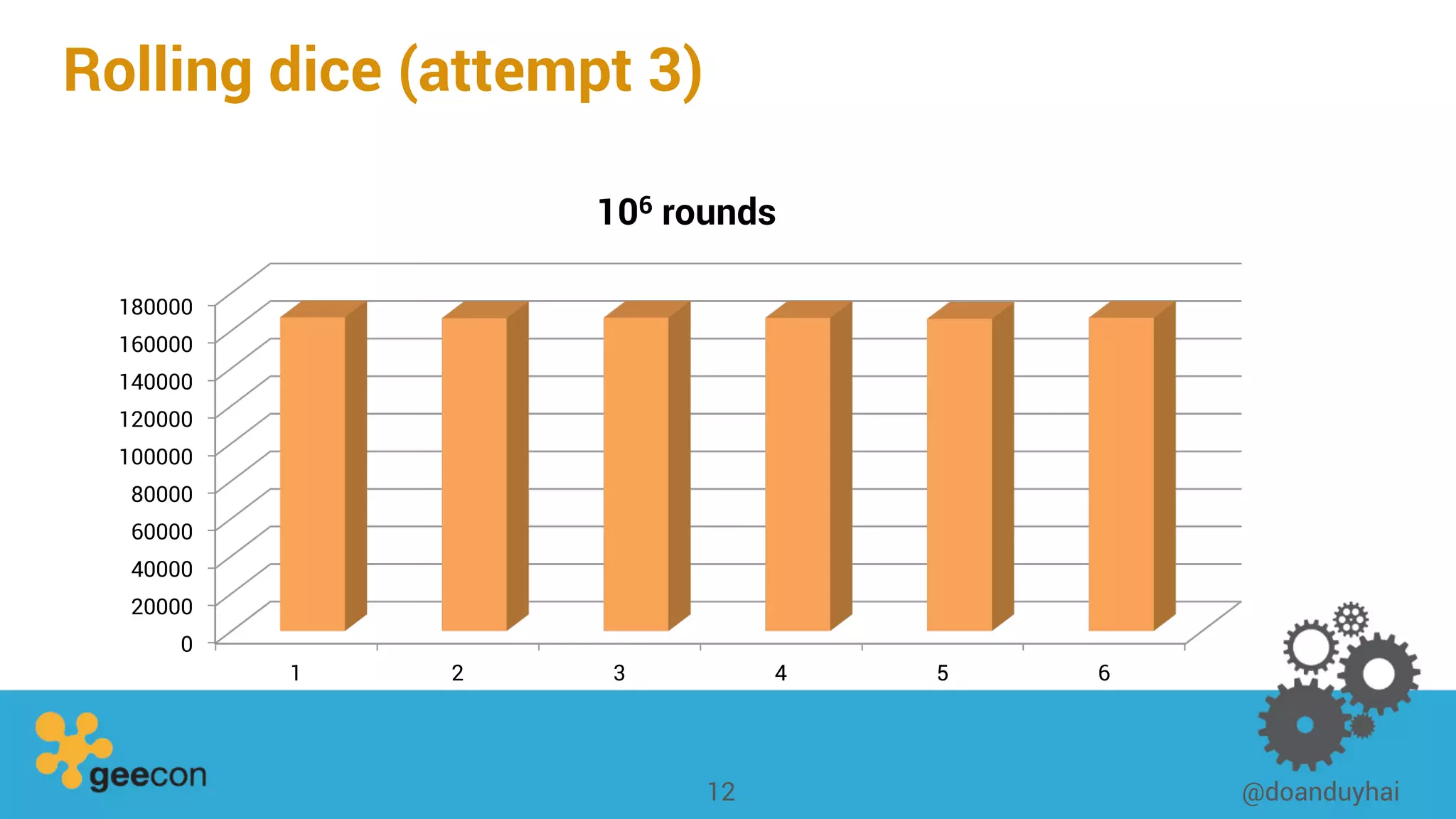
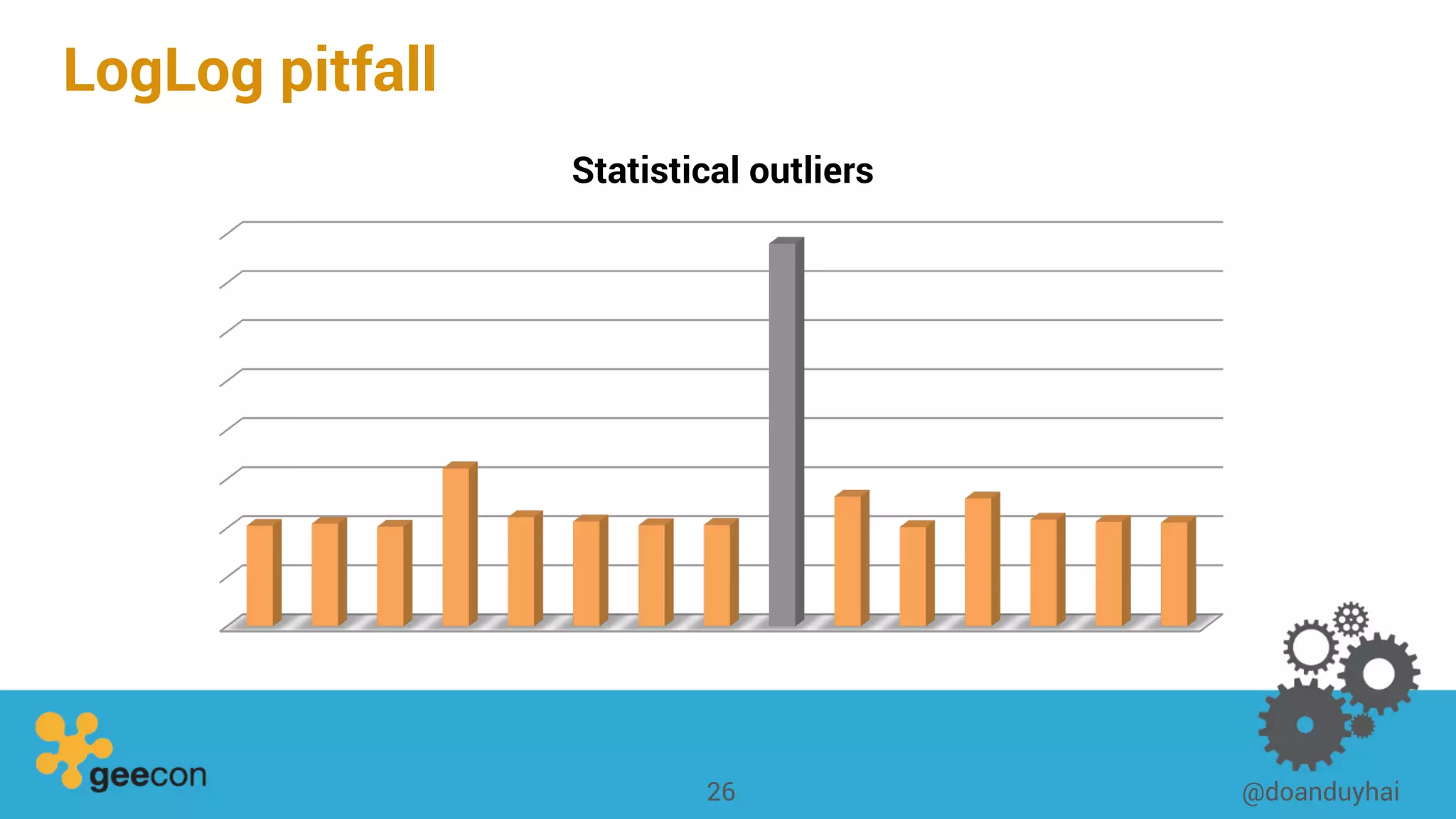
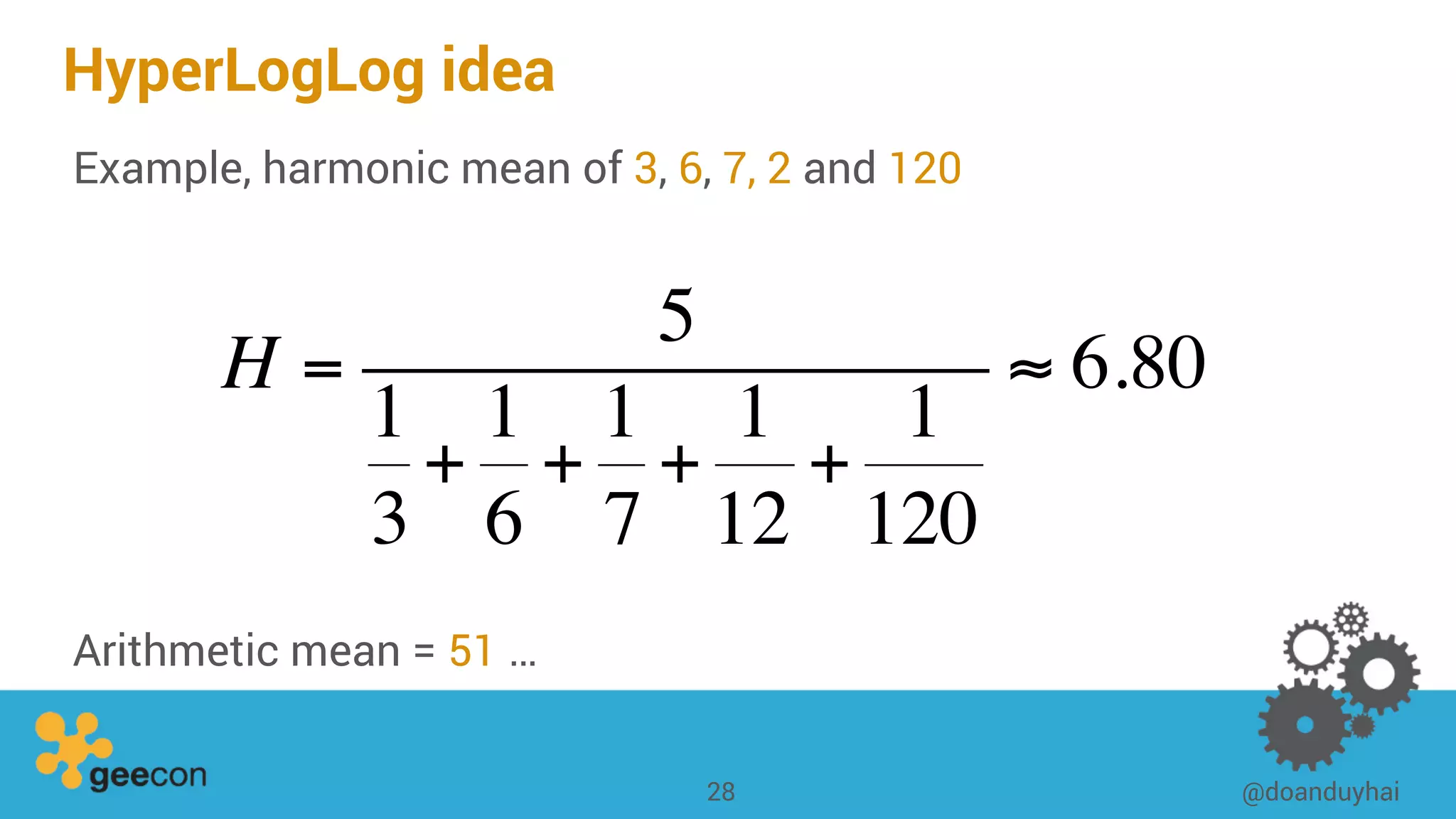
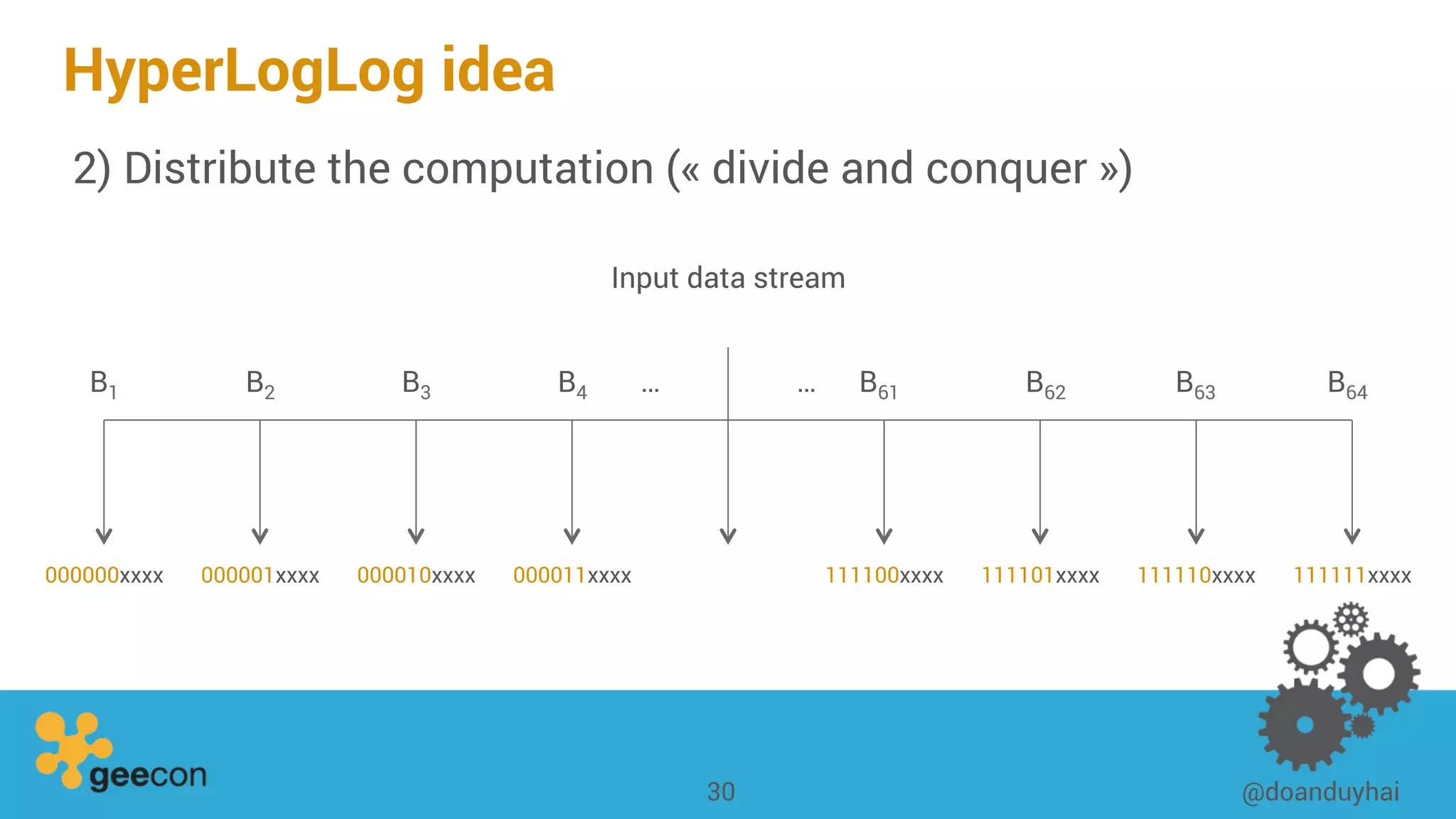
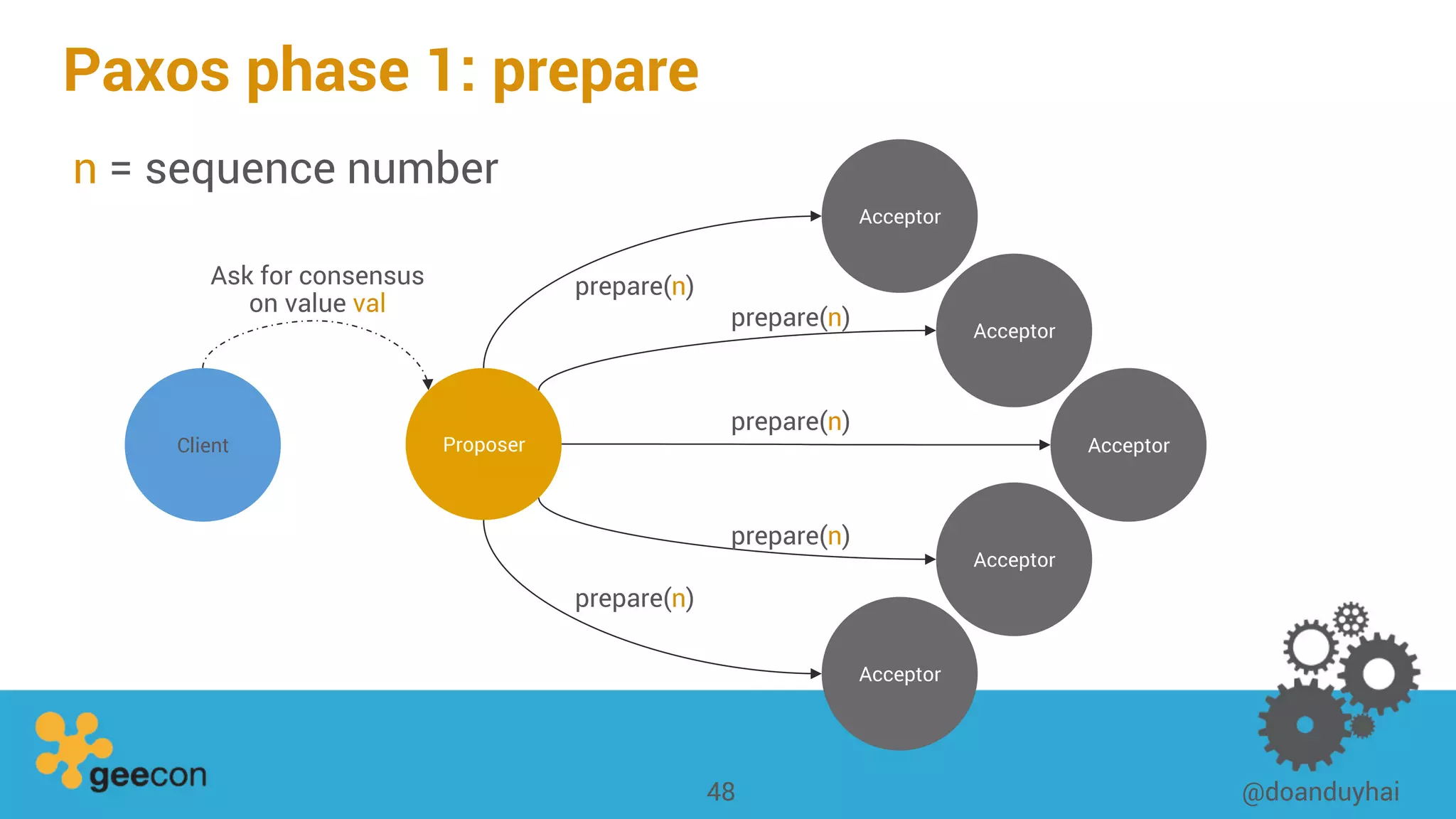
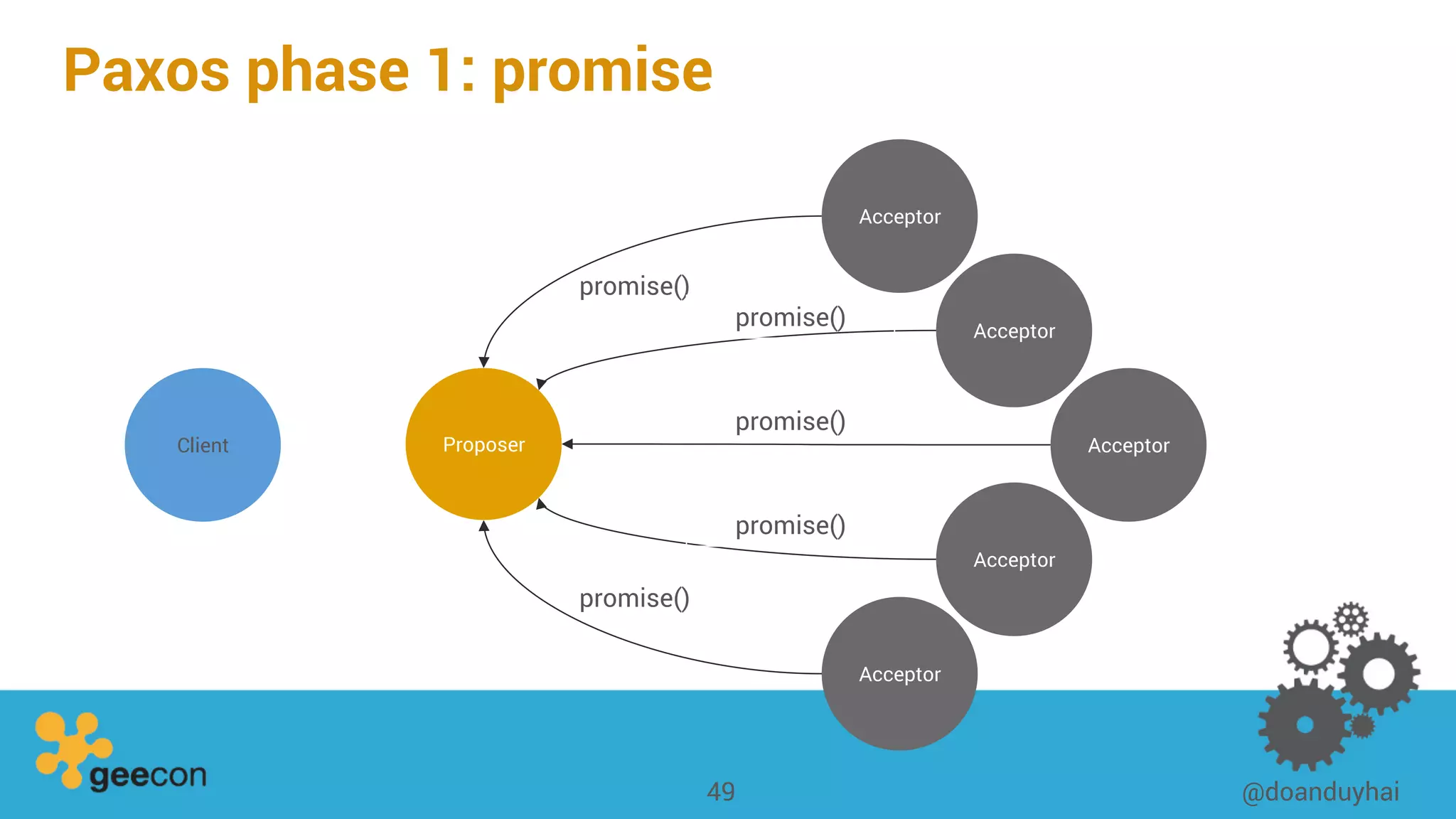
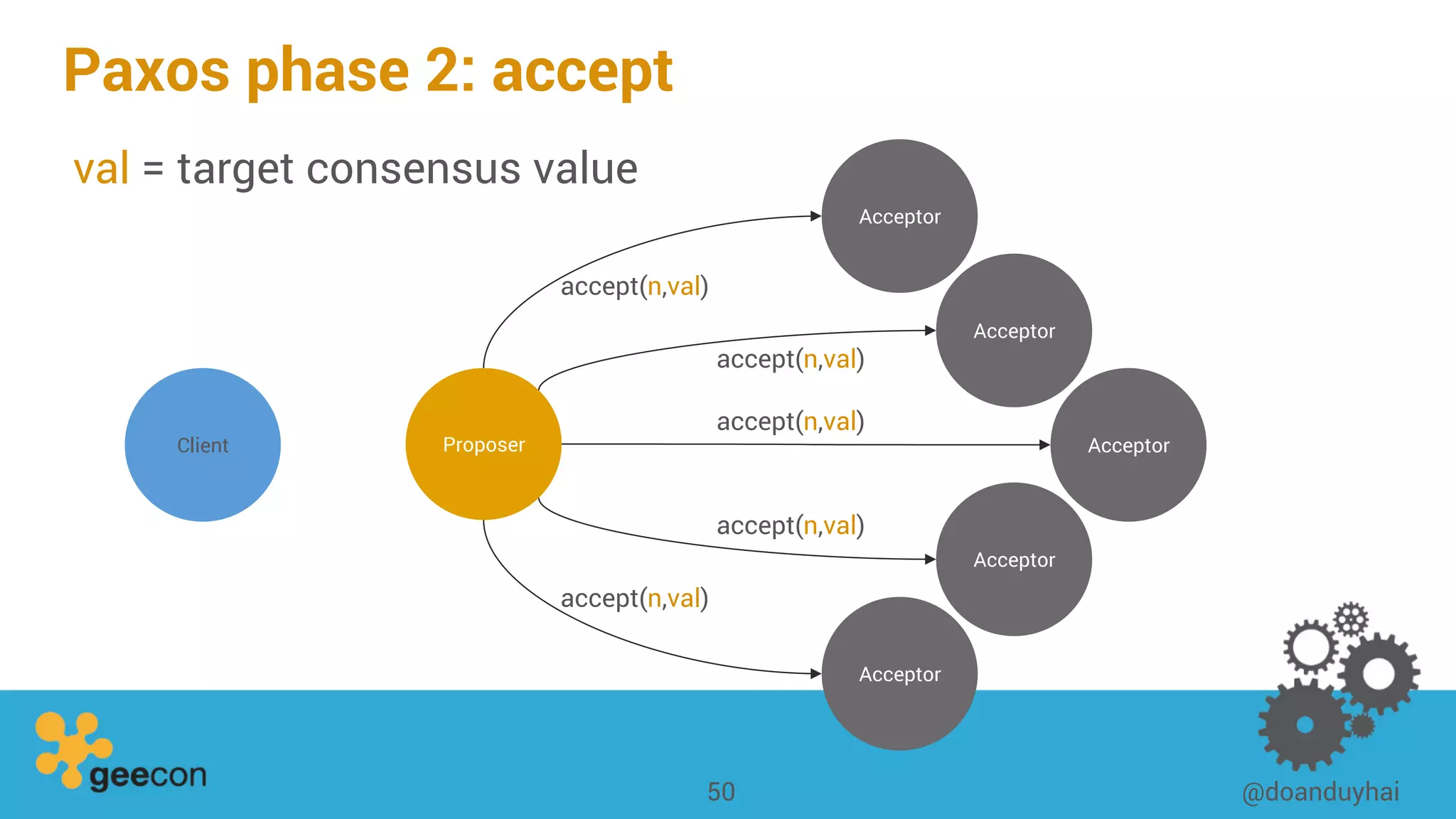
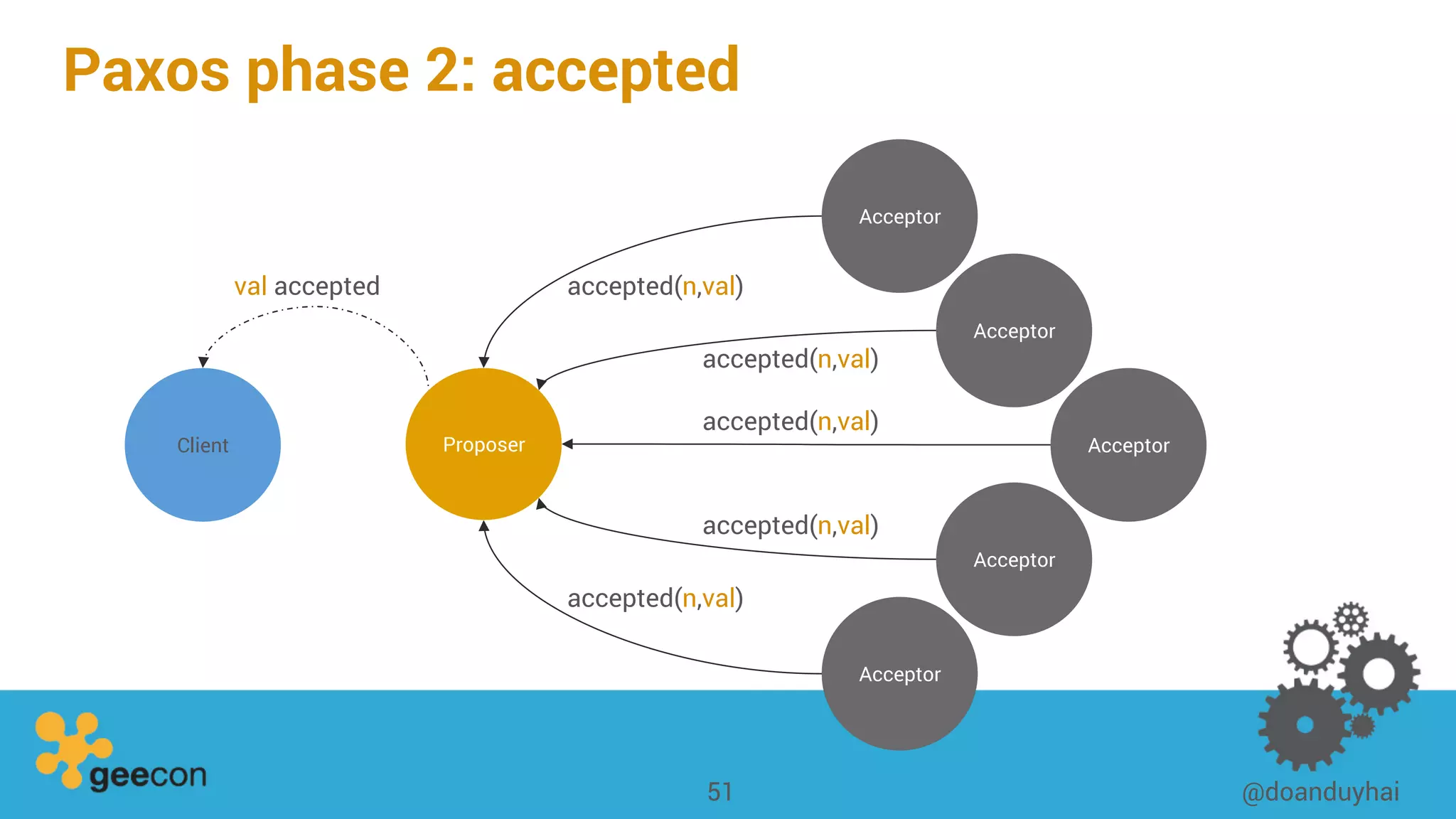
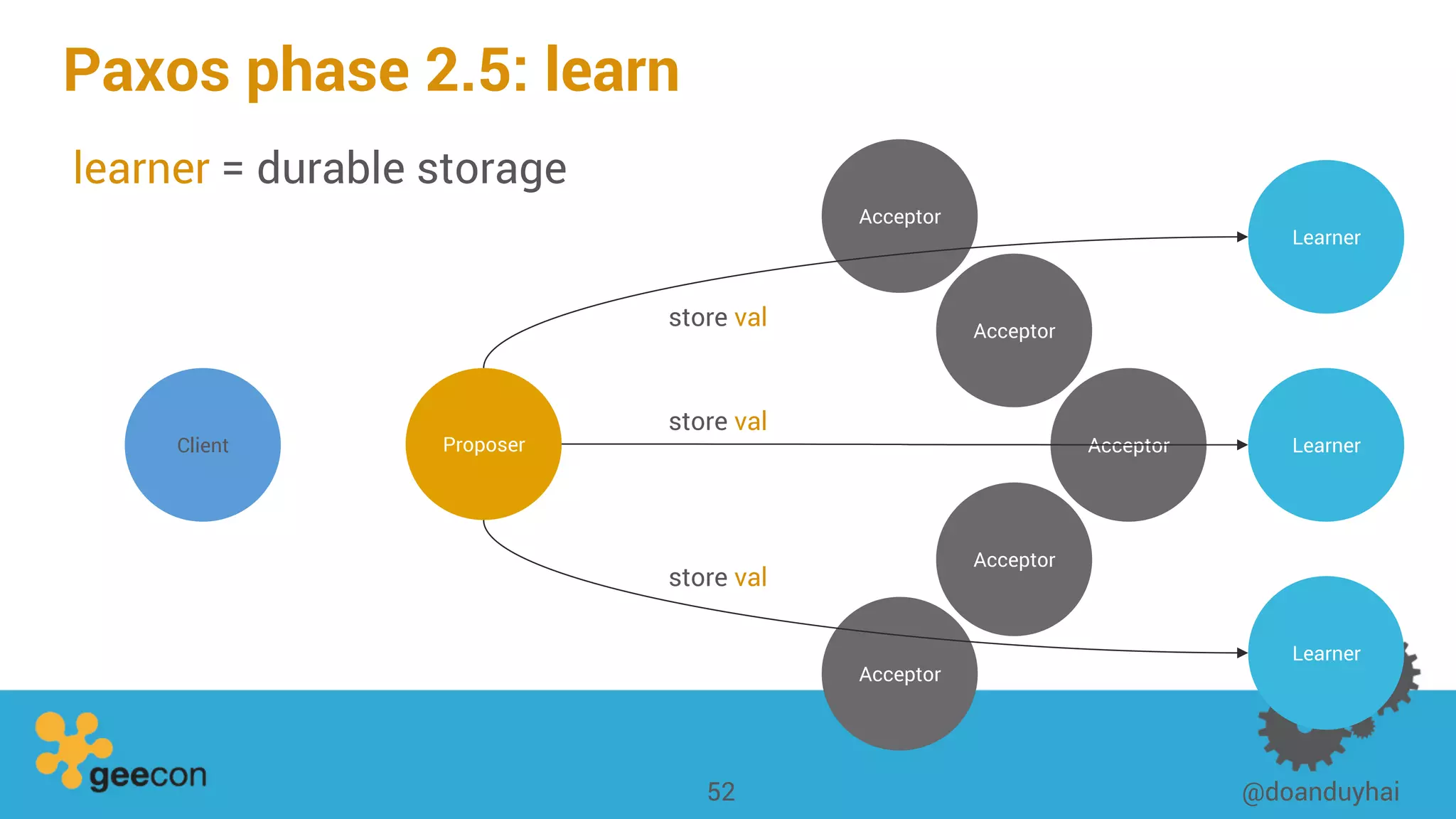
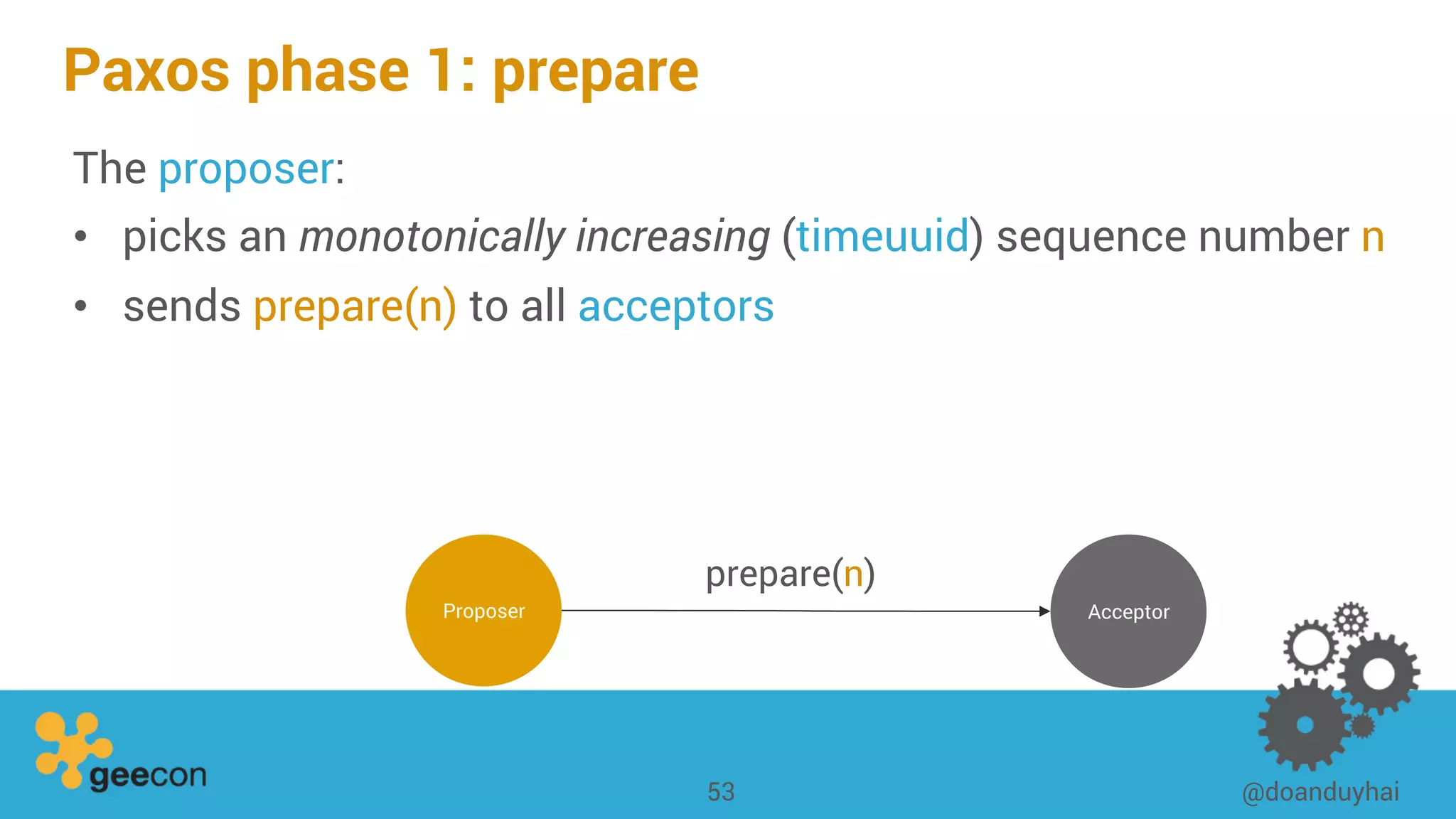
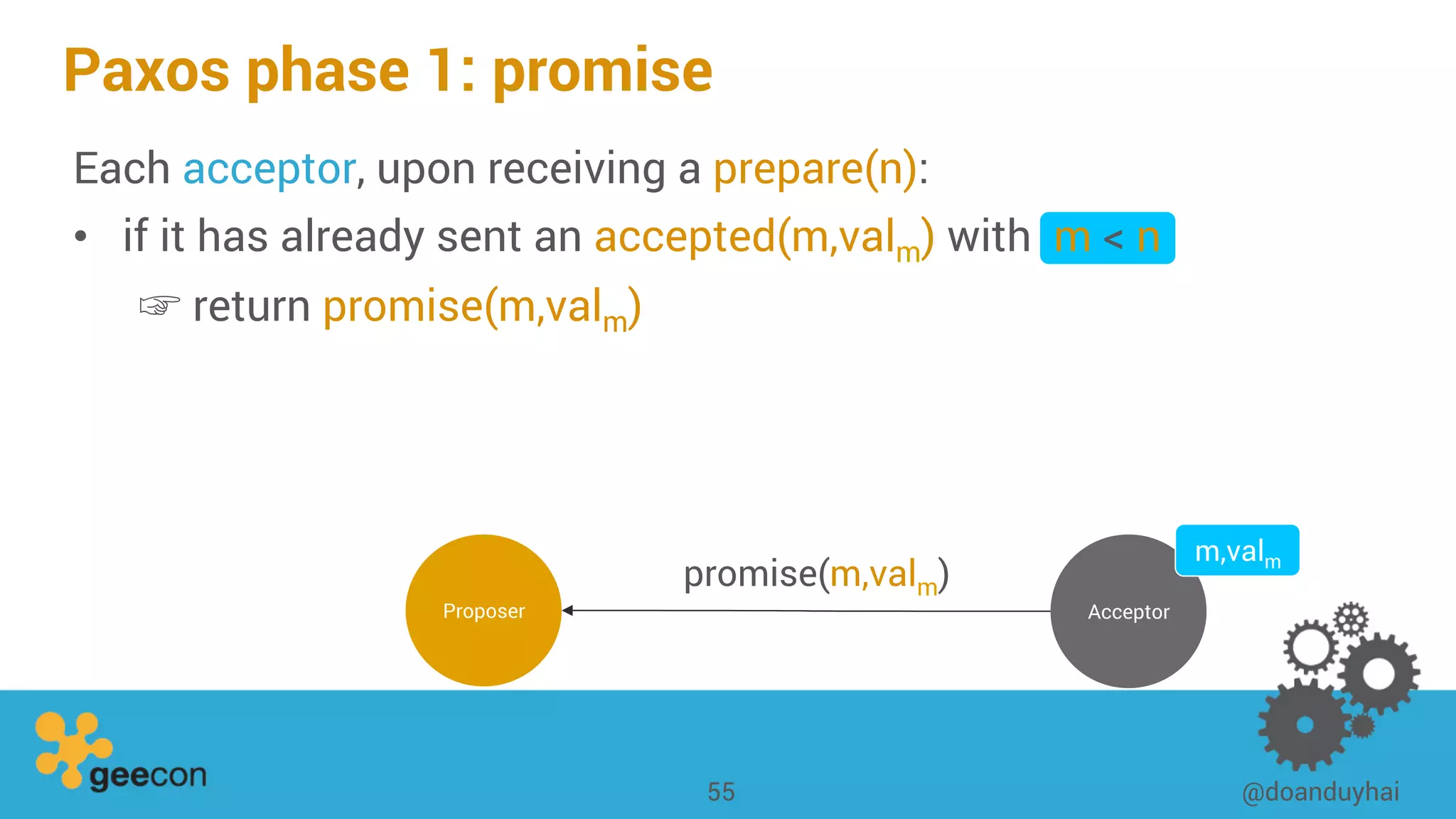
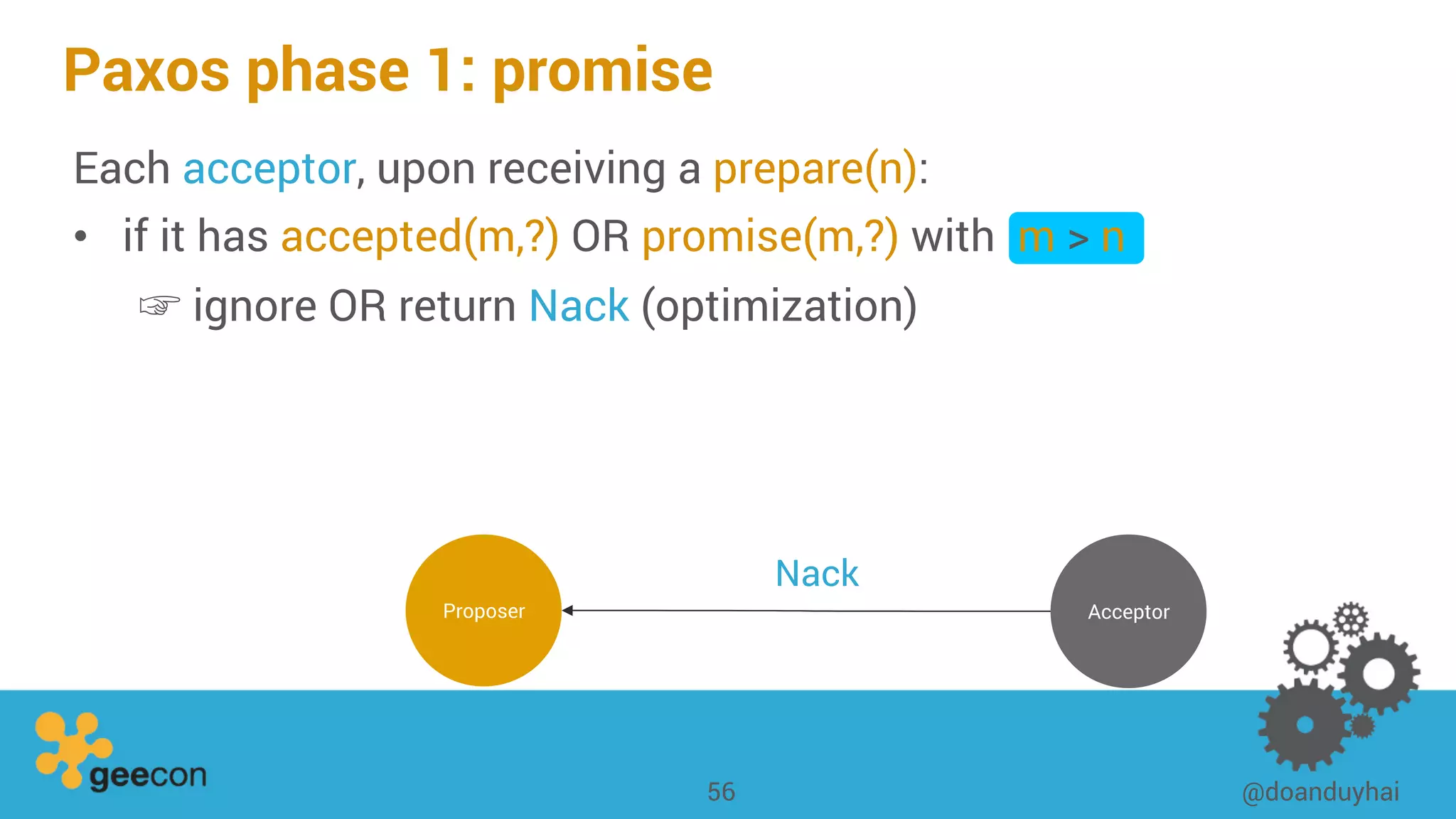
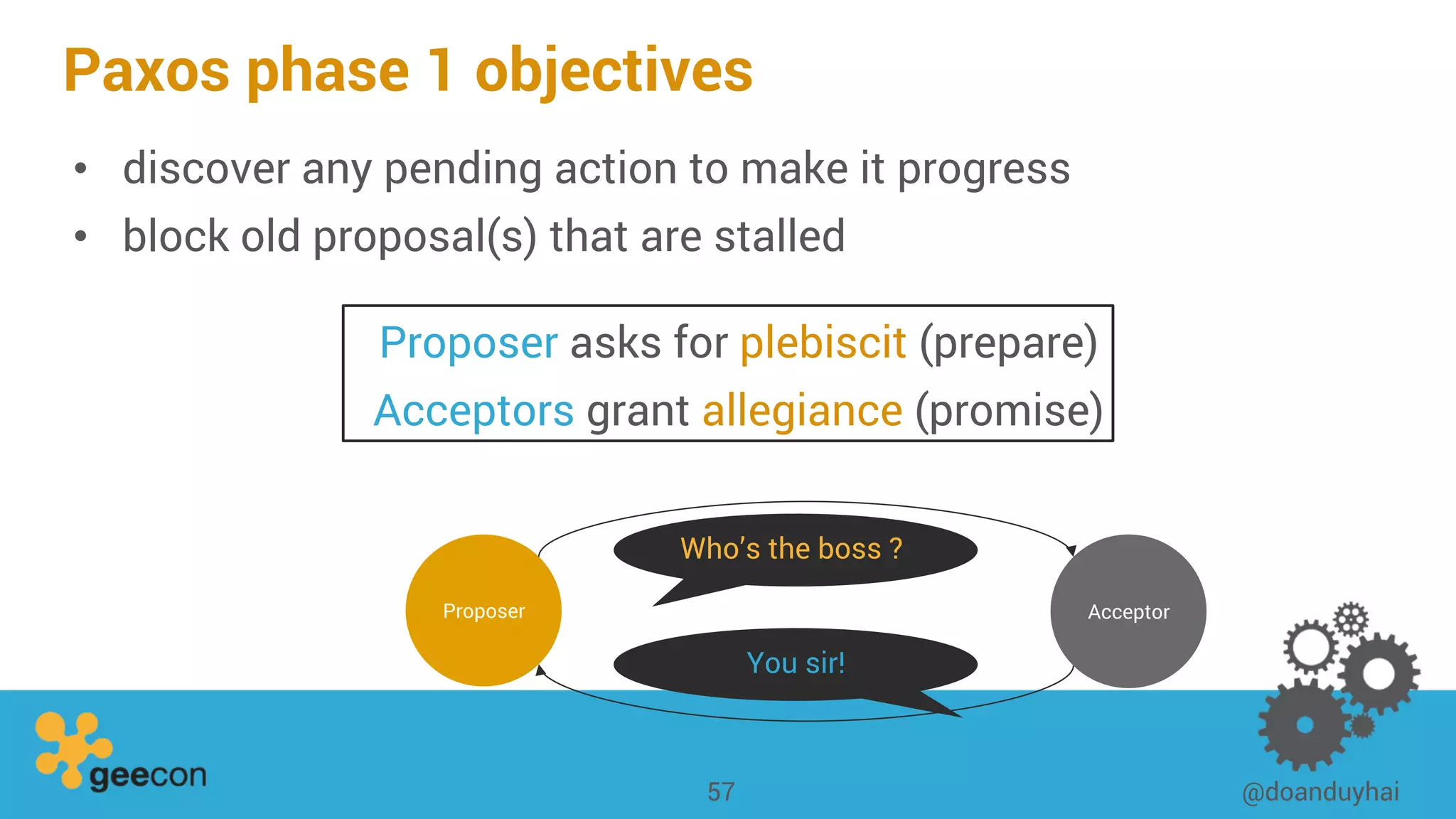
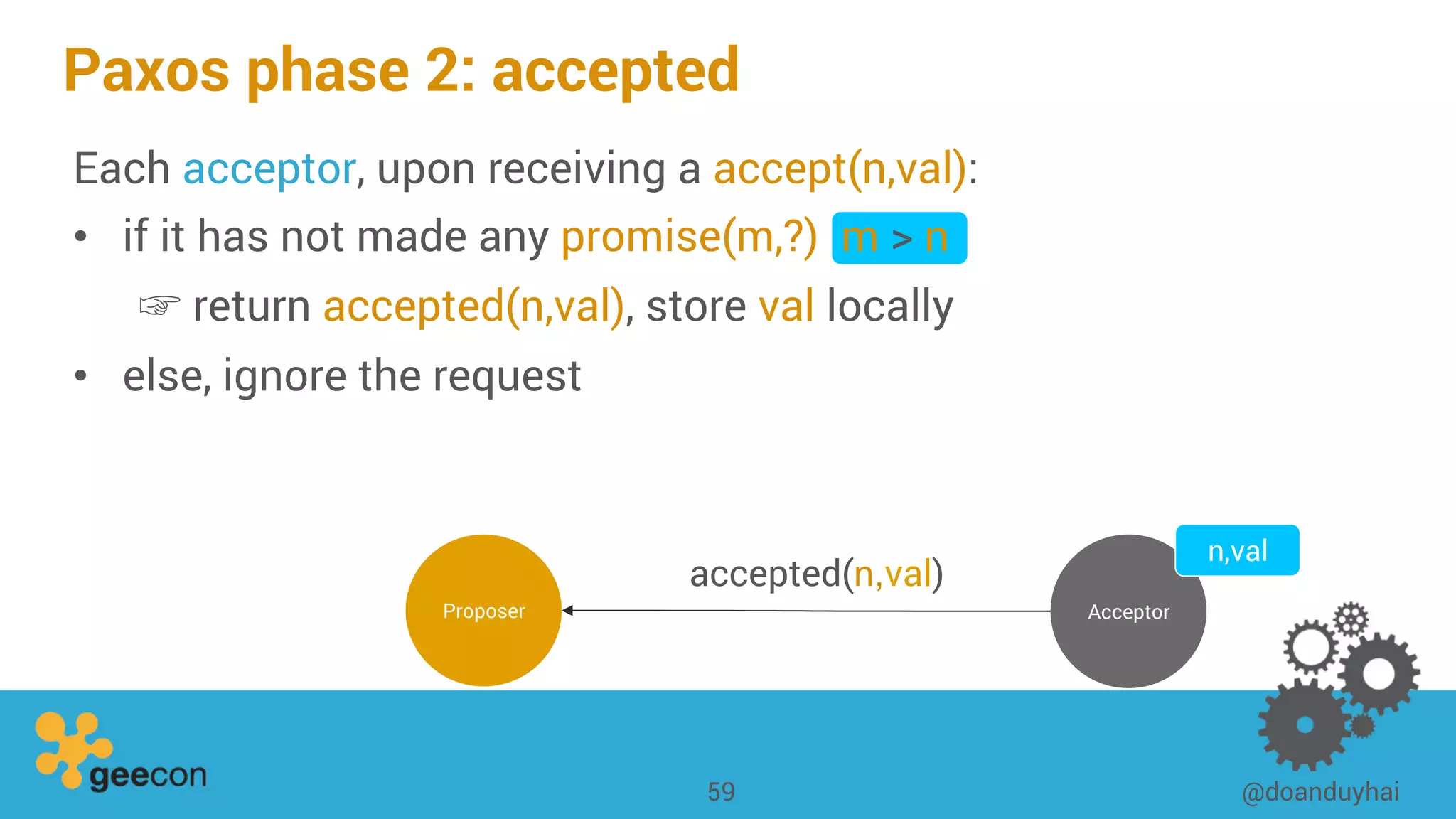
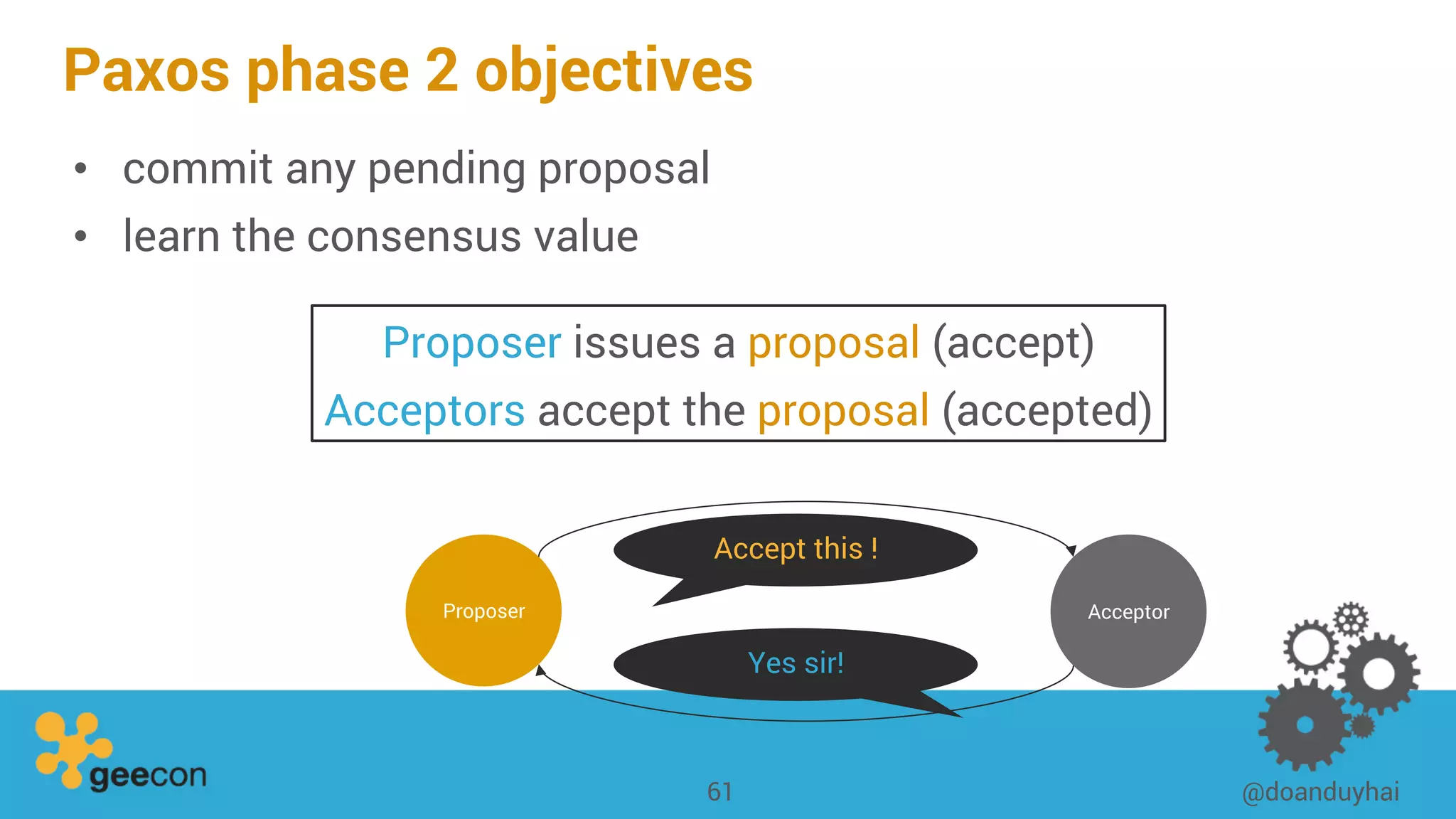
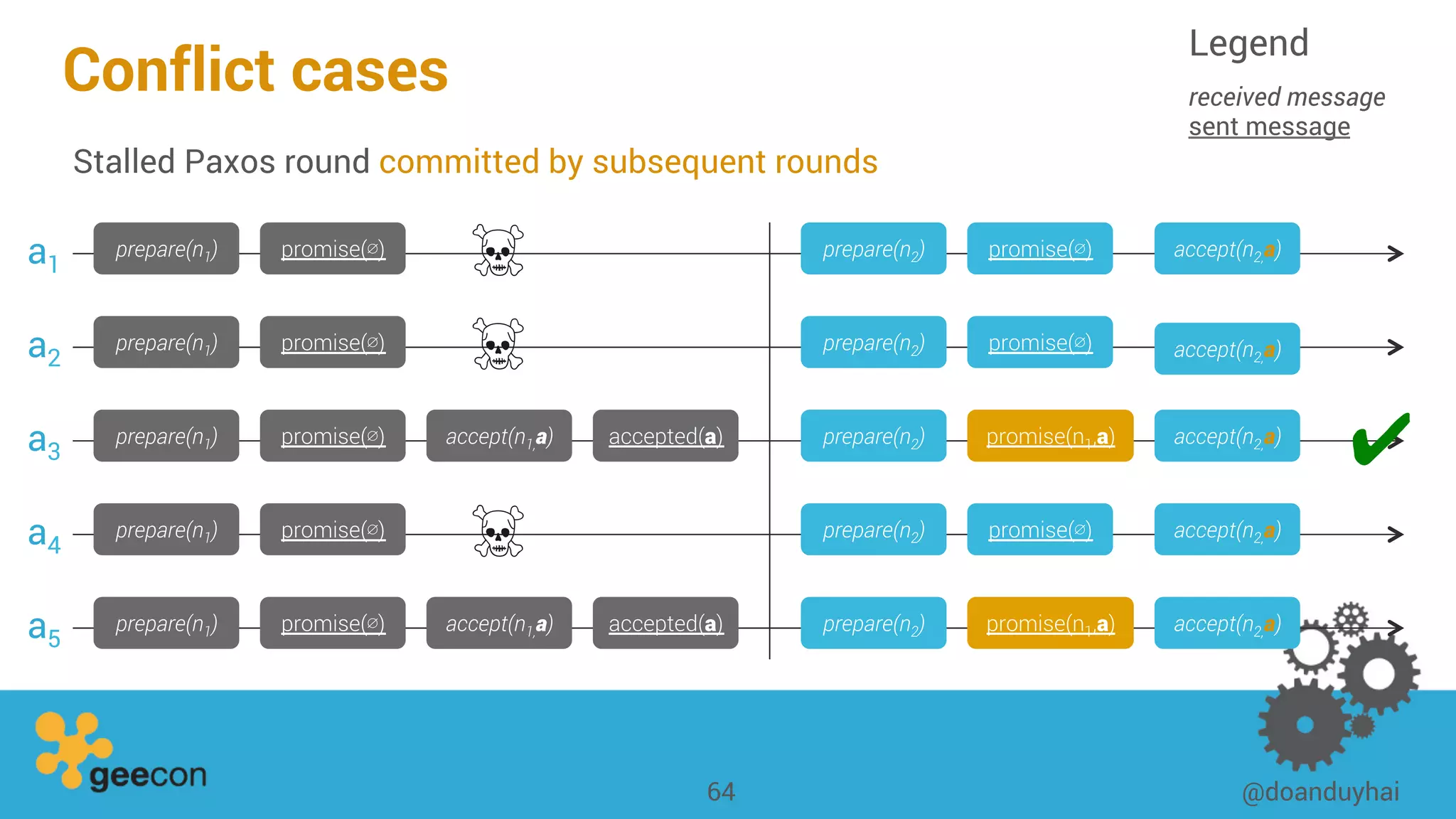
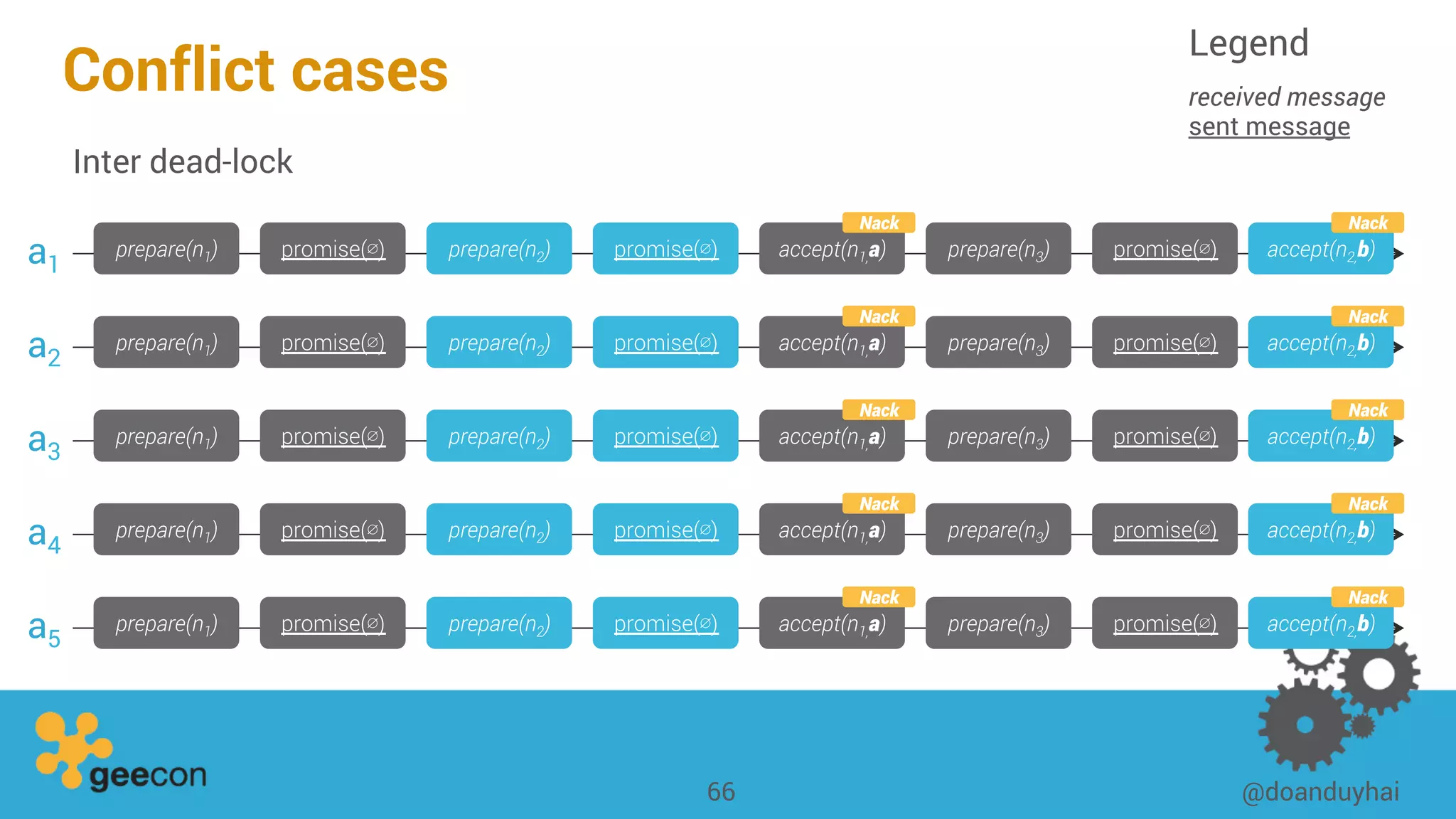
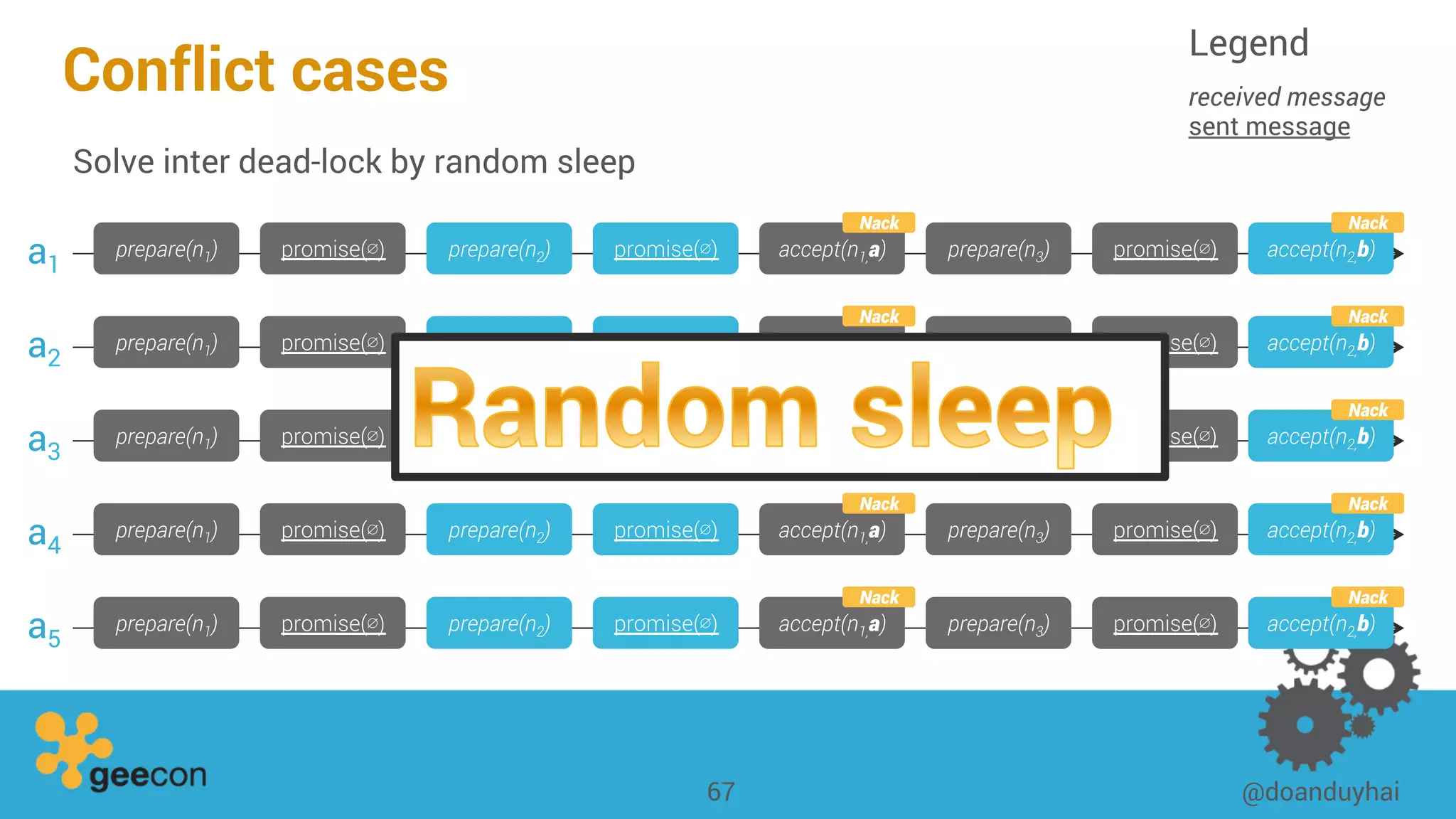
This document discusses distributed algorithms for big data. It begins with an overview of HyperLogLog for estimating cardinality and counting distinct elements in a large data set. It then explains how HyperLogLog works by using a hash function to distribute the data across buckets and applying the LogLog algorithm to each bucket before taking the harmonic mean. The document also covers Paxos for distributed consensus, explaining the phases of prepare, promise, accept and learn to reach agreement in the presence of failures.
Distributed algorithms for big data @ GeeCon
- 1. DISTRIBUTED ALGORITHMS FOR BIGDATA @doanduyhai Cassandra Technical Advocate Datastax @doanduyhai1
- 2. Who Am I? Duy Hai DOAN Cassandra technical advocate • talks, meetups, confs • open-source devs (Achilles, …) • OSS Cassandra point of contact ☞ duy_hai.doan@datastax.com ☞ @doanduyhai @doanduyhai2
- 3. Agenda High cardinality estimatewith HyperLogLog Distributed consensus with Paxos @doanduyhai3
- 4.
- 5. @doanduyhai5 The challenge Count thenumber of distinct elements, concurrently, in a high cardinality data set
- 6. @doanduyhai6 The challenge Count thenumber of distinct elements, concurrently, in a high cardinality data set
- 7. @doanduyhai7 The challenge Count thenumber of distinct elements, concurrently, in a high cardinality data set
- 8. Some possible solutions @doanduyhai8 Datastructure Required space Estimated cardinality Error margin Java HashSet 10 447 016 (10M) 67 801 0% Linear Probabilistic Counter 3 384 (3k) 67 080 1% HyperLogLog 512 70 002 3% Credits: http://highscalability.com/
- 9.
- 10. Rolling dice (attempt1) @doanduyhai10 0 2 4 6 8 10 12 14 16 18 20 1 2 3 4 5 6 100 rounds
- 11. Rolling dice (attempt2) @doanduyhai11 0 50 100 150 200 1 2 3 4 5 6 103 rounds
- 12. Rolling dice (attempt3) @doanduyhai12 0 20000 40000 60000 80000 100000 120000 140000 160000 180000 1 2 3 4 5 6 106 rounds
- 13.
- 14. LogLog algorithm(simplified) 1) Choosea very distributive hash function H 2) For each incoming element in the data set (article_id, login, uuid…), apply H 3) Convert the hash into binary sequence 4) estimate the cardinality by observing the binary sequences @doanduyhai14 0111010010101… 0010010010001… 1010111001100… …
- 15. LogLog intuition Uniform probability: 50%of the bit sequences start with 0xxxxx 50% of the bit sequences start with 1xxxxx 1/4 of the bit sequences start with 00xxxxx 1/4 of the bit sequences start with 01xxxxx 1/4 of the bit sequences start with 10xxxxx 1/4 of the bit sequences start with 11xxxxx @doanduyhai15
- 16. LogLog intuition Look forthe position r of the 1st bit set to 1 starting from the left 000000001xxxx à r = 9 0001xxxxxxxxx à r = 4 000001xxxxxxx à r = 6 @doanduyhai16 000000…0001xxxxxxx rank r
- 17. LogLog intuition There are2r combinations of r - length bit sequences 000…0001, 000…0010, 000…0011,…, 111…1111 @doanduyhai17 000000…0001xxxxxxx rank r
- 18. LogLog intuition Uniform probability: 1/2rof the bit sequences start with 000000…0001xxx 1/2r of the bit sequences start with 000000…0010xxx … 1/2r of the bit sequences start with 111111…1111xxx @doanduyhai18
- 19.
- 20. @doanduyhai20 Reversing the logic Ihave as many chance to observe 000000…0001xxx than to observe 000000…0010xxx than to observe 000000…0011xxx etc…
- 21. @doanduyhai21 Reversing the logic IfI have observed 000000…0001xxx I should probably observe 000000…0010xxx and probably observe 000000…0011xxx etc…
- 22. @doanduyhai22 Reversing the logic IfI have observed 000000…0001xxx … there is probably 2r bit sequences of rank r …
- 23. @doanduyhai23 Reversing the logic IfI have observed 000000…0001xxx … there is probably 2r bit sequences of rank r … estimated cardinality
- 24. LogLog formula Let’s lookfor the longest position 0000…01xxx observed among all binary sequences carnidality n ≈ 2max(r) @doanduyhai24
- 25. LogLog pitfall Example: 1000distinct elements 0010000100xxxxxxxxxx 0011001010xxxxxxxxxx 0000000001xxxxxxxxxx … 000000000000001xxxxx à rank r = 15, n ≈ 215 ≈ 32768 WRONG! … 1100110100xxxxxxxxxx @doanduyhai25
- 26.
- 27. HyperLogLog idea 1) Eliminateand smooth out outlying elements ☞ harmonic mean @doanduyhai27 H = n 1 x1 + 1 x2 +...+ 1 xn Credits: Wikipedia
- 28. HyperLogLog idea Example, harmonicmean of 3, 6, 7, 2 and 120 Arithmetic mean = 51 … @doanduyhai28 H = 5 1 3 + 1 6 + 1 7 + 1 12 + 1 120 ≈ 6.80
- 29. HyperLogLog idea 2) Distributethe computation (« divide and conquer ») ☞ apply LogLog to n buckets p = prefix length (here 6) buckets count = 2p (here 64) @doanduyhai29 101101000xxxxxxx p bits
- 30. HyperLogLog idea 2) Distributethe computation (« divide and conquer ») @doanduyhai30 000000xxxx Input data stream B1 B2 B3 B4 B63 B64B62B61… … 000001xxxx 000010xxxx 000011xxxx 111100xxxx 111101xxxx 111110xxxx 111111xxxx
- 31. 101101000001xxxx HyperLogLog idea 3) ApplyLogLog on each bucket @doanduyhai31 p = bucket prefix r = rank for LogLog
- 32. HyperLogLog formula For eachbucket i, we compute the cardinality estimate for this bucket, Mi Mi ≈ 2max(ri) max(ri) = max rank found in bucket Mi @doanduyhai32
- 33. HyperLogLog formula Harmonic meanH(Mi) computed on all Mi, by definition H(Mi) ≈ n/b n = global cardinality estimate (what we look for) b = number of buckets ☞ n ≈ b • H(Mi) @doanduyhai33
- 34. HyperLogLog, the maths @doanduyhai34 H(xi) = b 1 x1 + 1 x2 +...+ 1 xb = b 1 1 xi i=1 b ∑ " # $ $ $ $ % & ' ' ' ' H(xi ) = b 1 xi i=1 b ∑ " # $ $ % & ' ' −1 = b xi −1 i=1 b ∑ " # $ % & ' −1
- 35. HyperLogLog, the maths Wereplace the xi in the previous formula by Mi Then we replace the Mi in the formula by 2max(ri) @doanduyhai35 H(Mi ) = b Mi −1 i=1 b ∑( ) −1 H(Mi ) = b 2i −max(ri ) i=1 b ∑ # $ % & ' ( −1
- 36. HyperLogLog, the maths InjectH(Mi) into the formula for cardinality estimate: n ≈ b･H(Mi) @doanduyhai36 n ≈ αbb2 2−max(ri ) i=1 b ∑ $ % & ' ( ) −1 n = cardinality estimate b = buckets count 𝛼b = corrective constant max rank observed in each bucket
- 37. HyperLogLog space requirement @doanduyhai37 Hashfunction length Max estimated card. Bucket size (bits) 16 bits 216 = 65536 log2(16) = 4 32 bits 232 ≈ 4.2 109 log2(32) = 5 64 bits 264 ≈ 1.8 1019 log2(64) = 6 max_estimated _cardinality = 2hash_ function_length bucket _ size = log2 (hash_ function_length) required _ space = bucket _count *bucket _ size
- 38. HyperLogLog accuracy @doanduyhai38 Buckets countRequired space (bytes) Accuracy 256 16bits: 128, 32bits: 160, 64bits: 192 6.25% 512 16bits: 256, 32bits: 320, 64bits: 384 4.59% 1024 16bits: 512, 32bits: 640, 64bits: 768 3.25% 2048 16bits: 1k, 32bits: 1.25k, 64bits: 1.5k 2.29% accuracy ≈ 1.04 bucket _count
- 39. Which use-cases ? Nbof unique visitors on high traffic web site Nb of unique clicks on popular articles/items TopN elements (visitors, items …) … @doanduyhai39
- 40. Some real-world implementations ApacheCassandra: distributed table size estimate Redis: out-of-the-box data structure DataFu (Apache Pig): standard UDF Twitter Algebird: algorithms lib for Storm & Scalding @doanduyhai40
- 41.
- 42. @doanduyhai42 The challenge Find aconsensus, in a distributed system, in the presence of random failures (hardware, network, …)
- 43. @doanduyhai43 The challenge Find aconsensus, in a distributed system, in the presence of random failures (hardware, network, …)
- 44. @doanduyhai44 The challenge Find aconsensus, in a distributed system, in the presence of random failures (hardware, network, …)
- 45. @doanduyhai45 2 phase commit? • blocking protocol by nature • requires human intervention if manager down
- 46. @doanduyhai46 3 phase commit? • inconsistent state when split-brain network partition
- 47. @doanduyhai47 Paxos • 2,5 networkround-trips • 3 roles • Proposer • Acceptor • Learner • needs a quorum of response
- 48. Paxos phase 1:prepare n = sequence number @doanduyhai48 Proposer Acceptor Client Acceptor Acceptor Acceptor Acceptor prepare(n) prepare(n) prepare(n) Ask for consensus on value val prepare(n) prepare(n)
- 49. Paxos phase 1:promise @doanduyhai49 Proposer Acceptor Client Acceptor Acceptor Acceptor Acceptor promise() promise() promise() promise() promise()
- 50. Paxos phase 2:accept @doanduyhai50 Proposer Acceptor Client Acceptor Acceptor Acceptor Acceptor accept(n,val) accept(n,val) accept(n,val) val = target consensus value accept(n,val) accept(n,val)
- 51. Paxos phase 2:accepted @doanduyhai51 Proposer Acceptor Client Acceptor Acceptor Acceptor Acceptor accepted(n,val) accepted(n,val) accepted(n,val) val accepted accepted(n,val) accepted(n,val)
- 52. Paxos phase 2.5:learn @doanduyhai52 Proposer Acceptor Client Acceptor Acceptor Acceptor Acceptor store val learner = durable storage Learner Learner Learner store val store val
- 53. Paxos phase 1:prepare The proposer: • picks an monotonically increasing (timeuuid) sequence number n • sends prepare(n) to all acceptors @doanduyhai53 Proposer Acceptor prepare(n)
- 54. Each acceptor, uponreceiving a prepare(n): • if it has not accepted(m,?) OR promise(m,valm) with m > n ☞ return promise(n,∅), store n locally ☞ promise not to accept any prepare(o) or accept(o,?) with o < n Paxos phase 1: promise @doanduyhai54 Proposer Acceptor promise(n,∅) n,∅
- 55. Paxos phase 1:promise Each acceptor, upon receiving a prepare(n): • if it has already sent an accepted(m,valm) with m < n ☞ return promise(m,valm) @doanduyhai55 Proposer Acceptor promise(m,valm) m,valm
- 56. Paxos phase 1:promise Each acceptor, upon receiving a prepare(n): • if it has accepted(m,?) OR promise(m,?) with m > n ☞ ignore OR return Nack (optimization) @doanduyhai56 Proposer Acceptor Nack
- 57. Paxos phase 1objectives • discover any pending action to make it progress • block old proposal(s) that are stalled Proposer asks for plebiscit (prepare) Acceptors grant allegiance (promise) @doanduyhai57 Proposer Acceptor Who’s the boss ? You sir!
- 58. Paxos phase 2:accept The proposer receives a quorum of promise(mi,valmi ) • if all promises are promise(n, ∅) then send accept(n,valn) • otherwise, take the valmi of the biggest mi and send accept(n,valmax(mi) ) @doanduyhai58 Proposer Acceptor accept(n,valmax(mi)) OR accept(n,valn)
- 59. Paxos phase 2:accepted Each acceptor, upon receiving a accept(n,val): • if it has not made any promise(m,?) m > n ☞ return accepted(n,val), store val locally • else, ignore the request @doanduyhai59 Proposer Acceptor accepted(n,val) n,val
- 60. Paxos phase 2.5:learn The proposer receives a quorum of accepted(n,val) • send val to the learners (durable storage) The consensus is found and its value is val This defines a round of Paxos @doanduyhai60 Proposer store val Learner
- 61. Paxos phase 2objectives • commit any pending proposal • learn the consensus value Proposer issues a proposal (accept) Acceptors accept the proposal (accepted) @doanduyhai61 Proposer Acceptor Accept this ! Yes sir!
- 62. Formal Paxos limits • once a consensus val is reached, we can’t change it! • needs to reset val for another Paxos round Multi-Paxos • many rounds of Paxos in //, impacting different partitions • each server can be Proposer, Acceptor & Learner Fast-Paxos, Egalitarian-Paxos, etc … @doanduyhai62
- 63. Conflict cases Failure ofa minority of acceptors @doanduyhai63 a1 a2 a3 a4 a5 prepare(n1) prepare(n1) prepare(n1) prepare(n1) prepare(n1) Legend received message sent message promise(∅) promise(∅) promise(∅) promise(∅) promise(∅) accept(n1,a) accept(n1,a) ☠ ☠ accepted(a) accepted(a) accept(n1,a) accepted(a) ✔︎
- 64. Conflict cases Stalled Paxosround committed by subsequent rounds @doanduyhai64 a1 a2 a3 a4 a5 prepare(n1) prepare(n1) prepare(n1) prepare(n1) prepare(n1) Legend received message sent message promise(∅) promise(∅) promise(∅) promise(∅) promise(∅) accept(n1,a) accept(n1,a) ☠ ☠ accepted(a) ☠ accepted(a) prepare(n2) prepare(n2) prepare(n2) prepare(n2) prepare(n2) promise(∅) promise(∅) promise(∅) promise(n1,a) promise(n1,a) accept(n2,a) accept(n2,a) accept(n2,a) accept(n2,a) accept(n2,a) ✔︎
- 65. Conflict cases Random failure,last plebiscit wins ! @doanduyhai65 a1 a2 a3 a4 a5 prepare(n1) prepare(n1) prepare(n1) Legend received message sent message promise(∅) promise(∅) promise(∅) accepted(n2,b)prepare(n2) prepare(n2) prepare(n2) promise(∅) promise(∅) promise(∅) ⚡️ ⚡️ ⚡️ ⚡️ accept(n1,a) Nack accept(n2,b) accept(n2,b) accept(n2,b) accept(n1,a) accept(n1,a) accepted(n2,b) accepted(n2,b) accept(n1,a) accept(n1,a) 💡 💡 💡 💡 Nack Nack accept(n2,b) accept(n2,b) ✔︎ ❌︎ accepted(n2,b) accepted(n2,b)
- 66. Conflict cases Inter dead-lock @doanduyhai66 a1 a2 a3 a4 a5 prepare(n1) prepare(n1) prepare(n1) Legend receivedmessage sent message promise(∅) promise(∅) promise(∅) prepare(n2) prepare(n2) prepare(n2) promise(∅) promise(∅) promise(∅) prepare(n1) promise(∅) prepare(n1) promise(∅) prepare(n2) promise(∅) prepare(n2) promise(∅) accept(n1,a) accept(n1,a) accept(n1,a) accept(n1,a) accept(n1,a) Nack Nack Nack Nack Nack prepare(n3) prepare(n3) prepare(n3) prepare(n3) prepare(n3) promise(∅) promise(∅) promise(∅) promise(∅) promise(∅) accept(n2,b) Nack accept(n2,b) Nack accept(n2,b) Nack accept(n2,b) Nack accept(n2,b) Nack
- 67. Conflict cases Solve interdead-lock by random sleep @doanduyhai67 a1 a2 a3 a4 a5 prepare(n1) prepare(n1) prepare(n1) Legend received message sent message promise(∅) promise(∅) promise(∅) prepare(n2) prepare(n2) prepare(n2) promise(∅) promise(∅) promise(∅) prepare(n1) promise(∅) prepare(n1) promise(∅) prepare(n2) promise(∅) prepare(n2) promise(∅) accept(n1,a) accept(n1,a) accept(n1,a) accept(n1,a) accept(n1,a) Nack Nack Nack Nack Nack prepare(n3) prepare(n3) prepare(n3) prepare(n3) prepare(n3) promise(∅) promise(∅) promise(∅) promise(∅) promise(∅) accept(n2,b) Nack accept(n2,b) Nack accept(n2,b) Nack accept(n2,b) Nack accept(n2,b) Nack
- 68. Which use-cases ? Reliablemaster election for master/slave architectures Distributed consensus Distributed Compare & Swap algorithm Distributed lock @doanduyhai68
- 69. Some real-world implementations ApacheCassandra: light weight transaction Google Chubby/Spanner: lock/distributed transactions Heroku: via Doozerd for distributed configuration data Neo4j(≥1.9): replaces Apache Zookeeper for high availablity @doanduyhai69
- 70.
- 71.
- 72.