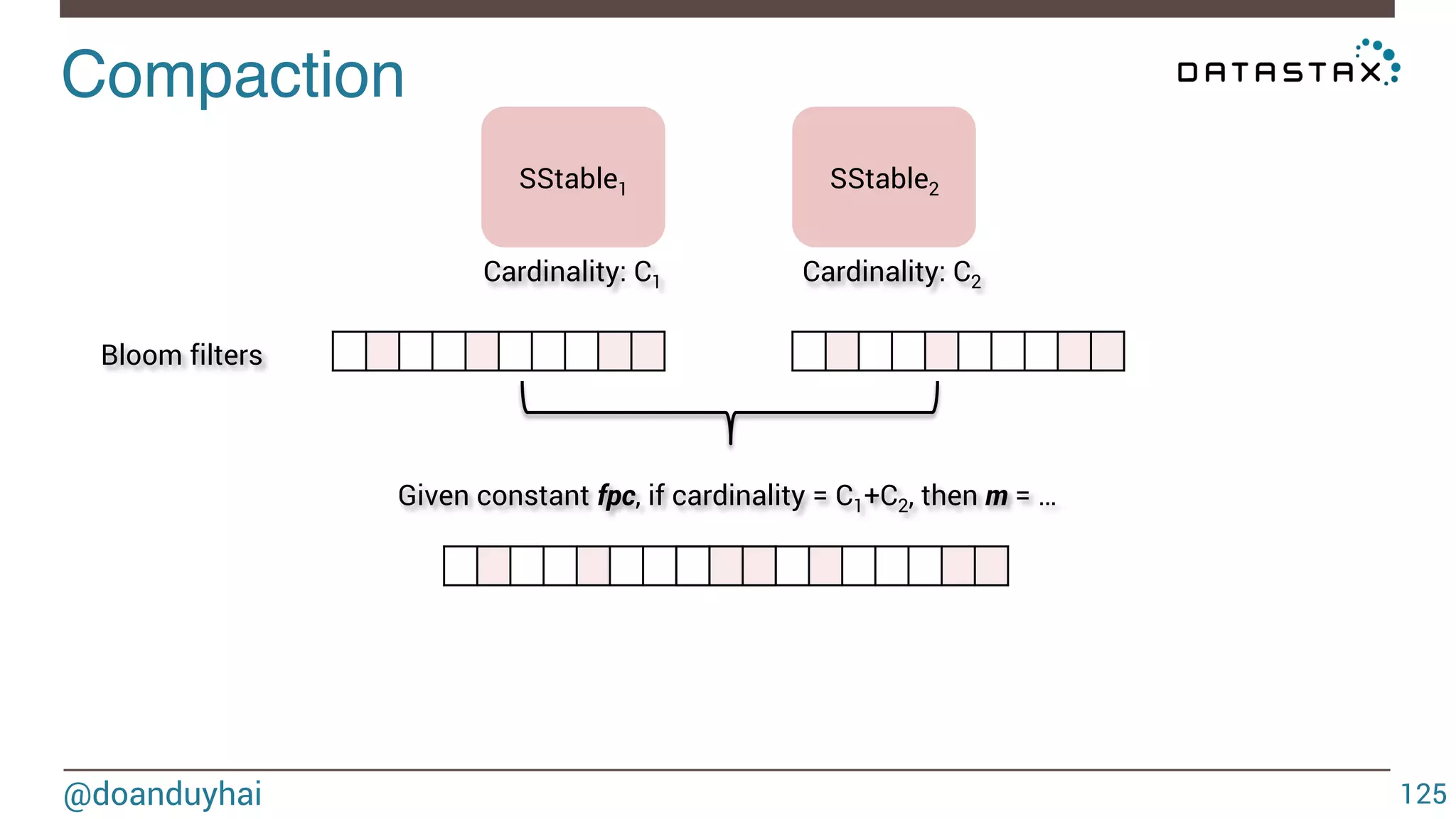
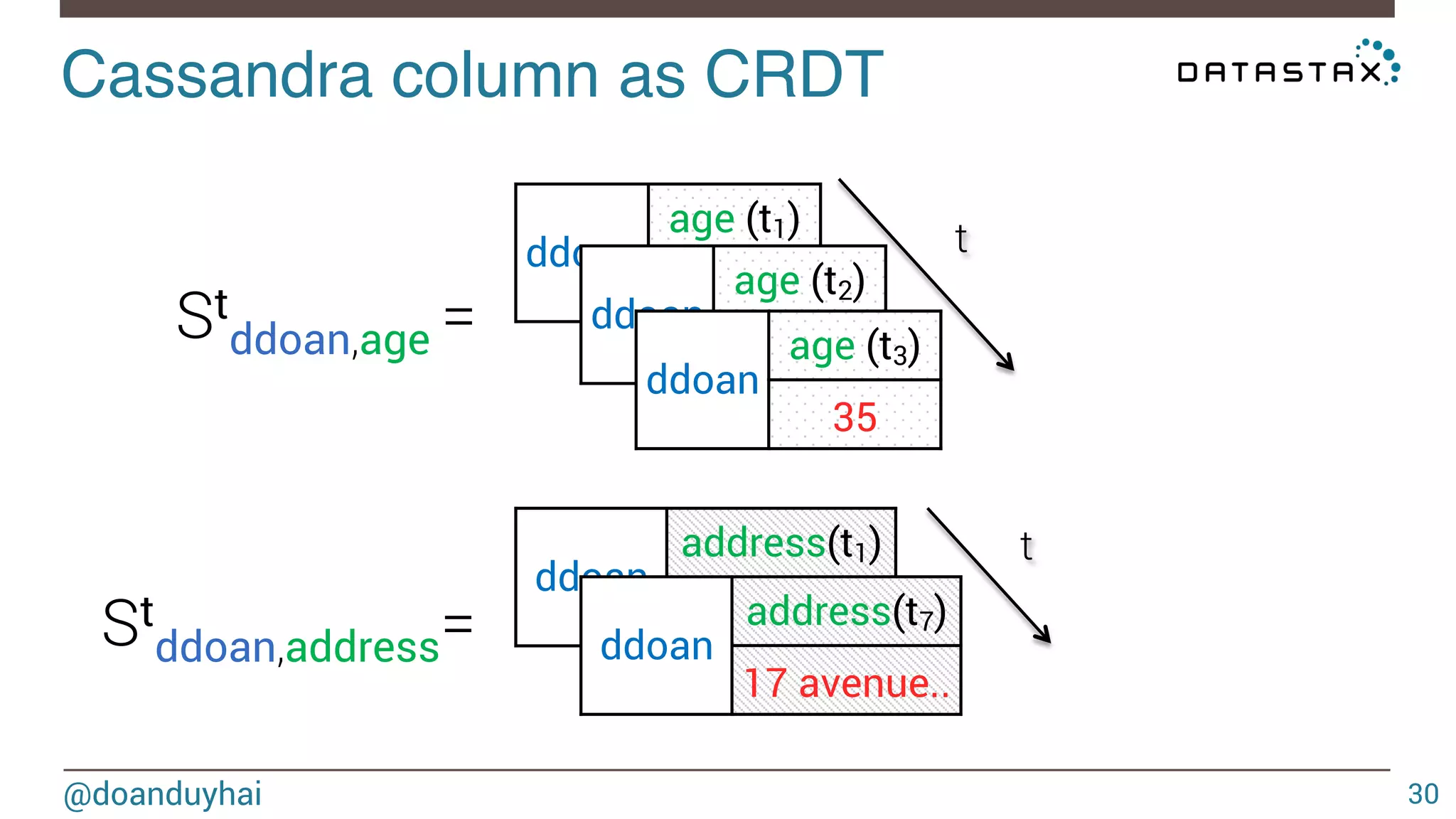
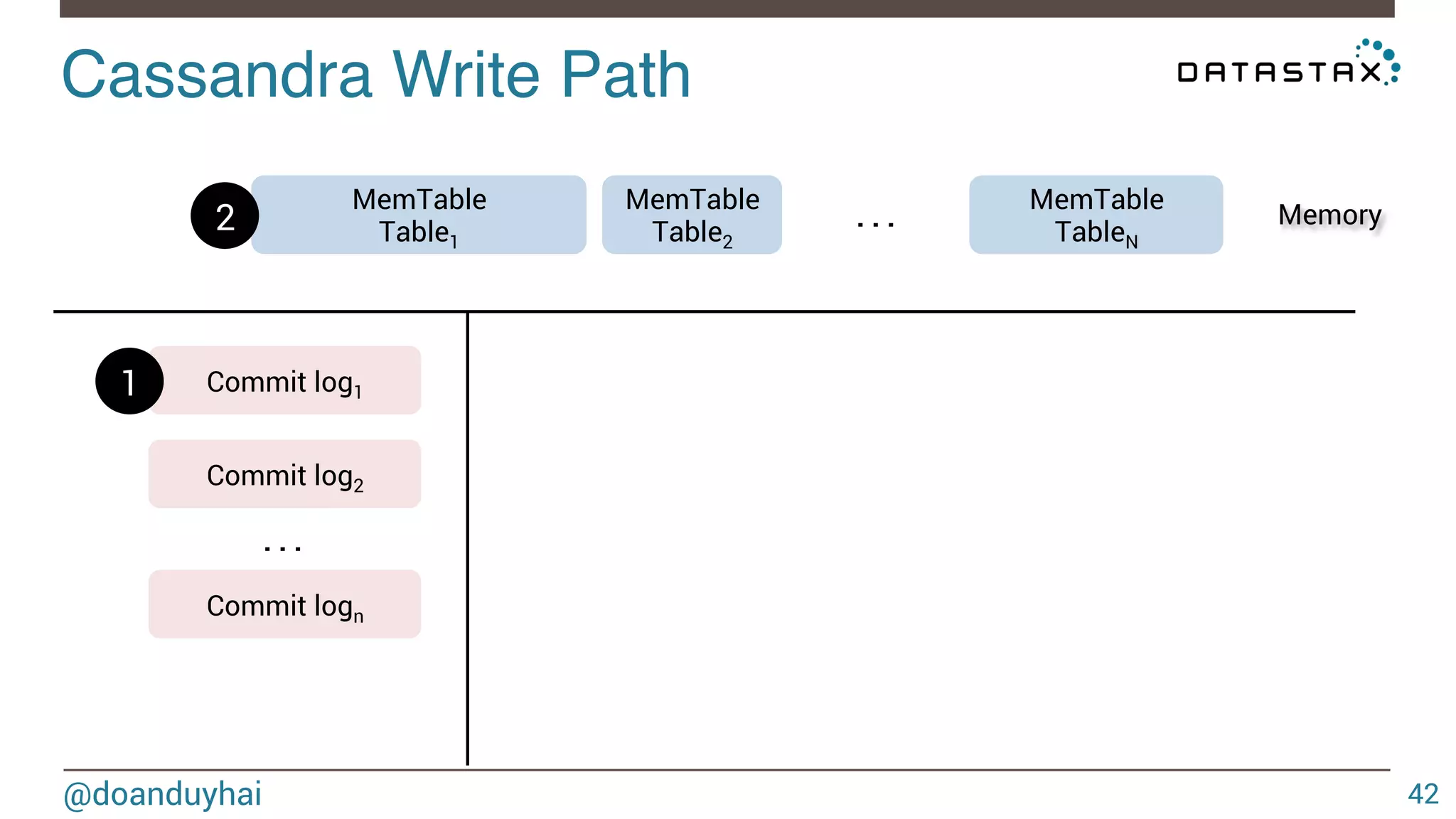
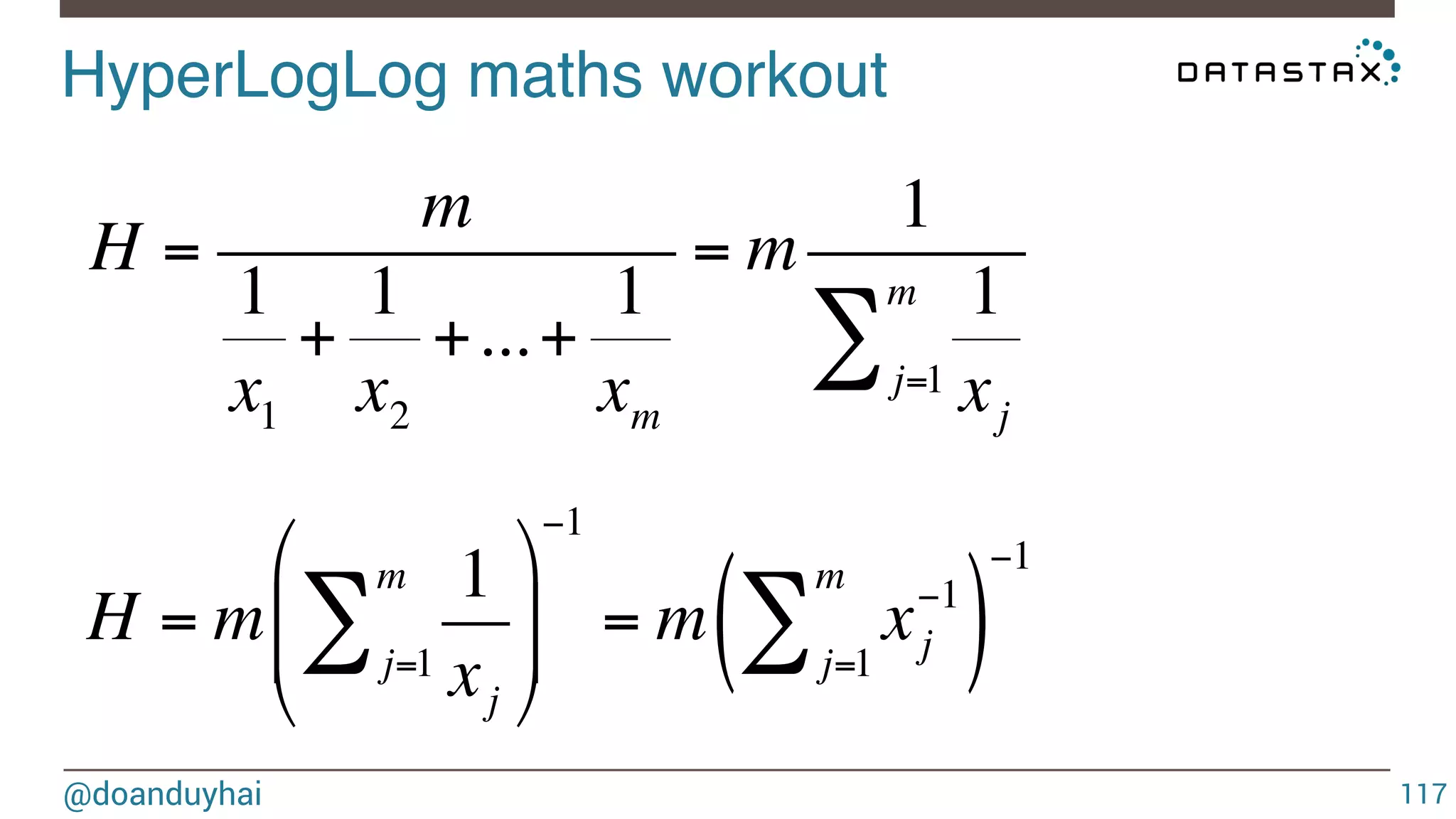Cassandra data structures and algorithms

Cassandra data structures & algorithms DuyHai DOAN, Technical Advocate @doanduyhai

Shameless self-promotion! @doanduyhai 2 Duy Hai DOAN Cassandra technical advocate • talks, meetups, confs • open-source devs (Achilles, …) • Cassandra technical point of contact • Cassandra troubleshooting

Agenda! @doanduyhai 3 Data structures • CRDT • Bloom filter • Merkle tree Algorithms • HyperLogLog

Why Cassandra ?! @doanduyhai 4 Linear scalability ≈ unbounded extensivity • 1k+ nodes cluster

Why Cassandra ?! @doanduyhai 5 Continuous availability (≈100% up-time) • resilient architecture (Dynamo) • rolling upgrades • data backward compatible n/n+1 versions

Why Cassandra ?! @doanduyhai 6 Multi-data centers • out-of-the-box (config only) • AWS conf for multi-region DCs Operational simplicity • 1 node = 1 process + 1 config file

Cassandra architecture! @doanduyhai 7 Data-store layer • Google Big Table paper • Columns/Columns Family Cluster layer • Amazon DynamoDB paper • masterless architecture

Cassandra architecture! @doanduyhai 8 API (CQL & RPC) CLUSTER (DYNAMO) DATA STORE (BIG TABLES) DISKS Node1 Client request API (CQL & RPC) CLUSTER (DYNAMO) DATA STORE (BIG TABLES) DISKS Node2

Data access! @doanduyhai 9 By CQL query via native protocol • INSERT, UPDATE, DELETE, SELECT • CREATE/ALTER/DROP TABLE Always by partition key (#partition) • partition == physical row

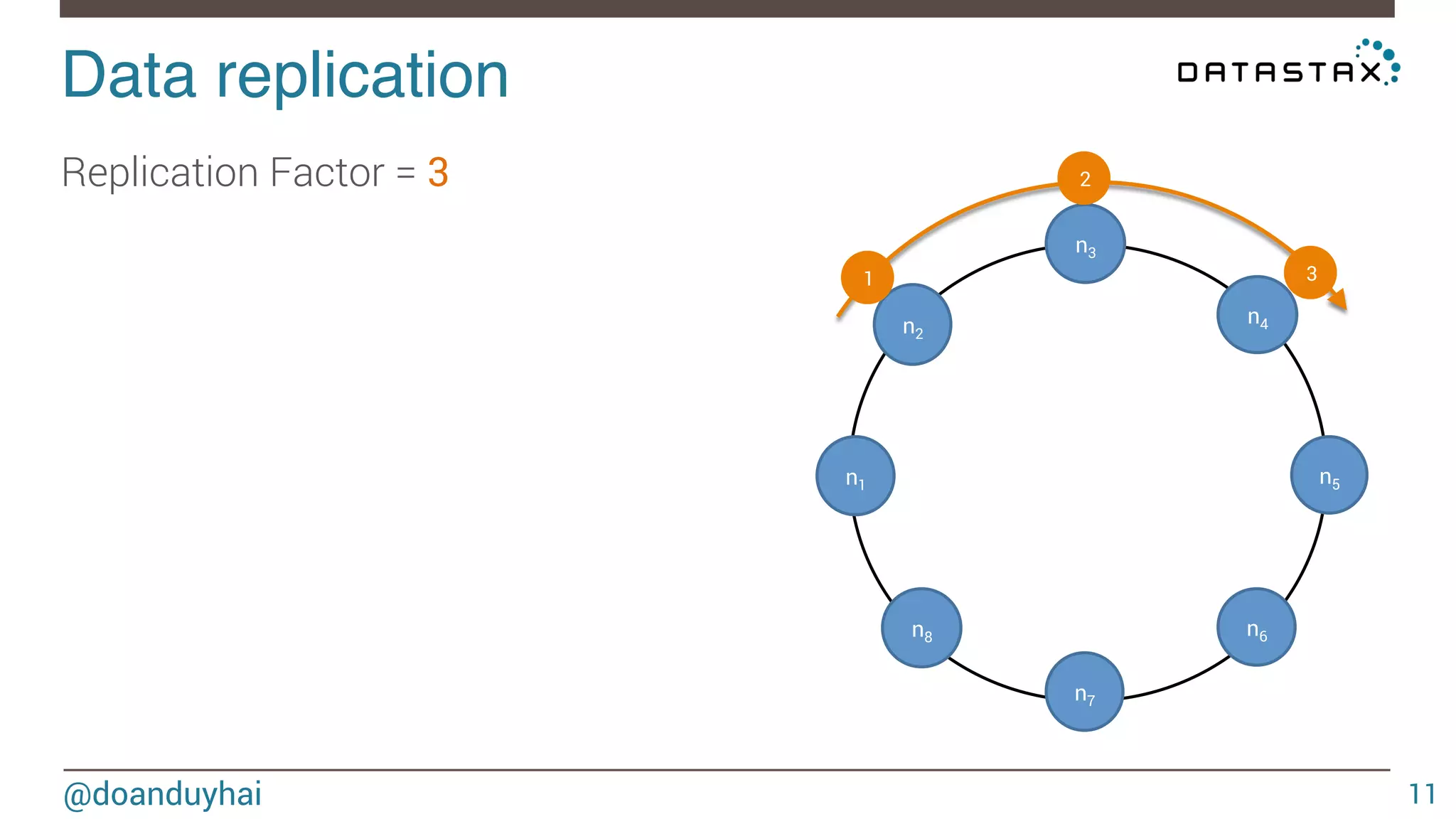
Data distribution! @doanduyhai 10 Random: hash of #partition → token = hash(#p) Hash: ]0, 2127-1] Each node: 1/8 of ]0, 2127-1] n1 n2 n3 n4 n5 n6 n7 n8

Data replication! @doanduyhai 11 Replication Factor = 3 n1 n2 n3 n4 n5 n6 n7 n8 1 2 3

Coordinator node! Incoming requests (read/write) Coordinator node handles the request Every node can be coordinator àmasterless @doanduyhai n1 n2 n3 n4 n5 n6 n7 n8 1 2 3 coordinator request 12

INSERT! INSERT INTO users(login, name, age) VALUES(‘ddoan’, ‘DuyHai DOAN’, 33); @doanduyhai 14 Table « users » ddoan age name 33 DuyHai DOAN

INSERT! INSERT INTO users(login, name, age) VALUES(‘ddoan’, ‘DuyHai DOAN’, 33); @doanduyhai 15 Table « users » ddoan age name 33 DuyHai DOAN #partition column names

INSERT! @doanduyhai ddoan age (t1) name (t1) 33 DuyHai DOAN 16 Table « users » INSERT INTO users(login, name, age) VALUES(‘ddoan’, ‘DuyHai DOAN’, 33); auto-generated timestamp (μs) .

UPDATE! @doanduyhai 17 Table « users » UPDATE users SET age = 34 WHERE login = ddoan; ddoan File1 File2 age (t1) name (t1) 33 DuyHai DOAN ddoan age (t2) 34

DELETE! @doanduyhai 18 Table « users » DELETE age FROM users WHERE login = ddoan; tombstone File1 File2 File3 ddoan age (t3) ý ddoan age (t1) name (t1) 33 DuyHai DOAN ddoan age (t2) 34

SELECT! @doanduyhai 19 Table « users » SELECT age FROM users WHERE login = ddoan; ? ? ? File1 File2 File3 ddoan age (t3) ý ddoan age (t1) name (t1) 33 DuyHai DOAN ddoan age (t2) 34

SELECT! @doanduyhai 20 Table « users » SELECT age FROM users WHERE login = ddoan; ✕ ✕ ✓ File1 File2 File3 ddoan age (t3) ý ddoan age (t1) name (t1) 33 DuyHai DOAN ddoan age (t2) 34

Cassandra columns! @doanduyhai 21 look very similar to … CRDT

CRDT Recap! @doanduyhai 22 CRDT = Convergent Replicated Data Types Useful in distributed system Formal proof for strong « eventual convergence » of replicated data

CRDT Recap! @doanduyhai 23 A join semilattice (or just semilattice hereafter) is a partial order ≤v equipped with a least upper bound (LUB) ⊔v, defined as follows: Definition 2.4 m = x ⊔v y is a Least Upper Bound of {x, y} under ≤v iff • x ≤v m and • y ≤v m and • there is no m′ ≤v m such that x ≤v m′ and y ≤v m′ It follows from the definition that ⊔v is: commutative: x ⊔v y =v y ⊔v x; idempotent: x ⊔v x =v x; and associative: (x⊔v y)⊔v z =v x⊔v (y⊔v z).

CRDT Recap! @doanduyhai 24 Definition 2.5 (Join Semilattice). An ordered set (S, ≤v) is a Join Semilattice iff ∀x,y ∈ S, x ⊔v y exists. Let’s define St k,n = set of Cassandra columns identified by • partition key k • column name n • assigned a timestamp t The ordered set (St #partition k,n, maxt) is a Join Semilattice column name(t1) … #partition column name(t2) …

Cassandra column as CRDT! @doanduyhai 25 Proof: • S1 k,n ≤ maxt (S1 k,n,S2 k,n) • S2 k,n ≤ maxt (S1 k,n,S2 k,n) • there is no Sx k,n ≤ maxt (S1 k,n,S2 k,n) such that S1 k,n ≤ Sx k,n and S2 k,n ≤ Sx k,n

Cassandra column as CRDT! @doanduyhai 26 Idempotent node1 node2 ! ddoan age (t2) 33 ddoan age (t2) 33 ddoan age (t2) 33 ddoan age (t2) 33 node3 coordinator

Cassandra column as CRDT! node1 node2 @doanduyhai 27 Commutative !ddoan age (t1) 33 ddoan age (t2) 34 coordinator ddoan age (t2) 34 node2 node1 ddoan age (t2) 34 ddoan age (t1) 33 coordinator ddoan age (t2) 34

Cassandra column as CRDT! node1 node2 @doanduyhai 28 Associative !ddoan age (t1) 33 ddoan age (t2) 34 ddoan age (t3) 35 ddoan age (t2) 34 node3 coordinator

Cassandra column as CRDT! @doanduyhai 29 ddoan File1 File2 address(t1) age (t1) 12 rue de.. 33 ddoan age (t2) 34 File3 File4 ddoan age (t3) 35 ddoan address(t7) 17 avenue..

Cassandra column as CRDT! @doanduyhai 30 ddoan age (t1) age (t2) 34 ddoan 33 ddoan age (t3) 35 St ddoan,age = St ddoan,address= ddoan address(t1) 12 rue de.. ddoan address(t7) 17 avenue.. t t

Eventual convergence! @doanduyhai 31 Proposition 2.1. Any two object replicas of a CvRDT eventually converge, assuming the system transmits payload infinitely often between pairs of replicas over eventually-reliable point-to-point channels.

Eventual convergence! @doanduyhai 32 Proposition 2.1. Any two object replicas of a CvRDT eventually converge, assuming the system transmits payload infinitely often between pairs of replicas over eventually-reliable point-to-point channels. ! ! eventually-reliable point-to-point channels à there is a network cable connecting 2 nodes …

Eventual convergence! @doanduyhai 33 The system transmits payload infinitely often between pairs of replicas

Eventual convergence! The system transmits payload infinitely often between pairs of replicas @doanduyhai 34 Repair

Eventual convergence! @doanduyhai 35 Strong hypothesis in the case of Cassandra CRDT !

Eventual convergence! @doanduyhai 36 maxtimestamp as merge function ! Strong hypothesis in the case of Cassandra CRDT !

Eventual convergence! @doanduyhai 37 Time is reliable … isn’t it ? !

Eventual convergence! @doanduyhai 38 NTP server-side mandatory

Bloom filters! by Burton Howard Bloom, 1970

Cassandra Write Path! @doanduyhai 41 Commit log1 . . . 1 Commit log2 Commit logn Memory

Cassandra Write Path! @doanduyhai 42 Memory MemTable Table1 Commit log1 . . . 1 Commit log2 Commit logn MemTable Table2 MemTable TableN 2 . . .

Cassandra Write Path! @doanduyhai 43 Commit log1 Commit log2 Commit logn Table1 Table2 Table3 SStable2 SStable3 3 SStable1 Memory . . .

Cassandra Write Path! @doanduyhai 44 MemTable . . . Memory Table1 Commit log1 Commit log2 Commit logn Table1 SStable1 Table2 Table3 SStable2 SStable3 MemTable Table2 MemTable TableN . . .

Cassandra Write Path! @doanduyhai 45 Commit log1 Commit log2 SStable3 . . . Commit logn Table1 SStable1 Memory Table2 Table3 SStable2 SStable3 SStable1 SStable2

Cassandra Read Path! @doanduyhai 46 Either in memory

Cassandra Read Path! @doanduyhai 47 Either in memory or hit disk (many SSTables)

Cassandra Read Path! @doanduyhai 48 How to optimize disk seeks ?

Cassandra Read Path! @doanduyhai 49 Only read necessary SSTables !

Cassandra Read Path! @doanduyhai 50 Bloom filters !

Bloom filters recap! @doanduyhai 51 Space-efficient probabilistic data structure. Used for membership test True negative, possible false positive

Bloom filters in Cassandra! @doanduyhai 52 For each SSTable, create a bloom filter Upon data insertion, populate it Upon data retrieval, ask the bloom filter for skipping

Bloom filters in action! @doanduyhai 53 #partition = foo h2 h3 1 0 0 1 0 0 1 0 0 0 Write h1

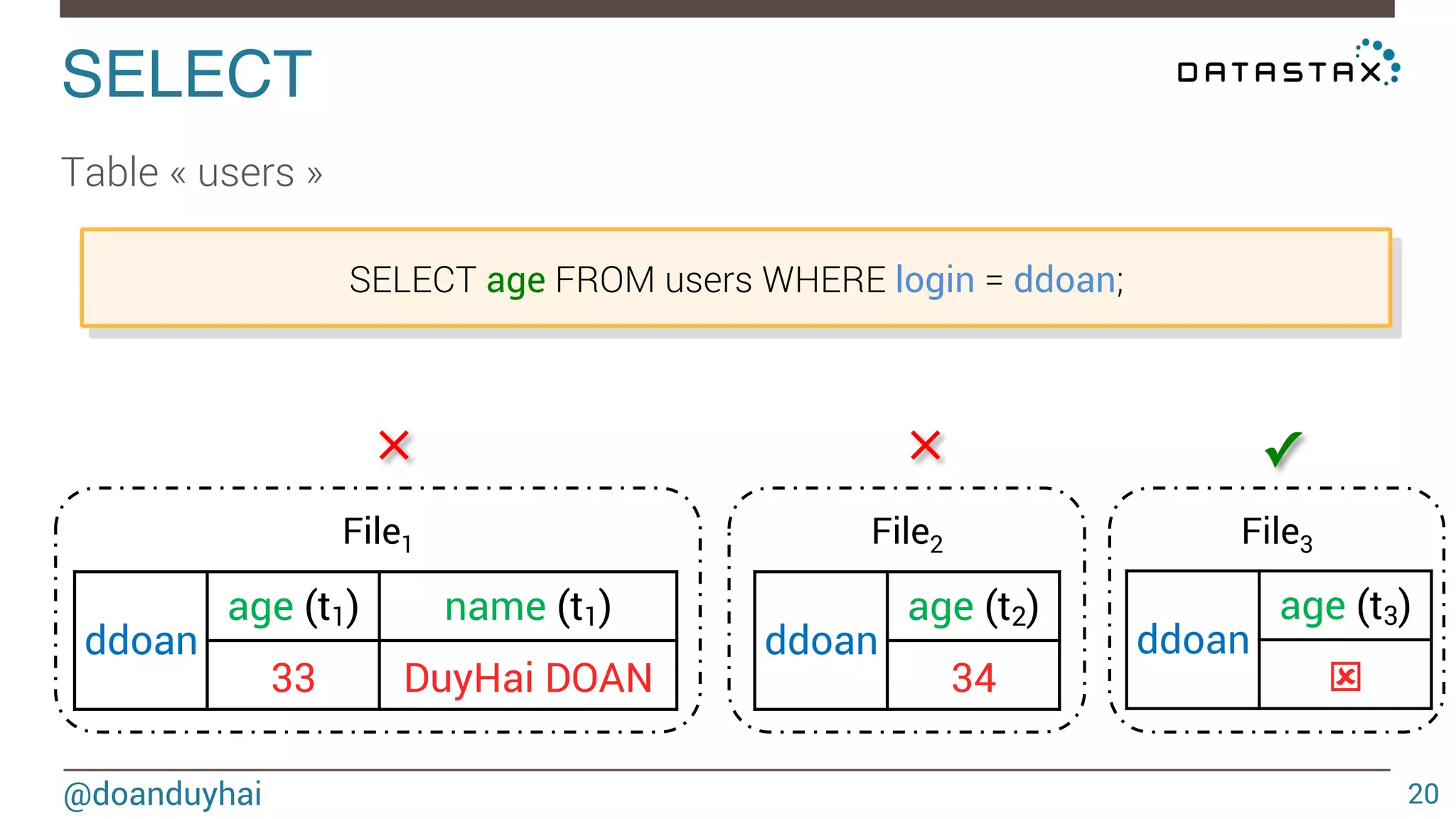
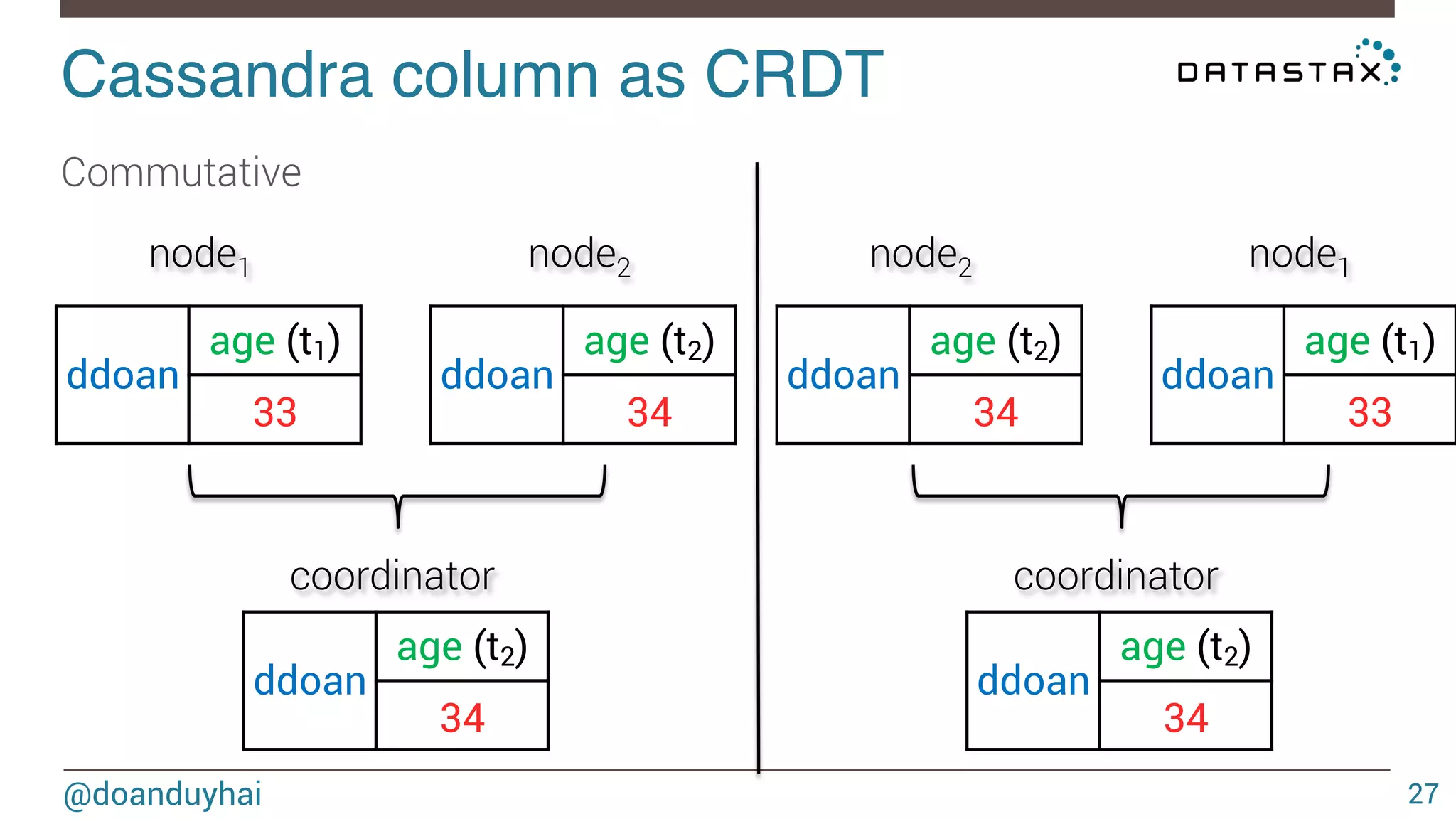
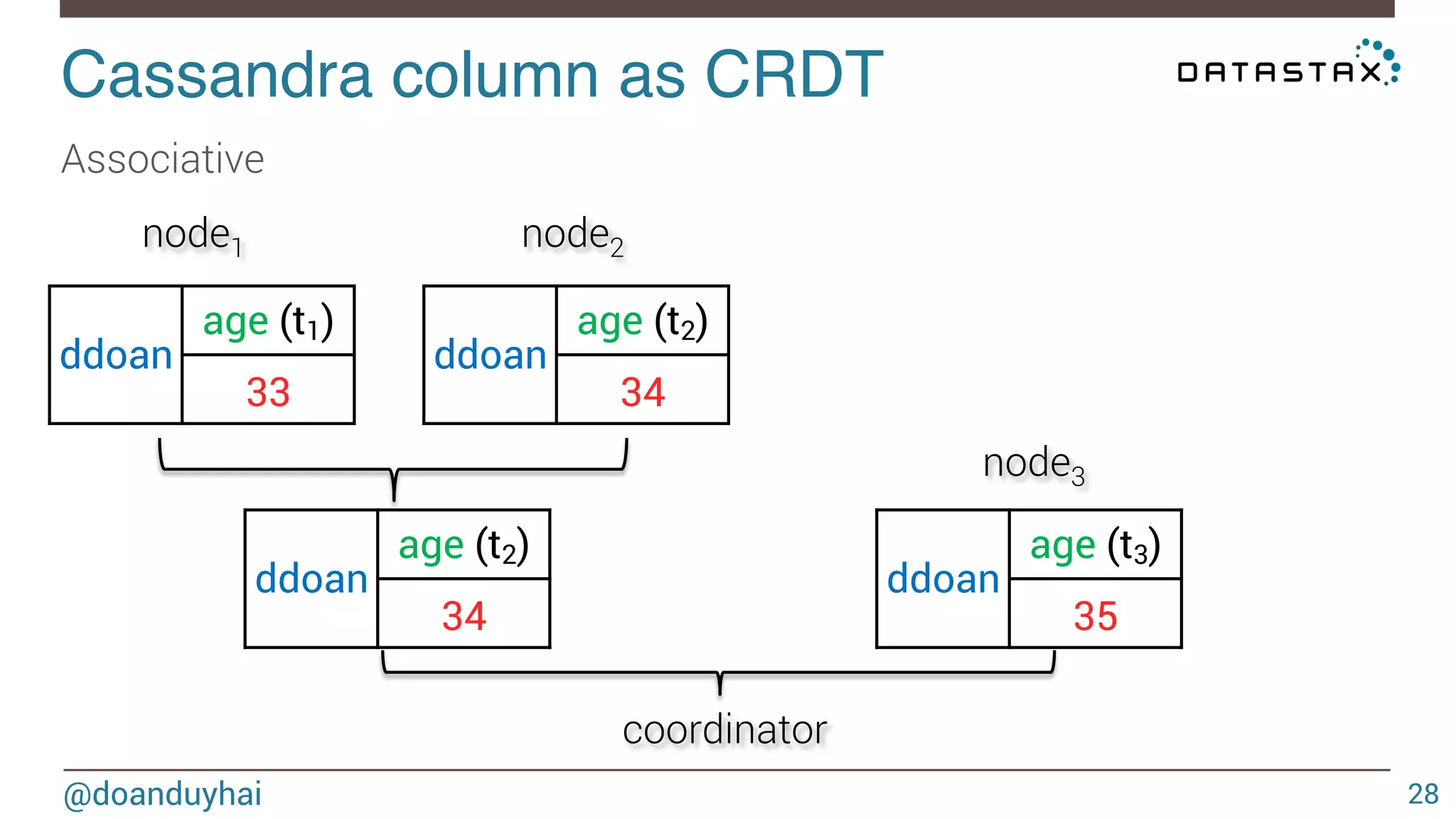
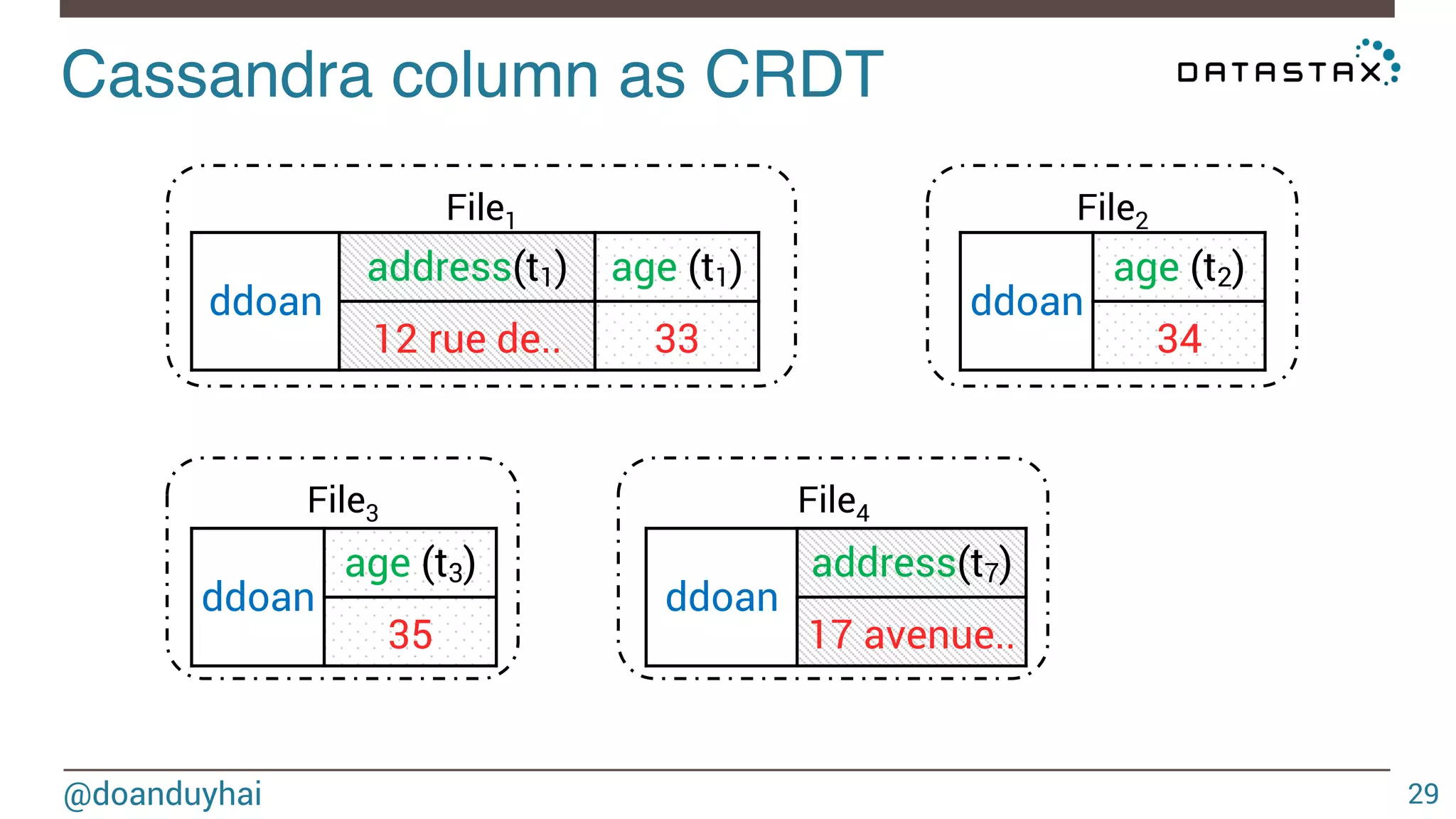
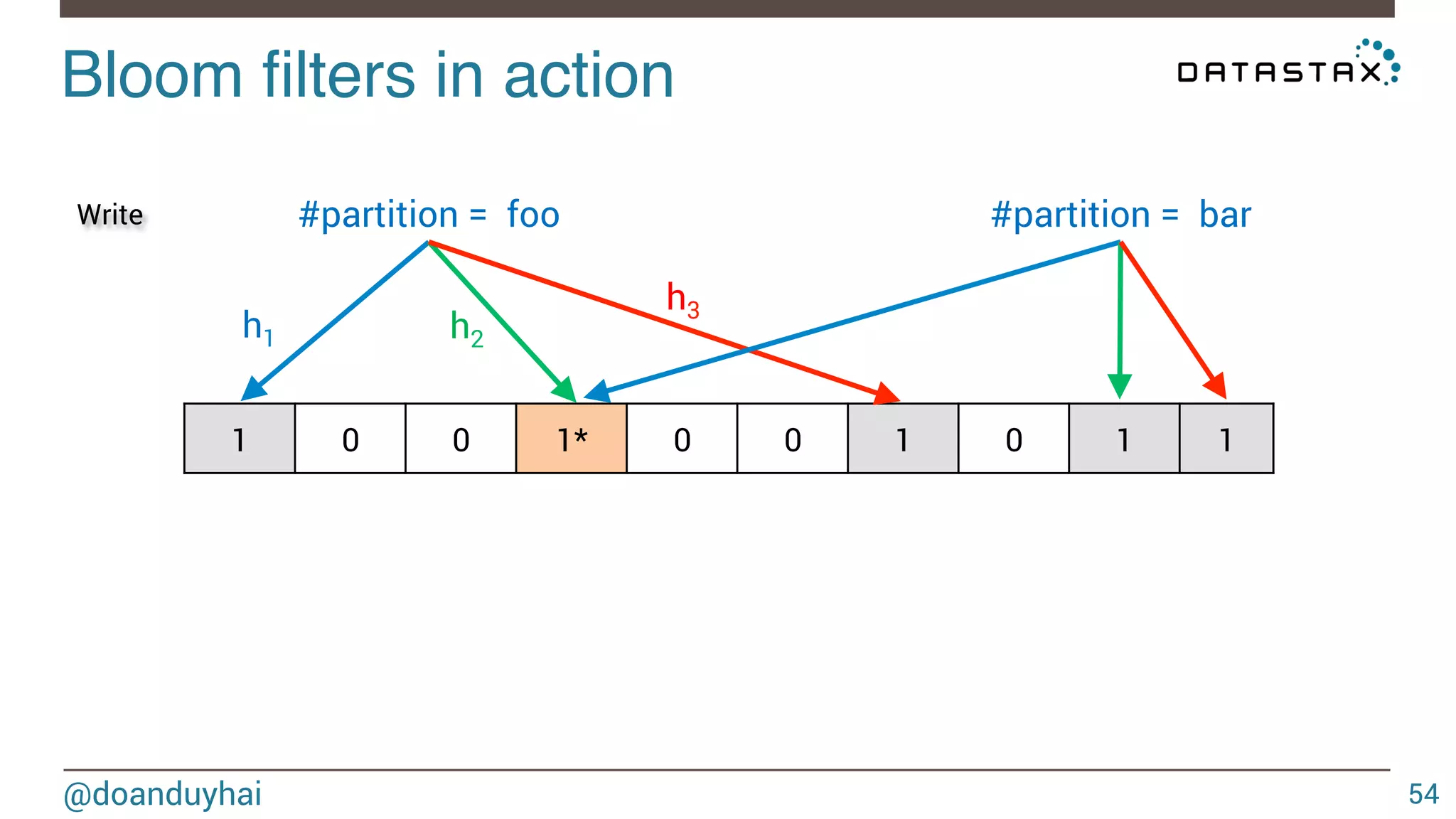
Bloom filters in action! Write #partition = bar h1 h2 @doanduyhai 54 #partition = foo h3 1 0 0 1* 0 0 1 0 1 1

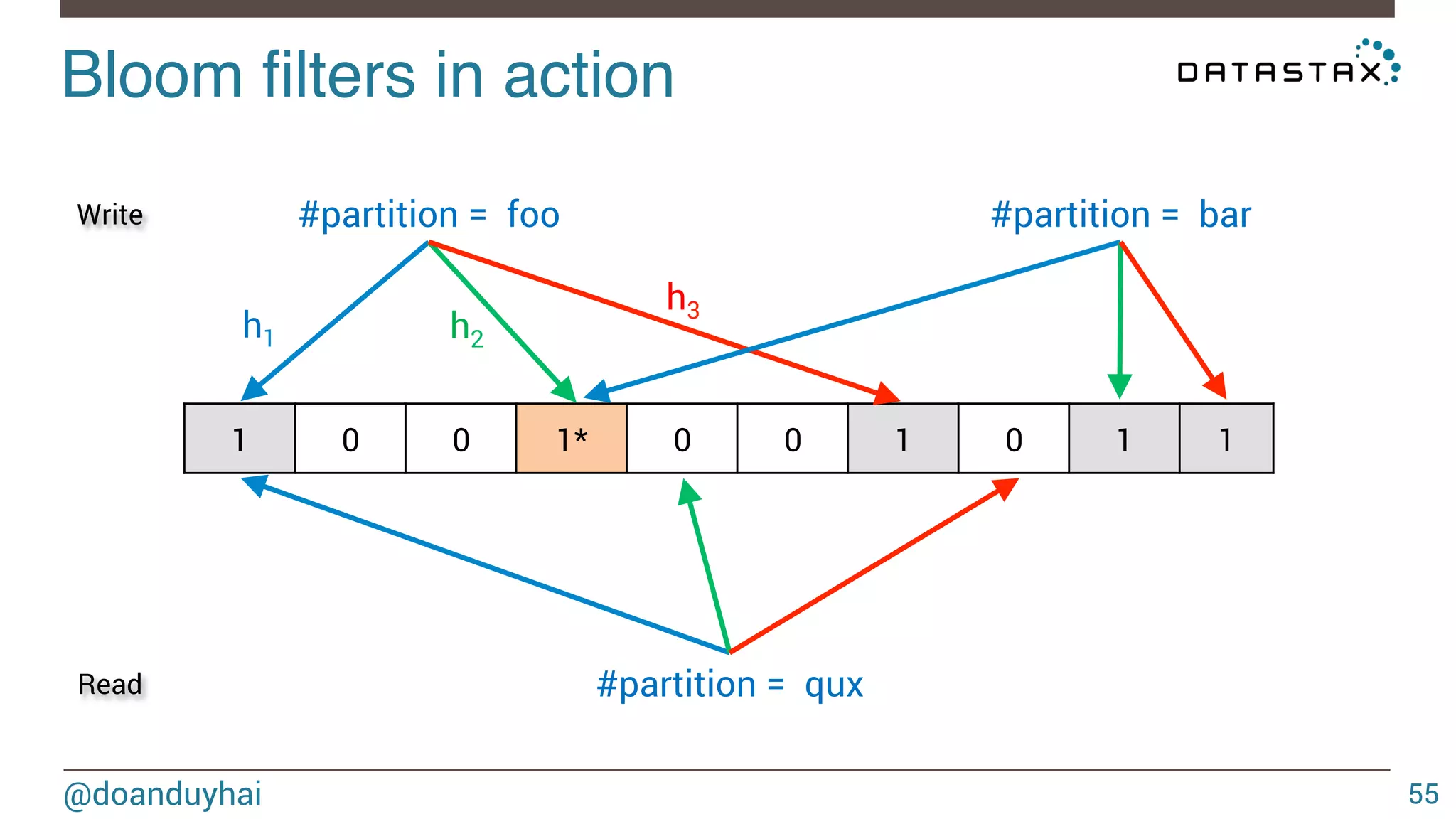
Bloom filters in action! Write #partition = bar h1 h2 @doanduyhai 55 #partition = foo h3 1 0 0 1* 0 0 1 0 1 1 Read #partition = qux

Bloom filters maths! @doanduyhai 56

Bloom filters maths! 1 0 0 1 0 0 1 0 0 0 @doanduyhai 57 probability of a bit to be set to 1: m bits 1 m 1− 1 m probability of a bit to be set to 0:

Bloom filters maths! @doanduyhai 58 probability with k … and n … of the bit to be set to 1: 1− 1− 1 m " # $ % & ' kn probability with k hash functions of the bit to be set to 0: 1− 1 m " # $ % & ' k probability with k … and n elements inserted … : 1− 1 m " # $ % & ' kn

Bloom filters maths! @doanduyhai 59 But why do we need to calculate probability of a bit: • to be set to 1 • then to be set to 0 • then back to 1 again ?

Bloom filters maths! @doanduyhai 60 Because of bits colliding on 1 when applying many k & n !

Bloom filters maths! @doanduyhai 61 For an element not in the SSTable, probability that all k hash functions return 1 (false positive chance, fpc): " kn 1− 1− 1 m " % ' & $# # $$ % & '' k ≈ 1− e −kn m " # $ % & ' k To minimize fpc: koptimal ≈ m n ln(2)

Bloom filters maths! @doanduyhai 62 $$$ fpc = 1− e − m n ln(2)n m " # % ''' & m n ln(2) " ) = 1− e ln( 1 2 # $ % & ' m n ln(2) = 1 2 m n ln(2) ln( fpc) = m n ln( 1 2 ) ln(2) = − m n ln(2)2 m = n ln( 1 fpc ) ln(2)2

Bloom filters maths! @doanduyhai 63 m = n ln( 1 fpc ) ln(2)2 For n = 109 of #partition • fpc = 10%, m ≈ 500Mb • fpc = 1%, m ≈ 1.2Gb

Bloom filters (notes)! @doanduyhai 64 Cannot remove elements once inserted (1-bit colliding) • cannot resize • collision increases with load

Merkle tree! by Ralph Merkle, 1987

Repairing data! The system transmits payload infinitely often between pairs of replicas @doanduyhai 67 Repair

Why repair ?! @doanduyhai 68 Data diverge between replicas because: • writing with low consistency for perf • nodes down • network down • dropped writes

Repairing data! @doanduyhai 69 Compare full data ? • read all data • I/O intensive • network intensive (streaming is expensive)

Repairing data! @doanduyhai 70 Compare full data ? • read all data • I/O intensive • network intensive (streaming is expensive) Compare digests ? • read all data • I/O intensive • network intensive (streaming is expensive)

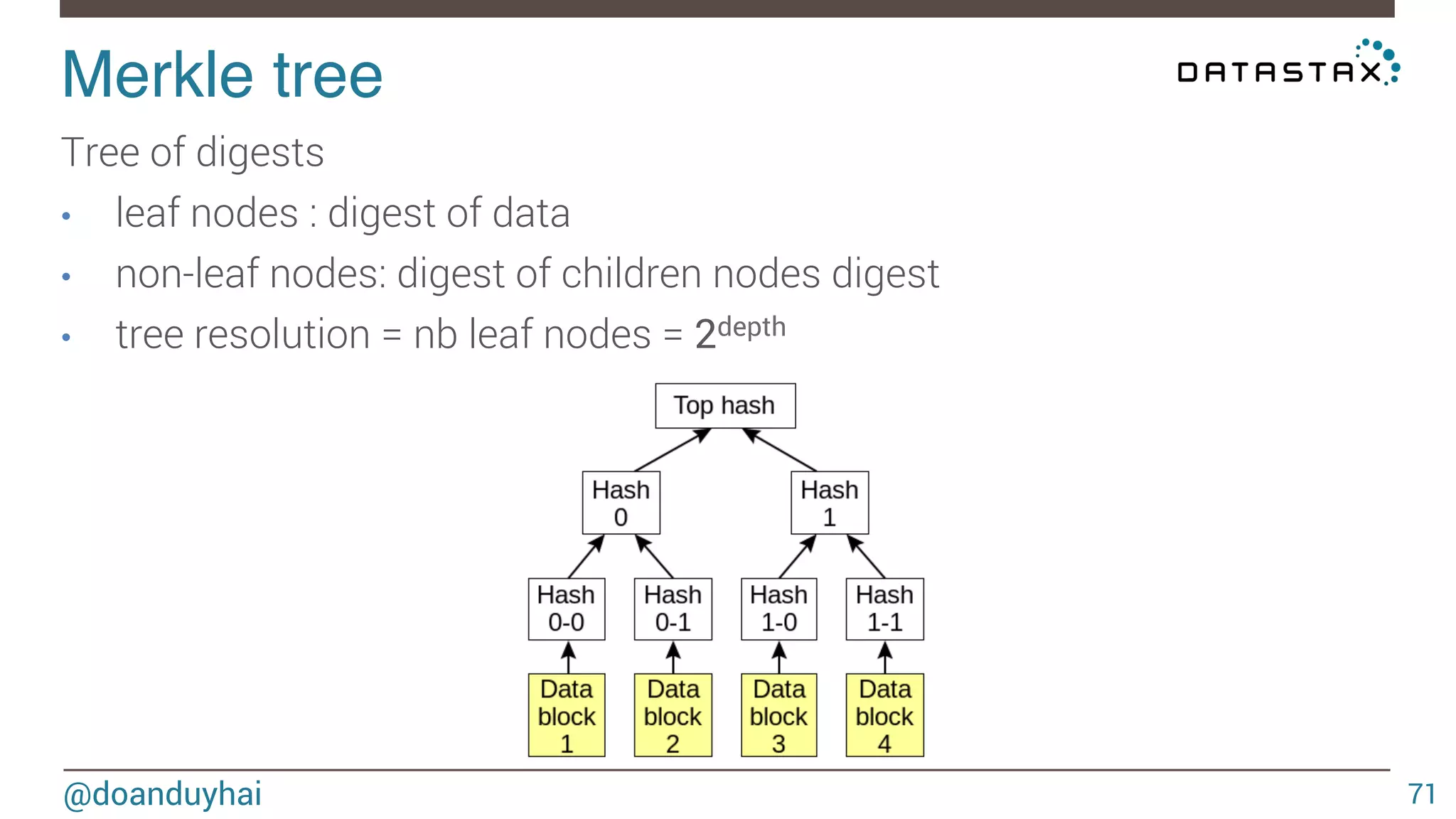
Merkle tree! @doanduyhai 71 Tree of digests • leaf nodes : digest of data • non-leaf nodes: digest of children nodes digest • tree resolution = nb leaf nodes = 2depth

Merkle tree in action! @doanduyhai 72 Depth = 15, resolution = 32 768 leaf nodes root … node node leaf1 leaf2 leaf3 n-partitions bucket n-partitions bucket n-partitions bucket

Merkle tree in action! @doanduyhai 73 Repair process • send the tree to replicas • compare digests, starting from root node • if mismatch, stream partition bucket(s) that differ

Merkle tree in action! @doanduyhai 74 If mismatch, stream partition bucket(s) that differ Example • 327 680 partitions • resolution = 32 768 à10 partitions/bucket • 1 column differs in 1 partition à 10 partitions streamed leaf 10-partitions

Over-streaming nightmare! @doanduyhai 75

Merkle tree in action! root node node node @doanduyhai 76 Improve tree resolution by increasing depth (dynamically) leaf1 node node leaf2 … leafN node node node node node leaf1 root node node node node node node node node node leaf3 … leafN leaf2

Merkle tree in action! root node node node node node @doanduyhai 77 Improve tree resolution by repairing by partition ranges leaf1 leaf2 … leafN root node node node leaf1 node node leaf2 … leafN root node node node leaf1 node node leaf2 … leafN

HyperLogLog! by late Philippe Flajolet, 2007

Cassandra Read Path! @doanduyhai 80 Remember that ? Table1 SStable1 Table2 Table3 SStable2 SStable3 SStable1 SStable2 SStable3

Cassandra Read Path! @doanduyhai 81 Even Bloom filter can’t save you if data spills on many SSTables

Cassandra Read Path! @doanduyhai 82 Compaction !

Compaction! @doanduyhai 83 Algorithm: • take n SSTables • load data in memory • for each St k,n apply the merge function (maxtimestamp) • remove (when applicable) tombstones • build a new SSTable

Compaction! @doanduyhai 84 Build a new SSTable à allocate memory for new Bloom filter

Compaction! @doanduyhai 85 But how large is the new Bloom filter ?

Compaction! @doanduyhai 86 SStable1 SStable2 Bloom filters same size ? double size? in between ?

Compaction! @doanduyhai 87 Bloom filter size depends on … elements cardinality (fpc constant)

Compaction! @doanduyhai 88 Bloom filter size depends on … elements cardinality (fpc constant) If we can count distinct elements in SSTable1 & SSTable2, we can allocate new Bloom filter

Compaction! @doanduyhai 89 Bloom filters SStable1 SStable2 Cardinality: C1 Cardinality: C2 Given constant fpc, if cardinality = C1+C2, then m = …

Compaction! @doanduyhai 90 But counting exact cardinality is memory-expensive ...

Compaction! @doanduyhai 91 Can’t we have a cardinality estimate ?

Cardinality estimators! @doanduyhai 92 Counter Bytes used Error Java HashSet 10 447 016 0% Linear Probabilistic Counter 3 384 1% HyperLogLog 512 3% credits: http://highscalability.com/

LogLog intuition! @doanduyhai 93 1) given a well distributed hash function h 2) given a sufficiently high number of elements n For a set of n elements, look that the bit pattern ∀ i ∈ [1,n], h(elementi) ≈ n/2 ≈ n/2 0xxxxx… 1xxxxx…

LogLog intuition! ≈ n/4 ≈ n/4 ≈ n/4 ≈ n/8 ≈ n/8 ≈ n/8 ≈ n/8 ≈ n/8 ≈ n/8 ≈ n/8 ≈ n/8 @doanduyhai 94 ∀ i ∈ [1,n], h(elementi) 01xxxx… 10xxxx… ≈ n/4 00xxxx… 11xxxx… 000xxx… 001xxx… 010xxx… 011xxx… 100xxx… 101xxx… 110xxx… 111xxx…

LogLog intuition! @doanduyhai 95 Flip back the reasonning. If we see a hash like this: 000 000 000 1… Since the hash distribution is uniform, we should also have seen: 000 000 001 0… and 000 000 001 1… and 000 000 010 0… and … 111 111 111 1… Thus an estimated cardinality of 210 elements for n

LogLog intuition! @doanduyhai 96 Toy example: n = 8, hash of 8 elements, 3 bit long: 000, 001, 010, 011, 100, 101, 110, 111 Uniform hash à equi-probability of each combination If I observed 001, I should have seen 000 too, and 010 too … If I observed 001, I should have seen 7 other combinations If I observed 001, n ≈ 8 (23)

LogLog intuition! @doanduyhai 97 1) given a well distributed hash function h 2) given a sufficiently high number of elements n If I find a hash starting with 01…, it’s likely that there are 22 distinct elements (n = 22) 001…, it’s likely that there are 23 distinct elements (n = 23) 0001…, it’s likely that there are 24 distinct elements (n = 24) … 00000000001…, it’s likely that there are 2r distinct elements (n = 2r) r

LogLog intuition! @doanduyhai 98 max(r) = longest 0000…1 position observed among all hash values n ≈ 2max(r)

LogLog intuition! @doanduyhai 99 Still, it’s a very terrible estimation … What if we have these hash values for n = 16: 10 x 010….. 5 x 100…. 1 x 000 000 001…

LogLog intuition! @doanduyhai 100 Still, it’s a very terrible estimation … What if we have these hash values for n = 16: 10 x 010….. 5 x 100…. 1 x 000 000 001… n ≈ 2max(r) ≈ 29 ≈ 512 ?

LogLog intuition! @doanduyhai 101 Still, it’s a very terrible estimation … What if we have these hash values for n = 16: 10 x 010….. 5 x 100…. 1 x 000 000 001… outlier & skewed distribution sensitivity n ≈ 2max(r) ≈ 29 ≈ 512 ?

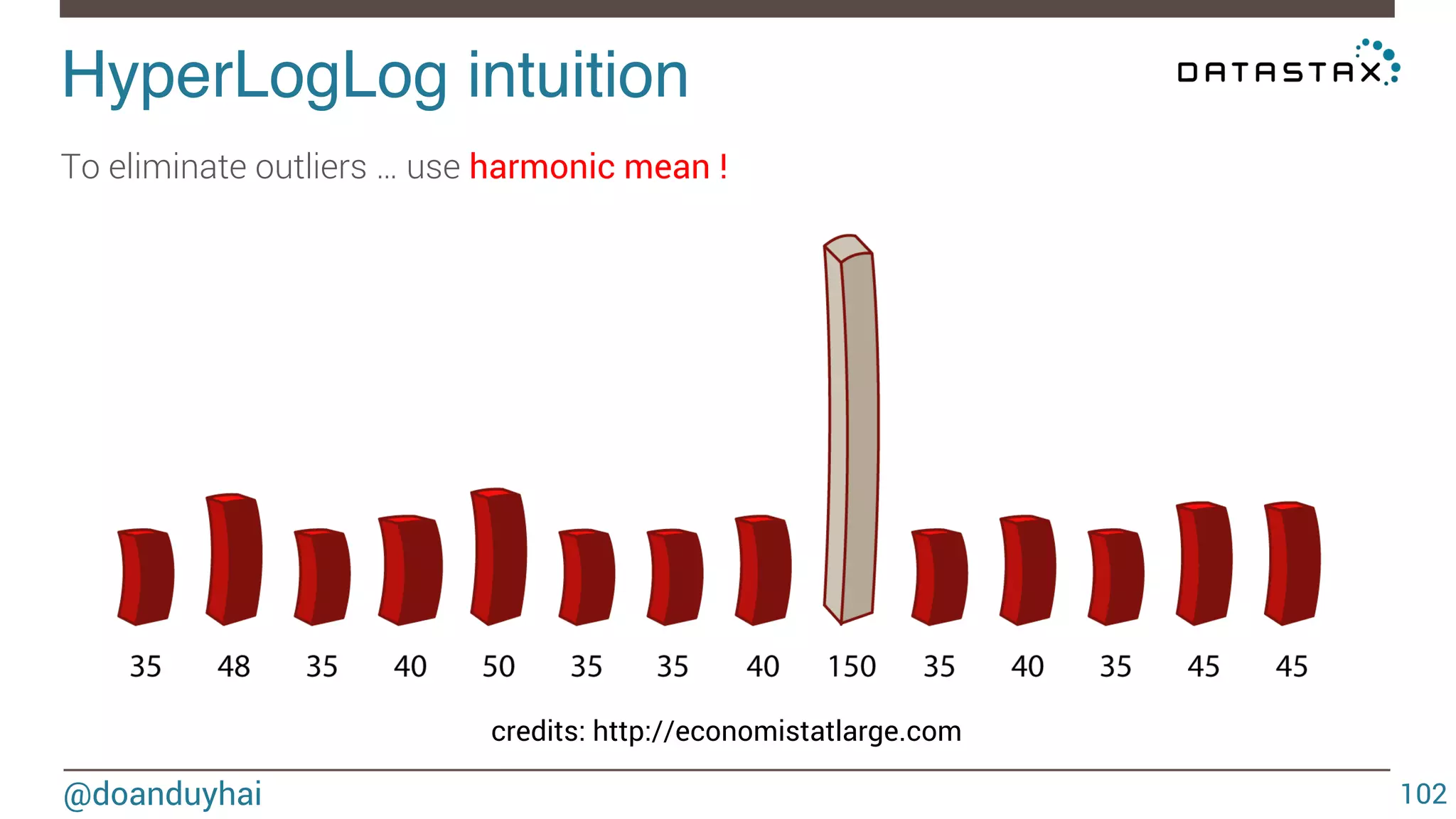
HyperLogLog intuition! @doanduyhai 102 To eliminate outliers … use harmonic mean ! credits: http://economistatlarge.com

HyperLogLog intuition! @doanduyhai 103 Harmonic means definition (thank you Wikipedia) H = m 1 x1 + 1 x2 +...+ 1 xm

HyperLogLog intuition! @doanduyhai 104 First, split the set into m = 2b buckets Bucket number is determined by first b bits h(element) = 001001 0100… b = 6, m = 32 buckets Buckets list: B1, B2, … B32 (index is 1-based)

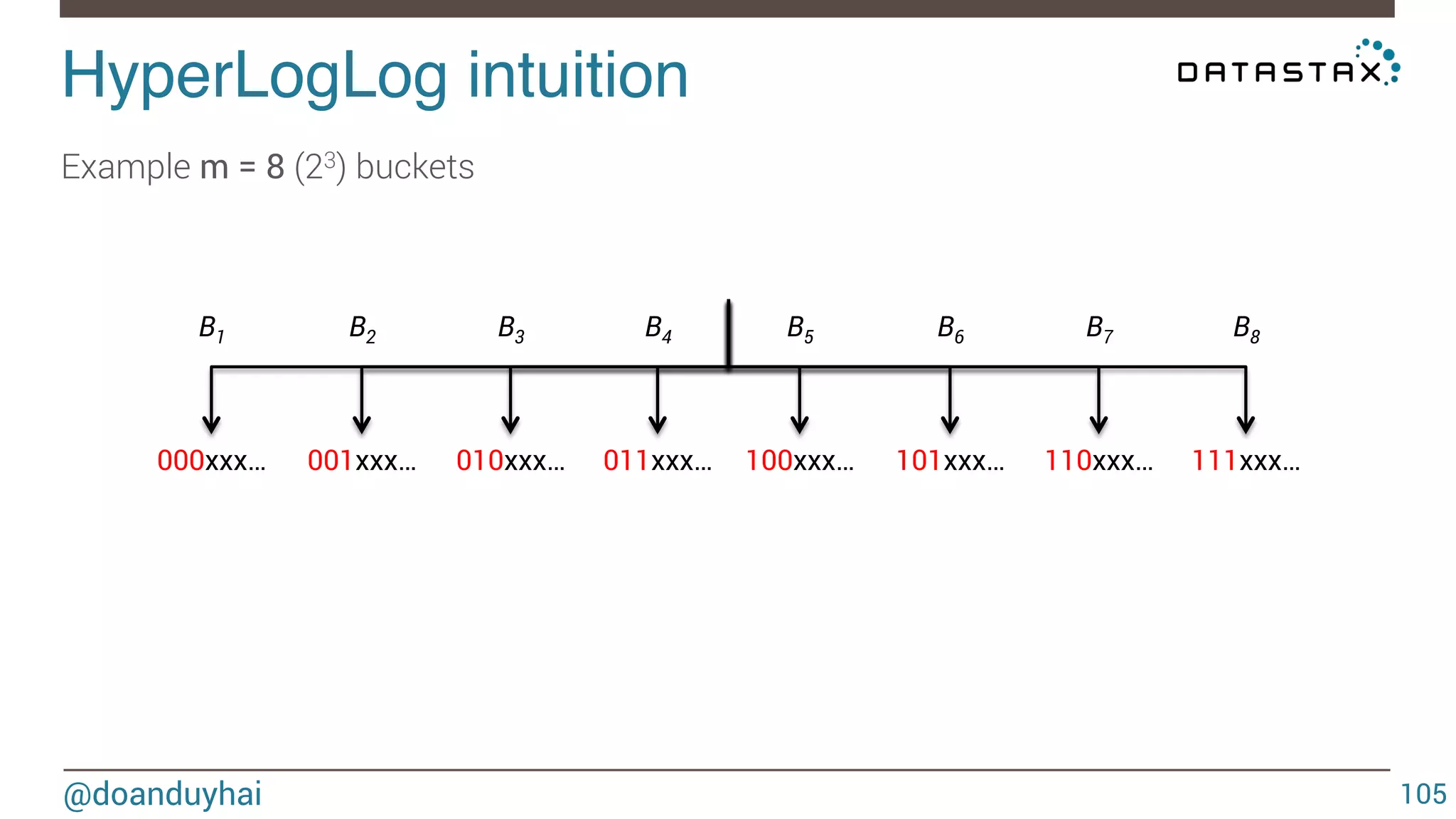
HyperLogLog intuition! B1 B2 B3 B4 B5 B6 B7 B8 @doanduyhai 105 Example m = 8 (23) buckets 000xxx… 001xxx… 010xxx… 011xxx… 100xxx… 101xxx… 110xxx… 111xxx…

HyperLogLog intuition! @doanduyhai 106 New intuition: • in each bucket j, there are ≈ Mj elements • harmonic mean (Mj) = H(Mj) ≈ n/m n ≈ mH(Mj)

HyperLogLog intuition! @doanduyhai 107 But how do we calculate each Mj ?

HyperLogLog intuition! @doanduyhai 108 Use LogLog !

HyperLogLog intuition! @doanduyhai 109 How to solve a big hard problem ?

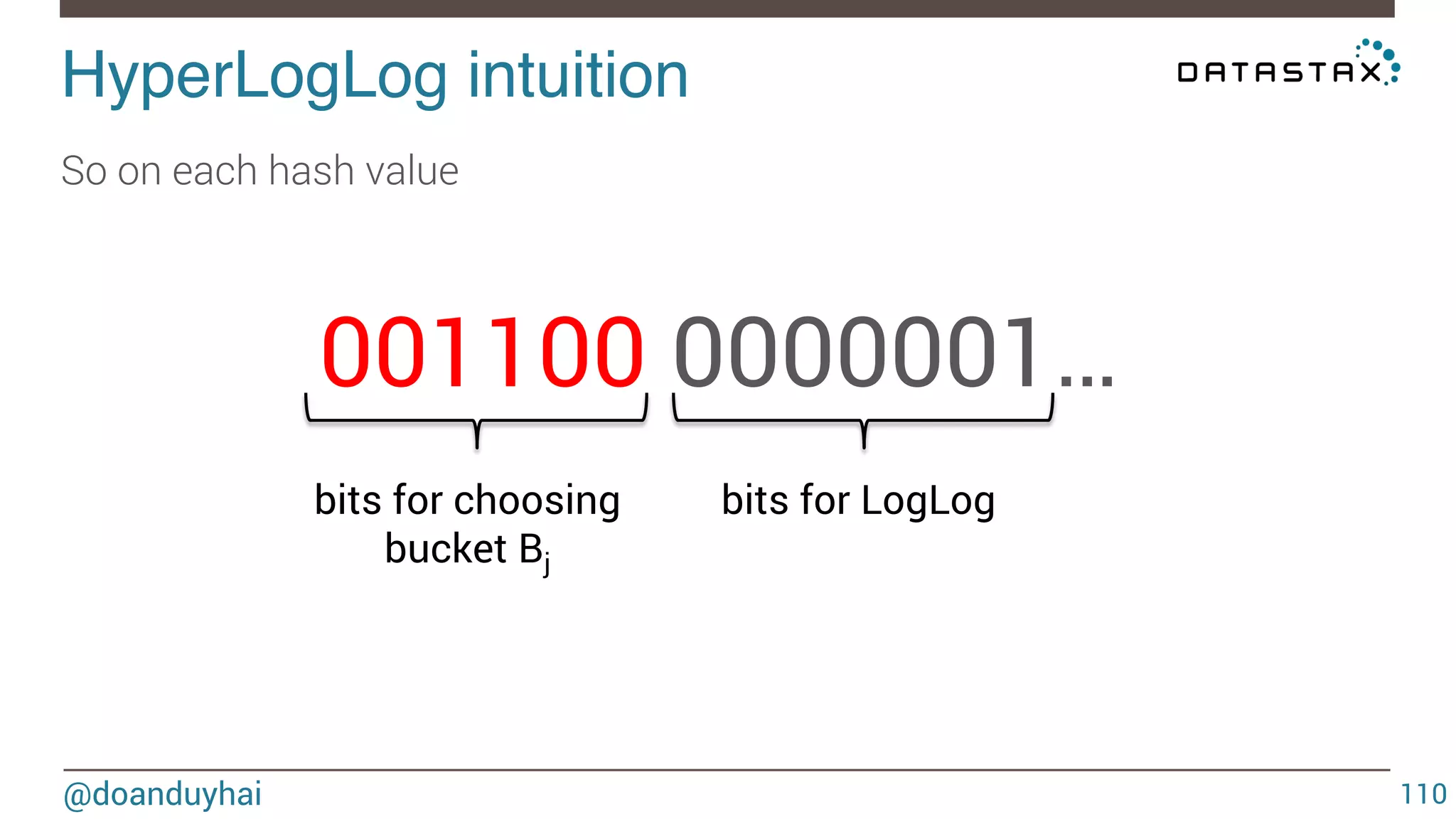
HyperLogLog intuition! @doanduyhai 110 So on each hash value 001100 0000001… bits for choosing bucket Bj bits for LogLog

HyperLogLog improvement! @doanduyhai 111 Greater precision compared to LogLog Computation can be distributed (each bucket processed separately)

HyperLogLog the maths! @doanduyhai 112

HyperLogLog formal definition! @doanduyhai 113 Let h : D → [0, 1] ≡ {0, 1}∞ hash data from domain D to the binary domain. Let ρ(s), for s ∈ {0, 1}∞ , be the position of the leftmost 1-bit. (ρ(0001 · · · ) = 4) It is the rank of the 0000..1 observed sequence Let m = 2b with b∈Z>0 m = number of buckets Let M : multiset of items from domain D M is the set of elements to estimate cardinality

HyperLogLog formal definition! @doanduyhai 114 Algorithm HYPERLOGLOG Initialize a collection of m registers, M1, . . . , Mm, to −∞ for each element v ∈ M do • set x := h(v) //hash of v in binary form • set j = 1 + ⟨x1x2 · · · xb⟩2 //bucket number (1-based) • set w := xb+1xb+2 · · · //bits for LogLog • set Mj := max(Mj, ρ(w)) //take the longest 0000..1 position observed in bucket Bj

HyperLogLog formal definition! @doanduyhai 115 mΣ −1 Compute Z = 2 //what is that Z ? −Mj j=1 # $ %% & ' (( Return n ≈ αmm2Z • αm as given by Equation (3) //what is that αm ? !

HyperLogLog maths workout! @doanduyhai 116 Mj = longest 0000...1 observed for bucket j. H(Mj) ≈ n/m H = m 1 x1 + 1 x2 +...+ 1 xm Remember our intuition n ≈ mH(Mj) ? Harmonic mean definition

HyperLogLog maths workout! @doanduyhai 117 H = m 1 x1 + 1 x2 +...+ 1 xm = m 1 1 xj m Σ j=1 H = m 1 xj m Σ j=1 " −1 = m xj % '' & $$# (Σm −1 )−1 j=1

HyperLogLog maths workout! @doanduyhai 118 (Σm −1 )−1 j=1 H = m xj mΣ Z = 2−Mj j=1 # $ %% −1 & ' (( compare it with let xj = 2Mj , the cardinality estimate for bucket Bj H = mZ

HyperLogLog maths workout! @doanduyhai 119 Remember our intuition n ≈ mH(Mj) ? n ≈ mH ≈ m2Z ☞ αmm2Z

HyperLogLog harder maths! @doanduyhai 120 What’s about the αm constant ?

HyperLogLog harder maths! @doanduyhai 121 You don’t want to dig into that, trust me …

HyperLogLog harder maths! @doanduyhai 122 8 pages full of this:

HyperLogLog harder maths! @doanduyhai 123 and this

HyperLogLog harder maths! @doanduyhai 124 and this…

Compaction! @doanduyhai 125 Bloom filters SStable1 SStable2 Cardinality: C1 Cardinality: C2 Given constant fpc, if cardinality = C1+C2, then m = …

Thank You @doanduyhai duy_hai.doan@datastax.com

Cassandra data structures and algorithms

More Related Content

What's hot

Similar to Cassandra data structures and algorithms

More from Duyhai Doan

Recently uploaded

In this document

Cassandra data structures and algorithms