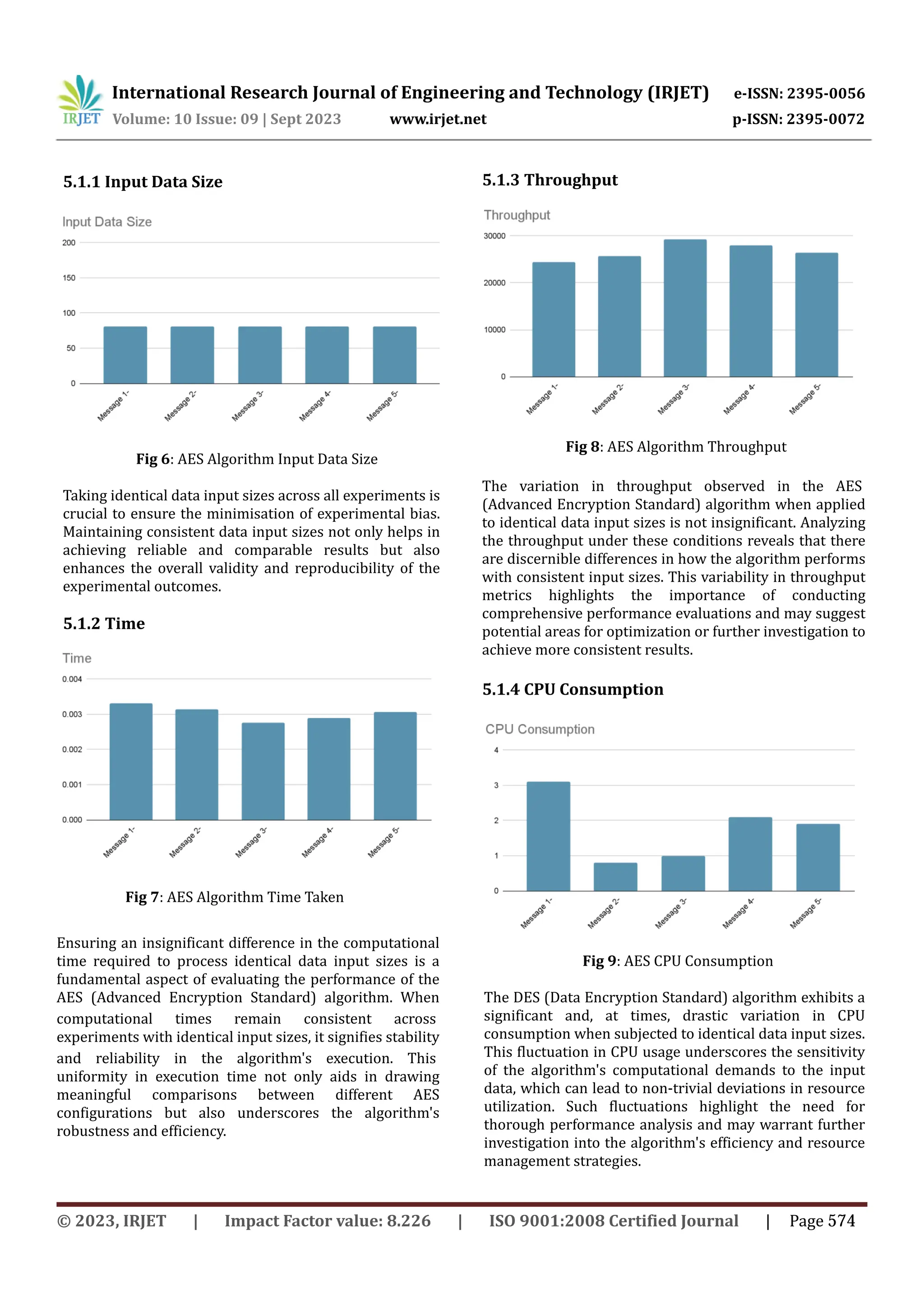
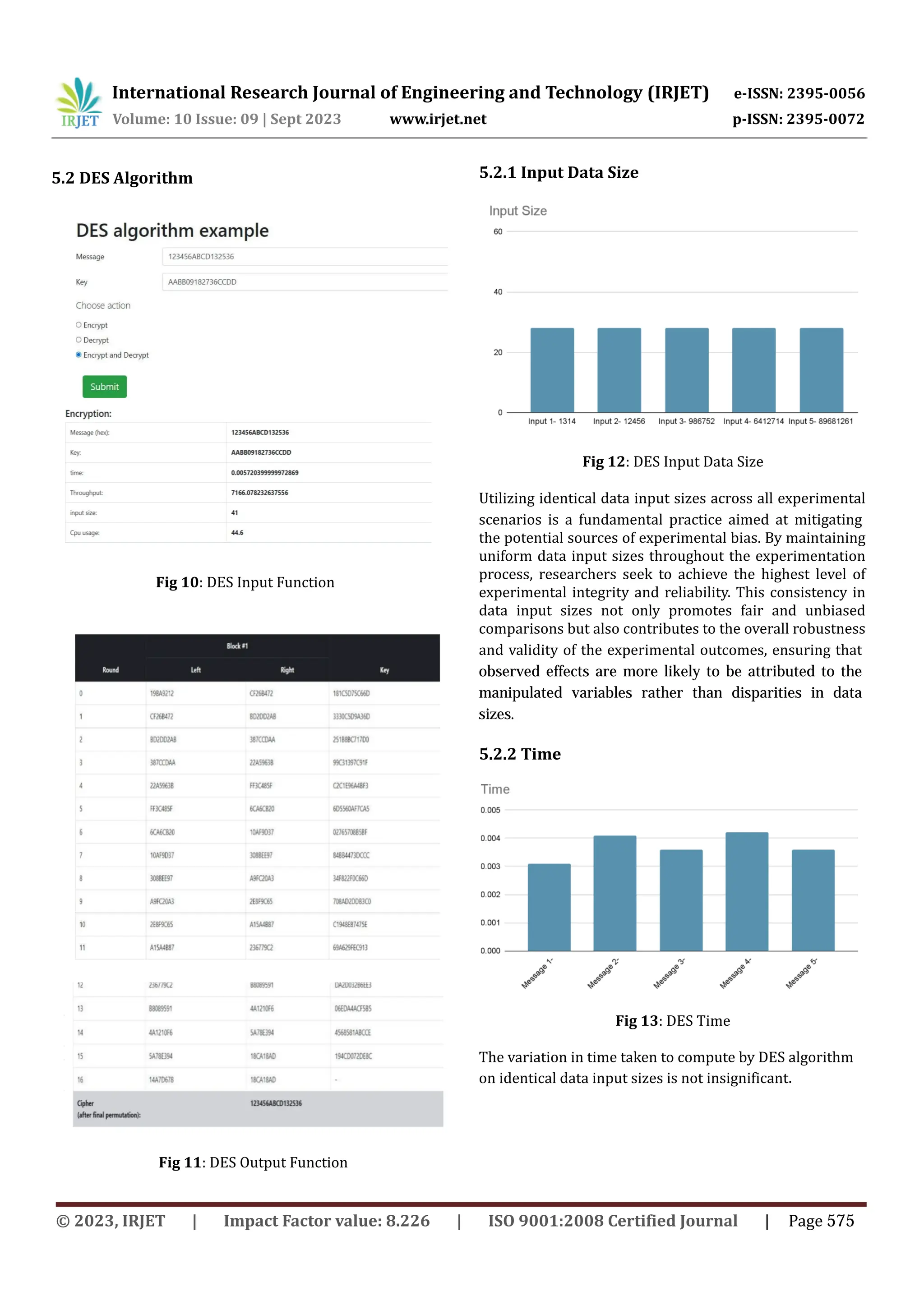
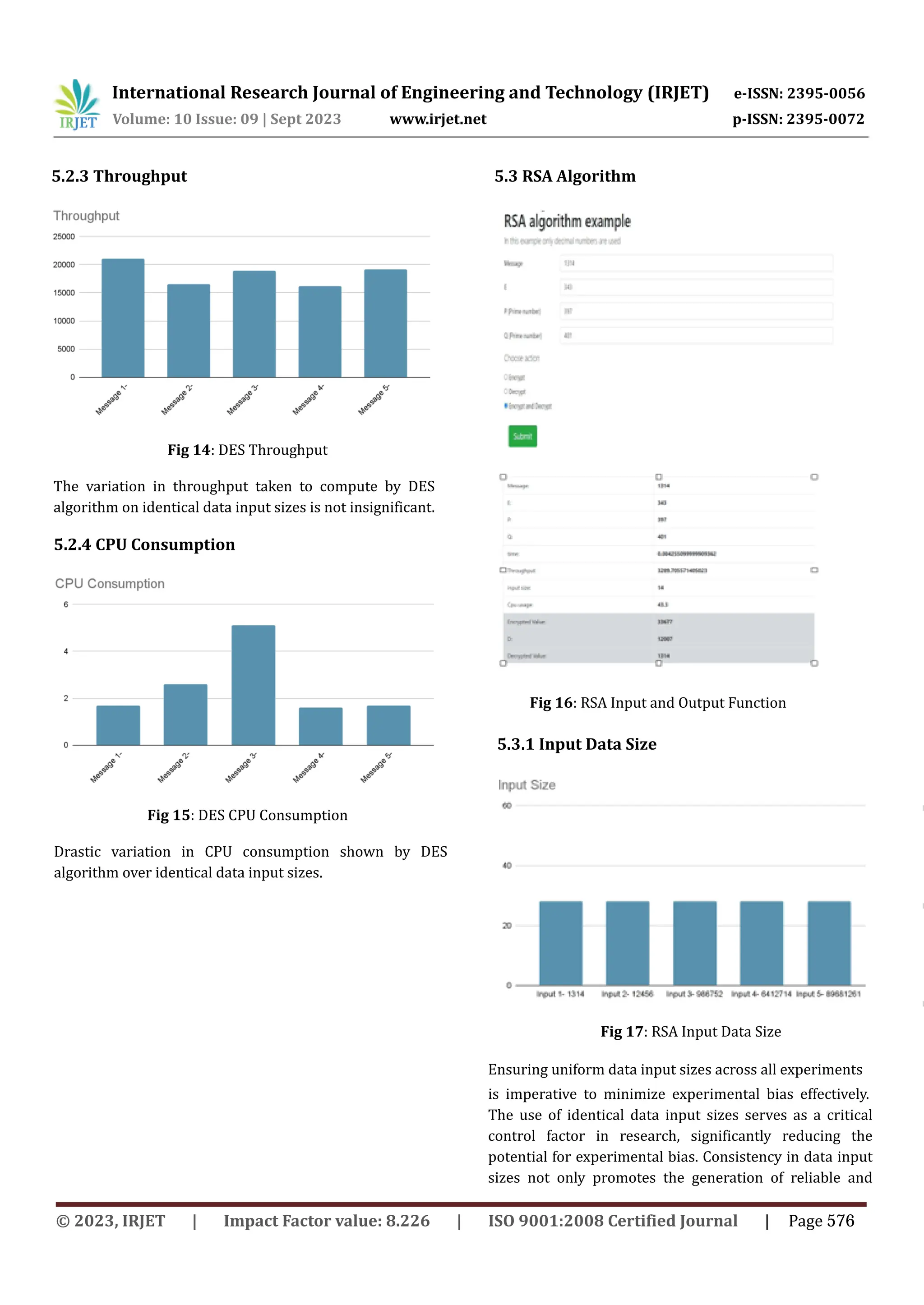
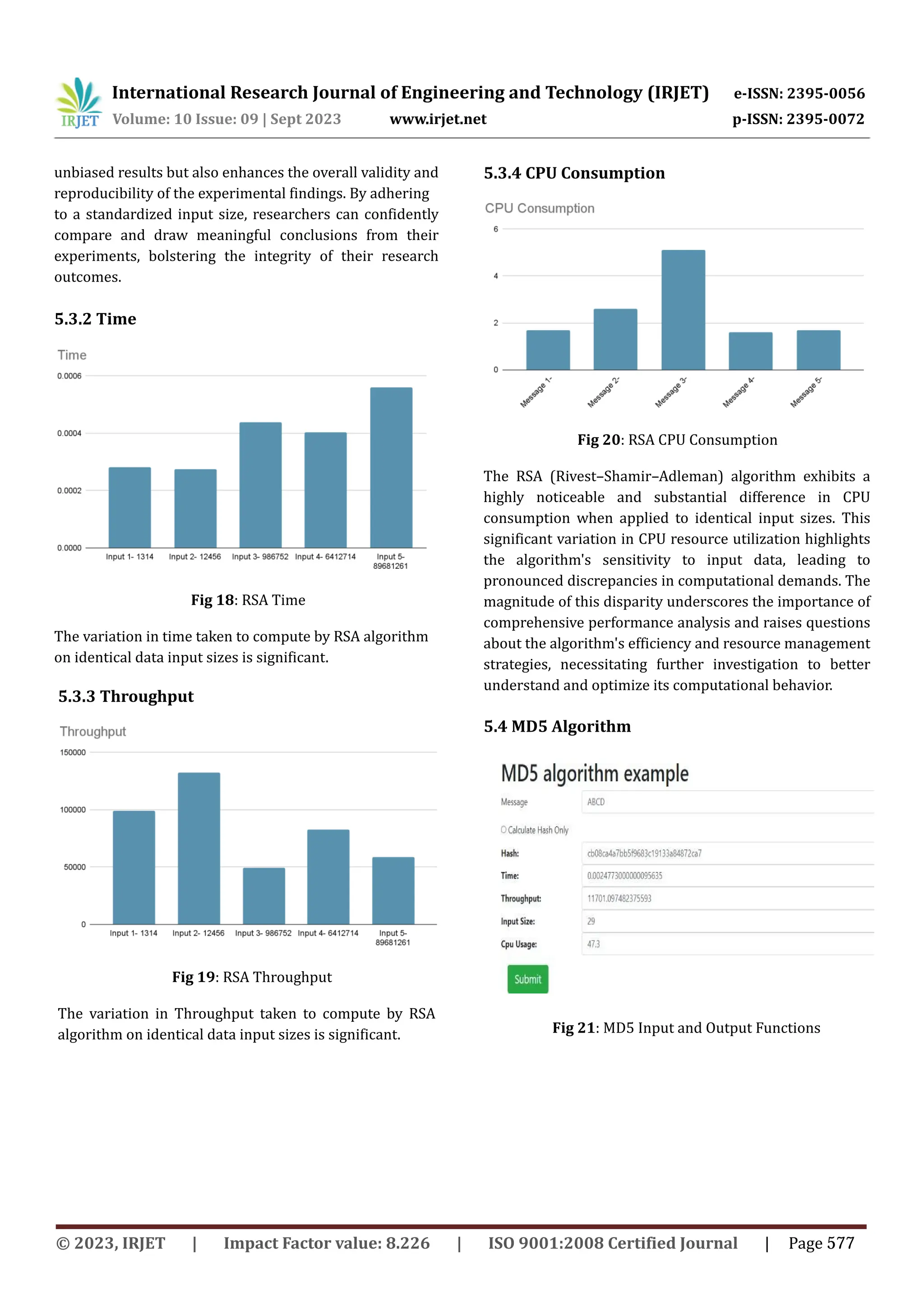
This document discusses the development and performance comparison of a modified RSA cryptographic algorithm with other algorithms like AES, DES, MD5, and RSA. It proposes creating a new algorithm that aims to perform better than existing algorithms in terms of security and efficiency. The document describes how the modified RSA algorithm would enhance security through techniques like padding, key management, use of randomness in key generation, longer key lengths, and secure hardware implementation. It outlines a plan to test the performance of the modified RSA algorithm against other algorithms and compare metrics like encryption/decryption speed and security level.






![International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 Volume: 10 Issue: 09 | Sept 2023 www.irjet.net p-ISSN: 2395-0072 Power Consumpti on Low High High High Time High Low Very High High Very High Low Low Low Confidenti ality High High Low High Table 1: Comparison of Results 6. CONCLUSIONS With data leaks and personal chats of people happening all the time, security has become a highly vital part of modern- day technology. The primitive form of the RSA algorithm has been shown to be a good and efficient security algorithm. It does, however, have some disadvantages. The public key and private key are both susceptible, and if someone obtains a person's private key, that person's whole data is at risk. As a result, in this project, we presented a method for making the RSA algorithm more secure and overcoming its flaws, so that even if a person's private key is released, a hacker will not be able to access private information. Because of this element of our project, it is extremely important in the field of data security. REFERENCE [1] Sheba Diamond Thabah, Mridupawan Sonowal, Rekib Uddin Ahmed, Prabir Saha,Fast and Area Efficient Implementation of RSA Algorithm,Procedia Computer Science, Volume 165,2019, Pages 525- 531, ISSN 1877-0509, doi: 10.1016/j.procs.2020.01.024 [2] Shakya, Aman & Karna, Nitesh. (2019). Enhancing MD5 hash algorithm using symmetric key encryption. ICCSP '19: Proceedings of the 3rd International Conference on Cryptography, Security and Privacy. 18-22. doi: 10.1145/3309074.3309087. [3] A. Mohammed Ali and A. Kadhim Farhan, "A Novel Improvement With an Effective Expansion to Enhance the MD5 Hash Function for Verification of a Secure E-Document," in IEEE Access, vol. 8, pp. 80290-80304, 2020, doi: 10.1109/ACCESS.2020.2989050. Throughpu t [4] Amorado, Ryndel & Sison, Ariel & Medina, Ruji. (2019). Enhanced Data Encryption Standard (DES) Algorithm based on Filtering and Striding Techniques. ICISS 2019: Proceedings of the 2019 2nd International Conference on Information Science and Systems. 252-256. doi: 10.1145/3322645.3322671. [5] V. S. Aparna, A. Rajan, I. Jairaj, B. Nandita, P. Madhusoodanan and A. A. S. Remya, "Implementation of AES Algorithm on Text And Image using MATLAB," 2019 3rd International Conference on Trends in Electronics and Informatics (ICOEI), 2019, pp. 1279-1283, doi: 10.1109/ICOEI.2019.8862703. [6] Abid, R., Iwendi, C., Javed, A.R. et al. An optimised homomorphic CRT-RSA algorithm for secure and efficient communication. Pers Ubiquit Comput (2021). https://doi.org/10.1007/s00779-021-01607-3 [7] Lin C-H, Hu G-H, Chan C-Y, Yan J-J. Chaos-Based Synchronized Dynamic Keys and Their Application to Image Encryption with an Improved AES Algorithm. Applied Sciences. 2021; 11(3):1329. https://doi.org/10.3390/app11031329 [8] Li, Y., HeLu, X., Li, M., Sun, Y., Wang, L. (2019). Implementation of MD5 Collision Attack in Program. In: Sun, X., Pan, Z., Bertino, E. (eds) Artificial Intelligence and Security. ICAIS 2019. Lecture Notes in Computer Science(), vol 11632. Springer, Cham. https://doi.org/10.1007/978-3-030-24274-9_54 © 2023, IRJET | Impact Factor value: 8.226 | ISO 9001:2008 Certified Journal | Page 580](https://image.slidesharecdn.com/irjet-v10i984-240108120722-f595e8aa/75/Development-and-performance-comparison-of-modified-RSA-algorithm-with-other-cryptographic-algorithms-13-2048.jpg)