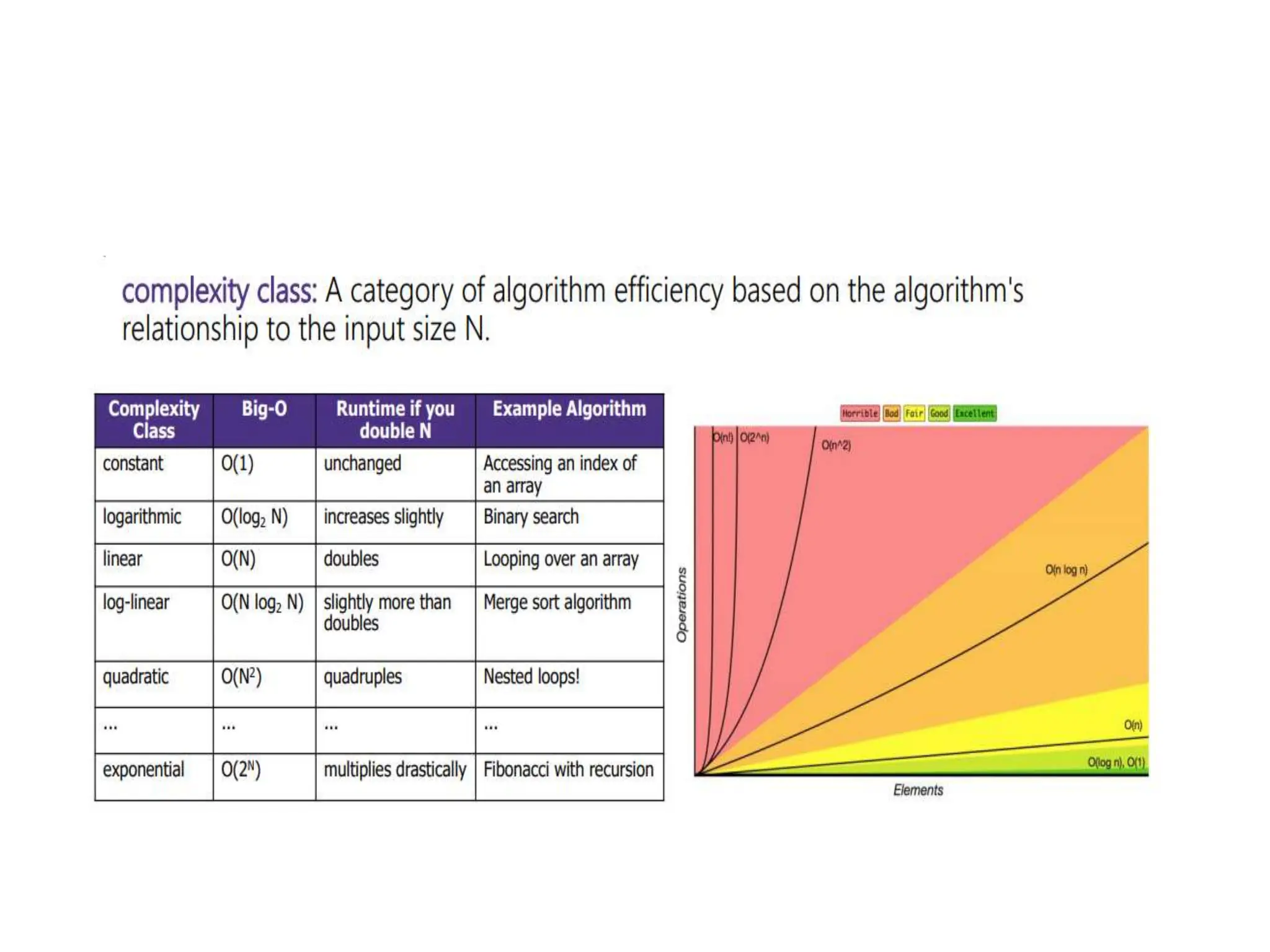
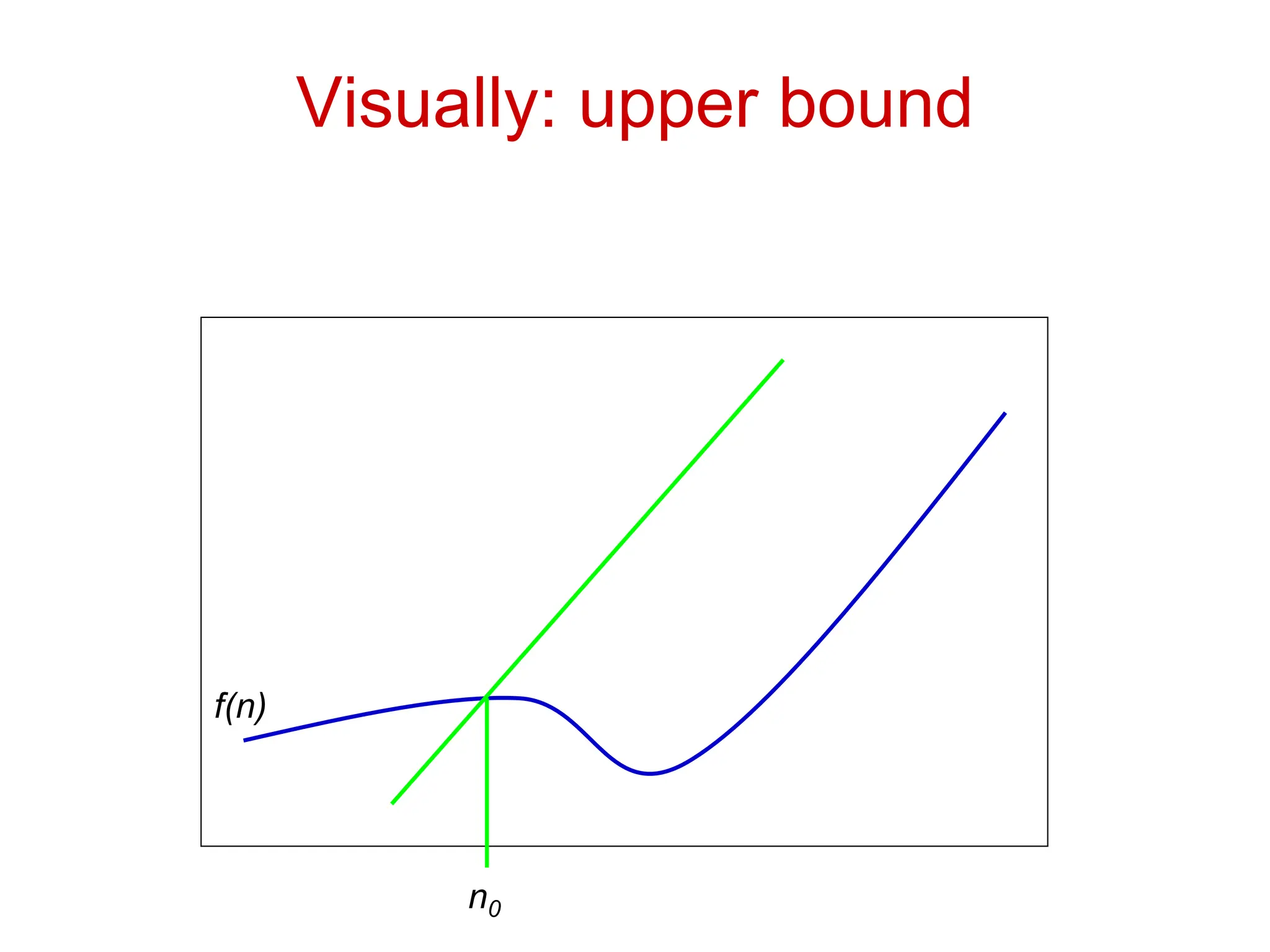
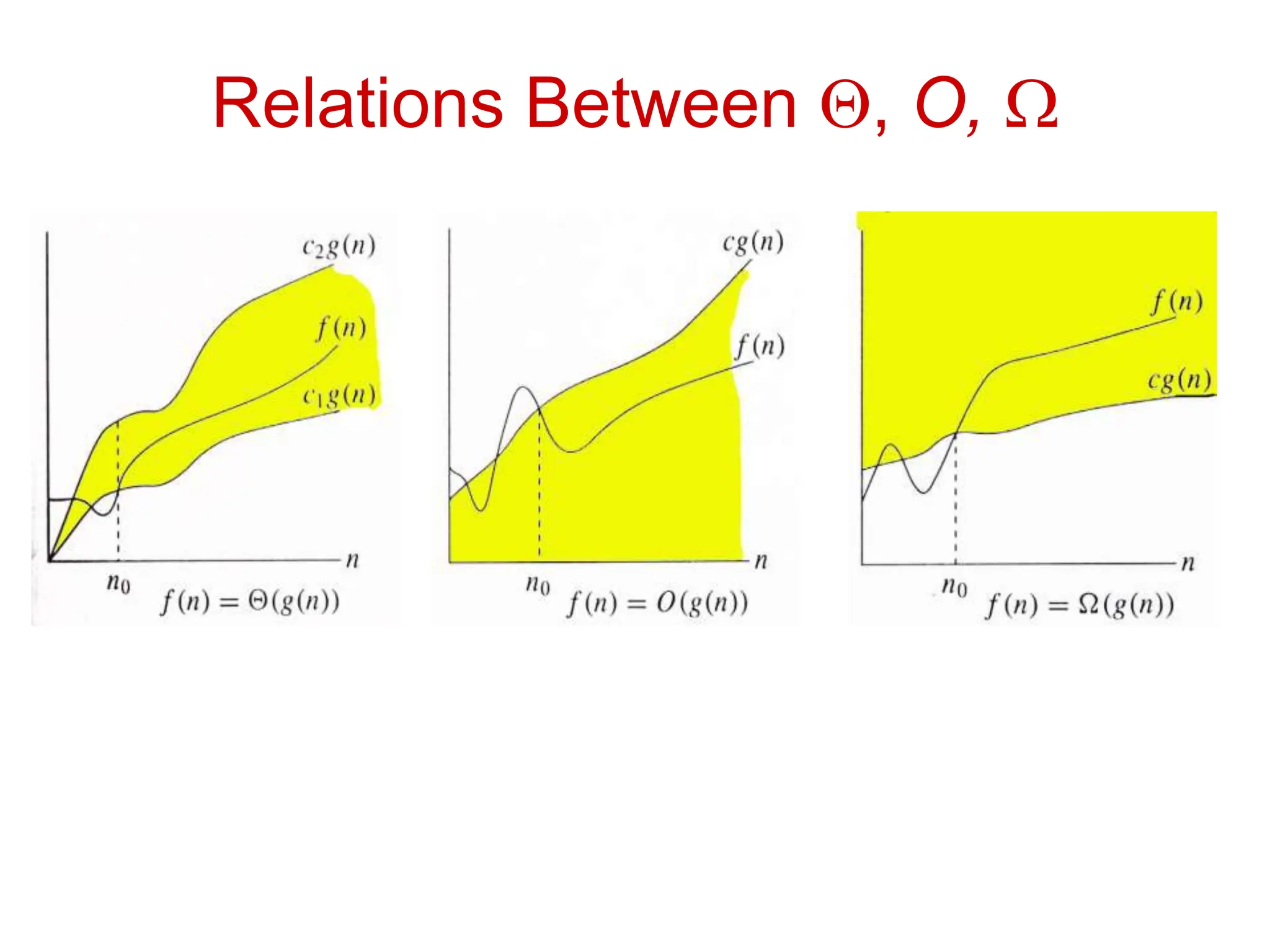
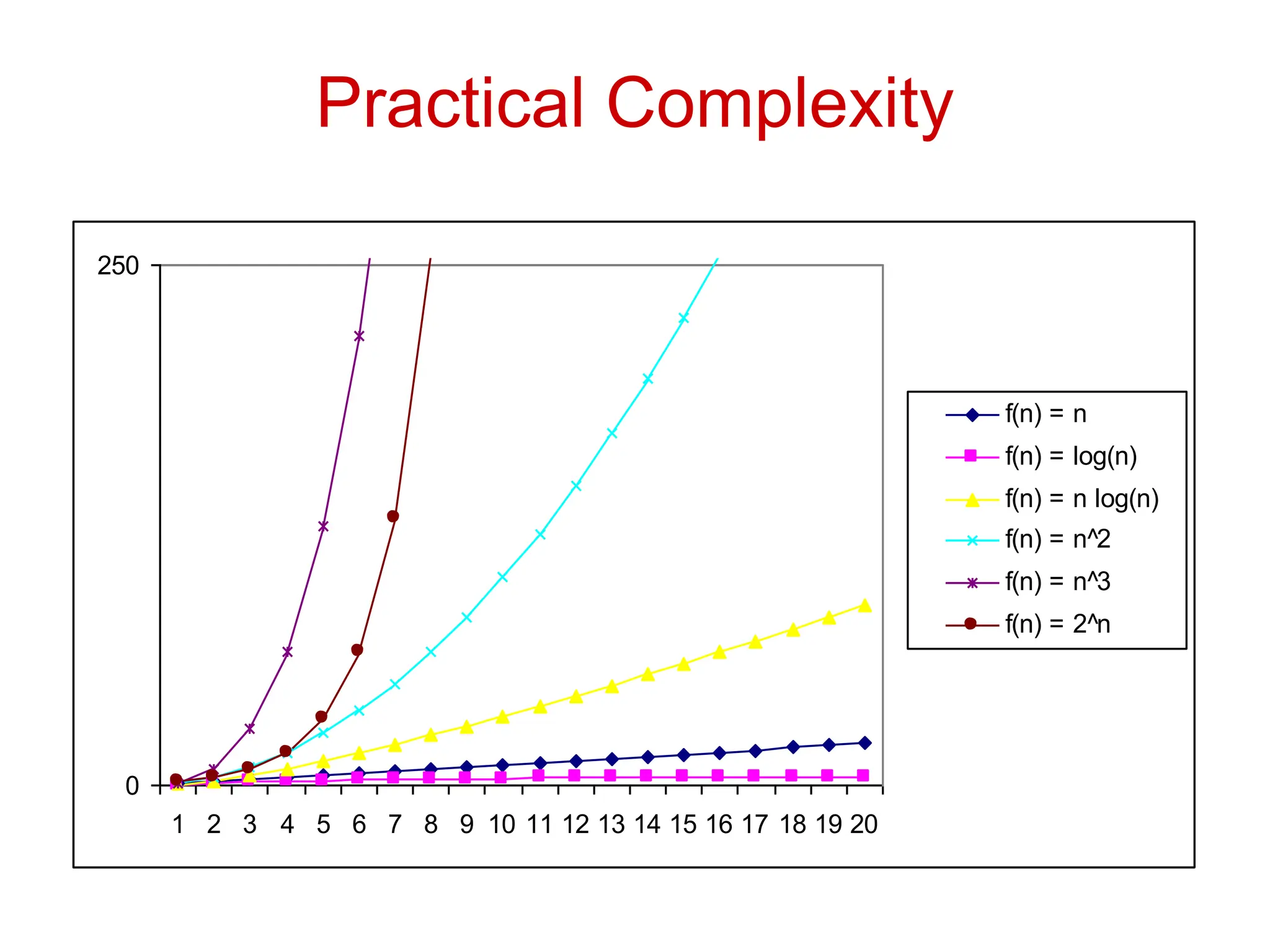
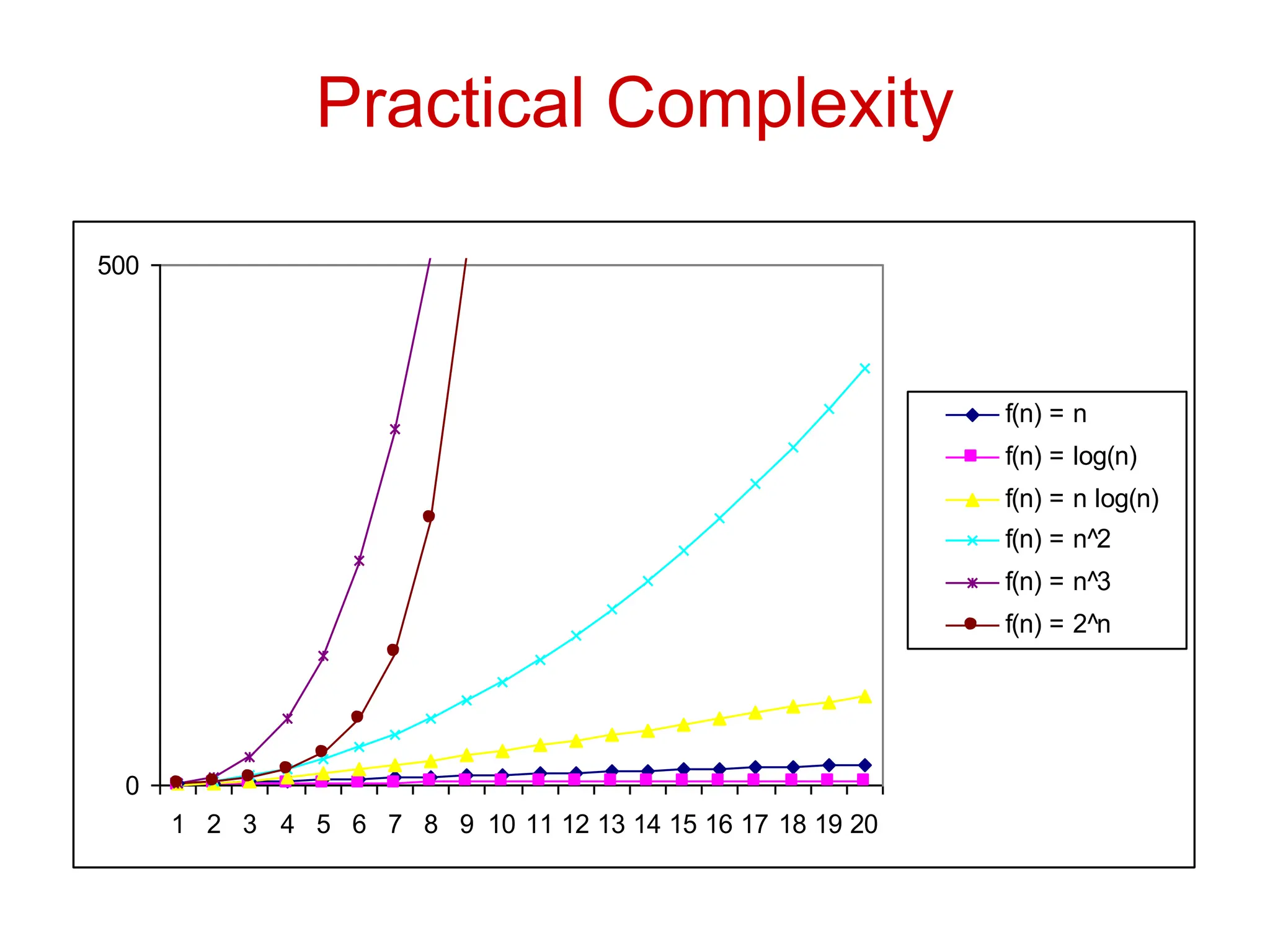
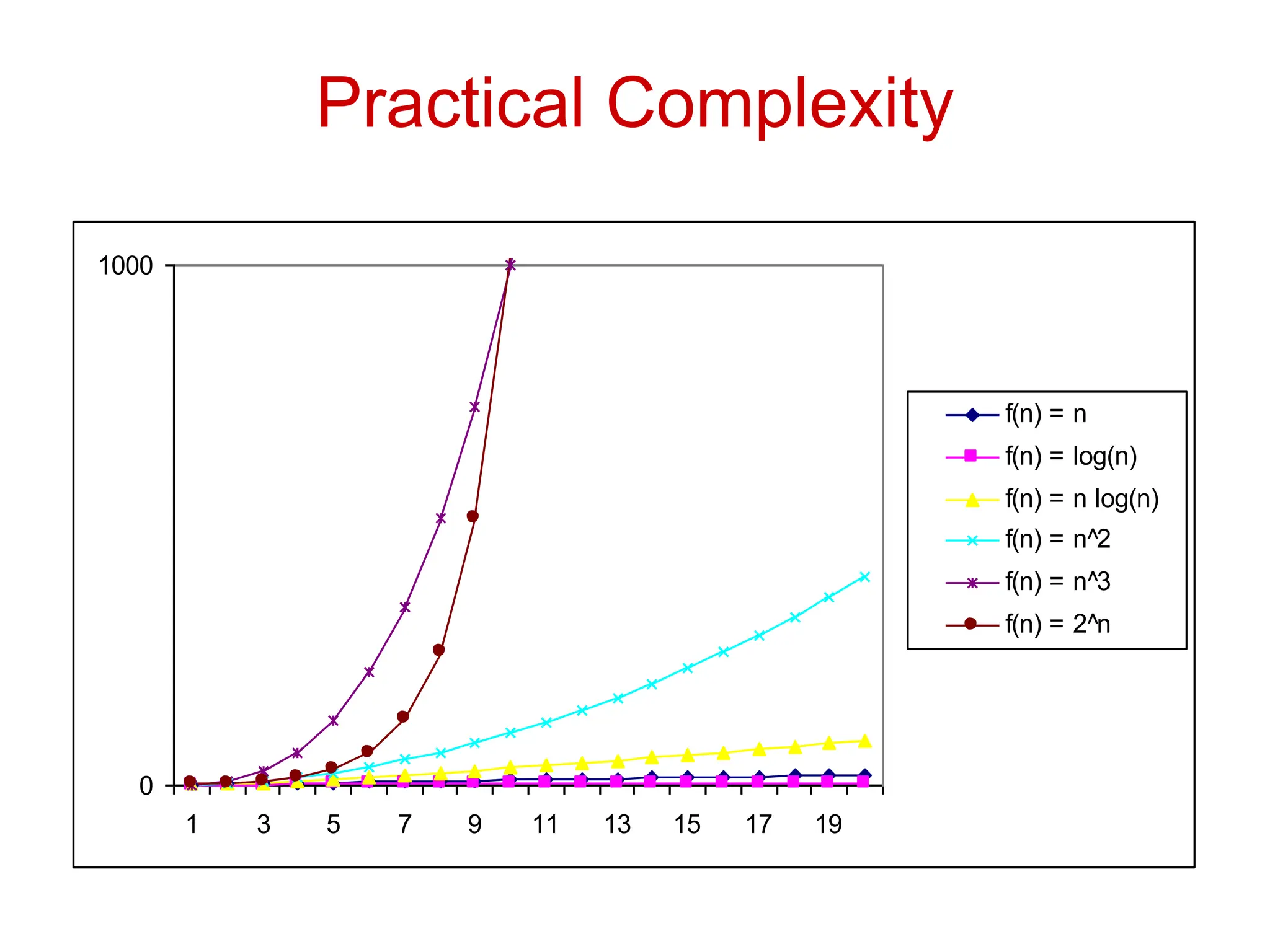
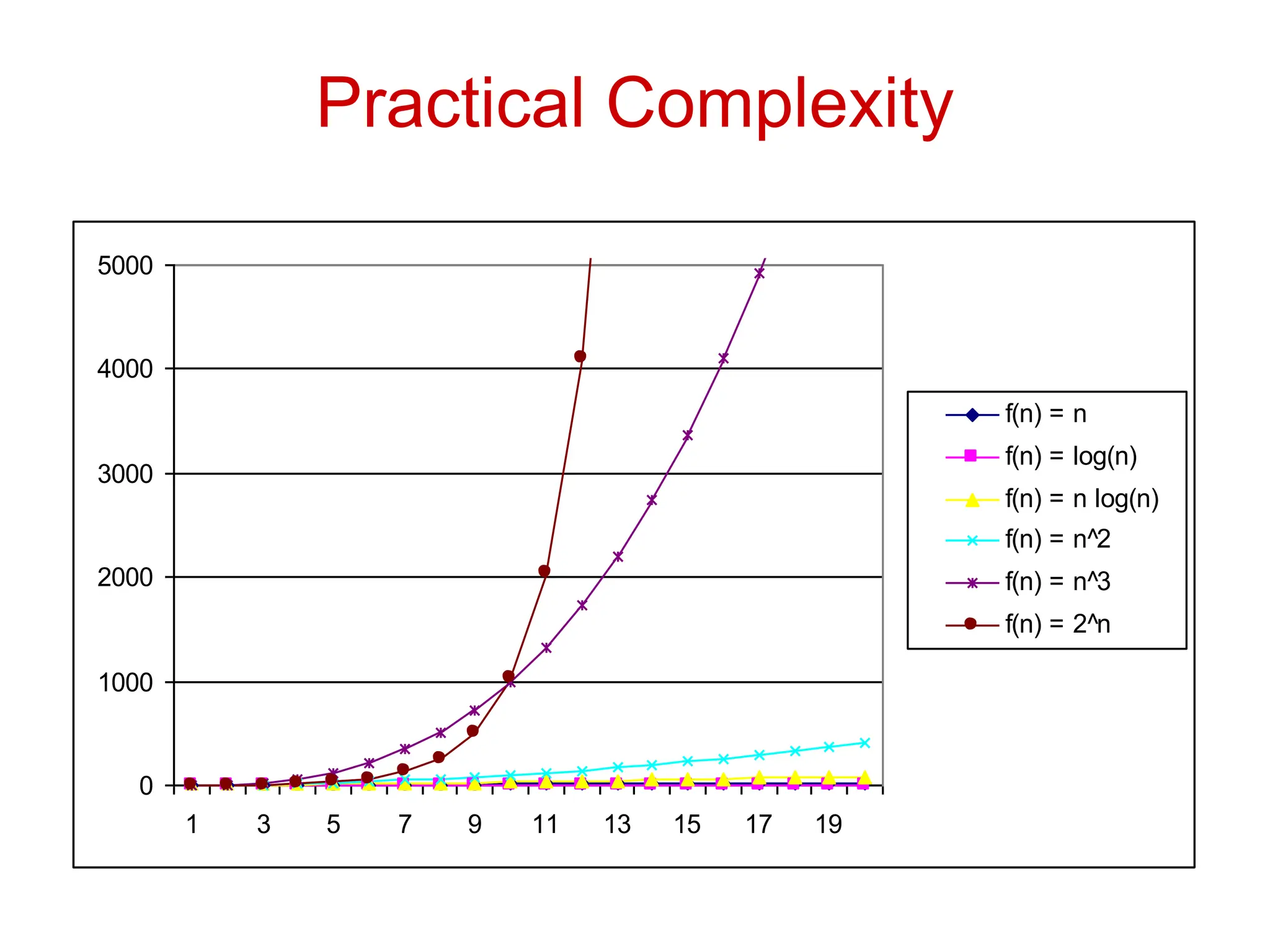
The document discusses asymptotic analysis and algorithmic complexity. It introduces asymptotic notations like Big O, Omega, and Theta that are used to analyze how an algorithm's running time grows as the input size increases. These notations allow algorithms to be categorized based on their worst-case upper and lower time bounds. Common time complexities include constant, logarithmic, linear, quadratic, and exponential time. The document provides examples of problems that fall into each category and discusses how asymptotic notations are used to prove upper and lower bounds for functions.