Download as PDF, PPTX
Data Structures and Algorithms - Lec 02.pdf
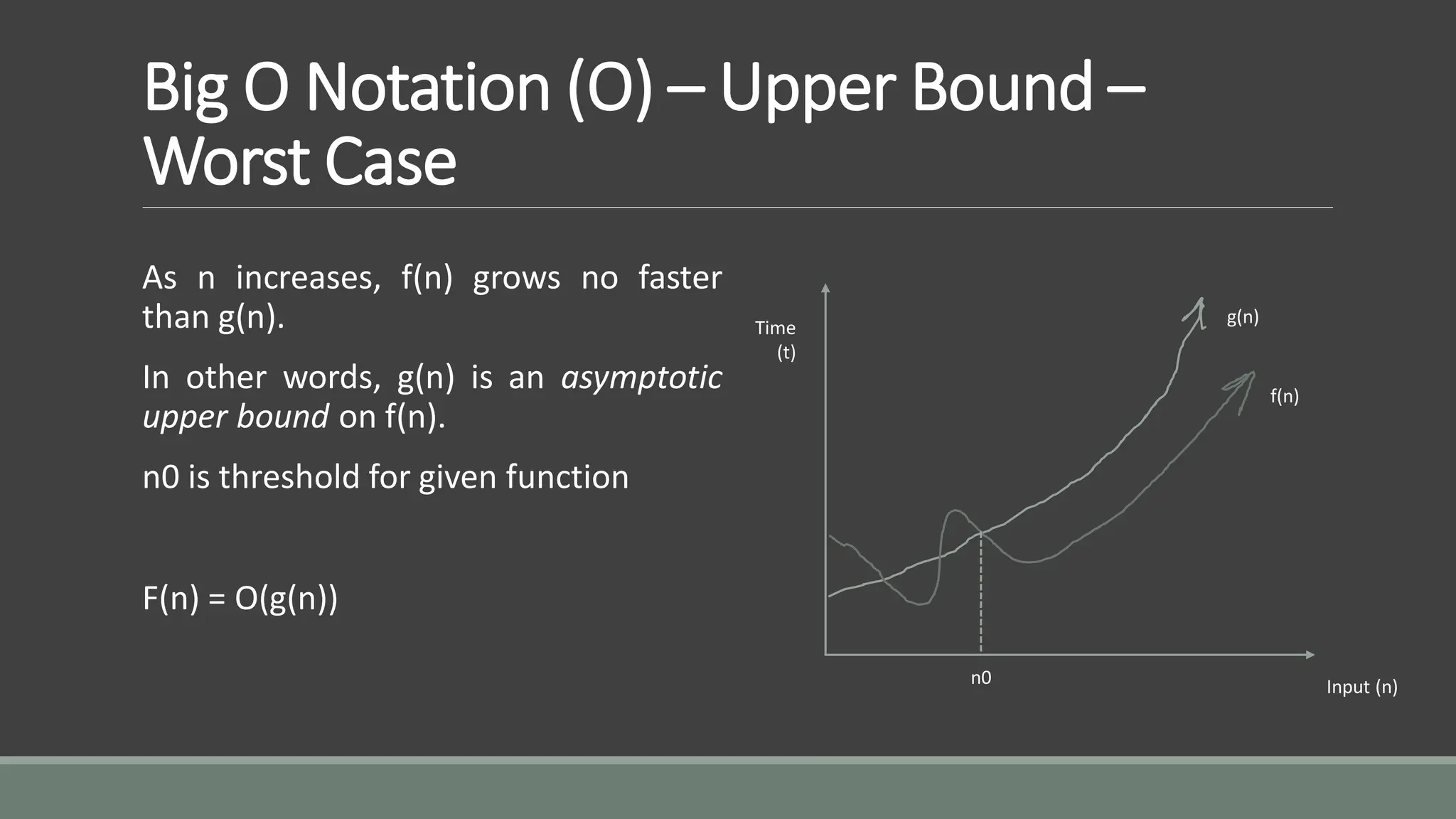
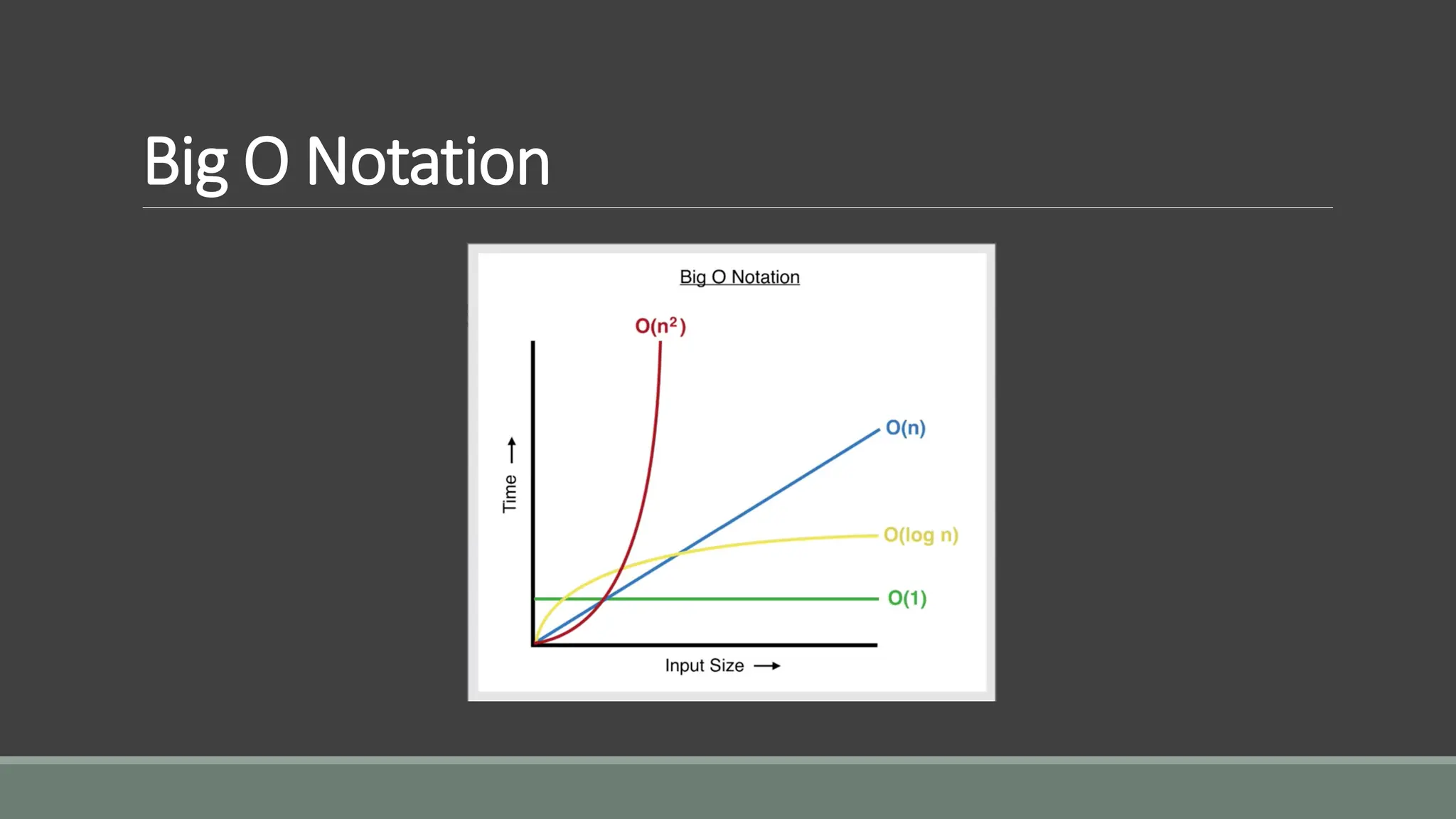
- 1. An Overview ofAlgorithms Lecture 02 Dhanushka Jayasinghe
- 2. Asymptotic Notation Aproblem may have numerous algorithmic solutions. In order to choose the best algorithm for a particular task, you need to be able to judge how long a particular solution will take to run. Need a way to compare algorithms with one another. Asymptotic Complexity is a way of expressing the main component of the cost of an algorithm, using idealized units of computational work.
- 3.
- 4. Asymptotic Notation Whenwe study algorithms, we are interested in characterizing them according to their efficiency. We are usually interesting in the order of growth of the running time of an algorithm, not in the exact running time. This is also referred to as the asymptotic running time. We need to develop a way to talk about the rate of growth of functions so that we can compare algorithms. Asymptotic notation gives us a method for classifying functions according to their rate of growth.
- 5. Fundamentals How todesign various algorithms for a single solution and how to analyze them. What will be the time taken by each one and what will be the memory required by each algorithm. Select the most suitable algorithm. Design Analyze Select
- 6. Asymptotic Notation Asymptotic Notationis a mathematical notation used to describe the asymptotic behavior of a function. EX: ◦ Algorithm A is twice as fast as Algorithm B ◦ If the number of items are increased by 50% ◦ Algorithm A is three times faster than Algorithm B ◦ If we have half as many items ◦ Algorithm A and B take equal time to run Therefore we need a comparison that is related to the number of items
- 7. Asymptotic Notation Big ONotation (O) ◦ Worst case – Upper Bound of function Big Omega Notation (Ω) ◦ Best case – Lower Bound of function Big Theta Notation (Ɵ) ◦ Average case
- 8. Big O Notation(O) – Upper Bound – Worst Case As n increases, f(n) grows no faster than g(n). In other words, g(n) is an asymptotic upper bound on f(n). n0 is threshold for given function F(n) = O(g(n)) Input (n) Time (t) f(n) g(n) n0
- 9. Big O Notation Ifwe can bind f(n) function by some other function g(n) in such a way that after some input n0, the value of g(n) is always greater than f(n) we call g(n) the upper bound of f(n). Definition: f(n) = O(g(n)) if there are two positive constants c and n0 such that |f(n)| <= c |g(n)| for all n >= n0 If f(n) is nonnegative, we can simplify the last condition to 0 <= f(n) <=c g(n) for all n >= n0 We say that “f(n) is big-O of g(n).”
- 10. Let’s we afunction f(n) 2n+6, f(n) = 2n+6 C g(n) = 4n 0 <= f(n) <=c g(n) all n >= n0 0 <= 2n+6 <= 4n , if n = 1; 1st 0 <= 8 <= 4 false 2nd 0 <= 10 <= 8 false 3rd 0 <= 12 <= 12 true 4th 0 <= 14 <= 16 true, therefor n >=3 0 <= 2n+6 <= 4n all n >=3 O ( g(n) ) C g(n) = 4n O(n) is time complexity of f(n) 2n+6 function
- 11. Activity Function 01 f(n) =2n2+10 c g(n) = 3n2 Function 02 f(n) = 2n2+n c g(n) = 3n2
- 12. Big O NotationComplexities O (1) = Constant time O (log n) = Logarithmic time O (n) = Liner time O (n log n) = Liner Arithmetic time O (nc) = Polynomial time O (cn) = Exponent time O (1) < O (log n) < O (n) < O (n log n) < O (n2) < O (2n)
- 13.
- 14. Dominative Factor Select themaximum complexity value f(n) = 3n2 + n + 1 O(n2) 1. f(n) = 2 log n + n log n + n 2. f(n) = 2n + n2 + 1
- 15. Big O Notation Insertin to an unordered array ◦ Time taken to insert an item into an unordered array is constant ◦ The time does not depend on the number of items ◦ Always time T=k
- 16. Big O Notation Linearsearch ◦ Proportional to number of items N ◦ T∝ N ◦ T=k*N
- 17.