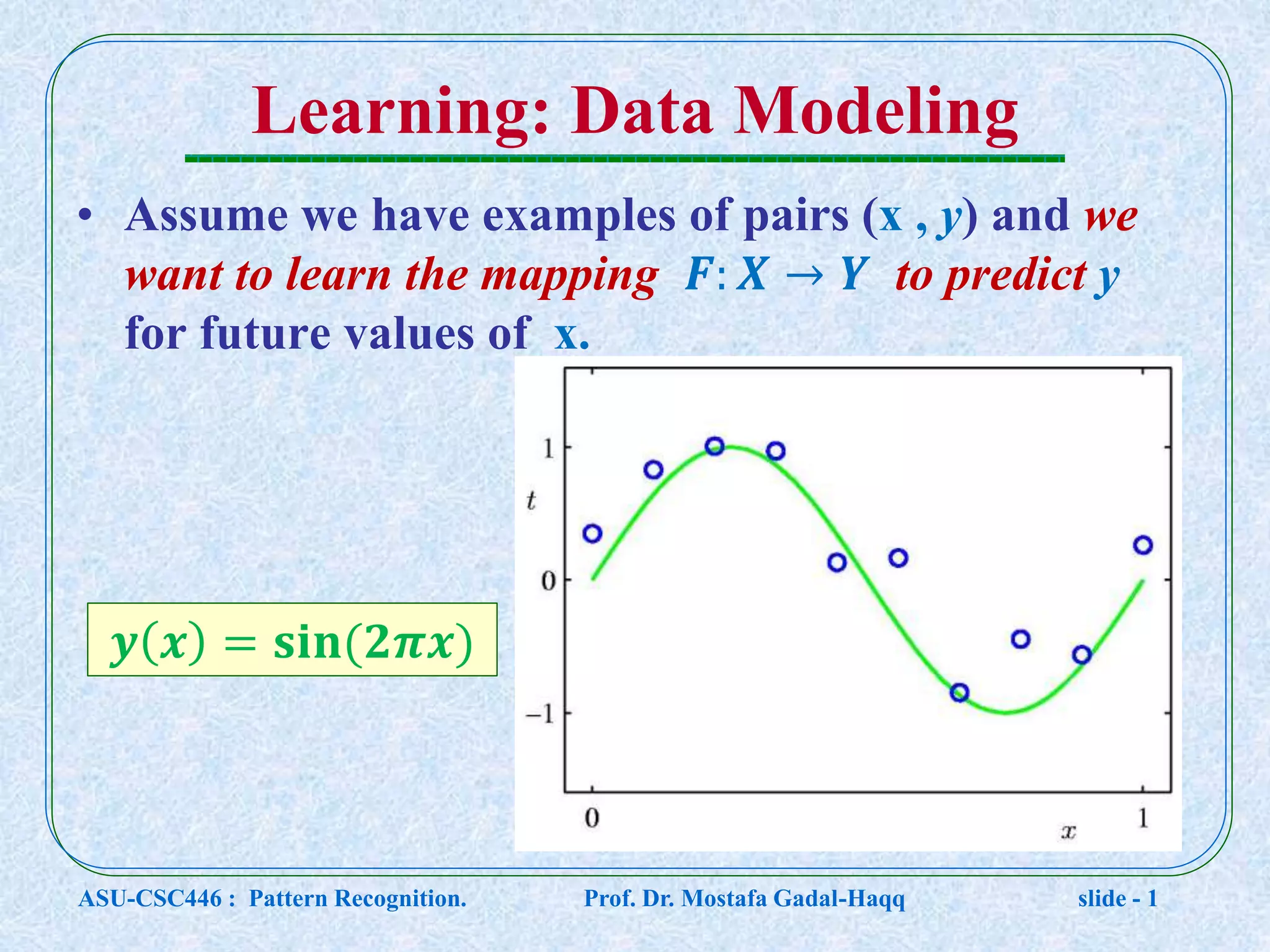
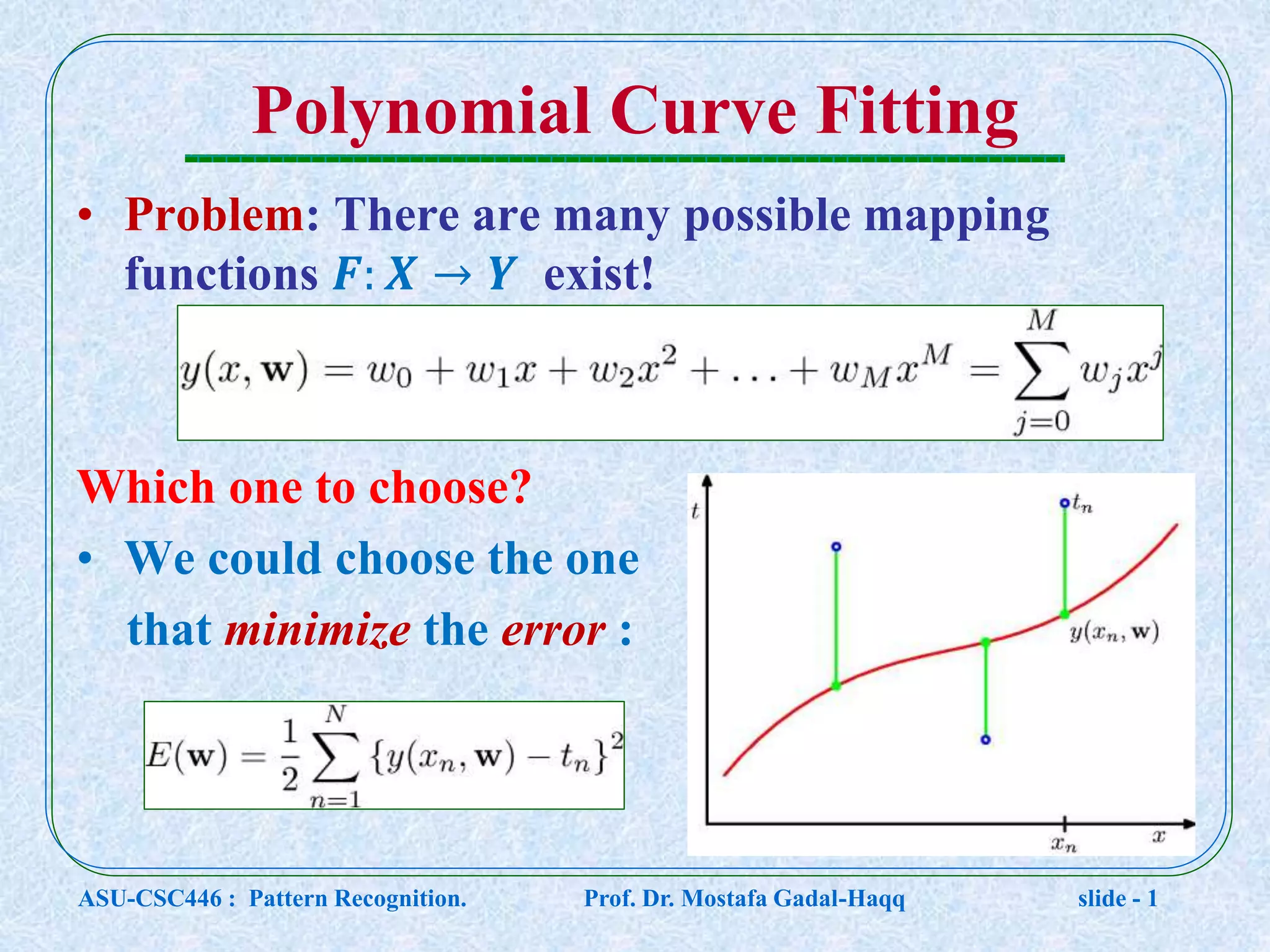
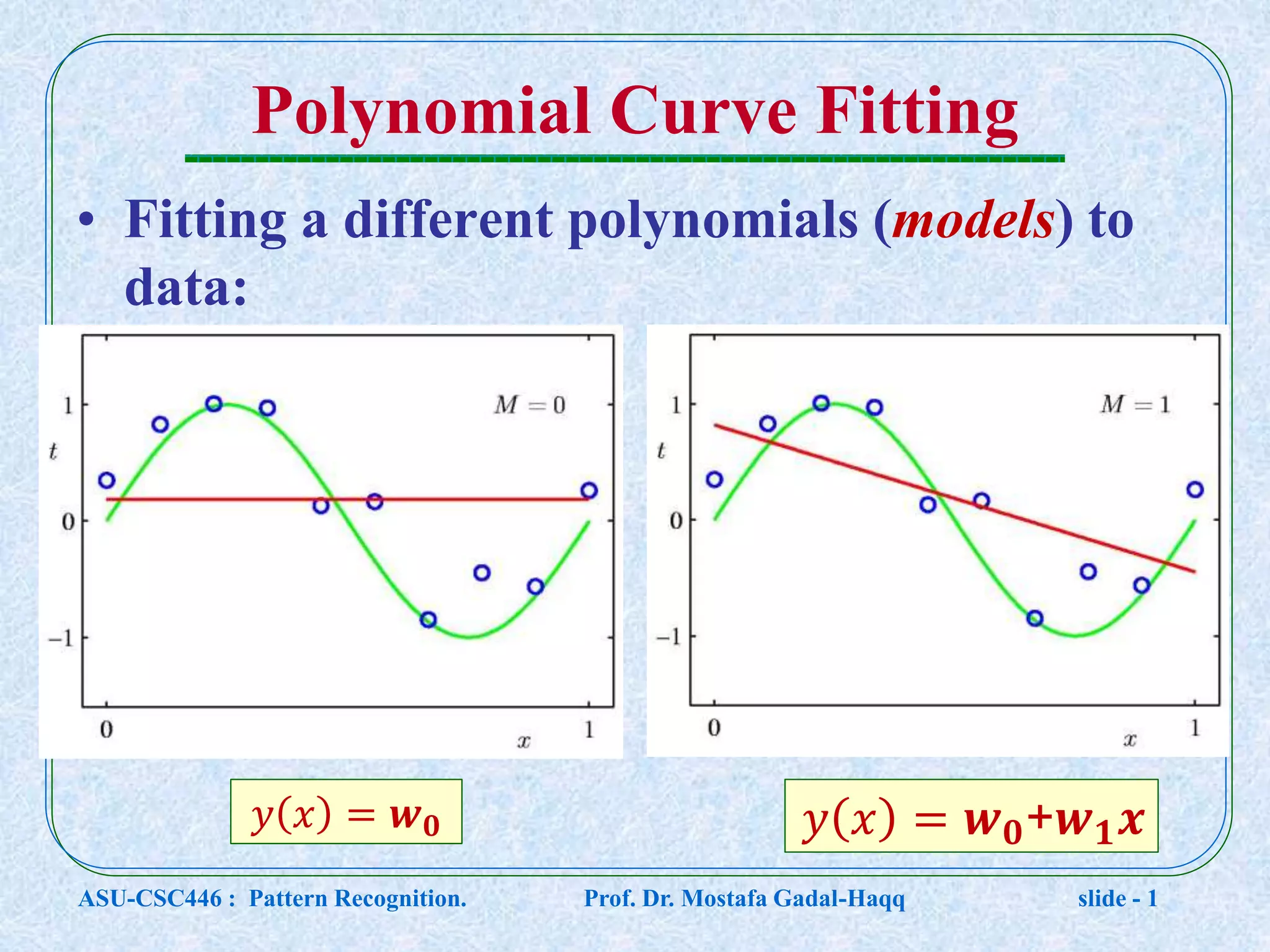
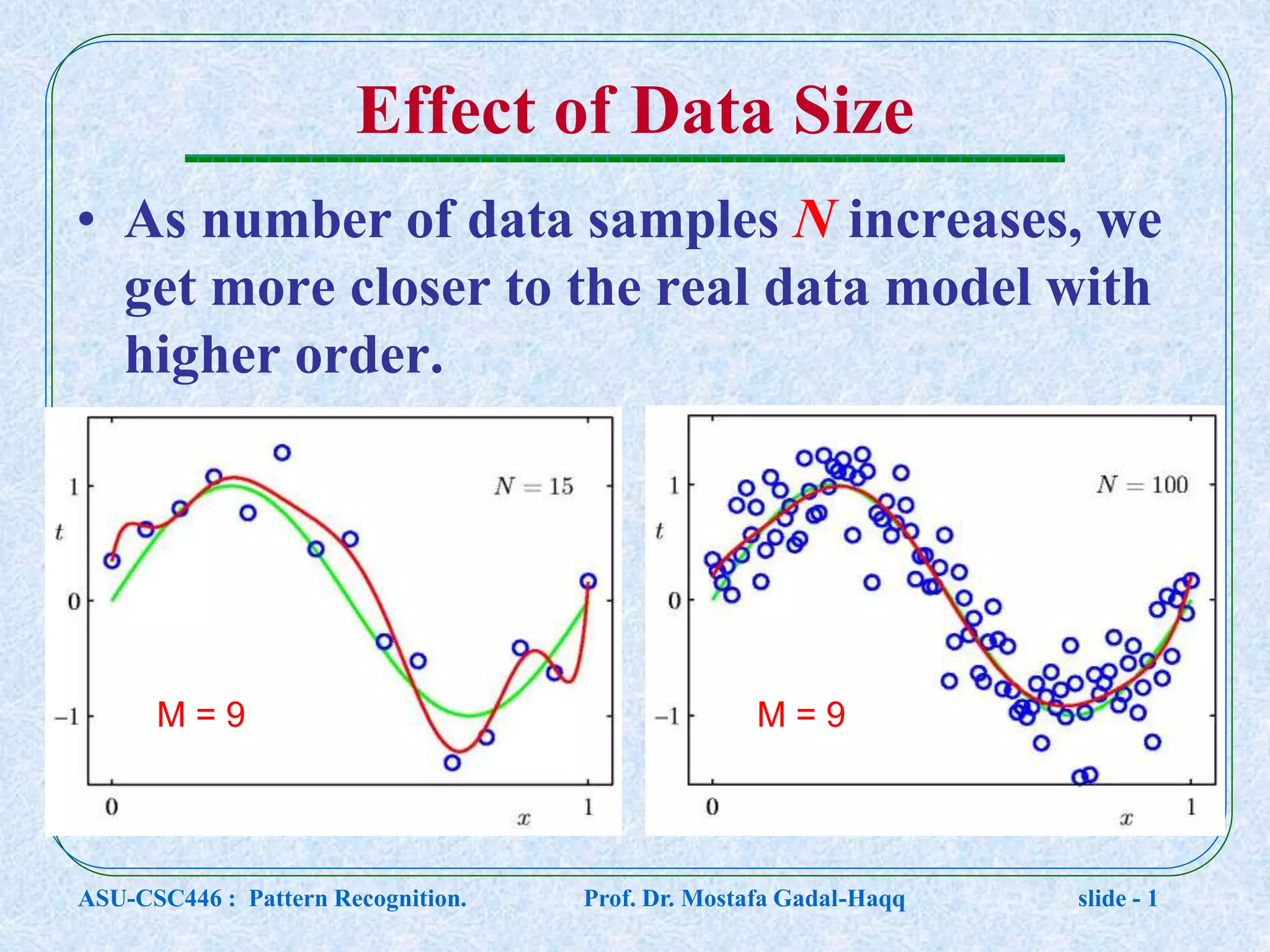
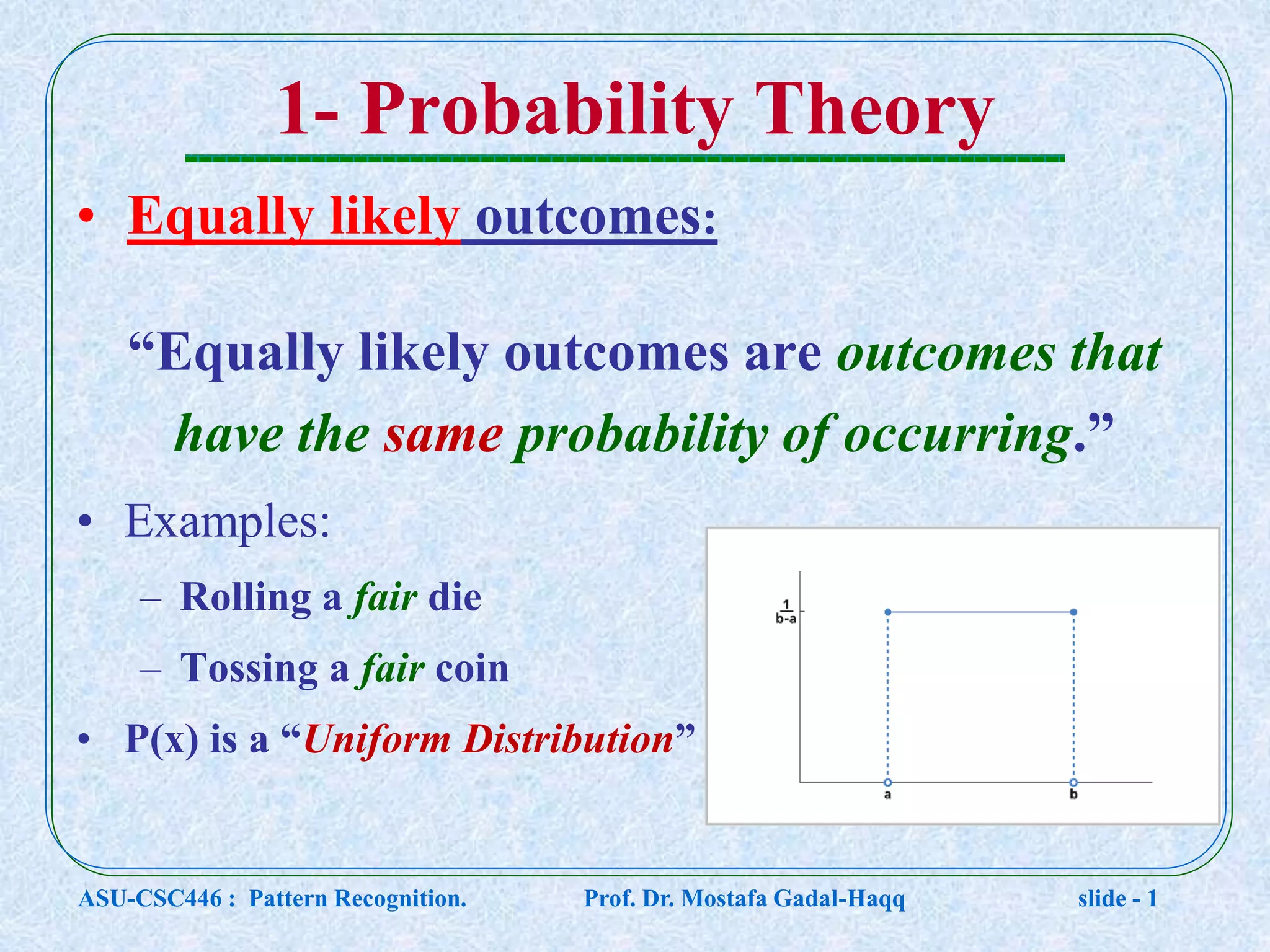
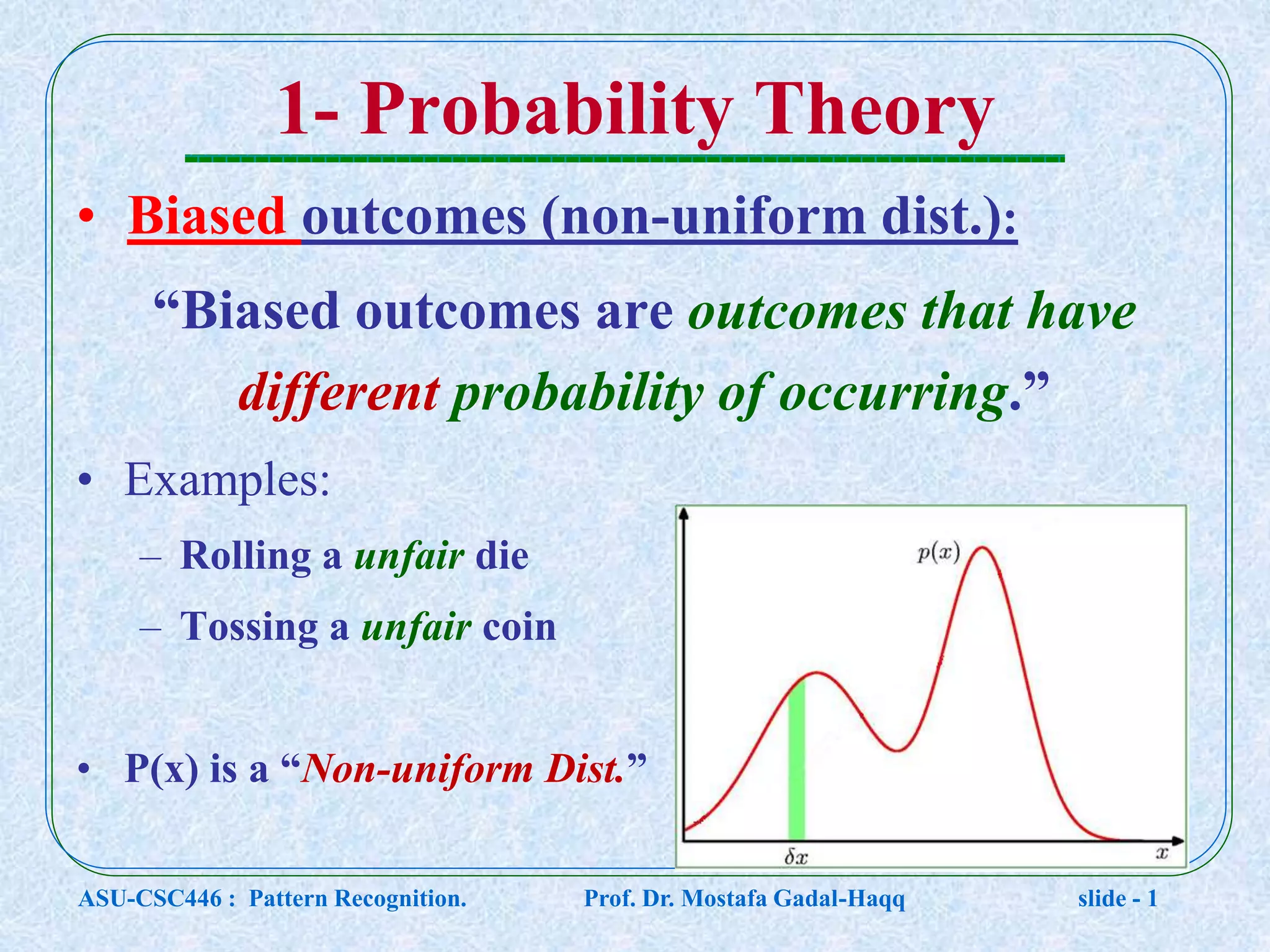
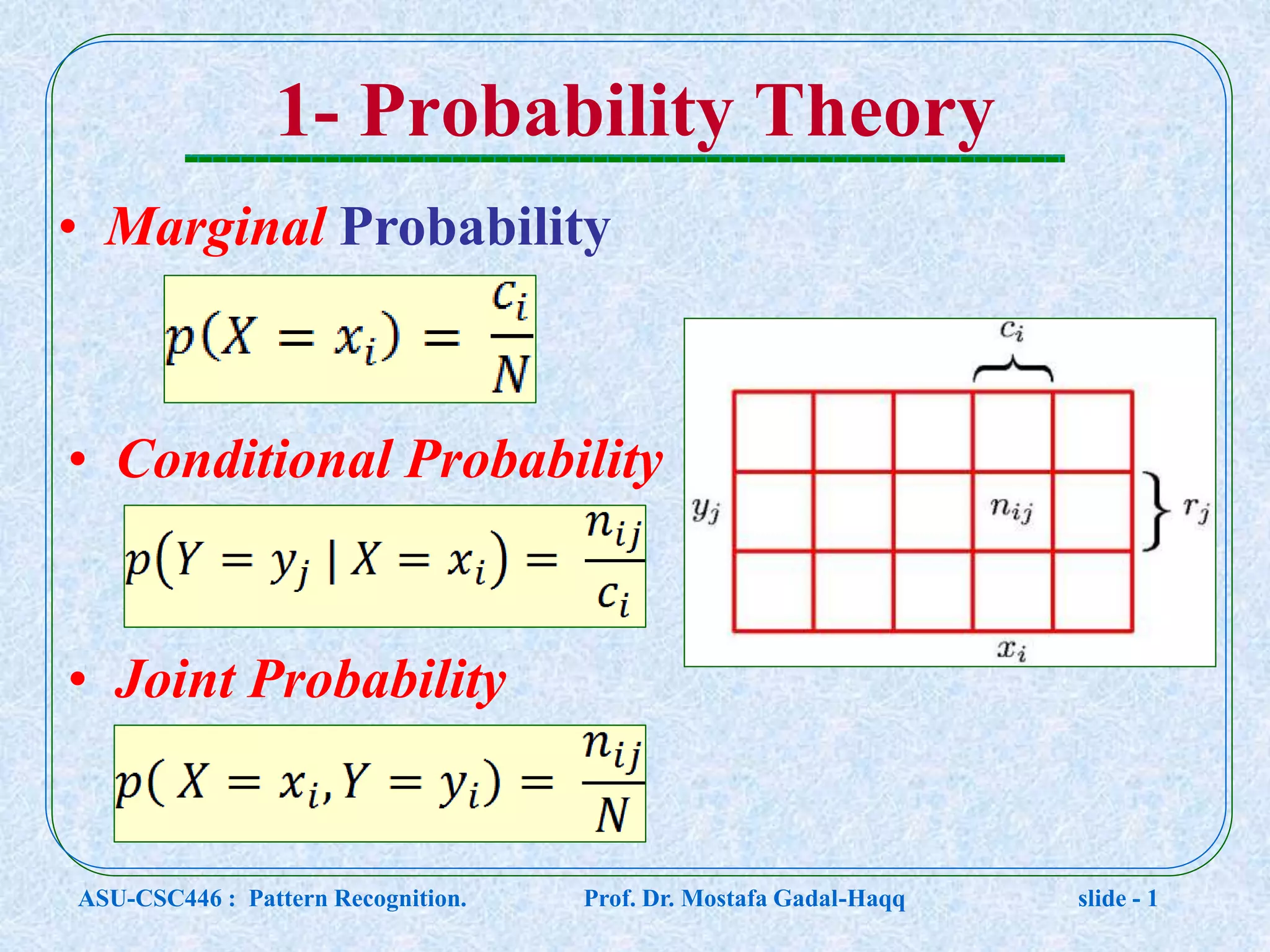
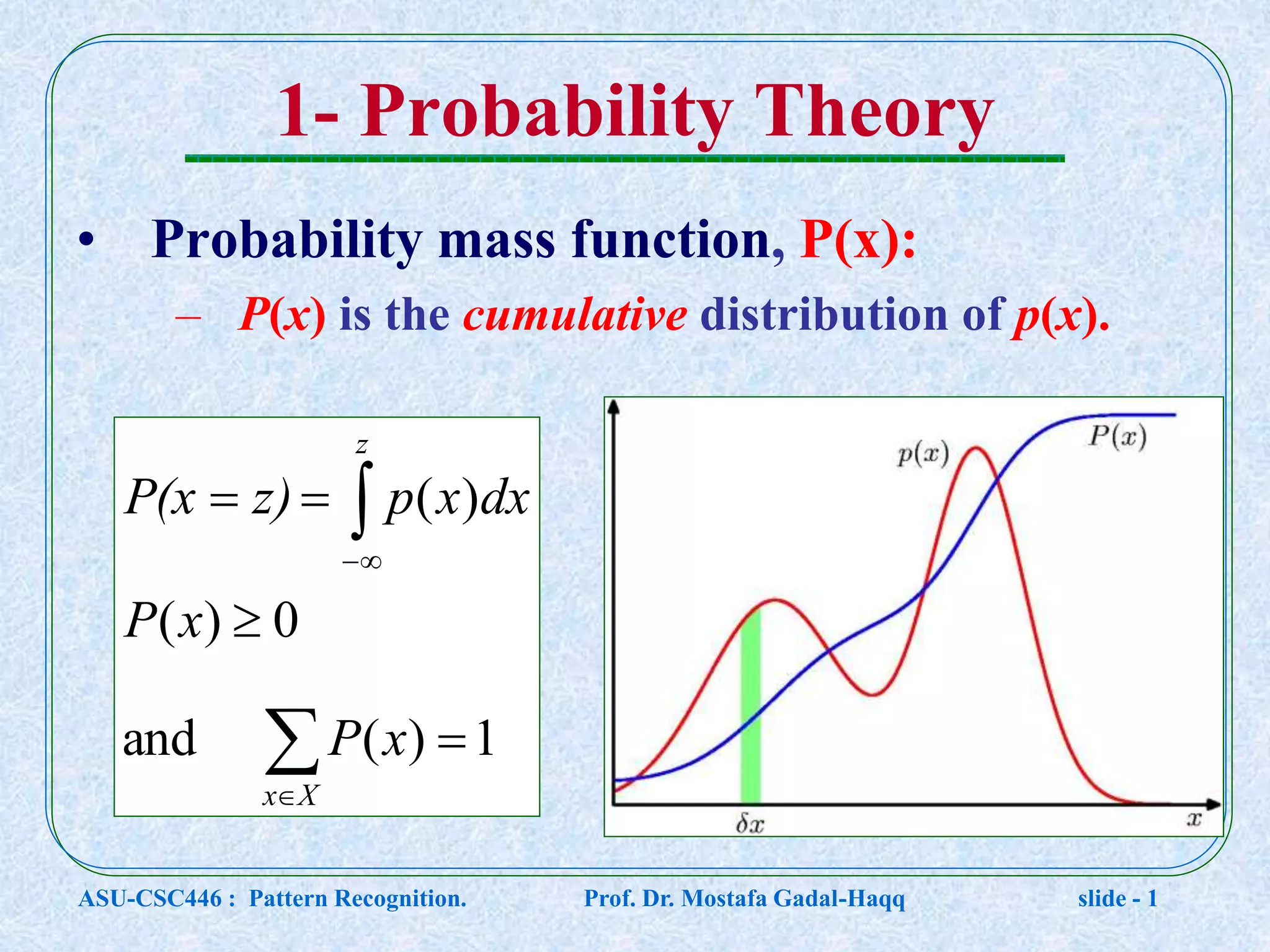
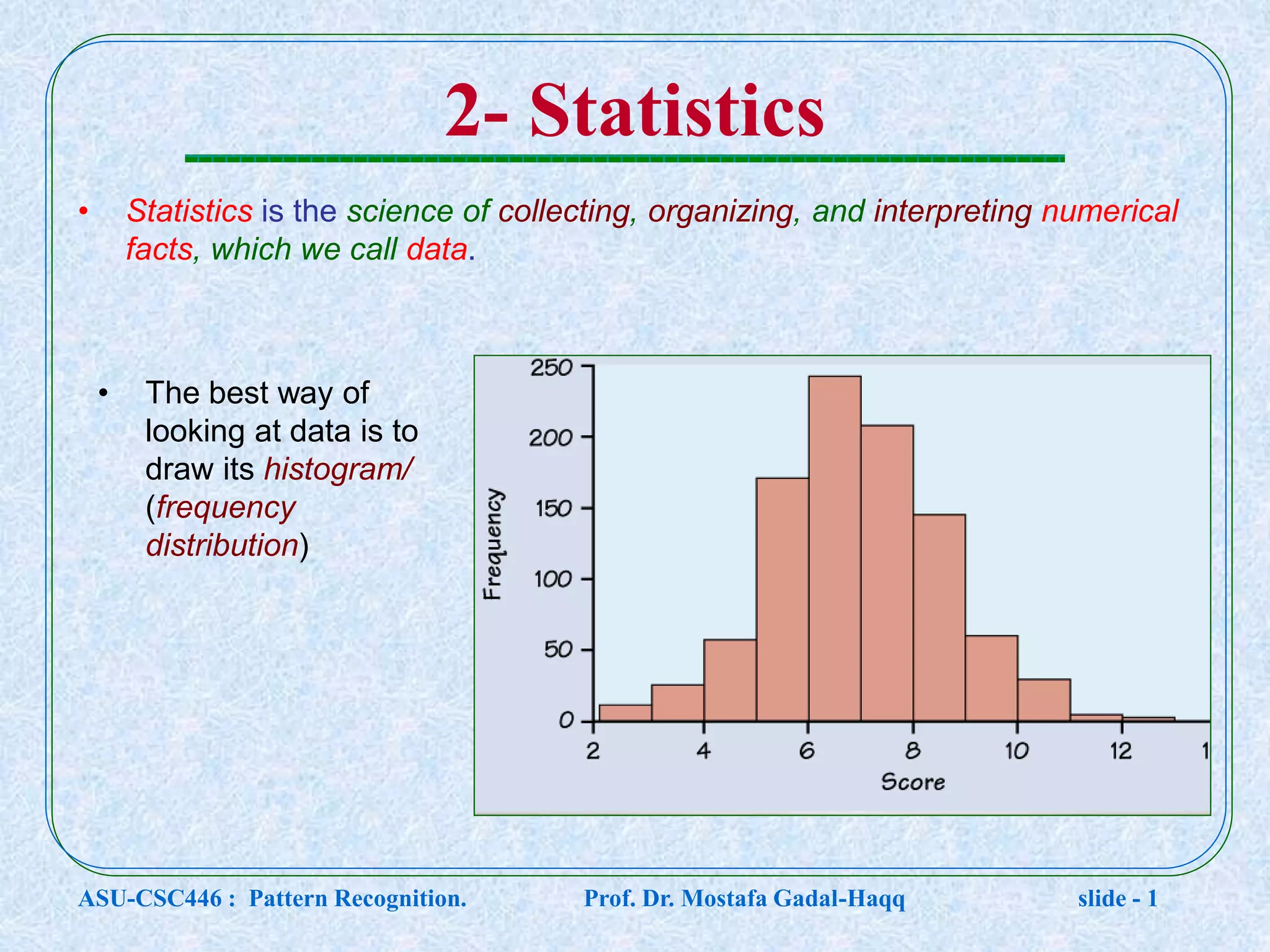
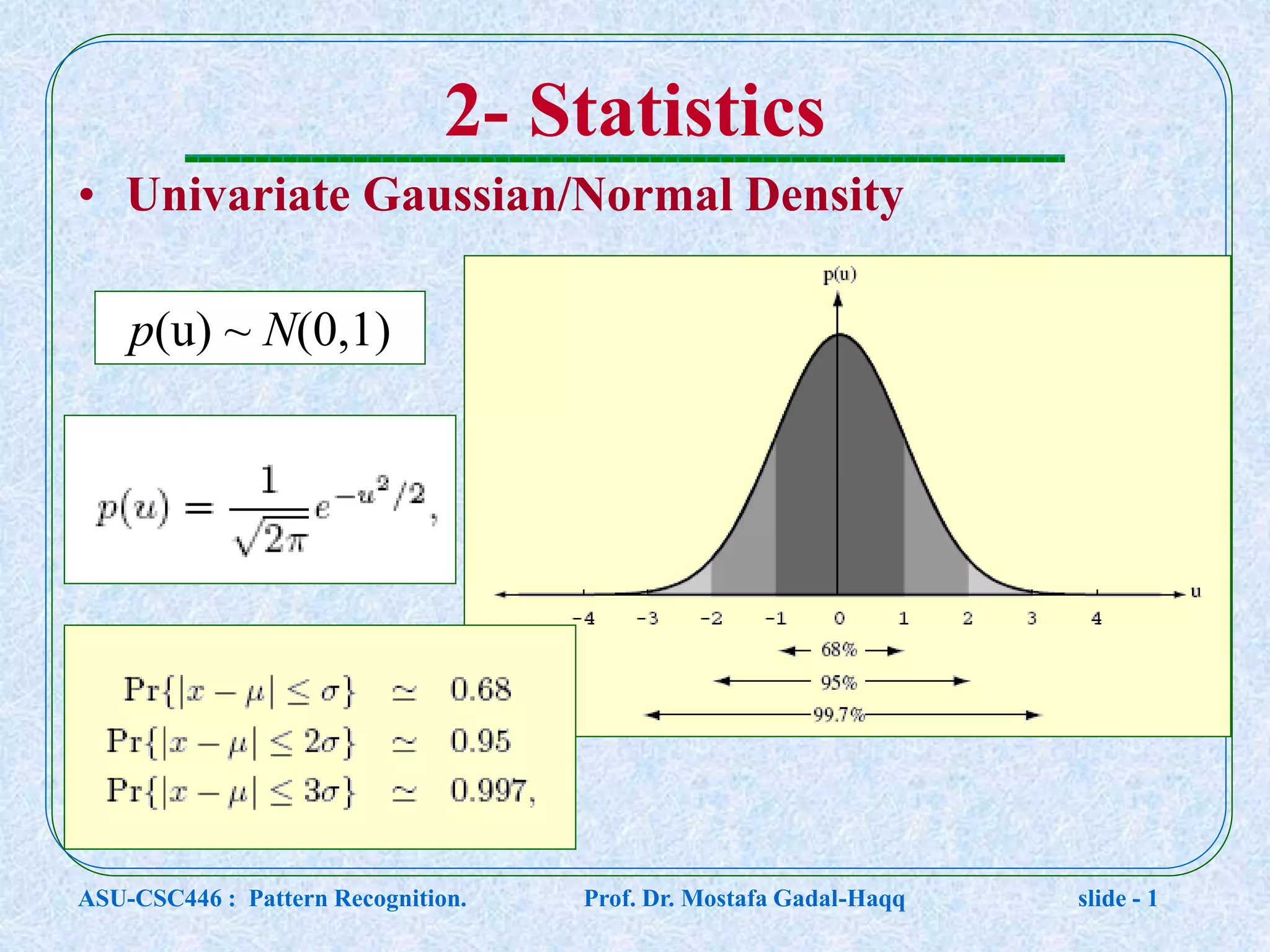
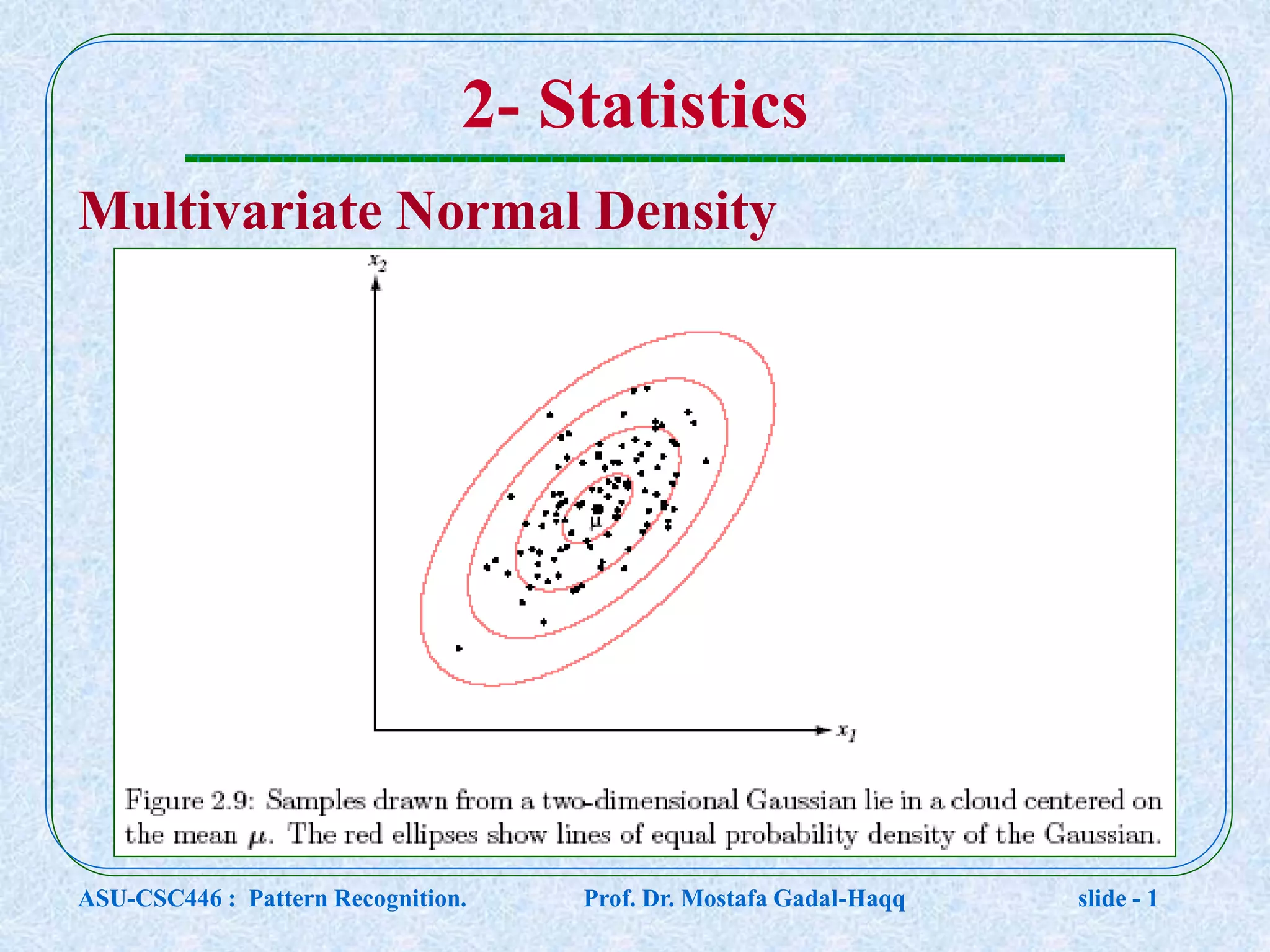
This document contains lecture notes for a pattern recognition course taught by Dr. Mostafa Gadal-Haqq at Ain Shams University. The notes cover mathematical foundations of pattern recognition including probability theory, statistics, and mathematical notations. Specifically, the notes define concepts like random variables, probability distributions, expected values, variance, and conditional probability. They also provide examples of applying these concepts to problems involving events, outcomes, and data modeling. The document concludes by noting that the next lecture will cover Bayesian decision theory.