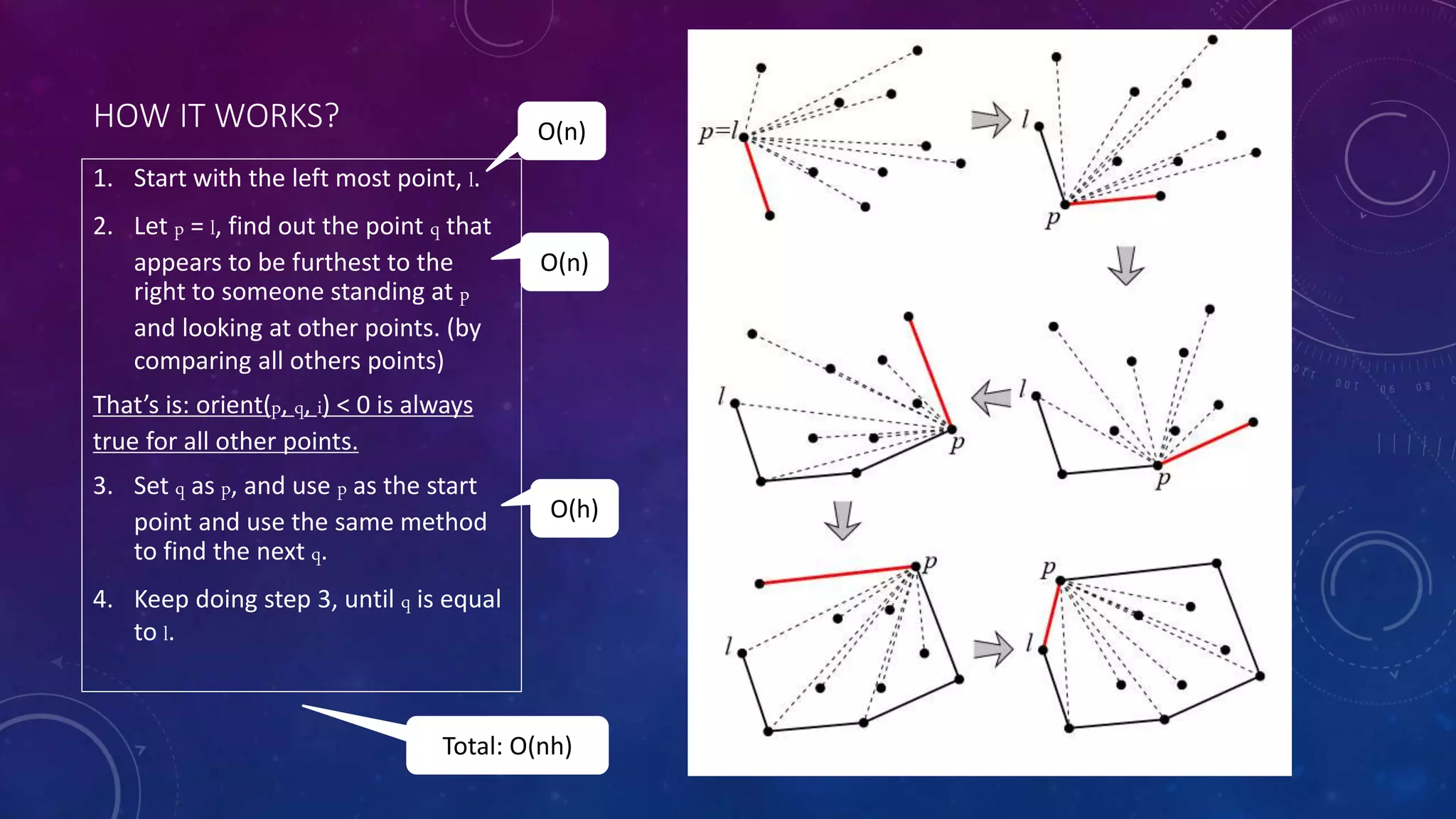
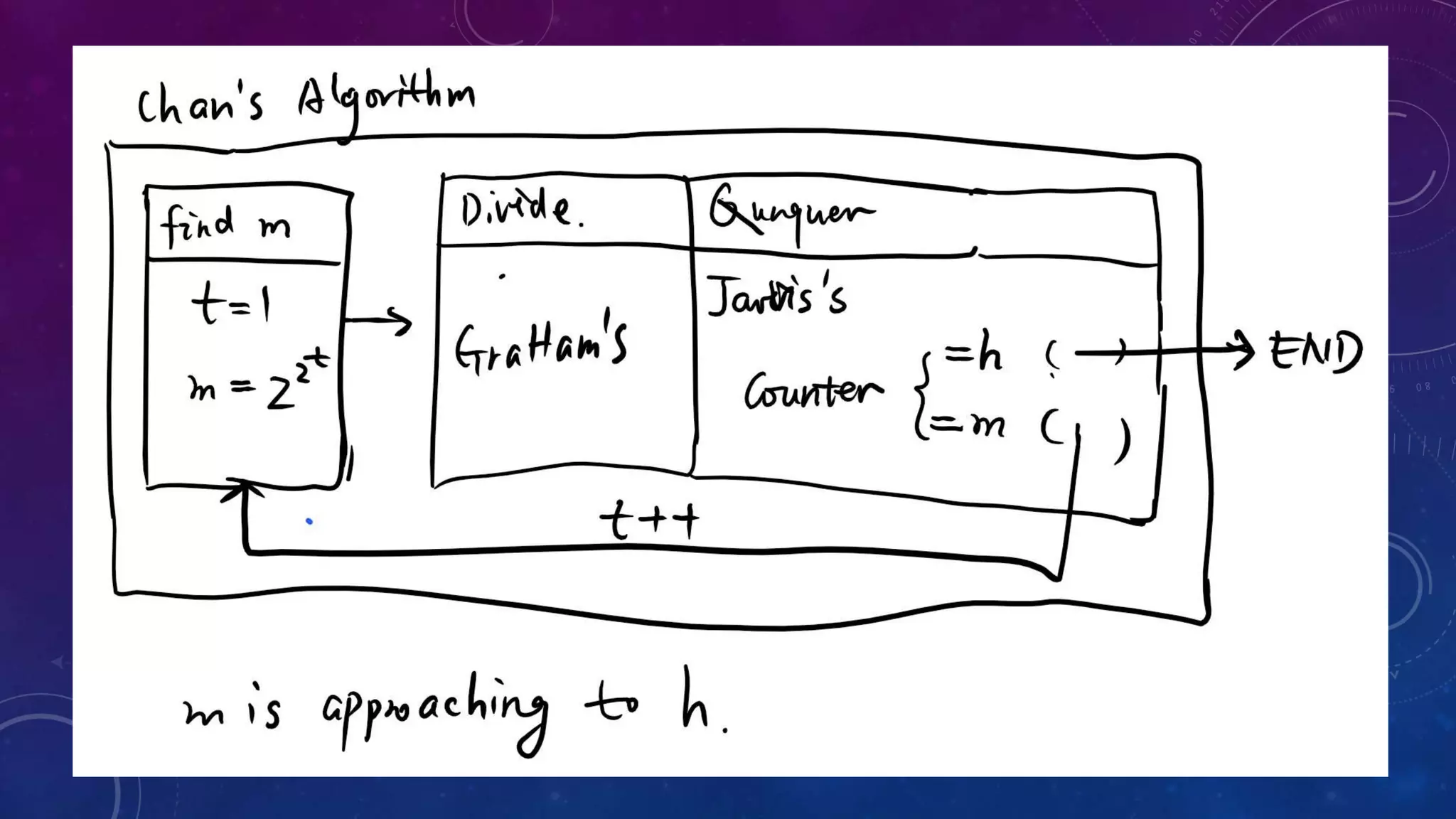
The document discusses the concept of the convex hull, defined as the smallest convex polygon containing a set of points in a plane. It introduces three algorithms for computing convex hulls: Jarvis's algorithm (O(nh)), Graham's algorithm (O(n log n)), and Chan's algorithm (O(n log h)), with Chan's being a combination of the former two and output-sensitive. The summary includes the working principles of each algorithm and emphasizes the importance of determining the optimal value of 'm' in Chan's algorithm.









![REFERENCES • [1]. https://en.wikipedia.org/wiki/Chan%27s_algorithm • [2]. http://tomswitzer.net/2010/12/2d-convex-hulls-chans-algorithm/ • [3]. http://jeffe.cs.illinois.edu/teaching/373/notes/x05-convexhull.pdf • [4]. http://www.utdallas.edu/~daescu/convexhull.pdf • [5]. http://www.geeksforgeeks.org/convex-hull-set-1-jarviss-algorithm-or-wrapping/ • [6]. http://www.geeksforgeeks.org/convex-hull-set-2-graham-scan/ 17](https://image.slidesharecdn.com/convexhull-presentation-160423214058/75/Convex-Hull-Chan-s-Algorithm-O-n-log-h-Presentation-by-Yitian-Huang-and-Zhe-Yang-17-2048.jpg)
