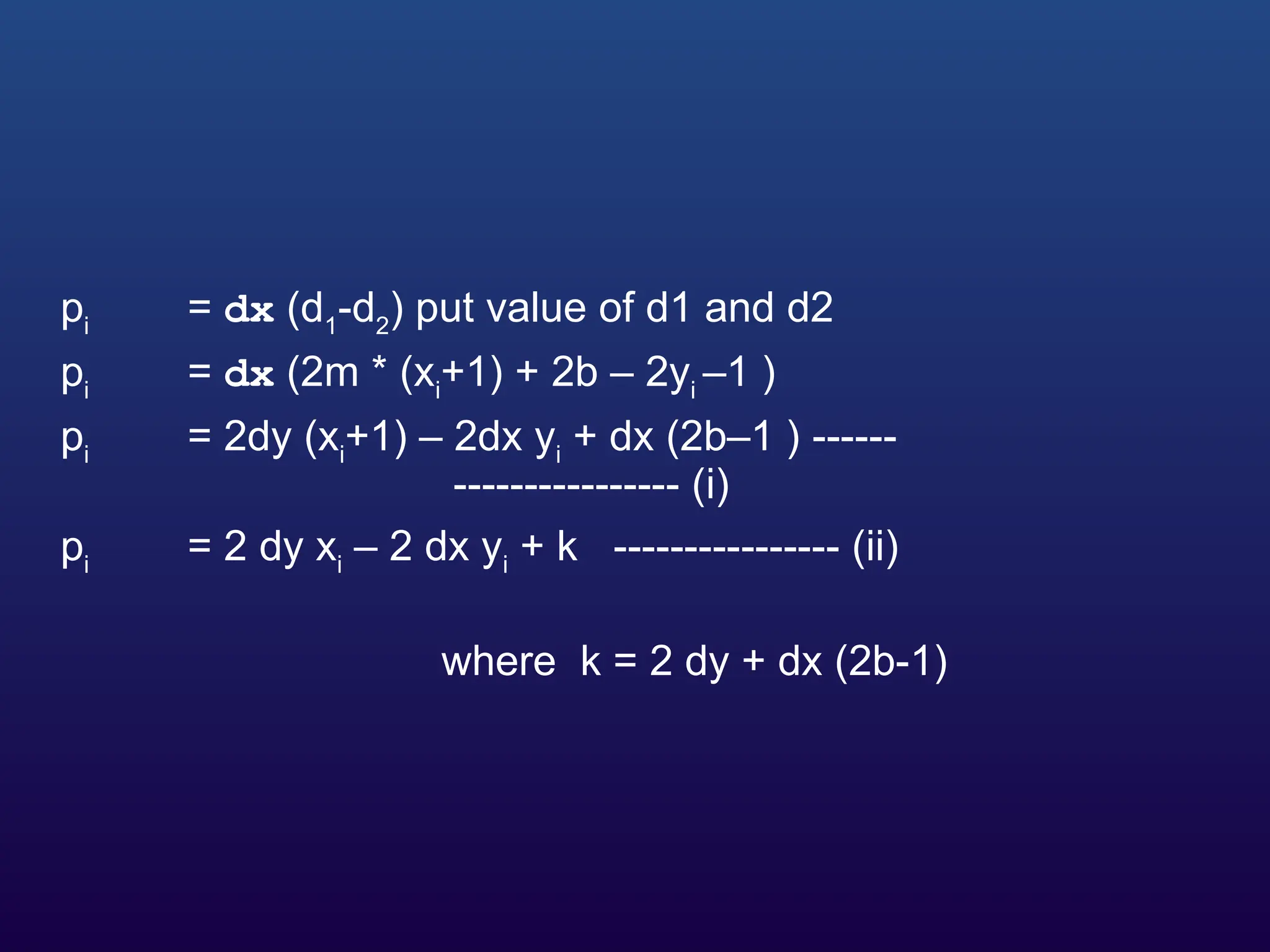The document discusses line drawing techniques in computer graphics, highlighting concepts such as the definition of points and lines, as well as three algorithms for drawing lines: the incremental line algorithm, the DDA algorithm, and Bresenham's algorithm. It details the mathematical foundations for each method, focusing on their efficiency and implementation in pixel representation. Additionally, the document describes performance improvements and alternative approaches to optimize the algorithms for graphic systems.