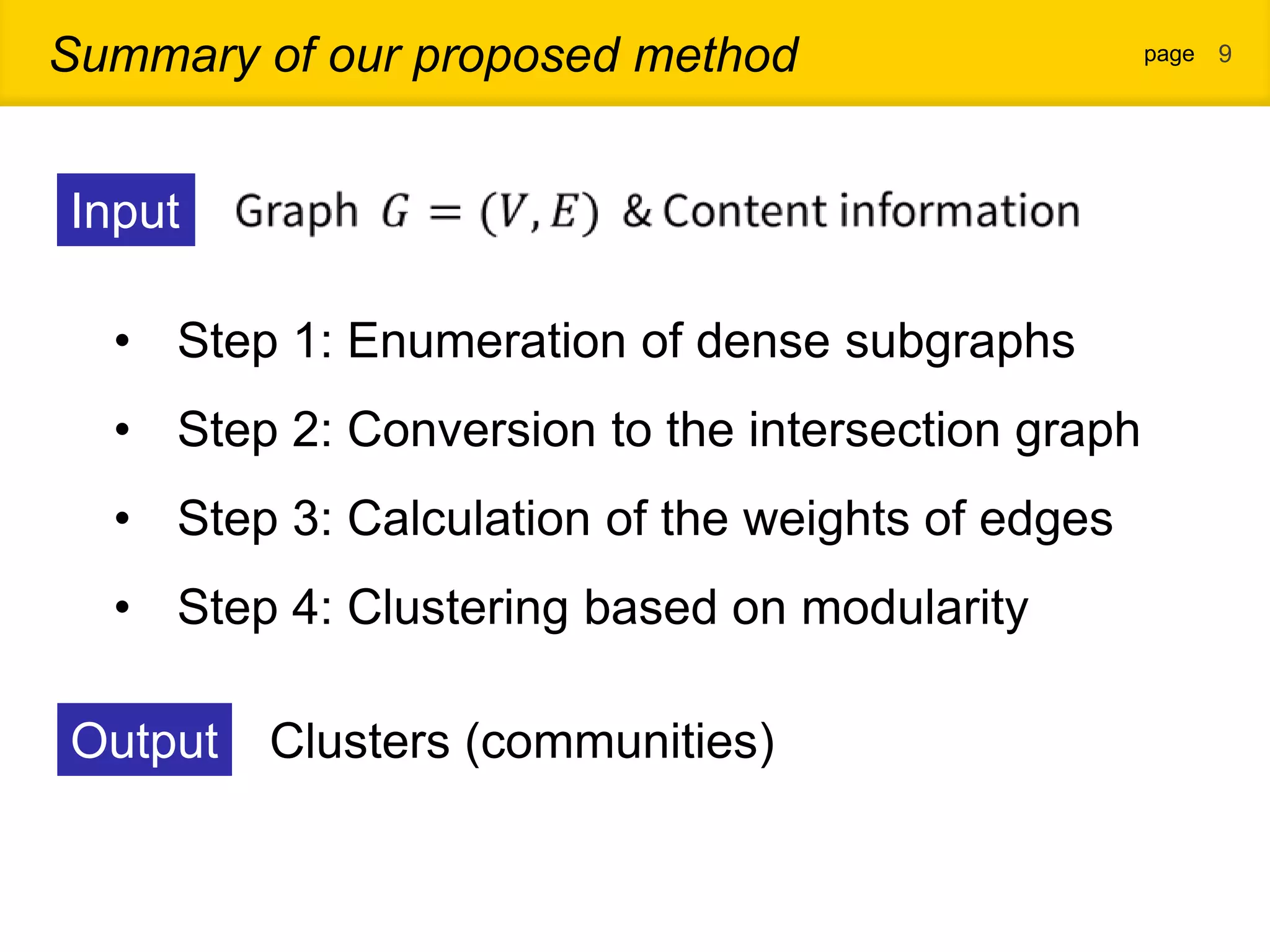
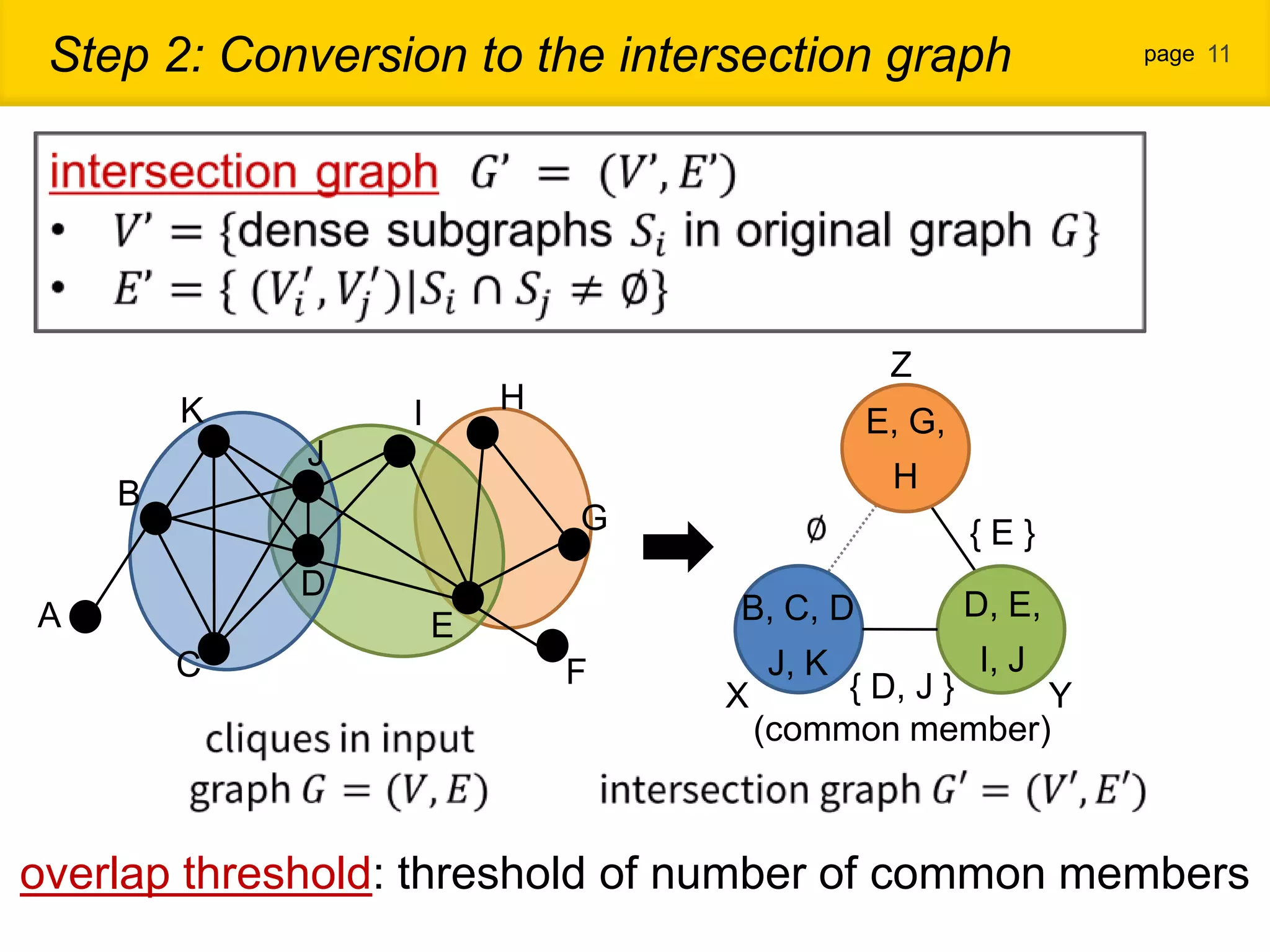
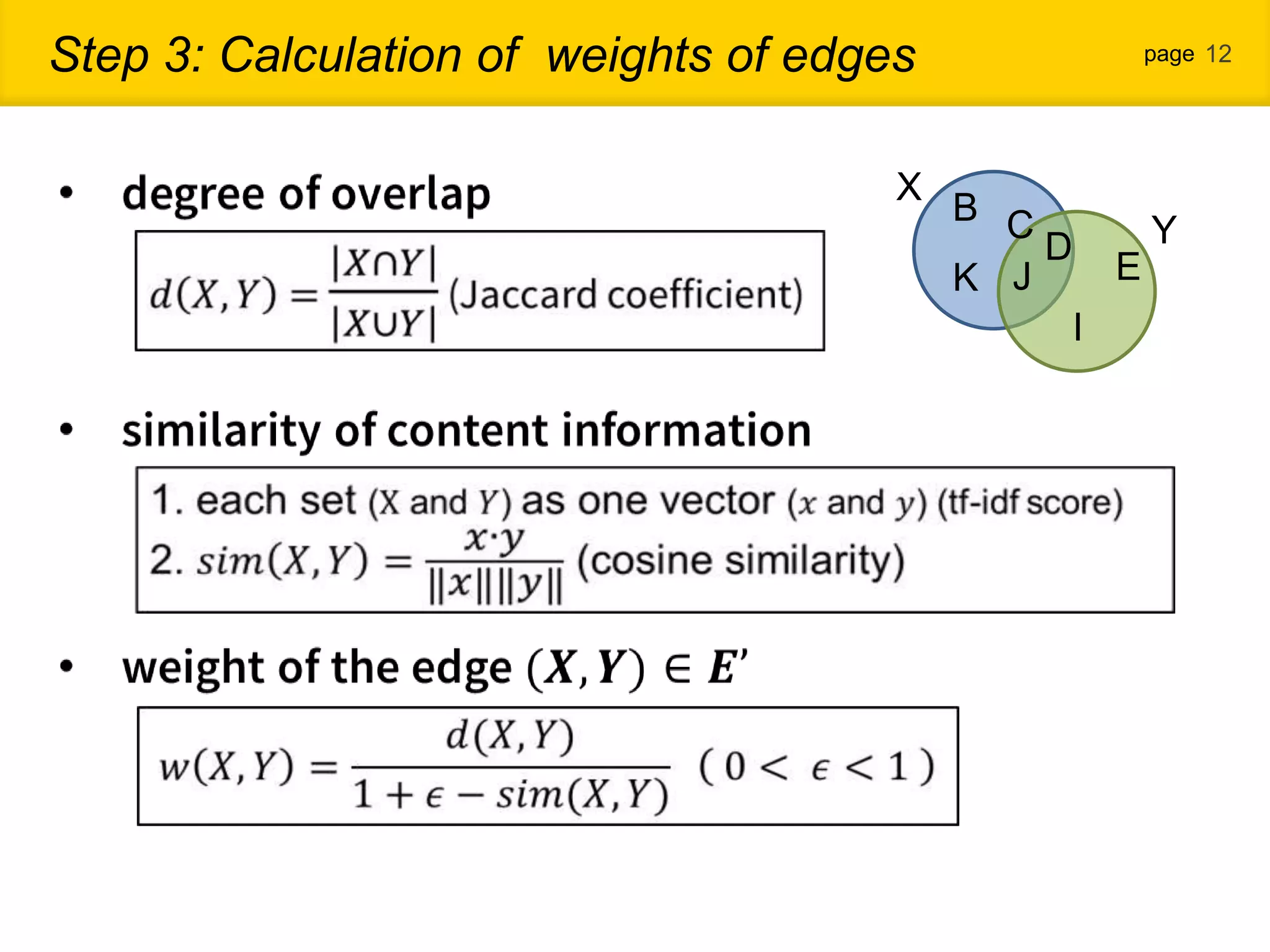
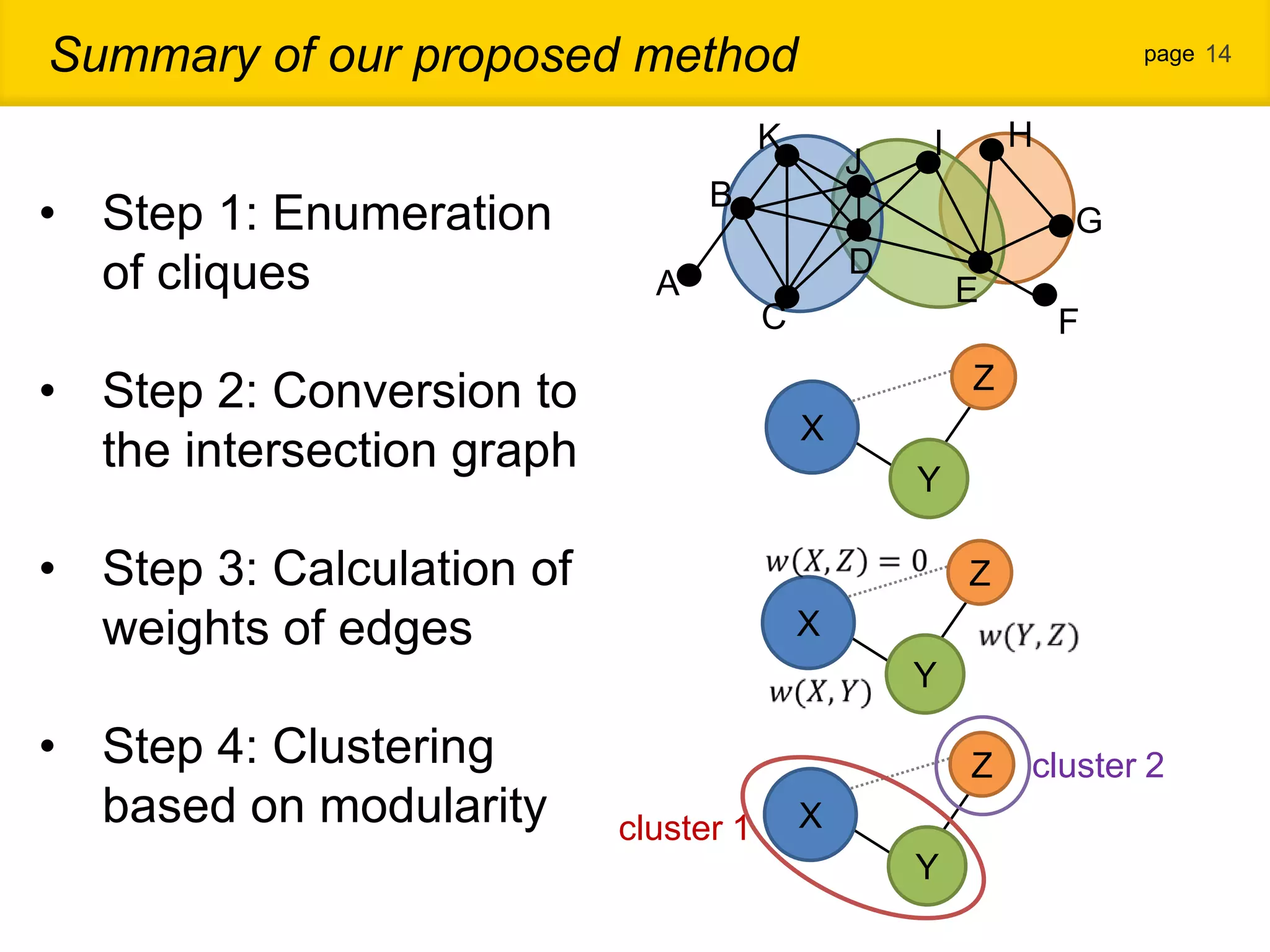
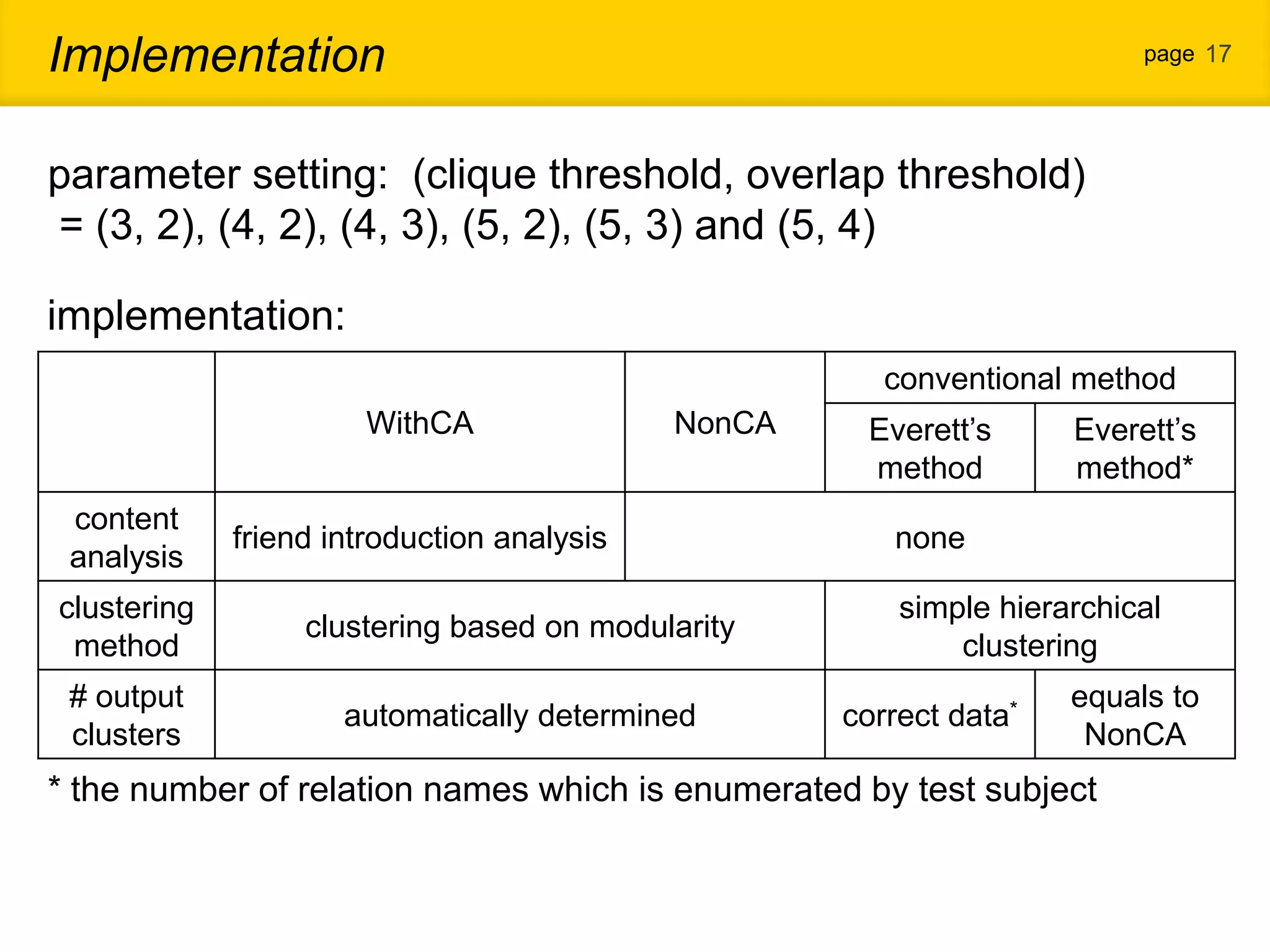
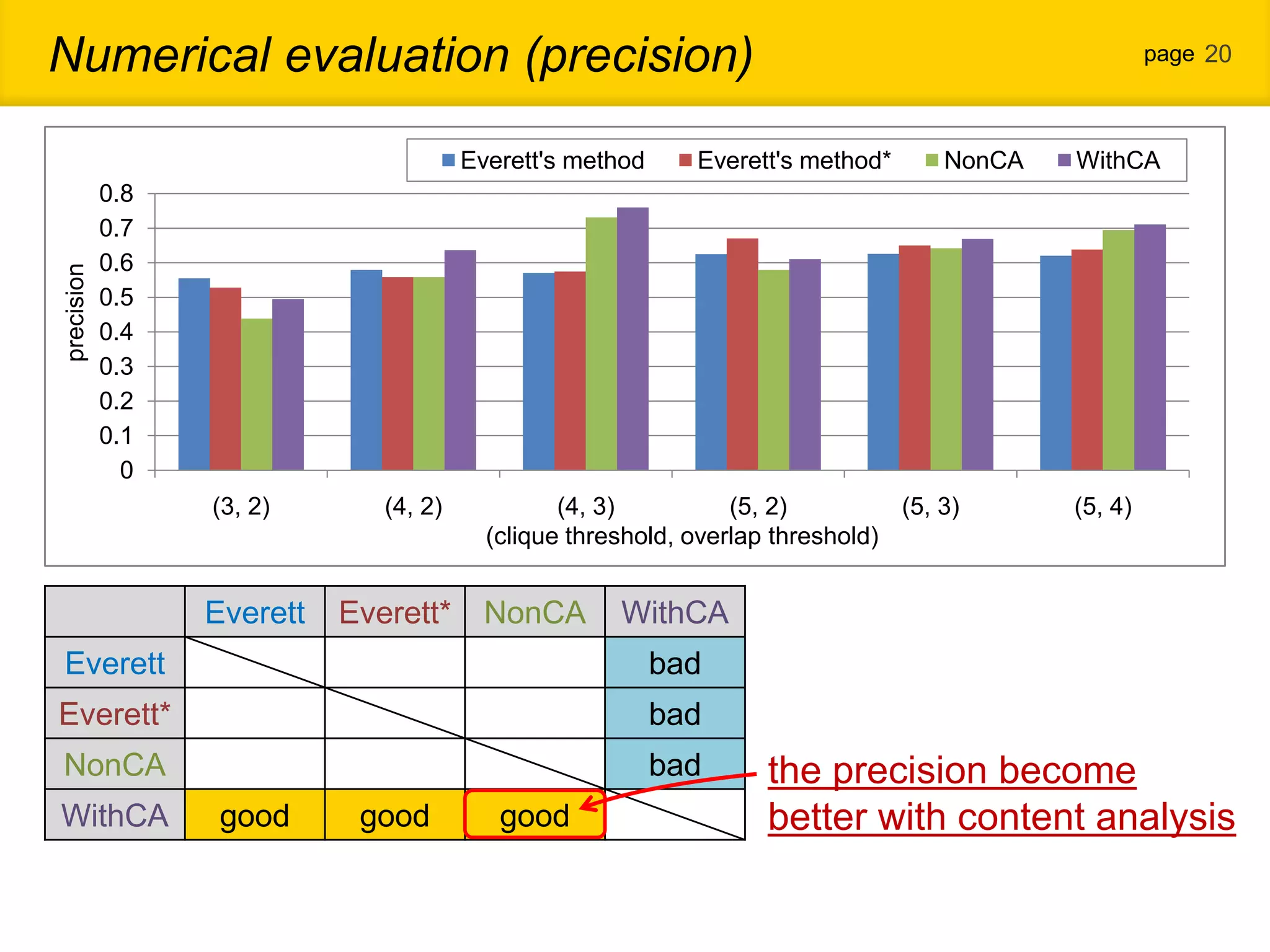
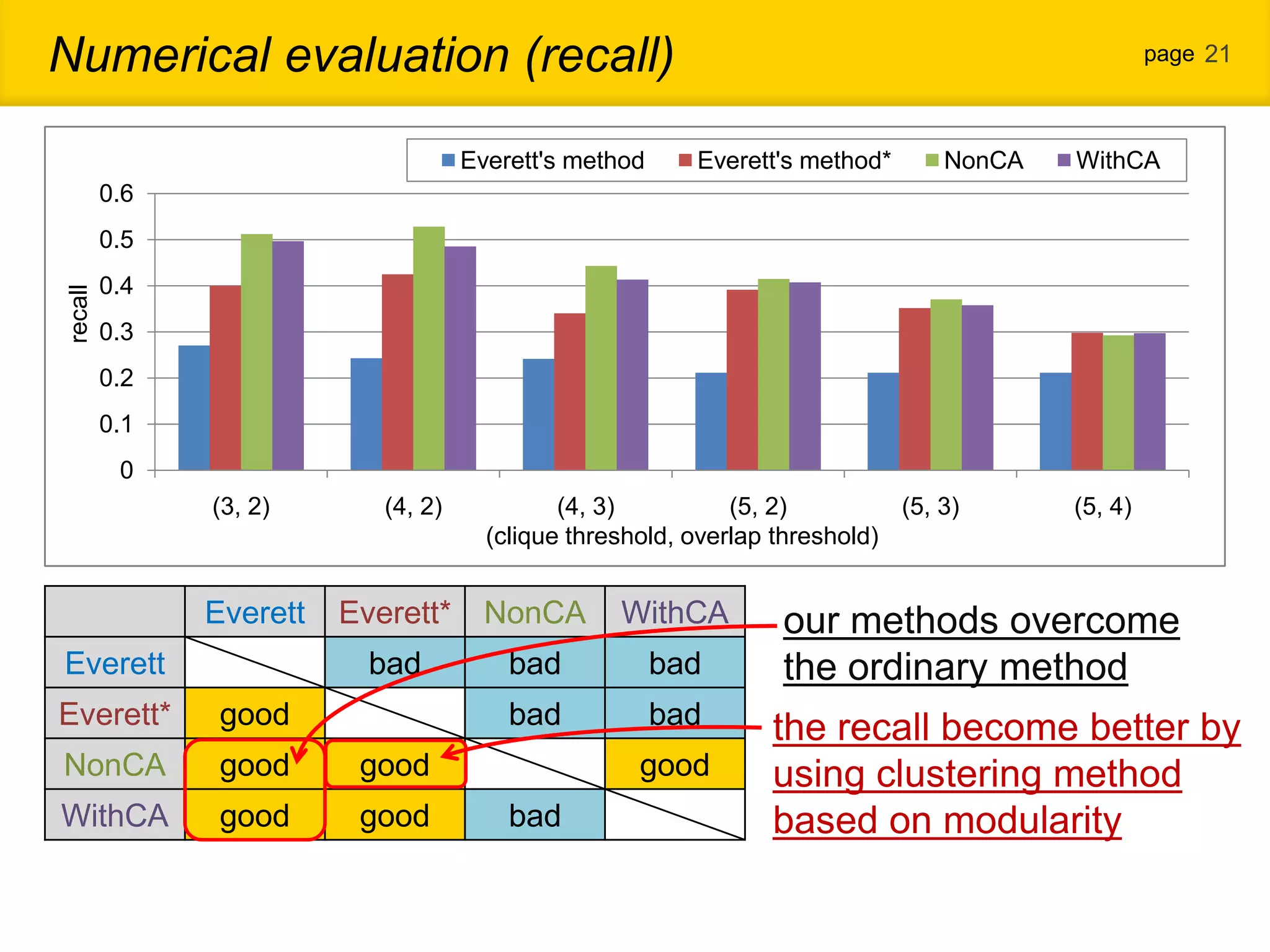
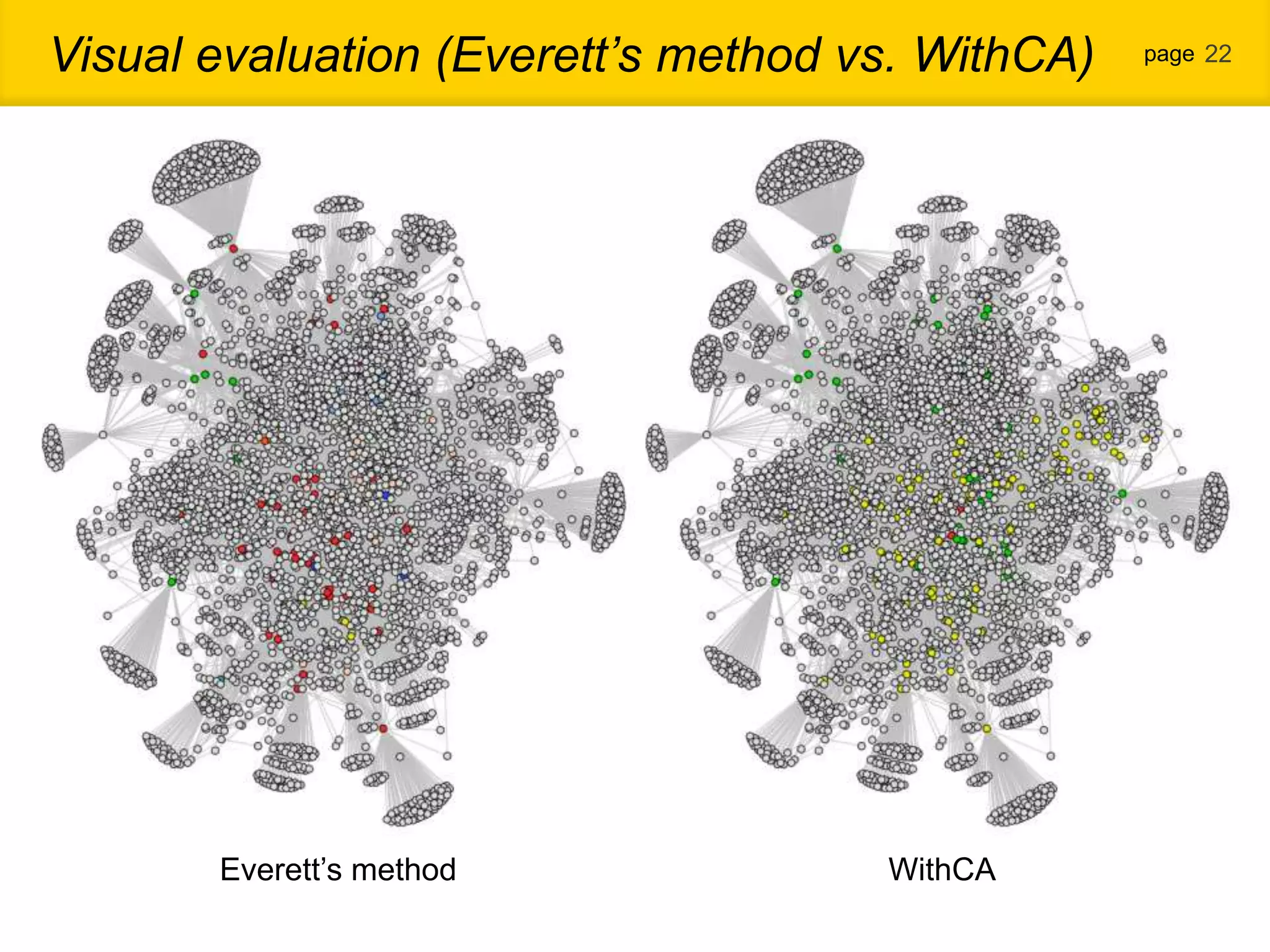
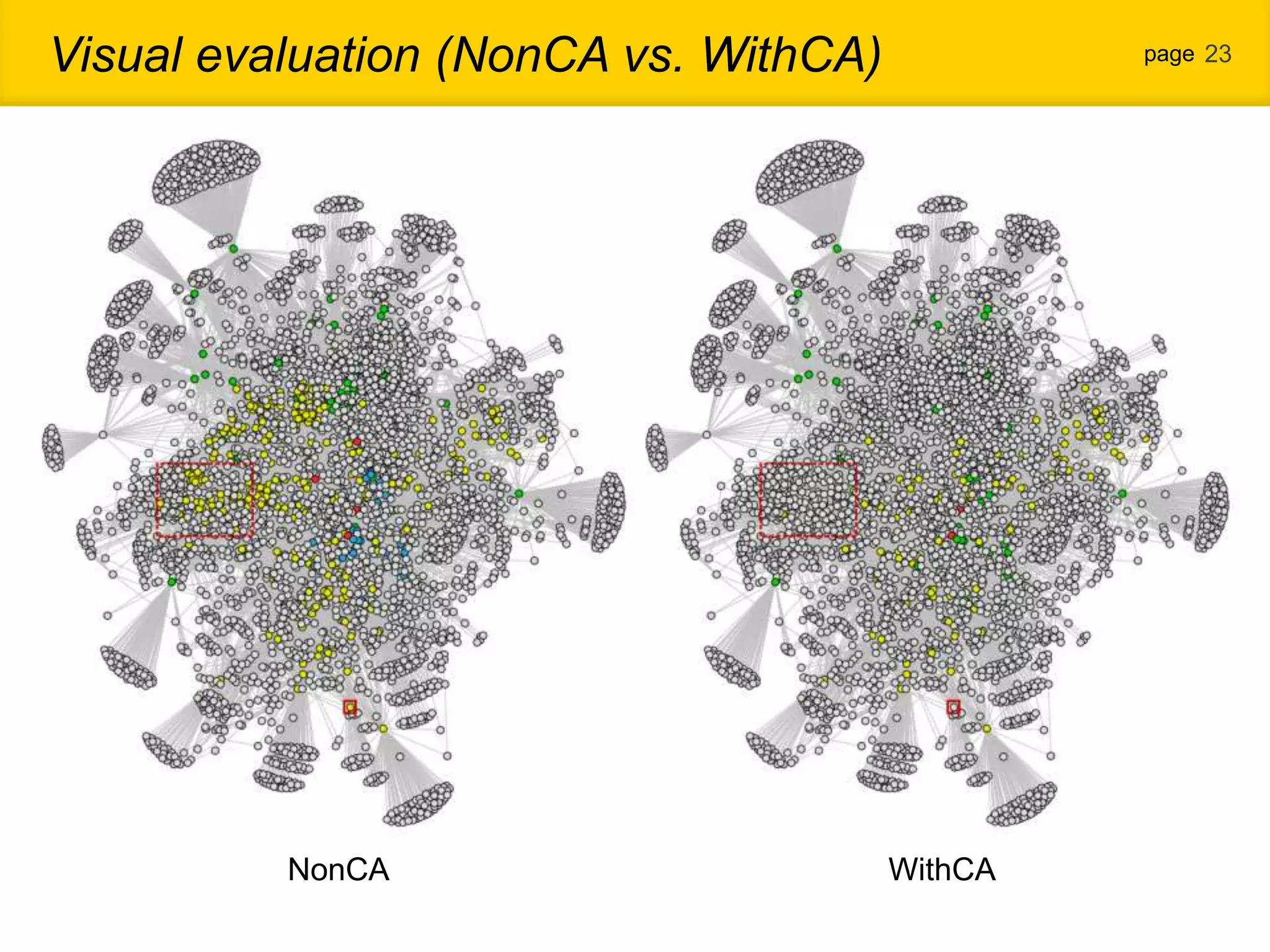
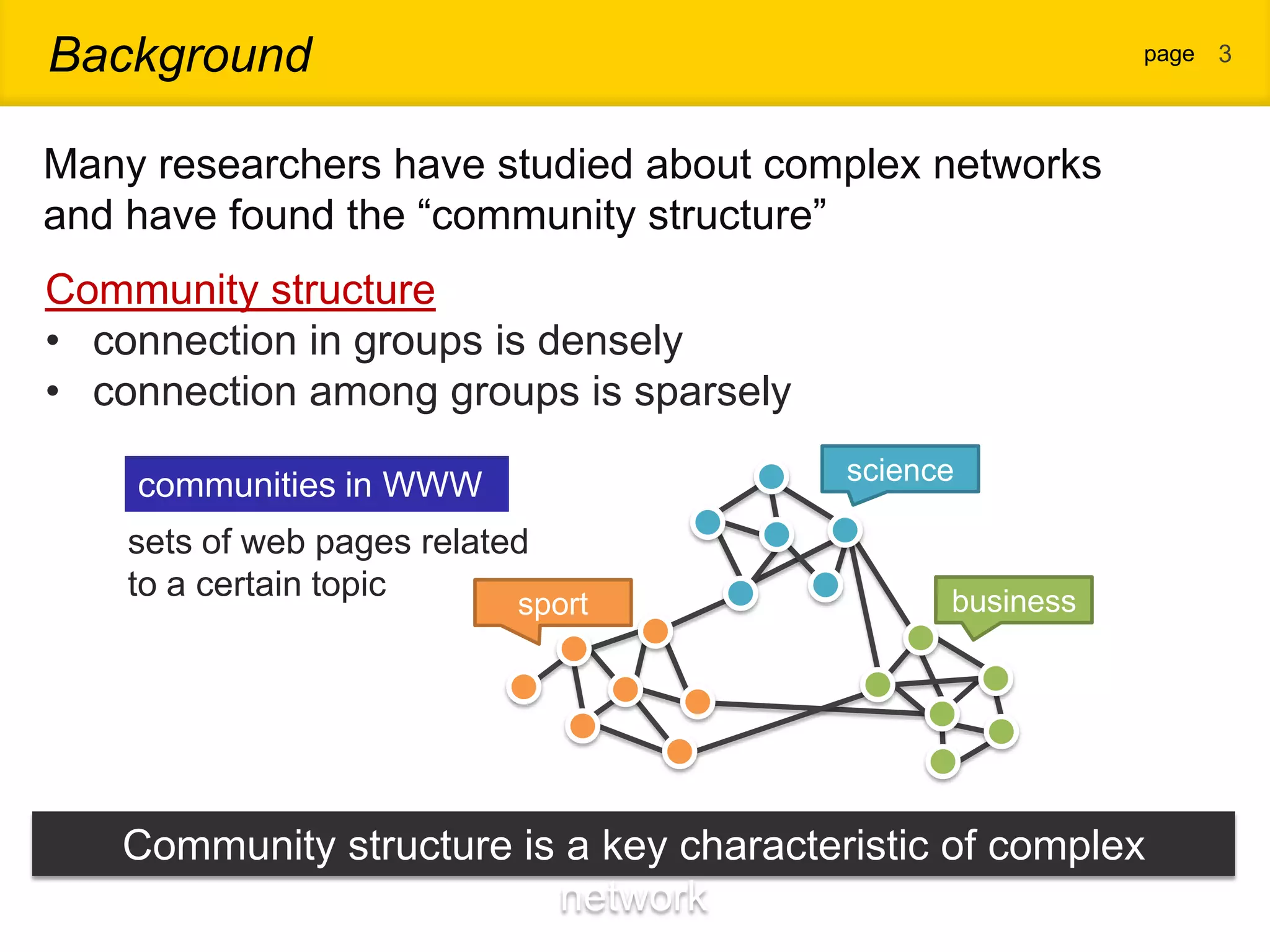
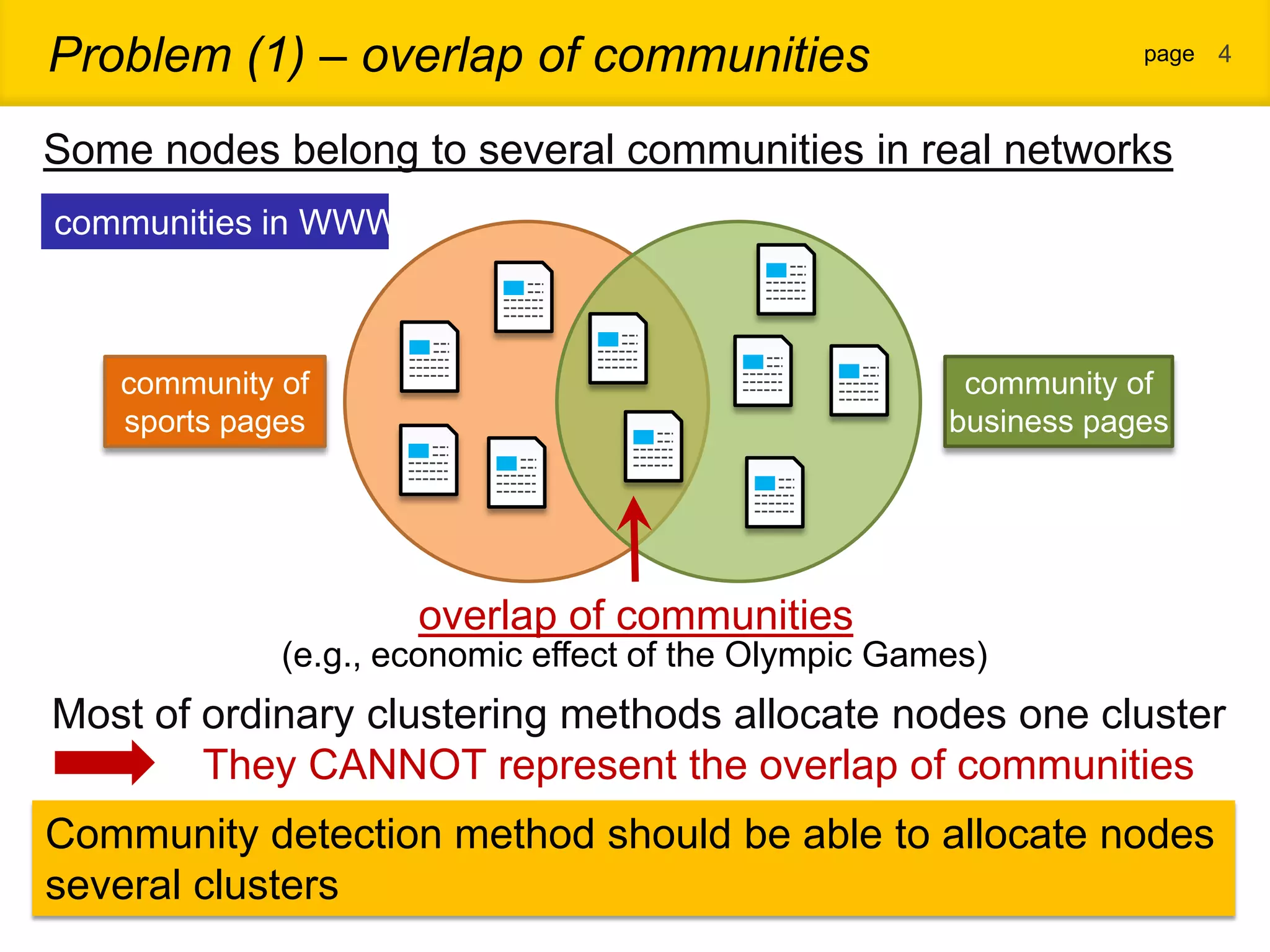
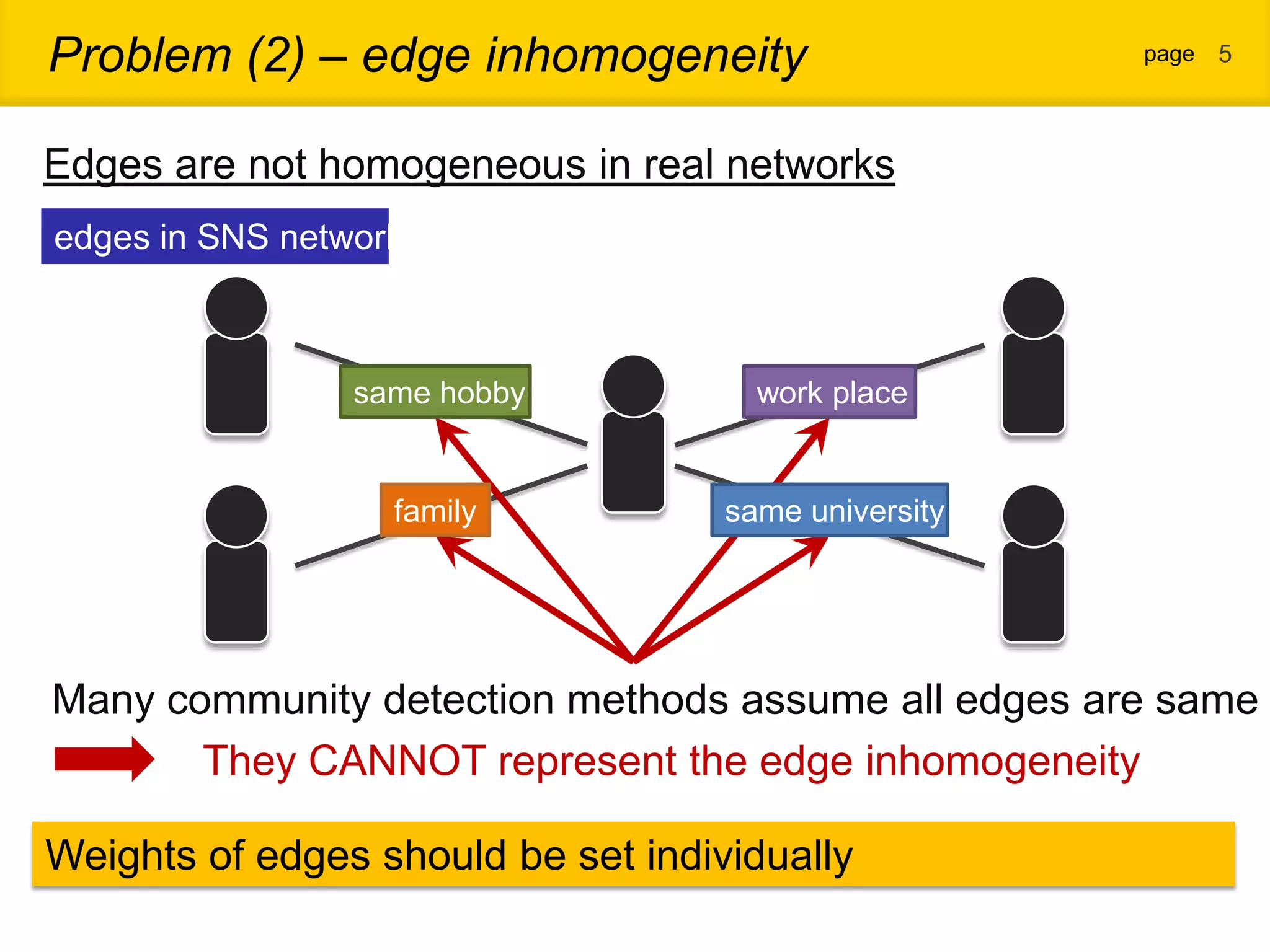
1. The document proposes a new community detection method for complex networks that addresses problems with existing methods, such as inability to represent overlapping communities or edge inhomogeneity. 2. The proposed method involves enumerating dense subgraphs, converting to an intersection graph, calculating edge weights using content analysis, and clustering based on modularity to automatically determine the optimal number of communities. 3. An evaluation on a real social network dataset found the proposed method outperformed conventional methods in recall, precision and F-measure.



![Purpose of this work page 7 We solve these three problems by proposing a new community detection method • A node may belong to several communities Using the idea of intersection graph [Everett & Borgatti, 1998] • Weights of edges are set individually Content information analysis • Number of communities are automatically determined Clustering based on modularity [Newman, 2003]](https://image.slidesharecdn.com/wi20124ss-130116213130-phpapp02/75/Community-Extracting-Using-Intersection-Graph-and-Content-Analysis-in-Complex-Network-7-2048.jpg)