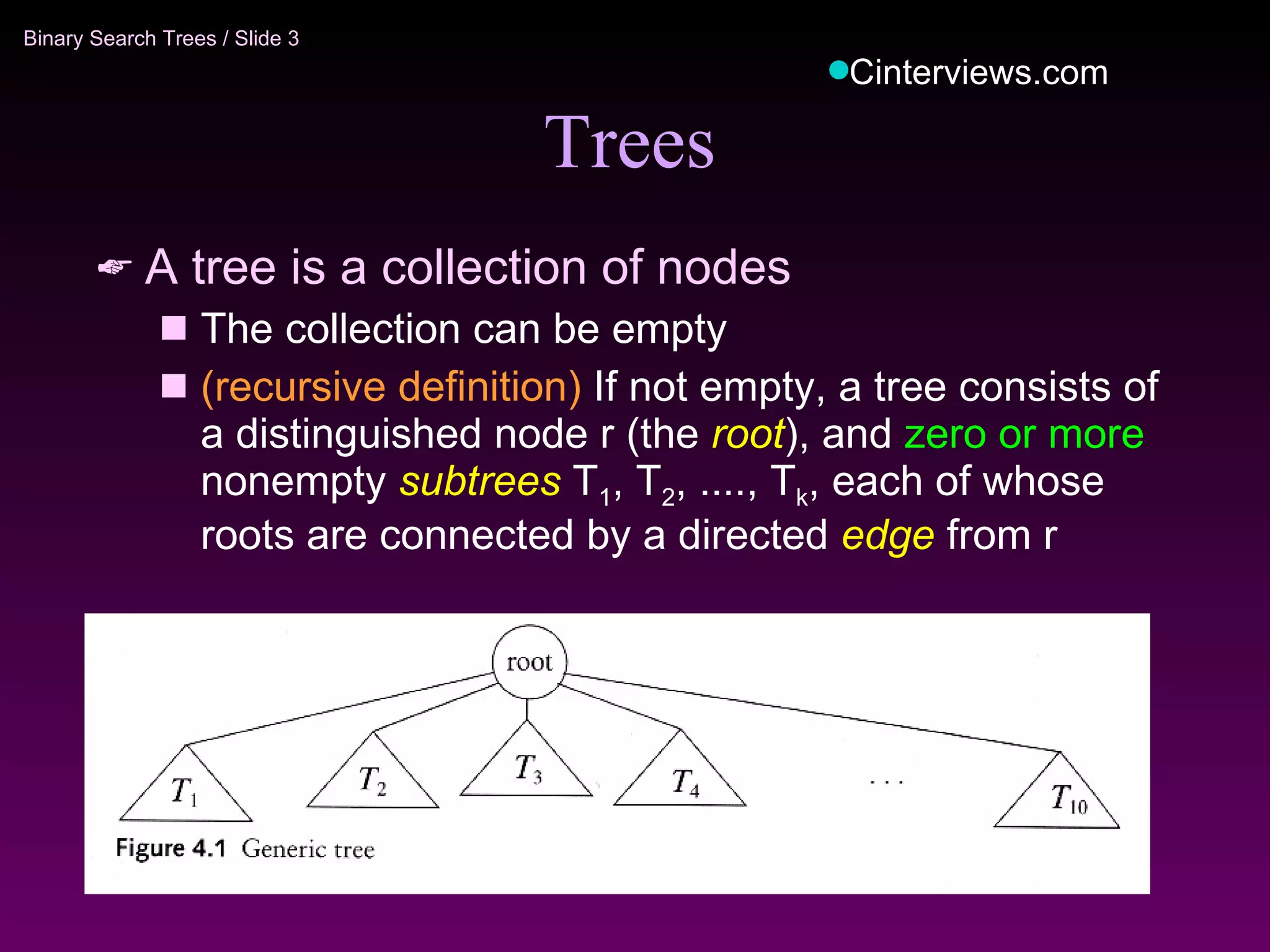
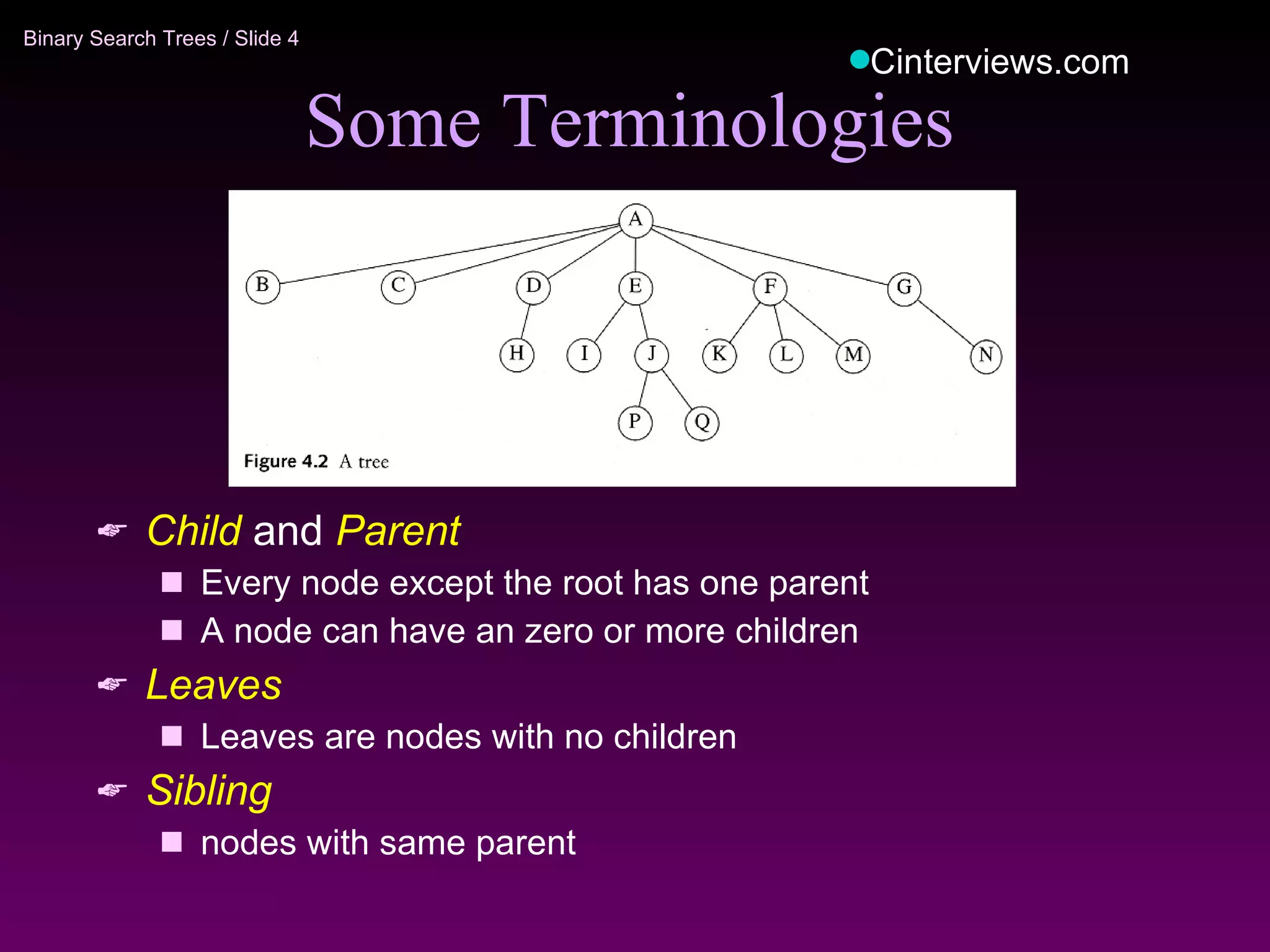
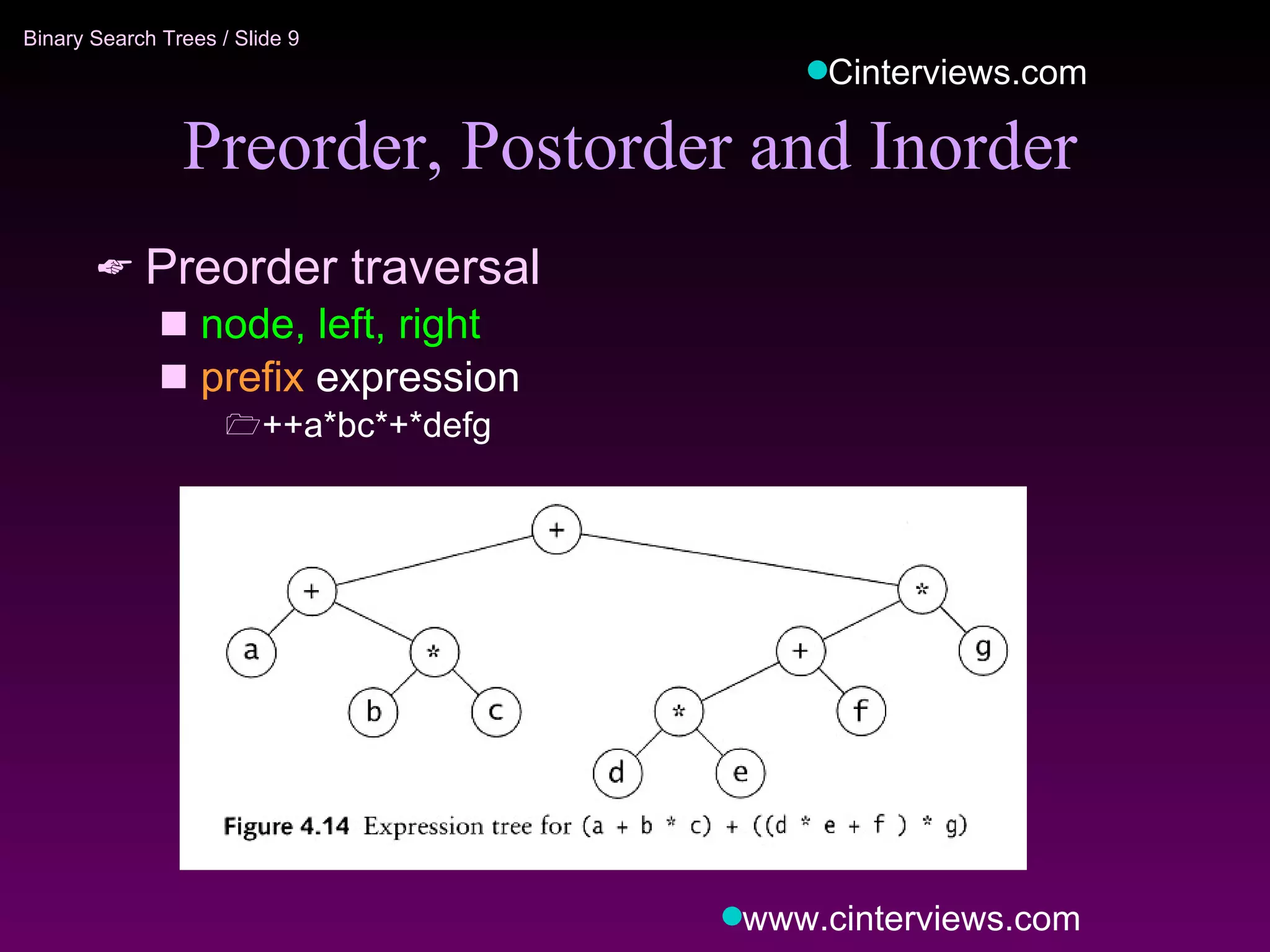
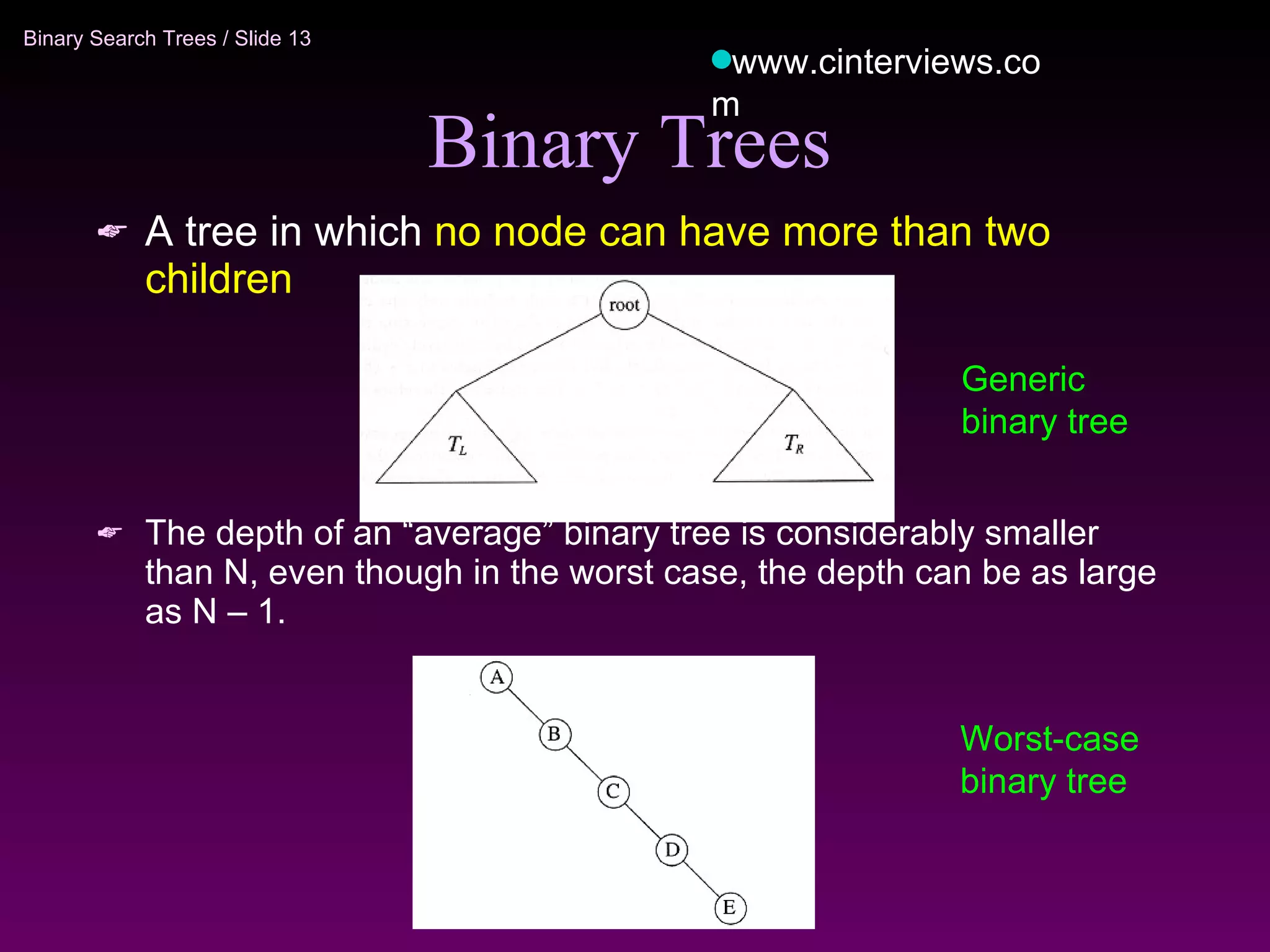
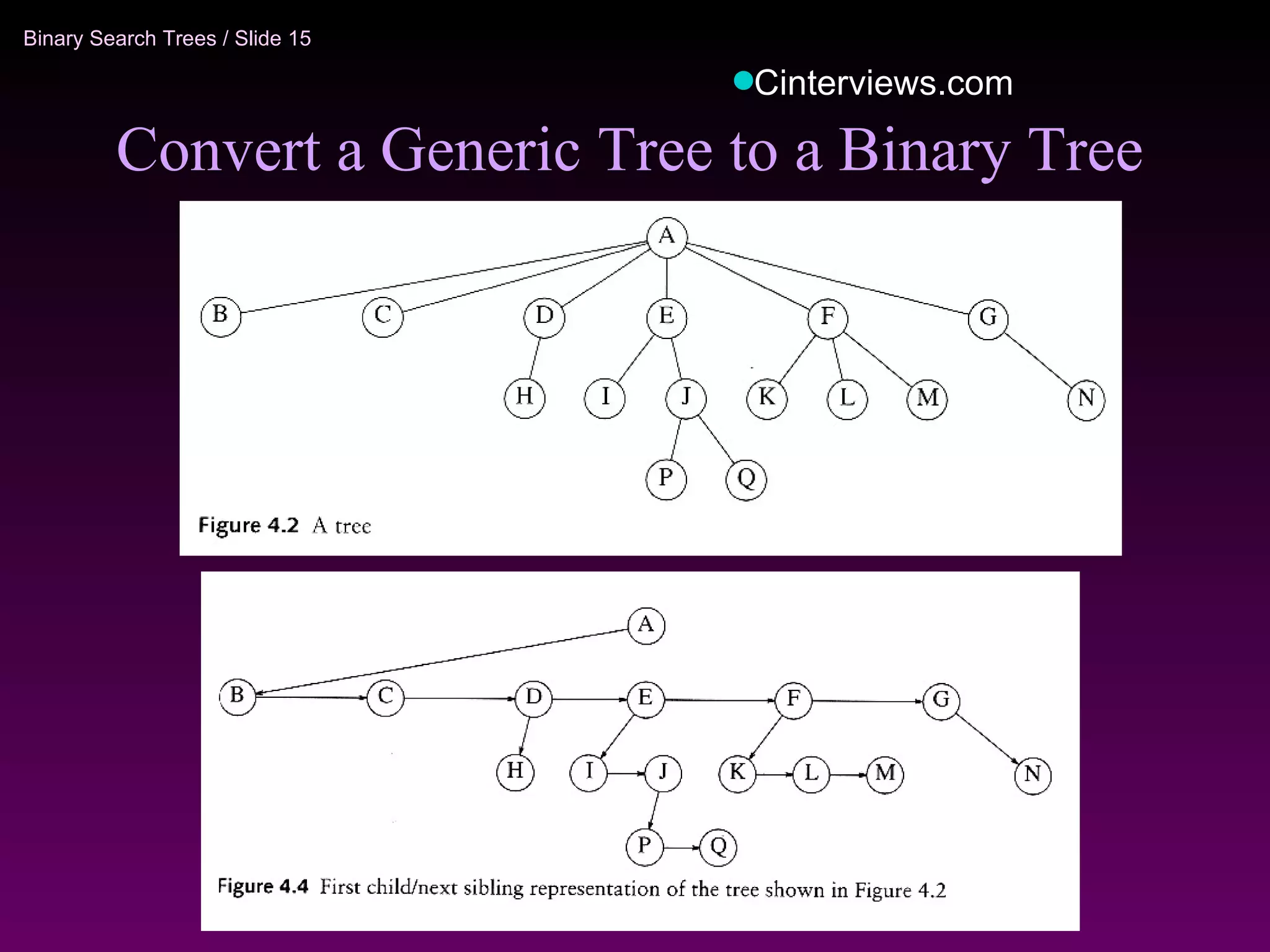
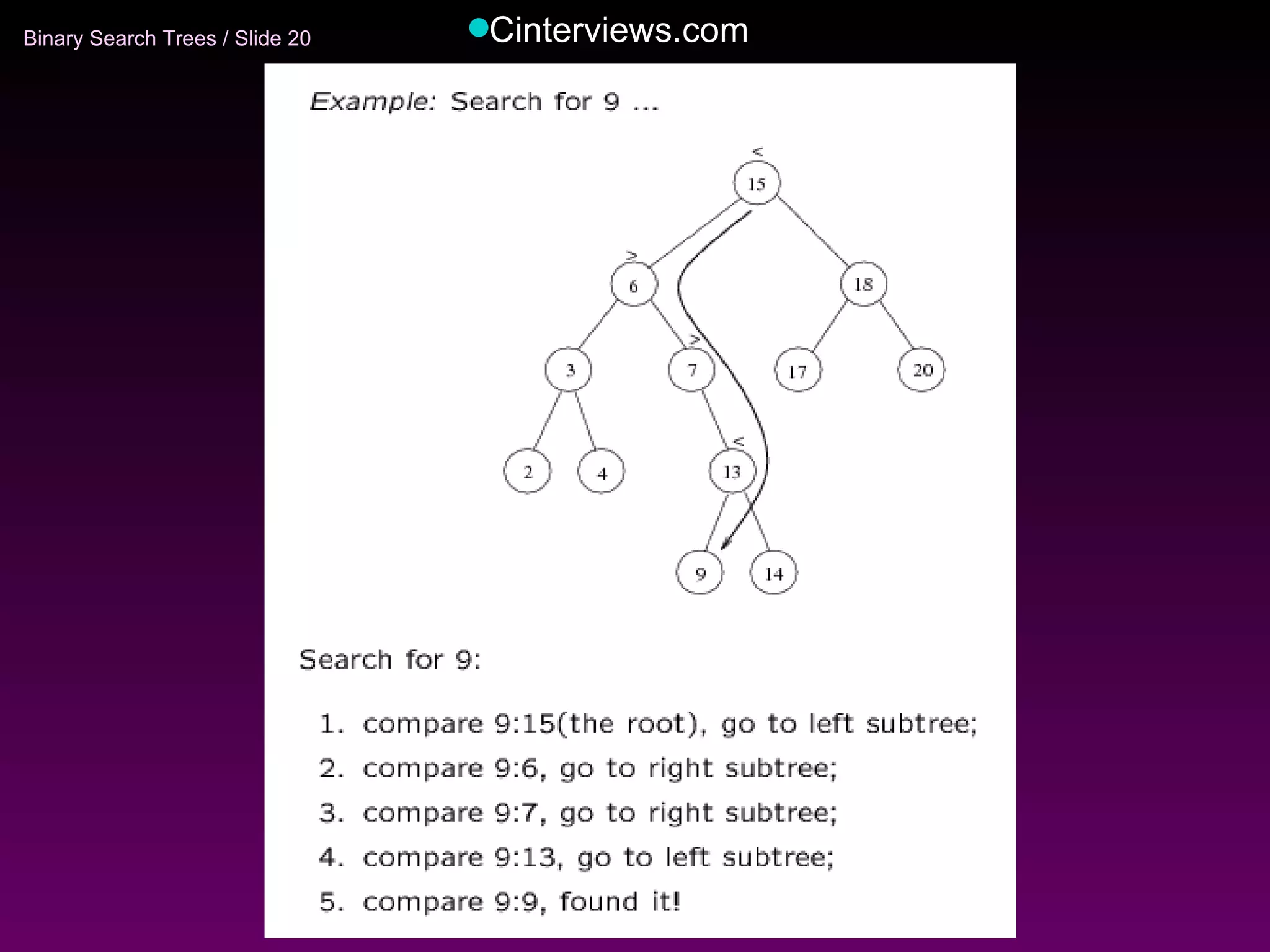
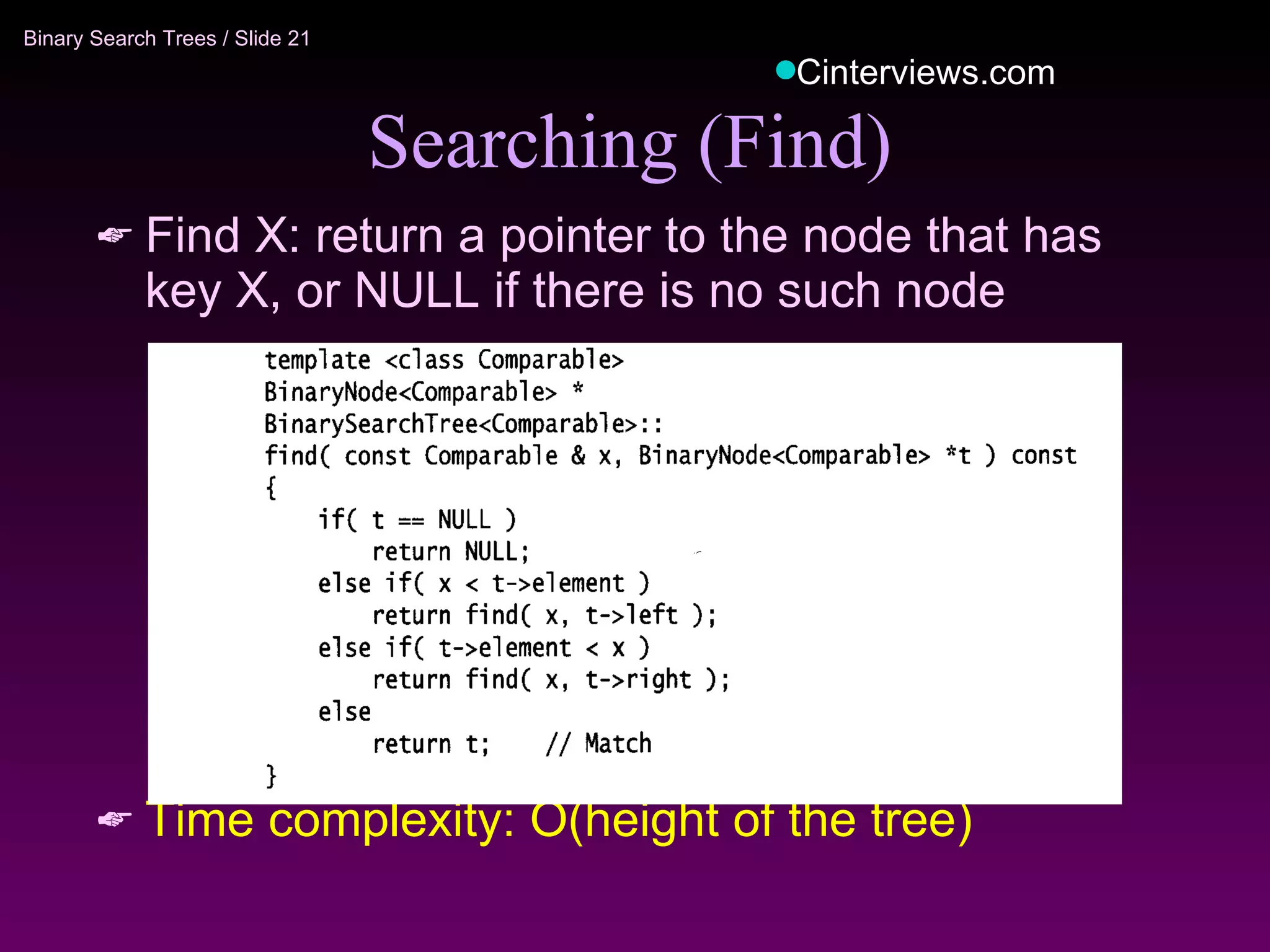
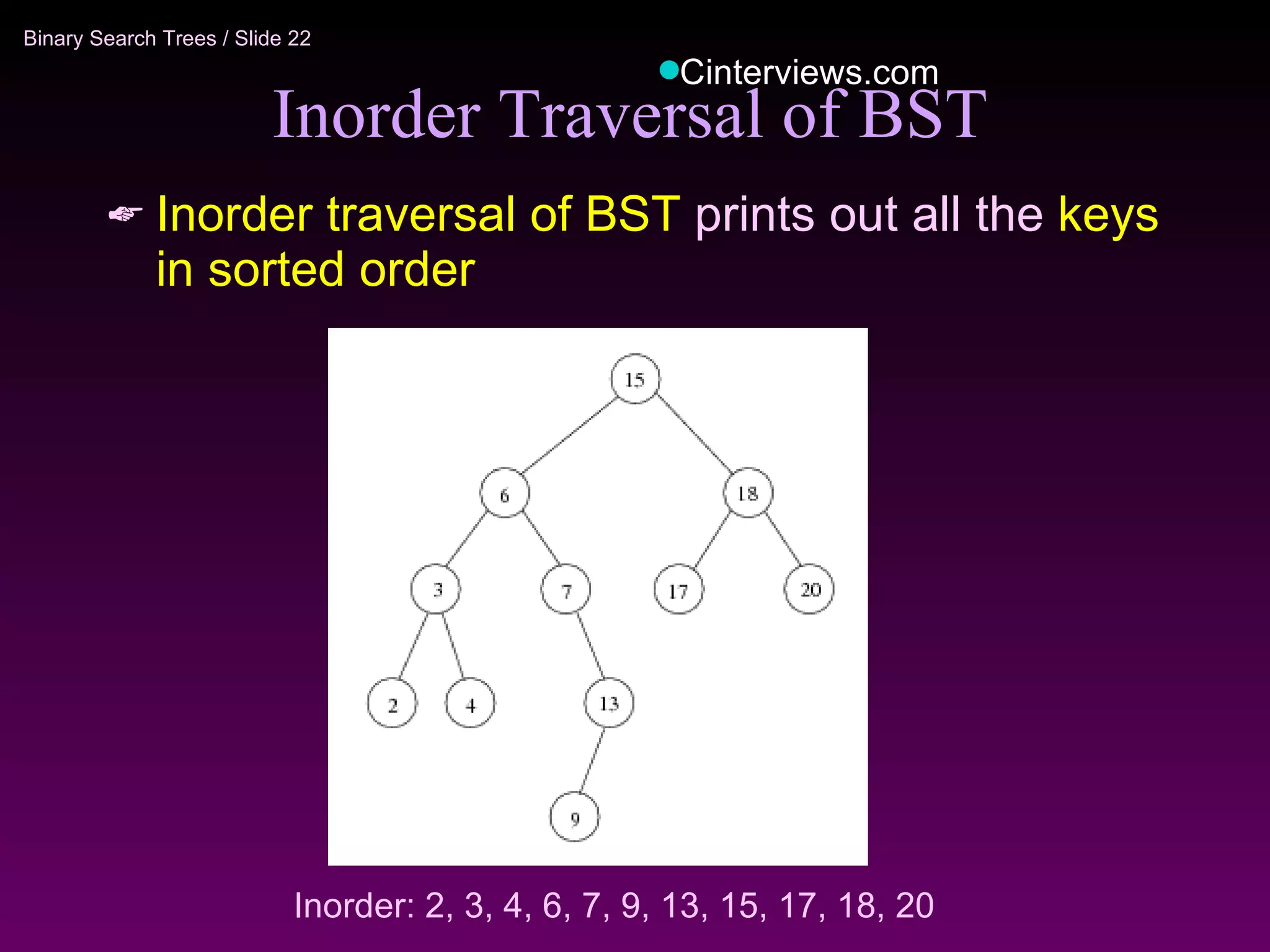
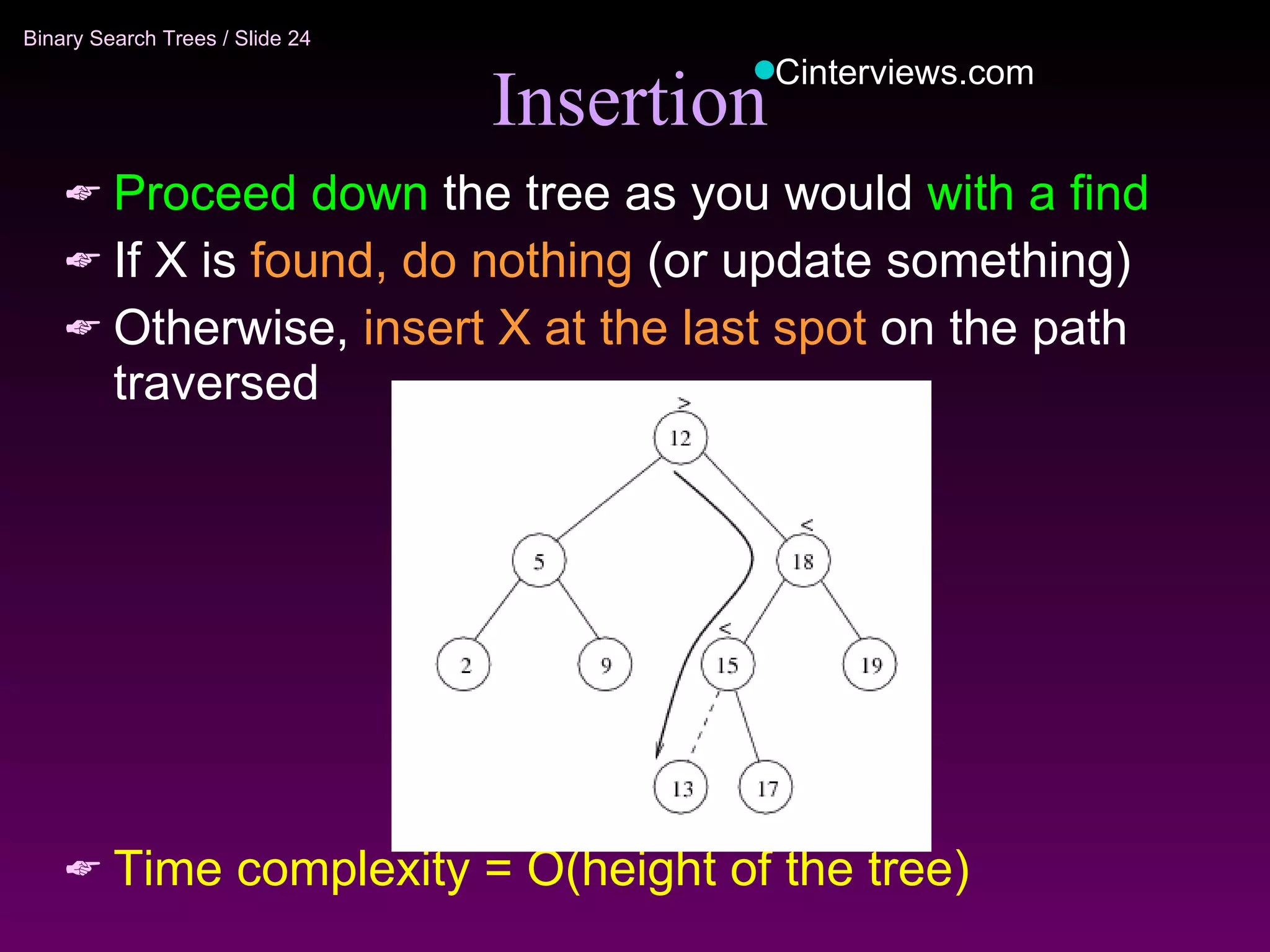
The document discusses binary trees and binary search trees. It defines key concepts like nodes, children, parents, leaves, height, and tree traversal. It explains that binary search trees allow searching, insertion, and deletion in O(log N) time by enforcing the property that all left descendants of a node are less than the node and all right descendants are greater. The operations of searching, insertion, deletion and their time complexities are outlined for binary search trees.