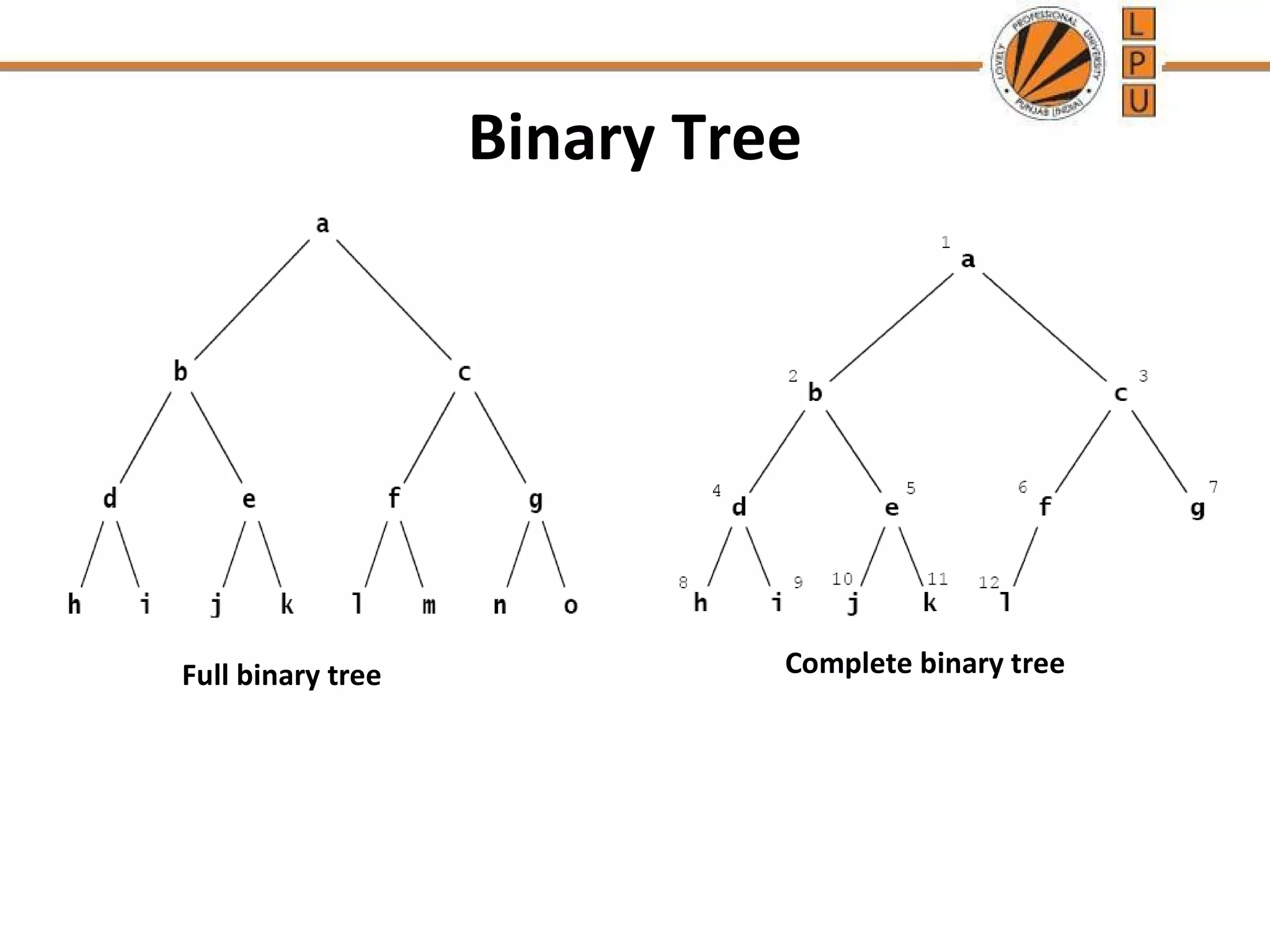
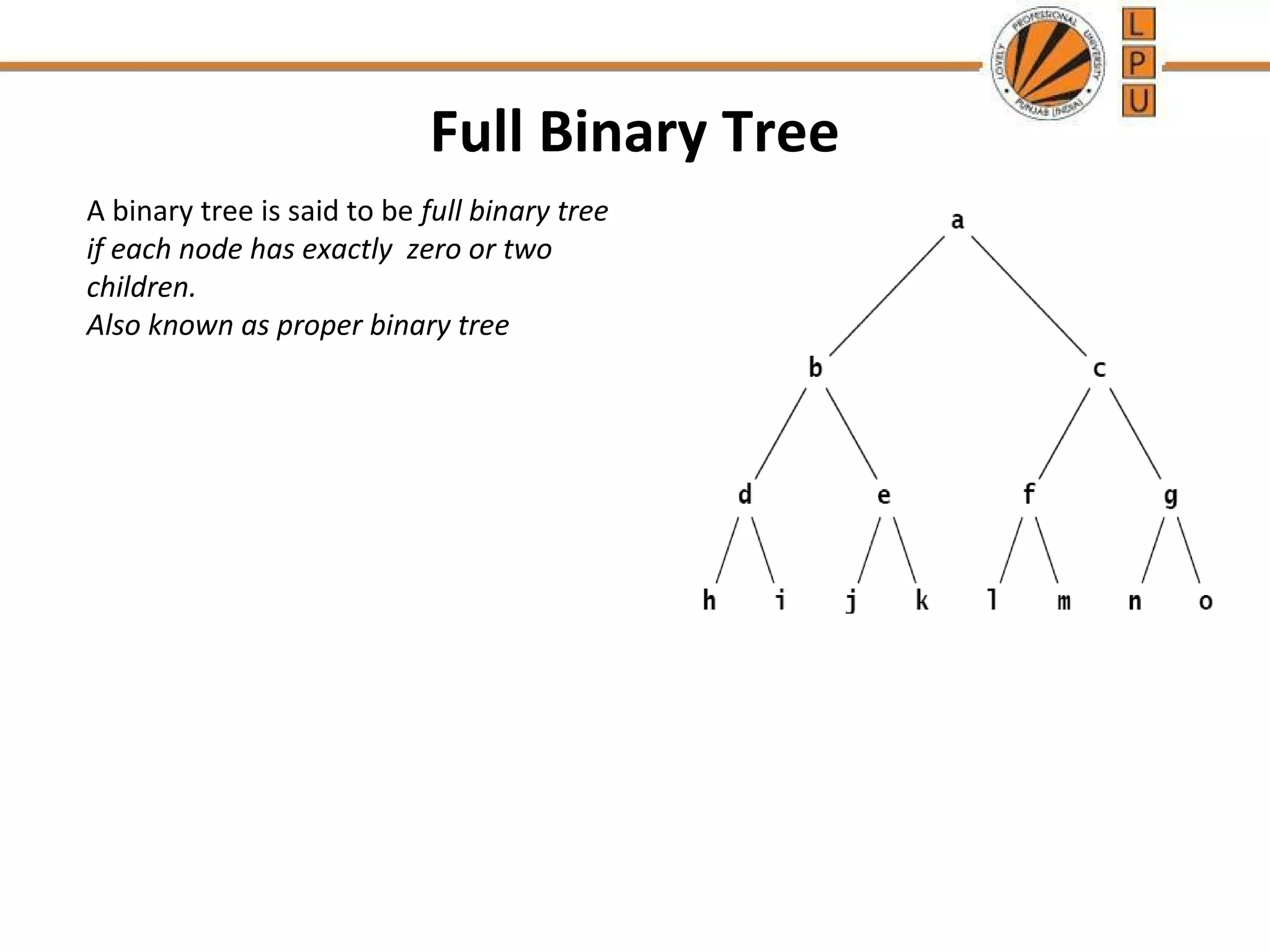
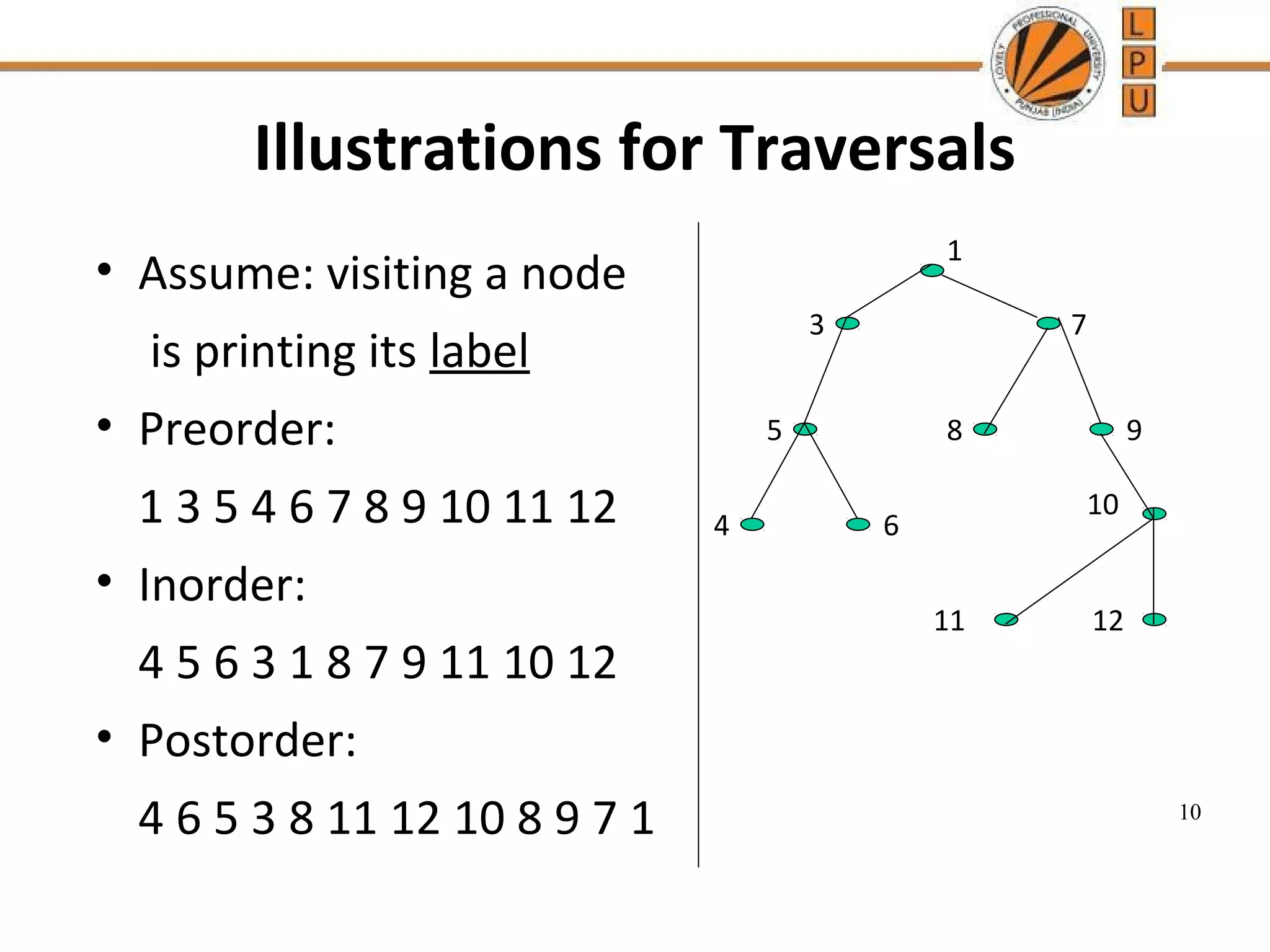
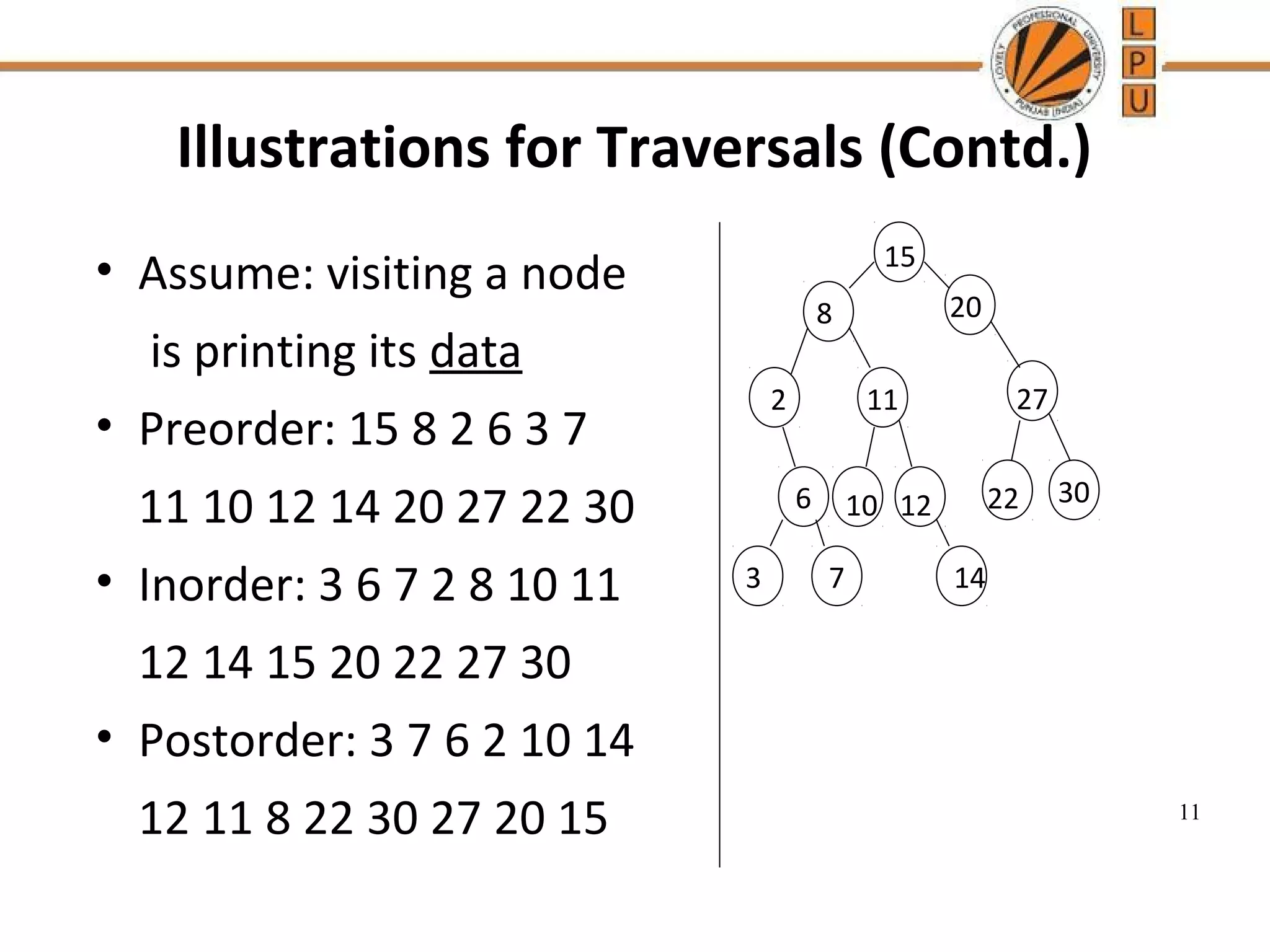
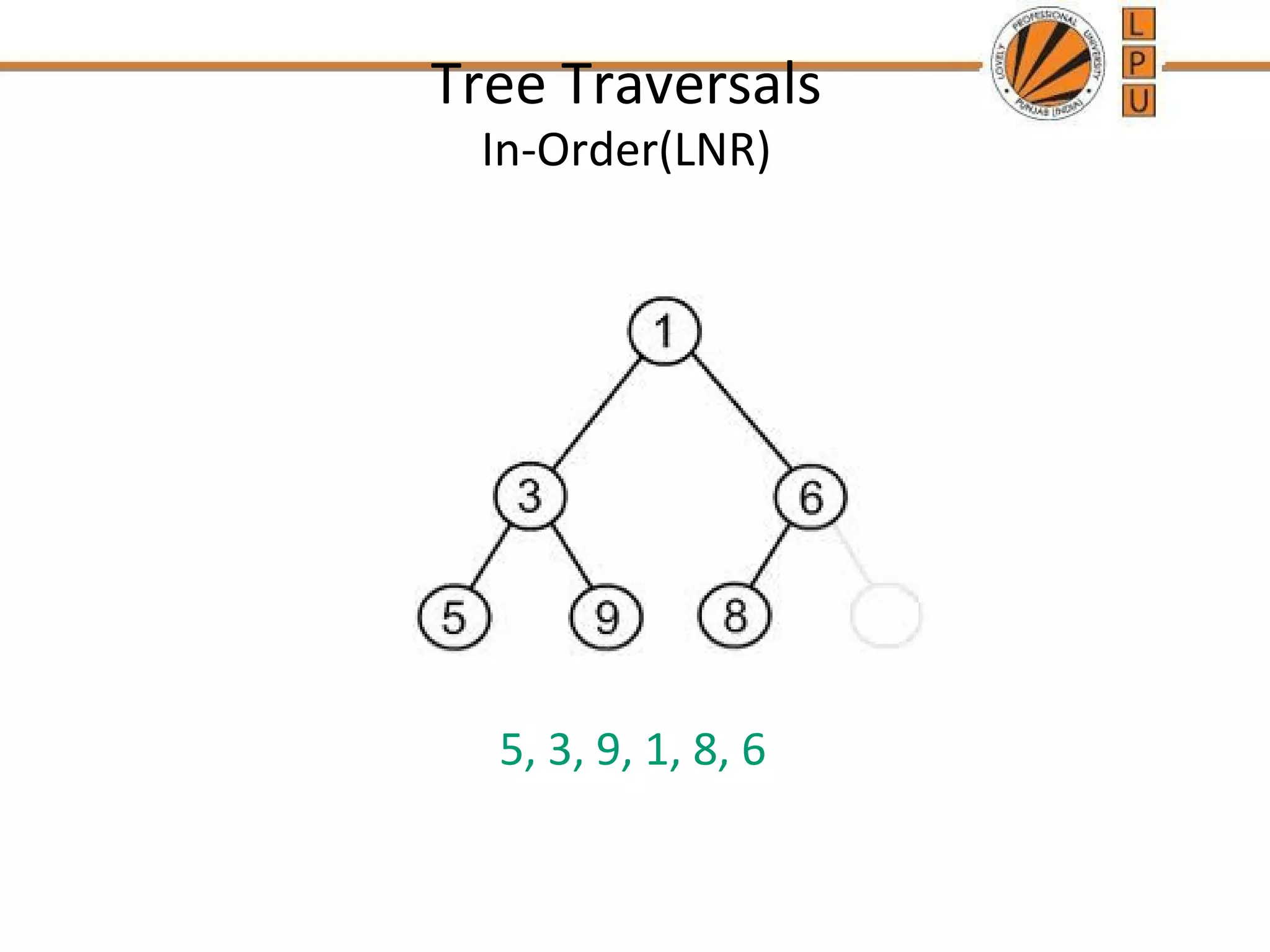
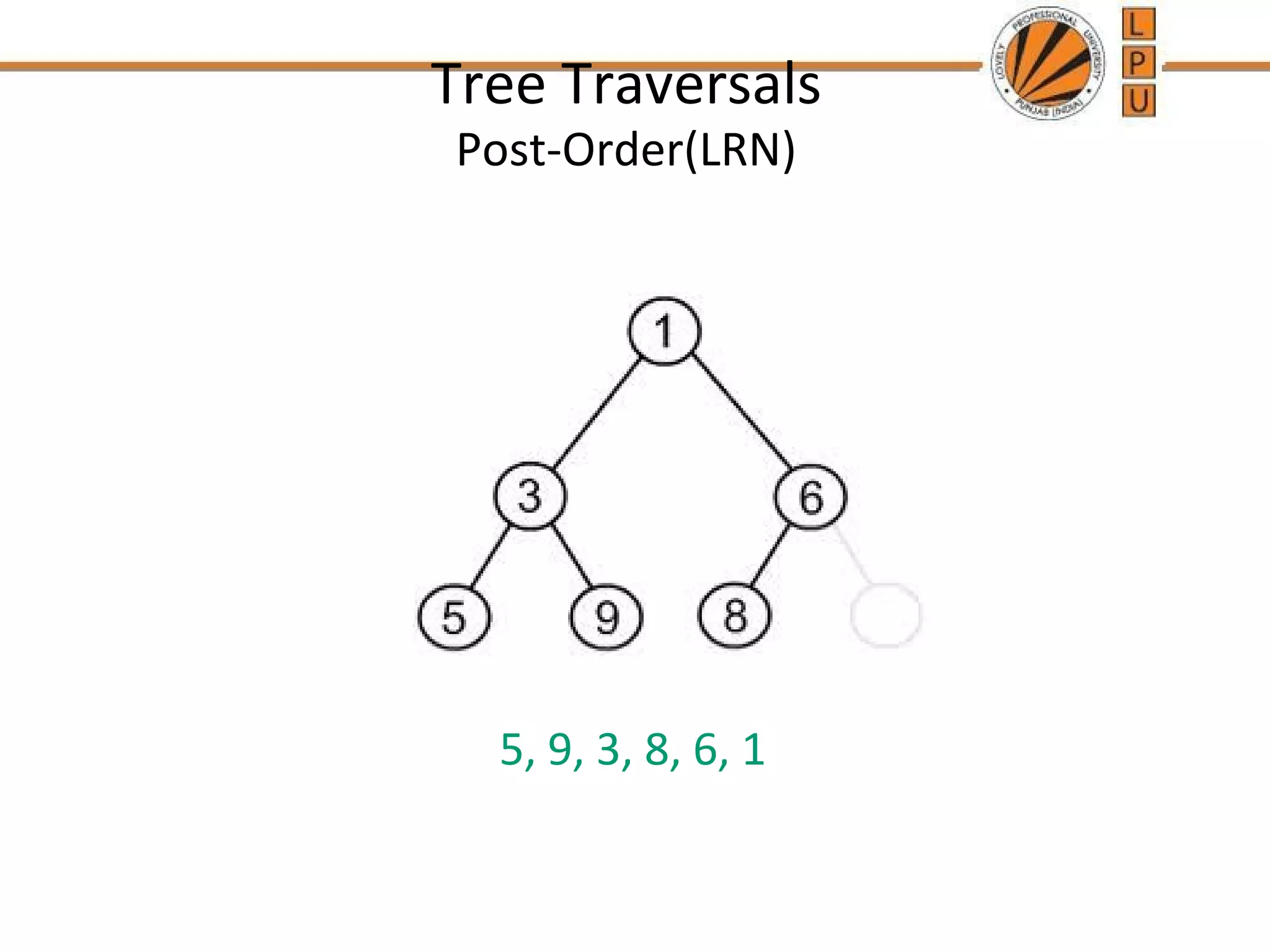
A binary tree is a tree data structure where each node has at most two children, described as left and right. There are different types of binary trees including full binary trees where each node has 0 or 2 children, and complete binary trees where all levels are fully filled except the lowest, which is filled from left to right. The document discusses properties of binary trees like the maximum number of nodes on each level and relationships between numbers of nodes and edges. It also describes common traversal techniques like preorder, inorder and postorder that visit nodes in different sequences, and provides pseudocode for algorithms to perform these traversals using a stack.




![• 4.if n is the number of nodes and e is the number of edges in an non-empty binary tree then n=e+1. • 5.if n0 is the number of leaf nodes (no child) and n2 is the number of nodes with two children in a non-empty binary tree then n0= n2+1 • 6.for a complete binary tree T with n nodes ,the height is floor[log2(n+1) -1]](https://image.slidesharecdn.com/2-141206172629-conversion-gate02/75/binary-tree-7-2048.jpg)




![• 1.[Initiaaly push NULL onto STACK and initialize PTR] Set TOP1.STACK[1]NULL and PTRROOT 2.Repeat steps 3 to 5 while PTR!=NULL 3.Apply PROCESS to INFO[PTR] 4.[Right Child?] If RIGHT[PTR]!=NULL [Push on STACK] TOPTOP+1 STACK[TOP]RIGHT[PTR] [End of if structure]](https://image.slidesharecdn.com/2-141206172629-conversion-gate02/75/binary-tree-16-2048.jpg)
![• 5.[Left Child ?] If LEFT[PTR]!=NULL, Set PTRLEFT[PTR] Else [pop from stack] PTRSTACK[TOP] TOPTOP-1 [End of if strucutre] [End of step 2 loop] 6.Exit](https://image.slidesharecdn.com/2-141206172629-conversion-gate02/75/binary-tree-17-2048.jpg)

![1.[Push NULL onto STACK and initialize PTR] TOP1,STACK[1]NULL and PTRROOT 2.Repeat while PTR!=NULL [Push left most path onto stack] a)TOPTOP+1 and STACK[TOP]PTR [Saves nodes] b)PTRLEFT[PTR] [updates PTR] [End of loop] 3.PTRSTACK[TOP] TOPTOP-1 [pops node from STACK]](https://image.slidesharecdn.com/2-141206172629-conversion-gate02/75/binary-tree-19-2048.jpg)
![4.Repeat steps 5 to 7 while PTR!=NULL [Backtracking] 5.Apply PROCESS to INFO[PTR] 6.[Right child?] If RIGHT[PTR]!=NULL a)PTRRIGHT[PTR] b)GOTO step 2 7.PTRSTACK[TOP] TOP=TOP-1 [Pops node] [end of step 4 loop] 8.Exit](https://image.slidesharecdn.com/2-141206172629-conversion-gate02/75/binary-tree-20-2048.jpg)

![1.[push NULL onto STACK and initialize PTR] Set TOP1,STACK[1]NULL,PTRROOT 2.[Push left-most path onto STACK] Repeat steps 3 to 5 while(PTR!=NULL) 3.TOPTOP+1 STACK[TOP]PTR [ Pushes PTR on STACK] 4.if RIGHT[PTR]!=NULL, then [Push on STACK] TOPTOP+1 and STACK[TOP]=-RIGHT[PTR]. [end of If strucutre]](https://image.slidesharecdn.com/2-141206172629-conversion-gate02/75/binary-tree-22-2048.jpg)
![Set PTRLEFT[PTR] [Updates pointer PTR] [End of Step 2 loop] 6.Set PTRSTACK[TOP] and TOPTOP-1 [Pops node from STACK] 7.Repeat while PTR>0. A)Apply PROCESS to INFO[PTR] B)Set PTRSTACK[TOP] and TOPTOP-1 [pops node from STACK] 8.If PTR<0 ,then: a)PTR-PTR b)Goto step 2. [End of If structure] 9.EXIT](https://image.slidesharecdn.com/2-141206172629-conversion-gate02/75/binary-tree-23-2048.jpg)