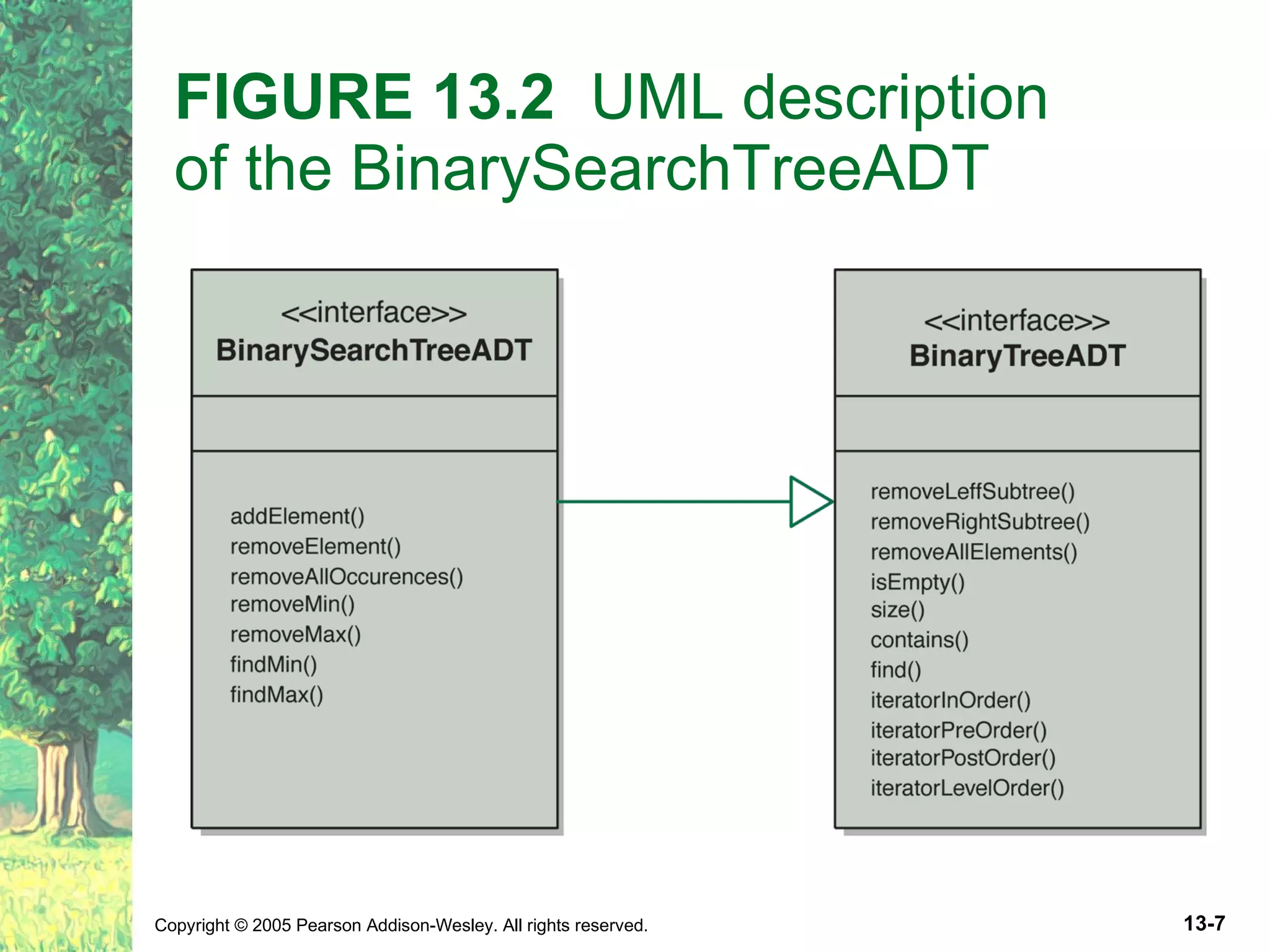
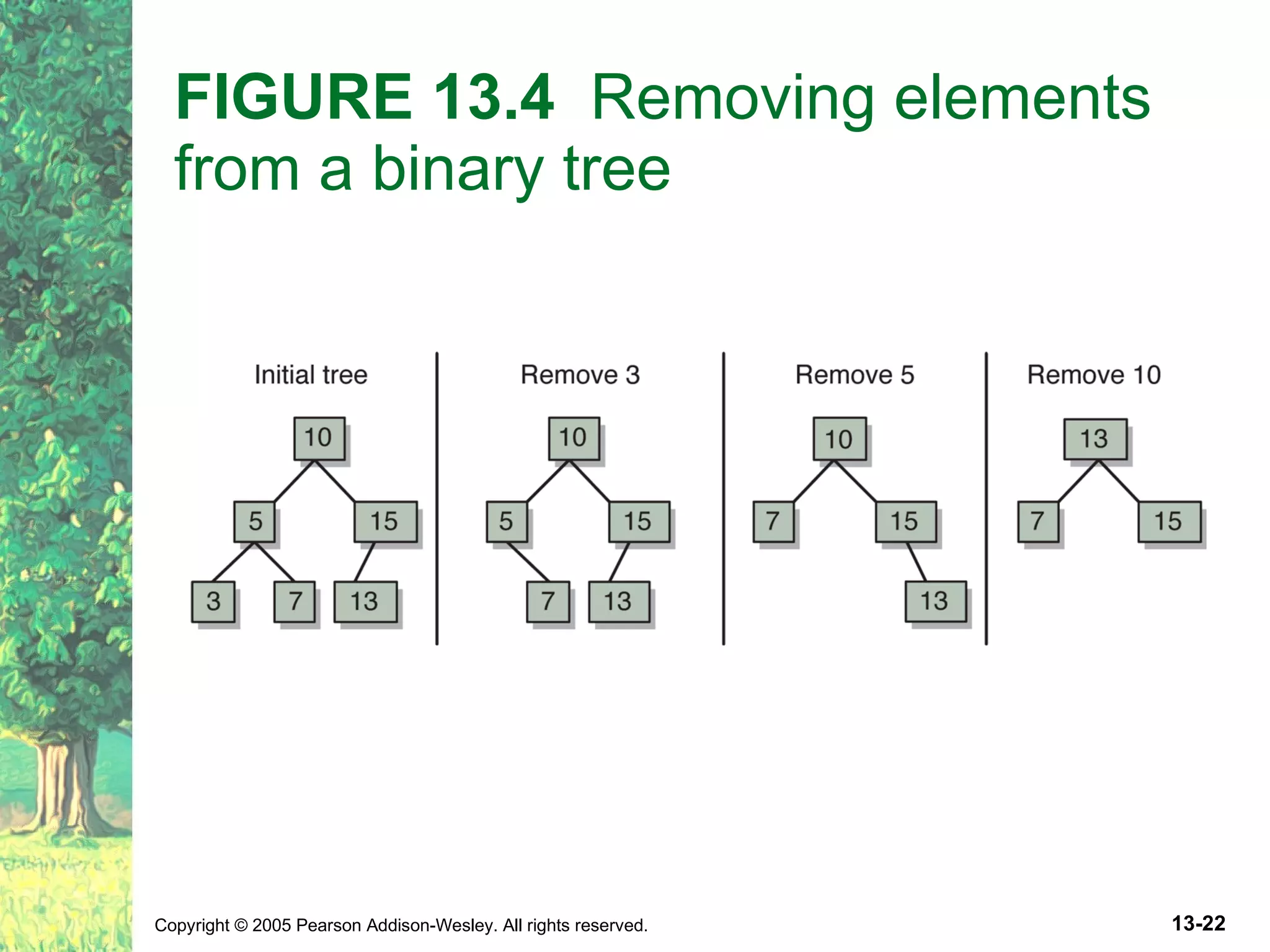
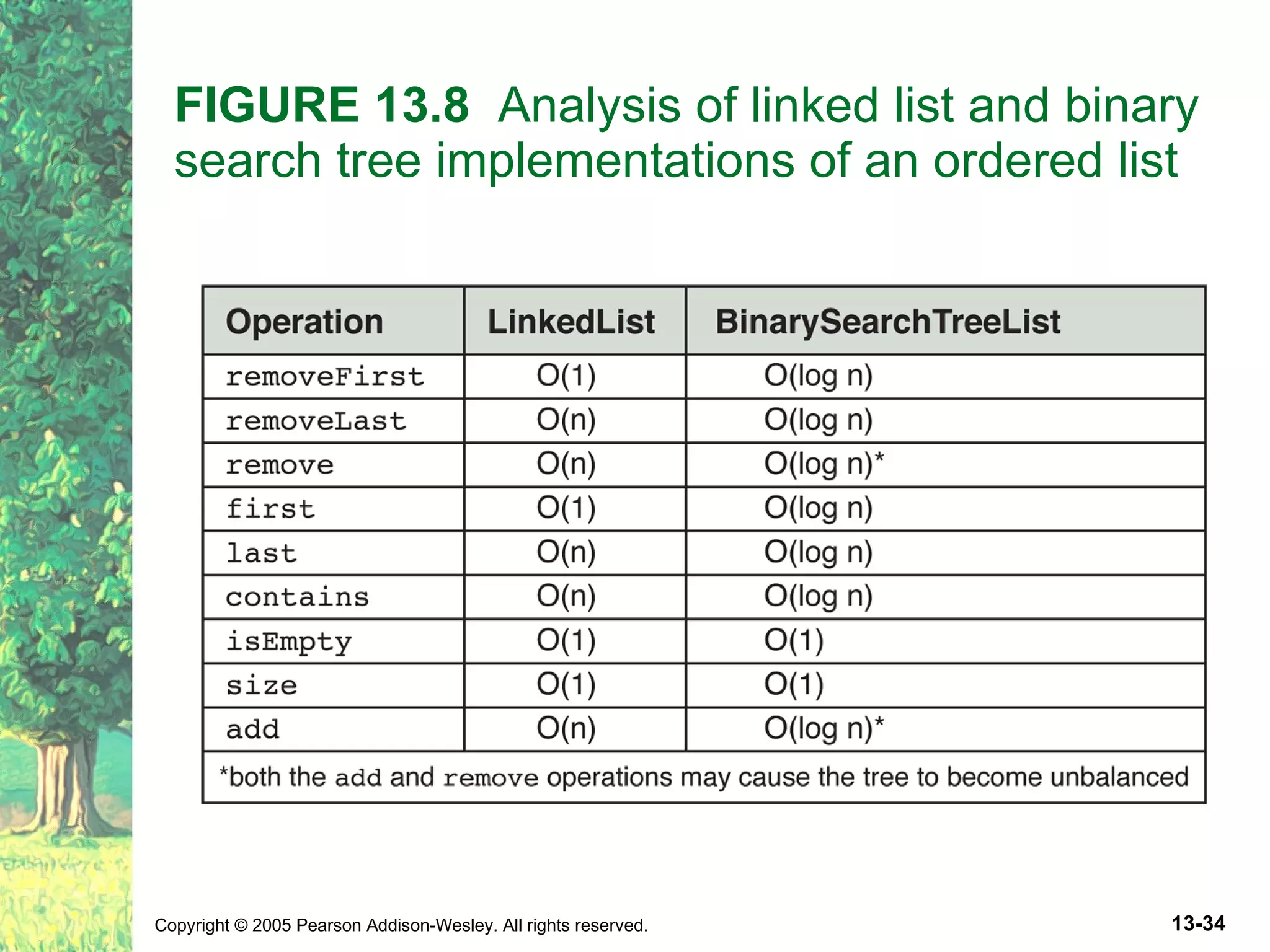
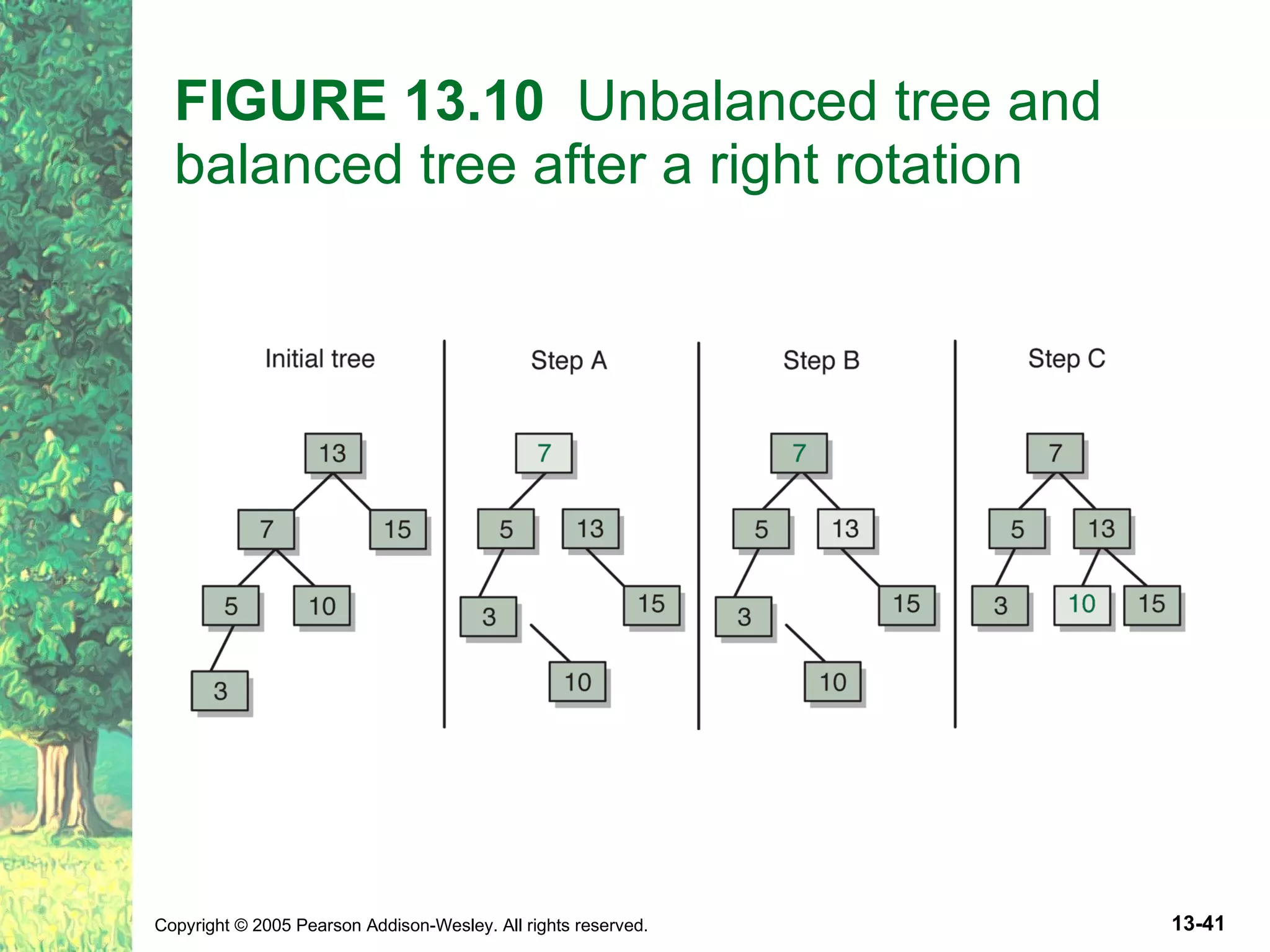
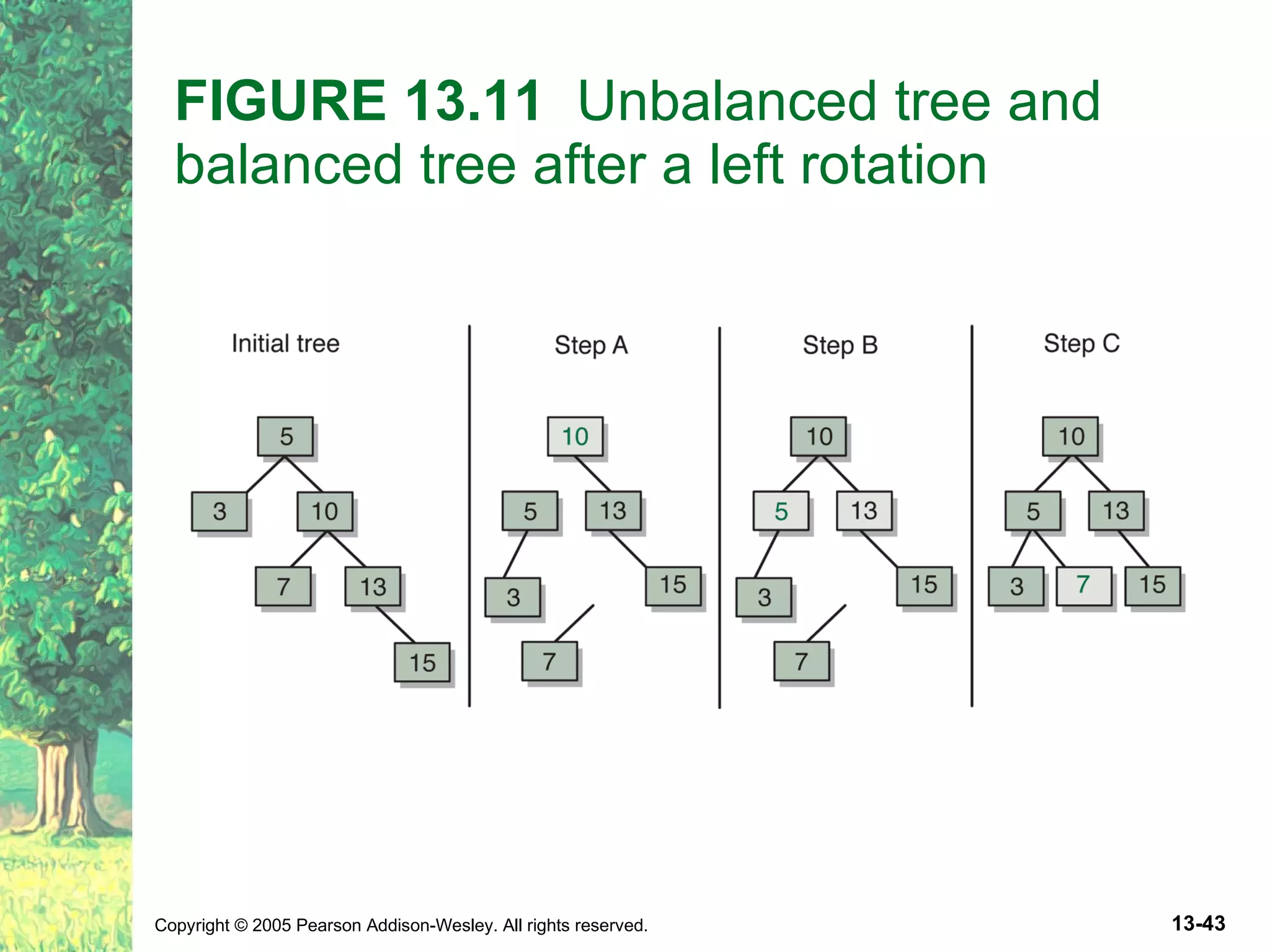
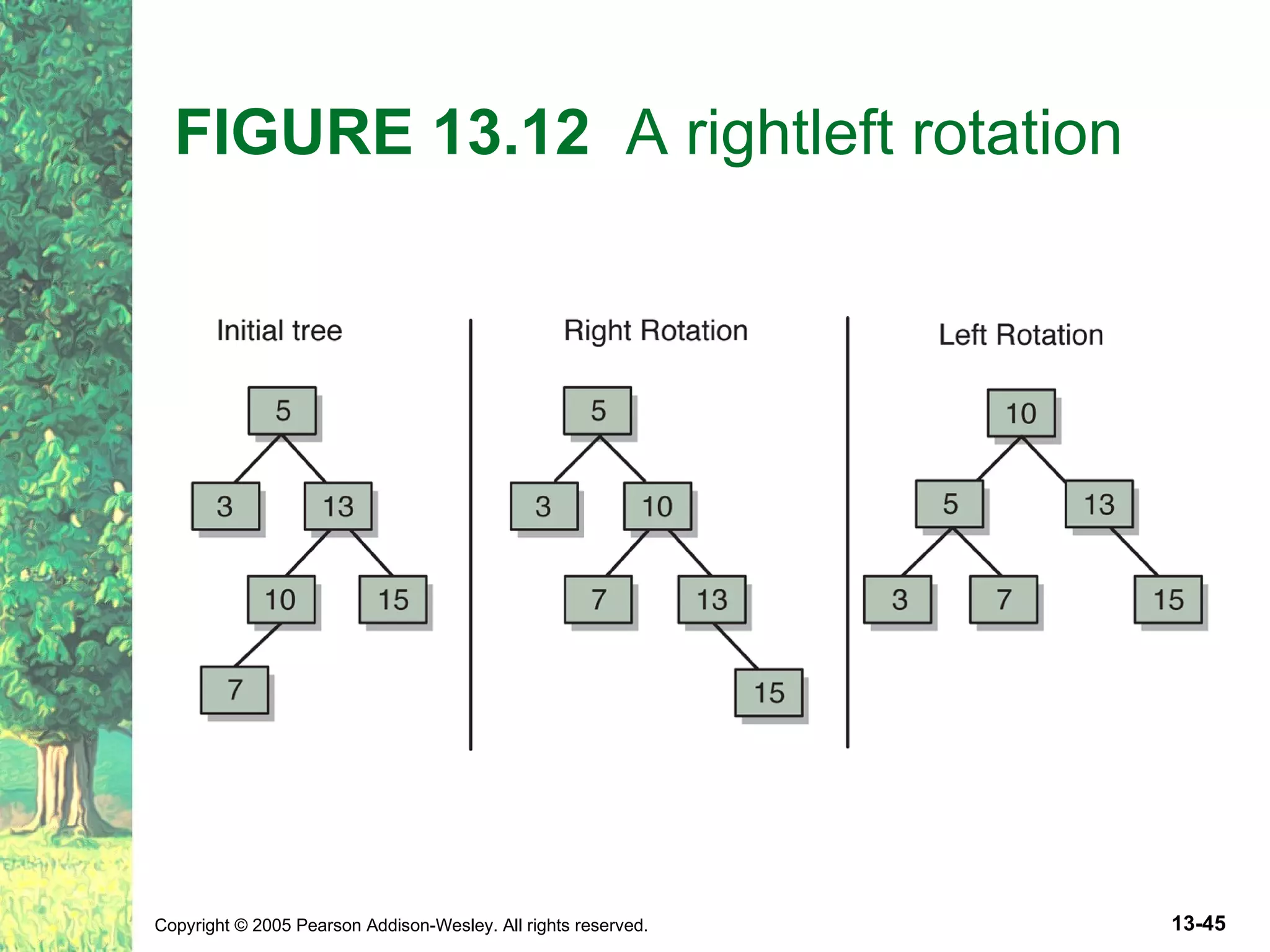
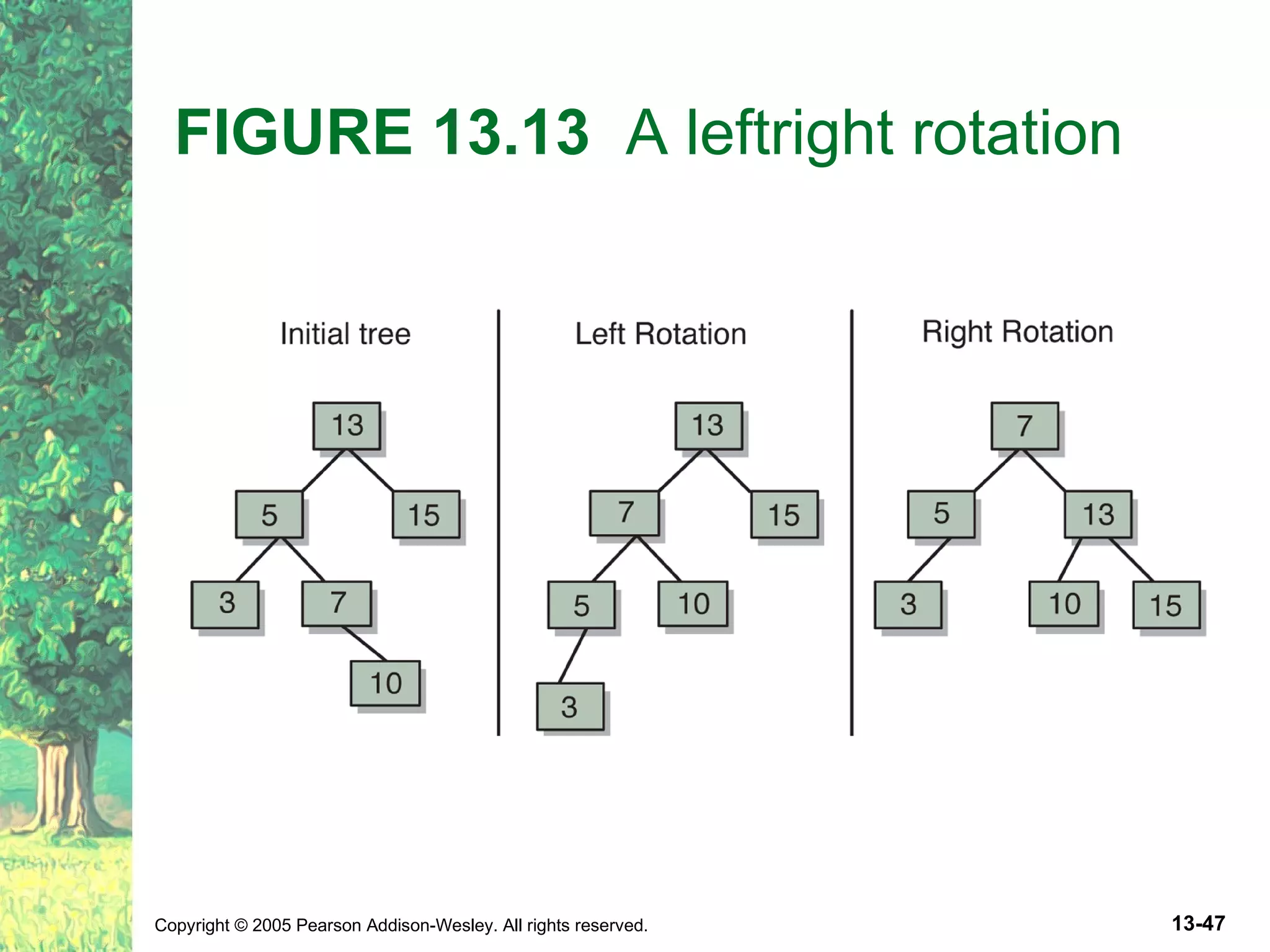
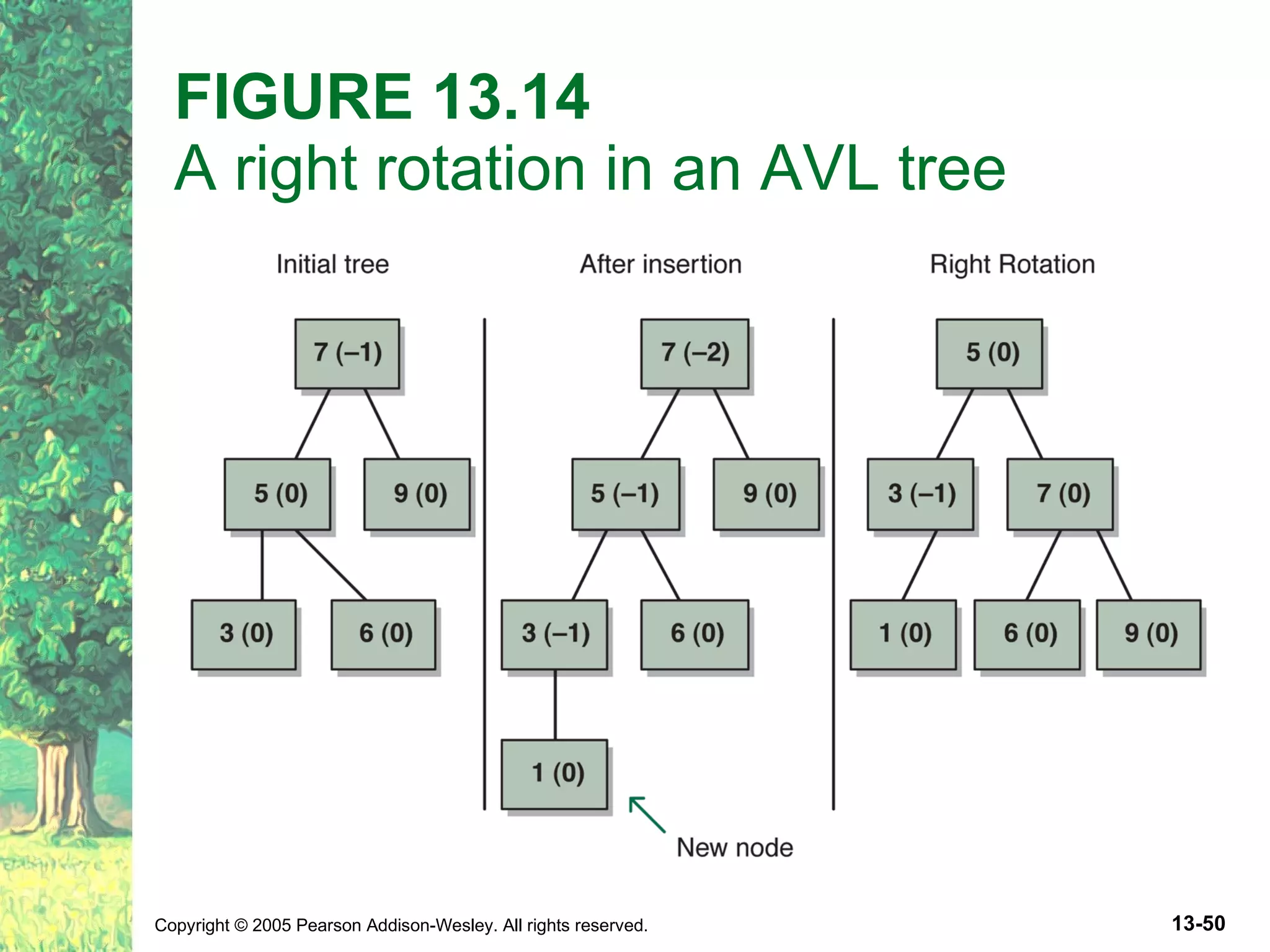
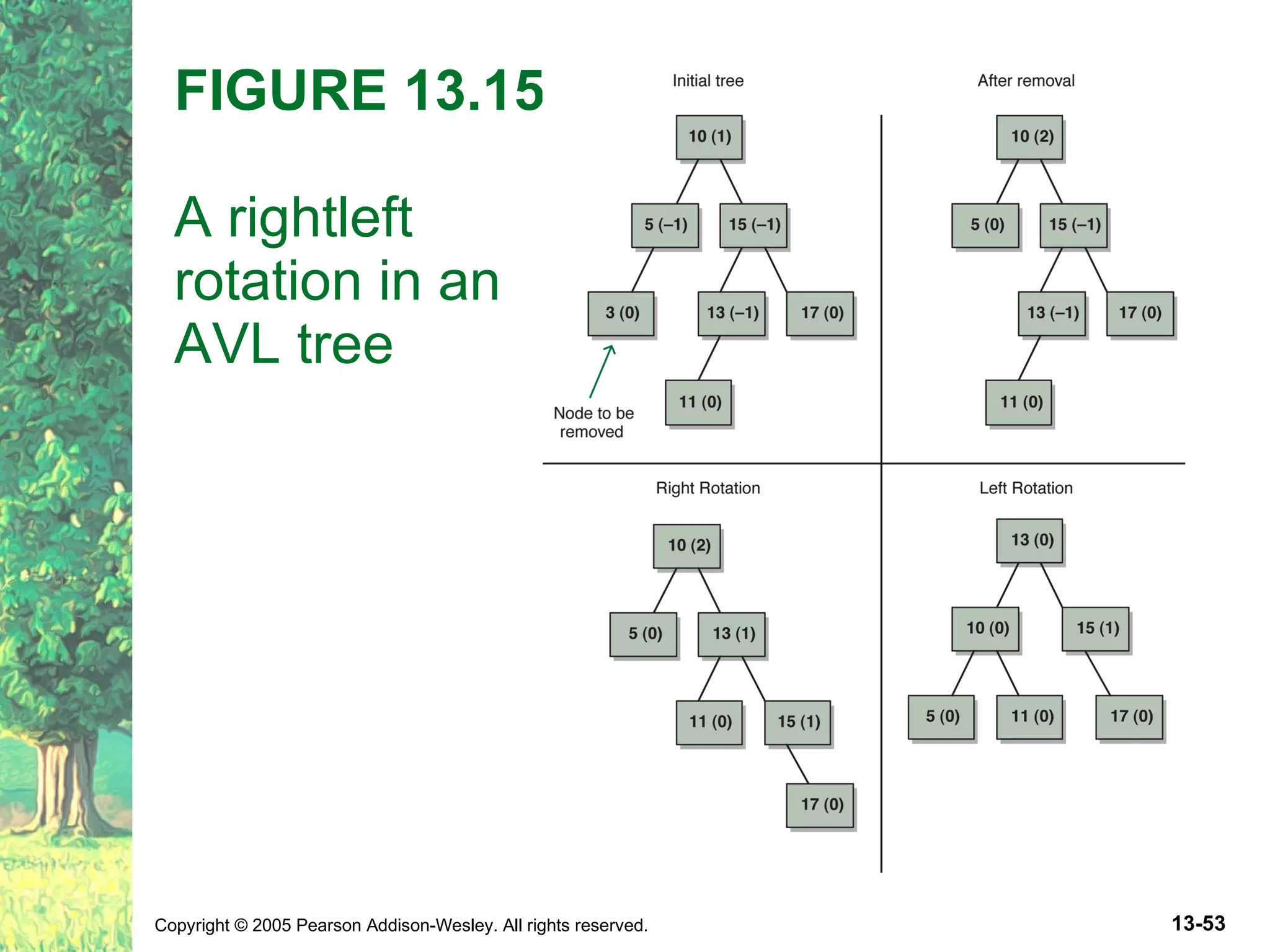
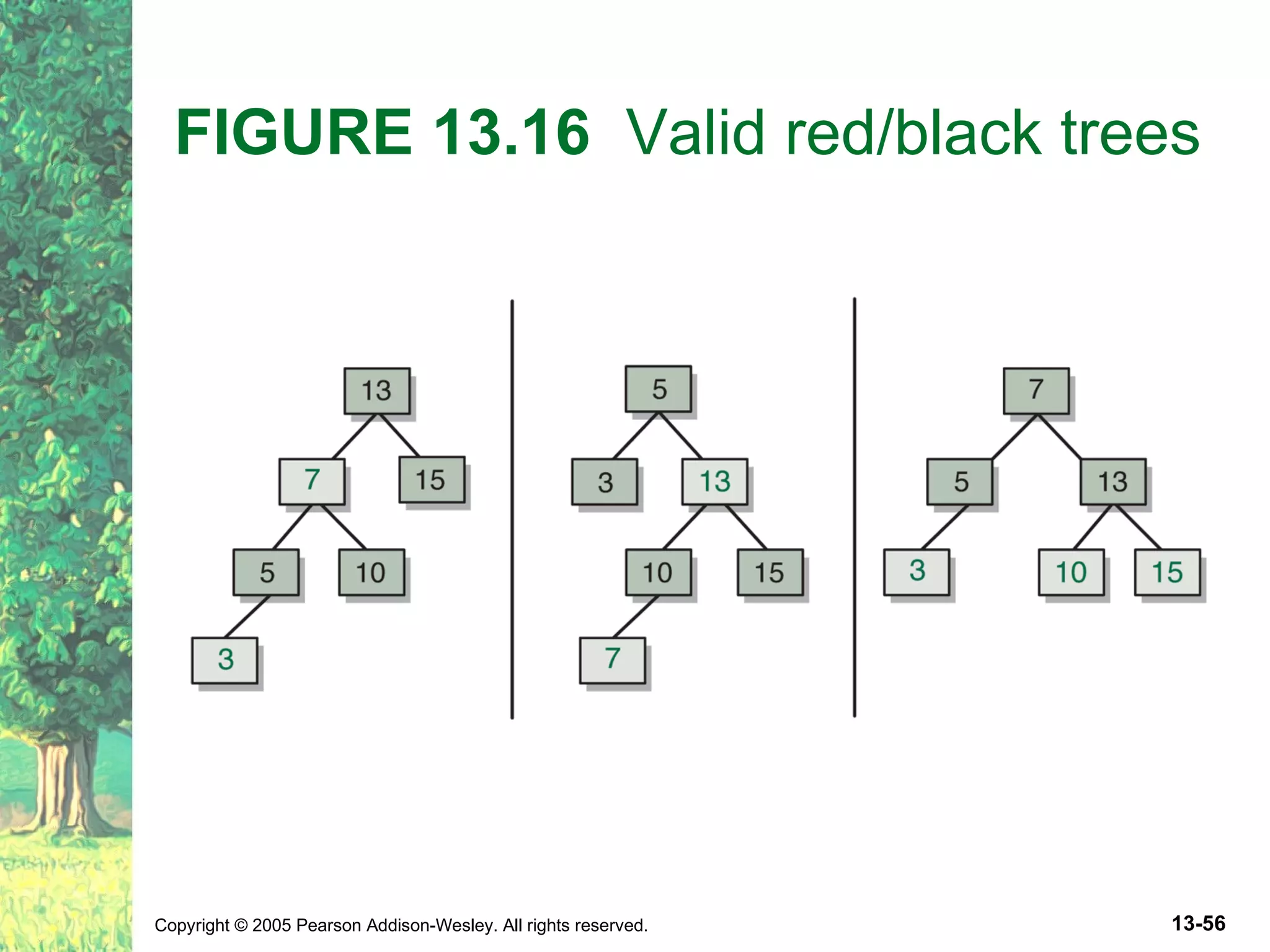
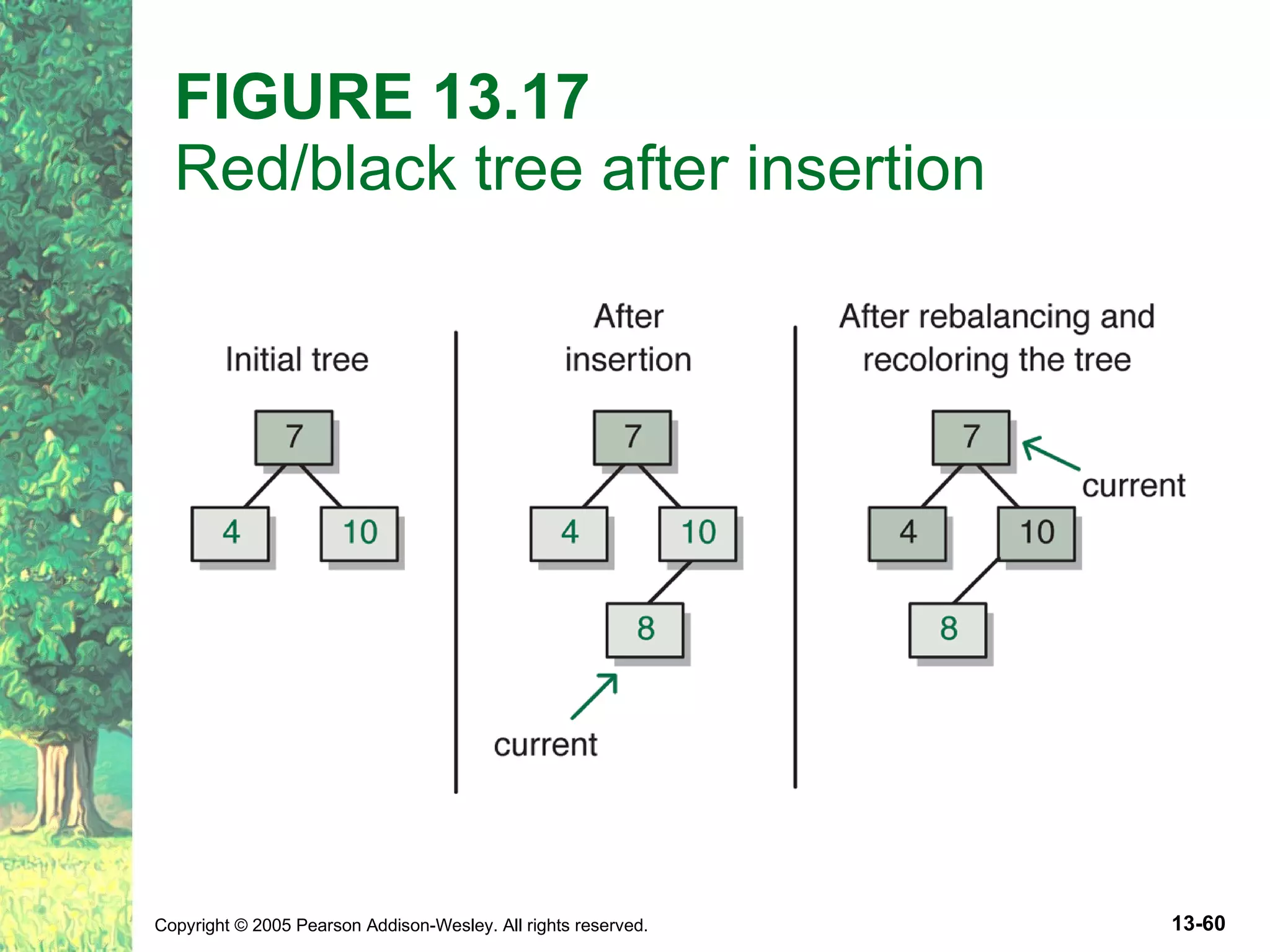
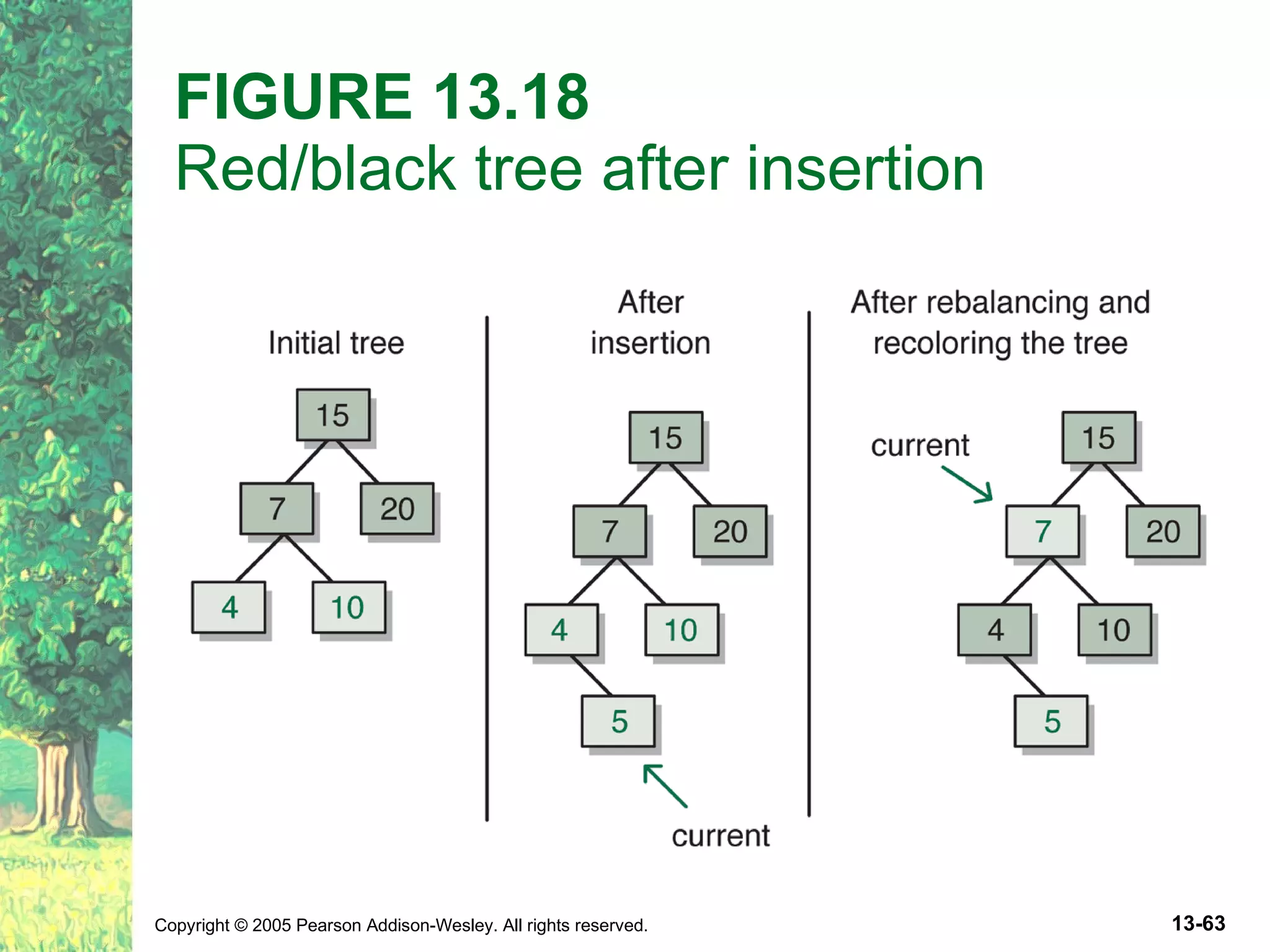
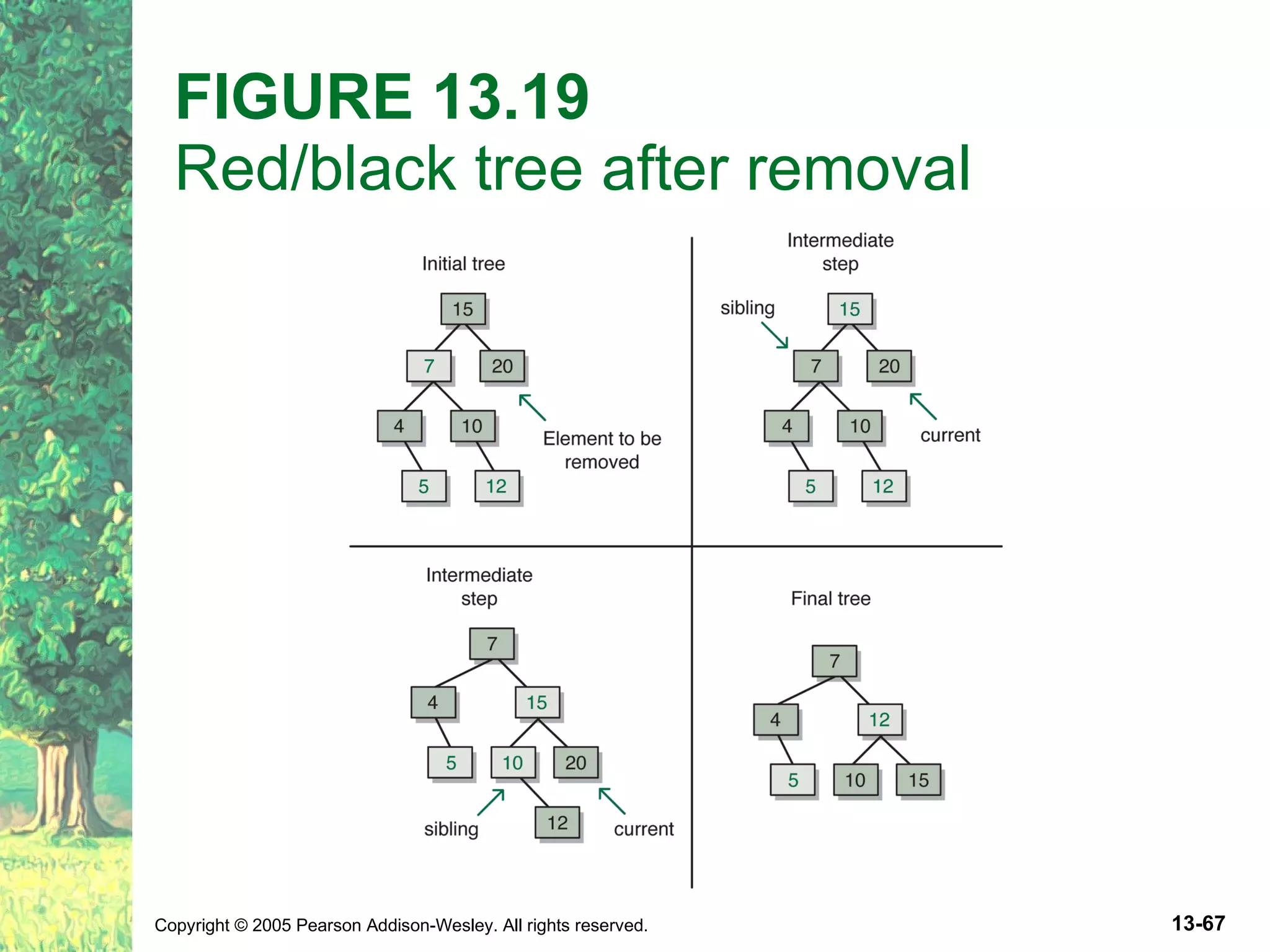
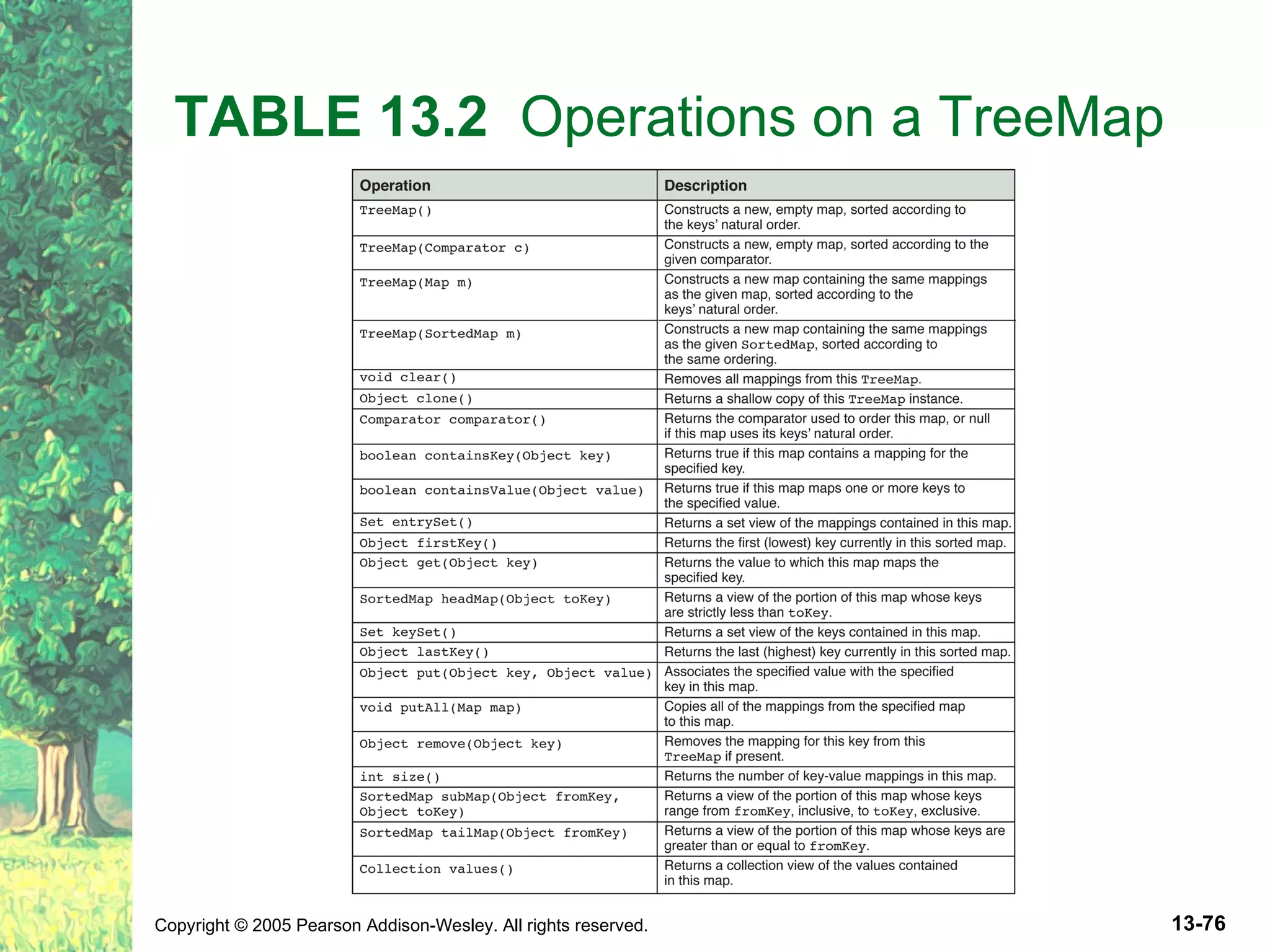
The document discusses binary search trees and their implementations. It defines binary search trees and their operations like adding and removing elements. It examines linked implementations of binary search trees and how to balance them using techniques like AVL trees and red-black trees. Rotations are used to rebalance the trees during insertion and deletion.