Basics of Data structure using C describing basics concepts

CHAPTER 2 1 Structures (records) struct { char name[10]; int age; float salary; } person; strcpy(person.name, “james”); person.age=10; person.salary=35000;

CHAPTER 2 2 Create structure data type typedef struct human_being { char name[10]; int age; float salary; }; or typedef struct { char name[10]; int age; float salary } human_being; human_being person1, person2;

CHAPTER 2 3 Unions Similar to struct, but only one field is active. Example: Add fields for male and female. typedef struct sex_type { enum tag_field {female, male} sex; union { int children; int beard; } u; }; typedef struct human_being { char name[10]; int age; float salary; date dob; sex_type sex_info; } human_being person1, person2; person1.sex_info.sex=male; person1.sex_info.u.beard=FALSE;

CHAPTER 2 4 Self-Referential Structures One or more of its components is a pointer to itself. typedef struct list { char data; list *link; } list item1, item2, item3; item1.data=‘a’; item2.data=‘b’; item3.data=‘c’; item1.link=item2.link=item3.link=NULL; Construct a list with three nodes item1.link=&item2; item2.link=&item3; malloc: obtain a node a b c

CHAPTER 2 5 Ordered List Examples  (MONDAY, TUEDSAY, WEDNESDAY, THURSDAY, FRIDAY, SATURDAYY, SUNDAY)  (2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King, Ace)  (1941, 1942, 1943, 1944, 1945)  (a1, a2, a3, …, an-1, an) ordered (linear) list: (item1, item2, item3, …, itemn)

CHAPTER 2 6 Operations on Ordered List  Find the length, n , of the list.  Read the items from left to right (or right to left).  Retrieve the i’th element.  Store a new value into the i’th position.  Insert a new element at the position i , causing elements numbered i, i+1, …, n to become numbered i+1, i+2, …, n+1  Delete the element at position i , causing elements numbered i+1, …, n to become numbered i, i+1, …, n-1 array (sequential mapping)? (1)~(4) O (5)~(6) X

Arrays 7 Outline 1. Introduction 2. Arrays 3. Declaring Arrays 4. Examples Using Arrays 5. Representation of arrays in memory 6. Dynamically allocated arrays 7. Array operations 1. Traversing 2. Inserting 3. Deleting 4. Searching 5. Sorting 8. Multidimensional arrays 9. Case Study: polynomials and sparse matrices

Introduction • Arrays – Structures of related data items – Static entity – same size throughout program – Dynamic data structures can also be created 8

Arrays 9 A linear array is a list of a finite number of homogeneous data elements (that is data elements of the same type) such that: 1. The elements of the array are referenced respectively by an index of n consecutive numbers 2. The elements of the array are stored respectively in successive memory locations

Arrays • Array – Group of consecutive memory locations – Same name and type • To refer to an element, specify – Array name – Position number • Format: arrayname[ position number ] – First element at position 0 – n element array named c: • c[ 0 ], c[ 1 ]...c[ n – 1 ] 10 Name of array (Note that all elements of this array have the same name, c) Position number of the element within array c c[6] -45 6 0 72 1543 -89 0 62 -3 1 6453 78 c[0] c[1] c[2] c[3] c[11] c[10] c[9] c[8] c[7] c[5] c[4]

Arrays • Array elements are like normal variables c[ 0 ] = 3; printf( "%d", c[ 0 ] ); – Perform operations in subscript. If x equals 3 c[ 5 - 2 ] == c[ 3 ] == c[ x ] 11

Declaring Arrays • When declaring arrays, specify – Type – Name – Number of elements arrayType arrayName[ numberOfElements ]; – Examples: int c[ 10 ]; float myArray[ 3284 ]; • Declaring multiple arrays of same type – Format similar to regular variables – Example: int b[ 100 ], x[ 27 ]; 12

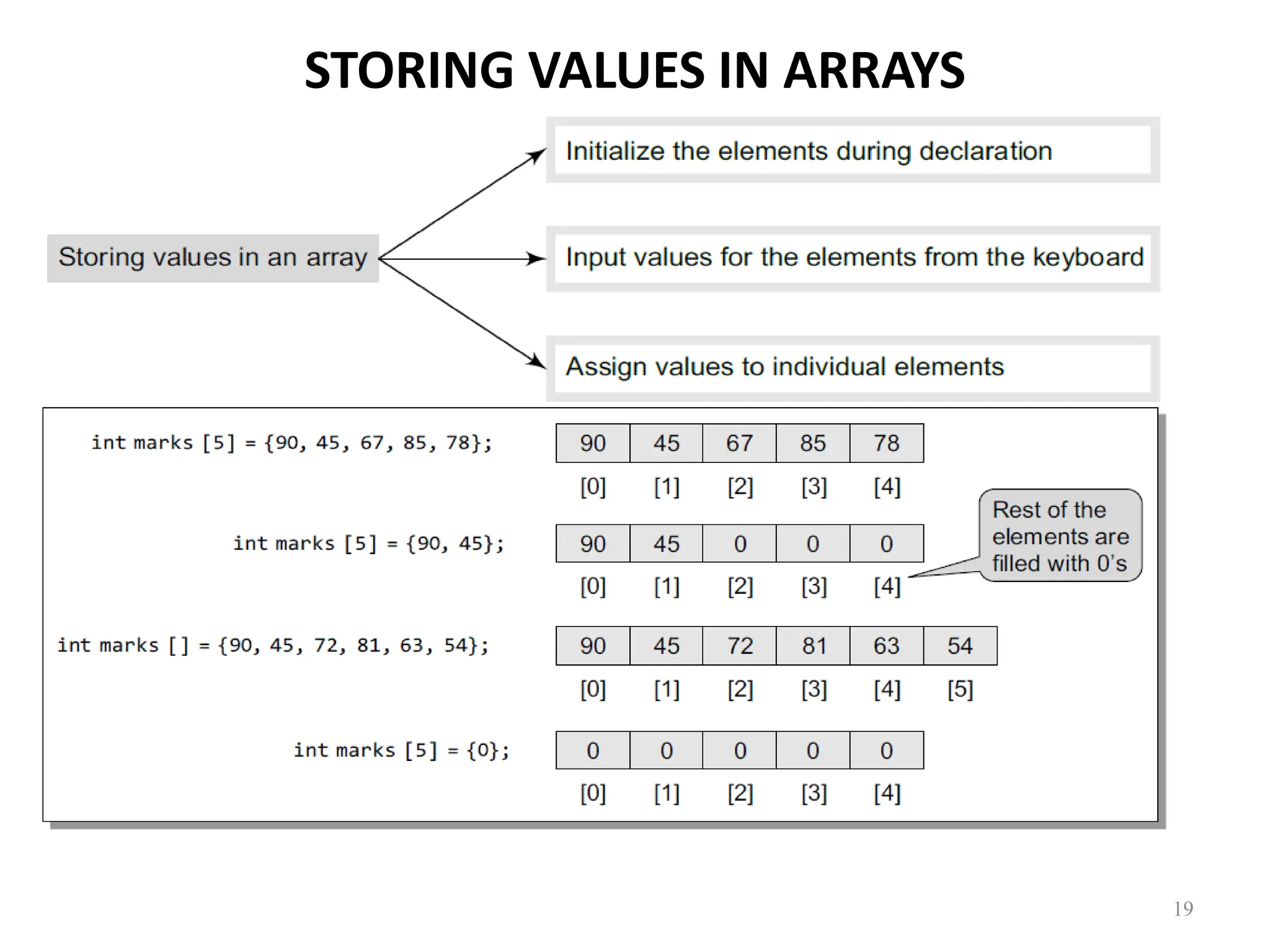
Examples Using Arrays • Initializers int n[ 5 ] = { 1, 2, 3, 4, 5 }; – If not enough initializers, rightmost elements become 0 int n[ 5 ] = { 0 } • All elements 0 – If too many a syntax error – C arrays have no bounds checking • If size omitted, initializers determine it int n[ ] = { 1, 2, 3, 4, 5 }; – 5 initializers, therefore 5 element array 13

Length of the array The length of an array is given by the number of elements stored in it. The general formula to calculate the length of an array is Length = upper_bound – lower_bound + 1 where upper_bound - is the index of the last element lower_bound - is the index of the first element 14

15 Ex: Let Age[5] be an array of integers such that Age[0] = 2, Age[1] = 5, Age[2] = 3, Age[3] = 1, Age[4] = 7 Show the memory representation of the array and calculate its length.

ACCESSING THE ELEMENTS OF AN ARRAY • To access all the elements, we must use a loop. • subscript must be an integral value or an expression that evaluates to an integral value. 16

Calculating the Address of an Array Elements 17 Address of data element, A[k] = BA(A) + w(k – lower_bound) A -is the array K - is the index of the element of which we have to calculate the address, BA – is the base address of the array A, w - is the size of one element in memory, Ex: size of int is 2. Given an array int marks[] = {99,67,78,56,88,90,34,85}, calculate the address of marks[4] if the base address = 1000. marks[4] = 1000 + 2(4 – 0) = 1000 + 2(4) = 1008

Example-2 calculating address An automobile company uses an array AUTO to record the number of auto-mobiles sold each year from 1932 to 1984. suppose Auto appears in memory at location 200 and w=4 words. Find the address of the array element for year k=1965 18 The address of the array element for the year k=1965 can be obtained : Loc(Auto[1932]) = Base (Auto)+w (1965 - lower bound) = 200 + 4 (1965-1932)= 332

20 Input values for the element from the key board Assign values to individual elements

OPERATIONS ON ARRAYS 21 There are a number of operations that can be preformed on arrays. 1. Traversing an array 2. Inserting an element in an array 3. Searching an element in an array 4. Deleting an element from an array 5. Merging two arrays 6. Sorting an array in ascending or descending order

27 Algorithm to Insert an Element in the Middle of an Array

28 Algorithm to delete an element from the middle of an array

31 • Design, develop and implement a program to merge two sorted arrays • Design, develop and implement a program to interchange the largest and smallest number in an array.

Dynamically allocated arrays 35

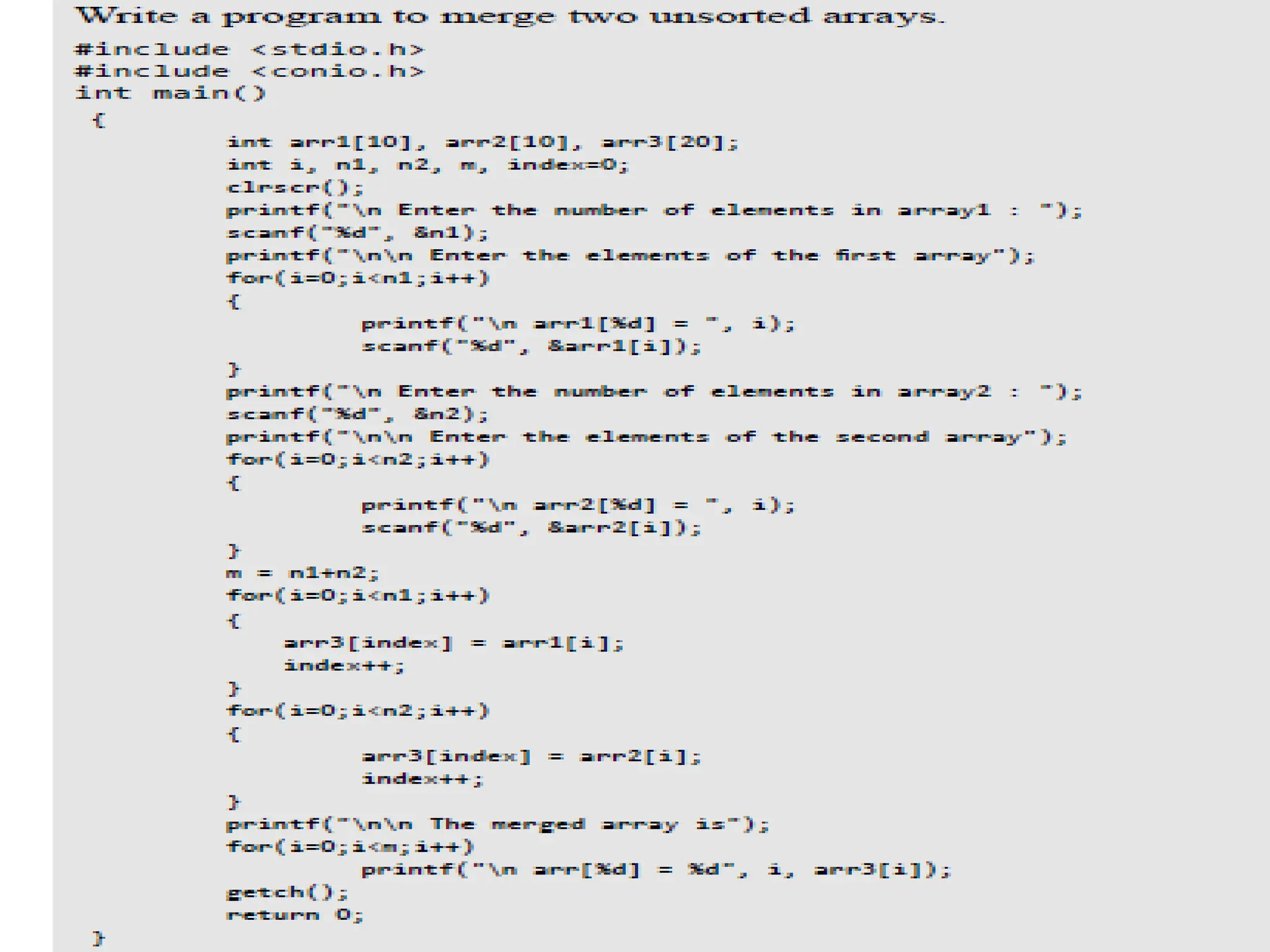
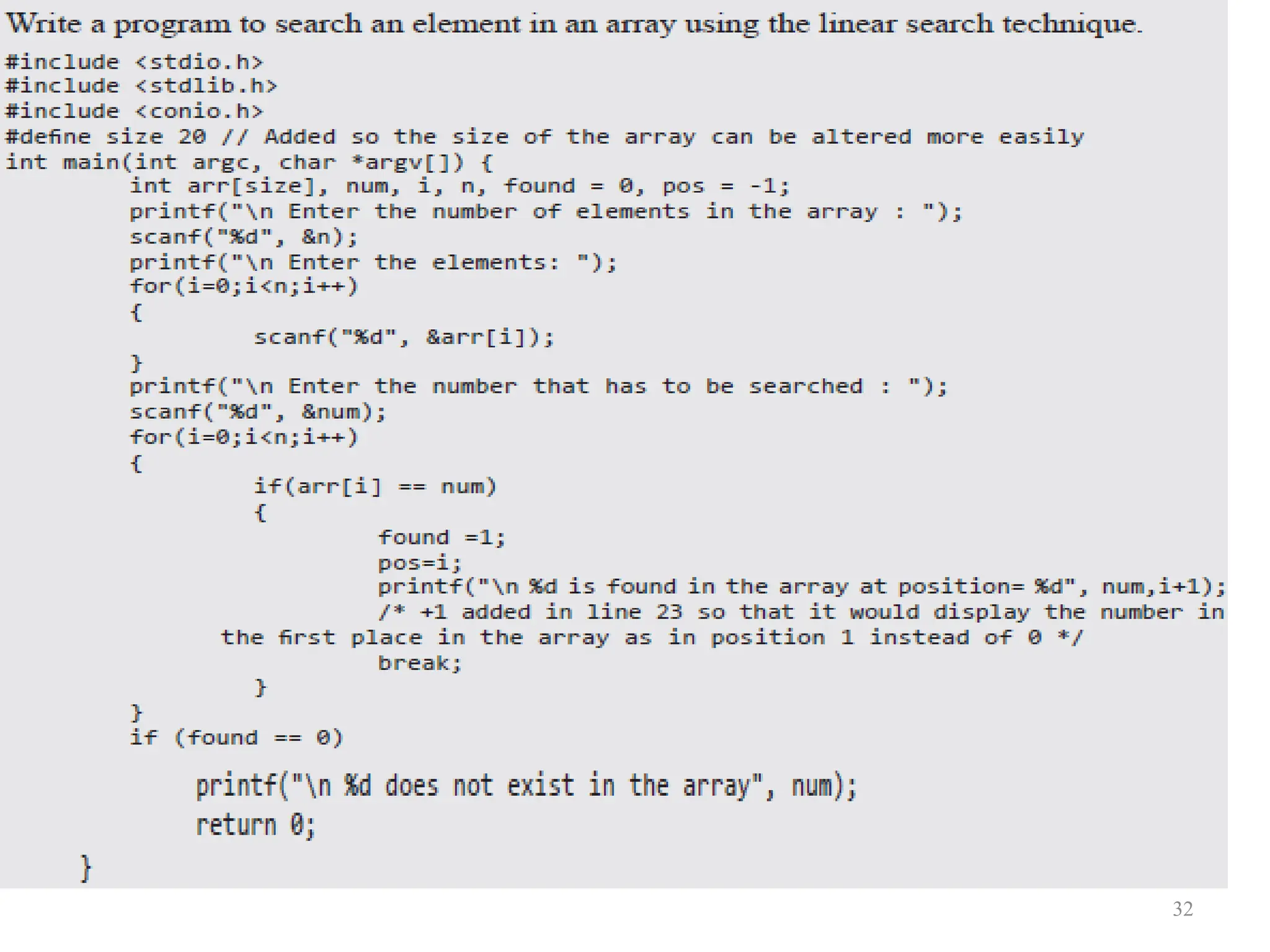
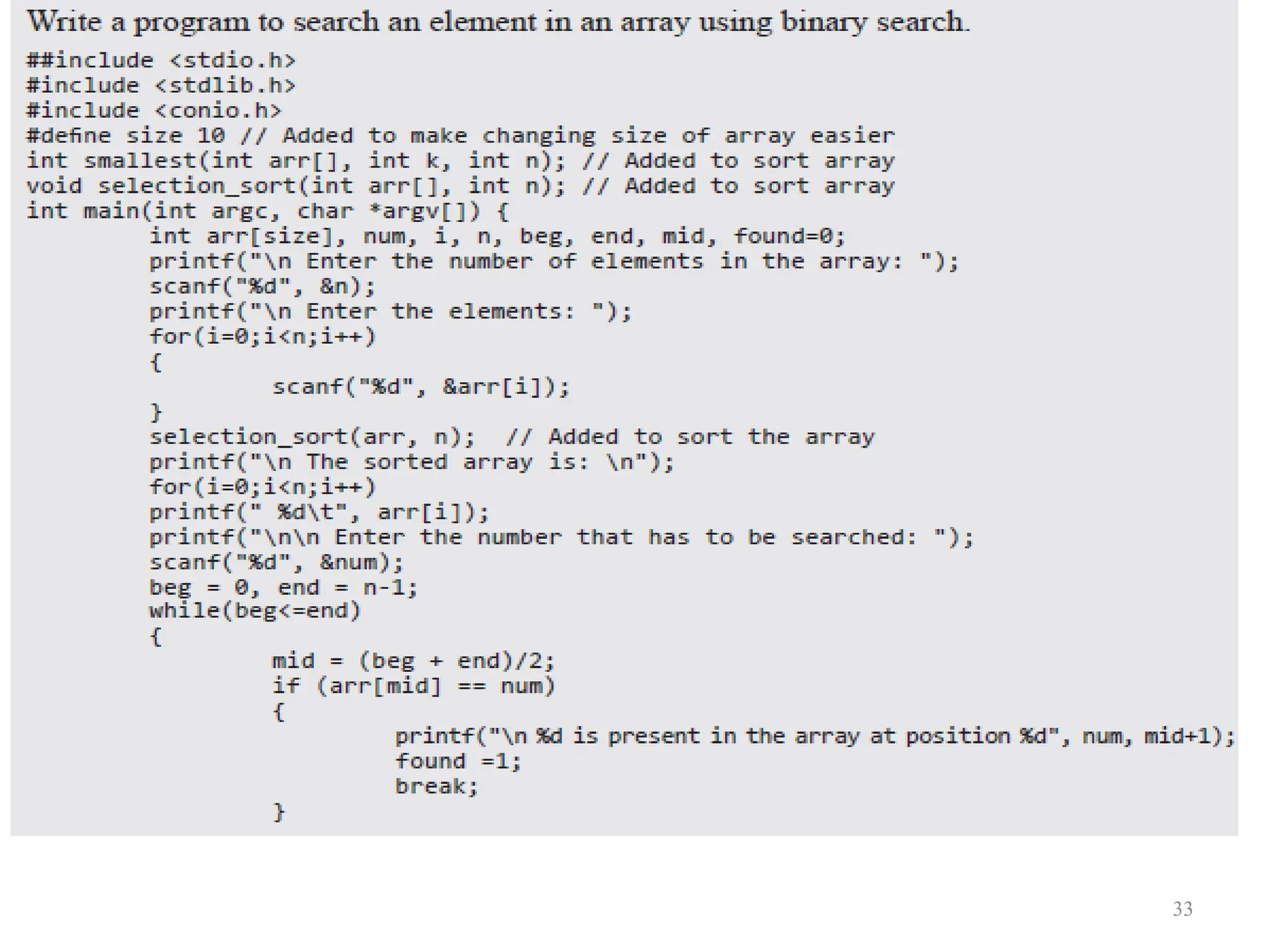
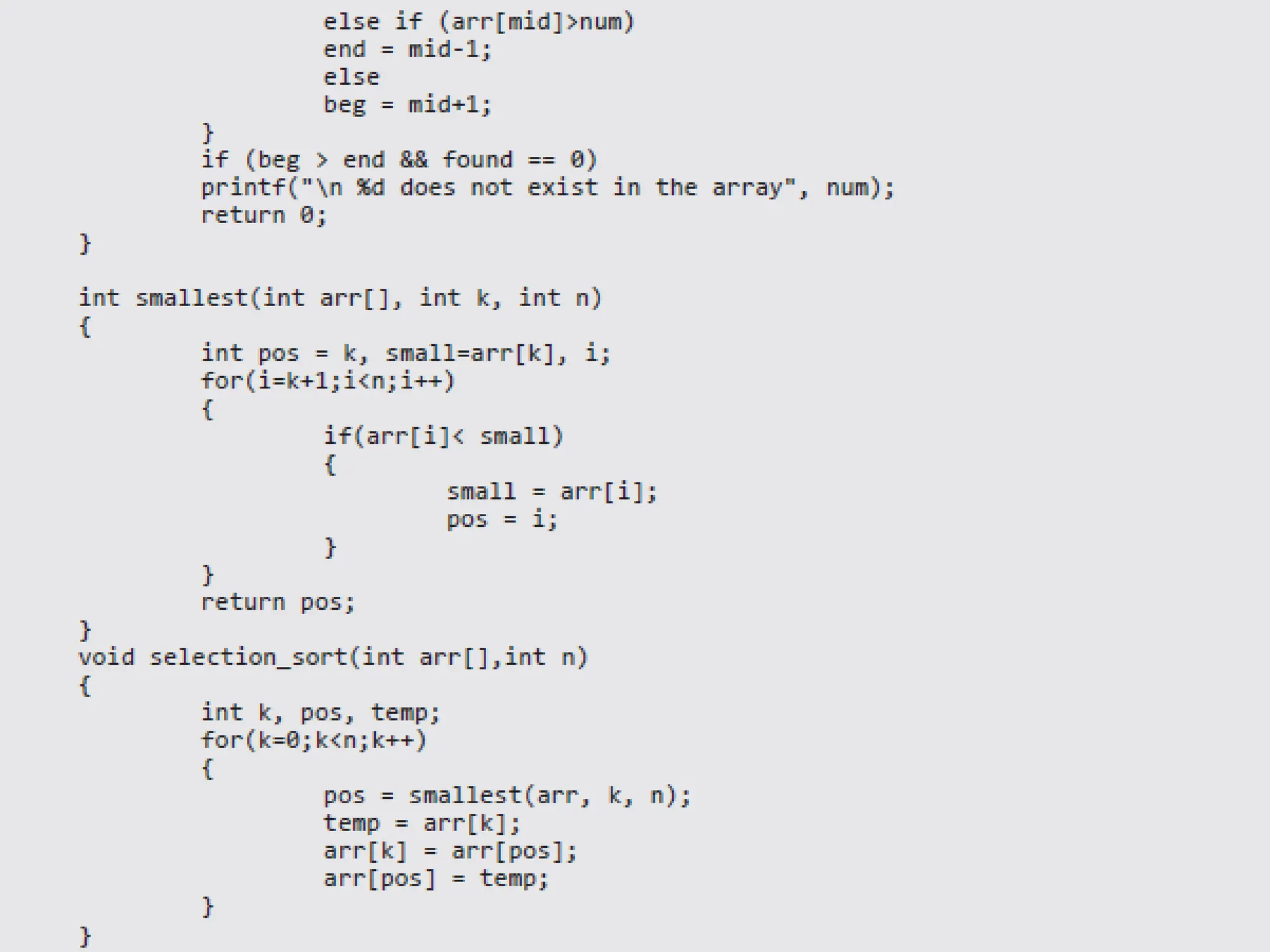
 2000 Prentice Hall, Inc. All rights reserved. 1. Initialize array 2. Loop 3. Print 37 1 /* 2 Histogram printing program */ 3 #include <stdio.h> 4 #define SIZE 10 5 6 int main() 7 { 8 int n[ SIZE ] = { 19, 3, 15, 7, 11, 9, 13, 5, 17, 1 }; 9 int i, j; 10 11 printf( "%s%13s%17sn", "Element", "Value", "Histogram" ); 12 13 for ( i = 0; i <= SIZE - 1; i++ ) { 14 printf( "%7d%13d ", i, n[ i ]) ; 15 16 for ( j = 1; j <= n[ i ]; j++ ) /* print one bar */ 17 printf( "%c", '*' ); 18 19 printf( "n" ); 20 } 21 22 return 0; 23 }

 2000 Prentice Hall, Inc. All rights reserved. Program Output 38 Element Value Histogram 0 19 ******************* 1 3 *** 2 15 *************** 3 7 ******* 4 11 *********** 5 9 ********* 6 13 ************* 7 5 ***** 8 17 ***************** 9 1 *

Examples Using Arrays • Character arrays – String “first” is really a static array of characters – Character arrays can be initialized using string literals char string1[] = "first"; • Null character '0' terminates strings • string1 actually has 6 elements – It is equivalent to char string1[] = { 'f', 'i', 'r', 's', 't', '0' }; – Can access individual characters string1[ 3 ] is character ‘s’ – Array name is address of array, so & not needed for scanf scanf( "%s", string2 ); • Reads characters until whitespace encountered • Can write beyond end of array, be careful 39

 2000 Prentice Hall, Inc. All rights reserved. 1. Initialize strings 2. Print strings 2.1 Define loop 2.2 Print characters individually 2.3 Input string 3. Print string Program Output 40 2 /*Treating character arrays as strings */ 3 #include <stdio.h> 4 5 int main() 6 { 7 char string1[ 20 ], string2[] = "string literal"; 8 int i; 9 10 printf(" Enter a string: "); 11 scanf( "%s", string1 ); 12 printf( "string1 is: %snstring2: is %sn" 13 "string1 with spaces between characters is:n", 14 string1, string2 ); 15 16 for ( i = 0; string1[ i ] != '0'; i++ ) 17 printf( "%c ", string1[ i ] ); 18 19 printf( "n" ); 20 return 0; 21 } Enter a string: Hello there string1 is: Hello string2 is: string literal string1 with spaces between characters is: H e l l o

Passing Arrays to Functions • Passing arrays – To pass an array argument to a function, specify the name of the array without any brackets int myArray[ 24 ]; myFunction( myArray, 24 ); • Array size usually passed to function – Arrays passed call-by-reference – Name of array is address of first element – Function knows where the array is stored • Modifies original memory locations • Passing array elements – Passed by call-by-value – Pass subscripted name (i.e., myArray[ 3 ]) to function 41

Passing Arrays to Functions • Function prototype void modifyArray( int b[], int arraySize ); – Parameter names optional in prototype • int b[] could be written int [] • int arraySize could be simply int 42

 2000 Prentice Hall, Inc. All rights reserved. 1. Function definitions 2. Pass array to a function 2.1 Pass array element to a function 3. Print 43 1 /* 2 Passing arrays and individual array elements to functions */ 3 #include <stdio.h> 4 #define SIZE 5 5 6 void modifyArray( int [], int ); /* appears strange */ 7 void modifyElement( int ); 8 9 int main() 10 { 11 int a[ SIZE ] = { 0, 1, 2, 3, 4 }, i; 12 13 printf( "Effects of passing entire array call " 14 "by reference:nnThe values of the " 15 "original array are:n" ); 16 17 for ( i = 0; i <= SIZE - 1; i++ ) 18 printf( "%3d", a[ i ] ); 19 20 printf( "n" ); 21 modifyArray( a, SIZE ); /* passed call by reference */ 22 printf( "The values of the modified array are:n" ); 23 24 for ( i = 0; i <= SIZE - 1; i++ ) 25 printf( "%3d", a[ i ] ); 26 27 printf( "nnnEffects of passing array element call " 28 "by value:nnThe value of a[3] is %dn", a[ 3 ] ); 29 modifyElement( a[ 3 ] ); 30 printf( "The value of a[ 3 ] is %dn", a[ 3 ] ); 31 return 0; 32 } Entire arrays passed call-by- reference, and can be modified Array elements passed call-by- value, and cannot be modified

 2000 Prentice Hall, Inc. All rights reserved. 3.1 Function definitions Program Output 44 33 34 void modifyArray( int b[], int size ) 35 { 36 int j; 37 38 for ( j = 0; j <= size - 1; j++ ) 39 b[ j ] *= 2; 40 } 41 42 void modifyElement( int e ) 43 { 44 printf( "Value in modifyElement is %dn", e *= 2 ); 45 } Effects of passing entire array call by reference: The values of the original array are: 0 1 2 3 4 The values of the modified array are: 0 2 4 6 8 Effects of passing array element call by value: The value of a[3] is 6 Value in modifyElement is 12 The value of a[3] is 6

Sorting Arrays • Sorting data – Important computing application – Virtually every organization must sort some data • Bubble sort (sinking sort) – Several passes through the array – Successive pairs of elements are compared • If increasing order (or identical ), no change • If decreasing order, elements exchanged – Repeat • Example: – original: 3 4 2 6 7 – pass 1: 3 2 4 6 7 – pass 2: 2 3 4 6 7 – Small elements "bubble" to the top 45

Case Study: Computing Mean, Median and Mode Using Arrays • Mean – average • Median – number in middle of sorted list – 1, 2, 3, 4, 5 – 3 is the median • Mode – number that occurs most often – 1, 1, 1, 2, 3, 3, 4, 5 – 1 is the mode 46

 2000 Prentice Hall, Inc. All rights reserved. 1. Function prototypes 1.1 Initialize array 2. Call functions mean, median, and mode 47 1 /* 2 This program introduces the topic of survey data analysis. 3 It computes the mean, median, and mode of the data */ 4 #include <stdio.h> 5 #define SIZE 99 6 7 void mean( const int [] ); 8 void median( int [] ); 9 void mode( int [], const int [] ) ; 10 void bubbleSort( int [] ); 11 void printArray( const int [] ); 12 13 int main() 14 { 15 int frequency[ 10 ] = { 0 }; 16 int response[ SIZE ] = 17 { 6, 7, 8, 9, 8, 7, 8, 9, 8, 9, 18 7, 8, 9, 5, 9, 8, 7, 8, 7, 8, 19 6, 7, 8, 9, 3, 9, 8, 7, 8, 7, 20 7, 8, 9, 8, 9, 8, 9, 7, 8, 9, 21 6, 7, 8, 7, 8, 7, 9, 8, 9, 2, 22 7, 8, 9, 8, 9, 8, 9, 7, 5, 3, 23 5, 6, 7, 2, 5, 3, 9, 4, 6, 4, 24 7, 8, 9, 6, 8, 7, 8, 9, 7, 8, 25 7, 4, 4, 2, 5, 3, 8, 7, 5, 6, 26 4, 5, 6, 1, 6, 5, 7, 8, 7 }; 27 28 mean( response ); 29 median( response ); 30 mode( frequency, response ); 31 return 0; 32 }

 2000 Prentice Hall, Inc. All rights reserved. 3. Define function mean 3.1 Define function median 3.1.1 Sort Array 3.1.2 Print middle element 48 33 34 void mean( const int answer[] ) 35 { 36 int j, total = 0; 37 38 printf( "%sn%sn%sn", "********", " Mean", "********" ); 39 40 for ( j = 0; j <= SIZE - 1; j++ ) 41 total += answer[ j ]; 42 43 printf( "The mean is the average value of the datan" 44 "items. The mean is equal to the total ofn" 45 "all the data items divided by the numbern" 46 "of data items ( %d ). The mean value forn" 47 "this run is: %d / %d = %.4fnn", 48 SIZE, total, SIZE, ( double ) total / SIZE ); 49 } 50 51 void median( int answer[] ) 52 { 53 printf( "n%sn%sn%sn%s", 54 "********", " Median", "********", 55 "The unsorted array of responses is" ); 56 57 printArray( answer ); 58 bubbleSort( answer ); 59 printf( "nnThe sorted array is" ); 60 printArray( answer ); 61 printf( "nnThe median is element %d ofn" 62 "the sorted %d element array.n" 63 "For this run the median is %dnn", 64 SIZE / 2, SIZE, answer[ SIZE / 2 ] );

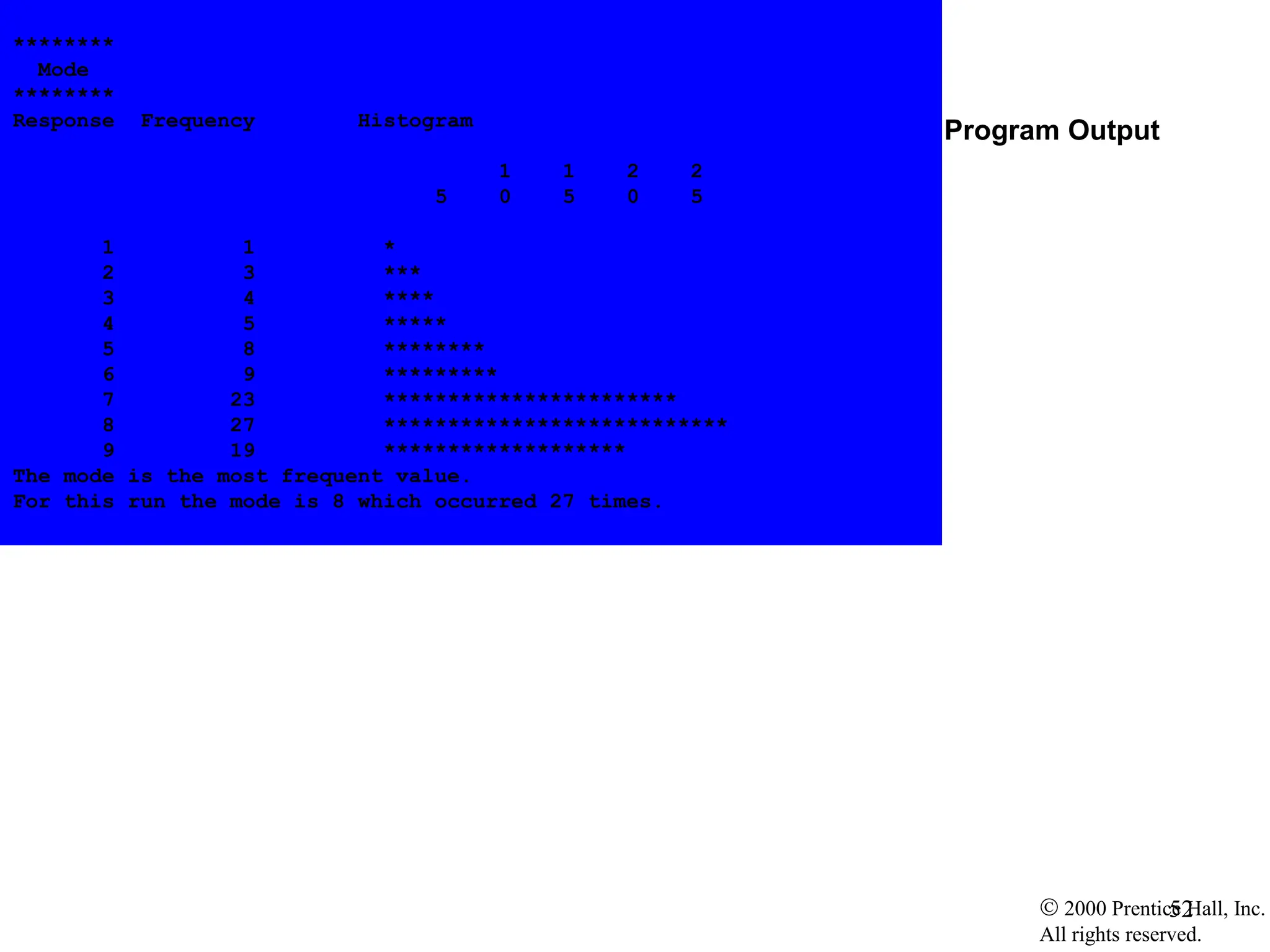
 2000 Prentice Hall, Inc. All rights reserved. 49 65 } 66 67 void mode( int freq[], const int answer[] ) 68 { 69 int rating, j, h, largest = 0, modeValue = 0; 70 71 printf( "n%sn%sn%sn", 72 "********", " Mode", "********" ); 73 74 for ( rating = 1; rating <= 9; rating++ ) 75 freq[ rating ] = 0; 76 77 for ( j = 0; j <= SIZE - 1; j++ ) 78 ++freq[ answer[ j ] ]; 79 80 printf( "%s%11s%19snn%54sn%54snn", 81 "Response", "Frequency", "Histogram", 82 "1 1 2 2", "5 0 5 0 5" ); 83 84 for ( rating = 1; rating <= 9; rating++ ) { 85 printf( "%8d%11d ", rating, freq[ rating ] ); 86 87 if ( freq[ rating ] > largest ) { 88 largest = freq[ rating ]; 89 modeValue = rating; 90 } 91 92 for ( h = 1; h <= freq[ rating ]; h++ ) 93 printf( "*" ); 94 3.2 Define function mode 3.2.1 Increase frequency[] depending on response[] Notice how the subscript in frequency[] is the value of an element in response[] (answer[]) Print stars depending on value of frequency[]

 2000 Prentice Hall, Inc. All rights reserved. 3.3 Define bubbleSort 3.3 Define printArray 50 95 printf( "n" ); 96 } 97 98 printf( "The mode is the most frequent value.n" 99 "For this run the mode is %d which occurred" 100 " %d times.n", modeValue, largest ); 101} 102 103 void bubbleSort( int a[] ) 104 { 105 int pass, j, hold; 106 107 for ( pass = 1; pass <= SIZE - 1; pass++ ) 108 109 for ( j = 0; j <= SIZE - 2; j++ ) 110 111 if ( a[ j ] > a[ j + 1 ] ) { 112 hold = a[ j ]; 113 a[ j ] = a[ j + 1 ]; 114 a[ j + 1 ] = hold; 115 } 116 } 117 118 void printArray( const int a[] ) 119 { 120 int j; 121 122 for ( j = 0; j <= SIZE - 1; j++ ) { 123 124 if ( j % 20 == 0 ) 125 printf( "n" ); Bubble sort: if elements out of order, swap them.

 2000 Prentice Hall, Inc. All rights reserved. Program Output 51 126 127 printf( "%2d", a[ j ] ); 128 } 129 } ******** Mean ******** The mean is the average value of the data items. The mean is equal to the total of all the data items divided by the number of data items (99). The mean value for this run is: 681 / 99 = 6.8788 ******** Median ******** The unsorted array of responses is 7 8 9 8 7 8 9 8 9 7 8 9 5 9 8 7 8 7 8 6 7 8 9 3 9 8 7 8 7 7 8 9 8 9 8 9 7 8 9 6 7 8 7 8 7 9 8 9 2 7 8 9 8 9 8 9 7 5 3 5 6 7 2 5 3 9 4 6 4 7 8 9 6 8 7 8 9 7 8 7 4 4 2 5 3 8 7 5 6 4 5 6 1 6 5 7 8 7 The sorted array is 1 2 2 2 3 3 3 3 4 4 4 4 4 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 The median is element 49 of the sorted 99 element array. For this run the median is 7

 2000 Prentice Hall, Inc. All rights reserved. Program Output 52 ******** Mode ******** Response Frequency Histogram 1 1 2 2 5 0 5 0 5 1 1 * 2 3 *** 3 4 **** 4 5 ***** 5 8 ******** 6 9 ********* 7 23 *********************** 8 27 *************************** 9 19 ******************* The mode is the most frequent value. For this run the mode is 8 which occurred 27 times.

Searching Arrays: Linear Search and Binary Search • Search an array for a key value • Linear search – Simple – Compare each element of array with key value – Useful for small and unsorted arrays 53

Searching Arrays: Linear Search and Binary Search • Binary search – For sorted arrays – Compares middle element with key • If equal, match found • If key < middle, looks in first half of array • If key > middle, looks in last half • Repeat – Very fast; at most n steps, where 2n > number of elements • 30 element array takes at most 5 steps – 25 > 30 so at most 5 steps 54 5

Multiple-Subscripted Arrays • Multiple subscripted arrays – Tables with rows and columns (m by n array) – Like matrices: specify row, then column 55 Row 0 Row 1 Row 2 Column 0 Column 1 Column 2 Column 3 a[ 0 ][ 0 ] a[ 1 ][ 0 ] a[ 2 ][ 0 ] a[ 0 ][ 1 ] a[ 1 ][ 1 ] a[ 2 ][ 1 ] a[ 0 ][ 2 ] a[ 1 ][ 2 ] a[ 2 ][ 2 ] a[ 0 ][ 3 ] a[ 1 ][ 3 ] a[ 2 ][ 3 ] Row subscript Array name Column subscript

Multiple-Subscripted Arrays • Initialization – int b[ 2 ][ 2 ] = { { 1, 2 }, { 3, 4 } }; – Initializers grouped by row in braces – If not enough, unspecified elements set to zero int b[ 2 ][ 2 ] = { { 1 }, { 3, 4 } }; • Referencing elements – Specify row, then column printf( "%d", b[ 0 ][ 1 ] ); 56 1 2 3 4 1 0 3 4

 2000 Prentice Hall, Inc. All rights reserved. 1. Initialize variables 1.1 Define functions to take double scripted arrays 1.2 Initialize studentgrades[][] 2. Call functions minimum, maximum, and average 1 /* 2 Double-subscripted array example */ 3 #include <stdio.h> 4 #define STUDENTS 3 5 #define EXAMS 4 6 7 int minimum( const int [][ EXAMS ], int, int ); 8 int maximum( const int [][ EXAMS ], int, int ); 9 double average( const int [], int ); 10 void printArray( const int [][ EXAMS ], int, int ); 11 12 int main() 13 { 14 int student; 15 const int studentGrades[ STUDENTS ][ EXAMS ] = 16 { { 77, 68, 86, 73 }, 17 { 96, 87, 89, 78 }, 18 { 70, 90, 86, 81 } }; 19 20 printf( "The array is:n" ); 21 printArray( studentGrades, STUDENTS, EXAMS ); 22 printf( "nnLowest grade: %dnHighest grade: %dn", 23 minimum( studentGrades, STUDENTS, EXAMS ), 24 maximum( studentGrades, STUDENTS, EXAMS ) ); 25 26 for ( student = 0; student <= STUDENTS - 1; student++ ) 27 printf( "The average grade for student %d is %.2fn", 28 student, 29 average( studentGrades[ student ], EXAMS ) ); 30 31 return 0; 32 } Each row is a particular student, each column is the grades on the exam.

 2000 Prentice Hall, Inc. All rights reserved. 3. Define functions 33 34 /* Find the minimum grade */ 35 int minimum( const int grades[][ EXAMS ], 36 int pupils, int tests ) 37 { 38 int i, j, lowGrade = 100; 39 40 for ( i = 0; i <= pupils - 1; i++ ) 41 for ( j = 0; j <= tests - 1; j++ ) 42 if ( grades[ i ][ j ] < lowGrade ) 43 lowGrade = grades[ i ][ j ]; 44 45 return lowGrade; 46 } 47 48 /* Find the maximum grade */ 49 int maximum( const int grades[][ EXAMS ], 50 int pupils, int tests ) 51 { 52 int i, j, highGrade = 0; 53 54 for ( i = 0; i <= pupils - 1; i++ ) 55 for ( j = 0; j <= tests - 1; j++ ) 56 if ( grades[ i ][ j ] > highGrade ) 57 highGrade = grades[ i ][ j ]; 58 59 return highGrade; 60 } 61 62 /* Determine the average grade for a particular exam */ 63 double average( const int setOfGrades[], int tests ) 64 {

 2000 Prentice Hall, Inc. All rights reserved. 3. Define functions 65 int i, total = 0; 66 67 for ( i = 0; i <= tests - 1; i++ ) 68 total += setOfGrades[ i ]; 69 70 return ( double ) total / tests; 71 } 72 73 /* Print the array */ 74 void printArray( const int grades[][ EXAMS ], 75 int pupils, int tests ) 76 { 77 int i, j; 78 79 printf( " [0] [1] [2] [3]" ); 80 81 for ( i = 0; i <= pupils - 1; i++ ) { 82 printf( "nstudentGrades[%d] ", i ); 83 84 for ( j = 0; j <= tests - 1; j++ ) 85 printf( "%-5d", grades[ i ][ j ] ); 86 } 87 }

 2000 Prentice Hall, Inc. All rights reserved. Program Output 60 The array is: [0] [1] [2] [3] studentGrades[0] 77 68 86 73 studentGrades[1] 96 87 89 78 studentGrades[2] 70 90 86 81 Lowest grade: 68 Highest grade: 96 The average grade for student 0 is 76.00 The average grade for student 1 is 87.50 The average grade for student 2 is 81.75

CHAPTER 2 61 Structure Polynomial is objects: ; a set of ordered pairs of <ei,ai> where ai in Coefficients and ei in Exponents, ei are integers >= 0 functions: for all poly, poly1, poly2  Polynomial, coef Coefficients, expon Exponents Polynomial Zero( ) ::= return the polynomial, p(x) = 0 Boolean IsZero(poly) ::= if (poly) return FALSE else return TRUE Coefficient Coef(poly, expon) ::= if (expon  poly) return its coefficient else return Zero Exponent Lead_Exp(poly) ::= return the largest exponent in poly Polynomial Attach(poly,coef, expon) ::= if (expon  poly) return error else return the polynomial poly with the term <coef, expon> inserted n e n e x a x a x p    ... ) ( 1 1 Polynomials A(X)=3X20+2X5+4, B(X)=X4+10X3+3X2+1 ADT for Polynomial

62 Polynomial Remove(poly, expon) ::= if (expon  poly) return the polynomial poly with the term whose exponent is expon deleted else return error Polynomial SingleMult(poly, coef, expon) ::= return the polynomial poly • coef • xexpon Polynomial Add(poly1, poly2) ::= return the polynomial poly1 +poly2 Polynomial Mult(poly1, poly2) ::= return the polynomial poly1 • poly2 *Structure 2.2:Abstract data type Polynomial (p.61) End Polynomial

63 /* d =a + b, where a, b, and d are polynomials */ d = Zero( ) while (! IsZero(a) && ! IsZero(b)) do { switch COMPARE (Lead_Exp(a), Lead_Exp(b)) { case -1: d = Attach(d, Coef (b, Lead_Exp(b)), Lead_Exp(b)); b = Remove(b, Lead_Exp(b)); break; case 0: sum = Coef (a, Lead_Exp (a)) + Coef ( b, Lead_Exp(b)); if (sum) { Attach (d, sum, Lead_Exp(a)); a = Remove(a , Lead_Exp(a)); b = Remove(b , Lead_Exp(b)); } break; Polynomial Addition #define MAX_DEGREE 101 typedef struct { int degree; float coef[MAX_DEGREE]; } polynomial; data structure 1:

CHAPTER 2 64 case 1: d = Attach(d, Coef (a, Lead_Exp(a)), Lead_Exp(a)); a = Remove(a, Lead_Exp(a)); } } insert any remaining terms of a or b into d *Program 2.4 :Initial version of padd function(p.62) advantage: easy implementation disadvantage: waste space when sparse

CHAPTER 2 65 Data structure 2: use one global array to store all polynomials A(X)=2X1000+1 B(X)=X4+10X3+3X2+1 2 1 1 10 3 1 1000 0 4 3 2 0 coef exp starta finisha startb finishb avail 0 1 2 3 4 5 6 *Figure 2.2: Array representation of two polynomials (p.63) specification representation poly <start, finish> A <0,1> B <2,5>

CHAPTER 2 66 MAX_TERMS 100 /* size of terms array */ typedef struct { float coef; int expon; } polynomial; polynomial terms[MAX_TERMS]; int avail = 0; *(p.62) storage requirements: start, finish, 2*(finish-start+1) nonparse: twice as much as (1) when all the items are nonzero

CHAPTER 2 67 void padd (int starta, int finisha, int startb, int finishb, int * startd, int *finishd) { /* add A(x) and B(x) to obtain D(x) */ float coefficient; *startd = avail; while (starta <= finisha && startb <= finishb) switch (COMPARE(terms[starta].expon, terms[startb].expon)) { case -1: /* a expon < b expon */ attach(terms[startb].coef, terms[startb].expon); startb++ break; Add two polynomials: D = A + B

CHAPTER 2 68 case 0: /* equal exponents */ coefficient = terms[starta].coef + terms[startb].coef; if (coefficient) attach (coefficient, terms[starta].expon); starta++; startb++; break; case 1: /* a expon > b expon */ attach(terms[starta].coef, terms[starta].expon); starta++; }

CHAPTER 2 69 /* add in remaining terms of A(x) */ for( ; starta <= finisha; starta++) attach(terms[starta].coef, terms[starta].expon); /* add in remaining terms of B(x) */ for( ; startb <= finishb; startb++) attach(terms[startb].coef, terms[startb].expon); *finishd =avail -1; } *Program 2.5: Function to add two polynomial (p.64) Analysis: O(n+m) where n (m) is the number of nonzeros in A(B).

CHAPTER 2 70 void attach(float coefficient, int exponent) { /* add a new term to the polynomial */ if (avail >= MAX_TERMS) { fprintf(stderr, “Too many terms in the polynomialn”); exit(1); } terms[avail].coef = coefficient; terms[avail++].expon = exponent; } *Program 2.6:Function to add anew term (p.65) Problem: Compaction is required when polynomials that are no longer needed. (data movement takes time.)

Sparse matrix 71 • A sparse matrix is a matrix in which most of the elements are zero. • By contrast, if most of the elements are nonzero, then the matrix is considered dense. • The number of zero-valued elements divided by the total number of elements is called the sparsity of the matrix (which is equal to 1 minus the density of the matrix).

Check matrix is sparse or not 72

CHAPTER 2 73                       0 0 0 28 0 0 0 0 0 0 0 91 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0 3 11 0 15 0 22 0 0 15 col1 col2 col3 col4 col5 col6 row0 row1 row2 row3 row4 row5 *Figure 2.3: Two matrices 8/36 6*6 5*3 15/15 Sparse Matrix sparse matrix data structure?

CHAPTER 2 75 Structure Sparse_Matrix is objects: a set of triples, <row, column, value>, where row and column are integers and form a unique combination, and value comes from the set item. functions: for all a, b  Sparse_Matrix, x  item, i, j, max_col, max_row  index Sparse_Marix Create(max_row, max_col) ::= return a Sparse_matrix that can hold up to max_items = max _row  max_col and whose maximum row size is max_row and whose maximum column size is max_col. SPARSE MATRIX ABSTRACT DATA TYPE

CHAPTER 2 76 Sparse_Matrix Transpose(a) ::= return the matrix produced by interchanging the row and column value of every triple. Sparse_Matrix Add(a, b) ::= if the dimensions of a and b are the same return the matrix produced by adding corresponding items, namely those with identical row and column values. else return error Sparse_Matrix Multiply(a, b) ::= if number of columns in a equals number of rows in b return the matrix d produced by multiplying a by b according to the formula: d [i] [j] = (a[i][k]•b[k][j]) where d (i, j) is the (i,j)th element else return error. * Structure 2.3: Abstract data type Sparse-Matrix (p.68)

CHAPTER 2 77 row col value row col value a[0] 6 6 8 b[0] 6 6 8 [1] 0 0 15 [1] 0 0 15 [2] 0 3 22 [2] 0 4 91 [3] 0 5 -15 [3] 1 1 11 [4] 1 1 11 [4] 2 1 3 [5] 1 2 3 [5] 2 5 28 [6] 2 3 -6 [6] 3 0 22 [7] 4 0 91 [7] 3 2 -6 [8] 5 2 28 [8] 5 0 -15 (a) (b) *Figure 2.4:Sparse matrix and its transpose stored as triples (p.69) (1) Represented by a two-dimensional array. Sparse matrix wastes space. (2) Each element is characterized by <row, col, value>. row, column in ascending order # of rows (columns) # of nonzero terms transpose

CHAPTER 2 78 Sparse_matrix Create(max_row, max_col) ::= #define MAX_TERMS 101 /* maximum number of terms +1*/ typedef struct { int col; int row; int value; } term; term a[MAX_TERMS] * (P.69) # of rows (columns) # of nonzero terms

Basics of Data structure using C describing basics concepts

More Related Content

Similar to Basics of Data structure using C describing basics concepts

Recently uploaded

Basics of Data structure using C describing basics concepts